1.5 Kräfte und Spannungen

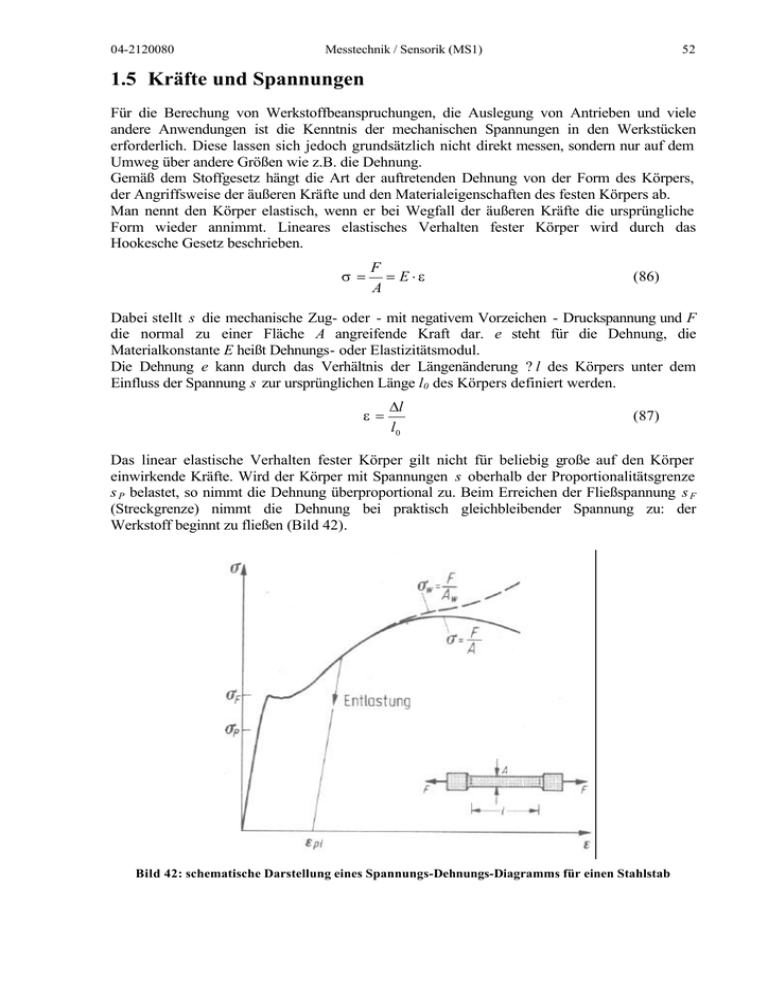
04-2120080
Messtechnik / Sensorik (MS1)
52
1.5 Kräfte und Spannungen
Für die Berechung von Werkstoffbeanspruchungen, die Auslegung von Antrieben und viele
andere Anwendungen ist die Kenntnis der mechanischen Spannungen in den Werkstücken
erforderlich. Diese lassen sich jedoch grundsätzlich nicht direkt messen, sondern nur auf dem
Umweg über andere Größen wie z.B. die Dehnung.
Gemäß dem Stoffgesetz hängt die Art der auftretenden Dehnung von der Form des Körpers,
der Angriffsweise der äußeren Kräfte und den Materialeigenschaften des festen Körpers ab.
Man nennt den Körper elastisch, wenn er bei Wegfall der äußeren Kräfte die ursprüngliche
Form wieder annimmt. Lineares elastisches Verhalten fester Körper wird durch das
Hookesche Gesetz beschrieben.
σ=
F
= E⋅ε
A
(86)
Dabei stellt s die mechanische Zug- oder - mit negativem Vorzeichen - Druckspannung und F
die normal zu einer Fläche A angreifende Kraft dar. e steht für die Dehnung, die
Materialkonstante E heißt Dehnungs- oder Elastizitätsmodul.
Die Dehnung e kann durch das Verhältnis der Längenänderung ? l des Körpers unter dem
Einfluss der Spannung s zur ursprünglichen Länge l0 des Körpers definiert werden.
ε=
∆l
l0
(87)
Das linear elastische Verhalten fester Körper gilt nicht für beliebig große auf den Körper
einwirkende Kräfte. Wird der Körper mit Spannungen s oberhalb der Proportionalitätsgrenze
s P belastet, so nimmt die Dehnung überproportional zu. Beim Erreichen der Fließspannung s F
(Streckgrenze) nimmt die Dehnung bei praktisch gleichbleibender Spannung zu: der
Werkstoff beginnt zu fließen (Bild 42).
Bild 42: schematische Darstellung eines Spannungs-Dehnungs-Diagramms für einen Stahlstab
04-2120080
Messtechnik / Sensorik (MS1)
53
Wird mit noch höheren Kräften belastet, nimmt die Dehnung weiter zu bis die
Querkontraktion des Körpers nicht mehr gleichmäßig verläuft. Der Körper beginnt sich an
einer Stelle einzuschnüren und reißt mit weiter zunehmender Belastung. Wird ein Körper bis
zu einer Spannung s < s F belastet und anschließend völlig entlastet, so nimmt er seine
ursprüngliche Länge wieder an. Die Belastungs- und Entlastungskurve fallen zusammen.
Belastet man den Körper jedoch mit einer Spannung jenseits der Fließgrenze s F, so verläuft
die Entlastungslinie parallel zur Belastungslinie im linear elastischen Bereich. Bei völliger
Entlastung geht die Dehnung dann nicht auf Null zurück, sondern es bleibt eine plastische
Dehnung epl erhalten (Bild 42).
Literatur:
[Schnell, 1992]
Schnell, Gross, Hauger, „Technische Mechanik Bd. 2“, 4. Auflage
04-2120080
Messtechnik / Sensorik (MS1)
54
1.6 Torsion von Stäben
An einem Stab angreifende mechanische Momente führen zu einer Torsion des Stabes. Diese
Momente führen zu Spannungen und Dehnungen im Stab und an seiner Oberfläche.
Mathematisch am einfachsten lassen sich Momente beschreiben, die an einem Stab mit Kreisoder Kreisringquerschnitt angreifen. Der Stab ist in diesem Fall gerade und der Querschnitt
und das Torsionsmoment sind längs der Mittelachse des Stabes konstant. Im Bild 43 ist
schematisch ein Stab der Länge l mit kreisringförmigem Querschnitt dargestellt. Der Stab hat
den Innenradius ri und den Außenradius ra. Die einzige äußere Belastung des Stabs ist das
axial am Ende angreifende Moment Mt . Das Moment ist positiv, da es am positiven
Schnittufer in die positive x-Richtung weist.
Bild 43: Schematische Darstellung des Stabes mit angreifendem Drehmoment Mt .
Die Schnittgröße Torsionsmoment ist unabhängig von x und überall gleich Mt . Bei der
Torsion von Stäben mit Kreisquerschnitt tritt keine Verwölbung auf, d.h. die Querschnitte
bleiben eben. Somit verdrehen sich alle Stabquerschnitte wie starre Scheiben um gewisse
Winkel gegeneinander. Der Torsionswinkel (Verdrehwinkel) f des Stabes ist proportional zur
Stablänge l und hängt mit dieser über den Proportionalitätsfaktor ? zusammen. Der Faktor ?
hat die Dimension m-1 und wird als Verdrillung bezeichnet.
ϕ = θ ⋅l
(88)
Es kann ein linear plastisches Verhalten des Stabes angenommen werden (s.a. Hooksches
Gesetz, Kap. 1.5), so dass die Verdrillung ? auch proportional zum angreifenden Torsionsmoment Mt ist. Die Torsionssteifigkeit (das Verhältnis Mt /?) hängt folglich nur von den
Radien ra und ri und den Werkstoffeigenschaften ab.
Bild 44: Schematische Darstellung der Torsion.
Im Bild 44 ist der Einfluss der Torsion auf den Stab schematisch dargestellt. Eine gerade
Mantellinie AB verformt sich auf der Oberfläche zur Schraubenlinie AC, die aber wegen der
betragsmäßig kleinen Formänderungen näherungsweise als geradlinig angenommen werden
kann. Die Scherung ?(r) ist gleich dem Winkel zwischen der Mantellinie AB und der
Schraubenlinie AC. Das führt zu der Gleichung
04-2120080
Messtechnik / Sensorik (MS1)
γ ( r) ⋅ l = ϕ ⋅ r
55
(89)
und damit zur Bestimmungsgleichung für die Scherung
γ ( r) =
ϕ ⋅r
=θ ⋅r
l
(90)
Nach dem Stoffgesetz ist die Scherung ?(r) über den Schubmodul G mit einer Schubspannung
t(r) verknüpft.
τ (r ) = G ⋅ γ ( r ) = G
ϕ ⋅r
= G ⋅θ ⋅ r
l
(91)
Der Schubmodul G ist eine Materialkonstante und steht in direktem Zusammenhang mit den
Materialkonstanten E (Elastizitätsmodul) und µ (Poissonzahl).
G=
E
2 ⋅ (1 + µ )
(92)
Die Schubspannungen nehmen linear mit dem Radius zu und erreichen ihr Maximum am
Außenradius. Das Moment aller Schubspannungen um den Kreismittelpunkt muss dieselbe
Größe haben wie das Torsionsmoment Mt . Damit ergibt sich bei einer Stabquerschnittsfläche
A die Gleichgewichtsbedingung
∫ r ⋅τ ( r ) dA − M
t
=0
(93)
A
Durch Einsetzen von Gleichung (91)
Gleichgewichtsbedingung:
für
t(r) erhält man daraus die folgende
G ⋅ θ ⋅ ∫ r 2 dA − M t = 0
(94)
A
Das Integral über die Fläche des Stabquerschnitts A wird als polares Flächenträgheitsmoment
IP bezeichnet.
I P = ∫ r 2 dA
(95)
A
Für einen kreisringförmigen Querschnitt lässt sich das Integral auflösen zu
IP =
π 4
(ra − ri 4 )
2
(96)
Mit Gleichung (94) kann die Verdrillung ? berechnet werden.
θ=
Mt
G ⋅ IP
(97)
Daraus folgt mit den Gleichungen (88) und (96) für den Verdrehwinkel f eines Stabes mit
Kreisringquerschnitt
ϕ=
Mt ⋅l 2
Mt ⋅ l
= ⋅
G ⋅ I P π G ⋅ (ra4 − ri 4 )
(98)
04-2120080
Messtechnik / Sensorik (MS1)
56
Die Dehnung ε an der Oberfläche des Stabs ist abhängig vom Winkel α, dem Winkel
zwischen der Stabachse und der bezüglich Dehnung betrachteten Richtung (vgl. Mohrscher
Spannungskreis [Schnell, 1998]). Senkrecht (a = 90°) und parallel zur Stabachse (a = 0°) tritt
keine Dehnung auf, wie sich leicht anhand der Bestimmungsgleichung für die Dehnung ε
erkennen lässt (vergleiche Mohrscher Spannungskreis, [Schnell, 1998]):
ε=
1 ra ⋅ ϕ
⋅
⋅ sin 2α
2
l
(99)
Mit Gleichung 98 ergibt sich für die Dehnung ε
ε=
r
M
1
⋅ 4 a 4 ⋅ t ⋅ sin 2α
π ra − ri G
(100)
Literatur:
[Schnell, 1998] Schnell, Walter, „Technische Mechanik – Elastostatik“, Springer Verlag
Berlin, 6.Auflage, 1998
04-2120080
Messtechnik / Sensorik (MS1)
57
1.7 Dehnungsmessung
1.7.1
Übersicht bekannter Messprinzipien
Die ältesten Dehnungsmessgeräte basieren auf mechanischen Messprinzipien, indem sie bei
gegebener Basislänge des Bauteils die Längenänderung mit einer beweglichen Schneide
abgreifen und mit Hebelübersetzung, Drehspiegel (Martens-Spiegelgerät) oder
Induktivaufnehmer vergrößert anzeigen. Da sie recht unhandlich sind, einen gleichförmigen
Spannungszustand voraussetzen und kaum dynamische Vorgänge erfassen können, ist ihr
Anwendungsbereich beschränkt.
Durch das Auftragen von Reißlack kann bei Dehnungsversuchen die Richtung der größten
Werkstückdehnung, die Hauptrichtung, ermittelt werden. Beim Reißlack handelt es sich um
einen spröden Lack, der bei Beanspruchung senkrecht zur Hauptdehnungsrichtung aufreißt.
Bei Kenntnis der Rissempfindlichkeit des Lacks kann man im Augenblick der Rissentstehung
die Größe der Dehnung an der betrachteten Stelle abschätzen.
Die Spannungsoptik ermöglicht es, durch Polarisationseffekte den Formänderungszustand an
flächigen Schnitten von durchsichtigen Kunststoffbauteilen unter Belastung bildlich
darzustellen. Als Werkstoffe werden z.B. Epoxid-, Polyester- und Acrylharze verwendet,
deren Brechungsindex unter Belastung richtungsabhängig wird (Doppelbrechung). Wird das
Messobjekt unter Belastung mit polarisiertem Licht durchleuchtet und durch einen Analysator
(Polarisationsfilter) betrachtet, so entsteht ein Muster aus farbigem Licht (bei der Einstrahlung
von Weißlicht) beziehungsweise hellen und dunklen Linien (bei der Einstrahlung von
monochromatischem Licht), aus dem man je nach Versuchsaufbau auf die Richtung der
Hauptspannungen (Isoklinen) beziehungsweise deren Größe (Isochromaten) schließen kann.
In speziellen Werkstoffen kann der Belastungszustand auch „eingefroren“ werden, indem das
Messobjekt bei erhöhter Temperatur belastet und unter anhaltender Beanspruchung abgekühlt
wird. So können dreidimensionale Modellwerkstücke nach dem Einfrieren in Scheiben zerteilt
und untersucht werden. Schließlich gibt es Kunststoffe, die ähnlich wie Reißlack auf
metallische Bauteile aufgetragen und im polarisierten Auflicht betrachtet werden.
Auf dem Messprinzip der Lichtinterferenz basiert die holografische Dehnungsmessung. Hier
werden Hologramme des selben Bauteils vor und während der Belastung überlagert. Das
entstehende Streifenmuster zeigt die Verformungen senkrecht zur Oberfläche in Vielfachen
der Lichtwellenlänge an.
Alle diese Dehnungsmessverfahren können nur diejenigen Formänderungen anzeigen, die seit
dem Beginn der Messung relativ zum Ursprungszustand aufgetreten sind. Die in einem
metallischen Werkstoff durch Eigenspannungen oder vorangegangene Belastungen
herrschenden Verzerrungen gegenüber dem spannungsfreien Zustand kann man durch
röntgenografische Messung der Abstände der Kristallgitterebenen bestimmen.
1.7.2
Dehnungsmessstreifen
Die im Überblick genannten Messprinzipien können nur eingeschränkt solche Dehnungszustände erfassen, die sich räumlich oder zeitlich stark ändern oder an unzugänglichen Stellen
auftreten. Hier setzt man zweckmäßigerweise die vom amerikanischen Wissenschaftler A.C.
Ruge 1938 erfundenen Dehnungsmessstreifen (DMS) ein. Ruge nutzte den schon von
Wheatstone und Thomson beschriebenen Effekt aus, dass sich der elektrische Widerstand
eines Drahts bei mechanischer Beanspruchung ändert.
04-2120080
1.7.2.1
Messtechnik / Sensorik (MS1)
58
Aufbau
Ein Dehnungsmessstreifen besteht aus einem elektrischen Leiter, im einfachsten Fall aus
einem Draht (z.B. Konstantan, 60% Cu, 40% Ni), der in einen Träger eingebettet ist und
mittels Kleber oder Kitt auf das zu untersuchende Bauteil aufgebracht wird. Er wird daher in
gleicher Weise wie das Messobjekt gedehnt. Aufgrund der Einbettung kann der Leiter nicht
ausknicken, so dass sich auch Stauchungen („negative Dehnungen“) erfassen lassen.
1.7.2.1.1
Hintergrund zur Widerstandsänderung
Der Widerstand eines Drahtes mit der Länge l, dem Durchmesser d, der Querschnittsfläche
A = pd2/4 und dem spezifischen Widerstand ? ergibt sich zu
R=
lρ 4lρ
=
A πd 2
(101)
Wird der Draht (einachsig) gedehnt, so ändern sich l, A und wegen der mit der
Gestaltänderung verbundenen Verschiebung in der Gitterstruktur auch der spezifische
Widerstand ? und damit der gesamte Widerstand R. Sind diese Änderungen infinitesimal
klein, so kann mittels des totalen Differentials folgender Zusammenhang zwischen der
Änderung dR des elektrischen Widerstandes und diesen sehr kleinen Änderungen berechnet
werden.
dR =
4ρ
4l
8lρ
dl + 2 dρ − 3 dd
2
πd
πd
πd
(102)
Werden die infinitesimal kleinen Änderungen dR, dρ, dl und dd der Größen R, ρ, l und d in
Gleichung 102 durch die immer noch kleinen Änderungen ∆R, ∆ρ, ∆l und ∆d, mit ∆ρ « ρ,
∆l « l und ∆d « d ersetzt, so folgt mit guter Genauigkeit die relative Widerstandsänderung
∆R/R.
∆R ∆l
∆d ∆ρ
=
−2
+
R
l
d
ρ
(103)
Bei einer Dehnung e = ?l/l in Längsrichtung des Drahts verändert sich der Durchmesser um
den Betrag eq = ? d/d = –µe (Poissonzahl µ = eq /e). Damit wird
∆R
∆ρ
∆ρ
= ε + 2µε +
= (1 + 2 µ ) ε +
R
ρ
ρ
(104)
Dividiert man diese Gleichung durch e, so ergibt sich der (dimensionslose) k-Faktor, der das
Verhältnis von Widerstands- zu Längenänderung angibt:
k=
∆R R
∆ρ ρ
= 1 + 2µ +
ε
ε
⇔
∆R
= k ⋅ε
R
(105)
Setzt man für metallische Werkstoffe µ = 35%, so erhält man für den k-Faktor
k = 1,7 +
∆ρ
ερ
(106)
Bei Dehnungsmessstreifen aus Metall liegt der k-Faktor bei etwa 2. Für Konstantan wird
k = 2,05 angegeben. Von der relativen Widerstandsänderung ? R/R geht also nur ein geringer
Beitrag auf die Änderung des spezifischen Widerstands zurück. Im Gegensatz dazu weisen
Halbleiter-DMS, bei denen der Dehnungsaufnehmer aus dotiertem Silizium oder Germanium
04-2120080
Messtechnik / Sensorik (MS1)
59
besteht, k-Faktoren von –100 bis +180 auf. Hier überwiegt bei weitem die Änderung des
spezifischen Widerstands. Allerdings ist der k-Faktor bei Halbleiter-DMS deutlich stärker
abhängig von der Temperatur. Die Beziehung zwischen k-Faktor und Dehnung ist also
nichtlinear.
1.7.2.1.2
Bauarten
Die ursprüngliche, auf Ruge zurückgehende Form ist der Draht-DMS. Zwischen zwei
harzgetränkte Papierstreifen wird ein gerader, zu einem Mäander geformter oder um einen
dritten Streifen zu einer flachen Spule gewickelter Draht geklebt. Diese Bauart wurde
weitgehend durch den Folien-DMS verdrängt, der wie eine gedruckte Schaltung hergestellt
wird. Auf einem Träger aus Kunststofffolie wird aus einer Metallschicht das Messgitter
herausgeätzt und mit einer weiteren Kunststoffschicht abgedeckt.
Bild 45: Verschiedene Bauarten von Dehnungsmessstreifen
Die Folien-DMS lassen sich einfacher und kostengünstiger herstellen (einfache Ausführungen
kosten weniger als 1 DM / 0,5 €). Das Messgitter kann beliebig geformt werden. Die
elektrischen Anschlüsse bilden in der Regel Lötstützpunkte, metallische Bänder oder dünne
Drähte. DMS werden mit sehr unterschiedlichen Messgitterlängen gefertigt. Im Normalfall
finden Längen von 6 bis 10 mm Verwendung. Die elektrischen Widerstände betragen zum
Beispiel 120, 350, 600 oder 1000 Ω. Der zulässige Messstrom beträgt meistens etwa 10 bis
20 mA.
Bild 46: Prinzipskizze eines Folien-DMS (Dicke nicht maßstäblich gezeichnet)
Für Messungen bei hohen Temperaturen gibt es Draht- oder Folien-DMS mit abnehmbarem
(Hilfs-) Träger. Bei der Anwendung werden sie mit der Gitterseite in eine Schicht aus
keramischem Kitt auf das Messobjekt gedrückt, der Träger abgezogen und das Gitter mit
einer weiteren Schicht Kitt abgedeckt.
Halbleiter-DMS enthalten wegen des hohen spezifischen Widerstands meist nur einen
einzelnen Silizium- oder Germaniumstreifen, der aus einem Einkristall herausgearbeitet, mit
Anschlüssen versehen und eingebettet wird. Wegen des hohen k-Faktors weisen sie nach
Gleichung 105 eine viel größere Dehnungsempfindlichkeit als metallische DMS auf.
Trotzdem werden sie wegen ihrer Temperaturempfindlichkeit und ihres hohen Preises
verhältnismäßig selten eingesetzt.
Um Dehnungen in verschiedenen Richtungen zu messen, verwendet man DMS-„Rosetten“,
die mehrere Messgitter in verschiedenen Richtungen tragen. Sie haben den Vorteil, dass bei
04-2120080
Messtechnik / Sensorik (MS1)
60
einmaligem Kleben die richtige Winkellage der Gitter zueinander gewährleistet ist. Sie sollten
deshalb immer dann verwendet werden, wenn man zweiachsige Spannungszustände zu
messen hat.
Aus den mit einer 90°-Rosette gemessenen Werten ergeben sich zwei orthogonale
Spannungen. Bei zunächst unbekanntem Spannungszustand des Messobjekts kann man
jedoch nicht davon ausgehen, dass es sich hierbei um die Hauptspannungen handelt, wenn
nicht aus der Werkstückgeometrie oder einem Vorversuch die Hauptrichtungen klar
hervorgehen. Bei unbekanntem Spannungszustand bevorzugt man daher eine 0°/45°/90°- oder
0°/60°/120°-Rosette und misst Dehnungswerte in drei Richtungen. Aus diesen drei Werten
können die Hauptspannungen mit ihren Richtungen rechnerisch ermittelt werden [Schnell,
1998]. Die Messgitter sind nebeneinander oder – für Anwendungen, bei denen wenig Platz
zur Verfügung steht oder sich die Dehnungswerte in der Oberfläche stark ändern –
übereinander (gestapelt) angeordnet.
Bild 47: 90°-Rosetten in Draht- und Folienausführung
Spezialausführungen sind z.B. Rosetten zur Messung der radialen und tangentialen Dehnung
einer Membran (in Druckaufnehmern) oder zur Messung von Spannungszuständen in einer
bestimmten Messobjektrichtung. Hierbei wird die Querdehnung des Messobjekts durch ein
zusätzliches Messgitter mitberücksichtigt, so dass die Widerstandsänderung proportional der
Spannung in Längsrichtung ist. Für die Messung von Eigenspannungen sind spezielle
Rosetten erhältlich (meist in 45°/90°-Ausführung). Nachdem man sie appliziert und
Messwerte aufgenommen hat, bohrt man in der Mitte der Rosette das Messobjekt mitsamt
Rosette an. Die Messstreifen auf der Rosette sind so angeordnet, dass sie nicht mit angebohrt
werden. Die durch die Bohrung teilweise entlastete Anordnung führt zu veränderten
Messwerten, aus denen sich die eingeprägten Spannungen oder die Eigenspannungen
ergeben.
1.7.2.2
Einsatz der DMS
Bei metallischen Basiswerkstoffen beträgt die zu messende Dehnung meist nur einige µm/m,
d.h. die relative Längenänderung der Messobjekte liegt in der Größenordnung von 10-6. Die
Widerstandsänderung (von Metall-DMS) liegt bei solchen Dehnungen in der gleichen
Größenordnung. Derartig kleine Widerstandsänderungen lassen sich beispielsweise mit der
Wheatstoneschen Brückenschaltung (siehe Kapitel Wheatstonesche Brückenschaltung)
erfassen.
Werden der oder die DMS gedehnt, so ist die Diagonalspannung der Brückenschaltung
(näherungsweise) proportional zur Dehnung, so dass man die Dehnung mittels DMS in Form
einer elektrischen Größe messen kann.
04-2120080
1.7.2.3
Messtechnik / Sensorik (MS1)
61
Ursachen von Messabweichungen
Bei der praktischen Arbeit mit Dehnungsmessstreifen treten eine Reihe von
Messabweichungen auf. Deren drei wichtigste Ursachen hängen mit ihrer Applikation,
Temperaturänderungen und unerwünschten Dehnungen zusammen.
1.7.2.3.1
Applikation
Bei der Applikation (dem Aufkleben) des DMS auf das Messobjekt muss besonders sorgfältig
gearbeitet werden. Abgesehen von den üblichen Vorkehrungen (gründliches Reinigen und
Entfetten der Klebefläche) muss ein spezieller DMS-Kleber verwendet werden.
Dieser Kleber ist spröder als andere, um die Dehnung möglichst schlupffrei zu übertragen.
Dadurch treten jedoch auch Spannungsspitzen an den Enden des DMS auf, welche die
Festigkeit der Klebung herabsetzen. Ein nicht einwandfrei geklebter DMS kann sich ablösen
oder kriechen (vor allem bei zu dicker Kleberschicht, falschem Kleber oder Lufteinschlüssen)
und daher falsche, meist zu niedrige Dehnungswerte anzeigen.
Um eine dünne, gleichmäßige Klebeschicht zu erzielen, enthalten einige Kleber
Lösungsmittel, andere sind kalt- und heißhärtende Ein- und Zweikomponentenkleber. Für
Hochtemperaturanwendungen können DMS angeschweißt oder eingekittet werden, während
es in anderen Fällen meist sinnvoll ist, eine Abdeckung zum Schutz vor Feuchtigkeit
anzubringen. Nähere Informationen über die verschiedenen Arten von Klebern, ihre
Kombinationsmöglichkeiten und Anwendung finden sich in den Unterlagen der Hersteller.
Bei anhaltender Dehnung, insbesondere bei höheren Temperaturen, tritt am Kleber und am
DMS Kriechen auf. Der DMS strebt in die Ausgangslage zurück, so dass sich die angezeigte
Dehnung verringert. Wird das Bauteil entlastet, kann eine Dehnung mit umgekehrtem
Vorzeichen angezeigt werden. Andererseits kann es vorkommen, dass der Basiswerkstoff
kriecht und nach Entlastung eine Restdehnung zurückbleibt, die von einem nicht kriechenden
DMS angezeigt wird. Im Gegensatz zu dynamischen Messungen sind Klebstoffe bei
statischen Messungen wegen der Kriecheffekte oft nur für niedrige Temperaturen geeignet.
Wesentlich sind Ort und Richtung der Applikation. Ausgehend von dem mechanischen
Spannungszustand muss man zunächst überprüfen, welche Dehnungen an der vorgesehenen
Stelle zu erwarten sind – eventuell kann durch einen Reißlackversuch die Hauptdehnungsrichtung bestimmt werden – und die DMS sorgfältig ausrichten. Eine Winkelabweichung von
5° ergibt eine Messabweichung von ca. 1%, die sich bei Anbringung mehrerer DMS noch
vergrößert. Zur Erfassung von mehrachsigen Spannungszuständen sind daher Rosetten
vorzuziehen. Vorausgesetzt wird dabei jedoch eine innerhalb der Messfläche homogene
Spannungsverteilung, da ein DMS die Dehnung über seine Länge mittelt und verschiedene
Messgitter einer Rosette unterschiedlichen Spannungszuständen ausgesetzt sein können. Im
Zweifelsfall sind entsprechend kleine DMS, Ketten von DMS oder gestapelte Rosetten zu
verwenden.
Ein DMS spricht in geringem Maß auch auf Dehnungen in Querrichtung an. Diese
„Querempfindlichkeit“ beträgt bei Draht-DMS in Mäanderform bis zu 2% der
Empfindlichkeit in Längsrichtung. Bei Folien-DMS ist sie jedoch praktisch zu
vernachlässigen, da die Metallstreifen in Querrichtung entsprechend breit ausgeführt werden.
Werden DMS auf nachgiebigen Werkstoffen oder dünnen Bauteilen angebracht, ist die
Rückwirkung zu beachten: Der aufgeklebte DMS versteift das Bauteil, so dass eine geringere
Dehnung auftritt und gemessen wird, als ohne DMS vorhanden wäre.
04-2120080
1.7.2.3.2
Messtechnik / Sensorik (MS1)
62
Temperatureinfluss
Wird die Messstelle mit dem DMS erwärmt, so treten drei Effekte auf:
- Das Basismaterial dehnt sich aus (Ausdehnungskoeffizient a l,b )
- Der Messdraht (oder die Messfolie) dehnt sich aus (Ausdehnungskoeffizient a l,d )
- Der spezifische Widerstand des Messdrahts ändert sich (Widerstandskoeffizient a w,d ).
Die resultierende spezifische Widerstandsänderung a w,D eines applizierten DMS bei
Temperaturänderung ?T beträgt damit
α w, D =
∆R
= α w ,d + k (α l ,b − α l ,d )
R∆T
(107)
Aus dieser Widerstandsänderung ergibt sich eine scheinbare Dehnung von
εs =
α w, D
k
⋅ ∆T
(108)
Es tritt zwar tatsächlich eine Dehnung auf, aber da man meist nur Dehnungen aufgrund von
mechanischer Belastung messen will, ist dieser Effekt unerwünscht. Man stellt deshalb den
Widerstandskoeffizienten a w,d durch Variation der Legierungszusätze oder der Wärmebehandlung des Materials des DMS so ein, dass gilt
α w,d = − k (α l ,b − α l , d )
(109)
Die scheinbare Dehnung ist dann Null. Der DMS ist somit für ein bestimmtes Basismaterial
temperaturkompensiert. Durch schnelle Temperaturänderungen können jedoch trotzdem
Messabweichungen auftreten. Insbesondere ist hier die Erwärmung durch den Brückenstrom
zu berücksichtigen. Man misst daher am besten entweder gleich nach dem Anlegen der
Speisespannung oder aber nachdem sich ein stationärer Zustand eingestellt hat. Bei
Mehrstellenmessungen mit Gleichspannung kann dazu die Speisespannung ständig an allen
Messstellen anliegen.
Um die verbleibenden Temperatureffekte auch noch auszugleichen, wird (bei einer
Halbbrücke) ein zweiter DMS in einen benachbarten Brückenzweig geschaltet und an einer
unbelasteten Stelle des Messobjekts angebracht (siehe Kapitel 1.2.4.1).
1.7.2.3.3
Unerwünschte Dehnungen
Auf die gleiche Weise wie Temperatureinflüsse lassen sich auch unerwünschte Dehnungen
durch geeignete Applikation und Schaltung von DMS eliminieren. Wird z.B. ein Balken
durch Normalkraft und Biegemoment beansprucht und will man nur das Biegemoment
ermitteln, so klebt man DMS an gegenüberliegenden Seiten des Balkens und schaltet sie in
dieselbe Halbbrücke. Ähnlich kann man z.B. den Einfluss von Biegemomenten und
Normalkräften an einer Torsionswelle eliminieren.
Literatur:
[Schnell, 1998] Schnell, Walter, „Technische Mechanik – Elastostatik“, Springer Verlag
Berlin, 6.Auflage, 1998