Stirling-Motor als Wärmekraftmaschine 2. Grundlagen

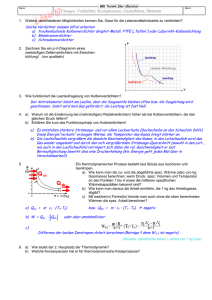
Stirling-Motor als Wärmekraftmaschine
1 von 3
Stirling-Motor als Wärmekraftmaschine
/ Stand: WS02 /
1. Ziel des Versuchs
Der Stirling-Kreisprozeß soll quantitativ mit Hilfe von Sensoren zur Messung von Druck, Temperatur,
Volumen und Drehzahl untersucht werden. Der thermische Wirkungsgrad des Stirling-Motors (als
Wärmekraftmaschine) bei der Umwandlung von Wärme in elektrische Energie soll bestimmt werden.
2. Grundlagen
(siehe auch Versuchsanleitung: „Stirling-Motor als Kältemaschine)
Der Stirling-Kreisprozeß wird in der Theorie durch 2 Isochore und 2 Isotherme definiert. Das
entsprechende pV-Diagramm sowie die jeweilige Position des Arbeits- und Verdrängerkolbens sind in
Abbildung 1 dargestellt. Arbeits- und Verdrängerkolben sind wie im Experiment (transparenter Motor
der Firma PHYWE) um 90° versetzt angeordnet. Das Verhältnis von mechanisch nutzbarer Energie
(eingeschlossene Fläche im pV-Diagramm) zu zugeführter Wärme entspricht dem thermischen
Wirkungsgrad:
ηthermisch = WpV / Q zu
[1]
ηthermisch :
Thermischer Wirkungsgrad
WpV
Abgegebene mechanische Arbeit
(eingeschlossene Fläche im pV-Diagramm)
Q zu:
Zugeführte Wärme
Mit Hilfe des 1.Hauptsatzes der Thermodynamik
dQ = dW + dU
[2]
und der allgemeinen Gasgleichung für ideale Gase
pV=nRT
(n : Molzahl)
[3]
läßt sich der thermische Wirkungsgrad des idealen Stirling-Kreisprozesses berechnen:
ηthermisch = 1 - Tmin / Tmax = ηCarnot
[4]
Dieser entspricht dem des Carnot-Prozesses, der den theoretischen maximalen Wirkungsgrad angibt,
den ein Kreisprozeß bei vorgegebenen Extremtemperaturen Tmin und Tmax erreichen kann. Reale
Kreisprozesse haben aufgrund verschiedener Effekte (z.B.: Prozesse nicht ideal adiabatisch oder
isotherm; Reibungseffekte; Wärmeverluste) kleinere thermische Wirkungsgrade. Unter Last
(elektrisch oder mechanisch) kann sich der Wirkungsgrad verändern.
Im Experiment wird die Wärmeenergie durch Verbrennen von Brennspiritus bereitgestellt. Die
thermische Leistung läßt sich durch Abwiegen der Alkoholmenge vor und nach dem Experiment
bestimmen. Kennt man die Brenndauer, so kann man mit Hilfe der gemessenen Massendifferenz sowie
des spezifischen Heizwertes (h = 25 kJ/g) die thermische Leistung (in Watt=Joule/s) berechnen.
Die abgegebene mechanische Energie WpV läßt sich durch Integration des aufgenommenen pVDiagramms ermitteln.
Stirling-Motor als Wärmekraftmaschine
2 von 3
Wird keine äußere (mechanische oder elektrische ) Last angeschlossen, so wird die gesamte
mechanische Energie in Reibungsenergie umgesetzt.
WReibung = WpV
[5]
Elektrische Last:
Die Achse des Stirling-Motors kann
über Schnurscheiben und einen Riemen an eine
Motor/Generator-Einheit angekoppelt werden. In der Schalterstellung "Generator" wird ein
Widerstand angeschlossen; Strom und Spannungsabfall werden gemessen, so daß sich die elektrische
Leistung bestimmen läßt:
Pel = U I
[8]
Die elektrische Leistung hängt von dem eingestellten Widerstand ab. In Abhängigkeit von der
elektrischen Last ändert sich die Drehzahl des Motors.
Abbildung 1: pV-Diagramm des idealen Stirling-Kreisprozesses; Position der Kolben
IV
3. Versuch
Stirling-Motor als Wärmekraftmaschine
3 von 3
Î Kalibrieren Sie die Sensoren für Temperatur, Volumen und Druck.
(siehe : Versuchsanleitung: „Stirling-Motor als Kältemaschine“)
Nach der Kalibrierung der Sensoren schließen Sie die Ausgänge für p und V an das Oszilloskop an.
Vor dem Starten des Motors wiegen Sie den mit Spiritus gefüllten Brenner. Stoppen Sie die gesamte
Brenndauer des Brenners und berechnen Sie daraus jeweils die zugeführte thermische Energie für
einen Umlauf (via Drehzahl).
Montieren Sie die Motor/Generator-Einheit auf der Grundplatte. Über einen Riemen wird die Einheit
an den Stirling-Motor angeschlossen. Parallel zu einer Lampenfassung liegen 2 Anschlußbuchsen, an
die der Schiebewiderstand (R ≤ 300 Ω) angeschlossen wird. Der Strom durch den Widerstand sowie
der Spannungsabfall über dem Widerstand werden mit den beiden Meßgeräten aufgenommen.
Hierdurch kann die elektrische Leistung Pel bestimmt werden.
Nach Einschalten des Motors warten Sie vor jeder Messung bis sich Drehzahl und Temperatur
stabilisiert haben. Übertragen Sie dann das pV-Diagramm vom Oszilloskop auf transparentes Millimeterpapier (liegt am Versuch aus). Für die Auswertung ist eine Genauigkeit von ¼ cm2 ausreichend.
Durch Einbeziehung der Kalibrierung für Druck und Volumen kann so PpV bestimmt werden. Notieren
Sie für jede Messung die Drehzahl n sowie die Temperaturen T1 und T2.
Î Variieren Sie den Widerstandswert (5 Werte) und messen Sie jeweils Strom, Spannung und
Drehzahl. Tragen Sie Pel als Funktion der Drehzahl auf und interpretieren Sie das Diagramm.
Î Messen Sie den thermischen Wirkungsgrad des Stirling-Motors ohne Last und vergleichen Sie das
Ergebnis mit dem theoretischen Wert.
ÎBerechnen Sie für die 5 Messungen mit Last und die Einzelmessung ohne Last jeweils den
thermischen Wirkungsgrad und den Carnot-Wirkungsgrad und vergleichen Sie die Resultate.
4. Sicherheitsaspekte
Es gelten die allgemeinen
Richtlinien und Vorschriften für Laboratorien (siehe Ordner
"Laborordnung Physik-Praktikum"). Spezielle - versuchsspezifische - Gesichtspunkte sind:
•
•
•
•
Sorgfältiger Umgang mit dem Spiritus-Brenner.
Glaszylinder des Motors im erhitzten Bereich nicht anfassen.
Start der elektrischen Messung mit maximalem Widerstandswert.
Vorsichtiger Umgang mit den Temperatursensoren (z.B. Zuleitungen nicht beschädigen ).
5. Vorbereitung
Literaturhinweis:
¾ Becker, Jodl, "Physikalisches Praktikum", VDI-Verlag 1991, S. 68ff
¾ Vorlesungsskript
Fragen:
• Wie berechnet man den thermischen Wirkungsgrad des idealen Stirling-Kreisprozesses ?
• Wie berechnen Sie die zugeführte thermische Energie im Versuch ?
• Wo liegen die Vor- bzw. Nachteile des Stirling-Heißluftmotors im Vergleich zum Otto-Motor
(z.B. Wirkungsgrad, Leistungskenndaten, Umweltverträglichkeit) ?