Musterabitur_EM-Felder_Relativität
Werbung
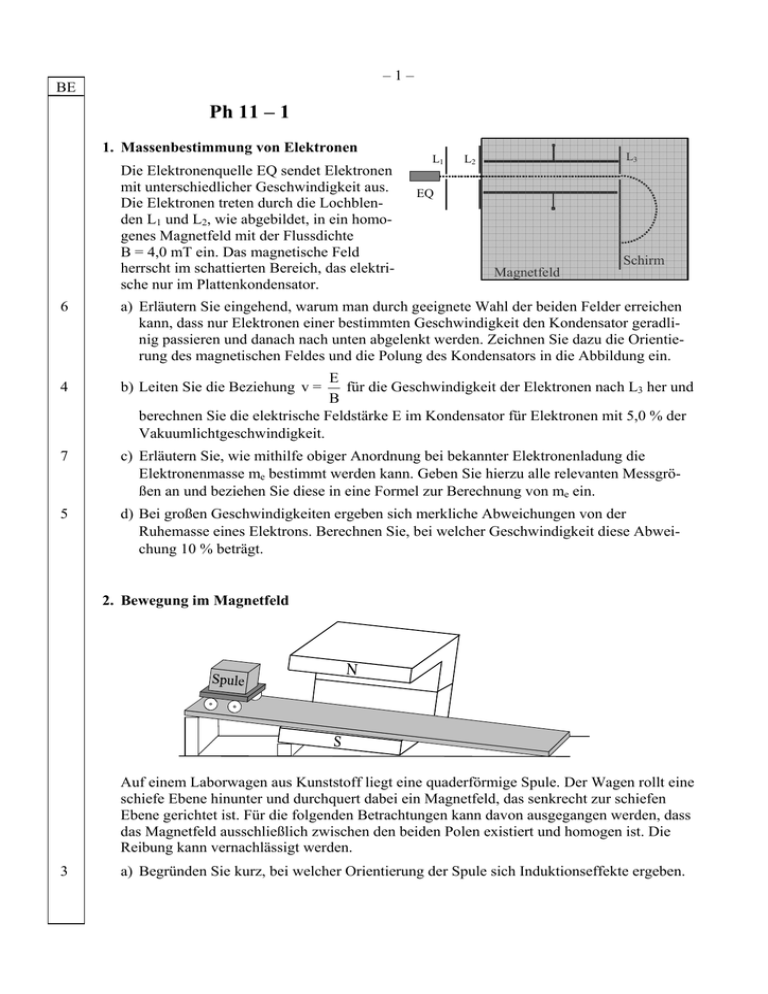
–1– BE Ph 11 – 1 1. Massenbestimmung von Elektronen L1 L3 L2 Elektronenquelle Die Elektronenquelle EQ sendet Elektronen mit unterschiedlicher Geschwindigkeit aus. Die Elektronen treten durch die Lochblenden L1 und L2, wie abgebildet, in ein homogenes Magnetfeld mit der Flussdichte B = 4,0 mT ein. Das magnetische Feld herrscht im schattierten Bereich, das elektrische nur im Plattenkondensator. EQ Schirm Magnetfeld 6 a) Erläutern Sie eingehend, warum man durch geeignete Wahl der beiden Felder erreichen kann, dass nur Elektronen einer bestimmten Geschwindigkeit den Kondensator geradlinig passieren und danach nach unten abgelenkt werden. Zeichnen Sie dazu die Orientierung des magnetischen Feldes und die Polung des Kondensators in die Abbildung ein. 4 b) Leiten Sie die Beziehung v = 7 c) Erläutern Sie, wie mithilfe obiger Anordnung bei bekannter Elektronenladung die Elektronenmasse me bestimmt werden kann. Geben Sie hierzu alle relevanten Messgrößen an und beziehen Sie diese in eine Formel zur Berechnung von me ein. 5 d) Bei großen Geschwindigkeiten ergeben sich merkliche Abweichungen von der Ruhemasse eines Elektrons. Berechnen Sie, bei welcher Geschwindigkeit diese Abweichung 10 % beträgt. E für die Geschwindigkeit der Elektronen nach L3 her und B berechnen Sie die elektrische Feldstärke E im Kondensator für Elektronen mit 5,0 % der Vakuumlichtgeschwindigkeit. 2. Bewegung im Magnetfeld Auf einem Laborwagen aus Kunststoff liegt eine quaderförmige Spule. Der Wagen rollt eine schiefe Ebene hinunter und durchquert dabei ein Magnetfeld, das senkrecht zur schiefen Ebene gerichtet ist. Für die folgenden Betrachtungen kann davon ausgegangen werden, dass das Magnetfeld ausschließlich zwischen den beiden Polen existiert und homogen ist. Die Reibung kann vernachlässigt werden. 3 a) Begründen Sie kurz, bei welcher Orientierung der Spule sich Induktionseffekte ergeben. –2– BE 8 b) Die Anschlüsse der Spule sind nicht verbunden. Die folgenden Diagramme zeigen die Geschwindigkeit v des Wagens bzw. die induzierte Spannung U, die an den Anschlüssen abgegriffen werden kann, in Abhängigkeit von der Zeit t. U v 0 0 t t Beschreiben und erklären Sie das Zustandekommen der Diagramme. 5 c) Jetzt wird an die Anschlüsse der Spule ein Strommessgerät angeschlossen und der Vorgang wiederholt. Beschreiben Sie qualitativ, was sich an der der Bewegung des Wagens gegenüber Teilaufgabe b ändert. Für welche Zeitbereiche erwarten Sie einen Ausschlag des Strommessgeräts? 3. Gestörter Rundfunkempfang Ein Sportplatz ist einseitig von einem Zaun begrenzt, der vollständig mit Blech beschlagen ist. In größerer Entfernung vom Zaun befindet sich der Sendedipol eines UKW-Senders. zum Sender c d d d Zaun Auf beiden Seiten des Zauns steht jeweils ein Sportler c bzw. d mit einem tragbaren Radio in einem bestimmten Abstand d vom Zaun. Trotz optimal eingestellter Empfänger haben beide sehr schlechten Radioempfang, doch kann einer der beiden Sportler durch eine geringfügige Veränderung seines Abstands vom Zaun die Empfangssituation deutlich verbessern, der andere nicht. 8 a) Erläutern Sie, warum anfangs beide Personen schlechten Radioempfang haben konnten und warum die Abstandsänderung nur bei einem der beiden zu einer Empfangsverbesserung führt. Im Metallzaun sind zwei Türen T1 und T2. Wenn beide offen sind, hat man hinter dem Zaun auf den skizzierten sechs Linien prakP tisch keinen Empfang. Der Abstand der Türmitten ist 10 m. T 11 b) Berechnen Sie die Wellenlänge und die Frequenz f des Senders unter Zuhilfenahme von Punkt P. Die Breite eines Kästchens in der Zeichnung entspricht 2 m in der Natur. Beschreiben Sie, an welchen Orten besonders guter Empfang herrscht. 1 [zur Kontrolle: f = 8 · 107 Hz] 3 60 c) Bestimmen Sie eine mögliche Länge eines optimal abgestimmten Sendedipols. T2 –3– BE Ph 11 – 2 1. Elektrische Feldstrukturen Zwei geladene Kugeln c und d sind 20 cm voneinander entfernt. Der Punkt A befindet sich genau in der Mitte zwischen den beiden Kugeln. Kugel c trägt die Ladung Q1 = + 3,2 · 10-9 As, der Betrag der Ladung auf Kugel d ist halb so groß. B C 1 A 2 7 a) Bestimmen Sie Betrag und Richtung der elektrischen Feldstärke im Punkt A. 7 b) Ergänzen Sie in der obigen Abbildung die Richtungen der Feldlinien. Zeichnen Sie Äquipotentiallinien durch die Punkte A, B und C ein. 3 c) Wie stellt sich das elektrische Feld für einen Beobachter in sehr großer Entfernung dar? 6 d) Beschreiben Sie ein selbst gewähltes Phänomen aus der Natur oder aus der Technik (z. B. Gewitterentstehung oder Funktionsprinzip der Xerographie), bei dem elektrische Felder eine entscheidende Rolle spielen. 2. Gold-Cap-Kondensatoren Ein „Gold Cap“ ist ein Kondensator mit sehr hoher Kapazität, der sich durch eine kleine Baugröße auszeichnet. Auf einem handelsüblichen Exemplar findet man die Aufschrift: „Gold Cap 2,3 V 10 F“. 3 a) Berechnen Sie die Plattenfläche, die ein Plattenkondensator bei einem Plattenabstand von 10 μm und einer Kapazität von 10 F hat? Zwei Gold Caps sind in der nachfolgenden Schaltung eingebaut. Der Schalter befindet sich zunächst in der Stellung „A“. –4– BE A B R U0 10 F 10 F Gold Cap 1 Gold Cap 2 5 b) Die Spannung U0 wird auf 2,0 V eingestellt. Bestimmen Sie die Ladung QA des Gold Cap 1 und die Energie EA, die in seinem elektrischen Feld gespeichert ist. Nun wird der Schalter von der Position „A“ in die Position „B“ umgelegt. 8 c) Berechnen Sie die Spannung, die sich lange Zeit nach Umlegen des Schalters an den beiden Kondensatoren einstellt, und die Gesamtenergie in beiden Feldern. Erläutern Sie, warum nun weniger Energie in den Feldern „steckt“ als bei Teilaufgabe b. 6 d) Statt des Gold Cap 2 soll nun eine Spule verwendet werden. Wieder wird zuerst der Schalter in Stellung „A“ gebracht und dann auf „B“ umgelegt. Skizzieren Sie qualitativ den zeitlichen Verlauf der Spannung am Gold Cap 1 und die Stromstärke durch den Widerstand ab dem Zeitpunkt des Umschaltens. 3. CD als Beugungsgitter Auf einer CD werden Informationen digital durch Vertiefungen in spiralförmigen Spurlinien gespeichert, die sich mit einem Laser im CD-Player auslesen lassen. Der Abstand g der nebeneinander liegenden Spurlinien beträgt 1,6 μm. Wenn man die Etikettbeschichtung der CD ablöst, kann man die CD als Beugungsgitter verwenden. Schirm Laser a 5 a) Der abgebildete Versuch soll zur Bestimmung der Wellenlänge des Lasers dienen. Skizzieren Sie das Interferenzbild auf dem Schirm und das Vorgehen zur Bestimmung der Wellenlänge. 6 b) Bei einem Versuch ergibt sich für den Abstand zwischen dem nullten und dem ersten Maximum 8,6 cm. Der Abstand zwischen CD und Schirm beträgt a = 20 cm. Berechnen Sie die Wellenlänge des verwendeten Lasers. 4 60 c) Beschreiben Sie die zu erwartenden Änderungen des Interferenzbildes, wenn der zunächst verwendete rote Laser durch einen grünen ersetzt wird und danach statt einer CD eine DVD verwendet wird, deren Spurlinien enger liegen.











