Vortrag 5 - Philipp - Kongruenzaxiome Hilbert

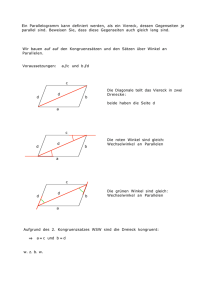
ℝ≇≆∄∃∊∉√∢
MAT746 · Seminar über Euklidische Geometrie · Philipp Becker
David Hilbert (1862-1943)
•  Den Begriffen aus der Anschauungswelt fehlt die notwendige
mathematische Exaktheit.
•  Gebäude der Geometrie soll nicht mehr auf wackeligen Füssen stehen.
•  Bestreben, die bislang v.a. auf Anschauung basierende und auf Euklid
zurückgehende Geometrie möglichst rein axiomatisch zu begründen.
Grundlagen der Geometrie (1899), veöffentlicht zur
Feier der Enthüllung des Gauß-Weber-Denkmals in
Göttingen.
(1886)
Hilbert’s “Grundlagen der Geometrie” (1899)
(1932)
•  Hilbert entwirft für die euklidische Geometrie ein vollständiges
Axiomensystem und darauf aufbauend eine streng axiomatisch
begründete Geometrie.
•  Jede Geometrie, die dem Hilbert’schen Axiomensystem
genügt, ist bis auf Isomorphie eindeutig bestimmt,
nämlich isomorph zum reellen 3D-Vektorraum.
Hilbert’s “Grundlagen der Geometrie” (1899)
Das Hilbert’sche Axiomensystem
•  Hilbert verwendet die drei Dinge Punkte, Geraden und Ebenen.
•  Hilbert verwendet die drei Beziehungen liegen, zwischen und kongruent.
•  kongruent wird als eine Beziehung zwischen Strecken und zwischen
Winkeln definiert. (andere Bezeichnung: gleich oder gleich lang; ≡)
Kongruenz von Segmenten: Wir formulieren die Axiome (C1) bis (C3)
C1 Gegeben sei das Segment AB sowie
ein Strahl r ausgehend vom Punkt C.
Dann ∃! D ∊ r sodass AB ≅ CD
C2 Sei AB ≅ CD und AB ≅ EF. Dann gilt
CD ≅ EF.
Jedes Segment ist kongruent zu sich
selbst.
C3 Gegeben seien die Punkte A, B, C, D,
E, F mit A*B*C und D*E*F.
Falls AB ≅ DE und BC ≅ EF, dann gilt
auch AC ≅ DF.
Vergleich der Hilbert’schen Axiome mit Euklid’s Aussagen
C1 Gegeben sei das Segment AB sowie
ein Strahl r ausgehend vom Punkt C.
Dann ∃! D ∊ r sodass AB ≅ CD
C2 Sei AB ≅ CD und AB ≅ EF. Dann gilt
CD ≅ EF.
Jedes Segment ist kongruent zu sich
selbst.
“Das was demselben gleich
ist, ist unter sich gleich.”
(Grundsatz 1 in Buch 1)
C3 Gegeben seien die Punkte A, B, C, D,
E, F mit A*B*C und D*E*F.
Falls AB ≅ DE und BC ≅ EF, dann gilt
auch AC ≅ DF.
“Gleichem das Gleiche
hinzugefügt ergibt Gleiches.”
(Grundsatz 2 in Buch 1)
Vergleich der Hilbert’schen Axiome mit Euklid’s Aussagen
•  Euklid beweist seine Postulate durch Konstruktionen
•  Hilbert dagegen geht von Existenzen aus:
z.B. existieren gewisse Punkte (Axiom C1) bzw. Winkel (Axiom C4)
•  Die Axiome (C1) bis (C3) sind nun unsere Werkzeuge, um Segmente
zu verschieben etc.
•  Wir verwenden sie, um die Propositionen zu beweisen.
Definition “Summe von Segmenten”
Seien AB und CD Segmente. Sei E∊r (s. Abb.) sodass CD ≅ BE.
(Die Existenz von E ist durch das Axiom (C1) gegeben.)
Dann ist AE die Summe der Segmente AB und CD
und wir schreiben
AE := AB + CD
Proposition“Kongruenz ist eine Äquivalenzrelation”
Kongruenz von Segmenten ist eine Äquivalenzrelation.
•  reflexiv: Jedes Segment ist kongruent zu sich selbst
Beweis: Axiom (C2).
•  symmetrisch: zu zeigen: AB ≅ CD impliziert CD ≅ AB.
Beweis: AB ≅ CD und AB ≅ AB (wegen Reflexivität)
Dann folgt mit Axiom (C2) CD ≅ AB
•  transitiv: zu zeigen: AB ≅ CD und CD ≅ EF impliziert AB ≅ EF.
Beweis: CD ≅ AB (wegen Symmetrie) und CD ≅ EF
Dann folgt mit Axiom (C2) AB ≅ EF
Bemerke: Häufige Verwendung von Axiom (C2) als Werkzeug für den Beweis.
Proposition“Summen kongruenter Segmente sind kongruent”
Gegeben seien die jeweils kongruenten Segmente AB ≅ A’B’
und CD ≅ C’D’.
Dann gilt AB + CD ≅ A’B’ + C’D’
Beweis: Tafel
Proposition“Subtraktion von Segmenten”
In der folgenden Proposition interpretieren wird Euklid’s Grundsatz:
“Gleichem das Gleiche weggenommen ergibt Gleiches”
Seien A, B, C Punkte, sodass A*B*C.
Sei r ein Strahl, ausgehend von D, mit E und F auf r.
Seien AB ≅ DE und AC ≅ DF.
Dann liegt E zwischen D und F (d.h. D*E*F)
und es gilt BC ≅ EF.
BC ist die Differenz von AC und AB. “Das Ganze ist grösser als ein Teil davon.” (Euklid)
d.h. aus A*B*C folgt, dass AB ≆ AC (es sei denn B=C).
Wir müssen “kleiner” und “grösser” definieren.
Definition: “kleiner” und “grösser”
Seien AB und CD (Linien-) Segmente.
Dann definieren wir:
AB < CD :⇔ ∃E mit C*E*D sodass AB ≅ CE.
Proposition zu “kleiner” und “grösser”
Die Definition “kleiner/grösser” ist kompatibel mit dem Kongruenz-Begriff:
(a)  Seien AB ≅ A’B’ und CD ≅ C’D’.
Dann gilt: AB < CD ⇔ A‘B‘ < C‘D‘
(b) Die Relation “<“ stellt eine Ordnungsrelation auf Kongruenzklassen dar:
i.  AB < CD, CD < EF ⇒ AB < EF.
ii.  Seien AB, CD Segmente. Es gilt genau eine der folgenden Aussagen:
AB < CD
AB ≅ CD
AB > CD
Beweis zu (b) i.: Tafel Anwendung: Kongruenz von Segmenten in der kartesischen Ebene
Ziel: Wir wollen den Begriff “Kongruenz” mit Leben füllen …
Die kartesische Ebene im ℝ2 soll ein Modell für die Axiome
(I1)-(I3), (B1)-(B4) und (C1)-(C3) sein.
Definiere die Distanz zwischen zwei Punkten A=(a1,a2) und B=(b1,b2) durch
(Euklidische Distanz / Metrik auf ℝ2)
Es gilt d(A,B) ≥ 0 und d(A,B) = 0 ⇔ A=B
Wir interpretieren nun den Kongruenz-Begriff wie folgt:
AB ≅ CD :⇔ d(A,B) = d(C,D)
Anwendung in der Ebene der reellen Zahlen
Wir wollen die Axiome (C1)-(C3)
überprüfen!
Tafel
Anwendung in der Ebene der rationalen Zahlen
Gelten die Axiome (C1) bis (C3) auch
in der kartesischen Ebene der rationalen Zahlen
•  (C2) gilt
•  (C3) gilt •  (C1) gilt jedoch i.A. nicht
Gegenbeispiel an Tafel
2?
Anwendung in der Taxi-Geometrie
Wir definieren eine andere Distanzfunktion:
à Die „taxicab geometry“
(C1)
Sei d(A,B) = δ und sei C=(c1,c2). Gesucht D auf dem Strahl mit Steigung m>0.
⇒ D=(c1+h, c2+mh)
⇒ d(C,D)=|c1 - (c1+h)| + |c2 - (c2+mh)| = h(1+m) == δ
⇒ h = δ/(1+m)
Die Koordinaten von D sind eindeutig: D = (c1+ δ/(1+m), c2 + mδ/(1+m))
Anwendung in der Taxi-Geometrie
Wir definieren eine andere Distanzfunktion:
à Die „taxicab geometry“
(C2)
Sei d(A,B) = δ
AB ≅ CD ⇔ d(A,B) = d(C,D) ⇒ d(C,D) = δ
AB ≅ EF ⇔ d(A,B) = d(E,F) ⇒ d(E,F) = δ
⇒ d(C,D) = δ = d(E,F) ⇒ CD ≅ EF
Anwendung in der Taxi-Geometrie
Wir definieren eine andere Distanzfunktion:
à Die „taxicab geometry“
(C3)
Wir zeigen, dass die taxicab-Distanzfunktion
additiv ist. Seien hierzu A, B und C Punkte auf
der Linie mit der Gleichung y=mx+b
⇒ A = (a1, a2)
B = (a1+h, a2+mh)
C = (a1+h+k, a2+m(h+k))
⇒ d*(A,B) = h(1+m)
d*(B,C)=|a1+h-a1-h-k| + |a2+mh-a2-mh-mk| = |-k| + |-mk| = k(1+m)
d*(A,C)= |a1-a1-h-k| + |a2-a2-mh-mk| = |-(h+k)| + |-(mh+mk)|= (h+k)(1+m)
⇒ d*(AB) + d*(B,C) = d*(A,C)
Anwendungen mit unterschiedlichen Distanzfunktionen
Frage: Wie sieht ein Kreis mit Mittelpunkt (0/0) und Radius 1
… in dieser Taxi-Geometrie aus?
… mit der supremum-Distanzfunktion aus? … und mit dieser? , falls AB horizontal oder senkrecht
, sonst Kongruenz von Winkeln
Winkel: Vereinigung von zwei Strahlen, die dem selben Punkt entspringen
•  Strahlen liegen nicht auf der gleichen Linie
•  180° „Winkel“ ist in diesem Sinne kein Winkel
Einführung vom Begriff der Kongruenz von Winkeln, in Zeichen
∢ BAC ≅ ∢EDF
Hilbert´s Axiome zur Kongruenz von Winkeln
C4 Gegeben sei der Winkel ∢ BAC und ein Strahl
DF ausgehend D.
Dann ∃! Strahl DE ausgehend von D sodass
∢ BAC ≅ ∢ EDF
C5 Gegeben seien drei Winkel α, β, γ mit
α ≅ β und α ≅ γ. Dann gilt β ≅ γ.
Jeder Winkel ist kongruent zu sich selbst.
C6 (SAS) Gegeben seien 2 Dreiecke ABC u. DEF,
wobei AB ≅ DE und AC ≅ DF und ∢ BAC ≅ ∢
EDF.
Dann sind die beiden Dreiecke kongruent und
es gilt:
BC ≅ EF, ∢ ABC ≅ ∢ DEF, ∢ ACB ≅ ∢ DFE.
Vergleich von Hilbert und Euklid
•  Hilbert betrachtet (C4) als Axiom: Aussage, dass ein solcher Winkel
existiert. Euklid beweist dies durch eine Konstruktion mit Lineal und
Winkelmesser (I.23)
•  Hilbert hat realisiert, dass Euklid seinen Kongruenzsatz (SWS),
zumindest seinen wesentlichen Inhalt, nicht beweisen kann (erstmals
angedeutet von Peletarius, 1557). Er führt die Aussage deshalb als
Axiom (C6) ein.
•  Die Einführung von (C6) ist essentiell, da dieses Axiom unabhängig
von den anderen Axiomen ist.
Wie bei der Kongruenz von Linien-Segmenten werden wir auch hier die
Axiome als Werkzeuge benutzen, um Propositionen zu beweisen.
Proposition: Kongruenz ist eine Äquivalenrelation
Kongruenz von Winkeln ist eine Äquivalenzrelation.
Beweis: Analog zum Beweis für Segmente unter Verwendung
von Axiom (C5) statt (C2).
Zur Summe von Winkeln
Die Summe von zwei Winkeln sollte wieder ein Winkel sein…
Sei ∢ BAC ein Winkel und der Strahl AD, ausgehend von A,
liege im Innern dieses Winkels. Dann können wir sagen:
∢ BAC ist die Summe von ∢ DAC und ∢ BAD.
Beginnend mit 2 gegebenen Winkeln kann es sein, dass die Summe kein
Winkel in „unserem Sinne“ mehr ist, z.B. wenn sie
•  180° = 2 rechte Winkel ist
•  grösser als 180° ist (die 2 ursprünglichen Winkel sind nicht mehr
im Innern des Summenwinkels)
Im Folgenden werden wir sehen, wie wir mit Summen und Ungleichheiten umgehen.
Definitionen: Ergänzungswinkel, Scheitelwinkel, rechter Winkel
Sei ∢ BAC ein Winkel und D ein Punkt auf der
Linie AC (s. Abb.), dann ergänzen sich die
Winkel ∢ BAC und ∢ BAD (Ergänzungswinkel)
Als Scheitelwinkel bezeichnen wir zwei
gegenüberliegende Winkel, wenn sich zwei
Linien schneiden.
Als rechten Winkel bezeichnen wir einen
Winkel α, welcher kongruent zu einem seiner
Ergänzungswinkel β ist.
Proposition zu Ergänzungswinkeln
Seien ∢ BAC und ∢ BAD sowie ∢ B´A´C´ und ∢ B´A´D´
jeweils Ergänzungswinkel, wobei ∢ BAC ≅ ∢ B´A´C´.
Dann gilt: ∢ BAD ≅ ∢ B´A´D´.
Diese Proposition entspricht Euklid´s (I.13):
„Winkel, die durch einen Strahl, der von einer Linie ausgeht, entstehen,
sind entweder rechte Winkel oder gleich zwei rechten Winkeln.
Ein Korollar zu Scheitelwinkeln
Scheitelwinkel sind kongruent.
Beweis: Die beiden Scheitelwinkel α und α´sind jeweils Ergänzungswinkel
von β. Der Winkel β ist kongruent zu sich selbst.
Wir haben zwei Paare von Ergänzungswinkeln: (α, β) und (α´, β).
Da β ≅ β , gilt gemäss vorheriger Proposition auch α ≅ α´.
Proposition zur Addition von Winkeln
Sei ∢ BAC ein Winkel und AD ein Strahl im Innern dieses Winkels.
Sei ∢ D´A´C´ ≅ ∢ DAC und ∢ B´A´D´ ≅ ∢ BAD, wobei die Strahlen A´B
´und A´C´nicht auf der gleichen Seite von A´D´ liegen (s. Abb.).
Dann beschreiben die Strahlen A´B´und A´C´ einen Winkel ∢ B´A´C´ (die
Summe!) und es gilt ∢ B´A´C´ ≅ ∢ BAC und A´D´ ist ein Strahl im
Innern von ∢ B´A´C´.
Kurz: Die Summen zueinander kongruenter Winkel sind kongruent.
Definition zur Ungleichheit von Winkeln
Gegeben seien zwei Winkel ∢ BAC und ∢ EDF.
Dann gilt:
∢ BAC < ∢ EDF :⇔ ∃ Strahl DG, ausgehend von D,
im Innern von ∢ EDF, sodass ∢ BAC ≅ ∢ GDF
Ungleichheit: Ordnungsrelation auf Kongruenzklassen
(a)  (α ≅ α´ und β ≅ β‘) ⇒ (α < β ⇔ α´ < β´)
(b)  Ungleichheit definiert eine Ordnungsrelation auf Kongruenzklassen
von Winkeln, d.h.
i.  α < β und β < γ, dann gilt α < γ
ii.  Für zwei beliebige Winkel α, β gilt genau einer der folgenden
Aussagen: α < β
α≅β
α>β
Beweis: Analog zur analogen Proposition über Segmente.
Proposition zu rechten Winkeln
Je zwei rechte Winkel sind zueinander kongruent.
Beweis: Diese Aussage kann tatsächlich bewiesen werden und muss nicht
- wie bei Euklid – als Axiom vorausgesetzt werden.
Die Axiome (C4)-(C6) in der kartesischen Ebene im ℝ2
Die Axiome (C4) bis (C6) gelten in der kartesischen Ebene.
Diese Aussage werden wir erst später zeigen und zwar sehr allgemein:
Jede kartesische Ebene über einen geordneten Körper, welcher gewisse
algebraische Anforderungen erfüllt, ist ein Modell für Hilbert´s Axiome.
Die Kongruenz-Axiome für Winkel in der Taxi-Geometrie
Wir nehmen die Betrags-Distanzfunktion:
à Die „taxicab geometry“
•  (C4) und (C5) gelten (Tafel)
•  (C6) gilt jedoch i.A. nicht
Gegenbeispiel: Wähle A=(0/0), B=(0.1/0.9), C=(1/0)
D=(0/0), E=(0.4/0.5), F=(0.5/-0.5)
Für ∆ABC gilt: d(A,B)=|0-0.1|+|0-0.9|=1 und auch d(A,C)=1.
tan(α)=| m´-m |
1+m´m
tan(α)=| 9-0 |= 9 (m´ = 9 (A nach B) und m = 0 (A nach C))
1+0.9
Für ∆DEF gilt: d(D,E)=|0-0.4|+|0-0.5|=1 und auch d(D,F)=1.
tan(γ)=| 1.25-(-1) |= 9 (m´ = 1.25 (D nach E) und m = -1 (D nach F))
1+(1.25·(-1))
Voraussetzungen erfüllt, aber: d(B,C) = 1.8 ≠ 1.1 = d(E,F)
⇒ BC ≆ EF Danke für eure Aufmerksamkeit!