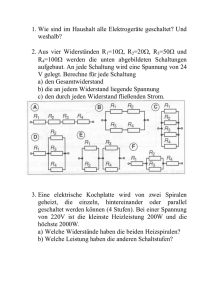
1 Elektrische Stromkreise und lineare Netzwerke /20

1
Elektrische Stromkreise und lineare Netzwerke
/20
Zwei Batterien G1 und G2 mit unterschiedlichen elektrischen Eigenschaften wurden
polrichtig parallel geschaltet und an den
Anschlussklemmen A, B mit einem Lastwiderstand RL = 10 Ω belastet.
Batteriedaten:
G1: Leerlaufspannung U01 = 12 V,
Innenwiderstand
Ri1 = 1 Ω
G2:
Leerlaufspannung U02 = 9 V,
Innenwiderstand
Ri2 = 2 Ω
1.1 Skizzieren Sie ein Ersatzschaltbild für die gesamte Anordnung mit
Verbraucherzählpfeilsystem. Stellen Sie ein allgemeines Gleichungssystem auf, mit dem sich die beiden Batterieströme IG1, IG2 und der Laststrom IL, sowie die Lastspannung UL berechnet werden können. Berechnen Sie IG1, IG2, IL, UL.
/8
1.2 Wandeln Sie die gesamte Schaltung in eine Ersatzspannungsquelle bezogen auf die Anschlussklemmen A, B um. Skizzieren Sie die zugehörige Schaltung und überprüfen Sie durch Rechnung den Laststrom IL.
/6
1.3 Nehmen Sie an, die beiden Batterien G1 und G2 werden polrichtig parallel geschaltet und im Leerlauf (RL = ∞ Ω) betrieben. Welche problematische
elektrische Größe tritt dann auf?
Benennen und berechnen Sie für diesen Fall die elektrische Größe.
/3
1.4 Kommentieren und bewerten Sie den Sachverhalt unter 1.3 und stellen
Sie eine begründete allgemeine Regel für die Parallelschaltung von Batterien auf!
/3
2
Sinusförmige Wechselgrößen
/20
Die Grafik zeigt einen Auszug aus
einem Laborprotokoll.
Die untersuchte Schaltung besteht
aus einer Parallelschaltung zweier
idealer Bauelemente.
Die Schaltung liegt an einer Wechselspannung von U=5V.
Durch den ohmschen Widerstand
fließt der Strom i1(t), ig(t) ist der Gesamtstrom der Schaltung.
2.1 Ermitteln Sie aus dem Diagramm die Effektivwerte der beiden Ströme
sowie deren Frequenz.
/3
2.2 Geben Sie den Nullphasenwinkel von ig(t) und den Phasenwinkel ϕ zwischen i1(t) und ig(t) an. Erläutern Sie die Begriffe Nullphasenwinkel und
Phasenverschiebungswinkel.
/6
2.3 Begründen Sie die Art des idealen Bauelements, das parallel zum
ohmschen Widerstand geschaltet ist. Bestimmen Sie den Wert des
ohmschen Widerstandes und des Blindwiderstandes. Ermitteln Sie die
Bauteilkenngröße des Blindwiderstandes bei einer Frequenz von
41,67Hz.
/7
2.4 Berechnen Sie den Momentanwert von i1(t) zum Zeitpunkt des positiven
Nulldurchgangs von ig(t).
/4
3
Komplexe R-L-C-Schaltungen
Die abgebildete Schaltung stellt einen
Ausschnitt aus dem Schaltplan eines
elektrischen Gerätes dar. Es wird eine
intern vorhandene Spannung U zum Betrieb eines Verbrauchers ZAB genutzt.
Von der Schaltung sind die folgenden
Werte bekannt:
IAB = 19 mA /-18,43°
R = 1 kΩ
L = 127,4 mH
C = 21,22 nF
f = 2,5 kHz
ZAB = 2,83kΩ /45°
/20
R
L
A
IAB
UAB
U
ZAB
C
B
3.1 Berechnen Sie die Blindwiderstände der Bauteile L und C.
/3
3.2 Ermitteln Sie den komplexen Wert der internen Spannungsquelle U.
/4
3.3 Wie groß sind die komplexen Teilspannungen an allen Widerständen?
Weisen Sie mit Hilfe des komplexen Zeigerdiagramms nach, dass nach dem
Kirchhoffschen Gesetz die Summe aller Spannungen gleich Null ist.
Maßstab: 10V =ˆ 1cm
/9
3.4 Der Lastwiderstand ZAB wurde geändert, sodass der Gesamtwiderstand der
Schaltung Zges = 3,16 kΩ /0° beträgt.
Welchen Wert hat ZAB angenommen?
Skizzieren Sie die Ersatzschaltung ZAB und benennen Sie die Bauteile.
/4
4
Grundlagen der Programmierung
/30
In Aufgaben 4.1 und 4.2 beziehen sich auf die Berechnung passiver Vierpole. Diese Vierpole können in zwei Gruppen eingeteilt werden:
die erste Gruppe umfasst Hoch- und Tiefpässe,
die zweite Gruppe enthält Bandpässe und Bandsperren.
Hochpass / Tiefpass
fg =
1
2 ⋅π ⋅ R ⋅ C
fg =
Bandpass / Bandsperre
R
2 ⋅π ⋅ L
f0 =
1
2 ⋅π ⋅ L ⋅ C
4.1
Erstellen Sie ein Struktogramm für ein Programm, das dem Anwender folgende Berechnungsmöglichkeiten zur Verfügung stellt:
Zunächst soll sich der Anwender entscheiden, für welche der beiden Gruppen (Hochpass/Tiefpass oder Bandpass/Bandsperre) er eine Berechnung
durchführen möchte.
Entscheidet er sich für Bandpass/Bandsperre muss er die Induktivität L und
die Kapazität C eingeben, anschließend wird die Resonanzfrequenz f0 berechnet und ausgegeben. Danach endet das Programm.
Fällt seine Wahl auf die Berechnung von Hochpass/Tiefpass muss er zunächst den Wert des Widerstandes R eingeben. Als nächstes muss er entscheiden, ob das Passverhalten durch eine Spule oder einen Kondensator
realisiert wird. Anschließend muss er den Wert der Kapazität C bzw. der Induktivität L eingeben. Das Programm berechnet dann die Grenzfrequenz fg
und gibt sie aus. Danach endet das Programm.
4.2
Erläutern Sie, wie das Programm für folgende Erweiterung verändert werden
muss. Eine Darstellung im Struktogramm ist nicht erforderlich.
Das Programm aus Aufgabe 1.1 soll so erweitert werden, dass der Anwender nach der Ausgabe der Ergebnisse die Möglichkeit hat, durch Eingabe
des Buchstabens ‚q’ das Programm zu beenden. Die Eingabe eines beliebigen anderen Buchstaben führt ihn zurück zur Auswahl „Hochpass/Tiefpass
oder Bandpass/Bandsperre“.
Die Aufgaben 4.3 und 4.4 beziehen sich auf
den nebenstehenden Quelltextauszug.
4.3
4.4
/8
/3
...
do
{
auswahl = Tastatur.liesChar();
}
while ( ??? )
...
Die Schleife im Quelltext soll erzwingen, dass die Variable ‚auswahl’ nur die
Werte ‚q’ oder ‚b’ annehmen kann.
Wie muss die Bedingung für die while - Anweisung lauten (Java-Quellcode)?
Begründen Sie, warum für diesen Anwendungsfall eine kopfgesteuerte
Schleife ungeeignet ist.
/2
/2
Die Aufgaben 4.5 bis 4.8 befassen sich mit dem belasteten Spannungsteiler. Die Ausgangsspannung U2 eines belasteten Spannungsteilers berechnet sich nach folgender Formel:
R2 L
U2 = U ⋅
R1 + R2 L
Hinweis:
R2L ist der Ersatzwiderstand der
parallel geschalteten Widerstände R2 und RL.
Belasteter Spannungsteiler
...
Eingabe: u, r1, r2, rL_min, rL_max
delta_rL ← (rL_max - rL_min) / 20
von rL ← rL_min bis rL_max
(Schrittweite ← delta_rL)
u2 ← u * parallel(r2, rL) / (r1 + parallel(r2, rL))
Ausgabe: u2
...
4.5
Erläutern Sie die Funktionsweise des im Struktogramm dargestellten Programmausschnitts.
4.6
Das Struktogramm enthält eine Schleife. Schreiben Sie den Java-Quellcode
dieser Schleife auf. Der Code der vor der Schleife befindlichen Anweisungen
muss nicht angegeben werden. Für die Bildschirmausgabe steht die Funktion
„System.out.print( )“ zur Verfügung.
4.7
Im Struktogramm ist der Aufruf einer Funktion „parallel(r2, rL)“ enthalten. Diese Funktion berechnet den Widerstand zweier parallel geschalteter Widerstände. Schreiben Sie den Java-Quellcode dieser Funktion auf.
4.8
Erläutern Sie anhand eines selbst gewählten Funktionsbeispiels folgende
Fachbegriffe:
- Rückgabedatentyp
- Rückgabewert
- formale Parameter
/4
/4
/4
/3
Abschlussprüfung Fachoberschule
2008 Elektrotechnik
1
Aufgabenvorschlag B
5
Objektorientierte Programmierung (OOP)
Die nebenstehende Schaltung dient als
Grundlage der Modellierung einer
Klasse zur Berechnung der drei Belastungsfälle Kurzschluss, Leerlauf und
Belastung mit RL einer technischen
Spannungsquelle.
/10
A
Ri
UKL
U0
B
5.1
Ergänzen Sie das unvollständige OOD-Klassendiagramm um die Widerstände Ri und RL und, beispielhaft für einen der beiden Widerstände, um
die Verwaltungsmethoden (set- und get-Methoden). (Die Lösung bitte auf
dem Arbeitsblatt und nicht hier auf dem Aufgabenblatt.)
BelasteteSpannungsquelle
- quellenspannung : double
...
+ BelasteteSpannungsquelle()
+ berechneUklBeiBelastung(lastWiderstand : double):double
/3
5.2
Im dem Konstruktor, der im obigen OOD-Klassendiagramm gegeben ist,
sollen alle Attribute initialisiert werden.
Stellen Sie die entsprechende Implementierung des Konstruktors als JavaQuellcode dar.
/3
5.3
Die Symbole „+“ bzw. „-“ des Klassendiagramms werden als „Modifizierer“
bezeichnet.
Erläutern Sie die Bedeutung dieser Symbole in der objektorientierten Programmierung.
/3
5.4
Schreiben Sie für ein Java-Objekt „belasteteUQuelle“ des Typs „BelasteteSpannungsquelle“ einen Methodenaufruf für die Methode
„berechneUklBeiBelastung(…)“ auf.
/1
FOS_IMT_B_08.doc
Abschlussprüfung Fachoberschule
2008, Elektrotechnik
Aufgaben
Seite 1 von 6