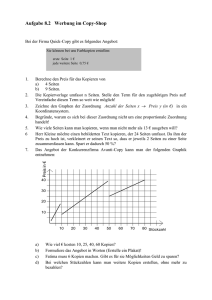
Mathematik

Mathematik-Verlag
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Quadratische Gleichungen
1. Wie lautet die p, q – Formel zur Lösung der
quadratischen Gleichung x2 + px + q = 0 ?
2. Berechne mit der p, q – Formel die
Lösungen der Gleichungen:
a) x2 − 3x − 4 = 0
b) x2 +
1
x−3=0
2
Karte 1
Lösung:
1. Die p, q – Formel lautet:
x1 = −
p
+
2
(p2 )
2
−q
p
und x 2 = − −
2
()
p 2
−q
2
2. a) Es ist: p = −3 und q = −4.
Durch Einsetzen in die p, q - Formel erhält man die
Lösungen: x1 = 4 und x2 = −1.
b) Es ist: p =
1
2
und q = −3.
Durch Einsetzen in die p, q - Formel erhält man die
Lösungen: x1 = 1,5 und x2 = −2.
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Quadratische Gleichungen
Wie muss man folgende Gleichungen umformen,
bevor man die p, q – Formel anwenden kann ?
Gib jeweils die Lösungen an.
a) x2 + 9x + 8 = −6
b) 2x2 − 8x − 10 = 0
Karte 2
Lösung:
Wichtig: Die p, q - Formel darf nur dann angewendet
werden, wenn auf einer Seite der Gleichung „0“ steht.
Außerdem darf vor „x2“ kein Faktor stehen.
a)
b)
x + 9x + 8 = −6
2
2x2 − 8x − 10 = 0
| +6
⇔ x2 + 9x + 14 = 0
⇔
⇒ x1 = −2 und x2 = −7
⇒ x1 = 5 und x2 = −1
| :2
x2 − 4x − 5 = 0
.
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Quadratische Gleichungen
Was muss man in folgender Gleichung beachten,
wenn man die Klammern ausmultipliziert bzw.
die quadratische Klammer auflöst ?
4 − (x + 1)(x − 2) − (x + 3)2 = −10
Berechne die Lösungen.
Karte 3
Lösung:
Wichtig: Steht vor einem Klammerprodukt oder einer
quadratischen Klammer ein Minuszeichen, muss man
zusätzliche Klammern setzen ! Sonst gibt es beim
Ausmultiplizieren einen Vorzeichenfehler.
4 − [(x + 1)(x − 2)] − [(x + 3)2] = −10
⇔ 4 − [x2 − 2x + 1x − 2] − [x2 + 6x + 9] = −10
⇔
4 − x2 + 2x − 1x + 2 − x2 − 6x − 9 = −10 | +10
⇔
−2x2 − 5x + 7 = 0
⇔
x + 2,5x − 3,5 = 0
2
| :(−2)
⇒ x1 = 1 und x2 = −3,5
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Bruchgleichungen
a) Wie bestimmt man die Definitionsmenge einer
Bruchgleichung ?
b) Gib die Definitionsmenge folgender Gleichung an:
1
+
6x
2
x+5
=
3
x −1
Karte 4
Lösung:
a) Die Zahlen, bei denen die einzelnen Nenner der
Bruchgleichung 0 werden, müssen aus der Definitionsmenge ausgeschlossen werden, da die Division durch 0
verboten ist. Man muss also jeden Nenner = 0 setzen und
nach x auflösen. Die Ergebnisse dieser Gleichungen
schreibt man in die geschweifte Klammer: D = IR \ { … }
b) 6x = 0 ⇔ x1 = 0
x + 5 = 0 ⇔ x2 = − 5
x − 1 = 0 ⇔ x3 = 1
Damit ist die Definitionsmenge: D = IR \ {0 ; −5 ; 1 }
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Geraden
a) Wie lautet die allgemeine Gleichung einer
Geraden g ?
.
g:
b) Was sind darin die Steigung und der
y-Achsenabschnitt ?
Karte 5
Lösung:
a) g: y = m ⋅ x + b bzw. y = m x + b
b) m ist die Steigung der Geraden. b nennt man den
y-Achsenabschnitt, da die Gerade g die y-Achse
immer im Punkt S y(0 | b) schneidet.
Tipp: Wenn man eine Gerade zeichnen soll, sollte die
Steigung m immer als Bruch vorliegen, damit man das
Steigungsdreieck zeichnen kann.
Z. B.: y = 1,5x + 2 =
3
2
x + 2 oder y = 2x − 1 = x − 1
2
1
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Geraden
a) Wie geht man vor, um das Schaubild einer
Geraden zu zeichnen ? Die Funktionsgleichung
der Geraden sei bekannt.
b) Zeichne jeweils das Schaubild der Geraden g und h
in ein Achsenkreuz:
g: y =
1
x−3;
2
h: y = −
3
x+2
4
Karte 6
Lösung:
a) Man trägt zunächst den Schnittpunkt Sy(0 | b) der Geraden
mit der y-Achse ein. Anschließend zeichnet man von Sy aus
anhand der Steigung m ein Steigungsdreieck.
Dazu sollte die Steigung m als Bruch vorliegen: m =
b)
z
.
n
y
2
g
2
-3
x
6
h
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Geraden
a) Wie bestimmt man die Funktionsgleichung einer
Geraden, von der zwei Punkte bekannt sind ?
Beschreibe das allgemeine Vorgehen.
b) Wie lautet die Funktionsgleichung der Geraden g,
die durch die Punkte A(2 | 6) und B(−1| 3) läuft ?
Karte 7
Lösung:
a) Man setzt die Koordinaten der beiden Punkte jeweils in die
Geradengleichung y = m⋅x + b ein. Dadurch erhält man ein
Gleichungssystem mit den Unbekannten m und b. Indem man
eine Gleichung von der anderen abzieht, fällt die Variable b
heraus, sodass die Steigung m berechnet werden kann.
Durch Einsetzen von m in eine der beiden Gleichungen kann
auch b berechnet werden.
b) A(2 | 6):
6 = m⋅2 + b
bzw. 6 = 2m + b (I)
B(−1 | 3): 3 = m ⋅ (−1) + b bzw. 3 = −m + b (II)
(I) − (II) ergibt: 3 = 3m ⇔ m = 1
Einsetzen in Gleichung (I) 6 = 2m + b ergibt: b = 4
Damit ist g: y = 1x + 4 bzw. y = x + 4
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Geraden
a) Wie bestimmt man die Gleichung einer
Geraden, von der die Steigung und ein Punkt
bekannt sind ?
Beschreibe das allgemeine Vorgehen.
b) Wie lautet die Gleichung der Geraden g,
die durch den Punkt P(− 4| 1) läuft und die
Steigung m = 2 hat ?
Karte 8
Lösung:
a) Man setzt die Steigung m und die Koordinaten des
bekannten Punktes in die Geradengleichung y = m⋅x + b
ein. Dadurch erhält man eine Gleichung, die nach b
umgestellt werden kann.
b) Einsetzen von m = 2 und P(− 4 | 1) in y = m⋅x + b
ergibt:
1 = 2 ⋅ (− 4) + b
⇔ 1 = −8 + b ⇔ b = 9
Damit ist g: y = 2x + 9
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Geraden
a) Gegeben ist die Gerade g: y = 2x + 1.
Was kann man über die Steigung der Geraden h
aussagen, wenn die Gerade h parallel zu g
verläuft ?
b) Bestimme die Gleichung der Geraden h,
wenn h durch den Punkt P(−3 | 5) geht.
Karte 9
Lösung:
a) Die Steigung der Geraden h ist ebenfalls m = 2.
Merke: Wenn zwei Geraden parallel zueinander verlaufen,
haben sie die gleiche Steigung m.
b) Einsetzen von m = 2 und P(−3 | 5) in y = m⋅x + b ergibt:
5 = 2 ⋅ (−3) + b
⇔ 5 = −6 + b ⇔ b = 11
Damit ist h: y = 2x + 11
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
a) Wie lautet die Scheitelform einer
quadratischen Funktion ?
b) Wie kann man anhand einer Scheitelform sehr
leicht die Koordinaten des Scheitelpunkts der
entsprechenden Parabel bestimmen ?
Karte 10
Lösung:
a) Die Scheitelform ist p: y = (x − b)2 + c.
b) Der Scheitelpunkt der entsprechenden Parabel p hat
die Koordinaten S(b | c).
Tipp: Die x-Koordinate des Scheitelpunkts ist immer die
Zahl, für die die Quadratklammer 0 wird. Die y-Koordinate
steht immer rechts von der Quadratklammer.
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
Bestimme jeweils die Koordinaten des
Scheitelpunkts der Parabeln:
a) p: y = (x − 3)2 + 1
b) p: y = (x + 1)2 − 4
c) p: y = x2 − 3
d) p: y = (x − 7)2
Karte 11
Lösung:
a) S(3 | 1)
b) S(−1 | − 4)
c) S(0 | −3)
d) S(7 | 0)
Hinweise zu c) und d):
In c) kann man statt y = x2 − 3 auch schreiben:
y = (x − 0)2 − 3.
In d) kann man statt y = (x − 7)2 auch schreiben:
y = (x − 7)2 + 0
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
a) Wie bestimmt man die Koordinaten des
Scheitelpunkts einer Parabel, deren
Gleichung in der Form y = x2 + px + q
angegeben ist ?
b) Berechne die Koordinaten des Scheitelpunkts
folgender Parabeln:
p1: y = x2 + 4x + 7 ; p2: y = x2 − 5x + 3
Karte 12
Lösung:
a)
Man muss die Gleichung y = x2 + px + q mithilfe einer
quadratischen Ergänzung in die Scheitelform
überführen. Erst dann kann man die Koordinaten des
Scheitelpunkts ablesen.
b)
p1: y = x2 + 4x + 7 = (x + 2)2 + 3 ⇒ S(−
−2 | 3)
p2: y = x2 − 5x + 3 = (x − 2,5)2 − 3,25 ⇒ S(2,5 | −3,25)
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
a) Wie geht man vor, um das Schaubild einer
Normalparabel zu zeichnen, wenn deren
Gleichung in der Form y = x2 + px + q
angegeben ist ?
b) Skizziere die Schaubilder der Parabeln
p1: y = x2 + 3x − 2 und p2: y = x2 − 6x − 4.
Karte 13
Lösung:
a)
Zum Zeichnen einer Normalparabel legt man die Parabelschablone am Scheitelpunkt an. Den Scheitelpunkt erhält
man, indem man die Gleichung y = x2 + px + q mithilfe einer
quadratischen Ergänzung in die Scheitelform umwandelt.
b)
P1: y = x2 + 3x − 2 = (x + 1,5)2 − 4,25 ⇒ S(−
−1,5 | − 4,25)
p2: y = x2 − 6x − 4 = (x − 3)2 − 13 ⇒ S(3 | −13)
Die Schaubilder ergeben sich durch Anlegen der Schablone an
die Scheitelpunkte.
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
Wie würdest du vorgehen, um die Schaubilder
folgender Parabelgleichungen zu zeichnen ?
a) p: y = (x − 4)2 − 5
b) p: y = −x2 + 2
c) p: y = −(x + 3)2 + 1
d) p : y =
1 2
x −2
2
Worauf muss man in b), c) und d) jeweils achten ?
Karte 14
Lösung:
Zum Zeichnen der Schaubilder muss man die Parabelschablone am Scheitelpunkt anlegen. Man muss also zuerst
die Koordinaten des Scheitelpunkts bestimmen. In b) und c)
muss man darauf achten, dass die Parabel wegen des
Minuszeichens vor dem quadratischen Term nach unten
geöffnet ist ! In d) kann man die Parabelschablone nicht
benutzen, da vor „x2“ noch ein Faktor steht. In diesem Fall
muss man eine Wertetabelle erstellen. Die Parabel in d) ist
gegenüber der Normalparabel gestaucht.
Die Scheitelpunkte sind:
a) S(4 | −5)
b) S(0 | 2)
c) S(−
−3 | 1)
© Mathematik-Verlag, www.matheverlag.com
d) S(0 | −2)
Kopieren und Ausdrucken verboten!
Algebra:
Geraden und Parabeln
a) Wie berechnet man die Schnittpunkte einer
Geraden bzw. Parabel mit der x-Achse ?
Die Gleichung der Geraden bzw. Parabel sei
bekannt. Beschreibe das allgemeine Vorgehen.
b) Berechne jeweils die Schnittpunkte mit
der x-Achse:
Gerade g: y = 4x + 3
Parabel p: y = x2 − 4x − 5
Karte 15
Lösung:
a) Die Schnittpunkte mit der x-Achse bestimmt man,
indem man in der Gleichung der Parabel bzw. Geraden für
y = 0 setzt und die Gleichung anschließend nach x
umformt. Beachte: Jeder Schnittpunkt mit der x-Achse
hat als y-Koordinate den Wert y = 0.
b)
Bei g: 0 = 3x + 4 ⇔ x = −0,75 ; S(−
−0,75 | 0)
Bei p: 0 = x2 − 4x − 5 ⇒ x1 = 5 und x2 = −1
Hier gibt es zwei Schnittpunkte mit der x-Achse:
S1(5 | 0) und S2(−
−1 | 0)
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln und Geraden
a) Wie berechnet man den Schnittpunkt einer
Geraden bzw. Parabel mit der y-Achse ?
Die Gleichung der Geraden bzw. Parabel sei bekannt.
Beschreibe das allgemeine Vorgehen.
b) Berechne jeweils den Schnittpunkt mit der y-Achse:
g: y = −0,5x − 8 ;
p: y = x2 + 7x − 3,5
Karte 16
Lösung:
a)
Die Schnittpunkte mit der y-Achse bestimmt man, indem
man in der Gleichung der Parabel bzw. Geraden für
x = 0 setzt und den y-Wert berechnet.
Beachte: Jeder Schnittpunkt mit der y-Achse hat als
x-Koordinate den Wert x = 0.
b)
Bei g: y = −0,5 ⋅ 0 − 8 = −8 ⇒ Sy(0 | −8)
Bei p: y = 02 − 4 ⋅ 0 − 5 ⇒ Sy(0 | −5)
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
a) Wie bestimmt man die Gleichung einer nach
oben geöffneten Normalparabel, wenn man die
Koordinaten ihres Scheitelpunkts kennt ?
Beschreibe das allgemeine Verfahren.
b) Was muss man beachten, wenn die
Normalparabel nach unten geöffnet ist ?
Karte 17
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
Wie lautet jeweils die Gleichung einer nach oben
geöffneten Normalparabel mit dem angegebenen
Scheitelpunkt ?
a) S(2 | −1)
b) S(−5 | 7)
c) S(0 | 4)
Gib die Parabelgleichung in der Form
y = x2 + px + q an.
Karte 18
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
Wie lautet jeweils die Gleichung einer nach
unten geöffneten Normalparabel mit dem
angegebenen Scheitelpunkt ?
a) S(−3 | 2)
b) S(4 | −1)
c) S(0 | −2)
Gib die Parabelgleichung in der Form
y = −x2 + px + q an.
Karte 19
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
a) Wie bestimmt man die Gleichung einer nach
oben geöffneten Normalparabel, von der
zwei Punkte A und B bekannt sind ?
Beschreibe das allgemeine Vorgehen.
b) Bestimme die Funktionsgleichung der
Parabel p, die durch die Punkte A(−6| 1) und
B(4 | 6) läuft.
Karte 20
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Geraden und Parabeln
a) Wie bestimmt man die gemeinsamen Punkte
zwischen zwei Parabeln bzw. zwischen einer
Parabel und einer Geraden ?
Beschreibe das allgemeine Vorgehen.
b) Berechne die gemeinsamen Punkte
zwischen den Parabeln p1 und p1:
p1: y = x2 − 2x − 2 und p2: y = −x2 + 6x − 8
Karte 21
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
Der Punkt A(−2 | 7) liegt auf der Parabel p:
y = x2 + 3x + q
a) Was muss man tun, um den Wert für den
Parameter q berechnen zu können ?
b) Bestimme den Wert für q und gib die
Koordinaten des Scheitelpunkts an.
Karte 22
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Parabeln
Eine nach oben geöffneten Normalparabel p1 hat
den Scheitelpunkt S1(4 | 2).
Die Parabel p1 wird um 3 Längeneinheiten nach
rechts und um 5 Längeneinheiten nach unten
verschoben. Man erhält so die Parabel p2.
a) Wie muss man vorgehen, um die Gleichung der
Parabel p2 zu bestimmen ?
b) Führe diese Rechnung durch.
Karte 23
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Abstand zweier Punkte
a) Mit welcher Formel kann man den Abstand
zweier Punkte A(a1 | a2) und B(b1 | b2) berechnen,
wenn deren Koordinaten bekannt sind ?
Versuche, die Formel an einem selbst gewählten
Beispiel herzuleiten.
b) Bestimme den Abstand zwischen den Punkten
A(4| 1) und B(1 | 3).
Karte 24
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Geraden
a) Der Punkt P(−3 | yp) liegt auf der Geraden g:
y=
2
x − 4. Berechne die y-Koordinate von P.
3
b) Der Punkt Q(− 4 | yp) liegt auf der Parabel p:
y = x2 − 3x + 7. Berechne die y-Koordinate von Q.
Karte 25
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Geraden und Parabeln
a) Der Punkt A(xA | 7) liegt auf der Geraden g: y = 3x − 2.
Wie kann man die x-Koordinate von A berechnen ?
b) Der Punkt B(xB|6) liegt auf der Parabel p: y = x2 + 4x + 10
Wie kann man die x-Koordinate von B berechnen ?
Karte 26
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Gleichungssysteme
a) Mit welchem Verfahren lässt sich folgendes
Gleichungssystem besonders einfach lösen ?
Begründe deine Antwort.
3x − 2y = 8
(I)
x + 2y = 4
(II)
b) Berechne mit diesem Verfahren die Lösungsmenge.
Karte 27
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Kegel
a) Wie kann man in einem Kegel eine der Strecken
h, r und s berechnen, wenn man zwei dieser
Strecken kennt ?
b) In einem Kegel ist: r = 5 cm und s = 8 cm.
Berechne die Kegelhöhe h.
c) In einem Kegel ist: h = 7,8 cm und r = 5,2 cm.
Berechne die Mantellinie s.
Karte 28
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Kegel
Von einem Kegel sind bekannt: V = 625 cm3 und r = 7,2 cm
a) Mit welcher Formel kann man aus diesen
Angaben sofort eine weitere Größe des Kegels
berechnen ? Welche Größe ist das ?
b) Tue dies, indem du diese Formel nach der
unbekannten Größe umstellst.
Karte 29
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Kegel
Von einem Kegel sind bekannt:
O = 540 cm2 und r = 9,8 cm.
a) Mit welcher Formel kann man aus diesen
Angaben sofort eine weitere Größe des Kegels
berechnen ?
b) Tue dies, indem du diese Formel nach der
unbekannten Größe umstellst.
Karte 30
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Kegel, Kugel und Zylinder
a) Bekannt sei das Volumen einer Kugel.
Was weiß man dann über einen Kegel, wenn von
einem „volumengleichen Kegel“ die Rede ist ?
b) Was bedeutet es, wenn ein Kegel und ein
Zylinder dieselbe Grundfläche haben ?
Karte 31
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Kugel
a) Welche Größe einer Kugel kann man berechnen,
wenn das Kugelvolumen bekannt ist ?
Stelle die entsprechende Formel nach dieser
Größe um.
b) Berechne die unbekannte Größe aus a) mit
dem Kugelvolumen V = 750 cm3.
Karte 32
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Kugel
a) Welche Größe einer Kugel kann man berechnen,
wenn die Kugeloberfläche O bekannt ist ?
Stelle die entsprechende Formel nach dieser
Größe um.
b) Berechne die unbekannte Größe aus a) mit
der Kugeloberfläche O = 485 cm2.
Karte 33
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Zylinder
a) Welche Größe eines Zylinders kann man
berechnen, wenn das Zylindervolumen und die
Zylinderhöhe bekannt sind ?
Stelle die entsprechende Formel nach dieser
Größe um.
b) Berechne die unbekannte Größe aus a) mit
dem Zylindervolumen V = 341 cm3 und der
Zylinderhöhe h = 15 cm.
Karte 34
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Kegel
a) Ein massiver Kegel wird durch einen Schnitt
entlang der Höhe halbiert. Aus welchen
Teilflächen besteht die Oberfläche einer der
Kegelhälften.
b) Berechne die in a) erwähnte Oberfläche,
wenn der Kegel den Radius r = 6,8 cm und die
Höhe h = 12,5 cm hat.
Karte 35
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramide
Für Berechnungen an quadratischen Pyramiden sind
drei rechtwinklige Dreiecke von Bedeutung. Zeichne
diese in die folgenden Figuren ein. Achte auf die
richtige Beschriftung der Dreiecksseiten.
.
Karte 36
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramide
a) Mit welcher Formel kann man die
Grundflächendiagonale d einer quadratischen
Pyramide und die Grundkante a ineinander
umrechnen ?
b) Berechne aus a = 9,6 cm die Diagonale d.
Berechne aus d = 7 cm die Grundkante a.
Karte 37
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
Die Abbildung zeigt eine quadratische Pyramide.
Wie lautet der Satz des Pythagoras in dem markierten
Dreieck ? Trage den rechten Winkel ein. Benutze für die
Seiten des Dreiecks die richtigen Bezeichnungen.
Karte 38
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
Die Abbildung zeigt eine quadratische Pyramide.
Wie lautet der Satz des Pythagoras in dem markierten
Dreieck ? Trage den rechten Winkel ein. Benutze für
die Seiten des Dreiecks die richtigen Bezeichnungen.
Karte 39
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
Die Abbildung zeigt eine quadratische Pyramide.
Wie lautet der Satz des Pythagoras in dem
markierten Dreieck ? Trage den rechten Winkel ein.
Benutze für die Seiten des Dreiecks die richtigen
Bezeichnungen.
Karte 40
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
Markiere den Neigungswinkel α einer Seitenfläche
gegen die Grundfläche der quadratischen Pyramide.
In welchem rechtwinkligen Dreieck kommt der
Neigungswinkel α vor ?
Karte 41
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
a) Aus welchen Teilflächen setzt sich die
Oberfläche einer quadratischen Pyramide
zusammen ?
b) Berechne die Oberfläche einer quadratischen
Pyramide mit a = 5 cm und hs = 8,4 cm.
c) Wie kann man mit den Angaben aus b) das
Volumen der Pyramide berechnen ?
Karte 42
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
a) Wie kann man aus der Grundkante a und der
Seitenkante s die Höhe h einer quadratischen
Pyramide berechnen ?
b) Berechne die Höhe h mit a = 7,3 cm und s = 12,5 cm.
h
Karte 43
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
a) Wie kann man aus der Höhe hs einer Seitenfläche
und der Pyramidenhöhe h die Grundkante a einer
quadratischen Pyramide berechnen ?
b) Berechne a mit hs = 6,8 cm und h = 5,4 cm
a
Karte 44
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
a) Wie kann man aus der Höhe hs einer Seitenfläche
und der Seitenkante s die Grundkante a einer
quadratischen Pyramide berechnen ?
b) Berechne die Höhe hs mit hs = 4,9 cm und s = 7,2 cm
a
Karte 45
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
Markiere den Neigungswinkel α einer Seitenkante
gegen die Grundfläche der quadratischen Pyramide.
In welchem rechtwinkligen Dreieck kommt der
Neigungswinkel α vor ?
.
Karte 46
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
a) Die Abbildung zeigt eine regelmäßige fünfseitige
Pyramide. Trage die Streckenbezeichnungen a,
h, hs und s in die Abbildung ein.
b) Wie nennt man diese Strecken ?
Karte 47
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
Für Berechnungen an regelmäßigen fünfseitigen
Pyramiden sind drei rechtwinklige Dreiecke von
Bedeutung. Zeichne diese in die folgenden Figuren
ein.
.
Karte 48
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
a) Die Abbildung zeigt ein gleichschenkliges
Dreieck. Trage die Höhe zur Basis a ein.
b) Was sind die Besonderheiten eines
gleichschenkligen Dreiecks ?
γ
b
α
b
a
β
Karte 49
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
a) Die Grundfläche einer regelmäßigen fünfseitigen
Pyramide besteht aus fünf gleichschenkligen
Dreiecken. Wie groß sind die Innenwinkel eines
dieser Dreiecke ? Fertige eine Skizze an.
b) Berechne in diesem Dreieck die Höhe h1
bezüglich der Grundseite a und die Länge b eines
Schenkels, wenn die Grundkante der Pyramide
a = 6,5 cm beträgt.
Karte 50
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
Die Grundfläche jeder regelmäßigen mehrseitigen
Pyramide besteht aus mehreren gleichschenkligen
Dreiecken. Berechne die Innenwinkel eines dieser
Dreiecke für
a) eine sechsseitige Pyramide,
b) eine achtseitige Pyramide,
c) eine neunseitige Pyramide.
Fertige jeweils eine Skizze eines der gleichschenkligen Dreiecke an.
Karte 51
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
a) Wie muss man vorgehen, um aus der
Grundkante a einer regelmäßigen mehrseitigen
Pyramide den Inhalt der Grundfläche G der
Pyramide zu berechnen ?
b) Die Grundkante a einer regelmäßigen neunseitigen
Pyramide ist a = 9,8 cm. Berechne daraus den
Inhalt der Grundfläche der Pyramide.
Karte 52
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Stereometrie:
Pyramiden
a) Aus welchen Teilflächen setzt sich der Mantel
einer regelmäßigen fünfseitigen Pyramide
zusammen ? Stelle eine Formel für die
Mantelfläche M auf.
b) Wie lautet die Formel der Mantelfläche M bei
einer regelmäßigen sechsseitigen (acht-, neunseitigen) Pyramide ?
Karte 53
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
a) Woran erkennt man in einem rechtwinkligen
Dreieck die Hypotenuse ?
b) Wovon hängt es ab, welche Seite in einem
rechtwinkligen Dreieck die Ankathete und
welche die Gegenkathete ist ?
Karte 54
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
Trage die Begriffe Ankathete, Gegenkathete und
Hypotenuse an der richtigen Stelle ein:
sin α =
cos α =
tan α =
.
Karte 55
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
a) Wie kann man in einem rechtwinkligen Dreieck
einen fehlenden Innenwinkel berechnen, wenn
man außer dem rechten Winkel noch einen
weiteren Innenwinkel kennt ?
b) Berechne in folgendem Dreieck den Winkel β:
.
35°
β
Karte 56
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
a) Mit welcher Formel kann man in jedem
Vieleck die Summe der Innenwinkel berechnen ?
b) Berechne den fehlenden Winkel β:
D
110°
.
A
54°
β
C
B
Karte 57
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
Berechne alle fehlenden Seiten und Winkel:
a)
b)
δ
25°
11
,4
α
cm
a
b
x
8,5 cm
γ
4,7 cm
Karte 58
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
a) Welche Hilfslinie sollte man zu Berechnungen in
gleichschenkligen Dreiecken immer einzeichnen ?
b) Berechne die fehlenden Winkel und die Strecke a:
cm
5,8
5,8
cm
γ
β
65°
a
Karte 59
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
a) Welche Hilfslinien sollte man zu Berechnungen in
Trapezen immer einzeichnen ?
b) Berechne die Strecke c:
cm
5,2
52°
70°
cm
6,4
c
10,7 cm
Karte 60
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
Wie viele rechtwinklige Dreiecke erkennst du in der
Figur ? Welche sind das ?
C
.
w
.
A
D
B
Karte 61
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
a) Wie kann man sehr leicht den Flächeninhalt eines
rechtwinkligen Dreiecks berechnen, wenn alle
Seiten bekannt sind ?
b) Das abgebildete Dreieck hat den Flächeninhalt
A = 14,25 cm2. Berechne die Länge der
fehlenden Seiten.
3,8
.
cm
b
c
Karte 62
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
Drücke die fehlenden Seiten des Dreiecks in
Abhängigkeit von e aus, ohne gerundete Werte zu
benutzen.
a)
b)
.
e
x
.
a
b
30°
y
45°
4e
Karte 63
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
Drücke die Länge der Strecke x in Abhängigkeit von e
aus, ohne gerundete Werte zu benutzen.
e 5
e
2
2
x
Karte 64
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Gleichungssysteme
a) Mit welchem Verfahren lässt sich folgendes
Gleichungssystem besonders einfach lösen ?
Begründe deine Antwort.
y = 2x − 5
(I)
3x + 4y = 13
(II)
b) Berechne mit diesem Verfahren die Lösungsmenge.
Karte 65
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
Für Berechnungen in rechtwinkligen Dreiecken mit
einer Formvariablen (e oder a) müssen oft Wurzelterme
umgeformt werden. Vereinfache folgende Terme und
mache im Ergebnis den Nenner rational, falls nötig.
a)
25e
2
b)
12e
2
2
c)
e 6
2
⋅
e 3
3
Karte 66
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Trigonometrie:
a) Gib in folgendem Dreieck die Seiten x und y
in Abhängigkeit von e an.
x
y
.
30°
5e
b) Bestimme außerdem den Flächeninhalt des
Dreiecks in Abhängigkeit von e.
Karte 67
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Algebra:
Gleichungssysteme
a) Mit welchem Verfahren lässt sich folgendes
Gleichungssystem besonders einfach lösen ?
Begründe deine Antwort.
y=x+5
(I)
y = 5x + 9
(II)
b) Berechne mit diesem Verfahren die Lösungsmenge.
Karte 68
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
erhöhter Grundwert
1. Was versteht man unter einem Zinsfaktor q ?
2. Wie kann man einen Zinsfaktor q sehr leicht in
den entsprechenden Zinssatz p % umwandeln ?
Tue dies mit folgenden Zinsfaktoren:
a) q = 1,05 ; p % =
b) q = 1,075 ; p % =
c) q = 1,0325 ; p % =
d) q = 1,16 ; p % =
.
.
Karte 69
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Zinsrechnung
1. Wie kann man einen Zinssatz p % in den
entsprechenden Zinsfaktor q umwandeln ?
2. Gib jeweils den Zinsfaktor q an:
a) p % = 6 % ; q =
b) p % = 4,5 % ; q =
c) p % = 2,25 % ; q =
d) p % = 12,7 % ; q =
Karte 70
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Zinsrechnung
a) Wie berechnet man die Zinsen, wenn man das
Start- und das Endkapital kennt ?
b) Wie kann man sehr schnell den Zinssatz für ein
Jahr berechnen, wenn man das Startkapital und
das Kapital am Ende dieses Jahres kennt ?
c) Ein Kapital von 1750 € ist nach einem Jahr auf
1820 € angewachsen. Wie viel Zinsen gab es in
diesem Jahr und wie hoch war der Zinssatz ?
Karte 71
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Zins und Zinseszins
a) Mit welcher Formel berechnet man das Endkapital Kn,
wenn ein Guthaben K0 mit konstantem Zinssatz über
mehrere Jahre verzinst wird ? Zinsen werden mitverzinst.
b) Ein Guthaben von 7500 € wird über 4 Jahre zu
einem festen Zinssatz von p % = 4,5 % verzinst.
Zinsen werden mitverzinst. Auf welchen Betrag ist
es nach 4 Jahren angewachsen ?
c) Stelle folgende Gleichung nach q um:
5200 = 3500 ⋅ q5
Karte 72
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Zins und Zinseszins
Ein Guthaben wird über mehrere Jahre zu verschiedenen Zinssätzen angelegt. Die Zinsen werden
mitverzinst.
a) Wie kann man sich die Entwicklung des Guthabens in
einer Tabelle veranschaulichen ? Erstelle eine solche
allgemeine Tabelle für 3 Jahre ohne Zahlenwerte.
b) Mit welcher Formel kann man aus einem
Startkapital K0 und den bekannten Zinssätzen das
Endkapital Kn berechnen ?
Karte 73
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Zins und Zinseszins
Mit der folgenden Tabelle soll die Entwicklung des
Startkapitals von 1500 € veranschaulicht werden.
Zinsen werden mitverzinst. Ergänze die Lücken.
Nach welchen Regeln muss man dabei vorgehen ?
Jahre
1.
Kapital am
Jahresanfang
1500 €
Zinsfaktor q
Kapital am
Jahresende
Zinsen
1,0375
2.
1,045
3.
1,0525
.
Karte 74
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Zins und Zinseszins
Ergänze in folgender Tabelle die Lücken und berechne
den Wert für x.
Jahre
1.
2.
3.
Kapital am
Jahresanfang
x
Zinsfaktor q
Kapital am
Jahresende
Zinsen
1,035
1,04
1,0425
2805,37 €
Karte 75
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Ratensparen
a) Wie funktioniert das jährliche Ratensparen ?
b) Wie kann man beim jährlichen Ratensparen die
Entwicklung eines Kapitals in einer Tabelle
veranschaulichen ?
Wie sieht eine solche Tabelle (ohne Zahlenwerte)
beim Ratensparen für 3 Jahre aus ?
c) Worauf muss man achten, wenn man beim
Ratensparen das jeweilige Kapital am Jahresanfang berechnen will ?
Karte 76
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Ratensparen
Herr Müller hat einen Ratensparvertrag mit einer
jährlichen Rate von 800 € abgeschlossen. Zinsen
werden mitverzinst. Ergänze die Lücken.
Jahre
Rate
Kapital am
Jahresanfang
Zinsfaktor q
1.
800 €
1,035
2.
800 €
1,04
3.
800 €
1,05
Kapital am
Jahresende
Zinsen
Karte 77
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
erhöhter und verringerter Grundwert
a) Wie lauten die beiden Formeln zur Berechnung
des erhöhten bzw. verringerten Grundwerts ?
Was bedeuten darin die Variablen ?
b) Wie kann man bei einer Textaufgabe sehr leicht
den „normalen“ Grundwert vom erhöhten bzw.
verringerten Grundwert unterscheiden ?
Karte 78
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
erhöhter Grundwert
1. Wie kann man einen Prozentsatz p % in den
entsprechenden Änderungsfaktor q+ umwandeln,
wenn der Grundwert um eben diesen Prozentsatz
erhöht wird ?
2. Gib für eine Erhöhung des Grundwerts die
entsprechenden Änderungsfaktoren an:
a) p % = 4 % ; q+ =
b) p % = 15 % ; q+ =
c) p % = 3,75 % ; q+ =
d) p % = 10,2 % ; q+ =
.
.
Karte 79
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
verringerter Grundwert
1. Wie kann man einen Prozentsatz p % in den
entsprechenden Änderungsfaktor q− umwandeln,
wenn der Grundwert um eben diesen Prozentsatz
verringert wird ?
2. Gib für eine Verringerung des Grundwerts
die entsprechenden Änderungsfaktoren an:
a) p % = 7 % ; q− =
b) p % = 12 % ; q− =
c) p % = 4,25 % ; q− =
d) p % = 15,5 % ; q− =
.
.
Karte 80
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
erhöhter und verringerter Grundwert
Wie kann man einen Veränderungsfaktor q sehr leicht
in den entsprechenden Prozentsatz p % umwandeln ?
Tue dies mit folgenden Veränderungsfaktoren:
a) q = 1,07 ; p % =
b) q = 1,045 ; p % =
c) q = 0,97 ; p % =
d) q = 0,875 ; p % =
.
.
Karte 81
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
erhöhter und verringerter Grundwert
a) Was versteht man unter den Begriffen „Rabatt“
und „Skonto“ ?
b) Ein Elektronik-Händler gewährt 15 % Rabatt auf
einen Taschenrechner, wenn ein Kunde
mindestens 30 Taschenrechner bestellt. Der Preis
ohne Rabatt beträgt 12,95 €. Außerdem erhält der
Kunde 2 % Skonto bei Barzahlung.
Wie viel muss ein Kunde für einen Taschenrechner
bezahlen, wenn er 40 Taschenrechner bestellt und
die Ware sofort bezahlt ?
Karte 82
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
erhöhter und verringerter Grundwert
a) Was versteht man unter den Begriffen
„Nettopreis“ und „Mehrwertsteuer“ ?
b) Welcher Wert ist bei „Mehrwertsteuer-Aufgaben“
immer der Grundwert, und welcher ist immer der
erhöhte Grundwert ?
c) In Deutschland liegt der derzeitige Mehrwertsteuersatz bei p % = 19 %. Wie groß ist der
entsprechende Änderungsfaktor q ?
Karte 83
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
erhöhter und verringerter Grundwert
a) Ein Paar Turnschuhe kostet in Deutschland
inklusive Mehrwertsteuer 45 €. Wie viel Euro
Mehrwertsteuer sind darin enthalten ?
Der Mehrwertsteuersatz in Deutschland beträgt
zurzeit 19 %.
b) Wie viel würden dieselben Turnschuhe in
Luxemburg (Mehrwertsteuersatz = 15 %) kosten,
wenn der Nettopreis der gleiche wäre ?
Karte 84
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Prozentrechnung
a) Mit welcher einfachen Formel berechnet man
Fragestellungen der Art „p % von G“ ?
Berechne 35 % von 780 kWh (Kilowattstunden).
b) Mit welcher einfachen Formel berechnet man
Fragestellungen der Art „W von G“ ?
Wie viel Prozent sind 28 Schüler von 448 Schülern ?
c) Wie berechnet man den Grundwert G, wenn man den
Prozentwert W und den Prozentsatz p % kennt ?
Tue dies mit p % = 4,5 % und W = 54 kg.
Karte 85
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Sachrechnen:
Prozentrechnung
a) Was ist bei Wahlen der Unterschied zwischen
Wahlberechtigung und Wahlbeteiligung ?
b) Was sind bei Wahlen der Grundwert und der
Prozentwert, wenn man die prozentualen
Stimmenanteile berechnen will ?
c) Bei einer Gemeindratswahl hat die Partei „Die
Bunten“ 25,6 % Stimmenanteile erhalten. Insgesamt
waren 28570 Bürger/innen wahlberechtigt. Die
Wahlbeteiligung lag aber nur bei 58 %. Wie viele
Stimmen haben „Die Bunten“ erhalten ?
Karte 86
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
a) Bei einem Würfelexperiment sind nach 10 Würfen
folgende Augenzahlen gefallen:
2;5;6;4;5;4;3;4;1;2
Erläutere anhand dieser Datenreihe die Begriffe
Merkmalswert, absolute Häufigkeit und relative
Häufigkeit.
b) Gib für die obige Datenreihe die absolute und
die relative Häufigkeit der Augenzahl 4 an.
Karte 87
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
a) Wie kann man eine relative Häufigkeit in Prozent
umrechnen ? Tue dies mit r =
3
.
4
b) Wie wandelt man eine Prozentangabe in einen
Bruch um ? Tue dies mit p % = 40 %.
c) Welche besondere Eigenschaft hat die Summe aller
relativer Häufigkeiten einer Datenreihe ?
Karte 88
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
a) Mit welchem Begriff kann man den Durchschnitt
einer Datenreihe noch bezeichnen ?
b) Wie kann man den Durchschnitt einer Datenreihe
berechnen ?
c) Ein Schüler hat im Laufe eines Schuljahrs folgende
Noten in Mathematik geschrieben:
2,3 | 3,3 | 2,7 | 2,1
Berechne seinen Notendurchschnitt.
Karte 89
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
a) Mit welcher Formel kann man den Durchschnitt
einer Datenreihe berechnen, wenn man von allen
Merkmalswerten xi die relativen Häufigkeiten ri
kennt ?
b) Berechne anhand der Häufigkeitstabelle den
Notendurchschnitt einer Klassenarbeit.
Note
relative
Häufigkeit:
1
2
3
4
5
6
0,12 0,18 0,15 0,20 0,18 0,17
Karte 90
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
a) Mit welchem Begriff kann man den Zentralwert
einer Datenreihe noch bezeichnen ?
b) Wie bestimmt man den Zentralwert einer
Datenreihe ?
c) Bei einem Würfelexperiment sind nach 10 Würfen
folgende Augenzahlen gefallen:
4;3;5;2;4;2;6;1;5;1
Bestimme den Zentralwert.
Karte 91
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
a) Mit welcher Formel berechnet man bei einem
Laplace-Experiment die Wahrscheinlichkeit
eines bestimmten Ereignisses ?
b) Gib die Wahrscheinlichkeit an, mit der beim
Würfeln eine Augenzahl größer als 4 erscheint.
Karte 92
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
Aus der abgebildeten Urne wird eine Kugel gezogen.
Berechne die Wahrscheinlichkeit für folgende Ereignisse.
A: Es wird eine weiße Kugel gezogen.
B: Es wird eine Nummer größer
als 1 gezogen.
C: Es wird eine graue Kugel mit
gerader Nummer gezogen.
5
1
2
3
4
Karte 93
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
Eine Münze wird zweimal hintereinander geworfen.
a) Veranschauliche dieses Zufallsexperiment in
einem Baumdiagramm. Achte auf die korrekte
Beschriftung der Äste und Knoten.
b) Nach welcher Regel werden die Wahrscheinlichkeiten der jeweiligen Ereignisse berechnet ?
Karte 94
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
Ein idealer Spielwürfel wird zweimal hintereinander
geworfen. Die Abbildung zeigt einen Ausschnitt des
entsprechenden Baumdiagramms. Ergänze die Lücken und
berechne jeweils die Wahrscheinlichkeit des Ereignisses am
Ende der Äste.
5
(
;
) p=
=
(
;
) p=
=
1
4
...
Karte 95
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!
Daten erfassen und Wahrscheinlichkeit:
a) Was ist beim Würfeln das Gegenereignis zu A:
„Die geworfene Augenzahl ist kleiner als 3“ ?
b) Wie kann man aus der Wahrscheinlichkeit eines
Ereignisses die Wahrscheinlichkeit des Gegenereignisses berechnen ?
c) Gib die Wahrscheinlichkeiten für das oben
erwähnte Ereignis A und das Gegenereignis A* an.
Karte 96
© Mathematik-Verlag, www.matheverlag.com
Kopieren und Ausdrucken verboten!