Universität Bayreuth - Didaktik der Physik!

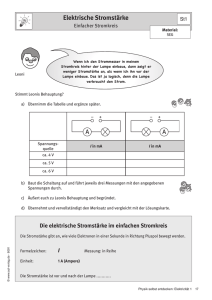
Universität Bayreuth
Physik Didaktik
Angewandte Fachdidaktik II
WS 05/06
Leitung: Dr. S. Weber
Referent: Alexander Thurn
31.10.2005
Alltagsvorstellungen und Präkonzepte
Schülerinnen und Schüler kommen nicht als unbeschriebene Blätter in den Unterrricht,
sondern sie bringen Vorkenntnisse, Assoziationen und Vorstellungen mit. Man spricht in der
Didaktik von Alltagsvorstellungen oder Präkonzepten.
1. Erläutern Sie an drei Beispielen von Präkonzepten, die typische Fehlvorstellungen
darstellen und nicht alle aus dem selben Bereich der Physik stammen sollen, warum
Alltagsvorstellungen im Unterricht bzw. bei der Unterrichtsvorbereitung
berücksichtigt werden müssen! Führen Sie dabei aus, worin jeweils die
Fehlvorstellung besteht!
Da alle Schülerinnen und Schüler bereits vor dem Fachunterricht in Physik individuelle
Vorerfahrungen und ein breit gestreutes aber meist aus physikalischer Sicht unvollständiges
Vorwissen über naturwissenschaftliche Sachverhalte oder Phänomene besitzen, muss die
Lehrkraft versuchen, diese Alltagsvorstellungen festzustellen, zu berücksichtigen und ihnen
durch seinen Unterricht gegebenenfalls entgegenwirken. Geschieht dies nicht in geeigneter
Weise, so entwickelt der Schüler daraus Misskonzepte oder Fehlvorstellungen, die
unreflektiert auf andere Sachverhalte übertragen werden können.
Anhand der drei folgenden Beispiele soll erläutert werden, wie man Präkonzepte die
Fehlvorstellungen darstellen, im Unterricht und bei der Unterrichtsvorbereitung
berücksichtigen muss.
Präkonzepte aus der Optik:
Fehlvorstellungen aus dem Bereich der Optik bestehen zum Beispiel darin, wie bzw. wieso
man etwas sehen kann, dabei können je nach Alter der Schülerinnen und Schüler verschiedene
Beobachtungen gemacht werden:
•
Bei der Gruppe der 10 – 11-jährigen ist die Vorstellung vom Lichtbad vorherrschend. Wird
ein Gegenstand gesehen, so machen sich Schüler dieses Alters keine Gedanken von woher
das Licht kommt. Licht ist - sofern man etwas sieht – überall, wodurch auch das Problem
der Schattenvorstellung auftritt. Die physikalische Ursache für diese Vorstellung liegt an
der Reflexion und Streuung des Sonnenlichts an allen Gegenständen der Umgebung.
Abb1: vorherrschende Fehlvorstellung bei 10 – 11- jährigen
Aus: „Fachdidaktik I (Version 4.0)“, Dr. S. Weber, S22
Bei dieser Fehlvorstellung muss die Lehrkraft zunächst darauf eingehen, dass es
eine Lichtquelle gibt, von der Strahlen ausgehen, die auf dem Objekt auftreffen
müssen um es erscheinen zu lassen. Darauf aufbauend muss erklärt werden, dass
die Strahlen der Lichtquelle vom Objekt reflektiert werden müssen, um zum
menschlichen Auge zu gelangen.
•
Bei 13 – 14-jährigen ist die Vorstellung einer Lichtquelle zwar vorhanden, ein Objekt kann
also gesehen werden, wenn es sich in der Umgebung einer Lichtquelle befindet. Die
Lichtquelle muss um das Objekt herum Licht erzeugen.
Abb 2: bei 13 – 14- jährigen auftretende Fehlvorstellung
Aus: „Fachdidaktik I (Version 4.0)“, Dr. S. Weber, S22
Hier muss darauf eingegangen werden, dass die Strahlen von der Lichtquelle auf
dem Objekt auftreffen und aber auch von diesem reflektiert werden müssen um
vom menschlichen Auge wahrgenommen zu werden.
•
Physikalisch richtig wird der Sehvorgang so beschrieben, dass ein Objekt nur dann sichtbar
ist, wenn das Licht von einer Lichtquelle auf ein Objekt trifft und von diesem mit
genügend Intensität ins Auge reflektiert wird.
Abb 3: physikalisch richtige Vorstellung
Aus: „Fachdidaktik I (Version 4.0)“, Dr. S. Weber, S22
Präkonzept zum Begriff der Energie
Viele Schüler sind der Ansicht, dass Energie ein Industrieprodukt ist, das erzeugt werden
kann, oder das Energie Treibstoff ist. Ist der Tank des Autos leer, so wurde die gesamte
Energie verbraucht, wohin sich diese verbrauchte Energie begibt, interessiert die Schüler
nicht. Die Fehlvorstellung ist also, dass Energie in der Sicht des Schülers nicht von einer
Energieform in die andere umgewandelt wird, sondern dass die Energie verbraucht wird.
Um diese Fehlvorstellung zu identifizieren, muss der Lehrer den Schülern geeignete Fragen
stellen. Die Antworten auf diese Fragen geben Auskunft darüber, welche (Fehl)vorstellungen
bei den Schülern vorhanden sind. Der Energieerhaltungssatz als richtiger physikalischer
Zusammenhang muss dabei durch einfache, deutliche Beispiele gefestigt werden, wobei
immer mit mechanischen Energieformen begonnen werden sollte, da hier Vorerfahrungen
existieren
z.B.: Ein Skifahrer, der den Berg herunter fährt und unten eine bestimmte Endgeschwindigkeit
besitzt, hat die Höhenenergie in kinetische Energie umgewandelt (wobei anfangs Luftreibung
und Reibungswiderstand zur Verdeutlichung keine Rolle spielen).
Präkonzept zur geradlinigen Bewegung
Ein Körper bewegt sich mit konstanter Geschwindigkeit auf einer Geraden, wobei er
drei Kräften ausgesetzt ist. In folgender Zeichnung sind nur zwei dieser drei Kräfte
eingezeichnet, die Schüler sollen die Zeichnung mit der dritten Kraft vervollständigen.
Abb 4: geradlinige Bewegung
Aus: http://didaktik.phy.uni-bayreuth.de/cgi-bin/testfragen_kraft.pl
Fehlvorstellungen zu diesem Problem sind:
•
Die Summe der beiden Kräfte hat bereits die Richtung der Bewegung, somit muss die
fehlende Kraft dieselbe Richtung haben.
Abb 5: Fehlvorstellung der Schüler, Kraft in Bewegungsrichtung
•
Existiert keine resultierende Kraft, die in Richtung der Bewegung zeigt, so muss der
Körper in Ruhe sein.
•
Die fehlende Kraft muss entgegen der Resultierenden der beiden anderen Kräfte zeigen,
jedoch aber kleiner sein als diese, damit sich der Körper fortbewegt.
Abb 6: Fehlvorstellung der Schüler, Kraft entgegen der Bewegungsr.
Physikalisch richtig ist, dass sich die Kräfte bei einer geradlinigen, konstanten Bewegung
gegenseitig aufheben (Trägheitssatz). Die Lehrkraft muss, nachdem die Präkonzepte der
Schüler aufgedeckt worden sind, durch geeignete Beispiele zeigen, dass sich die Kräfte die an
einem Körper angreifen, der sich mit einer konstanten Geschwindigkeit auf einer Geraden
bewegt gegenseitig aufheben. Hierbei können geeignete Gedankenexperimente die
Problematik des Trägheitssatzes bewusst machen.
Abb 7: Physikalisch richtige Vorstellung
2. Skizzieren Sie eine Unterrichtsstunde aus der Elektrizitätslehre, in der deutlich wird,
wie der Lehrer versucht, eine Fehlvorstellung in eine physikalisch richtige Erkenntnis
umzuwandeln! Nennen Sie Feinlernziele! Gehen Sie ausführlich auf die Einstiegsphase der Unterrichtsstunde ein.
In der folgenden Unterrichtseinheit soll die Fehlvorstellung des Stromverbrauchs bei Schülern
aufgegriffen werden.
Grobziel:
Grobziel dieses Unterrichts ist, den Schülern verständlich zu machen, dass der Strom eine
Erhaltungsgröße ist, d.h. wenn er durch einen Stromkreis mit mehreren Verbrauchern fließt,
nicht an jedem Verbraucher weniger wird.
Lernvorraussetzungen:
Die Schüler sollen:
• einen einfachen Stromkreis beschreiben und erklären können.
• den Begriff Spannung U kennen.
• den Begriff des Stromes I kennen.
• die Knotenregel bei einfachen Schaltungen kennen.
• einfache Reihen- und Parallelschaltungen von Verbrauchern kennen.
Feinlernziele:
FZ1: Kenntnis eines Modells zur Erklärung der Knotenregel für den Fall identischer
Verbraucher mit Hilfe des Wassermodells.
FZ2: An Experimenten überprüfen, dass die Stromstärke bei einer Reihenschaltung
von Verbrauchern überall im Stromkreis gleich ist.
FZ3: Fähigkeit die Stromstärken bei verschiedenen, kombinierten Parallel- und
Reihenschaltungen voraussagen zu können.
Um die Schüler zu motivieren, wird zu Beginn der Stunde ein Versuchsaufbau eines
Stromkreises mit einer Glühlampe gezeigt. Danach wird in den Stromkreis eine weitere
gleiche Glühlampe in Reihe geschaltet. Die Lampen leuchten dunkler. Die Schüler sollen
Gründe für dieses Verhalten nennen.
Die Antworten werden an der Tafel notiert und diskutiert.
Die Schüler werden gebeten, eine elektrische Schaltung an die Tafel zu zeichnen, die dem
aufgebauten Versuch entspricht. Der Schüler, der die Schaltung an der Tafel skizziert, darf die
anderen um Hilfe bitten, notfalls leistet der Lehrer Hilfestellung.
Nachdem die Skizze an der Tafel komplett ist, sollen die Schüler sie in das Heft übertragen.
Um einen genaueren Überblick über Fehlvorstellungen der Schüler zum Thema Stromverbrauch zu haben, wird ein Fragebogen ausgeteilt, wodurch sich die Schüler ihrer eigenen
Ideen bewusst werden sollen. Die Lehrkraft erkennt dabei die jeweiligen Fehlvorstellungen
der Schüler.
Der Fragebogen sieht folgendermaßen aus:
Aufgabe 1:
Die Birnchen im folgenden Stromkreis sind alle gleich.
Ergänze die Stromstärken in den Verzweigungen!
I1
I = 1,2 A
I1=...A
I2=...A
I3=...A
I2
I3
Abb 8: Skizze zur Parallelschaltung
Aus: „Fachdidaktik I (Version 4.0)“,
Dr. S. Weber, S20
Aufgabe 2:
Die Stromstärke im folgenden Stromkreis beträgt 0,4A.
Nun wird zuerst der Widerstand R1 und anschließend der Widerstand R2 geändert.
Batterie und Birnchen bleiben.
I=0,4A
R1=10 Ω
R2=10Ω
Abb 9: Skizze zur Reihenschaltung
Aus: „Fachdidaktik I (Version 4.0)“,
Dr. S. Weber, S21
1. Der Widerstand R1 wird durch den Widerstand R3 =20Ω ersetzt.
a) Die Stromstärke im Birnchen ist nun kleiner
b) Die Stromstärke ist genauso groß wie vorher
c) Die Stromstärke ist jetzt größer als 0,4 A
2. Der Widerstand R1 wird wieder eingesetzt.
Dann wird der Widerstand R2 durch den Widerstand R3 = 20Ω ersetzt.
a) Die Stromstärke im Lämpchen ist nun kleiner als 0,4 A
b) Die Stromstärke ist genauso groß wie vorher
c) Die Stromstärke ist größer als 0,4 A
Durch diese beiden Aufgaben wurde herausgefunden: Manche Schüler gehen davon aus, dass
der Strom grundsätzlich an jedem Verbraucher weniger wird.
Das Verhalten des Stromes bei der Parallelschaltung wird durch ein Analogmodell erklärt. Ein
Behälter, der drei Löcher in der Seitenwand hat, wird mit Wasser befüllt. An die Öffnungen
sind Schläuche mit gleichen Durchmesser angeschlossen. Das Wasser läuft durch diese
Leitungen in einen zweiten Behälter der wiederum einen Überlauf hat welcher in einen dritten
Behälter führt von dem das Wasser wieder zurückgepumpt wird. Dieses Modell stellt eine
Parallelschaltung von drei gleich großen Widerständen dar. Es fließt durch jeden Schlauch
(Leitung) die gleiche Menge an Wasser. Übertragen auf den Stromkreis lässt sich somit leicht
erklären, dass der Strom in einer Parallelschaltung mit gleichen Verbrauchern gleich groß ist.
-> FZ1 erreicht!
Skizze zum Analogmodell:
Flussrichtung des Wassers
Abb 10: Analogmodell zur Verdeutlichung einer Parallelschaltung
Um den Schülern die Reihenschaltung zu erklären, wird ein Versuchsaufbau benutzt. Es
werden zwei gleiche Widerstände R1 und R2 in Reihe geschalten. In den Stromkreis werden
jeweils nach den Widerständen zwei Strommessgeräte eingesetzt, um den Strom A1 und A2,
der in der Sichtweise der Schüler, nach jedem Verbraucher weniger wird, zu messen. Es
werden zwei Messungen mit gleichen und verschiedenen Widerständen durchgeführt, damit
die Schüler sehen, dass der Strom im Falle einer Reihenschaltung immer konstant ist.
Skizze zur Reihenschaltung:
-> FZ2 erreicht!
Um diese Feststellungen bei den Schülern zu festigen, wird ein Arbeitsblatt mit verschiedenen
Schaltungen ausgeteilt:
Abb. 11: Skizze zur Parallelschaltung mit Strommessgeräten
Aus: „Fachdidaktik I (Version 4.0)“, Dr. S. Weber, S26
In dieser Schaltung sind die Widerstände R1 und R2 parallel geschaltet. Die Stromstärken Ig, I1
und I2 werden durch die eingezeichneten Strommessgeräte gemessen. Zunächst sollen die
Schüler erklären welchen Ausschlag die Strommessgeräte ohne den angeschlossenen
Widerstand R3 haben. Dann wird der Widerstand R3 dazugeschaltet.
Wie verändern die Strommessgeräte ihren Ausschlag?
-> FZ3 erreicht!
Zweite Schaltung auf dem Arbeitsblatt:
Abb 12: Skizze einer kombinierten Reihen- und Parallelschaltung
Als Lernzielkontrolle wird eine kombinierte Schaltung aus parallel und in Reihe geschaltenen
Widerständen an die Wand projiziert. Die Schüler sollen nun beschreiben, wie sich die
Strommessgeräte verhalten, wenn man die verschiedenen Widerstände ändert. Die Antworten
werden an der Tafel mitprotokolliert und anschließend diskutiert.
3. Ein elektrisches Gerät wird über ein längeres Kabel an einem Generator
angeschlossen. (Das Gerät besitzt die Anschlussleistung von 1000W.) Erläutern sie
qualitativ, wodurch Verluste bei der Energieübertragung entstehen können! Der
Generator liefere eine Spannung derart, dass
a. 230V
b. 115V
am Gerät anliegen.
Vergleichen Sie die für die angegebenen Spannungen zu erwartenden Leitungsverluste
und erläutern sie das Ergebnis!
Werden Ladungen über längere Strecken durch ein Kabel transportiert, so entstehen
Leitungsverluste. Diese lassen sich durch den spezifischen Widerstand des Leiters (der meist
aus Kupferdraht besteht) begründen. Der Widerstand des Leiters ist ein Maß für die
Behinderung des Stromflusses zwischen Stromquelle und Verbraucher. Er hängt ab von der
Leitfähigkeit σ und der Geometrie des Leiters. Da es sich bei alltagsgebräuchlichen Kabeln
um zylinderförmige Körper handelt, hängt der Widerstand in diesem Fall von dem
Durchmesser d und der Länge l des Leiters ab. Die elektrische Energie die man als „Verlust“
bezeichnet, wird in Wärmeenergie umgewandelt und an die Umwelt abgegeben.
Um den quantitativen Verlust zu bestimmen, wurden neben den gegebenen Angaben folgende
Annahmen gemacht:
•
•
•
•
•
Es handelt sich um ein Kupferkabel
Leiterlänge l = 100m
Querschnittsfläche A = 1,5mm² (Handelsübliche Leitung)
Ω ⋅ mm²
Spezifischer Widerstand ρCu = 0,0178
m
(Literaturwert aus: Tabellenbuch Informations- und Kommunikationstechnik
Bildungsverlag EINS – Gehlen, 5.Auflage, S. 34)
Es handelt sich um Gleichspannung
Der Leiterwiderstand berechnet sich wie folgt:
RL =
ρ ⋅l
A
für eine Leiterlänge von l = 100m ergibt sich also ein Leiterwiderstand von
0,0178
RL =
Ω ⋅ mm²
⋅ 100m
m
= 1,18667Ω
1,5mm²
Da der Verbraucher eine Leistung von 1000W hat, muss bei einer Spannung von 230V
folgender Strom fließen:
P =U ⋅I ⇒ I =
P 1000VA
=
= 4,34783 A
U
230V
Bei einer Spannung von 115V beträgt der Strom:
P 1000VA
=
= 8,69565 A
U
115V
Somit ist der Widerstand R des Verbrauchers bei einer Spannung von 230V:
P =U ⋅I ⇒ I =
R=
U
230V
=
= 52,9Ω
I 4,34783 A
Bei einer Spannung von 115V beträgt der Widerstand des Verbrauchers:
R=
U
115V
=
= 13,225Ω
I 8,69565 A
Da der Widerstand des Leiters mit dem Gesamtwiderstand des Verbrauchers in Reihe
geschalten ist, gilt:
Rges = RV + RL
Das bedeutet im Falle von 230V Spannung:
Rges = 52,9Ω + 1,18667Ω = 54,08667Ω
Im Falle von 115 V Spannung:
Rges = 13,225Ω + 1,18667Ω = 14,41167Ω
Die Gesamtleistung beträgt also bei einer Spannung von 230 V:
P 230 = Rges ⋅ I ² = 54,08667Ω ⋅ (4,34783 A)² = 1022,4W
Bei einer Spannung von 115V beträgt die Gesamtleistung:
P115 = Rges ⋅ I ² = 14,41167Ω ⋅ (8,69565 A)² = 1089,7W
Die Verlustleistung im Falle von 230V Spannung beträgt:
PVerlust , 230 = P 230 − PV = 1022,4W − 1000W = 22,4W
dies entspricht 3,2% der Gesamtleistung.
Die Verlustleistung im Falle von 115V Spannung beträgt:
PVerlust ,115 = P115 − PV = 1089,7W − 1000W = 89,7W
dies entspricht 8,4% der Gesamtleistung.
Aus den Ergebnissen wird ersichtlich, dass eine höhere Spannung eine geringere
Verlustleistung mit sich bringt.