Suffix-Link Konstruktion α = a1...an βi = a1...ai Wir fügen β1 bis βn+1
Werbung
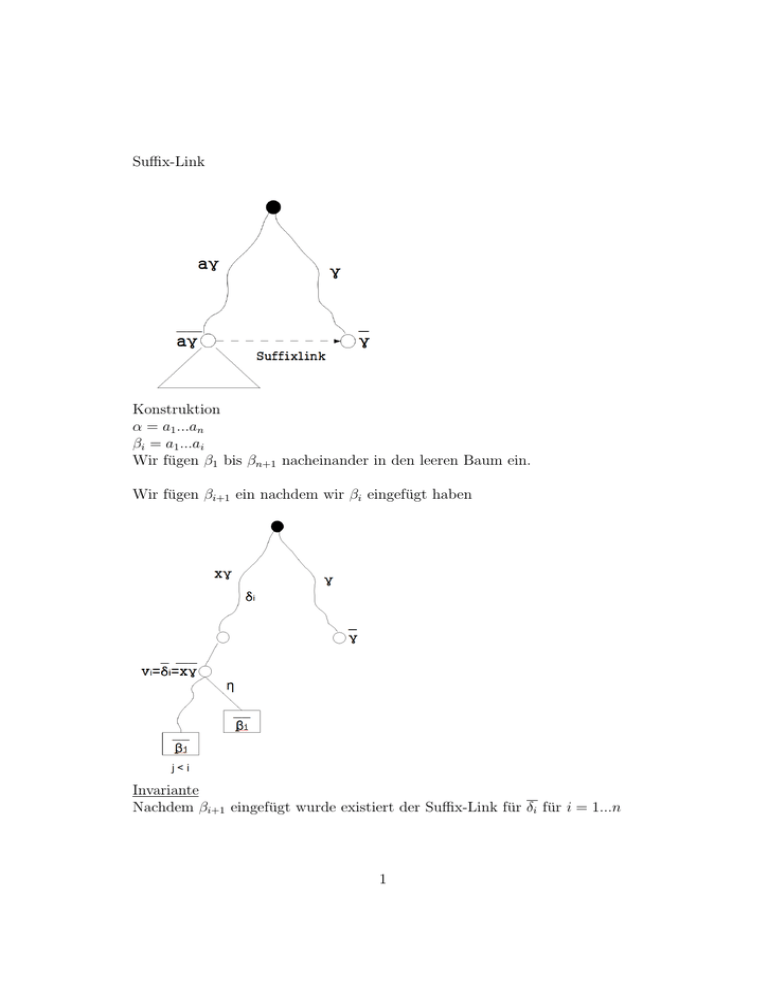
Suffix-Link Konstruktion α = a1 ...an βi = a1 ...ai Wir fügen β1 bis βn+1 nacheinander in den leeren Baum ein. Wir fügen βi+1 ein nachdem wir βi eingefügt haben Invariante Nachdem βi+1 eingefügt wurde existiert der Suffix-Link für δi für i = 1...n 1 ′ der Suffix-Link vom Großvater u von βi liefert Knoten u und Zerlegung γ = ′ γ1 γ2 . Von u aus Weg mit γ2 verfolgen (Der Weg ist vorhanden). Den Weg bestehend aus w1 , w2 ... wk zu verfolgen ist in O(k)-Zeit möglich (schnelles matching) denn bei wi gibt es weniger als |Σ| Ausgänge da die Anfangsbuchstaben der Beschriftungen alle verschieden sind. Nimm Kante wo Anfangsbuchstabe der Beschriftung mit aktuellem Zeichen von γ2 übereinstimmt. Das braucht konstante Zeit. Fallunterscheidung : Das Ende von γ2 wird erreicht Fall a : bei einem vorhandenen Knoten γ Fall b : Inmitten einer Kantenbeschriftung : schaffe neuen Knoten γ und spalte Kantenbeschriftung auf In jedem Fall setze den Suffix-Link von δi auf γ fügen danach noch η unterhalb von γ ein 2 Fall a : Vergleiche η Zeichen für Zeichen mit der Beschriftung bis man steckenbleibt (langsames matching). Falls dies inmitten einer Kantenbeschreibung passiert erzeugen wir einen neuen Knoten und zweigen den Rest von η : η2 zum neuen Knoten βi+1 ab Fall b : Erzeuge eine neue Kante von γ zu βi+1 mit Beschriftung η Laufzeitanalyse : betrachte Tiefe des aktuellen Knotens. Diese kann sich von Anfang bis Ende des Algorithmus um n verändern. Wird vermindert beim Übergang βi zum ′ Großvater u und per Suffix-Link zu u ′ es gilt d(u ) ≥ d(u) − 1 denn alle Knoten auf dem Weg von der Wurzel bis zu u haben einen Suffixlink zu einem Knoten auf dem Weg von der Wurzel ′ (einschlielich der Wurzel) bis zu u beim schnellen Matching Übergang von wi nach wi+1 O(1) Zeit Gewinn an Tiefe 1 beim langsamen Matching 3 im Fall b findet es nicht statt im Fall a Kosten O(|η1 |) Die Länge von δi+1 |δi+1 | = |η1 | + |γ| |η1 | = |δi+1 | − |γ| = |δi+1 | − |δi | − 1 Also insgesamt für das langsame Matching ∑ O( ni=1 |δi+1 | − |δi | + 1) = O(|δn+1 | − |δ1 | + n) = O(n) also insgesamt : O(n) Satz Der Algorithmus von McCreight konstruiert den Suffixbaum für ein Wort der Länge n in Zeit O(n) Anwendung von Suffixbäumen : 1. Stringmatching in linearer Zeit Text T mit |T | = n Muster P mit |P | = m • Konstruiere Suffixbaum für T - O(n) • verfolge darin Weg von der Wurzel der mit P beschriftet ist - O(m) • falls erfolgreich ist P in T als Teilwort • alle Vorkommen finden wir indem wir an der Stelle an der P endete den anhängenden Teilbaum betrachten. Falls wir die Blätter mit Positionen der entsprechenden Suffize markiert haben finden wir alle Positionen wo P in T endet. - O(k) mit k = #Blätter = Anzahl der Vorkommen von P in T Endscheidungsproblem in O(n + m) alle Vorkommen in O(n + m + k) = O(n + m) da k < n 2. Alternative zu KMP 2a Wenn wir den Text in O(n) vorverarbeiten dann knnen wir nach Mustern P1 , P2 ... suchen. Die Suchzeit betrgt dabei O(|Pi |) bzw O(|Pi | + ki ) um alle ki Vorkommen von Pi im Text zu finden. 2b Wenn wir ein Muster P in vielen Texten S1 , ..., Sl suchen wollen knnen wir diese Texte mit Sonderzeichen zusammenhängen S1 $S2 ...$Sl und fr den zusammengehängten Text einen Suffixbaum bauen. Eine Suche nach P findet dann alle Vorkommen in allen Texten. 4











