Direkt zu den Lösungen Teil 1

Schnittpunkt von Graphen
4
Die beiden Graphen schneiden sich im punkt S( 1 1 1 ).
Anmerkung:
Ob die Aufgabe zeichnerisch, rechnerisch oder durch probieren gelöst wird, ist
unerheblich. Dies begründet die Auswahl der Grenzfälle.
Weitere mögliche Lösungen:
Der Schnittpunkt hat die Koordinaten x = 1 und y = 1.
ODER (Grenzfall)
Beide Graphen werden richtig in ein Koordinatensystem gezeichnet und der
schnittpunkt ist erkennbar. Die Koordinaten des s'cnnittpunkts werden z. B. durch
gestrichelte Linien zu den Achsen angedeutet, aber nicht explizit angegeben.
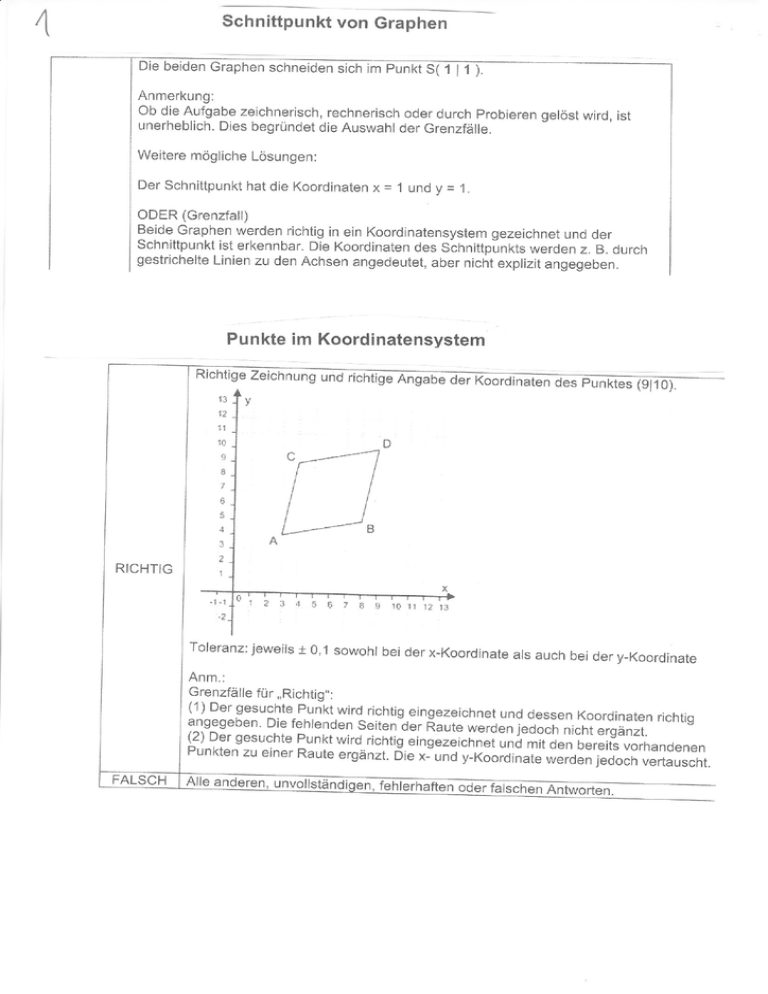
Punkte im Koordinatensystem
ni.ntig"
'. .] ,
RICHTIG
0i :;; ;;;;-il;TEl;
Toleranz: jeweils + 0,1 sowohl bei der x-Koordinate
als auch bei der y_Koordinate
Anm.:
Grenzfälle für,,Richtig,':
(1 ) Der gesuchte punkt wird richtig.eingezeichnet
und dessen Koordinaten richtig
angegeben. Die fehlenden Seiten der Raute
werden jeOo.n n,"nt ergänzt.
(2) Der gesuchte punkt wird richtig eingezeicnnet
unä-Äit äen bereits vorhandenen
Punkten zu einer Raute ergänzt. öie xlund y_k;il;;;i;;;rden
jedoch vertauscht.
Alle anderen unvollständ
fe
h le
rh aft e
n
od e r f aGärr e n Än
tuo
rt--e
n.
Abstand auf dem Wasser
?46a
1a 12 14 16 1d 20 22 24 26 2a
T-.1
t-l
RICHTIG
2 4 6 a 10 12 14 16 1a 20 22 24 26 2a 30 Fahrzeil
3a Fahrzeit ab
Hafen (min)
ab
Hafen (min)
T-'l
LJ
Abstand zum
Leuchttum (km)
246
B i0 r2
14 16
M
tal
2 A 6 a io 12 14 16 io 2a 22 24 26 2B 30
182022242628 30 Fahtzeft ab
Hafen (m'nl
I'
f,l
LJ
Fahtzeit ab
Hafen (min)
t.
fo,:Vqu Zur fr Pqilqq!,tu.j
ua Llusl*r*
-------.-.---.--.-.-l-\
XAt,oülrry
rJ
Linear und proportional
RICHTIG
)a
neln
Ein Stromanbieter verlangt eine monafliche Grundgebühr. Für
jede verbrauchte Kilowattstunde Strom ist zusätzlich eine
festgelegte cebühr zu zahlen.
a
D
Das Schwimmbecken eines Freibades ist zu Saisonbeoinn
leer. Vor der Eröffnung der Freibadsaison wird oas Schr-wimmbecken mit Wasser befüllt. Dabei ist dic nrn sr||n.la
einlaufende Wassermenge gleich.
E
n
tr
X
Ein Sparbetrag wird für drei Jahre mit einem festen Zinssatz
angelegt. Nach dem ersten Jahr werden auch die Zinsen
verztnst.
Wenn bereits 4 von 5 Kreuzen richtig gesetzt wurden, wird die Äufgäbe
als RICHTIG gewertet.
richtig
falsch
x
n
EI
n
Jede lineare Funktion ist auch eine proDortionale Funktion.
n
tr
Bei einer proportionalen Funktion gehört zum Doppelten des
x-Werts die Hälfte des y-Werts.
!
tr
Bei einer linearen Funktion hat die zugehörige Gerade immer
eine positive Steigung.
n
E
Für jedes Wertepaar x und y einer proportionalen Funktion hat
der Quotjent den gleichen Wert. (Dabei ist x, y*0.)
I
RICHTIG
Jede proportionale Funktion ist auch eine lineare Funktion.
'1
o]
cp -n
Tf,O=
o(o
NO-
=
6':l
<
F;{-O
8-äE
rbor
= -ol
+-35
t: o rjr
Olut-r
f;=9
-D
tY
9w
r^i gl
ö-g
3(D.
0]ü
c(D
o'"t
o;
'rn
I
ffiu)
(u-|<
+c {D
to==
itl LL
;+(D
rg
-r
O
'-
a
=gl
s*ö'
Y<J
(Jtf
:J
Srur
{fi :a
-.Ü L
f1\
N i-'
*e.
ä'-,
X-n
t- -r
J-1
(1.6
NOc'
g?m
lI: -r
i'<o
N=
JF
=aa
Xo
o=-
do
öE
äE
do
(o
o
c.
o
Q9ärtq
E
=J. si'
x N3
=':G
-=
11 rth<
J $ --O
o) =r<a
qo q 6
ctt
t_
*
JQ.nl
341
X:lob'mQ
3 ='5
E d.g
E*o
(t1 -{
N =-r
}-J(D
ö,FQ
ti5-5'
ä'J
=E
H
,- ='--$;{.
(Jt o- rD
c)o
c
(of =
F ciQ
ä
o =.*
=J
T='r
ä
o-o
äfir
-6(D
(,)
Fd
d-s
a6
s
bJci
ä= H
;'rco
-J
Eb
*fi;
är0(0.
äut
ür3
g.sd'
q7
$o
CA
a'=
rn Uro
ä rho
Ur
F(D
vro
a
:dq=
äo
EF
(Dc}
:U,
$
re :f
i
o-
f
(o
Xn
U=
o
o
;(o
o-
{D
a
nl
Ü,
qt
^-' rt
r
fT't
()
o
o(D
13
--1
LJf
gl
v,a
-l
3g)
ß)
r.Ll J
tu
6-g
o
U'
oo
iÄa
o ög
-J
-1
6-
o
=
t-
ta
N
ür. 6'
()(r
:to
a-F
Ecr
ci(D
5-'
0ä
o
C
u
=--
C
:f
F
=t
o
:f
o
:f
ßl
iD
=a
O-$
(D
3:.
;d
Ho
glÖ
fi/\ TJJ
:
0
ci'
-
Lt-r
f
o-
X
-LI
l'l
c(D
---r
lr,
CI
=
€
3'
rn
tl
$
o: e
-1
\
f
N6-'r
-os,
t})
G
tü
f-4
(o*
/?r l{
:f
:l
CI-
-I
Punlrt ge=tCht--...
L{
nicirtige Konstruktion UND Angabe eines richtigen Punktes
P(314)oDERP(3110)
RICHTIG
Zeichentoleranz bezüglich der x- und y-Koordinate des Punktes P: +1 mm'
Anm.: Koordinatenangaben bei P, die daraus folgend von den oben genannten
Werten um +0,2 abweichen, werden ebenfalls als RICHTIG akzeptiert'
Anm.: Der Kreis um Punkt D muss nicht vollständig gezeichnet werden. Es genügt,
den Kreisbogen so lang zu zeichnen, dass er zumindest einmal die
Mittelsenkrechte von ÄB schneidet.
AnStbeänesEeßpiels fur d, so dass sich keine Lösung ergibt
(d < 4 Längeneinheiten).
z.
8.:
d = kleiner als
4
Längeneinheiten
ODER d= 3 Längeneinheiten
Alle anderen Antworten.
Geschichte zur Graphik
Lj6a und Sven machen eing Radtour. Nach elnlger Zeit h6t Sven eine
Panne und sle müssen seln Rad teparieren. Für den Resl der Streck€
fahren beide mit höh€rEr Geschwlndlgkeit, um die versäumte Zeit
autzuholen.
Zeit ln Stunden
RolltrePPe
5
RICHTIG
iX*:ff:H::::raben
aus dem lntervan [10;
.11]
sind zu akzeptieren.
ODER (Grenzfall)
-10,5 q
1,4 min
RICHTIG
Graphik abgelesene Lösungen
Akzeptiert werden auch berechnete oder aus der
im Intervall [1 ,375 mini 1,5 min]
Einheit ist zulässig' sofern
Anm.: Die entsprechende Angabe der Zeit in anderer
dann die sewählte E]llellelggSgpglf!!
RICHTIG
i
(.
-
@ hn*
G/
G3
tr
ta['rrod{0u,,.
t q4t G/8 +5i +58 +ao), ?=5o
ln \ lr
/l'l
l,/ .^
^
71Lt ltlvv\
ScnofotaOenfigule-
f RtcurtG ltooooooo ooER tottrtittionen
n
200 Millionen
LKW Motonäder/ Bus
Mofas und andere
lsts{
n
f^
lM
aCf,oc,, tl,rr*i0ut
Joggen
{
Trainingspuls: mindestens:
A
RICHTIG
höchstens:140
ODER (Grenzfall)
höchstens: 141
Alle anderen AntwortenFALSCH
Z. B. nicht gerundete Werte:1012Q;1t!0,25
Ein Term für die unt'ere Grenze oGs rrainingspulses wird angegeber(x.teirt
Lebensalter in Jahren).
Anm.: Statt x kann jede beliebige Variable veruendet werden.
a
0,65 (200 - x)
RICHTIG
ODER 65/100 (200-x)
ODER 65
ok . (200 - x)
ODER (Grenzfall)
untere Grenze: 200 - x = t/i puls = v. 65 : 100
Alle unvollständigen, fehlerhafteÄ;aär falschen Antworlerl.
Z.B:
FALSCH
200-x.65/100
ODER (200-x) 65
ODER (200-35).65/100
ODER x< 65 %
\.l
J
.\ill\r+'-tJ{[lnn
.u
.]u
\,-\.
/\tl \
C,*
-Att
^
), urg5
.---) |
5n
ü{,t
-Tellaufgabe
SCHWEZ
Tellaufgabe
PORTUGAL
1
\-^
11 n I n
ttc,S[t}..süa c/"ftf,,-
tii-
4ü
Unregelmäßiges Vierect< Korrekte Beschreibung Oer Ze
Einzeichnen von geeigneten, der Beschreibung äntspreihenden Hirfsrinien in der
Abbildung UND Markierung der Strecken, dre gemessen werden müssen,
insbesondere verwendeter Höhen.
Die Lösung ist auch richtig, wenn Höhen und andere Strecken unqenau
eingezerchnet sind,
Zerlegungsmethode:
Anm.: Die Beschreibung der Zerregungsmethode ist korrekt, wenn die zerregung
des vierecks in Teilflächen beschrieben wird, deren Flächeninhalte mit einei Fo;mel
berechnet w-erden können (Das sind Rechtecke, Dreiecke, para erogramme und
Trapeze.) UND darauf hingewiesen wird, dass die summe dieser Flächeninhalte
den Flächeninhalt des Vierecks ergibt UND anhand der zeichnung verdeuflicht
wird, welche Strecken gemessen werden müssen.
Mögliche Zerlegungen (alle weiteren Zerlegungen, die der obigen Anmerkung
entsprechen, sind als richtig zu bewerten):
RICHTIG
lch zerlege das Viereck in Teilflächen, deren Flächeninhalte mit den
entsprechenden Flächenformeln berechnet werden können. Die Länaen kann ich
ausmessen. Die Summe der Flächeninhalte der Teilflächen eroibt de-n
Flächeninhalt des Vierecks.
ODER (Grenzfall)
Addiert man die Teilflächen, so erhält man den Flächeninhalt des Vierecks.
UND Skizze mit geeigneten Teilfiguren.
Anm.: Hier wurde zwar dre zerlegungsmethode nicht vollständig beschrieben, aber
die Abbildung lässt auf ein korrektes Verständnis schließen.
Yrww.lqb.hu.b€rtln,de
I Qf 3
'n",,,u,ru,
eralitätsenrwtckluns im B[dünssw€sen
Drehkörper
Eln Körper, dor aus fünf.gleich gfoßen Würfeln
b€steht, wtrd gedleht.
Welcher d€r folgenden Körper kann slch 6rgeben?
Kreuze an,
u
IRl-'o
L/n
I I t.v
t--]_f
L-, 1/
I
D
IF
FTA
\DU
Quadratfläche
B66timms d€n Fhchsnlnhalt des gegebonsn
euadrats.
6lb deln Ergobnls an.
-t{*=3{q*=11,'1{c.'".
RICHTIG
',)
' i.l
{rtl
4a
ftcC\rytc+,lt
(h)
U/
/5 \,30nr = 73, 5r,,',r
\v ? L(wid.*["flr^
ta\
--?.,t*^
')
+
\3/
O,t
'&/l l
Vl
I
UJ"LLcLKIÄ*.?.^
/.
,.
-|\
|
'\
\l
-'/./ ''
hA
$-c[rsrrck
r+
EcV
I
a-+
rl/1, --\
3t.t-rc1o-
I
Richtige Konstruktion des Punktes C, so dass das entstehende Dreieck ABC
gleichseitig ist. Dies kann beispielsweise auf folgende An und Weise geschehen:
Die Position von C lässt sich als Schnittounkt eines Kreises um A und ernes Kreises
um B, jeweils mit Radius I lB | , bestimmen.
ODER
ln A und in B werden 60"-Winkel an die Strecke AB abgetragen. C ist der
Schnittpunkt der beiden freien Schenkel.
ODER
l.B angetragen. C ist der
Schnittpunkt des zugehörigen freien Schenkels und der Mittelsenkrechte m.
In A oder in B wird ein 60"-Winkel an die Strecke
RICHTIG
Eine Beschreibung der Konskuktion ist jedoch nicht erforderlich.
Die fehlenden Maße müssen nicht eingetragen werden. Eine Beschriftung des
Punktes C, der Winkel oder der Seiten des Dreiecks ist nicht erforderlich.
Zeichentoleranz t 2 mm bzw. + 1"
Alle unvollständ igen, fehlerhaften oder falschen Konstruktionen.
Z.B.:
Konstruktion des Punktes C, ohne dass dieser mit den beiden anderen Punkten A
und B verbunden wird.
FALSCH
ODER
Es wird ein (anderes) gleichschenkliges Dreieck konstruiert.
ODER
Eine (mit Maßen beschriftete, aber) falsche Skizze wird anoefertiqt.
Anmerkungen:
Die erforderliche Zeichengenauigkeit für die Positlon von C auf m beträgt
t 2 mm. Eine Beschriftung des Punktes C ist nicht erforderlich.
Punkt C kann auch unterhalb von M eingezeichnet werden.
.
.
A*
Tellaufgabe 2
Spiegele die Figur an der Spiegelachse s.
Zeichne mit Geodreieck od6r Lineal.
T€ilaufgabe 3
Zeichne alle Spiegelachsen in diese FIgur ein.
.".dcwuatft
(rtf
Yrnz
f,ot et+l(nntüvi€ltt-
4S
0
30,ö "C
{c,}'c
nc.d66r..^,"-t
4
/3
&.
RICHTIG
Kw.
t
h
niöntige Antwort (32) UHO ricntlge Beschreibungdes Lösungsweges, in der
folgende Aspekte enthalten sind:
. Anna ist 45 min 16 km/h gefahren. Sie hat dabei einen Weg von 12 km
(0,75 h . 16 kmih) zurückgelegt.
. Insgesamt sind 12 km + I km = 20 km zu fahren.
. Da die Durchschnittsgeschwindigkeit für die Gesamtstrecke 20 km/h betragen
soll, hat sie für die verbleibenden 8 km noch eine Viertelstunde Zeit.
. D. h. sie müsste durchschnittlich so schnell fahren, dass sie in einer Stunde
32 km schaffen würde.
Z.B.:
. '16 km/h Durchschnittsgeschwindigkeit bedeutet, dass Anna in 45 Minuten
'12 Kilometer gefahren ist.
. Insgesamt sind also 20
km zu fahren.
. Sie hat somit für die restlichen 8 Kilometer noch 15 Minuten Zeit.
. Diese muss sie mit einer
von 32 km/h fahren.
AIle unvollständigen, fehlerhaften oder falschen Antworten.
FALSCH
Anna muss auf der Reststrecke durchschnittlich 32 km/h fahren, weil sie schneller
sein muss als auf den ersten 12 Kilometern, denn sie hat nur 15 Minuten Zeit.
46
i-f
(4 )
\t/
Sfcffiu
-tr
0
c'zwündec..u
.-i--l 0
ir nn I rr
.-D
I hc[L
Hc,I-U.,{fSf0-c{f
6 t'o'scl...ob,o LJarndq*o*Ju^
l-ft\.dt
b
= ]er-
.lo.s
,1
I.{h'
w^chl
}l Trqa
AT
Ungleichung erfüllen
Angabe von drei der Zahlen 0,
Oleictrungin lösen ist nicht schwierig
tra!
RICHTIG
4820
erkennbar durch Umformen gelöst
Die Lösung ist richtig, wenn dle Gleichung
wurde.
L.6..
7x-j4=
38 l+14
7x = 521 :7
52
7
ODER
7x=52
52
RICHTIG
7
Anmerkungen:
.
.
.
.
wird auch 7
Akzeptrert
'I
]
oDER
.
gerundete
7,4 ODER jedes andere korrekt
tol3"ill1,r""
richtig sein' ihre
umformungsschritte müssen mathematisch
Reihenfolge ist beliebig'
weitergerechnet' wird die Aufgabe als
Wird nach einem Rechenfehler folgerichtig
richtiq qewertet.
Aufgabe als
ffiä""[ ä; öäi"nung 7x - 14 = 42 korrekt gerechnet' wird die
richtig gewertet'
t-
*-ttr
blA+3=tl 5
llohsl"[,
O
'1
,50 *o
@ { ,5cr,,,o.
-[lk'z c*i_ sr0e,. h[0tu.
t
6,33
I-q[^5 slq]c s Kc.Ltr.rjlX 4 5l^<v"r
a0
Glücksrad drehen
+.4
Angabe des richtigen Winkels des Sektors C UND dessen Darstellung im
Glücksrad.
Anmerkungen:
. Wird der Sektor C nicht beschriftet, wird die Aufgabe als,,RICHTIG" gewertet.
. Sektor C kann auch neben Sektor A gezeichnet werden.
. Sektor C kann auch an anderen Stellen im Kreis einoezeichnet werden.
Sektor
Winkel
B
20"
a
30' 120'
Zeichentoleranz: 12'
RICHTIG
ODER (Grenzfall)
Der Winkel wird korrekt einctezeichnet. es fehlt iedoch das Gradmaß in der Tabelle.
Alle fehlerhaften oder falschen Antlvorten.
FALSCH
Z. B. Der Winkel wird korrekt anqegeben, jedoch wurde er nicht einqezeichnet.
J,
?. ft'n?{i!^[ c!üj Losr r^^'f du^*Bu,ldJlu. ( , 48c
nv\v\i,v\
u^
-D'30
8,4
-/\ r'll /\
1
rl
äsr[,.Q-
(i
\,
I
i
(q'
\5r
ü
?rdi,,Vl,r\
C- n'.n-[
ar
A,4.4*[""t"
Richtige Antwort (Ja) UND angemessene rechnerische oder verbale Begründung
durch-den Verweis auf das ermittelte Gesamtvolumen von 1300 ml (oder richtige
Angabe in anderer Einheit).
Ja, die Apfelsaftschorle passt in das Gefäß, denn insgesamt ergibt sich ein
Volumen von 1 ,3 Liter.
Lilb{'a-'kfttLLwrq--
@ 7,
@
5 tkr
3 Li{q-
\\/^lr
r i)
V
I /'.
ü Lwuu.f t\ t,U [Ä(.fu,1grtrr
===--=__
ti;
/l
RICHTIG
:)::---E:i-:"
-1--rt---7Tl-i --r-r
htrr.fcr*,c^(t\i
zutreffend
RICHTIG
nicht
zutreffend
Herr Goldmann sagt: ,,lch habe zwar den Gewinn des zweiten
Jahres wieder verloren, aber mir bleibt ja immer noch ein Gewinn
von 6 % aus dem ersten Jahr."
n
a
Frau Berger meint: ,,lch hätte diese Aktien nach dem ersten Jahr
verkaufen sollen. Jetzt habe ich insgesamt sogar einen Verlust
x
tr
n
E(
qemacht."
Die Firma schreibt in einem Werbeflyer: ,,Unsere Aktien haben in
den letzten drei Jahren einen durchschnittlichen Gewinn von
rc% + 25% - 25%) I 3 = zyo ercielt."