Computerorientierte Mathematik I

10
Kapitel 2
Probleme, Algorithmen, Programme:
Einige Beispiele
2.1
2.1.1
Temperatur Umrechnung
Das Problem:
Temperaturangaben in Fahrenheit sollen in Celsius umgerechnet werden.
2.1.2
Der Algorithmus:
Dafür nutzt man den Zusammenhang zwischen beiden Temperaturskalen. Beide Skalen haben eine
äquidistante Unterteilung mit folgenden Entsprechungen 1 :
0 Grad Fahrenheit ∼
= −17 79 Grad Celsius,
100 Grad Fahrenheit ∼
37 7 Grad Celsius.
=
9
Hieraus lässt sich die Temperatur C in Celsius als affin-lineare Funktion der Temperatur F in Fahrenheit berechnen, vgl. Abbildung 2.1:
5
C = (F − 32) .
9
Dies resultiert in den folgenden Algorithmus.
1 Der anekdotischen überlieferung zufolge kamen diese auf folgende Weise zustande. Fahrenheit wollte eines Tages eine
“normierte” Temperaturskala entwickeln. Es war gerade Winter und ziemlich kalt (nämlich −17 79 Grad Celsius). Da er sich
keine kältere Temperatur vorstellen konnte, normierte er diese zu 0. Anschließend wollte er die normale Körpertemperatur
des Menschen zu 100 normieren. Da er aber an diesem Tage leichtes Fieber hatte, wurden daraus 37 79 Grad Celsius.
Version vom 21. Oktober 2004
11
12
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
- C
−17, 78
0
37, 78 50
100
-
0
32
100
F
212
Abbildung 2.1: Die Celsius- und Fahrenheitskala.
Algorithmus 2.1 (Temperatur Umrechnung)
1. Einlesen von F
2. Umrechnung in C
3. Ausgabe von C
2.1.3
Das Programm
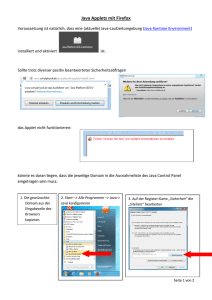
Wir sehen uns jetzt ein zugehöriges Java Programm an. Dieses erzeugt ein Applet, das in Abbildung 2.2 im Applet Launcher auf meinem Macintosh Rechner dargestellt ist.
Abbildung 2.2: Das Temperatur Applet.
Zunächst der Programmtext:
Programm 2.1 Temperatur.java
//Temperatur.java
//
// Transforms Fahrenheit to Celsius
import java.awt.*;
import java.applet.Applet;
import java.awt.event.ActionListener;
import java.awt.event.ActionEvent;
(1)
(1)
(1)
(2)
(3)
(3)
(3)
public class Temperatur extends Applet
(4)
13
2.1. TEMPERATUR UMRECHNUNG
{
(5)
// variables for the problem
double fahrenheit, celsius;
(6)
// objects for the graphical user interface
Label inputPrompt, outputPrompt1, outputPrompt2;
TextField input, output;
(7)
(7)
// setup the graphical user interface components
// and initialize labels and text fields
public void init() {
// define labels and textfields
inputPrompt = new Label("Geben Sie eine Temperatur "
+ "in Fahrenheit an und drücken Sie Return.");
outputPrompt1 = new Label("Die Temperatur in "
+ "Celsius beträgt");
outputPrompt2 = new Label(" Grad.");
(8)
(9)
(9)
(9)
(9)
(9)
input = new TextField(10);
input.addActionListener(new ActionListener() {
public void actionPerformed(ActionEvent e) {
calculateTemperature();
}
}); // action will be on input field
(10)
(11)
(11)
(11)
(11)
(11)
output = new TextField( 10 );
output.setEditable( false );
// disable editing in output field
(12)
(13)
(13)
// add labels and textfields to the applet
add(inputPrompt);
add(input);
add(outputPrompt1);
add(output);
add(outputPrompt2);
(14)
(14)
(14)
(14)
(14)
}
// process user’s action on the input text field
public void calculateTemperature() {
// get input number
fahrenheit = Double.parseDouble(input.getText());
// calculate celsius and round it to 1/100 degrees
celsius = 5.0 / 9 * (fahrenheit - 32);
(15)
(16)
(17)
14
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
// use Math class for round
celsius = Math.round(celsius * 100);
celsius = celsius / 100.0;
// show result in textfield output
output.setText(Double.toString(celsius));
}
}
(18)
(19)
(20)
(21)
(22)
Wir erläutern jetzt die Bedeutung der einzelnen Anweisungen gemäß der Nummerierung am rechten
Rand.
(1) Alles nach // bis zum Ende einer Zeile ist Kommentar. Die Kommentare enthalten den Namen
des Programms (Temperatur.java) und Informationen darüber, was das Programm tut.
Kommentare sollten auf Englisch sein, man weiß nie, wer das Programm einmal verwenden
muss.
(2) – (3) Das Programm benutzt Teile der von SUN entwickelten Bibliothek für Java. Die benötigten
Teile müssen dem Compiler per import-Anweisung mitgeteilt werden. Durch die Zeile import
java.awt.* in (2) werden alle Bibliotheksdateien geladen, die zum awt, dem abstract window
toolkit gehören. Die Import-Anweisungen (3) laden die Applet-Klasse, und zwei Klassen zur
Verarbeitung von Aktionen (ActionListener und ActionEvent).
Jede Klasse besteht grob gesprochen aus einer Kollektion von gleich gearteten Daten und Methoden, die auf diesen Daten arbeiten. Inzwischen gibt es Tausende von verfügbaren Klassen in
Java, und die Klassenbibliothek wird laufend erweitert. Eine Beschreibung aller jeweils in Java
verfügbaren Klassen findet man unter http://java.sun.com/j2se/1.4.2/docs/index.html.
(4) Deklariert das Hauptprogramm Temperatur. Jedes Hauptprogramm ist in Java selber eine
Klasse, was durch das Schlüsselwort class zum Ausdruck gebracht wird. Temperatur erweitert (Schlüsselwort extends) die vordefinierte Klasse Applet. Dies bedeutet, dass das
lauffähige Programm Temperatur als Applet zur Verfügung steht, also über das WWW geladen und mit Appletviewern oder HTML-Browsern ausgeführt werden kann, vgl. Abbildung 2.2
und Abbildung 2.3.2
Das Schlüsselwort public bringt zum Ausdruck, dass die Klasse Temperatur auch von anderen
Klassen benutzt werden darf. Alle durch import geladenen Klassen sind ebenfalls public,
d. h. die von ihnen bereit gestellten Methoden können von Temperatur benutzt werden.
(5) – (22) Die geschweiften Klammern {. . .} enthalten den Block der Klasse Temperatur. In ihm
wird festgelegt, was die Klasse leisten soll.
(6) Definiert die Variablen celsius, fahrenheit vom Datentyp double. Dieser bezeichnet Gleitkommazahlen doppelter Präzision (daher die Bezeichnung double), also im Rechner darstellbare reelle Zahlen mit großer Genauigkeit.
2 Man kann natürlich auch in Java eigenständige Programme schreiben; hierauf wird in den Übungen näher eingegangen.
2.1. TEMPERATUR UMRECHNUNG
15
celsius, fahrenheit können also reelle Werte annehmen, aber keine anderen wie z. B. Buchstaben oder Strings.
Die Bezeichner celsius und fahrenheit sind mnemonisch gewählt, d. h. aus den Namen lässt
sich leicht auf die Bedeutung schließen. Man sollte stets mnemonische Bezeichner verwenden.
(7) Deklariert die Objekte für das graphische User Interface, drei Label und zwei Textfelder. Label
sind Strings von Zeichen, und Textfelder sind rechteckige einzeilige Felder, die Text enthalten
können.
(8) Leitet die Definition der public Methode init() an. Diese wird automatisch beim Start des
Applets durch den Browser oder Appletviewer aufgerufen. Die Klammern () bedeuten, dass
die Methode keinen Input erwartet. Das Schlüsselwort void gibt an, dass die Methode keinen Outputwert erzeugt. Der Block der Methode wird wieder durch geschweifte Klammern
begrenzt.
(9) Definiert die Anfangseigenschaften der Labels. Für jedes in (7) deklarierte Label wird durch
new Label (...)
ein neues Objekt vom Typ Label erzeugt und mit dem in den Klammern angegebenen String initialisiert. Die Quotes ". . ." dienen als Begrenzer eines Strings, das + konkateniert zwei Strings
zu einem.
(10) Hierdurch wird ein neues Textfeld der Länge 10 (d. h. für 10 sichtbare Zeichen) eingerichtet und
der Variablen input zugewiesen. Dieses Textfeld ist jetzt unter dem Namen input ansprechbar.
(11) Diese (später näher erklärten 3 ) Anweisungen bewirken, dass das Textfeld input Aktionen
auslösen kann. Dies geschieht durch das Drücken der <Return> Taste. Der dem Textfeld hinzugefügte ActionListener startet beim Drücken der <Return> Taste die Methode mit dem
vorgeschriebenen Namen actionPerformed, die wiederum die von uns weiter unten in dem
Zeilen (15) – (20) definierte Methode calculateTemperature() startet.
(12) Richtet analog zu (10) das Textfeld output ein.
(13) Nutzt die Methode setEditable() der Klasse TextField, um output nicht-editierbar zu
machen.
(14) Hier werden durch die Methode add() der Klasse Applet alle Labels und Textfelder dem Applet hinzugefügt. Da keine weiteren Layoutanweisungen erfolgen, werden sie auf der verfügbaren
Appletfläche zeilenweise zentriert angeordnet. Dabei sind mehrere Komponenten pro Zeile
möglich.
(15) Leitet die Definition der public Methode calculateTemperature() ein, die die eigentliche
Rechnung und die Ein- und Ausgabe erledigt.
3
Hier wird eine anonyme Klasse definiert, die das Interface ActionListener präzisiert, vgl. Kapitel 7.3.8.
16
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
(16) Zunächst wird die in input angegebene Zahl der Variablen fahrenheit zugewiesen. Dies
erfolgt durch zwei ineinander geschachtelte Methoden. Die in input eingegebene Zahl ist
zunächst nur ein String. Dieser wird durch
input.getText()
eingelesen, anschließend durch die Methode parseDouble() der Klasse Double, also durch
Double.parseDouble() zu einer double Variablen konvertiert. Dieser Wert wird der double
Variablen fahrenheit zugewiesen.
Man könnte die Zeile (16) äquivalent auch in die folgenden Anweisungen zerlegen:
String str = input.getText(); // erzeugt String str
double temp = Double.parseDouble(str);
// erzeugt double temp aus str
fahrenheit = temp;
// weist den Wert von temp
// der Variablen fahrenheit zu
(17) Ist eine Zuweisung. Der Wert des Ausdruck (5.0 / 9) * (fahrenheit - 32) wird berechnet und der Variablen celsius zugewiesen. Da / sowohl die ganzzahlige Division mit Rest, als
auch die reellwertige Division bezeichnet, muss man (z. B. durch Angabe von 5.0 statt 5) dem
Compiler klar machen, dass hier die reellwertige Division gemeint ist. Beachte: 5 / 9 ergibt
den Wert 0, aber 5.0 / 9 den Wert 0.5555555555555556.
Hier findet die eigentliche Umrechnung statt. Alle anderen Anweisungen im Programm beziehen sich auf das User-Interface und die Ein- und Ausgabe.
(18) – (19) Um viele Nachkommastellen bei der Ausgabe zu vermeiden, wird das Ergebnis auf 2
Nachkommastellen gerundet. Dies geschieht durch Verwendung der Methode round() der
Klasse Math, die viele mathematische Standardfunktionen bereitstellt. round() rundet eine
double Zahl auf die nächstliegende ganze Zahl.
(20) Zeigt das Resultat im Ausgabefeld output. Die Methode toString() der Klasse Double
wandelt den double Wert celsius in einen String um, der dann mit der Methode setText()
der Klasse TextField für das Textfeld output benutzt wird.
Wir haben im Programm Temperatur.java einige wichtige Begriffe kennen gelernt: Variable, Zuweisung, Klasse, Methode.
Eine Variable ist (in erster Näherung) ein Name (Platzhalter) für Objekte (Daten) eines Typs, z. B. des
Typs “reelle Zahl”.
Sie belegt im Speicher einen bestimmten (dem Benutzer unbekannten) Speicherplatz, dessen Größe
vom vereinbarten Typ des Objekts abhängt. Dieser Speicherplatz ist unter dem Namen der Variablen
ansprechbar.
Eine Zuweisung aktualisiert den Wert (Inhalt) des Speicherplatzes.
17
2.1. TEMPERATUR UMRECHNUNG
Beispiel 2.1 Die Deklaration
double fahrenheit, celsius;
erzeugt im Speicher die (automatisch mit 0 initialisierten) Objekte
celsius
fahrenheit
0
0
.
Die Eingabe von 95 bewirkt folgendes. Durch
fahrenheit = Double.parseDouble(input.getText());
wird der Variablen fahrenheit der eingelesene Wert zugewiesen.
celsius
fahrenheit
0
95.0
Die Zuweisung
celsius = (5.0 / 9) * (fahrenheit - 32)
bewirkt die Auswertung des Ausdrucks (5.0 / 9) * (fahrenheit - 32) zu
(5.0/9) ∗ (95 − 32) =
5
· 63 = 35
9
und die Zuweisung an die Variable celsius.
celsius
fahrenheit
35.0
95.0
Man beachte: Ein Ausdruck hat einen Wert. Eine Zuweisung hat einen Effekt.
Eine Klasse besteht aus Variablen (auch Komponenten oder Datenfelder genannt) und Methoden (auch
Funktionen genannt). In Klassen sollen gleichartige Daten zusammengefasst werden und alle Methoden, sie zu verarbeiten, bereitgestellt werden. Die Komponenten und Methoden können durch
das Schlüsselwort public auch anderen Klassen zur Verfügung gestellt werden, bzw. durch das
Schlüsselwort private außerhalb der Klasse verboten werden. Der Zugriff auf eine public Methode
oder Komponente einer anderen Klasse erfolgt durch den “.”, wie in
Double.parseDouble() oder Math.round()
Klassen sind in Java auch Datentypen, man kann also Variable dieses Typs definieren, wie z. B.
TextField input;
Eine solche Variable wird auch als Instanz der Klasse oder Objekt bezeichnet. Instanzen (Objekte)
können die Methoden und Komponenten der Klasse benutzen. Der Zugriff geschieht wieder mit dem
“.” wie in
18
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
input.getText()
Methoden einer Klasse sind in anderen Programmiersprachen als Funktionen bekannt. Sie können ein
oder mehrere Argumente eines bestimmten Typs übergeben bekommen wie in
Math.round(celsius * 100)
und liefern Werte eines Rückgabetyps, bei Math.round vom Typ long, der für (lange) ganze Zahlen
steht. Argumenttypen und Rückgabetyp müssen in der Deklaration vereinbart werden, für Math.round
ist diese in der Klasse Math gegeben durch
long round(double a)
Dabei steht a für den zu übergebenden Wert vom Typ double.
Diese Bemerkungen sind nur eine sehr oberflächliche Einführung in Methoden und Klassen. Sie werden wesentlich detaillierter in Kapitel 7 behandelt.
Das Programm Temperatur.java wird4 durch den Befehl
javac Temperatur.java
kompiliert. Dies erzeugt die Datei Temperatur.class, die das Java Programm als Byte-Code enthält,
sowie eine Hilfsklasse Temperatur$1.class 5 .
In dieser Form kann es über das Internet durch Browser aus html-Seiten geladen und ausgeführt
werden, siehe Abbildung 2.3.
Abbildung 2.3: Darstellung des Applet Temperatur“ im Internet Explorer.
”
Dafür benötigt man eine html-Datei, die das Laden auslöst. Sie kann wie folgt aussehen.
Datei startApplet.html
<title>Temperatur</title>
4 in
5
meiner Unix shell
Diese zweite .class Datei rührt von der anonymen Klasse her, die den ActionListener präzisiert.
19
2.2. EINKOMMENSTEUERBERECHNUNG
<hr>
<applet codebase=. code="Temperatur.class" width=550 height=70>
</applet>
<hr>
<a href="Temperatur.java">The source.</a>
codebase gibt das directory an, in dem der code Temperatur.class zu finden ist. codebase=.
bedeutet also, dass sich dieser in der gleichen directory wie Temperatur.html befindet. Durch
width=550 und height=70 werden die Weite und Höhe des Applets (gemessen in Pixel) festgelegt.
Diese Werte können im Applet selbst6 bzw. im Appletviewer durch Veränderung der Fenstergröße, in
dem das Applet angezeigt wird, verändert werden. Abbildung 2.4 zeigt eine verkleinerte Darstellung
durch Änderung der Fenstergröße im Appletviewer. Sie zeigt deutlich, das die Objekte zeilenweise
zentriert auf das Applet gelegt werden.
Abbildung 2.4: Darstellung des Applet Temperatur“ bei Veränderung der Fenstergröße im Applet”
viewer.
Durch Laden der html-Datei startApplet.html in einen html-Browser (z. B. Internet Explorer)
oder einen Appletviewer steht dann das Applet ausführbar zur Verfügung.
2.2
2.2.1
Einkommensteuerberechnung
Das Problem
In einem (hypothetischen) Steuermodell sind Einkommensteuern S in Abhängigkeit des zu versteuernden Einkommens E zu zahlen. Das Steuermodell verwendet den sogenannten Stufen- oder Scheibentarif, in dem das Einkommen E in Scheiben unterteilt wird, die mit unterschiedlichen Sätzen besteuert
werden. Hier sind es 3 Scheiben:
E ≤ 20.000 e
20.000 < E ≤ 60.000
E > 60.000 e
6 durch
0 e Steuer
20% von E − 20.000
8.000 + 40% von E − 60.000
die Anweisung setSize( x, y ) in der Methode init()
20
2.2.2
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
Der Algorithmus
Aus dem Scheibentarif ergibt sich die Einkommensteuer S als stückweise lineare, monoton steigende
Funktion von E, vgl. Abbildung 2.5.
6 Steuer S in Te
24
!
!!
!
!
!!
!
!!
!
!!
8
Einkommen E in Te
-
0
20
40
60
80
Abbildung 2.5: Die Einkommensteuer Kurve.
Dies resultiert in den folgenden Algorithmus.
Algorithmus 2.2 (Steuer Berechnung)
1. Einlesen von E
2. Berechnung von S
3. Ausgabe von S
2.2.3
Das Programm
Ein entsprechendes Java Programm ist:
Programm 2.2 Steuer.java
// Steuer.java
//
// calculates taxes depending on the income in a
// piecewise linear fashion
import java.awt.*;
import java.applet.Applet;
import java.awt.event.ActionListener;
import java.awt.event.ActionEvent;
public class Steuer extends Applet {
// constants for tax calculation
final double noTaxBound = 20000,
lowRate = .2,
100
21
2.2. EINKOMMENSTEUERBERECHNUNG
lowTaxBound = 60000,
highRate = .4;
double income, tax;
// setup the graphical user interface components
// and initialize labels and text fields
Label inputPrompt, outputString;
TextField input;
Panel p1, p2; // use subdivision of applet into 2 panels
// for better layout
public void init() {
//set layout for applet so that eveything is left alligned
setLayout(new FlowLayout(FlowLayout.LEFT));
p1 = new Panel();
p2 = new Panel();
// define layout and color for panel p1
p1.setLayout(new FlowLayout(FlowLayout.LEFT));
p1.setBackground(Color.pink);
inputPrompt = new Label("Geben Sie das zu versteuernde "
+ "Einkommen an und drücken Sie Return. EURO");
input = new TextField(10);
input.addActionListener(new ActionListener() {
public void actionPerformed(ActionEvent e) {
calculateTax();
}
});
// action will be on input field
p1.add(inputPrompt);
p1.add(input);
// put prompt on panel
// put input on panel
// same for panel p2
p2.setLayout(new FlowLayout(FlowLayout.LEFT));
p2.setBackground(Color.yellow);
// this time we write the output into a label
outputString = new Label("Es sind " + tax
+ " EURO Steuern zu zahlen. Ihr Finanzamt.
p2.add(outputString);
// add panels to the applet
");
22
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
add(p1);
add(p2);
}
// process user’s action on the input text field
public void calculateTax() {
income = Double.parseDouble(input.getText());
if (income <= noTaxBound) {
// no tax
tax = 0;
} else if (income <= lowTaxBound) { // low rate applies
tax = lowRate * (income - noTaxBound);
} else {
tax = lowRate * (lowTaxBound - noTaxBound)
// low rate applies
+ highRate * (income - lowTaxBound);
// high rate applies
}
// round to Pfennig
tax = Math.round(tax * 100) / 100.0;
outputString.setText("Es sind " + tax
+ " EURO Steuern zu zahlen. Ihr Finanzamt.");
outputString.invalidate();
// marks outputString for updating when it changes
validate();
// tells applet to check for invalidations
// and update layout if necessary
}
}
Das entspechende Applet ist in Abbildung 2.6 dargestellt.
Hier sehen wir zusätzlich:
• Die Definition von Konstanten.
• Die if-Anweisung.
• Panels
• Layout-Anweisungen
2.2. EINKOMMENSTEUERBERECHNUNG
23
Abbildung 2.6: Das Steuer Applet.
Konstanten sollte man immer über Bezeichner ansprechen, da man so ihre Werte bei einer möglichen
Änderung nur an einer Stelle ändern muss. 7 Konstanten werden in Java über das Schlüsselwort final
gekennzeichnet.8 Sie müssen bei der Definition initialisiert werden.
Als Bezeichner (Identifikator) für Klassen, Methoden, Variablen, Kanstanten usw. kommen in Java
bestimmte Strings in Frage. Allgemein bestehen Strings aus 16-bit Unicode Zeichen. Diese Zeichen
sind bei den ersten 128 Zeichen mit dem ASCII-Zeichensatz und mit den ersten 256 Zeichen mit dem
ISO8859-1 (Latin 1) Zeichensatz verträglich. Bei 16 Bit sind insgesamt ca. 34000 Zeichen darstellbar,
so dass auch Zeichensätze exotischer Sprachen (äthiopisch, Bengali, Tamil . . .) darstellbar sind.
Als Bezeichner kommen solche Strings in Frage, die mit einem Unicode-Buchstaben beginnen und
nur aus Unicode-Buchstaben und Unicode-Ziffern bestehen. Zulässig sind also
input_1, Möhring,
nicht jedoch
3-Felder, no Tax Bound.
Die if-Anweisung (if-statement) hat in Java die Form
if (Bedingung) Anweisung1 else Anweisung2
wobei der else-Teil fehlen kann. Dabei ist Bedingung ein logischer Ausdruck. Logische Ausdrücke
sind in Java vom Typ boolean und können die Werte true und false für die beiden Wahrheitswerte
wahr und falsch annehmen.
Ist im if-statement der Wert von Bedingung gleich true, so wird Anweisung1 ausgeführt, ansonsten
(Bedingung ist “false”) Anweisung2 (bzw. nichts, falls der else-Teil fehlt).
Anweisung1 bzw. Anweisung2 können wieder if-statements sein, wodurch eine Verschachtelung wie
im obigen Programm auftritt.
Die Klasse Panel (aus java.awt) stellt eine Möglichkeit dar, die Oberfläche eines Applets zu untergliedern. In unserem Fall werden zwei Panels p1 und p2 definiert. Für beide Panels wird mit
setLayout() ein Layout festgelegt, nämlich ein linksbündiges Flowlayout. Ohne Layout Spezifi7 Ein Negativbeispiel war die Umstellung der Postleitzahlen; die Anzahl der Zeichen hierfür war meist nie als Konstante
deklariert worden, was einen immensen Umstellungsaufwand erforderte und ganze Programmsysteme lahmlegte.
8 Genau genommen sind Konstanten in Java Variable, deren Wert nicht mehr geändert werden darf.
24
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
zierung wird das zentrierte Flowlayout genommen (wie in Temperatur.java). Darüber hinaus
werden mit der Methode setBackground() Farben für diese Panels definiert. Die Argumente dieser
Methode sind Konstanten der Klasse Color, werden also (Zugriff auf Komponenten!) mit Color.pink
angesprochen.
Auch das gesamte Applet verwendet ein linksbündiges Flowlayout. Die Layoutanweisungen sind
nicht absolut, sondern ändern sich mit der Größe des Applets. Das linksbündige Flowlayout schreibt
nur vor, dass die Komponenten in der Reihenfolge der add() Befehle Zeile für Zeile eingefügt werden.
Die Ausgabe erfolgt diesmal über ein Label outputString, das in init() eingerichtet und initialisiert wird, und in calculateTax() mit der Methode setText() aktualisiert wird. Um die
Länge dem veränderten Text anzupassen, wird das Objekt outputString zunächst durch die Anweisung outputString.invalidate() als “verändert” markiert, und mit dem Aufruf der Methode
validate() für das Applet wird dieses angewiesen, outputString zu aktualisieren.
2.3
Primzahl
2.3.1
Das Problem
Zu einer gegebenen natürlichen Zahl n ∈ N, n > 0 soll die kleinste Primzahl p bestimmt werden, die
größer als n ist.9
2.3.2
Der Algorithmus
Der Algorithmus zur Lösung dieses Problems basiert auf der folgenden Idee.
Prüfe die Zahlen n + 1, n + 2, n + 3, . . ., ob sie durch eine kleinere natürliche Zahl k > 1 ohne Rest
teilbar ist. Die erste Zahl z, die das nicht ist, ist die gesuchte Primzahl.
Algorithmus 2.3 (Primzahl)
Lese die Zahl n ein
Setze z := n
Wiederhole
Erhöhe z um 1
überprüfe ob z Primzahl ist
bis z Primzahl ist
Gebe z aus
Der Test, ob z eine Primzahl ist, geschieht nach folgender Idee:
9
N bezeichnet die Menge der natürlichen Zahlen 0, 1, 2, . . .
25
2.3. PRIMZAHL
Teile z durch alle Zahlen k = 2, 3, . . . (bis k · k > z) und prüfe ob der Rest 0 ist. Ist dies für ein k der
Fall, so ist z keine Primzahl, andernfalls (d. h. keines der k teilt z ohne Rest) ist z eine Primzahl.
Diese Idee führt zu dem folgenden Algorithmus. Hierin ist teilerGefunden eine sogenannte Boolesche
Variable, also eine Variable, die nur die Werte wahr oder falsch annimmt. Die geschweiften Klammern
{. . .} enthalten Kommentare.
Algorithmus 2.4 (Primzahltest)
Setze k := 2
Setze teilerGefunden := falsch {noch kein Teiler gefunden}
Solange (teilerGefunden = falsch) und (k · k ≤ z) führe aus
Teile z ganzzahlig durch k. Sei rest der entstehende Rest
Falls rest = 0 so setze teilerGefunden := wahr
Setze k := k + 1
{z ist Primzahl falls teilergefunden = falsch beim Austritt aus der Schleife}
Algorithmus 2.3 und 2.4 werden jetzt in ein Java Programm umgesetzt.
Programm 2.3 Primzahl.java
// Primzahl.java
//
// input: natural number n
// output: smallest prime number p with p > n
//
// method: apply prime test to n+1, n+2, ... until prime is found,
//
prime testing of z is done by testing numbers k = 2 ...
//
k * k <= z if they are factors of z
//
import
import
import
import
with
java.awt.*;
java.applet.Applet;
java.awt.event.ActionListener;
java.awt.event.ActionEvent;
public class Primzahl extends Applet {
Label inputPrompt;
// declare Label
TextField input, output; // declare textfields for input and output
int n,
z,
k;
boolean
// the input integer read from terminal
// candidate for the prime, set to n+1, n+2 etc.
// possible divisor of z
divisorFound;
// Boolean, indicates that a divisor
// k of z has been found
26
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
// setup the graphical user interface components
// and initialize labels and text fields
public void init() {
// set layout
setLayout(new FlowLayout(FlowLayout.LEFT));
inputPrompt = new Label("Geben Sie die Zahl n ein "
+ "und drücken Sie Return.");
input = new TextField(10);
input.addActionListener(new ActionListener() {
public void actionPerformed(ActionEvent e) {
// call method for finding next prime
findPrime();
}
});
// action will be on input field
// output will be text in a field
output = new TextField(60);
output.setEditable(false);
output.setBackground(Color.yellow);
add(inputPrompt);
add(input);
add(output);
// put prompt on applet
// put input on applet
// put output on applet
}
// function for finding next prime number
public void findPrime() {
// get input number
n = Integer.parseInt(input.getText());
z = n;
do {
z++;
k = 2;
divisorFound = false;
// so far no divisor of z has been found
while (!divisorFound && k*k <= z) {
// check if k is a divisor of z
if (z % k == 0) {
divisorFound = true;
}
k++;
} //end while
27
2.3. PRIMZAHL
} while (divisorFound);
// define the output string
String str = "Die nächstgrößere Primzahl nach "
+ n + " ist " + z + ’.’;
// put the sting into the output field
output.setText( str );
}
}
Das entsprechende Applet ist in Abbildung 2.7 dargestellt.
Abbildung 2.7: Das Primzahl Applet.
Neu sind hier folgende Konstrukte für Schleifen:
while (Fortsetzungsbedingung) Anweisung
bzw.
do Anweisung while (Fortsetzungsbedingung)
Im ersten Fall wird Anweisung so oft ausgeführt, wie Fortsetzungsbedingung gilt. Diese Bedingung
wird vor jedem Eintritt in die Schleife überprüft. Evtl. wird die Schleife also auch kein mal durchlaufen.
Im zweiten Fall erfolgt die Überprüfung der Fortsetzungsbedingung nach jeder Abarbeitung von Anweisung. Anweisung wird also mindestens einmal ausgeführt.
Neu sind ferner folgende Operatoren:
!
logische Negation
&&
logisches und
%
Rest bei ganzzahliger Division, 8 % 3 ergibt 2
Bei der Ausgabe wird zunächst der String str-durch Konkatenation von Zeichenketten und Werten
von Variablen erzeugt. Dieser wird dann als String im Textfeld output ausgegeben.
Betrachten wir das Programm für das Zahlenbeispiel n = 50. Tabelle 2.1 dokumentiert die Veränderung
der Werte der Variablen n, z, k, divisorFound während des Programmablaufs (von oben nach unten).
28
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
Tabelle 2.1: Werte der Variablen in Programm 2.3
n
0
50
50
50
50
50
50
z
0
0
50
51
51
51
51
k
0
0
0
0
2
2
2
divisorFound
false
false
false
false
false
false
false
50
51
3
false
50
50
51
51
3
4
true
true
50
50
50
50
52
52
52
52
4
2
2
2
true
true
false
false
50
50
52
52
2
3
true
true
50
50
50
50
53
53
53
53
3
2
2
2
true
true
false
false
50
50
53
53
3
3
false
false
50
50
53
53
4
4
false
false
50
50
53
53
5
5
false
false
Aktion im Programm
Default Initialisierung bei Definition
nach Einlesen in n
nach z = n
nach z++
nach k = 2
nach divisorFound = false
Eintritt in while-Schleife
z % k = 51 % 2 6= 0
nach k++
neuer Eintritt in while-Schleife
z % k = 51 % 3 = 0
“then” statement ausgeführt
nach k++
kein neuer Eintritt in while-Schleife
neuer Eintritt in do-Schleife
nach z++
nach k = 2
nach divisorFound = false
Eintritt in while-Schleife
z % k = 52 % 2 = 0
“then” statement ausgeführt
nach k++
kein neuer Eintritt in while-Schleife
neuer Eintritt in do-Schleife
nach z++
nach k = 2
nach divisorFound = false
Eintritt in while-Schleife
z % k = 53 % 2 6= 0
nach k++
neuer Eintritt in while-Schleife
z % k = 53 % 3 6= 0
nach k++
neuer Eintritt in while-Schleife
z % k = 53 % 4 6= 0
nach k++
neuer Eintritt in while-Schleife
z % k = 53 % 5 6= 0
29
2.3. PRIMZAHL
n
50
50
z
53
53
k
6
6
divisorFound
false
false
50
50
53
53
7
7
false
false
50
50
53
53
8
8
false
false
Aktion im Programm
nach k++
neuer Eintritt in while-Schleife
z % k = 53 % 6 6= 0
nach k++
neuer Eintritt in while-Schleife
z % k = 53 % 7 6= 0
nach k++
k*k = 8 ∗ 8 > 53
⇒ kein neuer Eintritt in while-Schleife
divisorFound hat Wert false
⇒ kein neuer Eintritt in do-Schleife
⇒ z = 53 ausgegeben
Die Korrektheit des Programms folgt aus den Vorüberlegungen10 :
- Die while-Schleife testet alle in Frage kommenden natürlichen Zahlen k ≤
von z sind.
√
z ob sie Teiler
- Die do-Schleife terminiert mit einem z, für das kein Teiler gefunden wurde.
- Da es zu jeder Zahl n eine Primzahl p mit p > n gibt, terminiert auch die do-Schleife nach
endlich vielen Schritten (keine Endlosschleife).
Der Algorithmus kann auf verschiedene Weisen verbessert und schneller gemacht werden.
1. Die if-Anweisung
if (z % k == 0) {divisorFound = true;}
kann ersetzt werden durch die (allerdings schwer lesbare) Zuweisung
divisorFound = (z % k == 0);
Dabei ist z % k == 0 ein Boolescher Ausdruck, dessen Wert der Variablen divisorFound
zugewiesen wird.
2. Es kommen nur ungerade Zahlen als Primzahlen in Frage. Daher kann man als ersten Wert von
z die erste ungerade Zahl > n nehmen und dann stets z um 2 erhöhen.
3. Da z ungerade gewählt wird, kommen nur ungerade Zahlen k als Teiler von z in Frage.
Der Einbau dieser Änderungen (Anfang und Ende wie in Programm 2.3):
10
Dabei wird vorausgesetzt, dass nur natürliche Zahlen eingegeben werden. Für andere typzulässige Eingaben wie zum
Beispiel negative ganze Zahlen wird nichts ausgesagt. Solche Eingaben könnte man natürlich durch entsprechende Fallunterscheidungen “abfangen”.
30
KAPITEL 2. PROBLEME, ALGORITHMEN, PROGRAMME
. . .
if (n % 2 == 0) z = n - 1; else z = n;
// this makes z + 2 smallest odd number > n
do {
z += 2;
k = 3;
divisorFound = false;
while (!divisorFound && k*k <= z) {
divisorFound = (z % k == 0);
k += 2;
}\\endwhile
} while (divisorFound);
. . .
Dabei ist k += 2 äquivalent zu k = k + 2.
4. Eine andere Verbesserung besteht darin, in der while-Schleife eine unnötige Erhöhung der
Variablen k zu vermeiden. Dies kann erreicht werden durch:
if (z % k == 0) {
divisorFound = true;
} else {
k += 2;
}
2.4
Literaturhinweise
Die Beispiele sind [OSW83] entnommen. Dort finden sich insgesamt 100 Beispielaufgaben für einfache Programme und zugehörige Lösungsalgorithmen (allerdings in Pascal).
Weitere Beispiele für einfache Java Programme findet man in [DD01, CW98, Krü02].