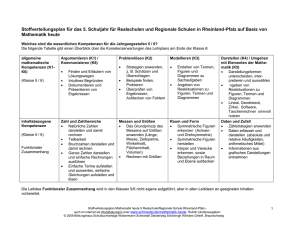
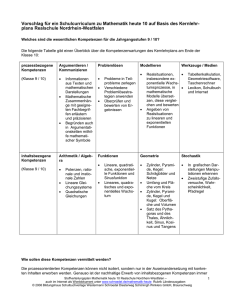
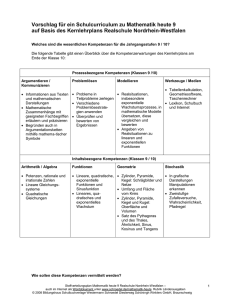
Inhaltsbezogene Kompetenzbereiche
Werbung

Von den Rahmenvorgaben des Bildungsplans 2015 zum Schulcurriculum Anregungen für Mathematik in der Sekundarstufe 1 auf der Grundlage von Sekundo 5 (978-3-507-85000-2) Der Stoffverteilungsplan geht von folgenden Voraussetzungen aus: 1. Im Mittel stehen in der Klasse 5 insgesamt ca. 170 Unterrichtsstunden für Mathematik pro Schuljahr zur Verfügung 2. Der Band 5 des Unterrichtswerkes „Sekundo“ wird „Seite für Seite“ abgearbeitet (aber nicht immer „Aufgabe für „Aufgabe“). 3. Die jeweils angegebene Zahl von Unterrichtsstunden für die einzelnen Lerneinheiten ist nur als grobe Orientierungshilfe zu verstehen. Anforderungen, die für das mittlere Niveau bzw. nur für das erweiterte Niveau vorgeschrieben sind, sind mit „M“ bzw. mit „E“ gekennzeichnet. Themen, die über die Regelanforderungen hinausgehen, sind mit + gekennzeichnet. Die prozessorientierten Kompetenzen können nicht unabhängig von den Inhalten vermittelt werden. Sie werden in allen inhaltlichen Bereichen in unterschiedlichster Form eingeübt. Dazu enthält das Schülerbuch eine Vielzahl von Projektseiten und Aufgabenstellungen, die einen besonderen Schwerpunkt auf die Förderung einer speziellen prozessbezogenen Kompetenz setzen. Sie sind exemplarisch in der nachfolgenden Übersicht aufgeführt. Inhalte von SEKUNDO Band 5 (978-3-507-85000-2) 1. Kapitel: Zahlen und Daten Stunden Seiten im Buch 20 Stunden 6–8 Fragebogen auswerten, Strichlisten, Tabellen und Diagramme anlegen Natürliche Zahlen darstellen, vergleichen, ordnen und runden + Wissen – Anwenden – Vernetzen Zahlen im Zehnersystem und am Zahlenstrahl darstellen Zahlen runden und darstellen am Zahlenstrahl Diagramme lesen und zeichnen Große Zahlen (Millionen, Milliarden, Billionen) schätzen, lesen und darstellen 9 – 10, 12 – 13, 16 14 – 15 9 – 13 16 – 17 18 19 – 21 Kompetenzen nach Klasse 6 gemäß Bildungsplan von 2015 Inhaltsbezogene Kompetenzbereiche Zahl – Variable – Operation (1) die Prinzipien des dezimalen Stellenwertsystems beschreiben, auch im Vergleich zum römischen Zahlensystem (M) und im Vergleich zu einem anderen Zahlensystem (E) (2) natürliche Zahlen bis zur Größenordnung Billion lesen und nach Hören schreiben (6) (natürliche) Zahlen und Punkte am Zahlenstrahl einander zuordnen, vergleichen und anordnen (19) Zahlenwerte und Größenangaben runden und gerundete Angaben interpretieren Funktionaler Zusammenhang (2) (einfache) Muster (zum Beispiel Zahlenfolgen) erkennen, verbal beschreiben und diese fortsetzen Daten und Zufall (2) Urlisten, Stricklisten, Häufigkeitstabellen anfertigen Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig + Systematisches Schätzen – Vermischte Aufgaben M, E Zahlen im Zweiersystem und mit römischen Zahlzeichen darstellen TÜV und Diagnosetest 22 – 23 24 – 26 27 – 28 (5) Aus Diagrammen (Balkendiagramm, Säulendiagramm, Streifendiagramm) Zahlenwerte entnehmen (6) Daten grafisch darstellen (Balken- und Säulendiagramm) Prozessbezogene Kompetenzbereiche Probleme lösen 2. Informationen aus den gegebenen Texten, Bildern und Diagrammen entnehmen (8/6) 3. durch Verwendung verschiedener Darstellungen (informative Figur, verbale Beschreibung, Tabelle, Graph, symbolische Darstellung, Koordinaten) das Problem durchdringen oder umformulieren(8/7) 6. das Problem durch Zerlegen in Teilprobleme oder das Einführen von Hilfsgrößen oder Hilfslinien vereinfachen (22/1-5) 14. Fehler analysieren und konstruktiv nutzen (19/4) Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen 1. zwischen natürlicher Sprache und symbolisch-formaler Sprache der Mathematik wechseln (16/1, 8) 3. zwischen verschiedenen mathematischen Darstellungen wechseln (24 – 25) 2. Kapitel: Addition und Subtraktion 20 Stunden 29 – 32 Im Kopf und am Zahlenstrahl addieren und subtrahieren mit Operatoren und Umkehroperatoren arbeiten Termschreibweise (+) und Rechengesetze kennen, Rechenvorteile nutzen BLEIB FIT: Wiederholung von 33 34 – 35 36 Kommunizieren 1. Mathematische Einsichten und Lösungswege schriftlich dokumentieren oder mündlich darstellen und erläutern (9/6; 21/15) 2. Ergebnisse strukturiert präsentieren (13/23) 3. eigene Überlegungen in kurzen Beiträgen sowie selbstständige Problembearbeitungen in Vorträgen verständlich darstellen (22/1) Inhaltsbezogene Kompetenzbereiche Zahl – Variable – Operation (12) einfache Rechnungen sicher im Kopf durchführen, unter anderem, um Ergebnisse überschlägig zu überprüfen (13) Natürliche Zahlen schriftlich addieren und subtrahieren (19) Zahlenwerte und Größenangaben runden und gerundete Angaben interpretieren (22) Rechnungen unter Verwendung der Umkehroperation überprüfen (23) Sachsituationen aus der eigenen Erfahrungswelt durch (einfache) Zahlterme beschreiben (24) Fachbegriffe für Rechenarten (Addition, Subtraktion), Rechenoperationen (addieren, subtrahieren) und Rechenoperanden (Summand, Minuend (M,E), Subtrahend (M,E) Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig Grundwissen Überschlagsrechnen, Schriftliches Addieren und Subtrahieren Texte lesen, verstehen und komplexe Sachzusammenhänge modellieren und Probleme lösen - Sachrechnen mit Geldbeträgen TÜV und Diagnosetest 37 – 41 42 – 44 verwenden (25) bei der Berechnung von Zahltermen Rechengesetze (M,E) und Rechenvorteile nutzen (26) den Wert von Zahltermen mit Klammern in einfachen Fällen berechnen (27) einfache Zahlterme mit den Fachbegriffen Summe, Differenz beschreiben (28) einfache Aufgaben mit Unbekannten durch ausprobieren oder Rückwärtsrechnen lösen 45 – 46 Prozessbezogene Kompetenzbereiche Probleme lösen 1. das Problem mit eigenen Worten beschreiben (31/14) 6. das Problem durch Zerlegen in Teilprobleme oder das Einführen von Hilfsgrößen oder Hilfslinien vereinfachen (39) 9. durch Vorwärts- oder Rückwärtsarbeiten Lösungsschritte finden (41/16, 18, 19) 15. Lösungswege vergleichen (41/11) Modellieren 1. wesentliche Informationen entnehmen und strukturieren (37/7) Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen 1. zwischen natürlicher Sprache und symbolisch-formaler Sprache der Mathematik wechseln (30/7; 34/5) 2. mathematische Darstellungen zum Strukturieren von Informationen, zum Modellieren und zum Problemlösen auswählen und verwenden (30/6) 4. Berechnungen ausführen (35/1) 5. Routineverfahren anwenden und miteinander kombinieren (41/11) 6. Algorithmen reflektiert anwenden (39) Kommunizieren 1. Mathematische Einsichten und Lösungswege schriftlich dokumentieren oder mündlich darstellen und erläutern (44/1) 3. eigene Überlegungen in kurzen Beiträgen sowie selbstständige Problembearbeitungen in Vorträgen verständlich darstellen (39) 4. bei der Darstellung der Ausführungen geeignete Medien einsetzen (32/1) 7. aus Quellen (Texten, Bildern und Tabellen) und aus Äußerungen anderer mathematische Informationen entnehmen (42-43) 8. Äußerungen und Informationen analysieren und beurteilen (42/3) Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig 3. Kapitel: Körper, Flächen und Linien 16 Stunden 47 – 48 Körper charakterisieren und nach Anleitung Würfel und Quader basteln Kopfgeometrie: an Würfel- und Quadernetz gedanklich operieren und Netze zeichnen BLEIB FIT: Wiederholung von Grundwissen Flächen und Kanten von Körpern begrifflich erfassen, Körpereigenschaften nennen Begriffe senkrecht, parallel, lotrecht und waagerecht sachgerecht verwenden und zur Beschreibung von Körpern nutzen Kantenmodelle basteln + Wissen – Anwenden – Vernetzen Rechteck und Quadrat als Seitenflächen von Quadern und Würfeln kennen und Eigenschaften in Sachanwendungen nutzen TÜV und Diagnosetest 49 – 50 51 52 53, 55 54 56 – 57 58 – 60 61 – 62 4. Kapitel: Multiplikation und Division 28 Stunden 63 – 65 Fachbegriffe bei Multiplikation und Division verwenden und im Kopf rechnen Großes Einmaleins und Quadratzahlen 66 – 67 Inhaltsbezogener Kompetenzbereich Raum und Form (1) Lagebeziehungen von Strecken und Geraden (parallel, senkrecht) untersuchen (6) Vierecke (Quadrat, Rechteck) identifizieren und deren spezielle Eigenschaften beschreiben (7) vorgegebene Körper (Quader, Würfel, Prisma (M, E), Zylinder, Pyramide, Kegel und Kugel) erkennen und benennen (14) Netze von Quadern und Würfeln zeichnen (15) einem vorgegebenen Netz (Quader, Würfel) den geraden Körper zuordnen (G) Prozessbezogene Kompetenzbereiche Argumentieren und Beweisen 1. in mathematischen Zusammenhängen Vermutungen entwickeln und als mathematische Aussage formulieren (50/9) 13. Aussagen auf ihren Wahrheitsgehalt prüfen und Beweise führen (E) (58/8) Probleme lösen 14. Fehler analysieren und konstruktiv nutzen (49/3; 55/5) Modellieren 7. zu einer Situation passende mathematische Modelle (z.B. geometrische Modelle,) konstruieren (48) Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen 1. zwischen natürlicher Sprache und symbolisch-formaler Sprache der Mathematik wechseln (59/3) 3. zwischen verschiedenen mathematischen Darstellungen wechseln (50/7,8) Kommunizieren 6. Ausführungen mit geeigneten Fachbegriffen darlegen (52/1; 53/1) Inhaltsbezogener Kompetenzbereich Zahl – Variable – Operation (12) einfache Rechnungen sicher im Kopf durchführen, unter anderem, um Ergebnisse überschlägig zu überprüfen (13) Natürliche Zahlen schriftlich multiplizieren und dividieren (14) Die Quadratzahlen von 1² bis 15² (bzw. bis 20², E) wiedergeben und erkennen Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig Kopfrechnen mit Zehnern, Hundertern und Tausendern Operatoren und Umkehroperatoren anwenden BLEIB FIT: Wiederholung von Grundwissen Halbschriftliches Multiplizieren Rechenregeln kennen, Rechenvorteile nutzen, Kopfrechentricks und Rechengesetze zu Rechengeschichten Rechenwege (Terme) erstellen Texte lesen, verstehen und bearbeiten Schriftliches Multiplizieren, das Ergebnis durch einen Überschlag abschätzen Schriftliches Dividieren - auch mit Rest Texte lesen und verstehen, zu Problemstellungen sachgerechte Modellierungen vornehmen sowie Lösungen finden und darstellen TÜV und Diagnosetest 68 69 70 71 72 – 75 76 77 78 – 81 82 – 85 86 – 88 89 – 90 (22) Rechnungen unter Verwendung der Umkehroperation überprüfen (23) Sachsituationen aus der eigenen Erfahrungswelt durch (einfache) Zahlterme beschreiben (24) Fachbegriffe für Rechenarten (Multiplikation, Division), Rechenoperationen (multiplizieren, dividieren) und Rechenoperanden (Faktor, Dividend, Divisor (M,E) verwenden (25) bei der Berechnung von Zahltermen Rechengesetze (M,E) und Rechenvorteile nutzen (26) den Wert von Zahltermen mit Klammern in einfachen Fällen berechnen (27) einfache und zusammengesetzte (E) Zahlterme mit den Fachbegriffen Produkt, Quotient beschreiben (28) einfache Aufgaben mit Unbekannten durch ausprobieren oder Rückwärtsrechnen lösen Prozessbezogene Kompetenzbereiche Argumentieren und Beweisen 1. in mathematischen Zusammenhängen Vermutungen entwickeln und als mathematische Aussage formulieren (65/15) 2. eine Vermutung anhand von Beispielen auf ihre Plausibilität prüfen oder anhand eines Gegenbeispiels widerlegen (67/10; 81/21) 13. Aussagen auf ihren Wahrheitsgehalt prüfen und Beweise führen (E) (65/15) Probleme lösen 2. Informationen aus den gegebenen Texten, Bildern und Diagrammen entnehmen (77/1,2) 5. durch Untersuchung von Beispielen und systematisches Probieren zu Vermutungen kommen und diese auf Plausibilität überprüfen (85/10) 8. das Aufdecken von Regelmäßigkeiten oder mathematischen Mustern für die Problemlösung nutzen (67/9; 81/22) 10. Sonderfälle oder Verallgemeinerungen untersuchen (88/1) 11. das Problem auf Bekanntes zurückführen oder Analogien herstellen (83/7; 88/3,4) 13. kritisch prüfen, inwieweit eine Problemlösung erreicht wurde (88/1) 15. Lösungswege vergleichen (75/5) Modellieren 1. wesentliche Informationen entnehmen und strukturieren (77/1; 86; 87) 4. relevante Größen und ihre Beziehungen identifizieren (86; 87) 7. zu einer Situation passende mathematische Modelle (z.B. arithmetische Operationen,) auswählen (68/1) Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen 1. zwischen natürlicher Sprache und symbolisch-formaler Sprache der Mathematik wechseln (73/1; 76) 3. zwischen verschiedenen mathematischen Darstellungen wechseln (73/1) 4. Berechnungen ausführen (79/1) 6. Algorithmen reflektiert anwenden (74/1) 5. Kapitel: Zeichnen und Konstruieren 24 Stunden 91 92 – 93 Geometrische Grundbegriffe Gerade, Strecke und Strahl erkennen und darstellen Begriffe senkrecht, parallel und Abstand präzisieren und in Sachanwendungen nutzen Lagebeschreibungen von Punkten und Gebieten in (Stadt-)Plänen und im Quadratgitter – Muster im Quadratgitter BLEIB FIT: Wiederholung von Grundwissen + Wissen – Anwenden – Vernetzen Spiegeln, Achsensymmetrien erkennen, Symmetrieeigenschaften von Figuren nennen symmetrische Figuren basteln Rechtecke, Quadrate, Parallelogramme und Rauten (E), Drachen und Trapeze 94 – 98 99 – 102 103 105 – 106 106 – 109 110 111 – 116 Kommunizieren 1. Mathematische Einsichten und Lösungswege schriftlich dokumentieren oder mündlich darstellen und erläutern (75/1) 4. bei der Darstellung der Ausführungen geeignete Medien einsetzen (75/1) 5. vorläufige Formulierungen zu fachsprachlichen Formulierungen weiterentwickeln (64/5) 7. aus Quellen (Texten, Bildern und Tabellen) und aus Äußerungen anderer mathematische Informationen entnehmen (77/1,2; 86; 87) 8. Äußerungen und Informationen analysieren und beurteilen (88/1) Inhaltsbezogene Kompetenzbereiche Raum und Form (1) Lagebeziehungen von Strecken und Geraden (parallel, senkrecht) mithilfe eines Geodreiecks untersuchen (4) Achsensymmetrie bei Figuren erkennen und die Symmetrieachse identifizieren (6) Vierecke (Quadrat, Rechteck, Raute (E), Drachen (E), Parallelogramm (E), Trapez (E)) identifizieren und deren spezielle Eigenschaften beschreiben (8) sicher mit Geodreieck und Lineal umgehen und damit geometrische Objekte zeichnen (10) zueinander parallele bzw. senkrechte Linien mithilfe eines Geodreiecks zeichnen (11) den Abstand zwischen Punkt und Gerade sowie den Abstand zwischen Parallelen (M, E) bestimmen (12) Punkte, Strecken, Figuren in vorgegebenen (G) / selbstständig skalierten (M, E) zweidimensionalen kartesischen Koordinatensystemen darstellen (13) Achsenspiegelungen durchführen Funktionaler Zusammenhang (3) Punkte in ein Koordinatensystem eintragen und die Koordinaten von Punkten ablesen (7) aus maßstäblichen Darstellungen Originallängen erschließen Prozessbezogene Kompetenzbereiche Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig (E) zeichnen, ihre wesentlichen Eigenschaften kennen und danach klassifizieren TÜV und Diagnosetest Argumentieren und Beweisen 13. Aussagen auf ihren Wahrheitsgehalt prüfen und Beweise führen (E) (114/5; 116/4) 117 – 118 Probleme lösen 11. das Problem auf Bekanntes zurückführen oder Analogien herstellen (112/6) 14. Fehler analysieren und konstruktiv nutzen (97/4; 98/7) Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen 1. zwischen natürlicher Sprache und symbolisch-formaler Sprache der Mathematik wechseln (92/1; 99/1,2) 3. zwischen verschiedenen mathematischen Darstellungen wechseln (94/1; 95/1) 6. Algorithmen reflektiert anwenden (111/1) 8. Hilfsmittel (z.B. Geodreieck und Zirkel) problemangemessen auswählen und einsetzen (95/2; 96/2; 97/1) 6. Kapitel: Größen 26 Stunden 119 – 121 122 – 127 mit Geldbeträgen rechnen Längen schätzen, messen, unter Verwendung der Kommaschreibweise umwandeln und mit ihnen rechnen Figuren maßstäblich vergrößern und verkleinern und Entfernungen auf Landkarten messen Maßeinheiten für Massen kennen, schätzen, messen, unter Verwendung der Kommaschreibweise umwandeln und mit ihnen rechnen im Internet Daten recherchieren und mit großen Größen rechnen, BLEIB FIT: Wiederholung von Grundwissen 128 – 130 131 – 134 135 Kommunizieren 1. Mathematische Einsichten und Lösungswege schriftlich dokumentieren oder mündlich darstellen und erläutern (106/1) Inhaltsbezogene Kompetenzbereiche Messen (1) Messvorgänge und die Verwendung von Einheiten erläutern (2) im Umfeld Massen und Zeitspannen erläutern (3) Größenangaben durch Maßzahl und Einheit darstellen (5) Einheiten für Masse, Zeit(spanne), Geld, Länge verwenden und (in benachbarte Einheiten G) umwandeln (6) alltagsbezogene Repräsentanten als Schätzhilfe für Größenangaben verwenden (8) mit Größenangaben rechnen und dabei Einheiten korrekt anwenden Funktionaler Zusammenhang (7) aus maßstäblichen Darstellungen Originallängen erschließen (8) bei einfachem, vorgegebenen Maßstab Zeichnungen anfertigen (G) / maßstäbliche Zeichnungen nach Vorgaben anfertigen (M) / maßstäbliche Zeichnungen anfertigen, auch mit selbstgewähltem, geeignetem Maßstab (E) 136 Prozessbezogene Kompetenzbereiche Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig Zeiteinheiten umwandeln und mit Zeitangaben (Dauern) rechnen Texte sinnentnehmend lesen und Daten aus Tabellen entnehmen und sachbezogen modellieren - Sachrechnen mit Alltagsbezug TÜV und Diagnosetest 137 – 140 141 – 144 145 – 146 Argumentieren und Beweisen 1. in mathematischen Zusammenhängen Vermutungen entwickeln und als mathematische Aussage formulieren (135) Probleme lösen 1. das Problem mit eigenen Worten beschreiben (125/6) 2. Informationen aus den gegebenen Texten, Bildern und Diagrammen entnehmen (121) 9. durch Vorwärts- oder Rückwärtsarbeiten Lösungsschritte finden (126/11) 15. Lösungswege vergleichen (125/1) Modellieren 1. wesentliche Informationen entnehmen und strukturieren (121) 2. ergänzende Informationen beschaffen und dazu Informationsquellen nutzen (139; 135) 4. relevante Größen und ihre Beziehungen identifizieren (135) 6. Grundvorstellungen zu mathematischen Operationen nutzen und die Eignung mathematischer Verfahren einschätzen (122/1; 131/1; 137/1) 7. zu einer Situation passende mathematische Modelle (z.B. arithmetische Operationen, geometrische Modelle, Terme und Gleichungen, stochastische Modelle) auswählen oder konstruieren (135) 11. die aus dem mathematischen Modell gewonnene Lösung in der jeweiligen Realsituation überprüfen (122/3) 7. Kapitel: Umfang und Flächeninhalt 18 Stunden 147 – 150 Flächen vergleichen, zerlegen und parkettieren mit gleichen Figuren und Quadratzentimetern Flächeninhalt und Umfang von Rechtecken berechnen und die zugehörigen Formeln kennen BLEIB FIT: Wiederholung von 151 – 154 155 Kommunizieren 1. Mathematische Einsichten und Lösungswege schriftlich dokumentieren oder mündlich darstellen und erläutern (123/4) 4. bei der Darstellung der Ausführungen geeignete Medien einsetzen (123/2) Inhaltsbezogene Kompetenzbereiche Zahl – Variable – Operation (23) Sachsituationen (auch aus der Geometrie) durch Zahlterme beschreiben (M,E) Messen (1) Messvorgänge und die Verwendung von Einheiten erläutern (2) im Umfeld Längen und Flächeninhalte messen (5) Einheiten für Flächeninhalt verwenden und (in benachbarte Einheiten G) umwandeln (9) den Umfang von Rechteck und Quadrat bestimmen Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig Grundwissen + Wissen – Anwenden – Vernetzen Maßeinheiten für den Flächeninhalt kennen und umrechnen, vermischte Sachaufgaben Texte lesen und verstehen, zu gegebenen Problemstellungen aus dem Themenbereich „Klassenraumgestaltung“ und „Tierhaltung“ sachgerechte Modellierungen vornehmen sowie Lösungen finden und darstellen TÜV und Diagnosetest 156 – 157 158 – 164 (11) die Formel für den Flächeninhalt eines Rechtecks mit dem Grundprinzip des Messens erklären (13) den Flächeninhalt von Quadrat und Rechteck berechnen und den Flächeninhalt von daraus zusammengesetzten Figuren bestimmen 165 – 166 167 – 168 Prozessbezogene Kompetenzbereiche Argumentieren und Beweisen 1. in mathematischen Zusammenhängen Vermutungen entwickeln und als mathematische Aussage formulieren (149/3; 152/9) 8. mathematische Verfahren und ihre Vorgehensweisen erläutern und begründen (151/4) 9. beim Erläutern und Begründen unterschiedliche Darstellungsformen verwenden (verbal, zeichnerisch, tabellarisch, formalisiert) (148/1) Probleme lösen 6. das Problem durch Zerlegen in Teilprobleme oder das Einführen von Hilfsgrößen oder Hilfslinien vereinfachen (148/7) 13. kritisch prüfen, inwieweit eine Problemlösung erreicht wurde (151/1) 14. Fehler analysieren und konstruktiv nutzen (151/1) 15. Lösungswege vergleichen (151/2) Modellieren 1. wesentliche Informationen entnehmen und strukturieren (165/1) 5. die Beziehungen zwischen diesen Größen mithilfe von Variablen, Termen, Gleichungen, Funktionen, Figuren, Diagrammen, Tabellen oder Zufallsversuchen beschreiben (165/1; 166/1) 6. Grundvorstellungen zu mathematischen Operationen nutzen und die Eignung mathematischer Verfahren einschätzen (158/3; 161) 8. Kapitel: Brüche und Dezimalzahlen 16 Stunden Kommunizieren 1. Mathematische Einsichten und Lösungswege schriftlich dokumentieren oder mündlich darstellen und erläutern (153/1) 2. Ergebnisse strukturiert präsentieren (158/1) 7. aus Quellen (Texten, Bildern und Tabellen) und aus Äußerungen anderer mathematische Informationen entnehmen (165/1; 166/1,3) Inhaltsbezogener Kompetenzbereich Zahl – Variable – Operation Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig Stammbrüche in Darstellungen (Bild, Grafik, Text) erkennen und Anteile von Größen bestimmen Bruch-Begriff und Bruch-Darstellung erarbeiten und Bruchteile von Größen ermitteln Bruchteile auf dem Nagelbrett Bruchteile von (Maß-)Zahlen als Darstellung von Rechen-Ergebnissen (Division) interpretieren und bestimmen + Brüche größer als 1 Addition und Subtraktion von Brüchen mit gleichem Nenner BLEIB FIT: Wiederholung von Grundwissen Dezimalzahlen darstellen (Stellenwerttafel, Zahlenstrahl), ordnen und runden Addieren und Subtrahieren von Dezimalbrüchen Informationen aus Texten, Bildern und Tabellen entnehmen und damit anwendungsorientierte Aufgaben lösen TÜV und Diagnosetest 169 – 171 172 – 174 175 176 177 178 – 180 181 182 – 185 186 – 188 189 – 191 192 – 193 (5) Brüche zur Beschreibung von Realsituationen verwenden, insbesondere unter den Aspekten Anteil, Operator (M, E) Maßzahl einer Größe (9) erläutern, dass zwischen zwei verschiedenen rationalen Zahlen stets beliebig viele weitere rationale Zahlen liegen (M,E) (10) in einfachen Fällen Brüche in Dezimalzahlen und abbrechende Dezimalzahlen in Brüche umwandeln (13) positive Dezimalzahlen schriftlich addieren und subtrahieren (18) (einfache G) positive rationale Zahlen in Bruch- und in Dezimaldarstellund addieren und subtrahieren (19) Zahlenwerte und Größenangaben (situationsgerecht M, E) runden und gerundete Angaben interpretieren Prozessbezogene Kompetenzbereiche Argumentieren und Beweisen 1. in mathematischen Zusammenhängen Vermutungen entwickeln und als mathematische Aussage formulieren (184/6) Probleme lösen 1. das Problem mit eigenen Worten beschreiben (178/8) 2. Informationen aus den gegebenen Texten, Bildern und Diagrammen entnehmen (189/1,2) 9. durch Vorwärts- oder Rückwärtsarbeiten Lösungsschritte finden (188/18) 15. Lösungswege vergleichen (186/1) Modellieren 1. wesentliche Informationen entnehmen und strukturieren (189/1) 4. relevante Größen und ihre Beziehungen identifizieren (189/1,2) 8. Hilfsmittel verwenden (175) Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen 3. zwischen verschiedenen mathematischen Darstellungen wechseln (174/1) Diagnosearbeiten 2 Stunden Aufgaben zur Diagnose des Leistungsstands am Ende des Schuljahrs aus allen Stoffgebieten 194 – 197 Übungen mit Selbstkontrolle und regelmäßige Lernstanderhebungen kontrollieren die Effektivität des Unterrichts, geben Lehrenden und Lernenden Rückmeldungen und bereiten auf Lernstanderhebungen vor. Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig Stoffverteilungsplan Sekundo 5 Baden-Württemberg – auch im Internet als Worddokument unter www.schroedel.de © 2015 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig