5. Akustik

5. Akustik
Autoren: Jens Fruhauf und Stephan Trumm
Version: 14.11.1997
26.11.1997 (AK)
Dieser Versuch beschaftigt sich mit der Ausbreitung von Schall, der Analyse von
Schall und der Psychoakustik. Sie werden dabei ein Schallpegelmegerat und
ein Audiometer als spezische Megerate kennenlernen. Ferner wird ein PC mit
\Soundkarte" zur Schallerfassung und Auswertung Verwendung nden.
5.1 Physikalische Grundlagen
Die Akustik behandelt die Entstehung, die U bertragung und den Empfang von Schall.
Als Schall bezeichnet man mechanische Schwingungs{ und Wellenvorgange in elastischen Medien (Gasen, Flussigkeiten, Festkorpern). Die Erkenntnis, da es sich bei
Schall um ein Wellenphanomen handelt, ist bereits 2000 Jahre alt. Ein romischer Architekt, der mit dem Bau von Amphitheatern beschaftigt war, verglich den Schall mit
Wellen im Wasser. Tabelle 5.1 zeigt eine grobe Frequenzeinteilung der verschiedenen
Schallbereiche.
Tabelle 5.1:
Frequenzeinteilung der verschiedenen Schallbereiche
Schallbereich
Frequenz
Infraschall
< 16 Hz
horbarer Schall 16 Hz < < 16 kHz
Ultraschall
16 kHz < < 10 MHz
Hyperschall
10 MHz < Interessant fur die Technik ist vor allem der Ultraschall. Die meisten Anwendungen
des Ultraschalls beruhen auf den hohen Beschleunigungen, die im Schallfeld auch bei
relativ geringer Leistung auftreten, da diese proportional 2 sind. Einige Anwendungen
sind :
Herstellung oder Verbesserung von Emulsionen,
Reinigung von Werkstucken,
Einleitung oder Beschleunigung von chemischen Reaktionen,
57
58
5. Akustik
Entgasen von Flussigkeiten,
Erwarmung und Trocknung von schallabsorbierenden Stoen,
Bohren, Frasen und Schneiden,
Aunden von Fehlern im Innern von Werkstoen.
Ein weiterer wichtiger Punkt ist der Schallschutz am Arbeitsplatz. Sie werden deshalb
in diesem Versuch auch etwas uber dB Werte und Psychoakustik lernen.
5.1.1 Megroen des Schallfeldes
Schall ist ein Wellenphanomen. Die Molekule des ubertragenden Mediums (z.B. Luft)
schwingen dabei parallel zur Ausbreitungsrichtung des Schalls vor und zuruck, wobei
sie im Medium Bereiche hoheren und niedrigeren Drucks erzeugen.
Schallgeschwindigkeit
Wir betrachten Schall naherungsweise als ebene Welle, die sich langs der positiven x{
Richtung fortpanzt. Dabei gehorcht die Auslenkung der Teilchen aus der Ruhelage
der Wellengleichung
= 0 cos (!t , kx);
0 ist die Schwingungsamplitude. Die Schallgeschwindigkeit ist die Ausbreitungsgeschwindigkeit der fortschreitenden Welle im Medium und ist durch die Beziehung
cs =
!
k
= 2k = gegeben. Dabei ist die Wellenlange , die Frequenz der Schallwelle. Die Schallausbreitung erfolgt sehr schnell, da das ubertragende Medium nicht mittransportiert werden
mu. cs hangt im wesentlichen von den Stoeigenschaften des Ausbreitungsmediums
ab. Da die Dichte eines Gases von der Temperatur abhangt, andert sich die Schallgeschwindigkeit mit der Temperatur.
Ein Experiment zur Bestimmung der Schallgeschwindigkeit wird in Versuch 1.2 vorgestellt. Um ein Gefuhl fur typische Schallgeschwindigkeiten in den verschiedenen Medien
zu bekommen, sind einige Werte in Tabelle 5.2 zusammengestellt.
Schallschnelle
Nicht zu verwechseln mit der Schallgeschwindigkeit ist die Schallschnelle u, die angibt,
mit welcher Geschwindigkeit sich die einzelnen Teilchen des Mediums bewegen.
u=
@
@t
= ,! 0 sin (!t , kx)
5.1 Physikalische Grundlagen
Tabelle 5.2:
59
Typische Schallgeschwindigkeiten (In Festkorpern und Flussigkeiten bei 200 C,
in Gasen bei 00 C und Normaldruck).
Festkorper
Aluminium
Blei
Eisen
[m/s] Flussigkeiten cs [m/s]
6420
Wasser
1464
1960
Alkohol
1170
5950
cs
Gase
Luft
Sauersto
Wassersto
Helium
Kohlendioxid
[m/s]
331,6
316
1284
965
259
cs
Schalldruck
Analog zur obigen Formel fur die Auslenkung der Teilchen erhalt man fur den Druck
im Schallfeld die Gleichung
pges = p0 + p sin (!t , kx)
mit dem Ruhedruck p0 (Atmospharendruck) und der durch die Schallwelle verursachten
Druckamplitude
p = cs ! 0 :
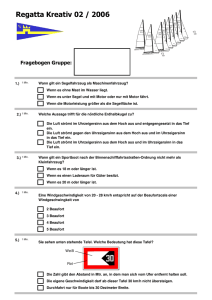
Bild 5.1:
Schallwelle in Luft: Oben eine schematische Darstellung der Dichte der Gasmolekule, unten der lokale Luftdruck im Vergleich zum Ruhedruck p0 .
Schallintensitat
Eine Schallquelle strahlt eine bestimmte Leistung (=Energie pro Zeit) ab. Um berechnen zu konnen, welcher Anteil dieser Leistung bei einem Mikrophon (oder Ohr)
ankommt, benotigen wir die Leistung pro Flache, die sog. Schallintensitat I .
Die Energiedichte e einer Welle ist aus der Mechanik bekannt (e = 12 !202); damit
erhalt man fur die Intensitat der Schallwelle die Beziehung
1
1 p2 / p2:
I = cs 02 ! 2 =
2
2 cs
60
5. Akustik
Die Schallintensitat hangt also quadratisch vom Schalldruck ab.
Um die Abhangigkeit der Schallintensitat vom Abstand von der Schallquelle zu bestimmen, betrachtet man eine isotrope (in alle Richtungen gleiche) Abstrahlung einer
punktformigen Schallquelle in den Raum. Da die Intensitat von der durchstrahlten
Flache abhangt und diese wie r2 (Kugelache) wachst, kann man leicht einsehen, da
die Schallintensitat mit dem Quadrat des Abstandes zur Schallquelle abnimmt:
I (r ) =
I0
:
r2
Diese Abstandsabhangigkeit soll im Versuch 1.1 uberpruft werden.
Schallpegel
In der Akustik sind Drucke uber viele Groenordnungen relevant. Deshalb benutzt man
in der Praxis den sog. Schalldruckpegel oder kurz Schallpegel L, der eine Umrechnung
des Schalldrucks bzw. der Schallintensitat in ein logarithmisches Ma darstellt:
L = 20 dB log
p
p0
!
= 10 dB log II
0
mit p0 = 20 Pa bzw. I0 = 10,12 W/m2 (Horschwelle bei 1 kHz). Dieses logarithmische
Ma hilft, Schall mit stark unterschiedlichen Intensitaten gleichzeitig auf einer Skala
darstellen zu konnen. Es ist das Verhaltnis zweier Schallfeldgroen. Die Groe im Nenner ist eine festgelegte Bezugsgroe. Naturlich bezieht sich L immer auf eine Frequenz
bzw. einen Frequenzbereich.
Rechnen mit Schallpegeln
Da der Schallpegel L eine logarithmische Groe ist, durfen beispielsweise zur Berechnung des Gesamtschallpegels bei der U berlagerung von zwei Schallquellen nicht einfach
die Pegel L1 und L2 addiert werden. Vielmehr ist hier mit den physikalischen Groen
p bzw. I zu rechnen.
Sind bei den zu berechnenden Schallfeldern die exakten Wellengleichungen bekannt, so
ist die zu betrachtende Groe der Schalldruck p. Es konnen Interferenzen auftreten,
die speziell beachtet werden mussen.
Im taglichen Leben (und in diesem Praktikum) werden Sie nur inkoharente Schallwellen (d.h. solche ohne exakt bestimmte Phasenlage) antreen. In diesem Fall ist die
Intensitat I / p2 die Groe, mit der gerechnet werden mu.
Um beispielsweise den gemeinsamen Pegel zweier gleicher Schallquellen L1 = L2 bzw.
I1 = I2 zu berechnen, addiert man die Intensitaten: Iges = I1 + I2 = 2I1. Damit folgt:
Lges
I I 1
= 10 dB log I = 10 dB log 2 I =
0
0I = 10 dB log I1 + log(2) = L1 + 3; 01 dB
0
Eine Verdopplung der Intensitat I entspricht also einer Zunahme des Schallpegels L
um etwa 3 dB; eine Erhohung um 10 dB oder 20 dB bedeutet eine Verzehn- bzw. Verhundertfachung der Intensitat.
5.1 Physikalische Grundlagen
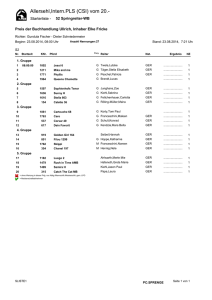
Bild 5.2:
61
Querschnitt durch das menschliche Ohr. (aus testo, Schallbel)
5.1.2 Psychoakustik
Das menschliche Ohr
Abbildung 5.2 zeigt den Aufbau des menschlichen Ohres. Die Ohrmuschel sammelt die
Luftschallwellen und leitet sie uber den aueren Gehorgang an das Trommelfell weiter.
Diese Teile bilden das Auenohr . Im Mittelohrbereich benden sich in der Paukenhohle
Hammer , Ambo und Steigbugel , die durch das Trommelfell in mechanische Schwingungen versetzt werden. Sie verstarken die Schallwellen (Auslenkungen im nm-Bereich!).
Auch die Resonanzwirkung des Gehorganges und das ovale Fenster beim U bergang
zum Innenohr wirken verstarkend. Die Eustachische Rohre ist die Verbindung vom
Mittelohr zum Nasen{Rachen Raum (Druckausgleich). Im Innenohr bendet sich das
Hororgan, die Schnecke , Diese ist mit Flussigkeit gefullt und setzt die empfangenen
Horimpulse in elektrische Nervenimpulse um, die dann zum Gehirn weitergeleitet werden. Das eigentliche Transformationsorgan ist das Cortische Organ dessen Haarzellen
die Fourieranalyse durchfuhren. Im Innenohr bendet sich auch der Vestibularapparat ,
der dem Gleichgewichtssinn zugeordnet ist.
Der Horbereich
Die beim Horschall auftretenden Druckschwankungen sind meist sehr gering. Bei einem
Normaldruck von 1013 mbar genugen schon A nderungen im Nanobar-Bereich, um eine
Reizung des menschlichen Ohres herbeizufuhren.
Das menschliche Ohr kann Drucke zwischen 10,5 Pa (untere Horgrenze) und 102 Pa
(Schmerzgrenze) wahrnehmen. Kein Megerat kann ohne Umschaltvorrichtung einen
derartig groen Bereich (7 Groenordnungen!) darstellen. Fur I0 = 10,12 W/m2 ndet man auch die Bezeichnung Horschwelle. Sie ist die vom menschlichen Ohr gerade noch wahrnehmbare Schallintensitat bei 1 kHz. Der zugehorige Druck ist 20 Pa.
Das entspricht einer Bewegung der Luftteilchen von nur 10,9 cm (zum Vergleich: Der
Durchmesser des Wasserstoatoms betragt 10,8 cm.).
62
5. Akustik
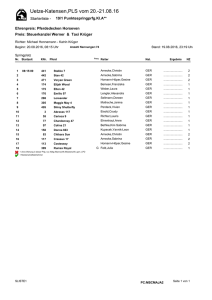
Bild 5.3:
Kurven gleicher Lautstarke Ls . (aus VDI, Physik fur Ingenieure)
Lautstarkeempnden
Die dB{Skala gibt jedoch nicht die genaue Horempndung wieder, da das menschliche
Horvermogen frequenzabhangig ist. Bei niedrigen und hohen Frequenzen ist die Empndlichkeit des Ohres geringer, wahrend sie bei etwa 1 kHz maximal ist. Der Schallpegel
mu also bei tiefen und hohen Frequenzen sehr viel hoher sein als am Empndlichkeitsmaximum, wenn in allen Fallen eine gleich starke Empndung hervorgerufen werden
soll. Der Mastab fur das Lautstarkempnden des Gehors ist die Lautstarke Ls (Einheit phon). Sie ist so gewahlt, da bei einer Schallfrequenz = 1 kHz der Wert der
Lautstarke (in phon) gleich dem Schalldruckpegel (in dB) ist.
Die Ermittlung der Lautstarke ist somit immer eine Vergleichsmessung. Fuhrt man
solche Vergleichsmessungen im gesamten Horbereich durch, so erhalt man Kurven gleicher Lautstarke (siehe Abbildung 5.3). Dabei gibt jede Kurve an, welcher Schallpegel L
in Abhangigkeit von der Frequenz notig ist, damit das Ohr eine bestimmte Lautstarke
Ls empndet. In diesem Diagramm ist zu sehen, da bei 1 kHz ein Pegel von 70 dB
ausreicht, um die gleiche Lautstarke (70 phon) hervorzurufen, wie sie ein Pegel von
80 dB bei 63 Hz erzeugt. Das menschliche Gehor nimmt Lautstarkeunterschiede von
Ls = 1 phon gerade noch wahr. Die Horschwelle liegt (fur alle Frequenzen) bei etwa
0 phon.
Das subjektive Lautstarkeempnden ist dabei keineswegs linear von der Schallintensitat
abhangig. Im Bereich ab 40 phon entspricht eine Verdoppelung der gehorten Lautstarke
einer Zunahme von Ls um etwa 10 phon { also einer um den Faktor 10 hoheren Intensitat. Unterhalb 40 phon ist das Ohr empndlicher.
Die A-Bewertung
Weil das Ohr unterschiedlich empndlich auf verschiedene Frequenzen reagiert, ware
die ideale Angabe der Lautstarke eines Gerausches der Wert in phon. Da dessen Bestimmung jedoch relativ kompliziert ist, wird allgemein die Lautstarke in der sog.
A-Bewertung angegeben. Dazu wird zu dem gemessenen Schallpegel (dem sog. unbe-
5.1 Physikalische Grundlagen
Tabelle 5.3:
63
Beispiele fur Lautstarken
leises Flustern
10 Phon
deutliche Sprache
50 Phon
Dusenugzeug
120 Phon
(100 m Entfernung)
Diskothek
100{130 Phon
Prelufthammer
130 Phon
(1 m Entfernung)
werteten Schallpegel) eine bestimmte Konstante addiert bzw. davon subtrahiert; Abbildung 5.4 zeigt diese in Abhangigkeit von der Frequenz. Die Angabe des Schallpegels
erfolgt dann in der Einheit dB(A). Ein 1 kHz-Ton mit 70 dB entspricht demnach auch
70 dB(A), ein 100 Hz-Ton der gleichen Intensitat jedoch nur etwa 53 dB(A) { weil er
entsprechend leiser gehort wird. Aufgrund dieser recht einfachen Umrechnung gelten
fur die A-bewerteten Mewerte die gleichen Rechenregeln wie fur die unbewerteten
Groen. Neben der A- wurden auch noch B-, C- und D-Bewertungskurven international standardisiert; allerdings entspricht die A-Bewertung bei Lautstarken unter 90 phon
(also in dem Bereich, mit dem man meistens zu tun hat) dem Lautstarkeempnden
des Menschen am besten. Sie ist deshalb die bei Schallpegelmessungen am haugsten
gebrauchte Bewertungskurve; auch in diesem Praktikum werden Sie nur un- und Abewertet messen.
10
Frequenz (Hz)
6300
10000
4000
1600
2500
1000
400
630
160
-10
250
100
63
25
40
Korrekturterme (dB)
0
-20
-30
-40
-50
Bild 5.4:
Bewertungskurven fur die A-bewertete Messung
5.1.3 Frequenzanalyse
In der Natur treten selten rein harmonische (sinusformige) Schwingungen auf. Musikinstrumente erzeugen zwar in erster Linie einen Sinuston (den Grundton), zusatzlich
aber auch Sinusschwingungen, deren Frequenzen ganzzahlige Vielfache der Grundtonfrequenz sind. Diese nennt man die Obertone; ihre Zusammensetzung hangt von der
Bauform des Klangkorpers ab und ist charakteristisch fur jedes einzelne Instrument.
64
5. Akustik
Tabelle 5.4:
Klassikation von Schallwellen nach Frequenz und Amplitude
Ton
sinusformige Schwingung mit konstanter Amplitude. Die Tonhohe wird durch die Frequenz, die
Tonstarke durch das Quadrat der Schwingungsamplitude bestimmt. (vgl. Abb. 5.5, oben links)
Klang
periodische, nicht rein sinusformige Schwingung,
die durch die U berlagerung des Grundtons mit
verschiedenen Obertonen zustande kommt.
Gerausch vollkommen unperiodischer Schwingungsvorgang. (vgl. Abb. 5.5, mitte rechts)
Knall
kurzer Schallimpuls, der Schwingungen eines
weiten Frequenzbereiches enthalt. Die Amplitude fallt rasch ab.
Gerausche und gesprochene Sprache sind U berlagerungen einer groen Anzahl von
Frequenzen, deren Zusammensetzung sich im zeitlichen Verlauf standig andert. Die vom
Ohr wahrgenommenen Schallwellen klassiziert man nach ihrem Frequenzspektrum
und dem zeitlichen Verlauf ihrer Amplitude (siehe Tabelle 5.4).
Grundlagen der Fourier-Analyse
Mathematisch lat sich beweisen, da man jedes beliebige, auch nicht periodische Signal
aus (unendlich vielen) harmonischen Schwingungen zusammensetzen kann. Dies nennt
man die Fourier-Synthese .
Die Fourier-Analyse ist die Umkehrung der Fourier-Synthese: Mit ihr kann man aus
der per Mikrofon aufgezeichneten Schwingung die enthaltenen Frequenzanteile errechnen.
Ist das Signal selbst periodisch, so enthalt es neben der Grundschwingung, die dieselbe
Frequenz wie das Signal besitzt, nur Oberschwingungen, deren Frequenzen ganzahlige
Vielfache der Grundfrequenz sind. In diesem Fall spricht man von einer Fourier-Reihe.
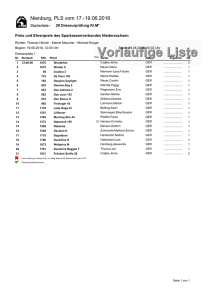
In Abbildung 5.5 sind verschiedene periodische Signale und ihre zugehorigen Frequenzspektren (Fourier-Spektren) abgebildet.
Im Versuch 2 werden Sie die Fourier-Spektren von verschiedenen Gerauschen und
Klangen und ihre Veranderung mit der Zeit untersuchen. Verwendet wird die sog.
Fast-Fourier-Transformation (FFT), die auf einem Computer in sehr kurzer Rechenzeit
brauchbare Ergebnisse liefert.
Ein optisches Analogon der Fourier-Analyse ist das Prisma, mit dem sich das weie
Sonnenlicht in seine Spektralanteile zerlegen lat.
Die Schwebung
Die einfachste Form von U berlagerungen ist die Schwebung. In Versuch 2.2 werden
Sie mit Stimmgabeln zwei harmonische Wellen erzeugen und ihre U berlagerung untersuchen. Abbildung 5.6 zeigt qualitativ die beiden (gleichlauten) Schwingungen mit den
5.1 Physikalische Grundlagen
Bild 5.5:
65
Zeitlicher Verlauf einiger akustischer Signale sowie die zugehorigen FourierSpektren
66
5. Akustik
Frequenzen 1 = T1,1, 2 = T2,1, deren Summe eine Welle mit der Frequenz 0 = (T 0),1
ergibt. Diese schwillt mit der Schwebungsfrequenz s = (Ts),1 an und ab. Es gilt:
+ 2
0 = 1
s = 1 , 2
2
Bild 5.6:
Schwebung. Im oberen Bild sind zwei harmonische Schwingungen mit leicht
unterschiedlicher Frequenz aufgetragen, unten ihre Summe. Beachten Sie, da
Ts keine echte Schwingungsdauer, sondern nur die Zeit zwischen zwei Minima
der Schwebung darstellt!
Die Summe der beiden Wellen lat sich dann schreiben als:
f (t)
= f1(t) + f2(t) = cos(21t) + cos(22t)
= 2 cos(2 0t) cos(2 2s t):
Im letzten Ausdruck der rechten Seite stellt der erste Kosinus die Schwingung dar, der
zweite die Modulation mit der Schwebungsfrequenz.
5.2 Metechnik
5.2.1 Schalldetektion
Im Rahmen des Versuchs werden Sie zwei Gerate zur Detektion von Schall benutzen.
Das Mikrophon gehort zu den elektroakustischen Wandlern, d.h. es wandelt den Schalldruck in elektrische Spannung um. Im Versuch wird als Memikrophon ein Kondensatormikrophon verwendet. Eine hauchdunne metallische Membran bildet mit dem
Mikrofongehause einen Kondensator, dessen Kapazitat sich je nach Auslenkung der
Membran andert. Die Spannung am Kondensator wird konstant gehalten, so da je
nach Membranbewegung ein Be{ bzw. Entladestrom iet, der mittels eines Widerstandes in eine mebare Spannung umgewandelt wird. Diese ist dann in erster Naherung proportional zur Geschwindigkeit der Membran und somit zur Geschwindigkeit
der Luftteilchen.
Zur quantitativen Messung von Schallpegeln verwendet man das Schallpegelmegerat.
Es besteht im wesentlichen aus einem Mikrophon und einem Eektivwertdetektor, der
5.2 Metechnik
67
die Signale des Mikrophons in Schallpegel umrechnet. Fur bewertete Messungen kann
ein Bewertungslter vor den Detektor geschaltet werden. Eine schematische Darstellung
der Komponenten eines Schallpegelmegerates zeigt Abbildung 5.7.
U bersteuerungsdetektor
Mikrofon
j
Vorverstarker
Bewertungslter
Halteschaltung
Verstarker
Eektivwertdetektor
Anzeige
93.7
Zeitkonstanten
\F"/\S"
Bild 5.7:
Schematischer Aufbau eines Schallpegelmegerates (nach testo, Schallbel)
5.2.2 Meprobleme
Schall hat die Eigenschaft, sich an Wanden, Decken und am Korper des MegeratBenutzers zu reektieren. Dadurch konnen Mefehler auftreten. Folgende Regeln sind
zu beachten:
Das Mikrophon des Megerates mit sehr gerichtet und mu daher immer auf die
Schallquelle zeigen.
Das Mikrophon soll mindestens 30 cm vom Korper gehalten werden, um Reexionen am Korper zu vermeiden. Ideal ware ein in Richtung der Schallquelle
ausgestreckter Arm. Wesentlich von Vorteil ist deswegen ein abnehmbares Mikrophon.
Schallpegel{Megerate sind zur Messung im Freifeld konzipiert. Von einem Freifeld
spricht man, wenn sich keine storenden Gegenstande im Schallfeld benden und somit
eine freie Schallausbreitung gewahrleistet ist. In der Praxis spricht man auch dann von
einem Freifeld, wenn die Reexionen so schwach sind, da sie gegenuber dem direkten
Feld der Schallquelle nicht mehr ins Gewicht fallen.
In einem geschlossenen Raum kann es zu Reexionen an den Wanden, der Decke
und den Einrichtungsgegenstanden kommen. Das dadurch entstehende Feld nennt man
Nachhallfeld.
Beispiel:
Buroraum mit Teppichboden, Vorhangen und Stellwanden ! Freifeld
68
5. Akustik
Kellerraum mit Betonwanden, ohne Moblierung, sehr stark hallend ! Nachhallfeld
In den Raumen des Praktikums werden Sie ein Mittel zwischen diesen beiden Extremen
vornden. In geringem Abstand zur Schallquelle werden Sie ein gutes Freifeld messen
konnen. Da die Intensitat des direkten Schalls mit der Entfernung von der Schallquelle
abnimmt, wahrend das Nachhallfeld im gesamten Raum etwa konstant ist, wird letzteres ab einem gewissen Abstand von der Schallquelle uberwiegen. Diesen Abstand nennt
man Hallradius. Auerhalb des Hallradius hangt dann der gemessene Schallpegel nicht
mehr vom Abstand zur Schallquelle ab.
5.3 Einfuhrung und Demonstrationen
Bevor Sie mit den Experimenten beginnen, wird der Betreuer Ihnen einige Fragen zum
Inhalt des Praktikums stellen, Ihnen einiges erklaren, und mit Ihnen eine einfuhrende
Messung durchfuhren.
5.3.1 Das Kundtsche Rohr
Das Kundtsche Rohr dient zum Nachweis stehender Wellen in Luft und anderen Gasen. Es eignet sich auch dazu, Wellenlangen zu bestimmen.
Das Rohr wird mit wenig Korkpulver befullt, und an einem Ende mit einem Schieber
verschlossen. In das andere Ende blast man mit einer Pfeife hinein, um eine stehende
Welle zu erzeugen. Mit dem Schieber wird wahrend des Versuches die schwingende
Lange des Rohres auf ein Vielfaches der halben Wellenlange eingestellt. (Warum?)
Wegen der Reexion der Schallwelle am Schieber bildet sich dabei im Rohr eine stehende Welle aus. An ihren Bauchen bewegt sich die Luft besonders stark, an den Knoten
dagegen kaum. Deshalb sammeln sich die Korkteilchen an den Knoten der Welle.
Neben diesem Eekt werden Sie noch kleinere Wellen sehen. Diese kann man auf Wirbelbildungen im Rohr zuruckfuhren.
Vermessen Sie nun die Wellenlange im Rohr und bestimmen Sie mit Hilfe des Computers und des Programms Analyse die Frequenz der Pfeife. Dabei wird Ihnen der
Betreuer die Bedienung des Systems demonstrieren.
Schatzen Sie aus diesen Daten die Schallgeschwindigkeit in Luft ab.
5.3.2 Das menschliche Ohr
An einem Modell des menschlichen Ohres wird Ihnen Ihr Betreuer den Horvorgang
erklaren. Siehe hierzu auch Abschnitt 5.1.2.
5.4 Versuchsdurchfuhrung
Hier sind die Experimente beschrieben, die Sie wahrend des Praktikums durchfuhren
sollen.
5.4 Versuchsdurchfuhrung
69
Tragen Sie alle Meergebnisse und Rechnungen in Ihr Protokollbuch ein und beantworten Sie auch die gestellten Fragen dort.
5.4.1 Ausbreitung von Schall
In diesem Teil sollen Sie sich mit den grundlegenden Eigenschaften der Ausbreitung
des Schallfeldes einer punktformigen Quelle beschaftigen.
Abstandsabhangigkeit der Intensitat
In diesem ersten Versuch sollen Sie bestimmen, wie die Intensitat des Schallfeldes einer
punktformigen Schallquelle vom Abstand von dieser Quelle abhangt.
1. Verwenden Sie den Kassettenrekorder als Schallquelle, als Signal dient das Terzpegelrauschen am Anfang der Praktikumskassette. Stellen Sie den Kassettenrekorder auf die Seite, so da der Lautsprecher oben steht. Drehen Sie den Lautstarkeregler auf Maximum.
2. Zum Messen der Schallintensitat dient das Schallpegelmegerat mit dem dazugehorigen Mikrophon.
Montieren Sie das Mikrophon so auf einen Reiter der Dreikantschiene, da es
genau so hoch wie der Lautsprecher steht (Ziehen Sie dazu die Gewindestange
mehr oder weniger weit aus dem Schaft.)
3. Messen Sie die Schallintensitat I in verschiedenen Abstanden x von der Schallquelle.
Beginnen Sie bei x = 4cm und fahren Sie in 1cm-Schritten fort. Ab 10cm genugt
es, wenn Sie in 2cm-Schritten weitermachen. Messen Sie solange, bis Sie an drei
verschiedenen Stellen in etwa den gleichen Pegel ermitteln.
Verschieben Sie dazu den Reiter auf der Dreikantschiene und lesen Sie auf der
Skala die Entfernung ab. Der Abstand zwischen Lautsprechermembran und -gitter
ist auf dem Kassettenrekorder angegeben.
Zum Schallpegelmegerat:
Verwenden sie die Einstellungen langsam und linear. Fangen Sie im hochsten
Mebereich 90 an, und verringern Sie ihn solange (erst 60, dann 30), bis Sie einen
deutlichen Zeigerausschlag sehen konnen. Der Mewert ergibt sich als Summe
der Mebereichsbasis (30dB, 60dB oder 90dB) und des an der Skala abgelesenen
Wertes.
Verwenden Sie den Spiegel oberhalb der Skala um den Wert parallaxenfrei abzulesen. Schauen Sie dazu so auf das Megerat, da der Zeiger sein Spiegelbild
verdeckt.
4. Zeichnen Sie ein doppelt-logarithmisches x-I -Diagramm. Beachten Sie dabei, da
Ihre Schallpegelwerte (in dB) die Schallintensitat bereits logarithmiert wiedergeben. Versuchen Sie durch die Skalierung der Achsen das Papier moglichst gut
70
5. Akustik
auszunutzen. Es mu dabei weder der Nullpunkt der Intensitat noch der des
Ortes in dem Diagramm zu sehen sein.
5. Beschreiben und erklaren Sie den Verlauf der Kurve. Schatzen Sie den Hallradius
rHall der Versuchsanordnung ab.
Schallgeschwindigkeit in Luft
Die Schallgeschwindigkeit soll aus der Laufzeit eines Schallsignals in Luft bestimmt
werden.
1. Verwenden Sie die Dreikantschiene als Laufstrecke und die beiden auf Reitern
montierten, kleinen, weien Mikrophone.
2. Zum Messen der Laufzeit dient das Programm Schallgeschwindigkeit.
Nach dem Einschalten des Rechners loggen Sie sich als Benutzer Akustik ohne
Pawort ein. Es erscheint dann automatisch das Hauptmenu, in dem Sie zwischen den Programmen Analyse und Schallgeschwindigkeit wahlen oder das
Programm beenden konnen.
Drucken Sie den Button Schallgeschwindigkeit, um dieses Modul zu starten.
3. Messen Sie die Schallaufzeit fur eine Strecke von l = 5cm
4. Stellen Sie dazu die beiden Mikrophone in diesem Abstand voneinander auf.
5. Starten Sie die Messung, indem Sie den Button Messung drucken.
6. Sie haben nun 5 Sekunden Zeit, ein Schallsignal durch den Zusammensto der
beiden Metallkugeln zu erzeugen.
Achten Sie dabei insbesondere darauf, da die Klickstelle und die beiden Mikrophone auf einer Geraden liegen, denn nur dann ist die Strecke zwischen den
Mikrophonen gleich dem Weg des Schallsignals.
7. Nach Ablauf der 5 Sekunden Aufnahmedauer zeigt das Programm die von den beiden Mikrophonen registrierten Signale an. Es erkennt dabei automatisch, wann
exakt der Knall registriert wurde und stellt am Bildschirm nur den relevanten
Ausschnitt der Signale dar. Sie sollten daher zwei zuerst ruhige Signale sehen,
die (zeitlich leicht versetzt) plotzlich heftig ausschlagen. Wiederholen Sie die Messung, falls der Knall nicht eindeutig zu identizieren sein sollte.
Suchen Sie in den beiden Signalen zwei sich entsprechende Stellen (z.B. jeweils
das erste Maximum) und markieren sie diese mit den beiden Markern. Lesen Sie
die Zeitdierenz ab.
Die Zeiten (die x-Achse ist die Zeitachse) werden in Sekunden angegeben. Dahinter steht eventuell eine Einheit, z.B. m fur Milli- und u fur Micro. 123.4m bedeutet
also 123,4 Millisekunden oder 0,1234 Sekunden.
5.4 Versuchsdurchfuhrung
71
Mit dem Button Skalierung konnen Sie die Darstellung der Kurve auf dem
Monitor optimieren. Die Skalen werden dann automatisch so eingeteilt, da die
Kurven die ganzen Fenster einnehmen.
8. Wiederholen Sie diese Messung (Schritte (4) bis (7)) fur Abstande von l = 10cm,
20cm, 40cm, 60cm, 70cm und 80cm.
9. Zeichnen Sie ein Weg-Zeit-Diagramm auf Millimeterpapier und berechnen Sie aus
den gemessenen Werten die Schallgeschwindigkeit.
Hinweis: Das Programm erkennt den Klick anhand eines Triggers. Sollten Sie Probleme
haben, weil der Trigger nicht auslost, andern Sie den Wert im Feld Trigger. Fragen
Sie dazu Ihren Betreuer.
5.4.2 Analyse von Schall
Im zweiten Teil des Praktikums sollen Sie die Wellennatur von Schall und typische
Wellenphanomene wie die U berlagerung zweier Wellenfelder kennenlernen.
Einfuhrung in die Fourier-Analyse
Machen Sie sich mit dem Programm Analyse und der Fourier-Analyse vertraut.
Lassen Sie sich dazu von Ihrem Betreuer drei Stimmgabeln geben, von denen sich zwei
untereinander um ca 50Hz und von der dritten um etwa 90Hz bis 120Hz. unterscheiden
sollen.
1. Starten Sie das Programm Analyse.
(Beenden Sie das Programm Schallgeschwindigkeit, wenn Sie es noch nicht
getan haben, um ins Hauptmenu zuruckzukommen.)
2. Schlagen sie eine Stimmgabel an und setzen Sie sie auf die Holzkiste auf.
Richten Sie das groe Mikrophon auf den Resonanzkorper und schalten Sie es
ein.
3. Mit dem Button Aufnahme konnen Sie die Aufnahme starten. Es werden durchgangig ca. 50ms lange Samples aufgenommen und (fast) in Echtzeit Fourieranalysiert.
Im Fenster Signal wird das Schallsignal und im Fenster Spektrum das berechnete Fourier-Spektrum angezeigt. Wenn Sie ein schones Signal (Sinus-Signal
mit einem Peak im Spektrum) sehen, konnen Sie durch erneutes Drucken des
Aufnahme-Buttons die Aufnahme anhalten.
4. Messen Sie mit Hilfe des Markers im Fenster Signal die Dauer einer vollen
Schwingung. (Messen Sie zum Beispiel den Abstand zwischen zwei benachbarten
Maxima.) Es steht allerdings nur ein Marker zur Verfugung, so da Sie zweimal
messen und die zwei Zeiten voneinander abziehen mussen. Berechnen Sie daraus
die Frequenz der Schwingung.
72
5. Akustik
5. Lesen Sie nun (ebenfalls mit Hilfe eines Markers) im Fenster Spektrum die Frequenz der Schwingung ab.
6. Vergleichen Sie nun die unter Punkt (4) berechnete und die unter (5) abgelesene
Frequenz mit der auf der Stimmgabel angegebenen.
7. Wiederholen Sie die Schritte (2) bis (6) nun fur die anderen beiden Stimmgabeln.
8. Versuchen Sie, aus den Ergebnissen die Grenzen der Leistungsfahigkeit des Programms zu erkennen.
Diese konnen Sie bei guter Kenntnis der Fourier-Analysis vielleicht selbst erklaren. Fragen Sie anderenfalls Ihren Betreuer.
Schwebungen
Nun sollen Sie zwei reine Sinustone zu einer Schwebung uberlagern.
Stimmgabeln als Musterbeispiel Mit den Stimmgabeln aus dem vorigen Versuch
sollen Sie nun Schwebungen erzeugen und charakterisieren.
1. Schlagen Sie die zwei ahnlichen Stimmgabeln an und setzen Sie sie zusammen
auf den Resonanzkorper auf.
2. Starten Sie wie vorhin die Aufnahme.
3. Um die Schwebung moglichst schon zu sehen, sollten Sie das Mikrophon von oben
auf die Kiste richten, und links und rechts davon je eine Stimmgabel stellen.
Bewegen Sie die Stimmgabeln so lange zum Mikrophon hin oder von ihm weg,
bis beide Peaks im Fenster Spektrum in etwa gleich hoch sind und stoppen Sie
dann die Aufnahme, wenn Sie die Schwebung gut sehen.
4. Beschreiben Sie das Spektrum (eventuell unter Angabe von Frequenzen, die Sie
wie oben mit dem Marker messen konnen) und damit die Art der U berlagerung.
5. Messen Sie mit dem Marker im Fenster Signal die Dauer der Schwebung und
bestimmen Sie so die Schwebungsfrequenz.
6. Bestimmen Sie ebenso die Schwingungsfrequenz indem Sie die Schwingungsdauer
messen. Welcher grundsatzliche Unterschied besteht zwischen Schwebungs- und
Schwingungsfrequenz ?
7. Berechnen Sie zum Vergleich die Schwebungs- und die Schwingungsdauer aus den
Frequenzangaben auf den beiden Stimmgabeln.
8. Beschreiben Sie kurz, was Sie horen. Welche Frequenz(en) haben der Ton oder
die Tone, die Sie horen ?
5.4 Versuchsdurchfuhrung
73
9. Drucken Sie das Signal und das Spektrum aus, indem Sie den Druck-Button
betatigen. Zeichnen Sie die Schwebungs- und die Schwingungsdauer in den Ausdruck ein.
10. Wiederholen Sie die gesamte Aufgabe (Schritte (1) bis (9)) mit einer anderen
Stimmgabelkombination.
Schwebungsfrequenz im horbaren Bereich Tiefe Tone sind uber groe Entfernungen weiter horbar als hohe. Deswegen mochte man Schisbruchigen eine Pfeife mitgeben, die moglichst tiefe Tone erzeugt. Wollte man einen tiefen Ton direkt erzeugen,
wurde die Pfeife (Orgelpfeife) sehr unhandlich.
1. Als Signal dient hier eine Rettungspfeife, wie sie an Schwimmwesten getragen
wird. Nehmen Sie wie oben das Signal auf. Das ist jedoch nicht ganz einfach und
verlangt ein gewisses Geschick.
2. Messen Sie die Einzelfrequenzen und berechnen Sie Schwebungs- und Schwingungsfrequenz.
Welche Frequenz(en) liegen im horbaren Bereich?
3. Drucken Sie auch hier wieder das Signal aus und zeichnen Sie die Schwingungsund Schwebungsdauer ein.
4. Was horen Sie ?
Konnen Sie die beiden hohen Frequenzen noch (vielleicht sogar getrennt) wahrnehmen?
Das Mehrfrequenzwahlverfahren als Anwendung Das Mehrfrequenzwahlverfahren
(MFV) ist eine Anwendung der Schwebung in der Signaltechnik. Die Anrufbeantworterfernabfrage ist nichts anderes als das Wahlmodul eines modernen Telephons, das
die Signale nicht direkt auf die Leitung gibt, sondern per Lautsprecher horbar macht,
damit diese von einem anderen Telephon aus in die Leitung eingespeist werden konnen.
1. Messen Sie die Einzelfrequenzen der von den einzelnen Tasten erzeugten Signale
und versuchen Sie, das hinter dem MFV stehende System zu erkennen. Sie mussen
dazu nicht unbedingt alle Tasten ausprobieren.
2. Sobald Sie das System verstanden haben lassen Sie sich von einem Kollegen eine
Taste vorspielen und erraten Sie diese anhand der vom Computer vorgenommenen
Frequenzanalyse.
Tone, Klange und Gerausche
Tone Mit Tonen hatten Sie ja schon reichlich zu tun. Was genau ist ein Ton?
Pfeifen Sie in das Mikrophon und betrachten Sie das Spektrum Ihres Pfeifens.
Wurden Sie das Pfeifen als Ton bezeichnen?
74
5. Akustik
Klange Nehmen Sie Signal und Spektrum folgender Klange, die Sie auf der Praktikumskasette nden, auf.
Stoppen Sie dazu die Aufnahme dann, wenn ein stabiles Spektrum zu erkennen ist.
Versuchen Sie bei den Instrumenten, einen reinen Ton zu erwischen. Passen Sie den
angezeigten Bereich des Spektrums so an, da Sie alle Frequenzanteile des Signals sehen
konnen. Charakterisieren Sie die Spektren kurz und drucken Sie sie aus.
1. Zwei Rechtecksignale mit unterschiedlichen Frequenzen
Warum sieht das Rechtecksignal auf dem Computer gar nicht so \rechteckig"
aus?
2. Bratsche
3. Cello
4. Querote
5. Singen Sie in das Mikrophon.
Schaen Sie es, einen sauberen Klang zu singen?
6. Wenn Sie sich (freiwillig) noch andere Klange "ansehen\ wollen, nden Sie auf
der Praktikumskassette noch die Klange von drei verschiedenen Weinglasern und
einer Rohrenglocke.
Gerausche Rauschen ist nicht gleich Rauschen. Man kann verschiedene Arten von
Rauschen nach ihrer spektralen Zusammensetzung unterscheiden.
1. Beobachten Sie die Spektren von "rosa\ und "weiem\ Rauschen eine Zeit lang,
drucken Sie die beiden Spektren aus und vergleichen Sie sie. Die Frequenzachse
sollte dabei die Frequenzen bis etwa 6 kHz umfassen.
2. Wenn Sie Zeit haben konnen Sie auch noch die Pegel in den Oktavbandern mit
dem Schallpegelmegerat ermitteln. Fragen Sie dazu Ihren Betreuer.
3. Vergleichen Sie die beiden Spektren und versuchen Sie die Begrie "rosa\ und
wei\ zu erklaren.
"Tip:
Aus welchem anderen Bereich der Physik kommen diese Begrie? Was bedeuten Sie dort?
4. Vergleichen Sie auch die beiden Horeindrucke.
Nach der Denition ist auch die menschliche Stimme ein Gerausch. Sprechen Sie in das
Mikrophon und bestimmen Sie die Tonlage Ihrer Stimme.
5.4.3 Rezeption von Schall - Psychoakustik
Im letzten Teil des Praktikums sollen Sie die Rezeption des Schalls durch den Menschen
und die Problematik einer zu hohen Larmbelastung kennenlernen.
5.4 Versuchsdurchfuhrung
75
Audiometrie
In der Audiometrie wird Ihr Gehor getestet. Sie bekommen einen Ton mit einer festen
Frequenz vorgespielt, der so lange lauter wird, bis Sie ihn wahrnehmen.
Hortest Testen Sie mit dem Audiometer ein Ohr. (Siehe Audiometeranleitung).
Zeichnen Sie dabei ein Frequenz-Lautstarke Diagramm Ihrer Horschwelle.
In jeder Gruppe ubernimmt ein Praktikant die Rolle des Arztes und der andere die des
Patienten.
Larmschutz Untersuchen Sie nun die Wirksamkeit von Ohrenstopseln, die z.B. in
der Produktion als Gehorschutz dienen.
Die Wirksamkeit von Gehorschutzeinrichtungen wird durch die Dampfung charakterisiert, unter der man die Abschwachung des Schallsignals versteht, die die jeweilige
Gehorschutzeinrichtung bewirkt. So bedeutet eine Dampfung um z.B. 25 dB, da ein
Schallsignal von ursprunglich 50 dB bzw. 125 dB nach der Dampfung nur noch einen
Schallpegel von 25 dB bzw. 100 dB hat.
1. Benutzen Sie einen Ohrenstopsel in dem Ohr, das Sie vorher getestet haben.
Warten sie nach dem Einfugen des Gehorschutzes in den Gehorgang ca. funf
Minuten, bis er sich an Ihren Gehorgang angepat hat und diesen wirklich dicht
verschliet.
2. Fuhren Sie mit diesem Ohr den Hortest noch einmal durch.
3. Ermitteln Sie die Dampfungscharakteristik des Gehorschutzes, indem Sie fur jede
Frequenz die Dampfung ausrechnen.
Um die Dampfung durch den Gehorschutz zu kompensieren mu die Schallquelle
einige dB lauter sein. Ihre (gemessene) Horschwelle liegt daher um diesen Betrag
hoher als bei der Messung ohne Ohrstopsel.
4. Zeichnen Sie ein Frequenz-Dampfungs-Diagramm.
In welchem Frequenzbereich ist die Dampfung am starksten ?
Gehorschadigung Dieser Versuch ist freiwillig.
Wenn Sie wollen, konnen Sie das Frequenz-Lautstarke-Diagramm aufnehmen, nachdem
Sie Ihr Gehor vorubergehend geschadigt haben, und die Art der Schadigung beschreiben. Fragen Sie dazu Ihren Betreuer.
Larmbelastung
Messen Sie verschiedene Gerauschkulissen auerhalb des Praktikumsraumes, z.B. in
einem Horsaal, in einer Maschinenhalle, in der Cafeteria, auf der Strae oder in einem
anderen Raum mit dem Schallpegelmegerat in A- und unbewerteter Messung.
76
5. Akustik
5.5 Aufgaben und Fragen
Beantworten Sie in Ihrem Versuchsprotokoll folgende Fragen:
1. Zur Schallwelle :
Welche Wellenlange hat ein Sinuston von 100 Hz, 440 Hz, 1 kHz, 10 kHz in Luft?
2. Zum Schallpegel :
Ein Motorrad erzeuge einen Schalldruckpegel von 80 dB(A)
(a) Welchen Schallpegel erzeugen zwei Motorrader?
(b) Wie viele Motorrader erzeugen einen Schallpegel, der als doppelt so laut
(d.h. ca. 90 dB(A) ) empfunden wird?
3. Zum Schalldruck :
Welcher Schalldruck p und damit welcher Schallpegel L herrschen in einem (theoretisch) absolut ruhigen Raum (d.h. bei keiner noch so geringen Bewegung der
Luft)?
4. Zur Lautstarkewahrnehmung :
Um welchen Faktor mu der Schalldruck p bei der Frequenz 31,5 Hz groer sein
als bei 1 kHz, damit man den Ton gerade noch hort (Vgl. Abbildung 5.3)?
5. Zur Schwebung :
Sie uberlagern zwei gleichlaute Schallquellen, die jeweils harmonische Schwingungen mit 1 = 999 Hz und 2 = 1000 Hz aussenden. Wie lautet die Schwingungsfrequenz, wie die Schwebungsfrequenz der resultierenden Schwebung? Welche Frequenz hat der Ton, den Sie horen?
Wie oft pro Sekunde schwillt dieser an?
6. Zur Bewertung von Schallpegelmessungen :
Bei welchen Anwendungen ist die Angabe von bewerteten Pegeln (in dB(A) oder
phon) sinnvoll, bei welchen die unbewertete Messung?
7. Zum Kundtschen Rohr :
Zeichnen Sie eine Skizze des Kundtschen Rohres mit Sandbergen. Zeichnen Sie
auch die Schallwellen ein und berechnen Sie aus der Demonstrationsmessung die
Schallgeschwindigkeit in Luft.
8. Zur Schallgeschwindigkeit in verschieden Gasen :
Erklaren Sie den "Mickey-Mouse\-Eekt beim Einatmen von leichten Gasen wie
Wassersto oder Helium.