Körper zum Selberbauen – Polydron
Werbung

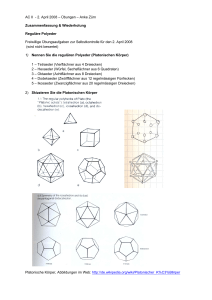
Mathematik zum Anfassen – Polydron Puntigam Manfred Körper zum Selberbauen – Polydron Was versteht man unter Polydron? Polydron ist ein von Edward Harvey erfundenes intelligentes Spielzeug, mit dem man verschiedene geometrische Figuren bauen kann. Es ist seit 40 Jahren bekannt und erfreut sich nicht nur in Großbritannien zunehmender Beliebtheit. Polydron ist speziell dafür ausgerichtet den modernen Geometrie Unterricht für Schüler als auch für die Lehrer interessanter und vor allem anschaulicher zu machen. Die Geometrie der Elemente; Wir bauen die Elemente Die platonischen Körper waren schon den Griechen bekannt. Ihre Namen gehen auf griechische Zahlenwörter zurück, die eine Beziehung zu den Anzahlen ihrer Flächen herstellen.Platon ordnete den fünf platonischen Körpern Elemente zu; Feuer Tetraeder Erde Hexaeder Würfel Luft Oktaeder Wasser Ikosaeder Universum Dodekaeder Seite 1/4 Mathematik zum Anfassen – Polydron Puntigam Manfred Didaktische Aufbereitung: Wie oben beschrieben gibt es 5 platonische Körper. Um bei den Schülern Interesse zu wecken könnte man zu Beginn der Präsentation etwas Spannendes über Platon und seine platonischen Körper erzählen. Danach legt man verschiedene Netze aus und fragt welcher Körper zu welchem Netz gehört. Wenn man nicht sicher ist kann man mit Hilfe von Polydron das Rätsel lösen. Zum Beispiel: Zu welchem Element gehört dieses Netz? 1. 2. 3. 4. 5. Feuer Wasser Erde Luft Universum Bitte schreib die richtige Zahl auf! Am Ende bekommen die Schüler die Möglichkeit die Zahlen die sie als Lösung herausbekommen haben (für jeden Körper eine) zusammen zu zählen. Die Lösung ergibt die Richtige Antwort auf die Abschlussfrage: Wie viele Ecken besitzt der Ikosaeder? (12) Es wäre auch möglich zu den anderen 20 Ausstellungsstücken einfache Fragen zu stellen um dann, nach der Ausstellung, eine Gesamtlösung zu bekommen. Sozusagen eine Schnitzeljagd. Seite 2/4 Mathematik zum Anfassen – Polydron Puntigam Manfred Basiswissen; Polyeder Was sind platonische Körper; Polyeder sind Körper, die von Polygonen, also von Vielecken, wie Dreiecken, Vierecken, Fünfecken usw. begrenzt sind. Polyeder heißen konvex, wenn zu je zwei Punkten aus dem Innern des Polyeders auch die Verbindungsstrecke zwischen diesen beiden Punkten ganz im Innern des Polyeders verläuft. Definition: Reguläres Polyeder Ein konvexes Polyeder heißt regulär, wenn alle Flächen zueinander kongruente, regelmäßige Vielecke sind und in jeder Ecke gleich viele Vielecke zusammenstoßen. Satz: Eulerscher Polyedersatz Für ein konvexes Polyeder mit e Ecken, k Kanten und f Flächen gilt e-k+f=2 Gibt es außer den fünf platonischen Körpern noch weitere reguläre Polyeder? Vereinbarung: • • • Ein Polyeder sei von regelmäßigen n-Ecken begrenzt, n ≥ 3 In jeder Ecke des Polyeders stoßen m Flächen zusammen m ≥ 3 Das Polyeder habe e Ecken, k Kanten und f Flächen. Dann gilt: Das Polyeder besteht aus f Fläche. Jede Fläche ist ein n-Eck, hat also n Kanten. Wir kommen also auf f ∙ n Kanten, haben dabei aber jede Kante bei zwei Flächen gezählt. Also gilt: f ∙n = 2 ∙ k Das Polyeder hat e Ecken. In jeder Ecke stoßen m Kanten (von m Flächen) zusammen. Wir kommen also auf e ∙ m Kanten, haben dabei aber jede Kante bei zwei Ecken gezählt. Also gilt: e ∙ m = 2 ∙ k Wir lösen diese beiden Gleichungen nach f bzw. e auf: f ∙n = 2 ∙ k ↔ f = 2 ∙ k / n ; e∙m=2∙k ↔ e= 2∙k/m Seite 3/4 Mathematik zum Anfassen – Polydron Puntigam Manfred Diese Ausdrücke setzen wir in die Eulersche Polyederformel ein und bekommen die Ungleichung: 1/m + 1/n > ½ Nun unter Verwendung dieser Ungleichung sieht man, dass für m und n nur ganz bestimmte Werte in Frage kommen können: m- Flächen pro Ecke m = 3, m = 3, m = 3, n-Eck n=3 n=4 n=5 Tetraeder Hexaeder (Würfel) Dodekaeder m = 4, n=3 Oktaeder m = 5, n=3 Ikosaeder Die fünf platonischen Körper sind also definitiv die einzigen relulären Polyeder! Literaturverzeichnis: Leitfaden Geometrie 3. Auflage www.polydron.co.uk Seite 4/4 Zu welchen Elementen gehören diese Netze? 1. Feuer 2. Wasser 3. Erde 4. Luft 5. Universum Antwort ist Nummer 4 1. Wasser 2. Erde 3. Luft 4. Universum 5. Feuer Antwort ist Nummer 5 1. Erde 2. Luft 3. Universum 4. Feuer 5. Wasser Antwort ist Nummer 3 Abschlussfrage: Wie viele Ecken besitzt der Ikosaeder? (12)