AC II - 2. April 2008 – Übungen – Anke Zürn Zusammenfassung

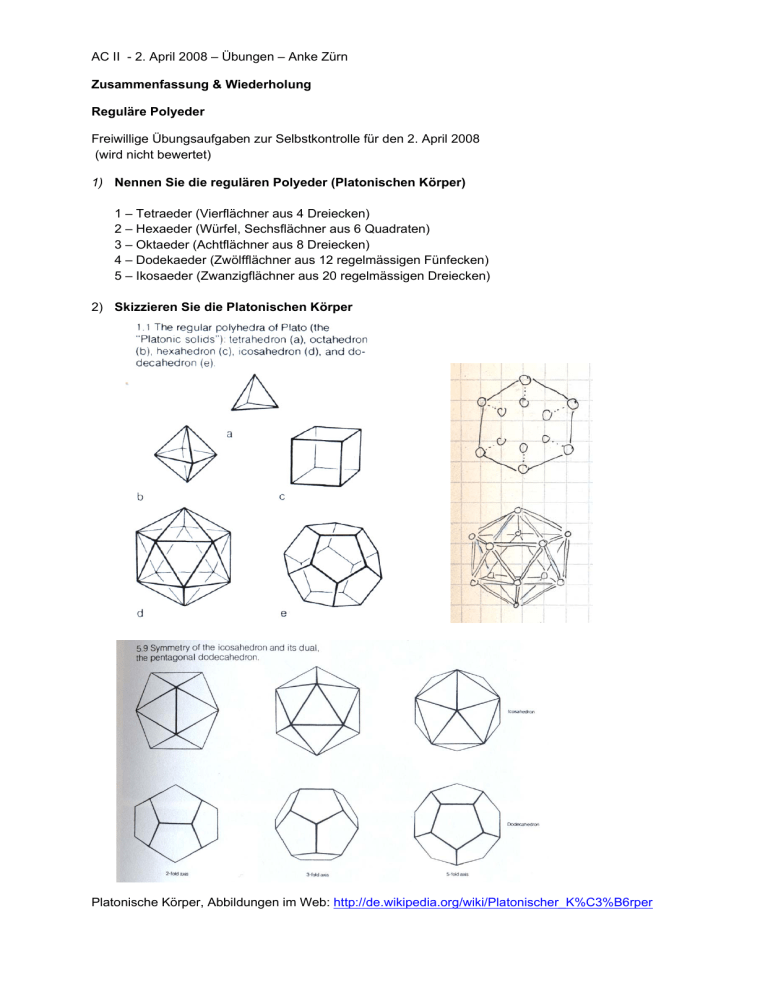
AC II - 2. April 2008 – Übungen – Anke Zürn
Zusammenfassung & Wiederholung
Reguläre Polyeder
Freiwillige Übungsaufgaben zur Selbstkontrolle für den 2. April 2008
(wird nicht bewertet)
1) Nennen Sie die regulären Polyeder (Platonischen Körper)
1 – Tetraeder (Vierflächner aus 4 Dreiecken)
2 – Hexaeder (Würfel, Sechsflächner aus 6 Quadraten)
3 – Oktaeder (Achtflächner aus 8 Dreiecken)
4 – Dodekaeder (Zwölfflächner aus 12 regelmässigen Fünfecken)
5 – Ikosaeder (Zwanzigflächner aus 20 regelmässigen Dreiecken)
2) Skizzieren Sie die Platonischen Körper
Platonische Körper, Abbildungen im Web: http://de.wikipedia.org/wiki/Platonischer_K%C3%B6rper
3) Worauf bezieht sich ihr Name? „
Auf die Anzahl der Flächen.
ACHTUNG PRÜFUNG: Flüchtigkeitsfehler
Wenn ein Oktaeder genannt ist, denken Sie bitte an 8 Flächen!!!
(zeichnen Sie bitte keinen Würfel - der hat zwar acht Ecken aber nur 6 Flächen!)
4) Wodurch zeichnen sich die regulären Polyeder aus?
Alle Ecken, Kanten und Flächen sind untereinander gleichartig/kongruent. Jede Ecke (Kante, Fläche)
kann auf jede andere Ecke (Kante, Fläche) abgebildet werden.
5) Duale Körper
a) Nennen sie die jeweiligen dualen Körper zu den Platonischen Körpern.
b) Wie konstruiert man den jeweils dualen Körper? Skizzieren Sie ein Beispiel.
Tetraeder – Tetraeder
Hexaeder – Oktaeder
Ikosaeder – Dodekaeder
(das Tetraeder ist zu sich selbst dual)
Konstruktion: Die Mittelpunkte jeder Fläche des ursprünglichen Körpers bilden die Ecken des dualen
Körpers. Am einfachsten ist dies mit einem Hexaeder zu zeigen.
Zeichen sie einen Würfel in Parallelprojektion. Markieren Sie die Mittelpunkte aller 6 Flächen und
verbinden Sie diese mit den 4 benachbarten Mittelpunkten. Es entsteht der Oktaeder im Würfel.
6) Nennen Sie eine Beziehungen zwischen Ecken, Kanten und Flächen für konvexe Polyeder
Eulersche Polyedersatz für konvexe Polyeder:
E–K+F=2
(Anzahl der Ecken) – (Anzahl der Kanten) + (Anzahl der Flächen) = 2
Anmerkung: Allgemeiner formuliert wird es in der Euler-Schläfli-Gleichung.
Für den dreidimensionalen Raum gilt: E – K + F – C = 0
E = Anzahl Ecken, K = Anzahl Kanten, F = Anzahl Polyederflächen, C = Anzahl der
Zellen/Volumenelemente. Für sphärische Körper (Kugel, Platonische Körper, konvexe Polyeder
allgemein) und Parkettierungen der unendliche Ebene gilt C = 2.
Achtung – aufpassen – englischen Literatur – nicht verwechseln:
edge (englisch) = Kante !!! vertex/vertices (englisch) = Eckpunkt/e
face (englisch) = Fläche
Anhang: Koordinationspolyeder zur Darstellung von Kristallstrukturen
Oft werden zur Darstellung von Kristallstrukturen Polyeder verwendet. Sie sollten deshalb die wichtigsten
Polyeder aus unterschiedlichen Richtungen erkennen und skizzieren können (Abbildung unten: Tetraeder
(orange) und Oktaeder (blau).
Beispiel: In einer Verbindung AXn ist das Atom A immer oktaedrisch von sechs X-Atomen umgeben. Zur
Darstellung der Kristallstruktur werden häufig nur die Koordinationspolyeder skizziert (Abb. unten c)
Modelle zum Basteln: