reale probleme und mathematik - Max-Brauer

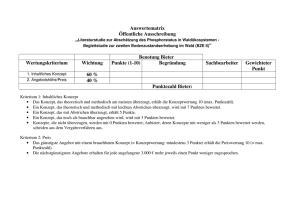
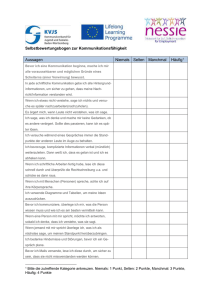
Mathematik: Selbstgestellte Aufgabe in der Oberstufe
Die selbstgestellte Aufgabe in Mathematik
REALE PROBLEME UND MATHEMATIK*
Was?
Für eine selbstgestellte Aufgabe in Mathematik bieten sich insbesondere reale Problembereiche an,
für die auf mathematischem Wege eine Antwort gegeben werden kann.
Hier wären folgende Themenfelder denkbar:
1. Bevölkerungsexplosion; oder?
2. Arbeit für alle!?!
3. Wie moralisch ist Politik?
4. AIDS und Grippe: zwei "moderne" Epidemien?
5. Fast food und big body? Gibt es Alternativen?
6. Wachstum, Wachstum – Boom über alle Grenzen?
7. Werden die Reichen immer reicher?
8. Energie"Hunger" - Umweltbelastung und andere Folgewirkungen
9. "Zeit"- beschleunigte informationstechnische Evolution: nachbiologische
Lebewesen?
10. Zeitbeschleunigung: bio- und gentechnische Evolution - Menschen nach Maß?
11. Crash-sh-sh: ... und Folgen
Wie?
Ziel: Selbstständiges
Formulieren von
Fragen und deren
Bearbeitung
Beim "Eintauchen" in das von euch ausgewählte reale Problem geht es dann
insbesondere auch darum, dass ihr selbstständig und eigenverantwortlich eine
konkrete Frage entwickelt, die euch erstens interessiert und über die ihr
zweitens intensiver und ausdauernd nachdenken wollt.
Erarbeitung von
Zusammenhängen,
Wechselwirkungen
oder Beziehungen
zwischen
Einflussgrößen;
gegebenenfalls
Ableitung von
Trends.
Mathematisch geht es darum, dass ihr Zusammenhänge, Wechselwirkungen
oder Verteilungen diskutiert und aufarbeitet, etwa:
Zusammenhänge und Abhängigkeiten u.a. von: Zeit und Information,
Zeit und Krankheit, Zeit und Produktzahlen, Kapital und Zins, Währung und
Kursgewinn, Preis und Menge, Nachfrage und Preis, Weg und Zeit, Arbeit und
Leistung ...
Wechselwirkungen und Zusammenwirkungen u.a. in Form von:
Eskalationen, schwachen Kopplungen, starken Rückkopplungen,
"Schmetterlingseffekten" ...
Verteilungen u.a. als Aufzeichnung von Beziehungen oder
statistischen Erhebungen.
•
•
•
•
Aufstellen von
Tabellen, Graphen,
Formeln; Annahmen
kenntlich machen;
Interpretieren
Tabellarische und graphische Darstellungen sind ein Mittel, das euch bei euren
Erkenntnissen helfen kann. Wollt ihr dann auch noch mögliche Trends oder
Tendenzen von Abläufen oder Entwicklungen feststellen, weil sie in eurem
späteren oder beruflichen Leben eine Rolle spielen könnten, dann steckt die
Zusammenhänge in eigens dazu erfundene "Formeln" oder "Sprachmuster"
und interpretiert sie, indem ihr von unterschiedlichen Annahmen ausgeht.
* Die Materialien stammen von der Internetplattform des Projektes „Modellieren mit Mathe“, herausgegeben von Willi van Lück
und sind für den Einsatz im Unterricht und Anpassungen für den eigenen Unterricht freigegeben. Internetadresse:
www.schule.suedtirol.it/blikk/angebote/modellmathe/medio.htm
Mathematik: Selbstgestellte Aufgabe in der Oberstufe
Hilfe?
Die Informationen zu den einzelnen Themenfeldern sind auf der Internetplattform des Projektes
„Modellieren mit Mathe“zu finden
Internetseite: www.schule.suedtirol.it/blikk/angebote/modellmathe/medio.htm
(am besten in Google Projektnamen einfügen und anklicken.) Hier finden sich unterstützende
Hinweise zum realen und mathematischen Hintergrund. Um genauere Informationen zum Umgang mit
dieser Internetplattform zu erhalten oder für weitergehende inhaltliche Beratung, wende dich an
deinen Mathelehrer!
Bewertung?
Das Ergebnis der selbstgestellten Aufgabe muss verschriftlicht abgegeben werden.
Die relevanten Bewertungskriterien können dem angefügten Bewertungsbogen entnommen werden.
Mathematik: Selbstgestellte Aufgabe in der Oberstufe
BEWERTUNG DER SELBSTGESTELLTEN AUFGABE
Gruppe/ Schüler: _________________________________________________________
Thema:_________________________________________________________________
1. Reales Problem/ Untersuchungsfrage
Kriterien:
- Klarheit
- gelungene Zuspitzung
Sonstiger Kommentar:
Punktzahl (mit 10% gewertet): --- / 15
2. Reales Modell
Kriterien:
- zentrale Zusammenhänge erkannt (wichtige Bestimmungsgrößen erkannt)
- Annahmen deutlich gemacht, sinnvoll reduziert
Sonstiger Kommentar:
Punktzahl (mit 20% gewertet): -- / 15
3. Mathematisches Modell
Kriterien:
- Klarheit im Zusammenhang zwischen Annahmen und Übersetzungen in die Sprache der
Mathematik (Qualität der Erläuterungen)
- mathematischer Anspruch/ Schwierigkeit
Sonstiger Kommentar:
Punktzahl (mit 40% gewertet): -- / 15
4. Mathematisches Ergebnis
Kriterien:
- Art der Darstellung (Tabelle, Formel, Graph)
- Richtigkeit des mathematischen Formalismus
- Rückinterpretation
Sonstiger Kommentar:
Punktzahl (mit 20% gewertet): -- / 15
5. Verschriftlichung
Kriterien:
- Struktur/ Aufbau
- Ordentliche Darstellung
- Quellenangaben
Sonstiger Kommentar:
Punktzahl (mit 10% gewertet): / 15
1 (10%)
2 (20%)
3 (40%)
4 (20%)
5 (10%)
Gesamtpunktzahl
Note
Mathematik: Selbstgestellte Aufgabe in der Oberstufe
MÖGLICHE FRAGESTELLUNGEN ZU DEN EINZELNEN THEMENBEREICHEN:
1. Bevölkerungsexplosion; oder?
•
•
•
Korreliert in einigen ausgesuchten Ländern die Geburtenrate mit der Nutzung von
Verhütungsmitteln, mit der Analphatenrate, mit dem Nahrungsangebot (bzw. dem Hunger)
und mit ... Sind die Familienplanung oder ein breites Bildungsangebot oder die wirtschaftliche
Entwicklung oder ... ein Ausweg aus der Bevölkerungsexplosion?
Wie könnte u.a. für Deutschland (vom Grundsätzlichen her) eine Rentenformel aussehen, mit
der sowohl die Jugendlichen als auch die Rentner gleichmäßig belastet würden?
Wie wirken sich religiöse oder weltanschauliche Grundüberzeugungen auf die Anzahl der
Neugeborenen aus?
2. Arbeit für alle!?!
•
•
•
Erstellt eine Umfrage: Zu welchen Zugeständnissen (Konzessionen) sind Jugendliche bereit,
um eine Ausbildungsstelle zu finden? Muss die Arbeit (a) interessant sein, (b) Sicherheit vor
Arbeitslosigkeit bieten, (c) vielfältig sein, (d) viel Geld einbringen (e) Aufstiegsmöglichkeiten
bieten ... ?
Korrelieren die Entwicklungen (etwa das Wirtschaftswachstum mit der Zahl der Arbeitsplätze
oder die Zahl der Arbeitsplätze mit der Zunahme der Neuen Technologien oder ...)? Wie ist
dies bezüglich möglicher Zusammenhänge, Folgewirkungen und/oder Lösungsmöglichkeiten
zu interpretieren?
Wie lassen sich für die Industrieländer und Schwellenländer sowie für die wirklich "armen
Länder" Arbeitsmodelle konstruieren, die regional und/oder weltweit eine dauerhafte Arbeit
bringen würden? Welche wichtigen Parameter (Einflussfaktoren) sind dabei jeweils und immer
zu berücksichtigen?
3. Wie moralisch ist Politik?
•
•
•
•
•
•
Wie steht es mit der Wahrheit und der Wahrhaftigkeit unserer Politiker und Manager? Wie
realistisch ist es, dass ein Wahlversprechen auch wirklich eingelöst wird? ... Ist es abhängig
von Konsumflauten oder Investitionsrückgängen? Wie groß ist in unserer Gesellschaft das
Vertrauen in die Institutionen des Bundestages oder der Parteien? Was sagen die
zurückgehenden Mitgliederzahlen in den Parteien aus? Steht in den Parteiprogrammen und
Wahlprogrammen auch wie die "Guten Taten" finanziert werden sollen? Wer verspricht vor
einer Wahl immer das Meiste? Recherchiert im Internet aussagefähige Daten und wertet sie
aus! Oder: Nehmt eure eigenen Daten, die ihr mit einer Stichproben-Befragung ermittelt habt,
und wertet diese aus.
Politisches Handeln ist abhängig von der "erpresserischen Macht" der wirtschaftlichen
Lobby... . Was bewirken eigentlich die so genannten "Alten" in unserer Gesellschaft mit ihren
Aufmärschen? ... Gelten heute also wieder die "Gesetze des Dschungels"? Modelliert den
Machterhalt einer Regierung, also u.a. die Abhängigkeit des politischen Handelns (a) von der
wirtschaftlichen Lobby, (b) vom Verhalten der älteren Generation oder (c) als "Gesetze des
Dschungels" ...
4. AIDS und Grippe: zwei "moderne" Epidemien?
Nimmt die Gesamtzahl der Menschen, die mit HIV leben und schließlich an Aids sterben,
eigentlich immer weiter und stetig zu?
Müssen wir uns Sorgen machen, dass sich das HI Virus auch bei uns ausbreitet oder ist AIDS
nur ein Problem in den Entwicklungsländern?
Haben wir die Epidemie einer Grippe oder von SARS oder von Ebola oder ... ebenfalls zu
befürchten? Wie viel Menschen sterben an einer Grippe? Nimmt diese Zahl zu?
Warum ist die Sicherheit von Gesellschaft und Wirtschaft betroffen?
Mathematik: Selbstgestellte Aufgabe in der Oberstufe
5. Fast food und big body? Gibt es Alternativen?
•
•
Modelliert und simuliert für eine übergewichtige Person zunächst den Fall, dass das einmal
erreichte Gewicht konstant gehalten wird. Simuliert sodann für dieselbe übergewichtige
Person eine Gewichtsabnahme (a) durch Reduktion der Nahrungsaufnahme und (b) durch
Reduktion der Nahrungsaufnahme begleitet mit regelmäßigem leichten Sport.
Analyse folgender Fragestellungen:  Wie hat sich etwa der Fett- oder Fleischkonsum in den
letzten Jahrzehnten verändert?  Wie haben sich die Aufnahme von Nährstoffen und von
Essensgewohnheiten geändert?  Wie hat sich insgesamt das Körpergewicht in der
Bevölkerung der Industrienationen geändert?  Welche Berechnungs-Formel passt am
Besten in unsere Fast Food Gesellschaft, um so etwa wie ein Normalgewicht zu definieren?
6. Wachstum, Wachstum – Boom über alle Grenzen?
7. Werden die Reichen immer reicher?
8. Energie"Hunger" - Umweltbelastung und andere Folgewirkungen
9. "Zeit"- beschleunigte informationstechnische Evolution: nachbiologische
Lebewesen?
10. Zeitbeschleunigung: bio- und gentechnische Evolution - Menschen nach
Maß?
11. Crash-sh-sh: ... und Folgen