Kap_4
Werbung
Vorlesungsmitschrift Graphentheorie
4
F¨
arbung in Graphen
F¨
arbung in Graphen
Definition : Eine zul¨assige F¨arbung ist eine F¨arbung der Knoten des ( ungerichteten ) Graphen, so daß je zwei adjazente Knoten verschiedene Farben
haben.
Trivial ist, daß n verschiedene Farben immer eine zul¨assige F¨arbung sind
( Anzahl Knoten = Anzahl Farben ).
Definition : Die chromatische Zahl eines Graphen G ist die kleinste Anzahl
von Farben f¨
ur eine zul¨assige F¨arbung. Symbol : χ(G)
Beispiele :
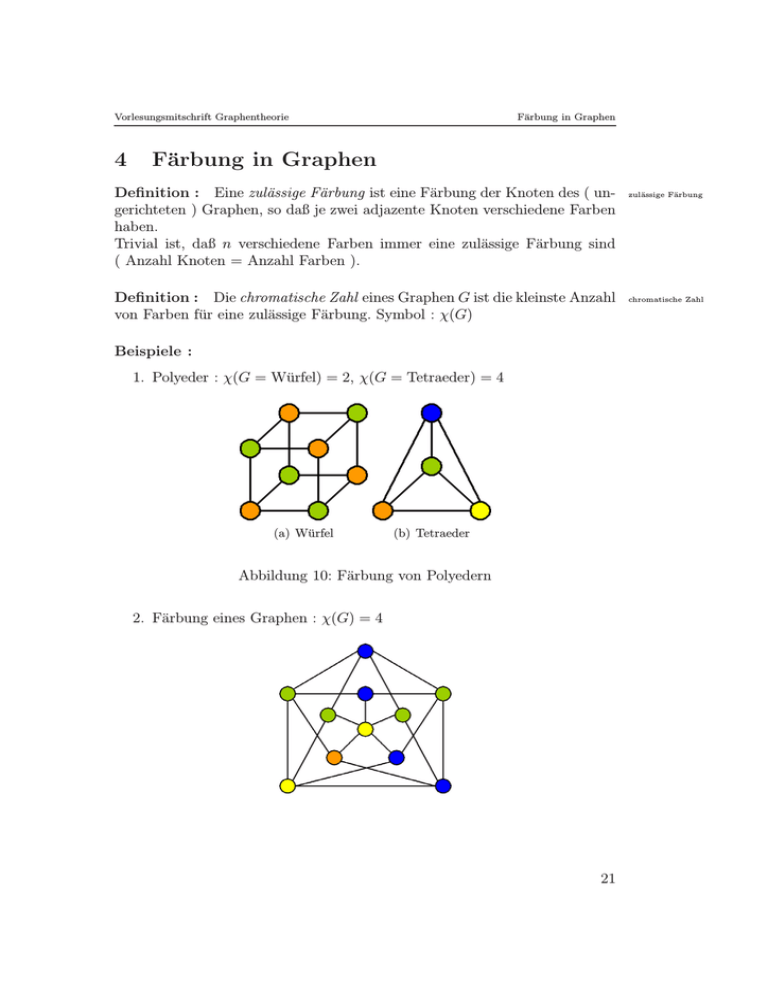
1. Polyeder : χ(G = W¨
urfel) = 2, χ(G = Tetraeder) = 4
(a) W¨
urfel
(b) Tetraeder
Abbildung 10: F¨arbung von Polyedern
2. F¨arbung eines Graphen : χ(G) = 4
21
zul¨
assige F¨
arbung
chromatische Zahl
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
3. F¨arben einer Landkarte : Eine Landkarte ist ein planarer Graph2 . Die
Knoten sind durch die L¨ander gegeben. 2 Knoten werden durch eine
Kante verbunden, wenn die L¨ander eine gemeinsame Grenze haben.
Abbildung 11: F¨arbung einer Landkarte
Jede Landkarte kann mit vier Farben zul¨assig gef¨arbt werden ( Vierfarbensatz )
4. Party mit n G¨asten : Die G¨aste stellen die Knoten dar. Jede Kante
zwischen zwei Knoten bedeutet, daß die jeweiligen zwei G¨aste nicht
miteinander harmonieren. Gesucht ist eine zul¨assige F¨arbung des Graphen, die einer Verteilung der G¨aste auf verschiedene Tische ohne Disharmonien entspricht.
Einfache Aussagen :
1. F¨
ur einen vollst¨andigen Graphen G mit n Knoten gilt : χ(G) = n
2. F¨
ur einen Kreis G mit gerader L¨ange gilt : χ(G) = 2
3. F¨
ur einen Kreis G mit ungerader L¨ange gilt : χ(G) = 3
2
¨
in der Ebene ohne Uberschneidungen
der Kanten darstellbar
22
Vierfarbensatz
Vorlesungsmitschrift Graphentheorie
4.1
F¨
arbung in Graphen
F¨
arbung mit 2 Farben
Satz : Ein Graph G = (X, K) hat eine zul¨assige F¨arbung mit 2 Farben ⇔
G hat keinen Kreis mit ungerader L¨ange.
Beweis :
⇒“: trivial ( siehe Aussage 3 )
”
⇐“:
”
In jeder Zusammenhangskomponente von G wird folgendermaßen gef¨arbt :
1. W¨ahle x0 aus der Knotenmenge der Zusammenhangskomponente beliebig. Alle Knoten y mit Distanz D(x0 , y) = gerade erhalten die Farbe
F1 . Alle Knoten y mit Distanz D(x0 , y) = ungerade erhalten die Farbe
F2 .
2. Noch zu zeigen : 2 adjazente Knoten x1 und x2 haben nicht die gleiche
Farbe. Indirekter Beweis :
Annahme : x1 und x2 seien adjazent und haben die gleiche Farbe F1 (
oder F2 ).
k¨
urzester Weg von x0 nach x1
k¨
urzester Weg von x0 nach x2
Kante von x1 nach x2
:
:
:
gerade ( ungerade ) L¨ange
gerade ( ungerade ) L¨ange
L¨ange 1
uck zu x0 ist offenbar stets ein
Der Weg von x0 u
¨ber x1 und x2 und zur¨
Kreis ungerader L¨ange !
Zwei-Farben-Algorithmus
Algorithmus : Beginne mit einem beliebigen Knoten x0 aus X. Bilde
sukzessive um x0 konzentrische Schalen gleichgef¨arbter Knoten, solange dies
m¨oglich ist.
Die Schalen enthalten genau die Knoten gleicher Distanz von x0 . Eine zul¨assige F¨arbung ist m¨oglich, wenn in keiner Schale adjazente Knoten existieren.
Gegeben sei ein ungerichteter zusammenh¨angender Graph G = (X, K)
mittels Nachfolgerliste nf der L¨ange 2m und zugeh¨origer Indexliste inf der
L¨ange n + 1. Außerdem ist ein Startknoten x0 ∈ X mittels des Indexes i0
gegeben.
Gesucht ist die Entscheidung, ob eine zul¨assige F¨arbung mit 2 Farben
m¨oglich ist. Falls ja, Angabe der F¨arbung der Knoten mittels farbe.
23
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
Listing 2: Zwei-Farben-Algorithmus
1
2
3
VAR N ,M , I0 : i n t e g e r;
TYPE PListe = array [1.. N +1] OF i n t e g e r;
KListe = array [1..2* M ] OF i n t e g e r;
4
5
6
7
8
9
P R O C E D U R E Z w e i F a r b e n ( nf : KListe ; inf , Farbe , D : PListe );
VAR i ,j ,k , Dakt , F a r b e A k t : i n t e g e r;
unfaerbbar
: b o o l e a n;
BEGIN
FOR i :=1 TO N DO D [ i ]:= -1;
10
11
12
D [ I0 ]:=0; Dakt :=0; Farbe [ I0 ]:=0;
u n f a e r b b a r := false ; F a r b e A k t :=0; // A n f a n g s i n i t i a l i s i e r u n g
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
REPEAT
FOR i :=1 TO N DO BEGIN
IF D [ i ] = Dakt THEN BEGIN
FOR j := inf [ i ] TO inf [ i +1] -1 DO BEGIN
k := nf [ j ];
IF D [ k ] = -1 THEN BEGIN
D [ k ]:= Dakt +1;
Farbe [ k ]:=1 - F a r b e A k t;
END
ELSE
IF D [ k ] = Dakt THEN u n f a e r b b a r := TRUE ;
END ;
END ;
END ;
Dakt := Dakt +1;
F a r b e A k t :=1 - F a r b e A k t;
UNTIL ( Dakt = N ) OR ( u n f a e r b b a r );
END ;
24
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
Beispiel :
1
2
3
4
5
Nachfolgerliste :
j
nf[j]
1
2
2
1
3
3
4
5
i
Index- und F¨arbeliste : inf[i]
farbe[i]
5
2
1
1
6
4
→
→
→
→
→
7
3
2 3 4
2 5 7
gesucht
2
1, 3, 5
2, 4
3, 5
2, 4
8
5
9
2
5
9
10
4
6
11
Die Abarbeitung des Zwei-Farben-Algorithmus liefert folgende L¨osung:
i
farbe[i]
1
0
2
1
3
0
4
1
5
0
25
Vorlesungsmitschrift Graphentheorie
4.2
F¨
arbung in Graphen
Maximalgrad und Greedy-Algorithmus
Definition : Der Maximalgrad eines Graphen G ist definiert durch
Maximalgrad
δ(G) := max d(xi ).
i=1,2,...,n
Offensichtlich gilt: χ(G) ≤ δ(G) + 1 .
Eine zul¨assige F¨arbung mit h¨ochstens δ(G) + 1 Farben ermittelt der
Greedy-Algorithmus :
Greedy-Algorithmus
Schritte :
1. x1 ∈ X erh¨alt Farbe 0; i = 2
2. x1 , x2 , . . . , xi−1 ∈ X seien bereits gef¨arbt
(a) Betrachte die in Γ(xi ) ∩ {x1 , x2 , . . . , xi−1 } vergebenen Farben
j1 , j2 , . . . , jr
(b) xi erh¨alt die Farbe ji = min({0, 1, 2, . . . , δ(G)} \ {j1 , j2 , . . . , jr })
(c) i := i + 1
3. Solange i < n + 1 fahre mit Schritt 2 fort.
26
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
Beispiel :
Der Greedy-Algorithmus ben¨otigt f¨
unf Farben, um den obigen Graphen zul¨assig
zu f¨arben.
Durch Vertauschen der Knotennummern 10 und 12 wird eine Farbe weniger
ben¨otigt.
Eine eventuell g¨
unstigere Knotennummerierung kann durch den folgenden
Algorithmus erreicht werden :
1. i := n, Gi := G
2. Ermittle in Gi einen Knoten xi mit minimalem Grad di.
(a) Bilde Gi−1 dadurch, daß xi und alle inzidenten Kanten entfernt
werden
(b) i := i − 1
3. Solange i > 0, setze in Schritt 2 fort.
Der Greedy-Algorithmus liefert jetzt eine zul¨assige F¨arbung mit h¨ochstens
δ (G) + 1 Farben, wobei δ (G) := maxi=1,2,...,n d (xi ).
27
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
Fu
¨ r obiges Beispiel :
i
1
2
3
4
5
6
7
8
9
10
11
12
xi
xi
di
1
12
2
2
11
2
3
10
2
4
9
2
5
8
1
6
7
2
7
4
2
8
3
1
9
2
1
10
6
2
11
1
0
12
5
1
(a) Ausgangsf¨arbung
(b) F¨
arbung nach Neunummerierung
Also reichen sogar 3 Farben f¨
ur eine zul¨assige F¨arbung.
Bemerkung : Es gibt eine Nummerierung der Knoten, so daß der GreedyAlgorithmus zu einer zul¨assigen F¨arbung mit χ(G) Farben f¨
uhrt.
28
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
Backtracking-Algorithmus :
1. x1 , x2 , . . . , xi−1 seien zul¨assig gef¨arbt, dann
(a) wird xi zun¨achst mit der ersten Farbe gef¨arbt,
(b) vertr¨agt sich diese Farbe mit den bereits gef¨arbten Nachbarn von
xi , so geht man zu xi+1 ,
uft,
(c) wenn nicht, dann wird die n¨achste Farbe f¨
ur xi u
¨ berpr¨
uft, so geht
(d) sind alle c Farben f¨
ur xi mit negativem Resultat u
¨berpr¨
man zu xi−1 zur¨
uck und ¨andert die Farbe f¨
ur xi−1 .
2. Nach Abarbeitung von 1. tritt eine der folgenden Situationen ein:
(a) man erreicht den letzten Knoten xn , kann diesen zul¨assig f¨arben
und hat damit eine zul¨assige F¨arbung des Graphen mit h¨ochstens
c Farben gefunden,
(b) man steht wieder am Anfang des Algorithmus, was bedeutet, dass
eine zul¨assige F¨arbung des Graphen mit c Farben nicht m¨oglich
ist (alle M¨oglichkeiten wurden durchprobiert).
Beispiel :
(a) Graph G
(b) c = 2
(c) c = 3
Abbildung 12: Backtracking-Algorithmus
F¨
ur c = 2 entsteht ein Farb¨anderungsverlauf mit dem Ergebnis, daß eine
zul¨assige F¨arbung mit 2 Farben nicht m¨oglich ist. F¨
ur c = 3 entsteht ein
g¨
ultiger Farb¨anderungsverlauf und somit eine zul¨assige F¨arbung.
29
Vorlesungsmitschrift Graphentheorie
4.3
F¨
arbung in Graphen
Das Vier-Farben-Problem, der Fu
¨nf-Farben-Satz
Graphentheoretisch lautet das Vier-Farben-Problem : Jeder planare Graph
G hat die chromatische Zahl χ(G) ≤ 4.
Vier-Farben-Problem
Historie des Vier-Farben-Problems :
1850
1976
in letzter Zeit
Vermutung von de Morgan, u
¨ber 125 Jahre ungel¨ost
K. Appel, W. Hahen, ( H. Heesch ) : Betrachtung von
ca. 1950 Arten von planaren Graphen, Computerl¨osung
N. Robertson, D. Sanders, P. Seymow, R. Thomas : Vereinfachung des Beweises, Reduktion auf ca. 650 F¨alle
bisher kein Beweis ohne Computerhilfe
Eulersche Polyederformel :
Sei G ein zusammenh¨angender planarer Graph mit n Knoten, m Kanten und
g Gebieten ( einschließlich des sog. Außengebietes ). Dann gilt :
m + g =2
n − Knoten
Kanten
Gebiete
Bemerkung : Aus einem Polyeder entsteht durch Projektion ein planarer
Graph.
(a) Polyeder
(b) planarer Graph
Abbildung 13: Projektion eines Polyeders auf einen planaren Graph
Der Quader hat n = 8 Ecken, m = 12 Kanten und g = 6 Fl¨achen; der planare
Graph n = 8 Knoten, m = 12 Kanten und g = 6 Gebiete ( einschließlich des
Außengebietes ).
30
Eulersche Polyederformel
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
Beweis der Eulerschen Polyederformel :
Induktionsanfang : f¨
ur m = 0 folgt, daß n = 1 und g = 1
Induktionsvoraussetzung : f¨
ur m > 0 sei die Behauptung richtig
Induktionsbehauptung : die Eulersche Polyederformel ist richtig f¨
ur einen zusammenh¨angenden planaren Graphen G mit m + 1 Kanten
Induktionsbeweis :
1. Fall : G enthalte keinen Kreis. Dann muß g = 1 und n = m + 2 sein.
Folglich : (m + 2) − (m + 1) + 1 = 2.
2. Fall : G enthalte einen Kreis. Es wird eine Kante aus dem Kreis entfernt. Dadurch verschmelzen zwei Gebiete. Nach Induktionsvoraussetzung gilt :
n − m + (g − 1) = 2
⇒
n − (m + 1) + g = 2
Aussagen :
1. F¨
ur einen planaren Graphen G mit n ≥ 3 Knoten gilt : m ≤ 3n − 6
2. In einem planaren Graphen G gibt es mindestens einen Knoten x mit
d(x) ≤ 5.
Beweis zu Aussage 1 : G sei zusammenh¨angend ( ansonsten f¨
ur jede
Zusammenhangskomponente )
1. Fall : g = 1 ( d.h. G hat Baumstruktur ). Aus der Baumstruktur folgt,
daß m = n − 1 sein muß. F¨
ur n ≥ 3 gilt sicher n − 1 ≤ 3n − 6.
2. Fall : g ≥ 2. F¨
ur ein Gebiet i in G ist
die L¨ange li des umlaufendes
Kreises ≥ 3. Somit ergibt sich : 2m = gi=1 li ≥ 3g. Wenn man nun die
umgeformte Eulersche Polyederformel g = 2 − n − m einsetzt, ergibt
sich folgende Absch¨atzung : 2m ≥ 6 − 3n + 3m und damit m ≤ 3n − 6.
Beweis zu Aussage 2 : F¨
ur n ≤ 6 ist die Aussage klar. Sei nun n > 6
und d(x) ≥ 6 f¨
ur alle x ∈ X angenommen. Dann gilt : 6n ≤ 2m, was im
Widerspruch zu m ≤ 3n − 6 steht.
31
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
Fu
¨nf-Farben-Satz :
F¨
unf-Farben-Satz
1879 zeigte A. Kempe einen Beweis f¨
ur das Vier-Farben-Problem. 1890 entdeckte P. Heawood einen Fehler in diesem Beweis, der jedoch bei der F¨arbung
mit 5 Farben nicht auftritt.
Kempes Beobachtung ist die folgende : Sei G zul¨assig gef¨arbt. F¨
ur zwei Farben i, j wird definiert :
Xij = {x ∈ X|x ist mit i oder j gef¨arbt}
Gij = der durch Xij erzeugte Teilgraph
Beispiel :
12
11
10
12
10
9
1
2
9
1
5
8
6
3
6
3
4
7
(a) Graph G
4
7
(b) Graph G13 mit getauschten Farben
Z sei eine Zusammenhangskomponente von Gij . Nun werden in Z die Farben
getauscht“: x wird mit der Farbe i gef¨arbt, falls x vorher mit der Farbe j
”
gef¨arbt war, und umgekehrt.
Die neue F¨arbung wird nach G u
¨bertragen. Die neue F¨arbung ist in G zul¨assig
und die Anzahl der Farben bleibt gleich.
Beim Beweis des F¨
unf-Farben-Satzes, dass jeder planare Graph mit 5 Farben
zul¨assig gef¨arbt werden kann, wird dieser Farbentausch Kempes genutzt..
32
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
Beweis des Fu
¨nf-Farben-Satzes:
Induktionsanfang : f¨
ur n = 1 trivial
Induktionsvoraussetzung : f¨
ur n sei die Behauptung richtig
Induktionsbeweis :
Sei G ein planarer Graph mit n + 1 Knoten, Sei x ∈ X ein Knoten mit
d(x) ≤ 5. Sei G der durch X \ {x} erzeugte Teilgraph von G. Nach der
Induktionsvoraussetzung besitzt G eine zul¨assige F¨arbung mit 5 Farben.
1. Fall : Verwenden die Nachbarn von x nicht alle 5 Farben, so ist eine
zul¨assige F¨arbung von G mit 5 Farben trivial.
2. Fall : Die 5 Nachbarn xi von x benutzen alle 5 Farben i, wobei i =
1, . . . , 5. Die Knoten xi laufen um x im Uhrzeigersinn.
x1
x5
x2
x
x3
x4
Ziel ist es, die Knoten x1 bis x5 mit 4 Farben zul¨assig f¨arben.
Es werden die Teilgraphen Gij mit 1 ≤ i, j ≤ 5 von G nach der Idee von
Kempebetrachtet, konkret G13 .
1. Fall : Es gibt keinen Weg in G13 von x1 nach x3 . x1 liege in einer
Zusammenhangskomponente Z von G13 . In Z werden die Farben 1 und
3 getauscht. Insgesamt bleibt eine zul¨assige F¨arbung von G erhalten.
x1 und x3 sind jedoch beide mit der Farbe 3 gef¨arbt. Die Farbe 1 kann
f¨
ur x verwendet werden.
x1
Z
x5
x2
x
x4
x3
33
Vorlesungsmitschrift Graphentheorie
F¨
arbung in Graphen
2. Fall : Es gibt einen Weg in G13 von x1 nach x3 . Zusammen mit x und
den beiden Kanten von x nach x1 und x3 ergibt sich ein Kreis GK .
x1
Gk
x5
x2
x
x3
x4
Jeder Weg von x2 nach x4 in G muß einen Knoten xK von GK benutzen. xK ist mit Farbe 1 oder 3 gef¨arbt. Somit liegen x2 und x4
in unterschiedlichen Zusammenhangskomponenten von G24 . Das heißt,
auf G24 kann der 1. Fall angewendet werden.
x1
Gk
x5
x2
x
xk
x4
x3
34











