Praktische Informatik 1

Bäume
  A^
 Wenn aA und lA^ und rA^, so (a,l,r)A^.
Def. Wurzel, Unterbaum, Kind, Teilbaum
Knoten von x: Wurzel eines nichtleeren Teilbaumes von x
Blatt: Knoten ohne Nachfolger (d.h. ein Teilbaum der Gestalt (a,  ,  ) ) heißt.
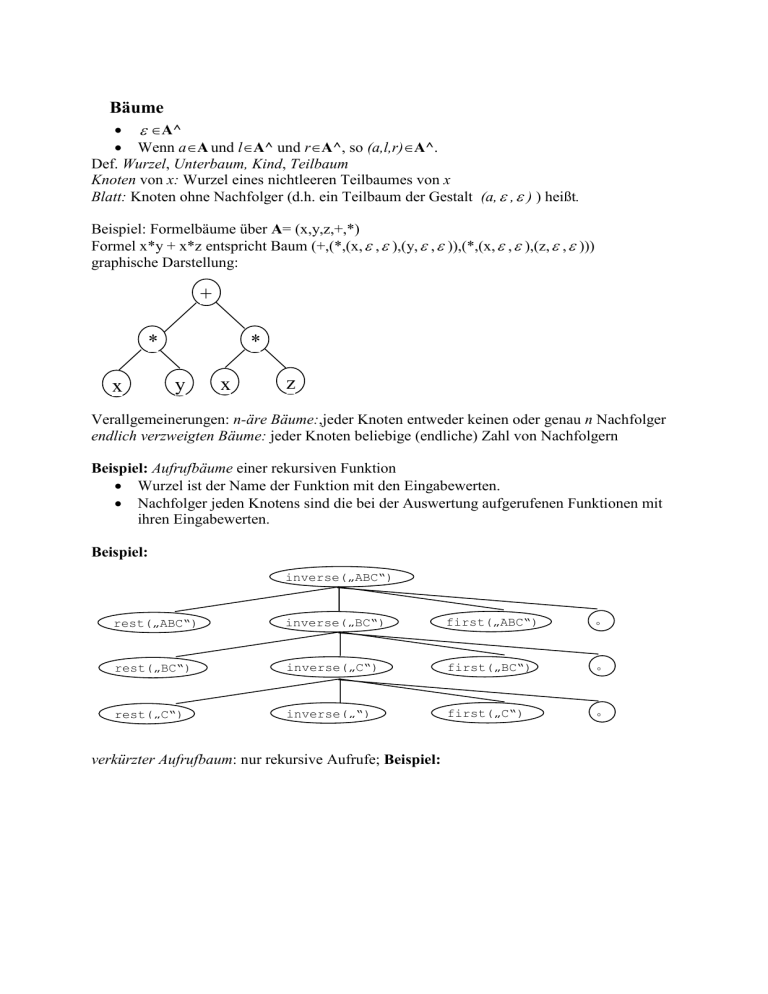
Beispiel: Formelbäume über A= (x,y,z,+,*)
Formel x*y + x*z entspricht Baum (+,(*,(x,  ,  ),(y,  ,  )),(*,(x,  ,  ),(z,  ,  )))
graphische Darstellung:
+
*
x
*
y
x
z
Verallgemeinerungen: n-äre Bäume:,jeder Knoten entweder keinen oder genau n Nachfolger
endlich verzweigten Bäume: jeder Knoten beliebige (endliche) Zahl von Nachfolgern
Beispiel: Aufrufbäume einer rekursiven Funktion
 Wurzel ist der Name der Funktion mit den Eingabewerten.
 Nachfolger jeden Knotens sind die bei der Auswertung aufgerufenen Funktionen mit
ihren Eingabewerten.
Beispiel:
inverse(„ABC“)
)
rest(„ABC“)
inverse(„BC“)
first(„ABC“)
°
rest(„BC“)
inverse(„C“)
first(„BC“)
°
rest(„C“)
inverse(„“)
first(„C“)
°
verkürzter Aufrufbaum: nur rekursive Aufrufe; Beispiel:
fib(5)
fib(3)
fib(4)
fib(3)
fib(2)
fib(2)
fib(2)
fib(1)
fib(1)
Aufrufkomplexität: Anzahl der Knoten im verkürzten Aufrufbaum
Beispiel: Aufrufkomplexität der Fibonacci-Funktion:
1, falls n  2

fibComp(n)  
1  fibComp(n  1)  fibComp(n  2), sonst
Theorem: fibComp(n)  2 * fib(n)  1
Bew. Induktion nach n. Für n=1,2 klar, für n>2:
fibComp(n)  1  fibComp(n  1)  fibComp(n  2)  I .V . 1  2 * fib(n  1)  1  2 * fib(n  2)  1
 2 * ( fib(n  1)  fib(n  2))  1  2 * fib(n)  1
Mit Gleichung von Binet:
n
n
2  1  5   1  5  
 
  1.

fibComp(n) 
5  2   2  


Wertetabelle
N
3
5
10
20
30
40
50
60
70
80
90
100
fibComp(n)
3
9
109
13529
1.6*106
2*108
2.5*1010
3*1012
3.8*1014
4.6*1016
5.7*1018
7*1020
Zeitaufwand für n=100 bei 10.000 Aufrufen pro Sekunde etwa 2,2 Milliarden Jahre
Graphen
Graph: bildliche Darstellung einer binären Relationen über einer endlichen Grundmenge
 Kreis (Knoten): Element der Grundmenge
 Pfeil (Kante): Elemente in der Relation enthalten
Beispiel: Relation {(A,B),(B,C),(C,B),(C,A),(B,D),(C,D)}
B
A
C
D
Symmetrische Relation: Pfeile immer in beide Richtungen (ungerichteter Graph).
Alternative Definition: Graphen als Tupel (V,E)
 V eine endliche Menge von Knoten (vertices)
 E eine endliche Menge von Kanten (edges)
 zu jeder Kante genau ein Anfangs- und ein Endknoten.
Quelle: Knoten, der nicht Endknoten ist
Senke: Knoten, der nicht Anfangsknoten ist
Isolierter Knoten: weder Anfangs- noch Endknoten
Weitere alternative Definition: Adjazenzmatrix
 Graph ist endliche Matrix (Tabelle) mit booleschen Werten
 Zeilen und Spalten sind mit der Grundmenge beschriftet
 Eintrag X gibt an, ob das Paar (Zeile, Spalte) in der Relation enthalten
A B C D
A
X
B
X X
C X X
X
D
Graphen können Zyklen enthalten: keine einfache induktive Definition möglich
endlich verzweigte Bäume sind zyklenfreie Graphen mit genau einer Quelle
Kapitel 2: Informationsdarstellung
2.1 Bits und Bytes, Zahl- und Zeichendarstellungen (siehe Gumm/Sommer * Kap.1.2/1.3)
Darstellung, Repräsentation: Abbildung von Informationen in maschinell verarbeitbarer Form
Bit (binary digit): kleinste Einheit der Informationsdarstellung (genau zwei Werte)
Realisierungsmöglichkeiten: an/aus, geladen/ungeladen, weiss/schwarz,
magnetisiert/entmagnetisiert, reflektierend/lichtdurchlässig, …
Ein Bit repräsentiert den kleinstmöglichen Informationsgehalt (Antwort auf Ja/Nein-Frage)
Repräsentation komplexerer Informationen durch Tupel oder Folgen von Bits.
Beispiel: Himmelsrichtungen (8 Möglichkeiten, durch Bitfolge der Länge 3 codiert)
000 = Nord
001 = Nordost
010 = Ost
011 = Südwest
100 = Süd
101 = Südost
110 = West
111 = Nordwest
2n mögliche Bitfolgen der Länge n (| |=2  |
n
|=2n)
Byte: Folge von 8 Bit; ein Byte kann repräsentieren (z.B.):
ein Zeichen (falls das Alphabet weniger als 28 Zeichen enthält)
eine Zahl zwischen 0 und 255,
eine Zahl zwischen -128 und +127,
Farbcodierung eines Punkts in einer Graphik, genannt „Pixel“ (picture element)
8 Bit: Byte
16 Bit: Halbwort
32 Bit: Wort
64 Bit: Doppelwort
128 Bit: Quadwort
210 = 1024  1000 = 103
Präfixe:
 k =
 M =
 G =
 T =
 P =
 E =
1024 = 210
 103
2
20
1024 = 1048576=2  106
10243 = 230
 109
10244 = 240
 1012
5
50
1024 = 2
 1015
10246 = 260
 1018
(k = Kilo)
(M = Mega)
(G = Giga)
(T = Tera)
(P = Peta)
(E = Exa)
1 GByte: entweder 230 = 10243 = 1.073.741.824 oder 109 = 1.000.000.000 Byte.
gängige Größenordnungen:
 Notiz: ~200 B
 Brief: ~3 kB
 Dos-Programm: ~300 kB
 Diskettenkapazität: 1,44 MB
 Windows-Programm: ~ 1 MB
 Musiktitel: ~40 MB (im MP3-Format ~4 MB)
 Zip-Diskette: ~120 MB
 Hauptspeichergröße: 512 MB – 2GB
 CD-ROM Kapazität: ~ 700 MB
 DVD (Digital Versatile Disk): ~ 4,7 bzw. ~ 9 GB
 Festplatte: ~80-600 GB.