Vorlesung 4 - Deutsches Elektronen

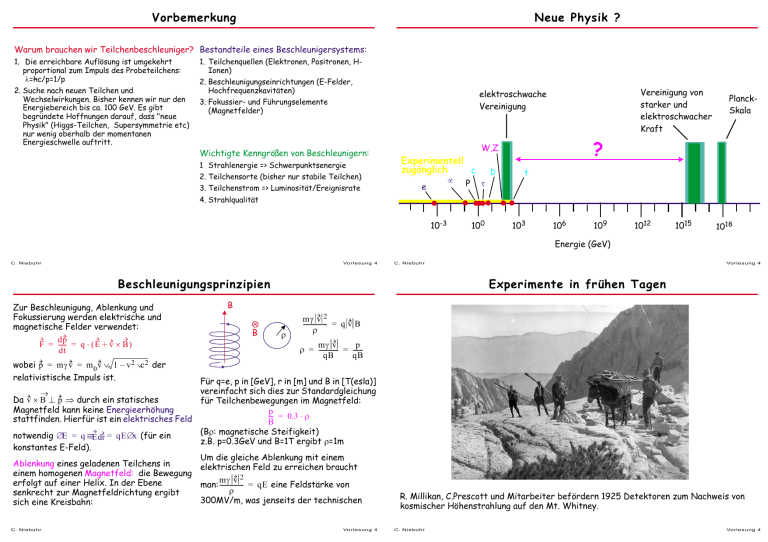
Vorbemerkung
Neue Physik ?
Warum brauchen wir Teilchenbeschleuniger? Bestandteile eines Beschleunigersystems:
1. Die erreichbare Auflösung ist umgekehrt
proportional zum Impuls des Probeteilchens:
λ=hc/p=1/p
2. Suche nach neuen Teilchen und
Wechselwirkungen. Bisher kennen wir nur den
Energiebereich bis ca. 100 GeV. Es gibt
begründete Hoffnungen darauf, dass "neue
Physik" (Higgs-Teilchen, Supersymmetrie etc)
nur wenig oberhalb der momentanen
Energieschwelle auftritt.
1. Teilchenquellen (Elektronen, Positronen, HIonen)
2. Beschleunigungseinrichtungen (E-Felder,
Hochfrequenzkavitäten)
Wichtigte Kenngrößen von Beschleunigern:
1 Strahlenergie => Schwerpunktsenergie
2. Teilchensorte (bisher nur stabile Teilchen)
3. Teilchenstrom => Luminosität/Ereignisrate
Vereinigung von
starker und
elektroschwacher
Kraft
elektroschwache
Vereinigung
3. Fokussier- und Führungselemente
(Magnetfelder)
?
W,Z
Experimentell
zugänglich
c
µ
e
P
b
τ
PlanckSkala
t
4. Strahlqualität
10-3
100
103
106
109
1012
1015
1018
Energie (GeV)
C. Niebuhr
Vor lesung 4
C. Niebuhr
Beschleunigungsprinzipien
Zur Beschleunigung, Ablenkung und
Fokussierung werden elektrische und
magnetische Felder verwendet:
dp
F = ------ = q ⋅ ( E + v × B )
dt
wobei p = mγ v = m 0 v ⁄ 1 – v 2 ⁄ c 2 der
relativistische Impuls ist.
Experimente in frühen Tagen
B
B
ρ
mγ v 2
----------------- = q v B
ρ
mγ v
p
ρ = -------------- = ------qB
qB
Für q=e, p in [GeV], r in [m] und B in [T(esla)]
vereinfacht sich dies zur Standardgleichung
Da v × B ⊥ p ⇒ durch ein statisches
für Teilchenbewegungen im Magnetfeld:
Magnetfeld kann keine Energieerhöhung
p
---- = 0.3 ⋅ ρ
stattfinden. Hierfür ist ein elektrisches Feld
B
(Bρ: magnetische Steifigkeit)
notwendig ∆E = q ∫ E dr = qE∆x (für ein
z.B. p=0.3GeV und B=1T ergibt ρ=1m
konstantes E-Feld).
Um die gleiche Ablenkung mit einem
Ablenkung eines geladenen Teilchens in
elektrischen Feld zu erreichen braucht
einem homogenen Magnetfeld: die Bewegung
mγ v 2
erfolgt auf einer Helix. In der Ebene
man: ----------------- = qE eine Feldstärke von
ρ
senkrecht zur Magnetfeldrichtung ergibt
300MV/m, was jenseits der technischen
sich eine Kreisbahn:
C. Niebuhr
Vor lesung 4
Vor lesung 4
R. Millikan, C.Prescott und Mitarbeiter befördern 1925 Detektoren zum Nachweis von
kosmischer Höhenstrahlung auf den Mt. Whitney.
C. Niebuhr
Vor lesung 4
Historische Entwicklung
Einfache elektrische Beschleuniger
Prinzip:
Seit den 20er Jahren wurden verschieden Beschleunigertypen
entwickelt:
Entwicklungsschritte:
• Gleichspannungsbeschleuniger
• Van-de-Graaff-Beschleuniger
• Linearbeschleuniger
• Zyklotron
• Betatron
Cockroft-Walton-Generator (1930):
• Synchrotron
Potential wird elektrisch mit Hilfe
eines Kaskadengenerator aufgebaut.
• Collider
s p
C. Niebuhr
Vor lesung 4
p
p
C. Niebuhr
Ein Beschleuniger aus dem Alltag
p
p
p
Vor lesung 4
Van-de-Graff-Beschleuniger
Beim Van-de-Graff-Beschleuniger
(1931) wird das Potential auf
mechanischem Wege erzeugt.
Erfolgt eine Umladung spricht man
von einem Tandem-Beschleuniger,
da die Beschleunigungsspannung
zweimal durchlaufen werden kann:
1. negative Ionen werden erzeugt und
beschleunigt
2. die Ionen treffen auf eine dünne
Folie, verlieren Hüllenelektronen
("stripping") und werden dadurch zu
positiv geladenen Ionen
3. die positiven Ionen durchlaufen die
Beschleunigungsstrecke erneut
Vor allem nützlich für Ionen mit
Z>>1, da sich höhere Energien
erreichen lassen.
Emax ≈ 1 GeV
C. Niebuhr
Vor lesung 4
C. Niebuhr
Vor lesung 4
Linearbeschleuniger
Die Driftröhren werden
abwechselnd mit beiden Polen
mit hochfrequenter Wechselspannung verbunden, d.h. die
Teilchen werden jeweils
zwischen den Driftröhren
beschleunigt. In den Driftröhren ist das elektrische
Feld abgeschirmt (Faradaykäfig)
Betatron
Das Betatron wurde 1940 von D.Kerst (Univ.
Illinois) entwickelt. Die Beschleunigung
erfolgt in einem Transformatorkern: in einem
zeitlich veränderlichen Magnetfeld wird nach
dem Induktionsgesetz ein elektrisches
Wirbelfeld erzeugt. Befinde sich frei
bewegliche Elektronen in dem evakuierten
Rohr werden sie beschleunigt. Zusätzlich
wirkt das B-Feld als Haltefeld für den
Elektronenstrahl.
Protonen-LINAC
Für nichtrelativisische Teilchen (z.B. Protonen) muss die Länge der Driftröhren der
zunehmenden Geschwindigkeit angepasst werden, damit man mit konstanter HF-Frequenz
arbeiten kann ⇒ für Protonen Emax ≈ 50 MeV.
Im Fall von Elektron-LINAC’s bewegen sich dagegen die Teilchen von Anfang an fast mit
Lichtgeschwindigkeit. Hier erreicht man die Beschleunigung dadurch, dass man eine
stehende Welle in einem Hohlleiter erzeugt mit vPh < c und die Phasengeschwindigkeit so
auf die Teilchengeschwindigkeit abstimmt, dass die Teilchen immer das gleiche Feld
sehen.
C. Niebuhr
Vor lesung 4
Typische Frequenz des B-Feldes: 50-500Hz
Beschleunigung nur während einer Viertelperiode möglich.
Form und Wert des Feldes müssen so gewählt
werden. dass die Teilchen sowohl radial als in
z-Richtung auf einer stabilen Bahn laufen.
=> BHalte(Rs) = Bind(Rs)/2
B
Vakuumkammer
z
Bz
BR
R
Radiale und axiale
Stabilität gegeben falls:
B ( r ) ∝ r – n mit 0<n<1
Betatrons sind nicht für Protonen geeignet,
da wegen der hohen Masse die Dämpfung
fehlt und die Protonen zu langsam umlaufen =>
zu wenig effektive Beschleunigung
C. Niebuhr
Zyklotron
Vor lesung 4
Synchrotron
Aus dem Gleichgewicht von Lorentz- und Zentrifugalkraft
erhält man die Zyklotronfrequenz ωc :
mv
qB
mω 2 r = ------- ⋅ ωr = vBq ⇒ ω c = ------r
m
Das Teilchen wird bei r=0 eingeschossen und beschleunigt.
Dadurch wächst der Bahnradius, aber ωc bleibt unabhängig
von r, E und p konstant. Deshalb sind beim Zyklotron
Beschleunigungsfrequenz (HF) und Umlauffrequenz gleich.
Wenn der maximale Radius r=Rmax erreicht ist, erfolgt die
Ejektion des Strahls.
Das Prinzip, des 1945 von Veksler,
McMillan und Wideroe konstruierten
Synchrotrons besteht darin, die
Beschleunigungsfrequenz ωHF(t) und
das Magnetfeld B(t) synchron so zu
verändern, dass die Teilchen, deren
Umlauffrequenz und Impuls p wächst,
in den Beschleunigungszellen immer
eine beschleunigende Spannung
erfahren und gleichzeitig weiterhin
auf der vorgegebenen Bahn im Vakuum
gehalten werden.
Typische Parameter:
B = 1.5 T
ω = 50 MHz
U = 200-500 kV
Die Teilchen legen zum Teil riesige
Strecken zurück: 109 Umläufe
entsprechen ≈ 1013m. Demzufolge
müssen die Strahlen sehr effektiv
fokussiert werden.
=> 20-25 MeV Endenergie bei Strömen bis zu mA Stärke
können erreicht werden.
Wegen des großen relativistischen Massesnanstiegs kann
das Zyklotron nicht für Elektronen sondern nur für
schwerere Teilchen verwendet werden (ωHF≈ωc nur
konstant für γ≈1)
C. Niebuhr
Stromwicklung
Eisenjoch
Störungen führen zu Betatron- und
Synchrotron-oszillationen.
Wesentliche Elemente:
• Injektionslinac (Teilchen im Synchrotron
müssen schon relativistisch sein)
• Beschleunigungsstrecken (HF Klystrons)
• Ablenkmagnete (Dipole)
• Fokussiermagnete (Quadrupole)
Vor lesung 4
C. Niebuhr
Vor lesung 4
Hochfrequenzbeschleunigung
Strahlführung
Für ein Teilchen, das sich in die Richtung s bewegt gilt:
Zur Wellenleitung werden Hohlleiterelemente
verwendet.
Aus den Maxwellgleichungen und Randbedingungen
folgt: B-Feld parallel und E-Feld senkrecht zur
leitenden Oberfläche.
Leiter
B
1 ˙˙
Lösungen der Wellengleichung ∆E – ----- E = 0
c2
E
s
e
1
Daraus folgt ----------------------- = --- B y ( x, y, s ) .
p
R ( x, y, s )
Normalerweise sind die Abweichungen x von der Sollbahn klein gegen
den Ablenkradius R, daher ist eine Multipolentwicklung in x sinnvoll:

e
e
--- B y ( x ) = ---  B y ( 0 ) +
p
p

TM01 Welle: E s = E 0 ⋅ J 0 ( k c r ) ⋅ exp ( i ( ωt – k s s ) )
mit k = 2.405 ⁄ R und ω = c
k c2 + k s2 .
Dipol
Damit ergibt sich für die
Dipol:
Quadrupol:
Sextupol:
Oktupol:
c
ω
Phasengeschwindigkeit: v Ph = ---- = -------------------------- ≥ c
ks
kc 2
1 –  -----
 k
∂B y
C. Niebuhr
Vor lesung 4
x +
Quadrupol
Sextupol
∂x
S
y
x
S
C. Niebuhr
N
3
1 ∂ By 3
----x
3! ∂ x 3
+
R
Mitbewegtes Koordinatensystem

+ ...


Oktupol
Ablenkung
Fokussierung
Kompensation von Feldfehlern
Kompensation von Feldfehlern
C. Niebuhr
Vor lesung 4
Fokussierung mit Quadrupolen
N
2
1 ∂ By 2
----x
2! ∂ x 2
s
x
Man spricht von linearer Strahloptik, wenn nur Dipole und Quadrupole
verwendet werden.
Durch Einbringen von Irisblenden kann man
v Ph = c erreichen.
Bei einem Quadrupol gilt für die
Feldkomponenten: B x = g ⋅ y und B y = g ⋅ x .
Man erreicht dies durch hyperbelförmige
Polschuflächen, wobei sich jeweils zwei
Nordpole bzw. zwei Südpole gegenüberstehen.
y
v = ( 0, 0, v s ) mit B = ( B x, B y, 0 ) . Für die Ablenkung in x-Richtung gilt
für die Lorentzkraft: F x = – ev s B y . Die Zentrifugalkraft ist: F = mv s2 .
Tyische Werte für g =
Betatronschwingungen
∂B y
sind 20 T/m für
∂x
normalleitende Magnete mit Eisenpolschuhen und 100-200 T/m für supraleitende Quadrupole. Die auf Teilchenimpuls und Ladung normierte Fokussierungsg
stärke ist K = e --- .
p
In der Näherung für eine dünne Linse hat
ein Quadrupol der Länge l hat die
1
Brennweite f = ---------- (⇒ Impulsabhängig !)
K⋅l
Im Gegensatz zu einer optischen Linse
fokussiert ein Quadrupol allerdings immer
nur in einer Ebene. In der dazu senkrechten
Ebene wird dder Strahl defokussiert. In
der Praxis werden daher immer zwei
gegeneinander um 90° verdrehte
Quadrupole (Dublett) verwendet.
Vor lesung 4
Aufgrund der Rückstellkräfte in den fokussierenden Magneten führen die Teilchen um
die Sollbahn sogenannte Betatronschwingungen aus. Für die Abweichungen in x- und yRichtung gelten die Hill’schen Differentialgleichungen:
x'' ( s ) + K ( s )x ( s ) = 0
und
y'' ( s ) – K ( s )y ( s ) = 0
In einem horizontal fokussierenden Quadrupol gilt K ( s ) = K 0 > 0 , in einem horizontal
defokussierenden Quadrupol entsprechend K ( s ) = – K 0 < 0
Lösungen sind quasiharmonische, amplituden und frequenzmodulierte Schwingungen der
Form x ( s ) = A ( s ) ⋅ cos ( Φ ( s ) – Φ 0 ) (analog für y(s)), wobei für die Amplituden- und
Phasenfunktionen gilt: A ( s ) =
ε ⋅ β(s)
und
ε ist eine Konstante mit der Dimension [Länge]
dΦ
1
------- = ---------ds
β(s)
Die Betafunktion β ( s ) bestimmt die Ortsabhängigkeit der Amplitude und der
Wellenlänge der Betatronschwingung. Sie hängt nur von der Anordnung der Magnete ab.
In den meisten Fällen findet man in Beschleunigern periodische Magnetanordnung ⇒
β ( s ) ist evbenfalls periodisch.
C. Niebuhr
Vor lesung 4
Einhüllende aller Teilchenbahnen
Phasenellipse der Teilchenbewegung
Aus den Bewegungsgleichungen der
Teilchen ergibt sich, dass der
vorhandenen Phasenraum, der durch
die Größen x und x’ gegeben ist durch
eine Ellipse beschrieben wird, deren
Form sich bei der Bewegung durch den
Beschleuniger zwar ändert, deren
Gesamtfläche aber nach dem Theorem
von Liouville konstant bleibt. Es gilt:
1 + α2( s )
α ( s ) = – β' ( s ) ⁄ 2 und γ ( s ) = ----------------------β(s)
Für die Gesamtheit der Strahlteilchen, die
transversale Schwingungen um den Sollorbit
durchführen, ist die äußere Grenze aller
Teilchenbahnen gegeben durch:
E (s) = ε ⋅ β(s) .
Sie bestimmt die maximale transversale
Strahldimension. Wichtig für die Auslegung
der Vakuumkammern eines Beschleunigers.
Eine wichtige Größe ist auch die Anzahl der
Betatronschwingungen:
1
Q = -----2π
°∫
1
dΦ
-------ds = -----2π
ds
°∫
x’
1
----------ds .
β(s)
Für eine stabilen Betrieb muss unbedingt
vermieden werden, dass Q ganz- oder halbzahlige Werte annimmt, da sonst die
unvermeidlichen Feldfehler zu einem
resonanzartigen Anwachsen der Amplitude
und damit zum Strahlverlust führen würden.
x
Nicht jede Bahn erreicht die Einhüllende
und wenn, dann nicht an allen Stellen.
C. Niebuhr
Vor lesung 4
x
Entwicklung der Phasenellipse in einer Driftstrecke:
rot → blau → grün
Der ursprünglich fokussierte Strahl divergiert mehr
und mehr. Mit einem Quadrupol läßt sich dies wieder
umkehren.
Analog für y und y’.
C. Niebuhr
Resonanzen
Vor lesung 4
Synchrotronschwingungen & Phasenfokussierung
In der Praxis gibt es Kopplung zwischen
Schwingungen in x- und y-Richtung. Dann
lautet die Resonanzbedingung:
mν x + nν y = r , mit m,n,r ganze Zahlen.
Störung
Bisher haben wir nur transversale
Schwingungen betrachtet. Jeder
Beschleuniger hat eine endliche
Energieschärfe, d.h. die Teilchen
befinden sich in einem Impulsintervall
∆p (typisch∆p/p≈10-3 ) um den Sollwert
herum.
Für den Fall relativistischer Teilchen in
einem Kreisbeschleuniger ergibt sich
folgende Situation:
Teilchen mit höherem (niedrigerem)
Impuls p>p0 (p<p0) laufen auf einem
größeren (kleineren) Kreis als die
Sollteilchen und kommen daher etwas
später (früher) an der Beschleunigungsstrecke vorbei. Dies führt dazu, dass
sie ein reduziertes (erhöhtes) E-Feld
spüren und daher im Vergleich zu den
Soll-Teilchen abgebremst
(beschleunigt) werden.
Q ganzzahlig ⇒ Störung wird immer mit der
gleichen Phase angetroffen ⇒ Resonanz
Q nicht ganzzahlig ⇒ Störung hebt sich im
Mittel vieler Umläufe auf.
(Statt Q wird auch häufig der Buchstabe ν
verwendet)
C. Niebuhr
x’
Vor lesung 4
C. Niebuhr
Sollelektron
U
zu spät: p>p0
zu früh: p<p0
phasenstabiles
Gebiet
t
phaseninstabiles
Gebiet
Konsequenzen:
1. Teichen führen sogenannte Synchrotronschwingungen
in longitudinaler Richtung aus (Energie und Phase)
Beispiel HERA-p: 31.15 Betatron- aber nur 0.002
Synchrotron-Schwingungen pro Umlauf
2. phasenstabiler Bereich nur in einer Viertelperiode ⇒
Ausbildung von Teilchenpaketen
N.B. Für den Fall von nichtrelativistischen
Teilchen in einem Linearbeschleuniger gilt die
Situation analog, aber der stabile Bereich ist in
diesem Fall die ansteigende Flanke!
Vor lesung 4
Synchrotronstrahlung
Parameter von einigen Beschleunigern
In den Ablenkmagneten eines Kreisbeschleunigers erfahren die geladenen Teilchen eine
Zentripetalbeschleunigung, die zur Abstrahlung von Energie führt. Für die abgestrahlte
2 e2
e2c3
P = --- ------------ -------------------- ⋅ E 02 ⋅ B 2
Leistung P gilt folgender Zusammenhang:
3 4πε 0 ( m c 2 ) 4
0
p0 E 0
Für gegebenen Krümmungsradius ρ ist B = ------ ≈ --------eρ eρc
4
e2  E0  1
wird
U 0 = --------  ------------ --3ε 0  m c 2 ρ
und der Energieverlust pro Umlauf
Maschine
StrahlStart Energie
(GeV)
SLC
SLAC
1989
e–x e+
50 x 50
0.8
8300
0.0007
1.45 +1.47
460 /
440
–
LEP
CERN
1989
e–x e+
100 x 100
24 - 100
22
4-6
26.66
3368
816
KEK-B
Japan
1999
e–x e+
8 x 3.5
10000
0.002
e– / e+
1100 / 2600
3.02
116 /
112
452 /
452
PEP-II
SLAC
1999
e–x e+
9 x 3.1
3000
0.0042
e– / e+
990 / 2140
2.20
192 /
192
290 /
326
SppS
CERN
1981
pxp
315-450
6
3.8
p / p
6 / 3
6.91
744
232
210
0.396
p / p
81 / 22
6.28
774
216
e± / p
50 / 100
6.34
396 /
416
580 /
280
26.66
1232
788
0
4
–5 E 0
Numerisch ergibt sich für einen Elektronbeschleuniger: U 0 [ GeV ] = 8.85 ×10 -----ρ
E 0 in [GeV] und ρ in [m] einzusetzen ist.
wobei
TEVATRON 1987
pxp
1000x1000
Fermilab
Beispiel LEP: E0=100 GeV, ρ=4.2km ⇒ Energieverlust pro Umlauf = 2.8 GeV. Diese
enormen Verluste müssen ständig durch ein sehr leistungsfähiges Hochfrequenzbeschleunigungssystem ausgeglichen werden.
Wichtige Konsequenz: höhere Energien mit Elektronen lassen sich nur mit einem
Linearbeschleuniger realisieren.
C. Niebuhr
Luminosität BXTime
1030cm-2s-1 (µs)
Vor lesung 4
HERA
DESY
1992
e± x p
27.5 x 920
14 - 45
0.096
LHC
CERN
2005
pxp
7000x7000
10000
0.025
540
C. Niebuhr
Tevatron
Vor lesung 4
LEP am CERN
Large Electron Positron Collider:
Inbetriebnahme 1987 am Fermilab in Chicago
• Strahlteilchen: Protonen auf Antiprotonen
• Umfang:
6.3 km
• Energie:
1 TeV x 1TeV
• Luminosität:
Strahl Strom Umfang /
#
#
(mA)
Länge (km) Dipole Quads
210 x 1030 cm-2 s-1
• Zeit zwischen
Bunchcrossings: 0.396 µs
Wichtige Ergebnisse:
• Nachweis des Top-Quarks (1995)
Betrieb: 1989-2000
• Nachweis des Tau-Neutrinos (2000)
• Strahlteilchen:
• Umfang:
• Energie:
e+ e–
27 km
50-100 GeV
24 x 1030 cm-2 s-1
• Zeit zwischen Bunchcrossings: 22 µs
• Luminosität:
C. Niebuhr
Vor lesung 4
C. Niebuhr
Vor lesung 4
SLAC
HERA
Hadron Elektron Ring Anlage bei DESY
Stanford Linear Accelerator
• Länge:
e+ e–
3 km
• Energie:
50 GeV
• Luminosität:
2.5 x 10 30cm-2 s-1
• Strahlteilchen:
• Zeit zwischen Bunchcrossings: 8300 µs
• Feldgradient dE/ds:
C. Niebuhr
15 MV/m
Vor lesung 4
in Betriebseit 1992 in Hamburg
• Strahlteilchen:
e± p
• Umfang:
6.3 km
• Energie:
27GeV x 920 GeV
• Luminosität:
10 x 1030 cm-2 s-1
40 x 1030 cm-2 s-1
• Zeit zw. Bunchcrossings:
0.096 µs
Upgrade 2000
C. Niebuhr
TESLA
Vor lesung 4
33 km Supraleitende Kavitäten
• Kavitäten aus hochreinem Niob
• Betrieb bei 2û Kelvin
• Feldgradient: 25-30 MV/m
• Frequenz: 1.3 GHz
C. Niebuhr
Vor lesung 4
C. Niebuhr
Vor lesung 4
Kosmische Beschleuniger
Energien oberhalb von 1020 eV werden
beobachtet. Es ist ein Gegenstand
aktiver Forschung die Quellen und
Beschleunigungsmechanismen
aufzuklären.
C. Niebuhr
Vor lesung 4