Folien - Informatik Uni-Leipzig
Werbung

Schaltkreiskomplexität
Markus Lohrey
Universität Leipzig
http://www.informatik.uni-leipzig.de/alg/lehre/ws09_10/SCHALTKREISE/
Wintersemester 2009/2010
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
1 / 195
Literatur
Die folgenden Bücher dienten als Quellen für diese Folien:
Peter Clote und Evangelos Kranakis, Boolean Functions and
Computation Models, Springer
Howard Straubing, Finite Automata, Formal Logic, and Circuit
Complexity, Birkhäuser
Heribert Vollmer, Introduction to Circuit Complexity: A Uniform
Approach, Springer
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
2 / 195
Grundlegende Definitionen
Allgemeine Notationen
Seien fi : Ai → Bi (i ∈ I ) Funktionen mit Ai ∩ Aj = ∅ für i 6= j.
S
S
S
Dann ist i∈I fi : i∈I Ai → i∈I Bi die Funktion mit
µ[ ¶
fi (a) = fi (a).
∀i ∈ I ∀a ∈ Ai :
i∈I
Für eine Funktion f : {0, 1}∗ → {0, 1}∗ sei f ↾n : {0, 1}n → {0, 1}∗ die
Einschränkung von f auf Wörter der Länge n.
Eine Boolesche Funktion ist eine Funktion f : {0, 1}n → {0, 1}, wobei
n ≥ 0 die Stelligkeit von f , kurz arity(f ), ist.
Für n ≥ 0 sei die Abbildung ℓ : N → N definiert durch:
(
1
falls n = 0
ℓ(n) =
⌊log(n) + 1⌋ falls n > 0
D. h. ℓ(n) ist die Länge von n in Binärnotation.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
3 / 195
Grundlegende Definitionen
Gerichtete Graphen
Ein geordneter gerichteter Graph ist ein Paar G = (V , α) mit α : V → V ∗ .
Intuitiv ist α(v ) eine Liste der Knoten, die eine Kante zu v haben, d. h.
wenn α(v ) = v1 v2 · · · vm , dann gibt es die Kanten (vi , v ) in dem Graphen
(1 ≤ i ≤ n).
G = (V , α) ist azyklisch, wenn der gerichtete Graph
(V , {(u, v ) | u kommt in α(v ) vor}) azyklisch ist.
Für v ∈ V nennen wir |α(v )| ∈ N den Eingangsgrad von v
(Anzahl der eingehenden Kanten).
Es sei Out(G ) = {v ∈ V | ∀u ∈ V : v kommt in α(u) nicht vor}.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
4 / 195
Grundlegende Definitionen
Schaltkreise
Sei B eine (eventuell unendliche) Menge von Booleschen Funktionen.
Ein Schaltkreis über der Basis B mit n Eingängen ist ein Tupel
S = (V , α, λ, out) mit folgenden Eigenschaften:
GS = (V , α) ist ein geordneter gerichteter azyklischer Graph.
λ : V → B ∪ {x1 , . . . , xn } ist eine Abbildung, wobei für alle Knoten
v ∈ V gilt:
Wenn λ(v ) ∈ B dann gilt arity(λ(v )) = |α(v )|.
Wenn λ(v ) ∈ {x1 , . . . , xn }, dann gilt |α(v )| = 0.
out : {1, . . . , |Out(GS )|} → Out(GS ) ist eine Bijektion.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
5 / 195
Grundlegende Definitionen
Schaltkreise
Sei S = (V , α, λ, out) ein Schaltkreis über der Basis B mit n Eingängen.
Knoten von S bezeichnen wir im folgenden auch als Gatter. Gatter v mit
λ(v ) ∈ {x1 , . . . , xn } nennen wir Eingabegatter, Gatter in Out(GS ) nennen
wir Ausgangsgatter, und Gatter v mit |α(v )| > 0 nennen wir wesentliche
Gatter.
Die Größe des Schaltkreises S ist size(S) = |{v ∈ V | |α(v )| > 0}|
(Anzahl der wesentlichen Gatter).
Die Tiefe des Schaltkreises S ist depth(S) = maximale Länge (= Anzahl
der Kanten) eines Pfades von einem Eingabegatter zu einem
Ausgangsgatter.
Der Eingangsgrad von S ist indeg(S) = max{|α(v )| | v ∈ V }.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
6 / 195
Grundlegende Definitionen
Auswerten von Schaltkreisen
Sei S = (V , α, λ, out) ein Schaltkreis über der Basis B mit n Eingängen.
Sei g : {x1 , . . . , xn } → {0, 1} eine Abbildung.
Wir definieren valg : V → {0, 1} induktiv wie folgt:
Wenn λ(v ) = xj , dann valg (v ) = g (xj )
Wenn λ(v ) = f ∈ B und α(v ) = v1 v2 · · · vm , dann
valg (v ) = f (valg (v1 ), valg (v2 ), . . . , valg (vm )).
Sei m = |Out(GS )| die Anzahl der Ausgangsgatter von S. Der Schaltkreis
S definiert dann eine Abbildung valS : {0, 1}n → {0, 1}m wie folgt:
Sei b1 , . . . , bn ∈ {0, 1} beliebig.
Definiere g : {x1 , . . . , xn } → {0, 1} durch g (xi ) = bi für 1 ≤ i ≤ n.
Dann ist valS (b1 , . . . , bn ) = (valg (out(1)), . . . , valg (out(m))).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
7 / 195
Grundlegende Definitionen
Auswerten von Schaltkreisen
Bemerkung:
Ein Schaltkreis S kann als ein paralleler Algorithmus zur Berechnung der
Funktion valS angesehen werden.
Funktionen aus der Basis B bilden dabei die elementaren Operationen des
Algorithmus.
Falls unbeschränkt viele Prozessoren vorhanden sind, kann depth(S) als
die parallele Rechenzeit angesehen werden, während |S| als die sequentielle
Rechenzeit angesehen werden kann.
Problem: Ein Schaltkreis kann immer nur Eingaben einer festen Länge (=
Anzahl der Eingabegatter) verarbeiten.
Wir führen deshalb Schaltkreisfamilien ein.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
8 / 195
Grundlegende Definitionen
Schaltkreisfamilien
Eine Schaltkreisfamilie über der Basis B ist eine Folge F = (Si )i≥0 , wobei
Si ein Schaltkreis über der Basis B mit ni vielen Eingängen ist und
n0 < n1 < n2 < · · · gilt.
Häufig (aber nicht immer) wird ni = i gelten.
Eine solche Schaltkreisfamilie F definiert
S eine partielle Abbildung
valF : {0, 1}∗ → {0, 1}∗ durch valF = i≥0 valSi .
Beachte: valF ist im allgemeinen nur partiell definiert, da in F nicht für
jedes n ≥ 0 ein Schaltkreis mit genau n Eingängen existieren muss.
Hat jeder Schaltkreis Si genau ein Ausgangsgatter, so ist valF eine
partielle Funktion valF : {0, 1}∗ → {0, 1}. Wir können dann die Sprache
LF = {w ∈ {0, 1}∗ | valF (w ) = 1} definieren.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
9 / 195
Grundlegende Definitionen
Schaltkreisfamilien
Sei F = (Sn )n≥0 eine Schaltkreisfamilie.
Die Größe von F ist die Funktion sizeF mit sizeF (n) = size(Sn ).
Die Tiefe von F ist die Funktion depthF mit depthF (n) = depth(Sn ).
Für eine Basis B und Mengen S, D von monotonen Funktionen auf N sei:
SIZEDEPTH(S, D, B) = {valF | F ist eine Schaltkreisfamilie über der
Basis B mit sizeF ∈ S und depthF ∈ D}
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
10 / 195
Grundlegende Definitionen
Wichtige Basisfunktionen
Für n ≥ 0 definieren wir die folgenden Booleschen Funktionen:
V
n (x1 , . . . , xn ) = x1 ∧ x2 ∧ · · · ∧ xn
W
n (x1 , . . . , xn ) = x1 ∨ x2 ∨ · · · ∨ xn
¬(x) = 1 − x.
MAJn (x1 , . . . , xn ) = 1 genau dann, wenn x1 + x2 + · · · + xn ≥ n/2.
MODqn (x1 , . . . , xn ) = 1 (wobei q ≥ 1) genau dann, wenn
x1 + x2 + · · · + xn durch q teilbar ist.
Den Index n lassen wir häufig weg, da er sich aus der Argumentliste ergibt.
Bemerkung: Bei diesen Funktionen kommt es nicht auf die Reihenfolge der
Argumente an. In Schaltkreisen, deren Basisfunktionen eine Teilmenge
dieser Funktionen bilden, kommt es daher nicht auf die Ordnung der
eingehenden Kanten eines Gatters an.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
11 / 195
Grundlegende Definitionen
Wichtige Schaltkreiskomplexitätsklassen
Sei Bool2 = {¬,
Für i ≥ 0 sei:
V
2}
V
und Bool = {¬} ∪ { k | k ≥ 2}.
NCi = SIZEDEPTH(nO(1) , O(logi (n)), Bool2 )
ACi = SIZEDEPTH(nO(1) , O(logi (n)), Bool)
TCi = SIZEDEPTH(nO(1) , O(logi (n)), Bool ∪ {MAJk | k ≥ 2})
ACC(q) = SIZEDEPTH(nO(1) , O(1), Bool ∪ {MODqk | k ≥ 2})
CC(q) = SIZEDEPTH(nO(1) , O(1), Bool2 ∪ {MODqk | k ≥ 2})
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
12 / 195
Grundlegende Definitionen
Wichtige Schaltkreiskomplexitätsklassen
Bemerkungen:
NC steht für Nick’s class (nach Nick Pippenger), AC steht für
alternating circuits, und TC steht für threshold circuits.
Die Klassen NC0 , AC0 , TC0 , ACC(q) und CC(q) werden durch
Schaltkreisfamilien konstanter Tiefe definiert.
Alle Klassen sind durch Schaltkreisfamilien mit polynomiell
beschränkter Größe definiert. Deshalb ist auch der Eingangsgrad eines
jeden Gatters polynomiell beschränkt.
Für Funktionen aus NCi muss der Eingangsgrad in den Schaltkreisen
durch 2 beschränkt sein.
Wir können in den auf der
W vorherigen Folie definierten
Schaltkreisfamilien auch k -Gatter (k = 2 für NCi und CC(q))
verwenden (de Morgan).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
13 / 195
Grundlegende Definitionen
Schaltkreis-Komplexitätsklassen
Bereits NC0 enthält Funktionen, die nicht berechenbar sind.
Sei A ⊆ N eine unentscheidbare Menge natürlicher Zahlen.
Definiere z. B. die Funktion f : {0, 1}∗ → {0, 1} wie folgt:
(
0 falls |w | 6∈ A
f (w ) =
1 falls |w | ∈ A
Die Funktion f ist offensichtlich nicht berechenbar, kann aber durch
eine (recht triviale) Schaltkreisfamilie berechnet werden.
Dieses “Problem” entsteht, da wir keinerlei Forderung aufstellen, wie
der n-te Schaltkreis Sn einer Familie F aus n berechnet werden kann.
Man sagt auch, dass die Klasse SIZEDEPTH(S, D, B) eine
nicht-uniforme Klasse ist.
Es gibt auch eine uniforme Variante dieser Klasse. Bei dieser kann der
n-te Schaltkreis Sn “effizient” aus n berechnet werden (mehr dazu
später).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
14 / 195
Grundlegende Definitionen
Schaltkreis-Komplexitätsklassen
Satz 1
NC0 ⊆ AC0 ⊆ TC0 ⊆ NC1 ⊆ AC1 ⊆ TC1 ⊆ NC2 ⊆ · · ·
Beweis:
Alle Inklusionen sind trivial, bis auf TCi ⊆ NCi+1 .
V
V S
V
Hierzu genügt
es zu zeigen: , MAJ ∈ NC1 , wobei = n≥0 n und
S
MAJ = n≥0 MAJn .
V
mit einen binären Baum der Tiefe O(log(n))
n kann offensichtlich
V
bestehend aus 2 -Gattern berechnet werden.
MAJ ∈ NC1 wird aus Satz 8 folgen.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
15 / 195
Grundlegende Definitionen
Schaltkreis-Komplexitätsklassen
Satz 2
AC0 ⊆ ACC(q) ⊆ TC0
Beweis:
AC0 ⊆ ACC(q) ist trivial.
Für ACC(q)
⊆ TC0 genügt es zu zeigen: MODq ∈ TC0 , wobei
S
MODq = n≥0 MODqn .
Sei n die Eingabelänge. Es gilt
MODqn (a1 a2 · · · an )
=
⌊n/q⌋
_
k=1
(a1 + a2 + · · · + an = k · q).
Es genügt also, eine TC0 -Schaltkreisfamilie zu konstruieren, die testet, ob
von den n Eingabegattern genau r viele auf 1 gesetzt sind.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
16 / 195
Grundlegende Definitionen
Schaltkreis-Komplexitätsklassen
Hierfür genügt es wiederum, eine TC0 -Schaltkreisfamilie zu konstruieren,
die testet, ob von den n Eingabegattern mindestens r viele auf 1 gesetzt
sind.
1. Fall: 2r ≤ n.
a1 + a2 + · · · + an ≥ r ⇐⇒ MAJ(a1 , a2 , . . . , an , 1, . . . , 1 ) = 1
| {z }
n−2r viele
2. Fall: 2r > n.
a1 + a2 + · · · + an ≥ r ⇐⇒ MAJ(a1 , a2 , . . . , an , 0, . . . , 0 ) = 1
| {z }
2r −n viele
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
17 / 195
Grundlegende Definitionen
Untere Schranken
Drei Hauptresultate dieser Vorlesung sind:
Satz 3 (Smolensky 1987)
Wenn p eine Primzahl ist und t > 1 einen Primteiler verschieden von p
hat, dann gilt für jedes k > 0: MODt 6∈ ACC(p k ).
f
Definiere CC(q)
= SIZEDEPTH(∗, O(1), Bool2 ∪ {MODqk | k ≥ 2}).
Satz 4 (Smolensky 1987)
Wenn p eine Primzahl ist, dann gilt für jedes k > 0:
Satz 5 (Smolensky 1987)
V
f k ).
6∈ CC(p
Wenn p eine Primzahl ist, und t > 1 einen Primteiler verschieden von p
f k ).
hat, dann gilt für jedes k > 0: MODt 6∈ CC(p
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
18 / 195
Grundlegende Definitionen
Untere Schranken
Satz 6 (Korollar aus Satz 3)
Wenn p eine Primzahl ist und k > 0, dann gilt: ACC(p k ) ( TC0 .
Beweis: Angenommen es gilt ACC(p k ) = TC0 .
Also gilt für alle t > 1: ACC(t) ⊆ TC0 = ACC(p k ) und damit
MODt ∈ ACC(p k ).
Dies widerspricht Satz 3.
Eine der berühmten Vermutungen der Schaltkreiskomplexitätstheorie ist:
Vermutung 1
S
0
q>1 ACC(q) ( TC .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
19 / 195
Grundlegende Definitionen
Untere Schranken
Eine stärkere Vermutung ist:
Vermutung 2
Seien t, r > 1, so dass t einen Primteiler hat, der nicht r teilt. Dann gilt
MODt 6∈ ACC(r )
Vermutung 2 impliziert Vermutung 1:
S
Angenommen es gilt r >1 ACC(r ) = TC0 .
Dann gäbe es ein r > 1 mit MAJ ∈ ACC(r ) und damit ACC(r ) = TC0 .
Also gilt für alle t > 1: MODt ∈ TC0 = ACC(r ), was Vermutung 2
widerspricht.
Eine weitere berühmte Vermutung:
Vermutung 3
TC0 ( NC1 .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
20 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Addition
Für einen Bitstring b1 b2 · · · bn (n > 0, bi ∈ {0, 1}) sei
(b1 b2 · · · bn )2 =
n
X
i=1
bi · 2i−1 .
Für n ≥ ℓ(k) bezeichnen wir mit binn (k) den eindeutigen Bitstring
u ∈ {0, 1}n mit (u)2 = k.
Definiere ADDn : {0, 1}2n → {0, 1}n+1 wie folgt für alle u, v ∈ {0, 1}n :
Sei ADD =
Satz 7
S
ADDn (uv ) = binn+1 ((u)2 + (v )2 ).
n≥1 ADDn .
ADD ∈ AC0 .
Beweis: Wir implementieren den Carry-Look-Ahead-Algorithmus als
Schaltkreis konstanter Tiefe.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
21 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Addition
Seien a1 a2 · · · an und b1 b2 · · · bn zwei zu addierende Bitstrings.
Für alle 2 ≤ j ≤ n + 1 definiere
¶
j−1
j−1
_µ
^
CARRYj =
(ai ∧ bi ) ∧
(ak ∨ bk ) .
i=1
k=i+1
Dann gilt CARRYj = 1 genau dann, wenn bei der Addition ein Übertrag
an Position j ankommt.
Wir können damit die Outputgatter c1 , . . . , cn , cn+1 wie folgt definieren:
c1 = (a1 ∧ ¬b1 ) ∨ (¬a1 ∧ b1 )
µ
¶
¡
¢
ci =
¬CARRYi ∧ (ai ∧ ¬bi ) ∨ (¬ai ∧ bi ) ∨
¶
µ
¡
¢
für 2 ≤ i ≤ n
CARRYi ∧ (¬ai ∧ ¬bi ) ∨ (ai ∧ bi )
cn+1 = CARRYn+1
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
22 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Subtraktion
Definiere SUBn : {0, 1}2n → {0, 1}n wie folgt für alle u, v ∈ {0, 1}n :
(
0n
falls (u)2 < (v )2
SUBn (uv ) =
.
binn ((u)2 − (v )2 ) sonst
S
Sei SUB = n≥1 SUBn .
Korollar aus Satz 7
SUB ∈ AC0 .
Beweis: Sei A = (a1 · · · an )2 und B = (b1 · · · bn )2 .
In AC0 kann man leicht feststellen, ob A < B gilt; sei o.B.d.A. A ≥ B.
Berechne 2n − B in AC0 : Komplementiere jedes Bit in B und addiere 1.
Berechne nun mit Satz 7 C = A + 2n − B in AC0 .
Aus 2n > A ≥ B folgt 2n ≤ C < 2n+1 , d. h. das (n + 1)-te Bit in C ist 1.
Indem dieses Bit auf 0 gesetzt wird, erhalten wir C − 2n = A − B.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
23 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Addition
2
Definiere IADDn : {0, 1}n → {0, 1}2n wie folgt für alle
u1 , . . . , un ∈ {0, 1}n :
IADDn (u1 u2 · · · un ) = bin2n ((u1 )2 + (u2 )2 + · · · + (un )2 ).
S
Sei IADD = n≥1 IADDn .
Aus Satz 7 folgt IADD ∈ AC1 .
Es geht aber besser:
Satz 8
IADD ∈ NC1 .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
24 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Addition
Beweis:
Vorüberlegung: Seien A = (a1 a2 · · · an ), B = (b1 b2 · · · bn ) und
C = (c1 c2 · · · cn ) drei n-Bit Zahlen.
Dann können wir in NC0 aus A, B, C zwei (n + 1)-Bit Zahlen
D = (d1 d2 · · · dn dn+1 ) und E = (e1 e2 · · · en+1 ) berechnen mit
A + B + C = D + E:
e1 = 0
ei
di
= (ai−1 ∧ bi−1 ) ∨ (ai−1 ∧ ci−1 ) ∨ (bi−1 ∧ ci−1 ) für 2 ≤ i ≤ n + 1
= (ai ∧ ¬bi ∧ ¬ci ) ∨ (¬ai ∧ bi ∧ ¬ci ) ∨
(¬ai ∧ ¬bi ∧ ci ) ∨ (ai ∧ bi ∧ ci ) für 1 ≤ i ≤ n
dn+1 = 0
Idee: di ist die Summe modulo 2 aus ai , bi und ci . Das Bit ei+1 ist 1
genau dann, wenn ai + bi + ci ≥ 2.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
25 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Addition
Angenommen wir haben nun m viele r -Bit Zahlen.
der Überlegung auf der vorherigen Folie in NC0 m′
mit der gleichen Summe berechnen, wobei:
m
falls m ≡ 0
2 · 3
′
m−1
m = 2 · 3 + 1 falls m ≡ 1
m−2
2 · 3 + 2 falls m ≡ 2
Dann können wir mit
viele (r + 1)-Bit Zahlen
mod 3
mod 3
mod 3
Für m > 2 gilt m′ ≤ 45 m.
Beginnend mit n vielen n-Bit Zahlen, wenden wir nun dieses Verfahren
k = ⌈log5/4 (n)⌉ ∈ O(log(n)) mal an und erhalten 2 (n + k)-Bit Zahlen mit
der gleichen Summe.
Diese beiden Zahlen können in NC1 addiert werden.
Insgesamt erhalten wir so einen NC1 -Schaltkreis für IADD.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
26 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Multiplikation
Satz 9 (Korollar aus Satz 8)
Multiplikation von zwei n-Bit Zahlen (kurz MULT) ist in NC1 .
Beweis:
Sei A = (a1 a2 · · · an ) und B = (b1 b2 · · · bn ).
Für 1 ≤ i ≤ n können die n vielen (2n − 1)-Bit Zahlen
falls ai = 0
0
Bi = ( 0 · · · 0 b1 b2 · · · bn )2 falls ai = 1
| {z }
i − 1 viele
in NC0 berechnet werden.
Nach Satz 8 kann A · B = B1 + B2 + · · · + Bn in NC1 berechnet
werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
27 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Majority
Satz 10 (Korollar aus Satz 8)
MAJ ∈ NC1 und damit TC0 ⊆ NC1 .
Beweis:
Für Eingabebits a1 , . . . , an ∈ {0, 1} können wir nach Satz 8
BCOUNT(a1 , . . . , an ) = binℓ(n) (a1 + a2 + · · · + an )
in NC1 berechnen.
In AC0 (und damit NC1 ) können wir dann ermitteln, ob
BCOUNT(a1 , . . . , an ) ≥ n2 gilt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
28 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Addition von log(n) vielen Zahlen
Satz 11
Addition von ⌈log(n)⌉ vielen n-Bit Zahlen (kurz LOGIADD) ist in AC0 .
Beweis: Angenommen wir haben ℓ(n) (≥ ⌈log(n)⌉ viele n-Bit Zahlen
A1 , . . . , Aℓ(n) , wobei Ai = (ai,1 ai,2 · · · ai,n )2 .
n → {0, 1} kann in
Vorüberlegung: Jede Boolesche Funktion f : {0, 1}V
n
n
Tiefe
3 mit ≤ 2 · n vielen ¬-Gattern, ≤ 2 vielen n -Gattern, und einem
W
-Gatter
berechnet werden (DNF).
2n
Pℓ(n)
Also können wir alle Summen sk = i=1 ai,k (1 ≤ k ≤ n) in AC0
berechnen. Dies ist Stufe 1.
Jede dieser Summen benötigt ≤ ℓ(ℓ(n)) = ℓ(2) (n) Bits. Sei
sk =
ℓ(n)
X
i=1
Markus Lohrey (Universität Leipzig)
ℓ(2) (n)
ai,k =
X
sk,j 2j−1 .
j=1
Schaltkreiskomplexität
WS 2009/2010
29 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Addition von log(n) vielen Zahlen
Wir haben somit das Problem der Addition von ℓ(n) vielen n-Bit Zahlen
auf die Addition von ℓ(2) (n) vielen (n + ℓ(2) (n))-Bit Zahlen reduziert:
A1 + · · · + Aℓ(n) =
=
ℓ(n) n
X
X
ai,k 2
=
n
X
ℓ(n)
k−1
2
X
ai,k =
i=1
ℓ(2) (n)
X
j=1
ℓ(n)
n X
X
ai,k 2k−1
k=1 i=1
i=1 k=1
k=1
=
k−1
n
X
|k=1
n
X
k−1
2
k=1
ℓ(2) (n)
X
sk,j 2j−1
j=1
sk,j 2k+j−2
{z
}
≤ n + ℓ(2) (n) viele Bits
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
30 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Addition von log(n) vielen Zahlen
Wir iterieren nun dieses Verfahren:
Stufe 2: Die Addition von ℓ(2) (n) vielen (n + ℓ(2) (n))-Bit Zahlen kann auf
die Addition von ℓ(3) (n) vielen (n + ℓ(2) (n) + ℓ(3) (n))-Bit Zahlen reduziert
werden.
..
.
Stufe k: Die Addition von ℓ(k) (n) vielen (n + ℓ(2) (n) + · · · + ℓ(k) (n))-Bit
Zahlen kann auf die Addition von ℓ(k+1) (n) vielen
(n + ℓ(2) (n) + · · · + ℓ(k+1) (n))-Bit Zahlen reduziert werden.
Hierbei sei k die kleinste Zahl, so dass ℓ(k+1) (n) ≤ 2 (k ≈ log∗ (n)).
Wir haben somit nach Stufe k nur noch 2
(n + ℓ(2) (n) + · · · + ℓ(k+1) (n))-Bit Zahlen.
Behauptung: n + ℓ(2) (n) + · · · + ℓ(k+1) (n) ∈ O(n).
Also können die beiden in Stufe k erzeugten Zahlen in AC0 addiert werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
31 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Addition von log(n) vielen Zahlen
Wir behaupten nun, dass die Stufen 2–k in einem Schritt in AC0
durchgeführt werden können. Beachte hierzu:
Jedes der in Stufe k erzeugten Bits hängt nur von ℓ(k) (n) Bits aus
Stufe k − 1 ab.
Jedes der in Stufe k − 1 erzeugten Bits hängt nur von ℓ(k−1) (n) Bits
aus Stufe k − 2 ab.
..
.
Jedes der in Stufe 2 erzeugten Bits hängt nur von ℓ(2) (n) Bits aus
Stufe 1 ab.
Also hängt jedes der in Stufe k erzeugten Bits nur von
ℓ(2) (n) · ℓ(3) (n) · · · ℓ(k) (n) vielen Bits aus Stufe 1 ab.
Behauptung: ℓ(2) (n) · ℓ(3) (n) · · · ℓ(k) (n) ∈ O(log(n)).
Also können mit unserer Vorüberlegung die Stufen 2–k in einem Schritt in
AC0 durchgeführt werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
32 / 195
Schaltkreise für arithmetische Operationen
Nochmals itererierte Addition
Satz 12
IADD ∈ TC0 .
Beweis:
Sei Ai = (ai,1 ai,2 · · · ai,n )2 für 1 ≤ i ≤ n.
P
Schritt 1: Berechne sk = ni=1 ai,k ∈ {0, . . . , n} für 1 ≤ k ≤ n.
Dies geht P
in TC0 : Jedes Bit in sk kann durch ein ODER von Bedingungen
der Form ni=1 ai,k = r mit 0 ≤ r ≤ n ausgedrückt werden.
Im
PnBeweis von Satz 02 haben wir gesehen, wie man die Bedingung
i=1 ai,k = r in TC überprüfen kann.
Beachte: sk hat höchstens ℓ(n) viele Bits.
Sei sk = (sk,1 · · · sk,ℓ(n) )2 .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
33 / 195
Schaltkreise für arithmetische Operationen
Nochmals itererierte Addition
Schritt 2: Wie im Beweis von Satz 11 zeigt man:
n
X
i=1
Ai =
ℓ(n)
n
X
X
j=1 k=1
|
sk,j 2k+j−2
{z
}
≤ n + ℓ(n) viele Bits
Wir müssen also noch ℓ(n) viele Zahlen mit (n + ℓ(n)) Bits addieren.
Nach Satz 11 ist dies in AC 0 ⊆ TC0 möglich.
Korollar aus Satz 12
Multiplikation von zwei n-Bit Zahlen (kurz MULT) ist in TC0 .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
34 / 195
Schaltkreise für arithmetische Operationen
Nochmals itererierte Addition
Satz 13
Für jede Primzahl p gilt IADD, MULT 6∈ ACC(p k )
Beweis:
Offensichtlich gilt BCOUNT 6∈ ACC(p k ) (siehe Beweis von Satz 10):
BCOUNT ∈ ACC(p k ) Ã MAJ ∈ ACC(p k ) Ã TC0 ⊆ ACC(p k )
(Widerspruch zu Satz 6).
Aus BCOUNT 6∈ ACC(p k ) folgt aber sofort IADD 6∈ ACC(p k ).
Angenommen, es würde MULT ∈ ACC(p k ) gelten.
Wir zeigen, dass hieraus BCOUNT ∈ ACC(p k ) folgt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
35 / 195
Schaltkreise für arithmetische Operationen
Nochmals itererierte Addition
Seien a0 , . . . , an−1 die Eingabebits und sei ℓ = ℓ(n).
P
Pn−1 ℓ·i
ℓ·i und B =
Definiere A = n−1
i=0 ai · 2
i=0 2 .
Die Binärdarstellungen dieser Zahlen können in AC0 berechnet werden.
Die Binärdarstellung von A (bzw. B) besteht aus n Blöcken der Länge ℓ,
wobei der i-te Block aus ai (bzw. einer 1) gefolgt von ℓ − 1 Nullen besteht.
P
Pn−1
P2n−2
(i+j)·ℓ =
k·ℓ
Sei C = A · B = n−1
i=0
j=0 ai · 2
k=0 ck 2
(kann nach Annahme in ACC(p k ) berechnet werden).
Hierbei ist ck eine ℓ-Bit Zahl (der k-te Block der Länge ℓ in der
Binärdarstellung von C .
P
P
Es gilt ck = ki=0 ai und damit cn−1 = n−1
i=0 ai .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
36 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Multiplikation
Satz 14
Multiplikation von n vielen n-Bit Zahlen (kurz IMULT) ist in TC0 .
Beispiel: Sei Ai = (ai,1 · · · ai,n )2 .
Für j ≥ 1 sei pj die j-te Primzahl.
Aus dem Primzahlsatz folgt pj ∈ O(j · log(j)).
Insbesondere benötigt pj nur O(log(j)) viele Bits.
Also hat auch die Zahl 2k mod pj (0 ≤ k < n, 1 ≤ j ≤ n2 ) nur O(log(n))
viele Bits.
Schritt 1: Wir berechnen in TC0 die n3 vielen Zahlen
n
X
ai,k · (2k−1 mod pj )
Bi,j =
k=1
(1 ≤ i ≤ n, 1 ≤ j ≤ n2 ).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
37 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Multiplikation
Dies ist nach Satz 12 (IADD ∈ TC0 ) möglich.
Beachte: Die Zahlen 2k mod pj hängen nicht von der Eingabe ab, sie
können für jede Eingabelänge n fest in den Schaltkreis verdrahtet werden.
Jede der Zahlen Bi,j benötigt nur O(log(n)) viele Bits.
Wir können daher in konstanter Tiefe mit nO(1) vielen Booleschen Gattern
die Zahl
¶
µX
n
k−1
ai,k · (2
mod pj ) mod pj
Bi,j mod pj =
k=1
=
µX
n
k=1
ai,k · 2
k−1
¶
mod pj
= Ai mod pj
(1 ≤ i ≤ n, 1 ≤ j ≤ n2 ) berechnen.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
38 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Multiplikation
Schritt 2:
Die multiplikative Gruppe des Körpers Fpj ist zyklisch von Ordnung pj − 1.
Sei gj ∈ {2, . . . , pj − 1} ein Erzeuger dieser Gruppe.
Für m ∈ {1, . . . , pj − 1} sei Lj (m) ∈ {0, . . . , pj − 2} die eindeutige Zahl mit
Lj (m)
gj
≡ m mod pj
(diskreter Logarithmus).
Beachte: Die Abbildungen m 7→ Lj (m) (m ∈ {1, . . . , pj − 1}) und
m 7→ gjm mod pj (m ∈ {0, . . . , pj − 2}) können in konstanter Tiefe mit
nO(1) vielen Booleschen Gattern berechnet werden (da sie nur von
O(log(n)) vielen Bits abhängen).
Wir können daher aus den Zahlen Ai mod pj (1 ≤ i ≤ n, 1 ≤ j ≤ n2 ) in
AC0 die Zahlen Lj (Ai mod pj ) berechnen (nur falls Ai mod pj 6= 0).
In einem speziellen Bit merken wir uns, ob Ai mod pj = 0 gilt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
39 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Multiplikation
Schritt 3: Wir berechnen nun (A1 A2 · · · An ) mod pj wie folgt.
Falls Ai mod pj = 0 für ein 1 ≤ i ≤ n, so folgt (A1 A2 · · · An ) mod pj = 0.
Sei nun Ai mod pj 6= 0 für alle 1 ≤ i ≤ n.
Dann haben wir in Schritt 2 die diskreten Logarithmen Lj (Ai mod pj )
berechnet.
In TC0 können wir nach Satz 12 (IADD ∈ TC0 ) die Summen
n
X
Lj (Ai mod pj )
i=1
(1 ≤ j ≤ n2 ) berechnen.
Diese Summen benötigen nur O(log(n)) viele Bits.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
40 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Multiplikation
Daher können wir in konstanter Tiefe mit nO(1) vielen Booleschen Gattern
die Zahlen
¶
µX
n
Lj (Ai mod pj ) mod (pj − 1)
i=1
berechnen.
Nun gilt
Lj ((A1 A2 · · · An ) mod pj ) =
µX
n
i=1
¶
Lj (Ai mod pj ) mod (pj − 1)
Also haben wir nun Lj ((A1 A2 · · · An ) mod pj ) berechnet.
Hieraus können wir wieder in konstanter Tiefe mit nO(1) vielen Booleschen
Gattern die Zahl (A1 · A2 · · · An ) mod pj berechnen.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
41 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Multiplikation
Schritt 4:
Nach dem Chinesischen Restesatz (oder dem Beweis von diesen) gibt es
Zahlen u1 , . . . , un2 < p1 p2 · · · pn2 , so dass für jede natürliche Zahl x gilt:
¶
µX
n2
uj · (x mod pj ) mod (p1 p2 · · · pn2 ).
x mod (p1 p2 · · · pn2 ) =
j=1
Diese Zahlen u1 , . . . , un2 hängen wieder nur von der Eingabelänge n ab,
und können fest in den n-ten Schaltkreis verdrahtet werden.
Da MULT ∈ TC0 (Korollar aus Satz 12) können wir die Produkte
uj · ((A1 A2 · · · An ) mod pj ) in TC0 berechnen.
Sodann können wir nach Satz 12 (IADD ∈ TC0 ) die Summe
2
S=
n
X
j=1
in TC0 berechnen.
Markus Lohrey (Universität Leipzig)
uj · ((A1 A2 · · · An ) mod pj )
Schaltkreiskomplexität
WS 2009/2010
42 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Iterierte Multiplikation
Es gilt S ≤ n2 pn2 p1 p2 · · · pn2 .
Wir vergleichen nun in AC0 die Summe S mit jeder der Zahlen
K · (p1 p2 · · · pn2 ) für 0 ≤ K ≤ n2 pn2 .
Durch ein ODER können wir so die größte Zahl K mit
S ≥ K · (p1 p2 · · · pn2 ) bestimmen.
Dann berechnen wir in AC0 die Differenz (SUB ∈ AC0 )
S − K · (p1 p2 · · · pn2 ) = S mod (p1 p2 · · · pn2 )
= (A1 A2 · · · An ) mod (p1 p2 · · · pn2 ).
2
Nun gilt p1 p2 · · · pn2 ≥ 2n = (2n )n > A1 A2 · · · An .
Also gilt (A1 A2 · · · An ) mod (p1 p2 · · · pn2 ) = A1 A2 · · · An .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
43 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Division
Satz 15
Ganzzahlige Division von zwei n-Bit Zahlen (kurz DIV) ist in TC0 .
Beweis:
Sei A = (a1 a2 · · · an )2 und B = (b1 b2 · · · bn )2 > 0.
O.B.d.A. sei B > 1, sonst können wir A ausgeben.
Wir berechnen ⌊A/B⌋ indem wir zunächst eine n-Bit Approximation von
1/B berechnen.
Sei k die Position des höchsten 1-Bits in B, d. h. 2k−1 ≤ B < 2k .
Wegen B ≥ 2 gilt k ≥ 2.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
44 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Division
Im folgenden operieren wir mit rationalen Zahlen kleiner als 1. Dies kann
vermieden werden, indem alle Zahlen mit genügend großen 2er-Potenzen
multipliziert werden.
Schritt 1: Berechne ε := 1 − B/2k .
Dies ist mittels einer Subtraktion in AC0 möglich.
Wegen 2k−1 ≤ B < 2k gilt 1/2 ≤ B/2k < 1 und damit 0 < ε ≤ 1/2.
Ausserdem gilt
Markus Lohrey (Universität Leipzig)
2−k
2−k
1
=
.
=
k
B
1−ε
1 − (1 − B/2 )
Schaltkreiskomplexität
WS 2009/2010
45 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Division
Schritt 2: P
Berechne “parallel” alle Potenzen ε0 , ε1 , . . . , εn−1 und dann
C = 2−k · i<n εi .
Wegen Satz 14 (IMULT ∈ TC0 ) ist dies in TC0 möglich.
Es gilt:
X
1
−
εi
1−ε
=
i<n
X
i≥0
= εn ·
εi −
X
X
εi
i<n
εi
i≥0
1
1−ε
∈ [0, 2 · εn ]
= εn ·
⊆ [0, 2 · 2−n ]
= [0, 2−n+1 ]
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
46 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Division
Daher erhalten wir für die Zahl C :
X
1
1
−C =
− 2−k ·
εi
B
B
i<n
X
2−k
− 2−k ·
εi
=
1−ε
i<n
X ¢
¡
1
= 2−k ·
−
εi
1−ε
i<n
−k
∈ [0, 2
·2
−n+1
−(n+k−1)
= [0, 2
⊆ [0, 2
−n
]
]
)
Also stimmen C und 1/B in der Tat bis auf n Nachkommastellen überein.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
47 / 195
Schaltkreise für arithmetische Operationen
Beispiel: Division
Aus 0 ≤ 1/B − C < 2−n , d. h. C ≤ 1/B < C + 2−n folgt
A·C ≤
A
< A · C + A · 2−n
B
und damit wegen A < 2n (d. h. A · 2−n < 1)
⌊A/B⌋ − ⌊A · C ⌋ ∈ {0, 1}
Also ist entweder ⌊A · C ⌋ oder ⌊A · C ⌋ + 1 die korrekte Ausgabe.
Beide Zahlen können in TC0 berechnet werden (Multiplikation ist in TC0 ).
Welche der beiden Zahlen der korrekte Quotient ⌊A/B⌋ ist, kann durch
eine Kontrollmultiplikation (in TC0 ) sowie eine Kontrollsubtraktion (in
AC0 ) festgestellt werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
48 / 195
Uniforme Schaltkreise
Bemerkungen zur Uniformität
Wir haben bisher keinerlei Forderung an die Abbildung n 7→ Sn für eine
Schaltkreisfamilie F = (Sn )n≥0 gestellt
(nicht-uniforme Schaltkreisfamilien).
Für eine Basis B und Mengen S, D von monotonen Funktionen auf N sei:
USIZEDEPTH(S, D, B) = {valF | F = (Sn )n≥0 ist eine Schaltkreisfamilie
über der Basis B mit sizeF ∈ S und
depthF ∈ D und die Abbildung
1n 7→ Sn ist in logspace berechenbar}
uNCi ist die Klasse USIZEDEPTH(nO(1) , O(logi (n)), Bool2 );
analog ist uniformes uACi , uniformes uTCi , . . . definiert.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
49 / 195
Uniforme Schaltkreise
Bemerkungen zur Uniformität
Bemerkungen:
Für die Repräsentation des Schaltkreises Sn = (V , α, λ, out) kann
man davon ausgehen, dass V = {1, . . . , m} für eine Zahl m gilt. Ein
Gatter kann dann durch einen Bitstring der Länge ℓ(m) notiert
werden. Die Abbildungen α, λ, und out können dann durch ihre
Wertetabellen repräsentiert werden.
Wir sagen, dass eine Funktion f in DSPACE(g ) (g : N → N eine
monotone Funktion) berechenbar ist, falls f auf einer
deterministischen Turingmaschine M mit folgenden Eigenschaften
berechnet werden kann: (i) M kann vom Eingabeband nur lesen
(two-way), (ii) M kann auf das Ausgabeband nur schreiben (one-way
von links nach rechts), und (iii) M hat bei einer Eingabe der Länge n
ein Arbeitsband der Länge g (n), das beschrieben und gelesen werden
kann.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
50 / 195
Uniforme Schaltkreise
Bemerkungen zur Uniformität
Bemerkungen:
Eine Funktion ist logspace-berechenbar, falls sie in DSPACE(log(n))
berechnet werden kann.
Die hier eingeführte Uniformitätsforderung wird auch als
logspace-Uniformität bezeichnet. In der Schaltkreiskomplexitätstheorie
sind noch wesentlich stärkere Uniformitätsforderungen als
logspace-Uniformität (z. B. DLOGTIME-Uniformität) üblich.
Die meisten der bisher bewiesenen Resultate gelten auch für uniforme
Schaltkreiskomplexitätsklassen:
ADD, LOGIADD ∈ uAC0
IADD, MULT ∈ uTC0
Dies kann leicht durch eine genauere Analyse unserer Beweise gezeigt
werden (die konstruierten Schaltkreise sind sehr einheitlich aufgebaut).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
51 / 195
Uniforme Schaltkreise
Division ist in uTC0
Etwas schwieriger sieht die Situation für IMULT (iterierte Multiplikation)
und damit auch DIV (Division) aus.
Die im Beweis von Satz 14 konstruierte Schaltkreisfamilie ist nicht
offensichtlich uniform.
Die Situation konnte erst 2001 geklärt werden:
Satz 16 (Chiu, Davida, Litow bzw. Hesse, Allender, Barrington)
IMULT, DIV ∈ uTC0 .
In der Tat wurde von Hesse, Allender und Barrington eine stärkere
Uniformitätsforderung (DLOGTIME-Uniformität) verwendet.
Auf den sehr schwierigen Beweis dieses Satzes verzichten wir hier.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
52 / 195
Uniforme Schaltkreise
Schaltkreistiefe versus Platz
Satz 17
Sei f ∈ uNCk (k ≥ 1). Dann kann die Funktion f in DSPACE(logk (n))
berechnet werden.
Beweis: Sei F = (Sn )n≥0 eine Schaltkreisfamilie über der Basis Bool2 mit:
f = valF
sizeF ∈ nO(1)
depthF ∈ O(logk (n))
1n 7→ Sn ist berechenbar in DSPACE(log(n)).
Die Komposition einer DSPACE(log(n))-berechenbaren Funktion und einer
DSPACE(logk (n))-berechenbaren Funktion (k ≥ 1) ist wieder in
DSPACE(logk (n)) berechenbar (der Beweis aus den Folien Strukturelle
Komplexitätstheorie, S. 77, für die Komposition von zwei
logspace-berechenbaren Funktionen funktioniert immer noch).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
53 / 195
Uniforme Schaltkreise
Schaltkreistiefe versus Platz
Daher genügt es zu zeigen, dass die Abbildung
hx, Sn i 7→ valSn (x)
(x ∈ {0, 1}n )
in DSPACE(logk (n)) berechenbar ist.
Sei Sn = (V , α, λ, out) und sei dn ∈ O(logk (n)) die Tiefe von Sn .
O.B.d.A. habe Sn nur ein Ausgabegatter o (sonst können wir die Werte
aller Ausgabegatter von Sn bei Eingabe x nacheinander berechnen und auf
das Ausgabeband schreiben.
Zentrale Beobachtung: Ein Pfad von o zu einem beliebigen Gatter in Sn
kann in Platz dn abgespeichert werden:
Solch ein Pfad hat Länge höchstens dn , da dn die Tiefe von Sn ist.
Da jedes Gatter nur höchstens zwei Eingänge hat, kann ein Pfad der
Länge k durch einen Bitstring p ∈ {ℓ, r } der Länge k gespeichert
werden (ℓ steht für “links”, r steht für “rechts”).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
54 / 195
Uniforme Schaltkreise
Schaltkreistiefe versus Platz
Idee für die Auswertung von Sn in logspace:
Wir können uns den Schaltkreis Sn zu einem Baum (oder Booleschen
Term) aufgefaltet vorstellen.
Diesen könnten wir auswerten, indem wir den Baum “depth-first”
traversieren. Dabei muss man sich den aktuellen Knoten im Baum
und das aktuelle Zwischenergebnis merken.
Knoten des aufgefalteten Baums entsprechen Pfade in Sn , die an der
“Wurzel” o beginnen. Solch ein Pfad kann in logspace gespeichert
werden.
Für p ∈ {ℓ, r }i mit i ≤ dn sei γ(p) das eindeutige Gatter, welches vom
Ausgabegatter o durch Ablaufen des Pfades p erreicht wird.
Beachte: Für gegebenes pV∈ {ℓ, r }i kann γ(p) und damit auch
λ(γ(p)) ∈ {x1 , . . . , xn , ¬, 2 } in logarithmischen Platz berechnet werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
55 / 195
Uniforme Schaltkreise
Schaltkreistiefe versus Platz
Der folgende Algorithmus liefert valSn (x) zurück:
p := ε; v := undefined;
while true do
if v = undefined then
if λ(γ(p)) = xi then v := i-tes Symbol von x else p := pℓ endif
elseif p 6= ε
sei p = p ′ d mit d ∈ {ℓ, r };
if d = r then p := p ′
elseif λ(γ(p ′ )) = ¬ then p := p ′ ; v := 1 − v
elseif v = 0 then p := p ′
else p := p ′ r ; v := undefined
endif
else return(v )
endif
endwhile
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
56 / 195
Uniforme Schaltkreise
Schaltkreistiefe versus Platz
Dieser Algorithmus muss nur den Pfad p und den Wert v abspeichern.
Der Pfad p kann in Platz O(logk (n)) gespeichert werden, der Wert v
benötigt nur zwei Bits.
Wegen uTC0 ⊆ uNC1 erhalten wir das folgende Korollar:
Korollar
Die Funktionen ADD, IADD, MULT, IMULT, und DIV sind
logspace-berechenbar.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
57 / 195
Uniforme Schaltkreise
Schaltkreistiefe versus Platz
Zur Erinnerung: NL ist die Menge aller Probleme, die auf einer
nichtdeterministischen Turingmachine in logarithmischen Platz gelöst
werden können.
Satz 18
NL ⊆ uAC1 .
Beweis:
Sei L ∈ NL (L ⊆ {0, 1}∗ ).
Sei M eine nichtdeterministische Turingmaschine M, die L akzeptiert und
bei einer Eingabe der Länge n Platzbedarf log(n) hat.
Fixiere eine Eingabelänge n.
Wir konstruieren (in logspace) einen Schaltkreis Sn , welcher genau die
Eingaben aus L ∩ {0, 1}n erkennt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
58 / 195
Uniforme Schaltkreise
Schaltkreistiefe versus Platz
Lemma 19
Multiplikation von zwei Booleschen (n × n)-Matrizen ist in uAC0 .
Beweis von Lemma 19: Sei A = (ai,j )1≤i,j≤n und B = (bi,j )1≤i,j≤n
W
Das Ausgabebit (A · B)i,j = nk=1 (ai,k ∧ bk,j ) kann offensichtlich in uAC0
berechnet werden.
Aus Lemma 19 folgt sofort:
Lemma 20
Multiplikation von n Booleschen (n × n)-Matrizen ist in uAC1 .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
59 / 195
Uniforme Schaltkreise
Schaltkreistiefe versus Platz
Sei G (x) (x ∈ {0, 1}n ) der Konfigurationsgraph der Maschine M bei
Eingabe x ∈ {0, 1}n :
Knoten sind Konfigurationen, wobei das Arbeitsband Länge log(n)
hat und auf dem Eingabeband die Eingabe x steht. Solch ein Knoten
kann durch ein Tripel (u, p, i) mit u ∈ (Γ × {0, 1})log(n) , p ∈ Q und
1 ≤ i ≤ n (hierbei ist Γ das Bandalphabet und Q die Zustandsmenge
von M) repräsentiert werden.
Es gibt eine Kante von (u, p, i) nach (v , q, j) falls M in einem Schritt
von (u, p, i) nach (v , q, j) übergehen kann.
Unser Schaltkreis hat für jedes Paar h(u, p, i), (v , q, j)i ein Gatter.
Dieses Gatter soll sich bei Eingabe x = x1 x2 · · · xn genau dann zu 1
auswerten, falls es in G (x) eine Kante von (u, p, i) nach (v , q, j) gibt.
Hierzu muss der Schaltkreis nur auf das Bit xi zugreifen.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
60 / 195
Uniforme Schaltkreise
Schaltkreistiefe versus Platz
Sei A(x) die Adjazenzmatrix von G (x) und sei d die Dimension von A(x)
(= Anzahl der Knoten von G (x)).
Diese wird durch die Gatter h(u, p, i), (v , q, j)i repräsentiert.
Sei α0 die Startkonfiguration und sei αf die (o.B.d.A.) eindeutige
akzeptierende Konfiguration von M.
W
Dann gilt: x ∈ L ⇐⇒ di=0 (A(x))iα0 ,αf = 1.
Nach Lemma 20 können wir jede der Potenzen (A(x))i in uAC1
berechnen.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
61 / 195
Untere Schranken
Shannons Theorem
Sei F2 die Menge aller zweistelligen sowie nullstelligen Booleschen
Funktionen. Es gilt also |F2 | = 16 + 2.
Sei F (s, n) die Anzahl aller Booleschen Funktionen von {0, 1}n nach
{0, 1}, die sich durch einen Schaltkreis S über der Basis F2 mit
size(S) ≤ s berechnen lassen.
n
Beachte: Es gibt 22 viele n-stellige Boolesche Funktionen.
Satz 21 (Shannon)
Sei s =
2n
n.
Dann gilt limn→∞
Markus Lohrey (Universität Leipzig)
|F (s,n)|
n
22
= 0.
Schaltkreiskomplexität
WS 2009/2010
62 / 195
Untere Schranken
Shannons Theorem
Beweis: Da wir zusätzliche Dummy-Gatter zu einem Schaltkreis
hinzufügen können, können wir in der Definition von F (s, n) davon
ausgehen, dass size(S) = s gilt.
Sei S = (V , α, λ, out) ein Schaltkreis mit n Eingabegattern, und sei W die
Menge aller wesentlichen Gatter, |W | = s.
Der Schaltkreis S ist dadurch festgelegt, dass wir für jedes Gatter v ∈ W
den Wert λ(v ) ∈ F2 \ {0, 1} festlegen (16 Möglichkeiten) und
den Wert α(v ) = v1 v2 festlegen ((s + n + 2)2 ≤ 4s 2 Möglichkeiten für
genügend großes n).
Dies ergibt insgesamt (64s 2 )s = 64s s 2s Möglichkeiten.
Allerdings ergibt jede Permutation von W einen Schaltkreis, der die
gleiche Boolesche Funktion berechnet.
Also gilt F (s, n) ≤
64s s 2s
.
s!
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
63 / 195
Untere Schranken
Shannons Theorem
Mit Stirlings Formel (s! ∈ Ω((s/e)s ·
γ, δ, c):
F (s, n) ≤
√
s)) folgt (für geeignete Konstanten
64s s 2s
s!
≤
64s s 2s
√
γ · (s/e)s · s
≤
(64e)s s 2s
γ · ss
= δ · cs · ss
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
64 / 195
Untere Schranken
Shannons Theorem
Mit s = 2n /n folgt:
log(F (s, n)) − 2n ≤ log(δ) + log(c) · s + s · log(s) − 2n
= log(δ) + log(c) ·
2n 2n
+ (n − log(n)) − 2n
n
n
= log(δ) + log(c) ·
2n 2n log(n)
−
n
n
= log(δ) +
2n
(log(c) − log(n))
n
n
Also gilt log(F (s, n)/22 ) = (log(F (s, n)) − 2n ) → −∞ für n → ∞ und
= 0.
damit limn→∞ |F 2(s,n)|
2n
Aus dem Satz von Shannon folgt, dass “fast alle” n-stelligen Booleschen
Funktionen nicht durch Schaltkreise der Größe ≤ 2n /n berechnet werden
können (für große n).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
65 / 195
Untere Schranken
Gatter-Eliminationsmethode
Die große Misere der Schaltkreiskomplexität: Für eine “natürlich”
definierte explizite Funktion ist die beste bekannte untere Schranke für die
Größe eines Schaltkreises von der Form 3n − o(n).
Wir zeigen eine schwächere untere Schranke der Form 2n − 4 für die
Schwellenwertfunktion
(
Pn
1 falls
n
i=1 xi ≥ k
Tk (x1 , . . . , xn ) =
0 sonst
Satz 22
Sei 2 ≤ k ≤ n − 1, n ≥ 3. Jeder Schaltkreis über der Basis F2 , welcher Tkn
berechnet, hat Größe mindestens 2n − 4.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
66 / 195
Untere Schranken
Gatter-Eliminationsmethode
Beweis: Induktion über n ≥ 3.
n = 3: Dann gilt k = 2.
Die Funktion T23 hängt von allen drei Argumenten echt ab.
Daher hat jeder Schaltkreis über der Basis F2 für T23 mindestens
n − 1 = 2 = 2 · 3 − 4 Gatter mit Eingangsgrad 2.
Sei nun n ≥ 4 und 2 ≤ k ≤ n − 1.
Sei S ein Schaltkreis über der Basis F2 , welcher Tkn berechnet und eine
minimale Anzahl s von wesentlichen Gattern hat.
Es muss ein wesentliches Gatter g in S geben, so dass die beiden Eingänge
g1 und g2 für g jeweils Eingangsgrad 0 haben.
Gatter g kann nicht das Outputgatter von S sein.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
67 / 195
Untere Schranken
Gatter-Eliminationsmethode
Wäre g1 oder g2 mit einer Konstanten (0 oder 1) beschriftet, so könnten
wir g eliminieren, indem wir die in g berechnete Funktion (welche nur
höchstens ein Argument hat) in alle Gatter, die g als Eingabegatter haben,
integrieren.
Wir erhalten so einen Schaltkreis für Tkn mit s − 1 wesentlichen Gattern,
ein Widerspruch.
Also sind g1 und g2 Eingabegatter von S.
Falls g1 und g2 mit der gleichen Eingabevariablen xi beschriftet wären,
könnten wir wieder einen Schaltkreis für Tkn mit s − 1 wesentlichen
Gattern finden (Argument wie oben).
O.B.d.A. sei gi mit xi beschriftet (i ∈ {1, 2}).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
68 / 195
Untere Schranken
Gatter-Eliminationsmethode
Wenn wir nun x1 und x2 beliebig mit 0 und 1 belegen, erhalten wir eine
der folgenden 3 Booleschen Funktionen:
Tkn−2
falls x1 = x2 = 0
n−2
Tk−1
n−2
Tk−2
falls (x1 = 0 und x2 = 1) oder (x1 = 1 und x2 = 0)
falls x1 = x2 = 1
Da das Gatter g sich jedoch unter einer dieser 4 partiellen Belegungen
immer zu 0 oder 1 auswertet, muss es ein Gatter h 6= g geben, welches g1
oder g2 als Eingang hat.
O.B.d.A. habe h das Gatter g1 als Eingang.
Sei h′ der zweite Eingang von h (h′ = g ist möglich).
Wir setzen nun x1 auf b ∈ {0, 1}; den exakten Wert b fixieren wir noch.
n−1
Sei Sb der entstehende Schaltkreis, er berechnet Tk−b
.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
69 / 195
Untere Schranken
Gatter-Eliminationsmethode
In Sb können wir nun Gatter g eliminieren, indem wir die in g berechnete
Funktion (mit dem einzigen Argument x2 ) in die Gatter, die g als
Eingabegatter haben, integrieren.
Aber auch Gatter h kann in Sb eliminiert werden:
Falls h nicht das Output-Gatter ist, können wir wieder die in h
berechnete Funktion (mit dem einzigen Argument h′ ) in die Gatter,
die h als Eingabegatter haben, integrieren.
Falls h das Output-Gatter ist, so kann h′ kein Eingabegatter von S
(bzw. Sb ) sein, da sonst Tkn nur von 2 Argumenten abhängen würde.
Wir können dann die in h berechnete Funktion (mit dem einzigen
Argument h′ ) in das neue Outputgatter h′ integrieren.
Wir erhalten so einen zu Sb äquivalenten Schaltkreis Sb′ mit s − 2
wesentlichen Gattern.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
70 / 195
Untere Schranken
Gatter-Eliminationsmethode
Falls k = 2 gilt, setzen wir nun b = 0, falls 3 ≤ k ≤ n − 1 gilt, setzen wir
b = 1.
Es gilt dann 2 ≤ k − b ≤ n − 2.
n−1
Da Sb′ die Funktion Tk−b
berechnet, hat Sb′ nach Induktion mindestens
2(n − 1) − 4 wesentliche Gatter.
Also hat S mindestens 2n − 4 wesentliche Gatter.
Die im Beweis von Satz 22 verwendete Beweistechnik ist als gate
elimination method bekannt. Sie wird auch in den erwähnten unteren
Schranken der Form 3n − o(n) verwendet.
Die augenscheinliche Unfähigkeit, stärkere untere Schranken zu beweisen,
hat die Untersuchung eingeschränkter Schaltkreisfamilien (insbesondere
Familien mit konstanter Tiefe sowie monotone Schaltkreise) motiviert.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
71 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Wir beginnen nun mit den Beweisen für die Sätze von Smolensky
(Satz 3–5).
Sei K ein endlicher Körper.
Mit FK ,n bezeichnen wir die Menge aller Funktionen von {0, 1}n ⊆ K n
nach K .
Dies ist ein Vektorraum über K der Dimension 2n .
Ein Polynom p(x1 , . . . , xn ) ∈ K [x1 , . . . , xn ] ist reduziert, falls p(x1 , . . . , xn )
eine Summe von Monomen
Y
xi
c · XI = c ·
i∈I
mit c ∈ K , I ⊆ {1, . . . , n} ist (keine Teilausdrücke der Form xi2 ).
Unter dem Grad eines Polynoms p(x1 , . . . , xn ) verstehen wir das Maximum
aller Summen e1 + · · · + en , wobei k · x1e1 · · · xnen mit k 6= 0 ein Summand
von p(x1 , . . . , xn ) ist.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
72 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Lemma 23
Jede Funktion f ∈ FK ,n kann eindeutig durch ein reduziertes Polynom
dargestellt werden.
Beweis: Für a = (a1 , . . . , an ) ∈ {0, 1}n definiere χa : {0, 1}n → {0, 1}
durch:
(
1 falls a = b
χa (b) =
0 sonst
Dann wird χa durch das folgende Polynom repräsentiert:
Y
Y
(1 − xi )
xi ·
1≤i≤n,
ai =1
1≤i≤n,
ai =0
Also wird f ∈ FK ,n durch das folgende Polynom repräsentiert:
X
f (a) · χa
pf (x1 , . . . , xn ) =
a∈{0,1}n
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
73 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Da xi und xi2 auf {0, 1} übereinstimmen, können wir das Polynom pf
reduzieren.
Angenommen es gäbe zwei verschiedene reduzierte Polynome p(x1 , . . . , xn )
und q(x1 , . . . , xn ), die beide die Funktion f ∈ FK ,n repräsentieren.
Dann würde
r (x1 , . . . , xn ) = p(x1 , . . . , xn ) − q(x1 , . . . , xn ) 6= 0
die Nullfunktion auf {0, 1}n repräsentieren.
Da r (x1 , . . . , xn ) 6= 0, gibt es eine bezüglich ihrer Mächtigkeit minimale
Teilmenge I ⊆ {1, . . . , n}, so dass der Koeffizient des Monoms XI in
r (x1 , . . . , xn ) nicht 0 ist.
Sei ai = 1 für i ∈ I und ai = 0 für i ∈ {1, . . . , n} \ I .
Dann gilt r (a1 , . . . , an ) 6= 0, ein Widerspruch.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
74 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Lemma 24
k
Für jede Primzahl p gilt MODp ∈ CC(p).
Beweis: Induktion über k ≥ 1.
Der Fall k = 1 ist klar.
Sei nun k ≥ 2 und gelte die Aussage des Lemmas für k − 1.
Wir benutzen den folgenden einfachen Sachverhalt:
p k ist ein Teiler von x genau dann wenn gilt:
p k−1 teilt x.
p teilt |{y | 1 ≤ y ≤ x, p k−1 teilt y }|.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
75 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Um zu überprüfen, ob x1 + · · · + xn durch p k teilbar ist (x1 , . . . , xn sind die
Eingabebits), müssen wir daher die beiden folgenden Bedingungen
überprüfen:
(a) p k−1 teilt x1 + · · · + xn (geht nach Induktionsvoraussetzung in CC(p)).
(b) p teilt |{y | 1 ≤ y ≤ x1 + · · · + xn , p k−1 teilt y }|.
Eigenschaft (b) überprüfen wir wie folgt:
Für 1 ≤ i ≤ n sei
yi = (xi ∧ MODip
k−1
(x1 , . . . , xi )).
Dann ist (b) äquivalent zu MODpn (y1 , . . . , yn ) = 1.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
76 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Beweis von Satz 4:
Angenommen, es gilt
Lemma 24 impliziert
V
V
V
f k ), falls p prim ist und k > 0 gilt.
6∈ CC(p
f k ).
∈ CC(p
f
∈ CC(p).
Dann gäbe es also eine Zahl d, und für jedes n gäbe es einen Schaltkreis
Sn mit n Eingabegattern und:
valSn (x1 , . . . , xn ) = x1 ∧ · · · ∧ xn .
Sn hat Tiefe d.
Sn ist ein Schaltkreis über der Basis {¬,
V
2}
∪ {MODpk | k ≥ 2}.
Im folgenden arbeiten wir über dem Körper K = Zp .
Behauptung: Die Funktion valSn : {0, 1}n → {0, 1} kann durch ein
(o.B.d.A. reduziertes) Polynom pn ∈ Zp [x1 , . . . , xn ] vom Grad ≤ p d
repräsentiert werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
77 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Wir ordnen hierzu induktiv jedem Gatter g von Sn ein Polynom pg vom
Grad p depth(g ) (depth(g ) = Länge eines längsten Pfades von g zu einem
Eingabegatter) zu, welches die am Gatter g berechnete Funktion
repräsentiert.
Im folgenden sei d = depth(g ).
1. Fall: g ist mit der Eingabevariablen xi markiert. Dann sei pg = xi .
2. Fall: g ist mit ¬ markiert.
Sei h das Eingabegatter von g .
Nach Induktionsvoraussetzung ist ph ein Polynom vom Grad ≤ p d−1 ,
welches die am Gatter h berechnete Funktion repräsentiert.
Dann wird die am Gatter g berechnete Funktion durch das Polynom
pg = 1 − ph , welches Grad ≤ p d−1 ≤ p d hat, repräsentiert.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
78 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
3. Fall: g ist mit
V
2
markiert.
Seien h1 , h2 die Eingabegatter von g .
Nach Induktionsvoraussetzung ist phi ein Polynom vom Grad ≤ p d−1 ,
welches die am Gatter hi berechnete Funktion repräsentiert (i ∈ {1, 2}).
Dann wird die am Gatter g berechnete Funktion durch das Polynom
ph1 · ph2 , welches Grad ≤ 2 · p d−1 ≤ p d hat, repräsentiert.
4. Fall: g ist mit MODpk markiert.
Seien h1 , . . . , hk die Eingabegatter von g .
Nach Induktionsvoraussetzung ist phi ein Polynom vom Grad ≤ p d−1 ,
welches die am Gatter hi berechnete Funktion repräsentiert (1 ≤ i ≤ k).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
79 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Beachte: Für alle a ∈ Zp \ {0} gilt ap−1 = 1 in Zp (kleiner Fermat).
Also wird die am Gatter g berechnete Funktion durch das Polynom
pg = 1 − (ph1 + · · · + phk )p−1 ,
welches Grad ≤ (p − 1)p d−1 ≤ p d hat, repräsentiert.
Dies beweist die Behauptung.
Da valSn aber durch das reduzierte Polynom x1 · x2 · · · xn repräsentiert
wird, erhalten wir für n > p d einen Widerspruch zu Lemma 23.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
80 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Satz 25
Sei p eine Primzahl und sei q > 1 teilerfremd zu p. Dann gilt
V
∈ SIZEDEPTH(∗, O(1), Bool2 ∪ {MODpk , MODqk | k ≥ 2}).
Beweis:
Sei m > 0. Dann gibt es bis auf Isomorphie genau einen Körper GF(p m )
mit p m Elementen. Dieser Körper enthält Zp als Teilkörper.
Da p teilerfremd zu q ist (d. h. p ∈ Z∗q ), gibt es ein m > 0 mit
p m ≡ 1 mod q, d. h. q teilt p m − 1.
Da die multiplikative Gruppe des Körpers GF(p m ) genau p m − 1 Elemente
hat und zyklisch ist, gibt es ein Element g ∈ GF(p m ) mit
g q = 1 und g r 6= 1 für 1 ≤ r < q.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
81 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Für x ∈ {0, 1} gilt offensichtlich:
x = (g − 1)−1 · (g x − 1).
Das Polynom x1 · x2 · · · xn , welches die UND-Funktion repräsentiert, kann
somit durch einen Ausdruck der Form
X
cI g uI
I ⊆{1,...,n}
P
mit cI ∈ GF(p m ) und uI = ( i∈I xi ) mod q beschrieben werden.
GF(p m ) ist ein Vektorraum der Dimension m über Zp .
Wir fixieren eine Basis von GF(p m ), welche 1 ∈ GF(p m ) enthält.
Ein Element r ∈ Zp repräsentieren wir im folgenden durch den Bitstring
1r 0p−1−r .
Elemente aus GF(p m ) repräsentieren wir als m-dimensionale Vektoren über
Zp , d. h. als Bitstrings der Länge m · (p − 1).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
82 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Schritt 1: Berechne aus den Eingabebits x1 , . . . , xn , die m(p − 1)-Bit
Repräsentation von g uI , wobei I ⊆ {1, . . . , n}.
Hierzu überprüfen wir zunächst mittels q vielen MODq -Gattern, ob
P
i∈I xi ≡ s mod q (0 ≤ s < q) gilt.
Neben den Inputbits xi für i ∈ I müssen hierzu zusätzliche 1-Bits in die
MODq -Gatter eingegeben werden.
Wir erhalten so q Bits, von denen
P genau eines 1 ist. Diese Bits
repräsentieren den Wert uI = ( i∈I xi ) mod q.
Aus diesen Bits können wir mittels eines Schaltkreises konstanter Größe
die m(p − 1)-Bit Repräsentation von g uI berechnen.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
83 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Schritt 2: Berechne aus den (2n vielen) m(p − 1)-Bit Repräsentationen
von g uI (für I ⊆ {1, . . .P
, n}) die (p − 1)-Bit Repräsentation der
1-Koordinate von S = I ⊆{1,...,n} cI g uI .
Beachte: S ∈ GF(p m ) ist entweder 0 (falls x1 ∧ · · · ∧ xn = 0) oder 1 (falls
x1 ∧ · · · ∧ xn = 1).
Im ersten Fall ist die 1-Koordinate von S gleich 0, im zweiten Fall ist die
1-Koordinate von S gleich 1; daher genügt es in der Tat die 1-Koordinate
von S zu berechnen.
Aus der m(p − 1)-Bit Repräsentation von g uI berechnen wir zunächst
mittels eines Schaltkreises konstanter Größe die (p − 1)-Bit Repräsentation
der 1-Koordinate von cI · g uI (sei yI diese (p − 1)-Bit Repräsentation).
Wir müssen nun die yI modulo p addieren.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
84 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Hierzu schicken wir alle Bitstrings yI in ein MODp -Gatter mit
Eingangsgrad 2n · (p − 1).
Dann gilt x1 ∧ · · · ∧ xn = 1 g.d.w. dieses MODp -Gatter 0 liefert.
Lemma 26
Sei q ein Teiler von t > 1. Dann gilt MODq ∈ CC(t).
Beweis:
Für 0 ≤ s < t definiere die Funktion MODt,s : {0, 1}∗ → {0, 1} durch:
(
Pn
1 falls
t,s
i=1 xi ≡ s mod t
MOD (x1 , . . . , xn ) =
0 sonst
Indem man zusätzliche 1-Bits in ein MODt -Gatter füttert, erhält man
leicht MODt,s ∈ CC(t) für alle 0 ≤ s < t.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
85 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
MODq ∈ CC(t) folgt dann aus:
t/q−1
q
MOD (x1 , . . . , xn ) =
_
MODt,cq (x1 , . . . , xn ).
c=0
Beweis von Satz 5: Sei p prim und habe t > 1 einen Primteiler q 6= p.
f k ).
Dann gilt für jedes k > 0: MODt 6∈ CC(p
f k ).
Angenommen es gilt MODt ∈ CC(p
f
Lemma 24 impliziert MODt ∈ CC(p).
f
Lemma 26 impliziert MODq ∈ CC(p).
V f
Aus Satz 25 folgt dann ∈ CC(p).
Dies widerspricht aber Satz 4.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
86 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Wir kommen nun zum Beweis von Satz 3: MODt 6∈ ACC(p k ), falls p prim
ist und t einen Primteiler verschieden von p hat.
Problem bei ACC(p k ): Übersetzt man ein UND-Gatter mit Eingangsgrad n
in ein Polynom, so wird der Grad des Polynoms um den Faktor n größer.
Lösung: Approximation durch Polynome mit niedrigem Grad.
Lemma 27
Sei K ein endlicher Körper der Charakteristik p (p eine Primzahl).
Angenommen die Funktionen g1 , . . . , gr : {0, 1}n → {0, 1} werden durch
Polynome über K vom Grad ≤ d repräsentiert. Sei 1 ≤ ℓ ≤ n. Dann gibt
es eine Teilmenge D ⊆ {0, 1}n mit:
|D| ≥ 2n − 2n−ℓ
Die Funktion OR(g1 , . . . , gr ) := 1 − (1 − g1 ) · · · (1 − gr ),
eingeschränkt auf der Menge D, kann durch ein Polynom über K vom
Grad ≤ (|K | − 1) · ℓ · d repräsentiert werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
87 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Beweis: O.B.d.A. seien g1 , . . . , gr selbst Polynome vom Grad ≤ d.
Betrachte das Polynom
¶
r
ℓ µ
X
Y
|K |−1
ci,j gi )
1−(
f (x1 , . . . , xn ) = 1 −
,
j=1
i=1
wobei ci,j ∈ K für 1 ≤ i ≤ r , 1 ≤ j ≤ ℓ.
Dann hat f Grad ≤ (|K | − 1) · ℓ · d.
Da die multiplikative Gruppe von K zyklisch von Ordnung |K | − 1 ist,
liefert f immer einen Wert aus {0, 1}.
Fixiere nun eine Eingabe a ∈ {0, 1}n .
Wir zählen nun die Anzahl δ(a) aller Belegungen für die Faktoren ci,j ∈ K
(1 ≤ i ≤ r , 1 ≤ j ≤ ℓ), für die f (a) 6= OR(g1 (a), . . . , gr (a)) gilt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
88 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
1.Fall: gi (a) = 0 für alle 1 ≤ i ≤ r .
Dann gilt
OR(g1 (a), . . . , gr (a)) = 0 = f (a)
für alle Belegungen der ci,j , d, h. δ(a) = 0.
2.Fall: Es gibt ein 1 ≤ m ≤ r mit gm (a) = 1.
Dann gilt OR(g1 (a), . . . , gr (a)) = 1.
Ausserdem: Für alle 1 ≤ j ≤ ℓ gilt: Für
Prjede Wahl der ck,j mit k 6= m gibt
es genau eine Wahl für cm,j , so dass i=1 ci,j gi (a) = 0.
Es gibt also insgesamt nur |K |(r −1)·ℓ viele Belegungen der ci,j , so dass
P
r
i=1 ci,j gi (a) = 0 für alle 1 ≤ j ≤ ℓ.
Also gilt δ(a) = |K |(r −1)·ℓ .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
89 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Definiere nun einen bipartiten Graphen G wie folgt:
linke Knotenmenge: {0, 1}n (2n viele)
rechte Knotenmenge: Alle Belegungen für die ci,j ∈ K (1 ≤ i ≤ r ,
1 ≤ j ≤ ℓ) (|K |r ·ℓ viele)
Es gibt eine Kante zwischen a ∈ {0, 1}n und einer Belegung für die
ci,j ∈ K , falls unter dieser Belegung gilt: f (a) 6= OR(g1 (a), . . . , gr (a)).
Jeder der 2n vielen linken Knoten hat ≤ |K |(r −1)·ℓ viele rechte Nachbarn,
d. h. G hat ≤ 2n · |K |(r −1)·ℓ viele Kanten.
Also gibt es einen rechten Knoten (eine Belegung für die ci,j ∈ K ), der
≤ (2n · |K |(r −1)·ℓ )/|K |r ·ℓ = 2n /|K |ℓ ≤ 2n−ℓ
viele linke Nachbarn hat, d.h. es gibt eine Belegung für die ci,j ∈ K , unter
der f (a) = OR(g1 (a), . . . , gr (a)) für mindestens 2n − 2n−ℓ viele a ∈ {0, 1}n
gilt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
90 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Lemma 28
Sei K ein endlicher Körper der Charakteristik p (p eine Primzahl). Sei
F = (Sn )n≥0 eine Schaltkreisfamilie über der Basis
Bool ∪ {MODpk | k ≥ 2} mit:
Sn hat n Eingänge und einen Ausgang.
depth(Sn ) ≤ d (d ist eine Konstante)
size(Sn ) ≤ 2r (n) , wobei r (n) ∈ o(n1/2d )
Dann gibt es Polynome pn (x1 , . . . , xn ) (n ≥ 0), so dass für alle n ≥ 0 gilt:
√
Grad(pn ) ∈ o( n).
Die durch pn (x1 , . . . , xn ) berechnete Funktion stimmt mit valSn auf
einer Teilmenge von {0, 1}n der Mächtigkeit ≥ 2n − o(2n ) überein.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
91 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Beweis: O.B.d.A. gelte r (n) → ∞ für n → ∞ (falls r (n) durch eine
Konstante beschränkt ist, können wir r (n) auf log(n) setzen).
Wir wenden Lemma 27 wiederholt mit ℓ = 2 · r (n) ≥ 1 auf Sn an, und
ordnen so jedem Gatter g von Sn ein Polynom pg zu mit
Grad(pg ) ≤ ((|K | − 1) · ℓ)depth(g ) .
In jedem Schritt werden höchstens 2n−ℓ neue Fehler eingeführt.
Sei im folgenden d = depth(g ).
1. Fall: g ist mit der Eingabevariablen xi markiert. Dann sei pg = xi .
Hierbei werden keine Fehler eingeführt.
2. Fall: g ist mit ¬ markiert.
Sei h das Eingabegatter von g .
Nach Induktionsvoraussetzung ist ph ein Polynom mit
Markus Lohrey (Universität Leipzig)
Grad(ph ) ≤ ((|K | − 1) · ℓ)d−1 .
Schaltkreiskomplexität
WS 2009/2010
92 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Sei pg = 1 − ph ; dann gilt
Grad(pg ) ≤ ((|K | − 1) · ℓ)d−1 ≤ ((|K | − 1) · ℓ)d .
Hierbei werden keine neuen Fehler eingeführt.
W
3. Fall: g ist mit
markiert.
Seien h1 , . . . , hk die Eingabegatter von g .
Nach Induktionsvoraussetzung ist phi ein Polynom mit
Grad(phi ) ≤ ((|K | − 1) · ℓ)d−1
Nach Lemma 27 gibt es ein Polynom pg mit
Grad(pg ) ≤ ((|K | − 1) · ℓ) · ((|K | − 1) · ℓ)d−1 = ((|K | − 1) · ℓ)d ,
welches mit OR(ph1 , . . . , phk ) auf einer Menge der Mächtigkeit ≤ 2n−ℓ
nicht übereinstimmt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
93 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Hier werden also ≤ 2n−ℓ viele neue Fehler eingeführt.
4. Fall: g ist mit MODpk markiert.
Seien h1 , . . . , hk die Eingabegatter von g .
Nach Induktionsvoraussetzung ist phi ein Polynom mit
Grad(phi ) ≤ ((|K | − 1) · ℓ)d−1 .
Definiere
pg = 1 − (ph1 + · · · + phk )|K |−1 .
Dann gilt
Grad(pg ) ≤ (|K | − 1) · ((|K | − 1) · ℓ)d−1 ≤ ((|K | − 1) · ℓ)d .
Hier werden wieder keine neuen Fehler eingeführt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
94 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Sei nun pn das für das Ausgangsgatter von Sn berechnete Polynom.
Dieses hat Grad ≤ ((|K | − 1) · ℓ)d und stimmt mit valSn auf einer Menge
der Mächtigkeit ≥ 2n − size(Sn ) · 2n−ℓ überein.
Wegen ℓ = 2 · r (n) und r (n) ∈ o(n1/2d ) gilt:
√
Grad(pn ) ≤ ((|K | − 1) · ℓ)d = (2(|K | − 1) · r (n))d ∈ o( n)
Beachte: (2(|K | − 1))d ist eine Konstante.
Ausserdem gilt wegen r (n) → ∞:
size(Sn ) · 2n−ℓ ≤ 2r (n) · 2n−2·r (n) = 2n−r (n)
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
95 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Lemma 29
Seien p und q verschiedene Primzahlen. Dann gibt es keine
Schaltkreisfamilie F = (Sn )n≥0 über der Basis Bool ∪ {MODpk | k ≥ 2}
mit:
valF = MODq
depth(Sn ) ≤ d (d ist eine Konstante)
size(Sn ) ≤ 2r (n) , wobei r (n) ∈ o(n1/2d )
Beweis: Angenommen es gibt eine Schaltkreisfamilie F = (Sn )n≥0 über
der Basis Bool ∪ {MODpk | k ≥ 2} mit:
valF = MODq
depth(Sn ) ≤ d (d ist eine Konstante)
size(Sn ) ≤ 2r (n) , wobei r (n) ∈ o(n1/2d )
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
96 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Es gibt dann für jedes 0 ≤ s < q eine Schaltkreisfamilie Fs = (Ss,n )n≥0
über der Basis Bool ∪ {MODpk | k ≥ 2} mit:
valFs = MODq,s
depth(Ss,n ) ≤ d (d ist eine Konstante)
size(Ss,n ) ≤ 2r (n+q) , wobei r (n) ∈ o(n1/2d ), d. h. size(Ss,n ) ≤ 2r
wobei r ′ (n) ∈ o((n + q)1/2d )
′ (n)
,
Wegen o((n + q)1/2d ) = o(n1/2d ) gilt aber wieder r ′ (n) ∈ o(n1/2d ).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
97 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Wie im Beweis von Satz 25 finden wir eine Zahl m > 0 und ein
g ∈ GF(p m ) mit
g q = 1 und g r 6= 1 für alle 1 ≤ r < q.
Wieder gilt xi = (g − 1)−1 (g xi − 1) für xi ∈ {0, 1}.
Im folgenden sei yi = g xi 6= 0 (d. h. xi = (g − 1)−1 (yi − 1) und
yi = (g − 1)xi + 1.
Sei K = GF(p m ).
Wegen Lemma 28 gibt es Polynome pn,s (x1 , . . . , xn ) ∈ K [x1 , . . . , xn ] und
Mengen En,s ⊆ {0, 1}n (n ≥ 0, 0 ≤ s < q) mit:
√
Grad(pn,s ) ∈ o( n)
|En,s | ∈ o(2n )
∀x ∈ {0, 1}n \ En,s : pn,s (x) = MODq,s (x)
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
98 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Definiere das Polynom
pn (x1 , . . . , xn ) =
q−1
X
s=0
g s · pn,s (x1 , . . . , xn ) ∈ K [x1 , . . . , xn ]
√
vom Grad o( n) und die Mengen
En =
q−1
[
s=0
Dann gilt:
|En | ≤
Pq−1
s=0
En,s ⊆ {0, 1}n und Dn = {0, 1}n \ En .
|En,s | ∈ q · o(2n ) = o(2n ), d. h. |Dn | ∈ 2n − o(2n )
Für alle (x1 , . . . , xn ) ∈ Dn gilt
pn (x1 , . . . , xn ) =
q−1
X
s=0
Markus Lohrey (Universität Leipzig)
g s · MODq,s (x1 , . . . , xn ) = g x1 +···+xn = y1 · · · yn .
Schaltkreiskomplexität
WS 2009/2010
99 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Wir zählen nun die Anzahl σn aller Funktionen von Dn ⊆ {0, 1}n nach K
auf zwei verschiedene Weisen, und werden so zu einem Widerspruch
kommen.
n −o(2n )
1. Zählweise: Wegen |Dn | ∈ 2n − o(2n ) gilt σn ∈ |K |2
Beachte: Dies ist eine untere Schranke für σn .
2. Zählweise: Sei f : Dn → K beliebig.
Wegen Dn ⊆ {0, 1}n kann f durch ein reduziertes Polynom p(x1 , . . . , xn )
repräsentiert werden (Lemma 23), wobei diese Repräsentation nicht
unbedingt eindeutig sein muss.
Ersetze in p(x1 , . . . , xn ) jedes Vorkommen von xi durch (g − 1)−1 (yi − 1)
(1 ≤ i ≤ n).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
100 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Wir erhalten so einen Ausdruck der Form
Y
X
cI · YI mit YI =
yi und cI ∈ K .
(1)
Wir ersetzen nun in (1) jeden Teilausdruck YI mit |I | ≥ ⌈n/2⌉ durch
Y
yj−1 .
y1 · · · y n
(2)
i∈I
I ⊆{1,...,n}
j6∈I
Beachte: Für xi ∈ {0, 1} gilt
yi−1 = g −xi = (g −1 − 1)(g − 1)−1 (yi − 1) + 1.
Deshalb kann (2) approximiert werden durch
Y
pn (x1 , . . . , xn ) · ((g −1 − 1)(g − 1)−1 (yj − 1) + 1).
j6∈I
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
101 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Schließlich ersetzen wir jedes Vorkommen von yi wieder durch
(g − 1)xi + 1.
Wir erhalten so ein Polynom p ′ (x1 , . . . , xn ) mit:
√
Grad(p ′ ) ∈ ⌊ n2 ⌋ + o( n)
∀x ∈ Dn : p ′ (x) = f (x), d. h. p ′ repräsentiert f .
Wir können daher σn (Anzahl aller Funktionen von Dn nach K ) nach oben
abschätzen, indem wir (o.B.d.A. reduzierte) Polynome über K vom Grad
√
⌊ n2 ⌋ + o( n) zählen.
¡ ¢
Die Anzahl aller reduzierten Monome YI mit |I | = i ist ni .
Daher erhalten wir
σn ∈ |K |
Markus Lohrey (Universität Leipzig)
P⌊n/2⌋+o(√n)
i=0
Schaltkreiskomplexität
(ni) .
WS 2009/2010
102 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Um den gewünschten Widerspruch abzuleiten, müssen wir noch zeigen:
√
µ
¶ µ⌊n/2⌋+o(
X n) µn¶¶
2n − o(2n ) ∩
=∅
i
i=0
Dies folgt aus folgender Behauptung, denn
(2n − o(2n )) ∩ (2n−1 + o(2n )) = ∅.
P⌊n/2⌋+o(√n) ¡n¢
⊆ 2n−1 + o(2n )
Behauptung: i=0
i
Beweis der Behauptung: Es gilt
√
√
⌊n/2⌋+o( n) µ ¶
⌊n/2⌋ µ ¶
⌊n/2⌋+o( n) µ ¶
X
X
X
n
n
n
=
+
i
i
i
i=0
i=0
i=⌊n/2⌋+1
µ
¶
√
n
n−1
⊆ 2
+ o( n)
⌊n/2⌋ + 1
µ
¶
√
n
n−1
.
⊆ 2
+ o( n)
⌈n/2⌉
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
103 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
√ ¡ n ¢
Es genügt also zu zeigen: o( n) ⌈n/2⌉
⊆ o(2n ), oder alternativ:
µ
n
⌈n/2⌉
¶
√
∈ O(2n / n).
Sei zunächst n gerade.
√
Mit Stirlings Formel (n! ∈ Θ((n/e)n · n)) folgt:
µ
¶ µ
¶
µ
√ ¶
n
n
(n/e)n · n
=
∈ O
⌈n/2⌉
(n/2e)n · n/2
n/2
µ n√ ¶
2 n
= O
n/2
n √
= O(2 / n)
Der Fall n ungerade kann analog behandelt werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
104 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Beweis von Satz 3: MODt 6∈ ACC(p k ), falls p prim ist und t einen
Primteiler q 6= p hat.
Angenommen es gilt MODt ∈ ACC(p k )
Lemma 24 impliziert MODt ∈ ACC(p).
Lemma 26 impliziert MODq ∈ ACC(p).
Dies widerspricht aber Lemma 29.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
105 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Bereits 1984 konnten Furst, Saxe und Sipser mittels der probabilistischen
Restriktionsmethode zeigen, das PARITY = MOD2 6∈ AC0 gilt.
Die untere Schranke für PARITY wurde insbesondere von Hastad 1986
mittels seines Switching Lemmas verbessert:
Satz 30 (Hastads Switching Lemma, 1986)
Sei F eine Boolesche Formel in k-DNF (Disjunktion von Konjunktionen
mit höchstens k Literalen) in n Variablen.
Angenommen wir wählen zufällig t ≤ n Variablen aus, und setzen deren
Werte zufällig und unabhängig voneinander auf 0 oder 1. Sei G die
resultierende Formel (in n − t Variablen). Dann gilt:
Prob[G ist nicht äquivalent zu einer Formel in s-KNF] ≤
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
µ
(n − t)k 10
n
WS 2009/2010
¶s/2
106 / 195
Untere Schranken
Untere Schranken für Schaltkreise konstanter Tiefe
Erwähnt sollte auch noch der folgende Satz von Sipser werden, wobei
AC0k = SIZEDEPTH(nO(1) , k, Bool).
Satz 31 (Sipser, 1983)
Für alle k ≥ 1 gilt: AC0k+1 \ AC0k 6= ∅.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
107 / 195
Reguläre Sprachen und NC1
Reguläre Sprachen und NC1
Wir beginnen mit einigen algebraischen Grundlagen zu regulären Sprachen.
Satz 32
Sei L ⊆ Σ∗ . Dann ist äquivalent:
L ist regulär.
Es gibt einen Monoidhomomorphismus h : Σ∗ → M, wobei M ein
endliches Monoid ist, und S ⊆ M mit L = h−1 (S)
Beweis:
(1) Sei L regulär.
Sei A = (Q, Σ, δ, q0 , F ) ein vollständiger deterministischer endlicher
Automat mit L = L(A).
Hierbei ist δ : Q × Σ → Q.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
108 / 195
Reguläre Sprachen und NC1
Reguläre Sprachen und NC1
Sei M = (Q Q , ◦) (das Monoid aller Abbildungen von Q nach Q;
Transformationsmonoid auf Q) und definiere h : Σ∗ → M durch
h(a) = fa mit fa (q) = δ(q, a) für q ∈ Q, a ∈ Σ.
Für S = {f : Q → Q | f (q0 ) ∈ F } gilt L = h−1 (S).
(2) Sei h : Σ∗ → M ein Monoidhomomorphismus mit M endlich und sei
S ⊆ M mit L = h−1 (S).
Definiere den endlichen Automaten
A = (M, Σ, δ, 1, S),
wobei 1 das neutrale Element von M ist und δ(m, a) = mh(a) für m ∈ M
und a ∈ Σ.
Dann gilt w ∈ L(A) ⇔ δ(1, w ) ∈ S ⇔ 1h(w ) ∈ S ⇔ h(w ) ∈ S ⇔
w ∈ h−1 (S) = L.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
109 / 195
Reguläre Sprachen und NC1
Reguläre Sprachen gehören zu NC1
Satz 33
Sei L ⊆ {0, 1}∗ regulär. Dann gilt L ∈ NC1 (sogar L ∈ uNC1 ).
Beweis:
Sei L ⊆ {0, 1}∗ regulär.
Nach Satz 32 gibt es einen Monoidhomomorphismus h : {0, 1}∗ → M und
S ⊆ M mit M endlich und L = h−1 (S).
Sei m = |M|. Ein Element a ∈ M kann durch einen Bitstring code(a) der
Länge ℓ = ⌈log2 (m)⌉ kodiert werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
110 / 195
Reguläre Sprachen und NC1
Reguläre Sprachen gehören zu NC1
Es gibt somit feste Schaltkreise input, mult und output mit:
input hat ein Eingabegatter, ℓ Outputgatter, und liefert bei Eingabe
b ∈ {0, 1} die Ausgabe code(h(b)).
mult hat 2 · ℓ Eingabegatter, ℓ Outputgatter und liefert bei Eingabe
von code(a1 )code(a2 ) die Ausgabe code(a1 a2 ).
output hat ℓ Eingabegatter, 1 Outputgatter und liefert bei Eingabe
von code(a) die Ausgabe 1 g.d.w. a ∈ S.
V
Beachte: Jeder dieser Schaltkreise kann aus ¬-Gattern und 2 -Gattern in
konstanter Tiefe aufgebaut werden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
111 / 195
Reguläre Sprachen und NC1
Reguläre Sprachen gehören zu NC1
Der n-te Schaltkreis unserer Familie (n = Anzahl der Eingabebits) sieht
nun wie folgt aus.
Bei Eingabe x1 x2 · · · xn (xi ∈ {0, 1}) wird zunächst
code(h(x1 ))code(h(x2 )) · · · code(h(xn )) mittels einer Schicht von
input-Schaltkreisen berechnet.
Nun wird in einem binären Baum der Tiefe O(log(n)) der Wert
code(h(x1 )h(x2 ) · · · h(xn )) = code(h(x1 x2 · · · xn )) berechnet. Hierzu
benötigen wir 2n viele mult-Schaltkreise.
Schließlich wird mittels eines output-Schaltkreises (der
code(h(x1 x2 · · · xn )) als Eingabe erhält) überprüft, ob
h(x1 x2 · · · xn ) ∈ S, d. h. x1 x2 · · · xn ∈ h−1 (S) = L gilt.
Dieser Schaltkreis hat Tiefe O(log(n)) und O(n) viele Gatter.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
112 / 195
Reguläre Sprachen und NC1
Einfache Gruppen
Wir wollen im folgenden eine gewisse Umkehrung von Satz 33 beweisen.
Hierzu benötigen wir einfache Gruppen.
Sei G eine Gruppe und H eine Untergruppe von G . Dann ist H ein
Normalteiler von G (kurz H ⊳ G ), genau dann, wenn gilt:
∀g ∈ G : g −1 Hg = H.
Die Gruppe G ist einfach, falls 1 und G die einzigen Normalteiler von G
sind.
Äquivalent:
G ist einfach g.d.w. für jeden surjektiven Gruppenhomomorphismus
h : G → H gilt: H ∼
= G.
= 1 oder H ∼
Ist G endlich, so ist G ist einfach g.d.w. für jedes Element h ∈ G \ 1
gilt: Jedes Element von G kann als ein Produkt von Elementen aus
{g −1 hg | g ∈ G } dargestellt werden.
Für den zweiten Punkt beachte man: Ist G endlich, so ist die Menge aller
Produkte von Elementen aus {g −1 hg | g ∈ G } ist ein Normalteiler von G ,
der h 6= 1 enthält.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
113 / 195
Reguläre Sprachen und NC1
Einfache Gruppen und Kommutatoren
Beispiele:
(Zp , +) ist einfach, falls p eine Primzahl ist.
An ≤ Sn ist einfach für n ≥ 5. Sn ist die Gruppe aller Permutationen
von n Elementen. An (die alternierende Gruppe auf n Elementen) ist
die Untergruppe von Sn bestehend aus allen geraden Permutationen.
Eine Permutation σ auf {1, . . . , n} ist gerade, falls die Anzahl aller
Paare (i, j) mit 1 ≤ i < j ≤ n und σ(i) > σ(j) gerade ist.
A5 ist die kleinste nicht-Abelsche einfach Gruppe, sie hat 60 Elemente.
Sei G eine Gruppe. Der Kommutator von g , h ∈ G ist [g , h] = ghg −1 h−1 .
Die Kommutatoruntergruppe einer Gruppe G ist die Menge [G , G ] aller
Produkte g1 g2 · · · gn , wobei n ≥ 0 und g1 , . . . , gn Kommutatoren in G sind.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
114 / 195
Reguläre Sprachen und NC1
Kommutatoruntergruppe
[G , G ] ist in der Tat eine Untergruppe von G :
[G , G ] ist nach Definition unter Produkt abgeschlossen.
Es gilt [g , h]−1 = (ghg −1 h−1 )−1 = hgh−1 g −1 = [h, g ].
Für Kommutatoren g1 , . . . , gn gilt also
(g1 g2 · · · gn )−1 = gn−1 · · · g2−1 g1−1 ∈ [G , G ],
d.h. [G , G ] ist unter Inversenbildung abgeschlossen.
[G , G ] ist sogar ein Normalteiler von G , denn es gilt:
x −1 [g , h]x
= x −1 ghg −1 h−1 x
= (x −1 gx)(x −1 hx)(x −1 g −1 x)(x −1 h−1 x)
= (x −1 gx)(x −1 hx)(x −1 gx)−1 (x −1 hx)−1
= [x −1 gx, x −1 hx]
Für Kommutatoren g1 , . . . , gn gilt also
x −1 (g1 g2 · · · gn )x = (x −1 g1 x)(x −1 g2 x) · · · (x −1 gn x) ∈ [G , G ].
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
115 / 195
Reguläre Sprachen und NC1
Kommutatoruntergruppe
Beispiel: [Sn , Sn ] = An für n ≥ 2 (Übung).
Offensichtlich ist eine Gruppe G genau dann Abelsch, falls [G , G ] = 1 gilt.
Da [G , G ] ein Normalteiler von G ist, folgt:
Lemma 34
Ist G eine nicht-Abelsche einfache Gruppe, so gilt [G , G ] = G .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
116 / 195
Reguläre Sprachen und NC1
Wörter über Monoiden
Sei M ein Monoid und {x1 , . . . , xn } eine Menge von Variablen.
Ein Wort w ∈ (M ∪ {x1 , . . . , xn })∗ repräsentiert eine Funktion
fw : M n → M wie folgt:
Sei m = (m1 , . . . , mn ) ∈ M n .
Definiere ρm : (M ∪ {x1 , . . . , xn })∗ → M als den eindeutigen
Monoidhomomorphismus mit ρm (m) = m für m ∈ M und
ρm (xi ) = mi .
Dann gilt fw (m) = ρm (w ).
Ein Wort w ∈ (M ∪ {x1 , . . . , xn })∗ schreiben wir auch als w (x1 , . . . , xn )
und für fw (m1 , . . . , mn ) schreiben wir einfach w (m1 , . . . , mn ).
Für w , v1 , . . . , vn ∈ (M ∪ {x1 , . . . , xn })∗ ist w (v1 , . . . , vn ) das Wort, dass
aus w entsteht, indem jedes Vorkommen von xi durch vi ersetzt wird.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
117 / 195
Reguläre Sprachen und NC1
Der Satz von Maurer und Rhodes
Satz 35 (Maurer, Rhodes; 1965)
Sei G eine endliche, nicht-Abelsche, einfache Gruppe und sei f : G n → G
eine Funktion. Dann existiert ein Wort w ∈ (G ∪ {x1 , . . . , xn })∗ mit f = fw .
Beweis:
Seien g1 , g2 ∈ G mit g1 6= 1.
Da G einfach ist, kann g2 als Produkt von Elementen der Form hg1 h−1
(h ∈ G ) geschrieben werden.
Es gibt also ein Wort ug1 ,g2 ∈ (G ∪ {x1 })∗ mit:
ug1 ,g2 (g1 ) = g2 ,
ug1 ,g2 (1) = 1
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
118 / 195
Reguläre Sprachen und NC1
Der Satz von Maurer und Rhodes
Da G einfach und nicht-Abelsch ist, gilt G = [G , G ] nach Lemma 34.
Sei nun h ∈ G \ {1}.
Wegen h ∈ G = [G , G ] gibt es g1 , h1 , . . . , gr , hr ∈ G mit
h=
r
Y
[gi , hi ].
i=1
Wir definieren nun durch Induktion über m ≥ 1 Wörter
wm,h ∈ (G ∪ {x1 , . . . , xm })∗ mit
wm,h (h, . . . , h) = h,
wm,h (a1 , . . . , am ) = 1 falls 1 ∈ {a1 , . . . , am }.
Induktionsanfang: Definiere w1,h (x1 ) = uh,h (x1 ) und
w2,h (x1 , x2 ) =
r
Y
uh,gi (x1 )uh,hi (x2 )uh,gi (x1 )|G |−1 uh,hi (x2 )|G |−1 .
i=1
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
119 / 195
Reguläre Sprachen und NC1
Der Satz von Maurer und Rhodes
Dann gilt:
w2,h (h, h) =
r
Y
uh,gi (h)uh,hi (h)uh,gi (h)|G |−1 uh,hi (h)|G |−1
i=1
=
r
Y
|G |−1 |G |−1
hi
gi hi gi
i=1
=
r
Y
gi hi gi−1 hi−1 = h
i=1
sowie, für alle a ∈ G :
w2,h (a, 1) =
=
r
Y
i=1
r
Y
uh,gi (a)uh,hi (1)uh,gi (a)|G |−1 uh,hi (1)|G |−1
uh,gi (a)|G | = 1
i=1
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
120 / 195
Reguläre Sprachen und NC1
Der Satz von Maurer und Rhodes
Analog ergibt sich w2,h (1, a) = 1 für alle a ∈ G .
Induktionsschritt: Für m ≥ 2 definieren wir
wm+1,h = w2,h (wm,h , xm+1 ).
Dann gilt
wm+1,h (h, . . . , h) = w2,h (wm,h (h, . . . , h), h) = w2,h (h, h) = h
sowie, falls 1 ∈ {a1 , . . . , am , am+1 },
wm+1,h (a1 , . . . , am+1 ) = w2,h (wm,h (a1 , . . . , am ), am+1 )
(
w2,h (1, am+1 ) = 1 falls 1 ∈ {a1 , . . . , am }
=
w2,h (wm,h (a1 , . . . , am ), 1) = 1.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
121 / 195
Reguläre Sprachen und NC1
Der Satz von Maurer und Rhodes
Seien nun h, k ∈ G mit h 6= 1 und sei
G \ {k −1 } = {k1 , . . . , kt }.
Definiere
zk,h (x) = wt,h (uk1 k,h (k1 x), . . . , ukt k,h (kt x)).
Dann gilt
zk,h (k) = wt,h (uk1 k,h (k1 k), . . . , ukt k,h (kt k)) = wt,h (h, . . . , h) = h.
Ausserdem gibt es für alle g ∈ G \ {k} ein 1 ≤ i ≤ t mit ki g = 1 und
damit uki k,h (ki g ) = 1.
Also gilt
∀g ∈ G \ {k} : zk,h (g ) = 1.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
122 / 195
Reguläre Sprachen und NC1
Der Satz von Maurer und Rhodes
Sei nun h ∈ G \ 1, n ≥ 1 und g = (g1 , . . . , gn ) ∈ G n . Definiere
vg ,h (x1 , . . . , xn ) = wn,h (zg1 ,h (x1 ), . . . , zgn ,h (xn )).
Dann gilt
vg ,h (g ) = wn,h (zg1 ,h (g1 ), . . . , zgn ,h (gn )) = wn,h (h, . . . , h) = h.
Sei nun (h1 , . . . , hn ) ∈ G n \ {g }. Dann existiert ein 1 ≤ i ≤ n mit hi 6= gi
und damit zgi ,h (hi ) = 1.
Also gilt
∀x ∈ G n \ {g } : vg ,h (x) = 1.
Für eine Funktion f : G n → G sei schließlich
Y
wf (x1 , . . . , xn ) =
vg ,f (g ) (x1 , . . . , xn ).
g ∈G n
f (g )6=1
Dann gilt wf (g ) = f (g ) für alle g ∈ G n .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
123 / 195
Reguläre Sprachen und NC1
Barringtons Theorem
Satz 36 (Barrington 1989)
Sei G eine endliche, nicht-Abelsche, einfache Gruppe, sei L ∈ NC1 und
seien 0, 1 ∈ G zwei beliebige Elemente (0 6= 1; 1 muss nicht unbedingt das
neutrale Element von G sein).
Dann gibt es eine Folge (wn )n≥0 mit wn ∈ (G ∪ {x1 , . . . , xn })∗ , so dass
gilt:
Die Funktion n 7→ |wn | ist durch ein Polynom beschränkt.
Für alle a1 , . . . , an ∈ {0, 1} ⊆ G gilt:
(
1 falls a1 a2 · · · an ∈ L
wn (a1 , a2 , . . . , an ) =
0 sonst .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
124 / 195
Reguläre Sprachen und NC1
Barringtons Theorem
V
Beweis: Sei F = (Sn )n≥0 eine Schaltkreisfamilie über der Basis {¬, 2 }
mit:
valSn (a1 , . . . , an ) = 1 genau dann, wenn a1 · · · an ∈ L.
Die Tiefe von Sn ist beschränkt durch c · log2 (n) für eine Konstante c.
Nach Satz 35 gibt es Wörter and(x1 , x2 ) ∈ (G ∪ {x1 , x2 })∗ und
not(x1 ) ∈ (G ∪ {x1 })∗ mit:
and(a1 , a2 ) = (a1 ∧ a2 ) für a1 , a2 ∈ {0, 1}
not(a) = ¬a für a ∈ {0, 1}
Sei ℓ = max{|and(x1 , x2 )|, |not(x1 )|}.
Wir konstruieren nun für jedes Gatter g von Sn durch Induktion über
depth(g ) ein Wort wg (x1 , . . . , xn ), mit:
wg (x1 , . . . , xn ) repräsentiert die am Gatter g berechnete Boolesche
Funktion.
|wg | ≤ ℓdepth(g )
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
125 / 195
Reguläre Sprachen und NC1
Barringtons Theorem
1. Fall: g ist mit der Eingabevariablen xi beschriftet.
Dann sei wg (x1 , . . . , xn ) = xi .
2. Fall: g ist mit ¬ beschriftet. Sei h das Eingabegatter von g .
Dann sei wg (x1 , . . . , xn ) = not(wh (x1 , . . . , xn )).
à |wg | ≤ ℓ · |wh | ≤ ℓ · ℓdepth(h) = ℓdepth(g ) .
3. Fall: g ist mit
V
2
beschriftet. Seien h1 und h2 die Eingabegatter von g .
Dann sei wg (x1 , . . . , xn ) = and(wh1 (x1 , . . . , xn ), wh2 (x1 , . . . , xn )).
à |wg | ≤ ℓ · max{|wh1 |, |wh2 |} ≤ ℓ · max{ℓdepth(h1 ) , ℓdepth(h2 ) } = ℓdepth(g ) .
Sei schließlich wn (x1 , . . . , xn ) = wg (x1 , . . . , xn ), wobei g das Outputgatter
von Sn ist.
Dann gilt |wn | ≤ ℓc·log2 (n) ∈ nO(1) .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
126 / 195
Reguläre Sprachen und NC1
Starke Reduzierbarkeit
Wir definieren nun noch einen Reduktionsbegriff wie folgt.
Seien K , L ⊆ {0, 1}∗ Sprachen.
Für n ≥ 0 sei χnL = χL ↾{0, 1}n (die charakteristische Funktion von L
eingeschränkt auf Wörter der Länge n).
Wir schreiben K ≤strong L falls gilt:
K ∈ SIZEDEPTH(nO(1) , O(1), Bool2 ∪ {χnL | n ≥ 0}).
Wir schreiben K ≤1strong L, falls die Schaltkreisfamilie die folgende
Zusatzeigenschaft hat: Auf keinem Pfad von einem Eingabegatter zu
einem Ausgabegatter kommt mehr als ein Gatter aus {χnL | n ≥ 0} vor.
Beispiele:
k
Lemma 24 besagt MODp ≤strong MODp .
Lemma 26 besagt MODq ≤strong MODt , falls q Teiler von t ist
(hier liefert der Beweis sogar MODq ≤1strong MODt ).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
127 / 195
Reguläre Sprachen und NC1
Teilbarkeit von Monoiden und das syntaktische Monoid
Seien M und N Monoide. Wir schreiben N ¹ M (kurz: N teilt M), falls
ein Teilmonoid M ′ von M (die neutralen Elemente von M und M ′ müssen
nicht übereinstimmen) und ein surjektiver Monoidhomomorphismus
ψ : M ′ → N existiert.
Übung: ¹ ist transitiv.
Sei L ⊆ A∗ ein beliebige Sprache. Die syntaktische Kongruenz von L ist die
Relation ≡L ⊆ A∗ × A∗ mit:
u ≡L v ⇐⇒ ∀x, y ∈ A∗ : xuy ∈ L ↔ xvy ∈ L.
Übung: ≡ ist eine Kongruenzrelation auf dem freien Monoid A∗ .
Das Quotientenmonoid M(L) = A∗ /≡L ist das syntaktische Monoid von L.
Es gilt:
L ist regulär genau dann, wenn M(L) endlich ist.
Sei M ein Monoid. Es gilt M(L) ¹ M genau dann, wenn L = h−1 (S)
für einen Monoidhomomorphismus h : A∗ → M und S ⊆ M.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
128 / 195
Reguläre Sprachen und NC1
Auflösbare Gruppen
Eine Gruppe G ist auflösbar, falls eine Folge G = G0 , G1 , . . . , Gn−1 , Gn = 1
von Gruppen existiert mit:
Gi+1 ⊳ Gi für 0 ≤ i ≤ n − 1
Gi /Gi+1 ist Abelsch für 0 ≤ i ≤ n − 1.
Einige bekannte Eigenschaften auflösbarer Gruppen:
Sei H ⊳ G und seien H und G /H auflösbar. Dann ist auch G auflösbar
Jede Untergruppe einer auflösbaren Gruppe ist wieder auflösbar.
Ein Monoid M ist auflösbar, falls jede Gruppe, die Teilmonoid von M ist,
auflösbar ist.
Lemma 37
Sei das endliche Monoid M nicht auflösbar. Dann existiert eine
nicht-Abelsche einfache Gruppe H mit H ¹ M.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
129 / 195
Reguläre Sprachen und NC1
Auflösbare Gruppen
Beweis: Sei G eine nicht-auflösbare Gruppe in M.
Durch Induktion über |G | zeigen wir, dass eine nicht-Abelsche einfache
Gruppe H mit H ¹ G existiert.
Da G nicht auflösbar ist, kann G nicht Abelsch sein.
Falls G einfach ist, können wir H = G wählen.
Sei also G nicht einfach und sei N ⊳ G mit 1 6= N 6= G .
Da G nicht auflösbar ist, ist N oder G /N nicht auflösbar.
Beachte: Es gilt N ¹ G , G /N ¹ G und |N| < |G | > |G /N|.
Also können wir die Induktionsannahme anwenden.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
130 / 195
Reguläre Sprachen und NC1
1
NC -vollständige reguläre Sprachen
Satz 38
Sei L ⊆ {0, 1}∗ regulär. Falls M(L) nicht auflösbar ist, so gilt für alle
K ∈ NC1 : K ≤1strong L.
Für den Beweis benötigen wir noch das folgende technische Lemma:
Lemma 39
Sei M ein endliches Monoid und G eine einfache nicht-Abelsche Gruppe
mit G ¹ M. Sei M ′ ein Teilmonoid von M und ψ : M ′ → G surjektiv. Sei
η : A∗ → M ein surjektiver Monoidhomomorphismus. Dann existiert ein
r > 0 mit G ⊆ ψ(η(Ar ) ∩ M ′ ).
Beweis: Sei |G | = m.
Beachte: Für jedes Wort u ∈ η −1 (M ′ ) gilt ψ(η(u m )) = 1.
Da G einfach und nicht-Abelsch ist, gilt G = [G , G ].
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
131 / 195
Reguläre Sprachen und NC1
1
NC -vollständige reguläre Sprachen
Jedes Element von G ist also Produkt von Kommutatoren, d.h. für jedes
g ∈ G existiert ein Wort über A von der Form
wg =
sg
Y
m−1
ug ,i vg ,i ugm−1
,i vg ,i ,
i=1
mit ug ,i , vg ,i ∈ η −1 (M ′ ) und ψ(η(wg )) = g .
Qsg
Es gilt |wg | = m · ℓg mit ℓg = | i=1
ug ,i vg ,i |.
Sei r = kgV({|wg | | g ∈ G }).
Dann gibt es kg ≥ 1 mit r = m · ℓg · kg für alle g ∈ G .
Definiere
wg′
= wg
µY
sg
ugm,i vgm,i
i=1
Ã
ψ(η(wg′ ))
= g und
Markus Lohrey (Universität Leipzig)
|wg′ |
¶kg −1
= |wg | + (kg − 1) · |wg | = kg |wg | = r .
Schaltkreiskomplexität
WS 2009/2010
132 / 195
Reguläre Sprachen und NC1
1
NC -vollständige reguläre Sprachen
Beweis von Satz 38: Sei K ∈ NC1 und L ⊆ {0, 1}∗ regulär mit M(L)
nicht auflösbar.
Nach Lemma 37 existiert eine einfach nicht-Abelsche Gruppe G mit
G ¹ M(L).
Wähle Elemente 0, 1 ∈ G mit 0 6= 1.
Es gibt ein Teilmonoid M ′ von M(L) und einen surjektiven
Monoidhomomorphismus ψ : M ′ → G .
Sei ηL : A∗ → M(L) der kanonische Monoidhomomorphismus.
Nach Lemma 39 existiert ein r > 0 mit G ⊆ ψ(ηL ({0, 1}r ) ∩ M ′ ).
Also existiert für jedes Gruppenelement g ∈ G ein Wort vg ∈ {0, 1}r mit
ψ(ηL (vg )) = g .
Wir konstruieren einen Schaltkreis über der Basis Bool2 ∪ {χnL | n ≥ 0},
der K ∩ {0, 1}n erkennt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
133 / 195
Reguläre Sprachen und NC1
1
NC -vollständige reguläre Sprachen
Da K ∈ NC1 , existiert nach Satz 36 eine Folge (wn )n≥0 mit
wn ∈ (G ∪ {x1 , . . . , xn })∗ , so dass gilt:
|wn | ∈ nO(1) .
Für alle a1 , . . . , an ∈ {0, 1} ⊆ G gilt:
(
1 falls a1 a2 · · · an ∈ K
wn (a1 , a2 , . . . , an ) =
0 sonst .
Der Schaltkreis für Eingabelänge n konstruiert aus der Eingabe
a1 a2 · · · an ∈ {0, 1}n zunächst einen Wort u ∈ {0, 1}|wn |·r , indem:
in wn jedes Gruppenelement g ∈ G durch das Wort vg ∈ {0, 1}r
ersetzt wird, und
in wn jedes Vorkommen der Variable xi durch vai ersetzt wird.
Dann gilt ψ(ηL (u)) ∈ {0, 1} und (a1 a2 · · · an ) ∈ K ⇐⇒ ψ(ηL (u)) = 1.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
134 / 195
Reguläre Sprachen und NC1
1
NC -vollständige reguläre Sprachen
Sei S = ψ −1 (1) ⊆ M ′ ⊆ M(L).
Es gilt also (a1 a2 · · · an ) ∈ K ⇐⇒ ηL (u) ∈ S.
Da |S| eine Konstante ist, genügt es einen Schaltkreis zu entwerfen, der
ηL (u) = s überprüft (s ∈ S).
Für Wörter x, y ∈ {0, 1}∗ sei x −1 Ly −1 = {z ∈ {0, 1}∗ | xzy ∈ L}.
Dann gilt für alle z1 , z2 ∈ {0, 1}∗ :
z1 ≡L z2
⇐⇒
⇐⇒
∀x, y ∈ {0, 1}∗ : xz1 y ∈ L ↔ xz2 y ∈ L
∀x, y ∈ {0, 1}∗ : z1 ∈ x −1 Ly −1 ↔ z2 ∈ x −1 Ly −1
Der Wert ηL (u) wird also eindeutig dadurch festgelegt, indem man angibt,
zu welchen Mengen x −1 Ly −1 das Wort u gehört.
Nun gibt es aber nur endlich viele Mengen x −1 Ly −1 :
Sei A = (Q, {0, 1}, δ, q0 , F ) ein vollständiger deterministischer Automat
mit L = L(A).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
135 / 195
Reguläre Sprachen und NC1
1
NC -vollständige reguläre Sprachen
Dann erkennt A jede Menge x −1 Ly −1 , indem man als Anfangszustand
δ(q0 , x) wählt, und als Menge der Endzustände {q ∈ Q | δ(q, y ) ∈ F }
wählt.
Es gibt deshalb eine (nur von s ∈ M(L) abhängige) Liste von Paaren
′ , y ′ ) ∈ {0, 1}∗ × {0, 1}∗ mit:
(x1 , y1 ), . . . , (xℓ , yℓ ), (x1′ , y1′ ), . . . , (xm
m
ηL (u) = s
⇐⇒
⇐⇒
ℓ
^
i=1
ℓ
^
i=1
u∈
xi−1 Lyi−1
xi uyi ∈ L ∧
∧
m
^
i=1
m
^
i=1
−1
−1
u 6∈ x ′ i Ly ′ i
xi′ uyi′ 6∈ L
Letztere Bedingung kann mittels ℓ + m vielen “L-Gattern” überprüft
werden.
Beachte: In dem resultierenden Schaltkreis liegt auf jedem Pfad höchstens
ein L-Gatter.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
136 / 195
Reguläre Sprachen und NC1
1
NC -vollständige reguläre Sprachen
Für k ≥ 1 sei
TC0k = SIZEDEPTH(nO(1) , k, Bool ∪ {MAJk | k ≥ 2}).
Satz 40
Wenn TC0k ( TC0k+1 für alle k ≥ 1 gilt, dann TC0 6= NC1 .
Beweis: Gelte TC0 = NC1 .
Nach Satz 33 enthält TC0 jede reguläre Sprache.
Sei L ⊆ {0, 1}∗ eine beliebige reguläre Sprache, so dass M(L) nicht
auflösbar ist (existiert).
Dann gibt es ein k ≥ 1 mit L ∈ TC0k .
Nach Satz 38 gilt für jede Sprache K ∈ NC1 = TC0 : K ≤1strong L ∈ TC0k .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
137 / 195
Reguläre Sprachen und NC1
1
NC -vollständige reguläre Sprachen
Die in der Reduktion K ≤1strong L konstruierten Schaltkreise haben sogar
die Eigenschaft, dass ihre Tiefe nur von L (und nicht von K ) abhängt.
Sei diese Tiefe r .
Dann folgt TC0k+r = TC0 .
Reguläre Sprachen, deren syntaktisches Monoid auflösbar ist, sind
“einfacher” als solche mit nicht auflösbaren syntaktischen Monoid:
Satz 41 (Barrington, Therien; 1988)
Sei L regulär und M(L) auflösbar. Dann gilt: L ∈
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
S
q>0 ACC(q)
⊆ TC0 .
WS 2009/2010
138 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Semibeschränkte Schaltkreise
Wir wollen eine Schaltkreiskomplexitätsklasse zwischen NC1 und AC1
betrachten, bei der AND-Gatter beschränkten Eingangsgrad haben,
OR-Gatter aber unbeschränkten Eingangsgrad haben.
Vorsicht: Erlauben wir NOT-Gatter an beliebigen Positionen, so erhalten
wir wieder AC1 .
Lösung: Wir betrachten Schaltkreise, bei denen NOT-Gatter nur direkt
hinter Eingabegatter liegen dürfen.
Beachte: Diese Einschränkung würde in der Definition von NC1 und AC1
nichts ändern.
Ein Schaltkreis S = (V , α, λ, out) über der Basis Bool ist in
Negationsnormalform, falls für alle Gatter v ∈ V gilt:
Wenn λ(v ) = ¬, dann ist α(v ) ein Eingabegatter.
Eine Schaltkreisfamilie F = (Sn )n≥0 ist in Negationsnormalform, falls für
alle n ≥ 0 der Schaltkreis Sn in Negationsnormalform ist.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
139 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Die Klassen SAC1 und LOGCFL
Die Klasse SAC1 (das S steht für “semi”) ist definiert durch
SAC1 = {valF | F ist eine Schaltkreisfamilie in Negationsnormalform
W
V
über der Basis {¬, 2 } ∪ { n | n ≥ 2} mit
sizeF ∈ nO(1) und depthF ∈ O(log(n))}
Die Klasse uSAC1 entsteht aus SAC1 , indem man sich zusätzlich auf
logspace-uniforme Schaltkreisfamilien einschränkt.
Wir werden in diesem Kapitel eine Charakterisierung von uSAC1 mittels
kontextfreier Sprachen angeben.
Mit LOGCFL bezeichnen wir die Menge aller Sprachen, die logspace
reduzierbar auf eine kontextfreie Sprache sind:
LOGCFL = {K ⊆ {0, 1}∗ | ∃L ∈ CFL : K ≤log
m L}.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
140 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL = uSAC1
Man sagt auch: LOGCFL ist der Abschluss der kontextfreien Sprachen
unter logspace-Reduktionen.
Das Hauptresultat aus diesem Kapitel besagt:
Satz 42 (Venkateswaran 1987)
LOGCFL = uSAC1 (hier schränken wir uSAC1 auf Sprachen, d. h.
charakteristische Funktionen, ein).
Bevor wir den Satz zeigen, wollen wir eine einfache Konsequenz ableiten:
Natürlich gilt: uSAC1 ⊆ uAC1 ⊆ uNC2 .
Nach Satz 17 gilt außerdem: uNC2 ⊆ DSPACE(log2 (n)).
Also folgt:
Satz 43 (Lewis, Stearns, Hartmanis; 1965)
LOGCFL ⊆ DSPACE(log2 (n))
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
141 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Beweisbäume
Für den Beweis der Inklusion uSAC1 ⊆ LOGCFL im Beweis von Satz 42
benötigen wir das Konzept des Beweisbaums.
Sei S = (V , α, λ, out) ein Schaltkreis über der Basis Bool in
Negationsnormalform mit n Eingabegattern und einem Outputgatter.
Sei a = (a1 , a2 , . . . , an ) ∈ {0, 1}n eine Eingabe für S.
Ein Beweisbaum für S und a ist ein knotenbeschrifteter Baum T mit
folgenden Eigenschaften (wir sehen gleich, dass solch ein Baum nur dann
existiert, falls a ∈ LS ):
Jeder Knoten in T ist mit einem Gatter von S beschriftet, welches
sich bei Eingabe a zu 1 auswertet.
Die Wurzel von T ist mit dem Outputgatter von S beschriftet.
Jedes Blatt von T ist mit einem Gatter g beschriftet, so dass
λ(g ) ∈ {¬, x1 , . . . , xn }.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
142 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Beweisbäume
(Fortsetzung Definition Beweisbaum)
Sei der innereVKnoten v von T mit dem Gatter g beschriftet und
gelte λ(g ) = k , α(g ) = h1 · · · hk . Dann hat v genau k viele Kinder
in T und das i-te Kind ist mit hi beschriftet.
Sei der innereWKnoten v von T mit dem Gatter g beschriftet und
gelte λ(g ) = k , α(g ) = h1 · · · hk . Dann hat v genau ein Kind in T .
Dieses ist mit einem Gatter hi beschriftet, und hi wertet sich bei
Eingabe a zu 1 aus.
Das folgende Lemma ist offensichtlich:
Lemma 44
Sei S ein Schaltkreis über der Basis Bool in Negationsnormalform mit n
Eingabegattern und einem Outputgatter und sei a ∈ {0, 1}n eine Eingabe
für S. Dann gilt valS (a) = 1 genau dann, wenn ein Beweisbaum für S und
a existiert.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
143 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Beweisbäume
Problem: Die Anzahl der Knoten eines Beweisbaum für S und a wächst
i. A. exponentiell mit der Größe von S.
Dies gilt aber nicht für SAC1 -Schaltkreisfamilien:
Lemma 45
Sei F = (S
W Schaltkreisfamilie in Negationsnormalform über der
Vn )n≥0 eine
Basis {¬, 2 } ∪ { n | n ≥ 2} mit sizeF ∈ nO(1) und depthF ∈ O(log(n)).
Dann existiert ein Polynom p(n), so dass für alle n ≥ 0 und a ∈ {0, 1}n
gilt: Wenn a ∈ LF , dann existiert ein Beweisbaum für Sn und a mit
höchstens p(n) vielen Knoten.
Beweis:
Da in Sn nur 2-stellige AND-Gatter vorkommen und depthF ∈ O(log(n))
gilt, ist ein Beweisbaum für Sn und a ein binärer Baum der Tiefe
O(log(n)).
Solch ein Baum hat aber nur 2O(log(n)) = nO(1) viele Knoten.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
144 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
uSAC1 ⊆ LOGCFL
Beweis der Inklusion uSAC1 ⊆ LOGCFL in Satz 42
(nach McKenzie, Reinhardt, Vinay, 1999):
Sei F = (Sn )n≥0 eine logspace-uniforme Schaltkreisfamilie
in
V
W
Negationsnormalform über der Basis {¬, 2 } ∪ { n | n ≥ 2} mit
sizeF ∈ nO(1) und depthF ∈ O(log(n)).
Sei Sn = (Vn , αn , λn , outn ) für n ≥ 0.
O.B.d.A. sei Vn = {1, . . . , s(n)} für ein Polynom s(n).
O.B.d.A. sei 1 das (einzige) Outputgatter von Sn .
Nach Lemma 45 existiert ein Polynom p(n), so dass für alle n ≥ 0 und
a ∈ {0, 1}n gilt: Wenn a ∈ LF , dann existiert ein Beweisbaum für Sn und a
mit höchstens p(n) vielen Knoten.
Sei nun a = (a1 , a2 , . . . , an ) ∈ {0, 1}n eine Eingabe für S.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
145 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
uSAC1 ⊆ LOGCFL
Wir definieren eine Kodierung code(Sn , a) ∈ {0, 1, a, $, $∧ , $∨ , #}+ :
Für ein Gatter g ∈ {1, . . . , s(n)} mit λn (g ) = xi sei
code(g , a) = #ag $ai .
Für ein Gatter g ∈ {1, . . . , s(n)} mit λn (g ) = ¬, αn (g ) = h und
λn (h) = xi sei code(g , a) = #ag $(1 − ai ).
V
Für ein Gatter g ∈ {1, . . . , s(n)} mit λn (g ) = 2 und αn (g ) = h1 h2
sei code(g , a) = #ag $∧ ah1 $∧ ah2 .
W
Für ein Gatter g ∈ {1, . . . , s(n)} mit λn (g ) = k und
αn (g ) = h1 · · · hk sei code(g , a) = #ag $∨ ah1 $∨ ah2 $∨ · · · ahk .
Schließlich sei
code(Sn , a) =
µ s(n)
Y
g =1
Markus Lohrey (Universität Leipzig)
¶p(n)
#
code(g , a)
Schaltkreiskomplexität
WS 2009/2010
146 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
uSAC1 ⊆ LOGCFL
Definiere die Abbildung f : {0, 1}∗ → {0, 1, a, $, $∧ , $∨ , #}∗ durch:
f (w ) = code(Sn , w ), falls |w | = n.
Dann ist die Abbildung f logspace-berechenbar:
Die Abbildung 1n 7→ Sn ist logspace-berechenbar, da die
Schaltkreisfamilie F nach Annahme logspace-uniform ist.
Die Abbildung hSn , w i 7→ code(Sn , w ) ist offensichtlich auch
logspace-berechenbar.
Logspace-berechenbare Abbildungen sind unter Komposition
abgeschlossen.
Wir konstruieren nun einen festen Kellerautomaten P mit:
∀w ∈ {0, 1}∗ : w ∈ LF ⇐⇒ f (w ) ∈ L(P).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
147 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
uSAC1 ⊆ LOGCFL
Intuitiv gesprochen, versucht der Kellerautomat P einen Beweisbaum für
Sn und w ∈ {0, 1}n zu konstruieren.
P arbeitet wie folgt (das oberste Kellersymbol steht im folgenden immer
ganz rechts):
1
Zu Beginn schreibt P auf den Keller #a.
Beachte: 1 ist das Outputgatter von Sn , also legt P die Kodierung
des Outputgatters auf den Keller.
2
Nun macht P die folgenden Schritte (3)–(7) solange, bis der Keller
leer ist (dann akzeptiert P):
3
Laufe auf der Eingabe nicht-deterministisch zu einer Position, wo das
aktuelle Symbol # ist.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
148 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
uSAC1 ⊆ LOGCFL
4
Sei der aktuelle Kellerinhalt von der Gestalt · · · #ag und komme auf
′
dem Eingabeband ag x mit x ∈ {$, $∧ , $∨ } nach der aktuellen
Position.
Überprüfe, ob g = g ′ gilt (das kann ein Kellerautomat) und lehne ab,
falls g 6= g ′ .
Dabei wird (falls g = g ′ ) #ag vom Keller gepopt, und der
Eingabekopf wandert bis zur Position von x ∈ {$, $∧ , $∨ }
Intuition: P läuft zu einen Vorkommen von code(g , a), wobei g das
oberste Gatter auf dem Keller ist.
5
Falls x = $: Überprüfe, ob nach dem x eine 1 kommt.
Wenn nicht à Ablehnen
6
Falls x = $∧ : Sei $∧ ah1 $∧ ah2 # · · · der Inhalt des Eingabebandes ab
der aktuellen Position.
Pushe #ah1 #ah2 auf den Keller.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
149 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
uSAC1 ⊆ LOGCFL
7
Falls x = $∨ : Sei $∨ ah1 $∨ ah2 · · · $∨ ahk # · · · der Inhalt des
Eingabebandes ab der aktuellen Position.
Pushe nicht-deterministisch eines der Wörter #ahi (1 ≤ i ≤ k) auf
den Keller.
Bemerkungen:
Der Kellerautomat P kann auf dem Eingabeband nur von links nach
rechts laufen. Diese Einschränkung überwinden wir dadurch, dass wir
p(n) viele Kopien der Kodierung des Schaltkreises in code(Sn , a)
hintereinander schreiben.
p(n) viele Kopien reichen aus, da im Falle a ∈ LF ein Beweisbaum für
Sn und a mit höchstens p(n) vielen Knoten existiert.
Dies beendet den Beweis der Inklusion uSAC1 ⊆ LOGCFL.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
150 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Logspace-berechenbare Funktionen liegen in uSAC1
Für den Beweis der Inklusion LOGCFL ⊆ uSAC1 benötigen wir einige
Lemmata.
Nach Satz 18 gilt NL ⊆ uAC1 .
Eine Analyse des Beweises zeigt sofort, dass sogar NL ⊆ uSAC1 gilt.
Insbesondere gilt L ⊆ uSAC1 .
Das folgende Lemma verallgemeinert dies auf logspace-berechenbare
Funktionen.
Lemma 46
Sei f : {0, 1}∗ → {0, 1}∗ eine logspace-berechenbare Funktion mit der
Eigenschaft: |x| = |y | =⇒ |f (x)| = |f (y )|. Dann gilt f ∈ uSAC1 .
Beweis: Sei f : {0, 1}∗ → {0, 1}∗ eine logspace-berechenbare Funktion mit
der Eigenschaft: |x| = |y | =⇒ |f (x)| = |f (y )|.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
151 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Logspace-berechenbare Funktionen liegen in uSAC1
Sei ℓ : N → N definiert durch ℓ(n) = |f (0n )|.
Dann gilt ℓ(n) ∈ nO(1) und ℓ ist logspace-berechenbar (bei unärer
Kodierung von Zahlen).
Ausserdem gehört die Sprache
F = {1i 0w | w ∈ {0, 1}∗ , 1 ≤ i ≤ ℓ(|w |) und das i-te Bit von f (w ) ist 1}
zur Klasse L (Übung) und damit zu uSAC1 (nach obiger Bemerkung).
Sei F = (Sn )n≥0 eine uSAC1 -Schaltkreisfamilie mit LF = F .
Wir können damit einen uSAC1 -Schaltkreisfamilie zur Berechnung von f
bauen:
Der Schaltkreis für Eingabelänge n besteht aus jeweils einer Kopie des
Schaltkreises Sn+i+1 (1 ≤ i ≤ ℓ(n)), in dem die ersten i + 1
Eingabebits mit 01i belegt werden.
Das i-te Outputgatter (1 ≤ i ≤ ℓ(n)) ist das Outputgatter der Kopie
von Sn+i+1 .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
152 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Das folgende Lemma folgt sofort aus Lemma 46.
Lemma 47
∗
Wenn (CFL ∩ 2{0,1} ) ⊆ uSAC1 gilt, dann gilt auch LOGCFL ⊆ uSAC1 .
∗
Beweis: Angenommen es gilt (CFL ∩ 2{0,1} ) ⊆ uSAC1 .
Sei K ∈ LOGCFL.
Dann existiert eine logspace-berechenbare Funktion f : {0, 1}∗ → Σ∗ und
eine kontextfreie Sprache L ⊆ Σ∗ mit: x ∈ K ⇐⇒ f (x) ∈ L.
Sei Σ = {a1 , . . . , an } und ϕ : Σ∗ → {0, 1}∗ der Morphismus mit
ϕ(ai ) = 01i für 1 ≤ i ≤ n.
Indem wir L durch die kontextfreie Sprache ϕ(L) ⊆ {0, 1}∗ und f durch
die logspace-berechenbare Funktion ϕ ◦ f (erst f dann ϕ) ersetzen, können
∗
wir im folgenden davon ausgehen, dass L ∈ CFL ∩ 2{0,1} gilt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
153 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Die Funktion f : {0, 1}∗ → {0, 1}∗ muss nicht unbedingt die Eigenschaft
“|x| = |y | =⇒ |f (x)| = |f (y )|” haben; aber wir können diese Eigenschaft
wie folgt erzwingen:
Sei p(n) ein Polynom mit |f (x)| ≤ p(|x|) für alle x ∈ {0, 1}∗
(existiert, da f logspace-berechenbar ist).
Sei L′ = L01∗ (kontextfrei!) und f ′ (x) = f (x)01p(|x|)−|f (x)| für
x ∈ {0, 1}∗ (logspace-berechenbar!).
à (i) x ∈ K ⇐⇒ f ′ (x) ∈ L′ und (ii) |x| = |y | =⇒ |f ′ (x)| = |f ′ (y )|.
Nach Lemma 46 kann die Funktion f ′ durch uSAC1 -Schaltkreise berechnet
werden. Ausserdem kann die kontextfreie Sprache L′ nach Annahme durch
uSAC1 -Schaltkreise entschieden werden.
Hintereinanderschaltung dieser Schaltkreise liefert eine uSAC1 Schaltkreise
für die Sprache K .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
154 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Lemma 48 (Ruzzo; 1980)
Sei G = (N, Σ, S, P) eine kontextfreie Grammatik in Chomsky-Normalform
∗
und gelte A ⇒+
G s für A ∈ N und s ∈ (N ∪ Σ) mit |s| > 2. Dann existiert
+
eine Faktorisierung s = u1 vu2 und B ∈ N mit A ⇒+
G u1 Bu2 , B ⇒G v und
|v |, |u1 Bu2 | ≤ 98 · |s|.
Beweis:
Sei T ein Ableitungsbaum für die Ableitung A ⇒∗G s und sei n = |s|.
Da G in Chomsky-Normalform ist, ist T ein binärer Baum (falls wir die
mit Terminalsymbolen beschrifteten Blätter entfernen).
Für einen Knoten ν in T sei yield(ν) das Teilwort von s, dass entsteht,
wenn man die Blätter des in ν gewurzelten Teilbaums von T von links
nach rechts besucht.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
155 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Betrachte einen Pfad p in T mit den folgenden Eigenschaften:
p beginnt an der Wurzel von T und endet an einem Blatt.
Falls eine Kante (ν, ν1 ) von T zum Pfad p gehört und ν1 and ν2 die
Kinder von ν sind, dann gilt |yield(ν1 )| ≥ |yield(ν2 )|.
Sei ν der erste Knoten (von der Wurzel aus gezählt) auf dem Pfad p mit
yield(ν) ≤ 89 · n (existiert!).
Dann kann ν nicht die Wurzel von T sein; sei ν ′ der Elternknoten von ν.
Dann gilt yield(ν ′ ) >
8
9
· n.
Ausserdem kann ν kein Blatt von T sein:
Wäre ν ein Blatt von T , so würde gelten: |yield(ν)| = 1 und yield(ν ′ ) ≤ 2,
d. h. 2 ≥ yield(ν ′ ) > 98 · n, d. h. n < 89 · 2 < 3, ein Widerspruch zu n ≥ 3.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
156 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Sei ν mit dem Nichtterminal B ∈ N beschriftet und yield(ν) = v .
Also existiert eine Faktorisierung s = u1 vu2 mit
A ⇒+
G u1 Bu2 ,
B ⇒+
G v,
Wegen n > 2 und |v | ≥ |yield(ν ′ )|/2 >
4
9
8
· n.
9
· n gilt außerdem
|u1 Bu2 | = n − |v | + 1 < n −
Markus Lohrey (Universität Leipzig)
|v | ≤
4
8
· n + 1 ≤ · n.
9
9
Schaltkreiskomplexität
WS 2009/2010
157 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Beweis der Inklusion LOGCFL ⊆ uSAC1 in Satz 42:
∗
Wegen Lemma 47 genügt es zu zeigen: CFL ∩ 2{0,1} ⊆ uSAC1 .
Sei G = (N, {0, 1}, S, P) eine kontextfreie Grammatik, o.B.d.A. in
Chomsky-Normalform.
Wir V
konstruieren
W einen Schaltkreis Sn über der Basis
{¬, 2 } ∪ { n | n ≥ 2}, der L(G ) ∩ {0, 1}n erkennt.
Fixiere eine Eingabelänge n.
Im folgenden sei für eine Eingabe x = x1 x2 · · · xn mit x1 , . . . , xn ∈ {0, 1}:
x[i, j] = xi xi+1 · · · xj für 1 ≤ i ≤ j ≤ n
x[k + 1, k] = ε
x[i] = xi für 1 ≤ i ≤ n
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
158 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Definiere
A = {[m1 , n1 ]A1 [m2 , n2 ] · · · Ai [mi+1 , ni+1 ] | 0 ≤ i ≤ 3, A1 , . . . , Ai ∈ N,
1 ≤ m1 , ni+1 ≤ n,
mj ≤ nj + 1 (1 ≤ j ≤ i + 1),
nj + 1 < mj+1 (1 ≤ j ≤ i)}
Es gilt |A| ∈ O(n8 ).
Für w = [m1 , n1 ]A1 [m2 , n2 ] · · · Ai [mi+1 , ni+1 ] ∈ A sei
|w | = i +
i+1
X
j=1
(nj − mj + 1).
Wir fixieren nun eine Eingabe x ∈ {0, 1}n .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
159 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Wir interpretieren das Paar
(A, w ) = (A, [m1 , n1 ]A1 [m2 , n2 ] · · · Ai [mi+1 , ni+1 ]) ∈ N × A
als die Aussage A ⇒+
G x[m1 , n1 ]A1 x[m2 , n2 ] · · · Ai x[mi+1 , ni+1 ].
Wir schreiben dann valid(A, w ).
Beachte: Die Länge der Satzform x[m1 , n1 ]A1 x[m2 , n2 ] · · · Ai x[mi+1 , ni+1 ]
ist |w | (unabhängig von x).
Seien u, v ∈ A. Dann kann v in u eingesetzt werden, falls gilt:
u ist von der Form u1 [j, k]A[ℓ, m]u2 .
v ist von der Form [k + 1, k ′ ]s[ℓ′ , ℓ − 1] bzw. [k + 1, ℓ − 1].
Anzahl der Nichtterminale in u + Anzahl der Nichtterminale in v ≤ 4
Dann entsteht w = u1 [j, k ′ ]s[ℓ′ , m]u2 ∈ A bzw. w = u1 [j, m]u2 ∈ A durch
Ersetzen von A durch v in u, und wir schreiben dann (u, v ) ÃA w .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
160 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Ein Beweisbaum für (A0 , w0 ) ∈ N × A ist ein binärer Baum, dessen
Knoten mit Paaren aus N × A beschriftet sind, und für den gilt:
Die Wurzel ist mit (A0 , w0 ) beschriftet.
Ist ein innerer Knoten mit (A, w ) beschriftet so sind die beiden Kinder
mit Paaren (A, u) und (B, v ) beschriftet, wobei (u, v ) ÃB w gilt.
Jedes Blatt ist mit einem Paar (A, w ) beschriftet, wobei einer der
beiden folgenden Fälle gilt:
w = [k, k − 1]B[ℓ, ℓ − 1]C [m, m − 1] für Positionen
1 ≤ k < ℓ < m ≤ n + 1 und (A, BC ) ∈ P.
w = [k, k] für eine Position 1 ≤ k ≤ n mit (A, x[k]) ∈ P.
Offensichtlich gilt valid(A, w ), falls ein Beweisbaum für (A, w ) ∈ N × A
existiert.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
161 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Aber auch die Umkehrung (sogar eine Verschärfung davon) gilt:
Behauptung: Sei γ = 89 . Dann gilt valid(A, w ) genau dann, wenn ein
Beweisbaum der Höhe ≤ 2 · ⌈logγ (|w |)⌉ + 2 für (A, w ) existiert.
Beweis der Behauptung:
Es genügt zu zeigen: Wenn valid(A, w ), dann existiert ein Beweisbaum der
Höhe ≤ 2 · ⌈logγ (|w |)⌉ + 2 für (A, w ).
Sei w = [m1 , n1 ]A1 [m2 , n2 ] · · · Ai [mi+1 , ni+1 ] und gelte valid(A, w ), d. h.
A ⇒+
G x[m1 , n1 ]A1 x[m2 , n2 ] · · · Ai x[mi+1 , ni+1 ].
(3)
Wir zeigen durch Induktion über die Länge der Ableitung in (3):
Wenn i < 3, dann existiert für (A, w ) ein Beweisbaum der Höhe
≤ 2 · ⌈logγ (|w |)⌉ + 1.
Wenn i = 3, dann existiert für (A, w ) ein Beweisbaum der Höhe
≤ 2 · ⌈logγ (|w |)⌉ + 2.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
162 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
1. Fall: |w | = 1
Dann hat die Ableitung in (3) die Länge 1 und es muss w = [k, k] für eine
Position k mit (A, x[k]) ∈ P gelten.
Dann wählen wir als Beweisbaum einen Baum mit einem Knoten, der mit
(A, [k, k]) beschriftet ist.
Dieser Baum hat die Höhe 1 ≤ 2 · ⌈logγ (|w |)⌉ + 1.
2. Fall: |w | = 2
Dann hat die Ableitung in (3) die Länge ≤ 3.
Wir erhalten dann einen Beweisbaum für (A, w ) mit höchstens 3 Blättern,
der Höhe ≤ 3 hat.
Es gilt: 3 ≤ 2 · ⌈logγ (|w |)⌉ + 1.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
163 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Beispiel für den 2. Fall:
Sei w = [5, 6] und sei
A ⇒G BC ⇒G bC ⇒G bc
die Ableitung in (3), wobei b = x[5] und c = x[6].
Dann erhalten wir für (A, [5, 6]) den folgenden Beweisbaum:
(A, [5, 6])
(A, [5, 4]B[6, 6])
(A, [5, 4]B[6, 5]C [7, 6])
Markus Lohrey (Universität Leipzig)
(B, [5, 5])
(C , [6, 6])
Schaltkreiskomplexität
WS 2009/2010
164 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
3. Fall: |w | ≥ 3 und in w kommen genau 3 Nichtterminale vor, d. h.
w = [m1 , n1 ]A1 [m2 , n2 ]A2 [m3 , n3 ]A3 [m4 , n4 ].
Dann existiert eine Faktorisierung
x[m1 , n1 ]A1 x[m2 , n2 ]A2 x[m3 , n3 ]A3 x[m4 , n4 ] = y1 zy2
und ein Nichtterminal B, so dass gilt:
A ⇒+
G y1 By2 ,
B ⇒+
G z, und
in y1 By2 sowie z kommen jeweils nur 2 Nichtterminale vor.
Zu dieser Faktorisierung korrespondieren u, v ∈ A mit:
(u, v ) ÃB w = [m1 , n1 ]A1 [m2 , n2 ]A2 [m3 , n3 ]A3 [m4 , n4 ] und
in u und v kommen jeweils nur 2 Nichtterminale vor.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
165 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
+
Da die Ableitungen A ⇒+
G y1 By2 und B ⇒G z kürzer als die Ableitung (3)
sind, gibt es nach IH:
einen Beweisbaum T1 für (A, u) der Höhe ≤ 2 · ⌈logγ (|u|)⌉ + 1 und
einen Beweisbaum T2 für (B, v ) der Höhe ≤ 2 · ⌈logγ (|v |)⌉ + 1.
Es gilt ausserdem |w | = |u| + |v | − 1.
Wir erhalten dann einen Beweisbaum T für (A, w ) indem wir eine neue
mit (A, w ) beschriftete Wurzel hinzufügen, deren linker (bzw. rechter)
Teilbaum T1 (bzw. T2 ) ist.
Die Höhe von T können wir wie folgt abschätzen, wobei o.B.d.A. |u| ≥ |v |:
Höhe(T ) = 1 + max{Höhe(T1 ), Höhe(T2 )}
≤ 1 + 2 · ⌈logγ (|u|)⌉ + 1
= 2 · ⌈logγ (|u|)⌉ + 2
≤ 2 · ⌈logγ (|w |)⌉ + 2 (da |u| = |w | − |v | + 1 ≤ |w |)
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
166 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
4. Fall: |w | ≥ 3 und in w kommen höchstens 2 Nichtterminale vor.
Wegen Lemma 48 existiert eine Faktorisierung
x[m1 , n1 ]A1 x[m2 , n2 ] · · · Ai x[mi+1 , ni+1 ] = y1 zy2
und ein Nichtterminal B, so dass gilt:
A ⇒+
G y1 By2 ,
B ⇒+
G z, und
|y1 By2 |, |z| ≤
8
9
· |x[m1 , n1 ]A1 x[m2 , n2 ] · · · Ai x[mi+1 , ni+1 ]| =
8
9
· |w |.
Zu dieser Faktorisierung korrespondieren u, v ∈ A mit:
(u, v ) ÃB w und
|u|, |v | ≤
8
9
· |w |.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
167 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
+
Da die Ableitungen A ⇒+
G y1 By2 und B ⇒G z kürzer als die Ableitung (3)
sind, gibt es nach IH:
einen Beweisbaum T1 für (A, u) der Höhe ≤ 2 · ⌈logγ (|u|)⌉ + 2 und
einen Beweisbaum T2 für (B, v ) der Höhe ≤ 2 · ⌈logγ (|v |)⌉ + 2.
Wir erhalten einen Beweisbaum T für (A, w ) wie in Fall 3.
Die Höhe von T können wir wie folgt abschätzen:
Höhe(T ) = 1 + max{Höhe(T1 ), Höhe(T2 )}
≤ 1 + 2 · ⌈logγ (8/9 · |w |)⌉ + 2
= 1 + 2 · ⌈logγ (|w |) − 1⌉ + 2
= 2 · ⌈logγ (|w |)⌉ + 1
Dies beendet den Beweis der Behauptung.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
168 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Wir können nun den Schaltkreis für Eingabelänge n wie folgt konstruieren.
Die Menge der Gatter ist eine Obermenge von
V = {((A, w ), i) | (A, w ) ∈ N × A, 0 ≤ i ≤ 2 · ⌈logγ (n)⌉ + 2}.
Sei ((A, w ), i) ∈ V . Wir setzen:
1
Falls w = [k, k − 1]B[ℓ, ℓ − 1]C [m + 1, m] für 1 ≤ k < ℓ ≤ m ≤ n
und (A, BC ) ∈ P oder w = [k, k] für ein k mit (A, x[k]) ∈ P:
((A, w ), i) = 1
2
Falls die Bedingung in (1) nicht zutrifft und i ≥ 1:
_
((A, u), i − 1) ∧ ((C , v ), i − 1)
((A, w ), i) =
(u,v )ÃC w
3
((A, w ), i) = 0 in allen anderen Fällen.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
169 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
LOGCFL ⊆ uSAC1
Wir V
erhaltenWso eine Schaltkreisfamilie F über der Basis
{¬, 2 } ∪ { n | n ≥ 2} mit:
depthF ∈ O(log(n)) und sizeF ∈ O(n16 log(n))
F ist in Negationsnormalform.
Bei Eingabe x wertet sich das Gatter ((A, w ), i) zu 1 aus, g.d.w. es
einen Beweisbaum der Tiefe ≤ i für (A, w ) bei Eingabe x gibt.
F ist logspace-uniform (ist ziemlich offensichtlich).
Definieren wir das Gatter ((S, [1, n]), 2 · ⌈logγ (n)⌉ + 2) als das einzige
Ausgabegatter, so akzeptiert die resultierende Schaltkreisfamilie genau die
Sprache L(G ).
Dies beendet den Beweis von Satz 42.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
170 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Eine härteste kontextfreie Sprache
Im Beweis der Inklusion uSAC1 ⊆ LOGCFL hatten wir eine feste
kontextfreie Sprache L(P) ⊆ {0, 1, a, $, $∧ , $∨ , #}+ definiert mit:
∀K ∈ uSAC1 : K ≤log
m L(P).
Wegen uSAC1 = LOGCFL gilt also:
∀K ∈ CFL : K ≤log
m L(P).
Man sagt auch: L(P) ist eine härteste kontextfreie Sprache.
Eine solche wurde zuerst von Greibach 1973 konstruiert.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
171 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Die Klasse SAC1 birgt eine Asymmetrie in sich: UND-Gatter müssen
Eingangsgrad 2 haben, ODER-Gatter haben unbeschränkten Eingangsgrad.
Aus dem folgenden Satz folgt, dass wir die gleiche Klasse von Sprachen
erhalten, wenn wir den Eingangsgrad von ODER-Gattern auf 2
beschränken und UND-Gatter von beliebigen Eingangsgrad erlauben.
Satz 49 (Borodin, Cook, Dymond, Ruzzo, Tompa 1989)
Die Klassen SAC1 und uSAC1 (und damit auch LOGCFL) sind unter
Komplement abgeschlossen.
Für den Beweis von Satz 49 benötigen wir ein Lemma.
Zur Erinnerung: Die Schwellenwertfunktion Tkn (0 ≤ k ≤ n, n ≥ 1) ist:
(
Pn
1 falls
n
i=1 xi ≥ k
Tk (x1 , . . . , xn ) =
0 sonst
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
172 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Lemma 50
Für alle 0 ≤ k ≤ n gilt: Tkn kann durch einen
der Größe nO(1)
W
V Schaltkreis
und Tiefe O(log(n)) über der Basis {0, 1, 2 } ∪ { m | m ≥ 2} berechnet
werden.
Beweis: Der Schaltkreis ergibt sich aus der folgenden Rekursion:
T01 (x1 ) = 1
T11 (x1 ) = x1
Tkn (x1 , . . . , xn ) = 0 falls k > n
Tkn (x1 , . . . , xn ) =
k
_
j=0
Markus Lohrey (Universität Leipzig)
⌊n/2⌋
Tj
⌈n/2⌉
(x1 , . . . , x⌊n/2⌋ ) ∧ Tk−j (x⌊n/2⌋+1 , . . . , xn )
falls n ≥ 2 und k ≤ n.
Schaltkreiskomplexität
WS 2009/2010
173 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Beweis von Satz 49:
Sei F = (S
W Schaltkreisfamilie in Negationsnormalform über der
Vn )n≥0 eine
Basis {¬, 2 } ∪ { n | n ≥ 2} mit sizeF ∈ nO(1) und depthF ∈ O(log(n)).
Wir erweitern jeden Schaltkreis Sn um weitere Gatter, mit denen sich dann
das Komplement der Sprache LF entscheiden lässt.
Fixiere Eingabelänge n; s = Anzahl der Gatter von Sn , d = Tiefe von Sn .
Schritt 1: Wir wandeln Sn in einen äquivalenten Schaltkreis Tn um mit:
1 T besteht aus 2d + 1 vielen Schichten L , . . . , L
n
0
2d .
2 Die Eingänge eines Gatters aus L mit i ≥ 1 liegen in L
i
i−1 .
3 L besteht aus allen Eingabegattern und negierten Eingabegattern,
0
L2d besteht aus Gattern mit Ausgangsgrad 0, zu diesen gehört auch
das Outputgatter.
4 |L | = s für alle i ∈ {1, . . . , 2d}
i
5 In L
2i (L2i−1 ) liegen nur UND-Gatter (ODER-Gatter) für i ≥ 1.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
174 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Für alle 1 ≤ i ≤ 2d liegt in Li genau eine Kopie von jedem Gatter aus Sn .
V W
Die Markierung ( 2 , m ) solcher Gatter ergibt sich aus Forderung (5).
L0 besteht aus den originalen Eingabegattern und negierten
Eingabegattern von Sn . O.B.d.A. sind dies genau 2n viele.
Die Verdrahtung in Tn ist wie folgt:
Ist v ∈ Li eine Kopie eines Eingabegatters g oder eines negierten
Eingabegatters g für i ≥ 1 so sind alle Eingänge von v gleich der
Kopie von g aus Li−1 (wir kopieren den Wahrheitswert).
Ist v ∈ Li eine Kopie eines UND-Gatters (bzw. ODER-Gatters) g mit
i ≥ 3 ungerade (bzw. i ≥ 2 gerade), so sind alle Eingänge von v
gleich der Kopie von g aus Li−1 (wir kopieren den Wahrheitswert).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
175 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Ist v ∈ L1 eine Kopie eines UND-Gatters, so sind die Eingänge von v
bliebige Gatter aus L0 .
Ist v ∈ Li eine Kopie eines UND-Gatters (bzw. ODER-Gatters) g mit
i ≥ 2 gerade (bzw. i ≥ 3 ungerade oder (i = 1 und in Sn sind alle
Eingänge von g (evtl. negierte) Eingabegatter)), so sind die Eingänge
von v die Kopien der Eingänge von g in Sn aus Li−1 .
Ist v ∈ L1 eine Kopie eines ODER-Gatters g und sind in Sn nicht alle
Eingänge von g Eingabegatter oder negierte Eingabegatter, so sind
die Eingänge von v bliebige Gatter aus L0 .
Dann kann man leicht durch Induktion über i zeigen: Sei 0 ≤ i ≤ d und
sei g ein Gatter aus Sn , so dass i die maximale Länge eines Pfades in Sn
von einem Eingabegatter oder negierten Eingabegatter zu g ist. Sei v ∈ Lk
eine Kopie von g mit k ≥ 2i. Dann wertet sich v in Tn zum gleichen
Wahrheitswert wie g in Sn aus.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
176 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
In der weiteren Konstruktion werden Schwellenwertgatter zum Schaltkreis
hinzugefügt. Diese werden am Ende mittels Lemma 50 eliminiert.
Schritt 2: Für 0 ≤ i ≤ d und eine Eingabe x ∈ {0, 1}n sei
Ei (x) = {v ∈ L2i | v wertet sich bei Eingabe x zu 1 aus}.
Wir fügen nun für alle Gatter v ∈
Gatter v c zu Tn hinzu.
S2d
i=1 Li
aus Tn und alle 0 ≤ c ≤ s ein
Falls v ∈ L2k mit k ≥ 1 (d. h. v ist ein UND-Gatter) und
v0 , v1 ∈ L2k−1 die Eingänge von v sind, dann ist v c ein ODER-Gatter
mit den Eingängen v0c und v1c .
Falls v ∈ L2k−1 mit k ≥ 1 (d. h. v ist ein ODER-Gatter), und sind
v1 , . . . , vm ∈ L2k−2 die Eingänge von v , dann ist v c ein Tc∗ -Gatter mit
den Eingängen L2k−2 \ {v1 , . . . , vm }.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
177 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Wir fixieren im folgenden eine Eingabe x für Tn .
Behauptung 1: Sei v ∈ L2i ∪ L2i−1 ein Gatter aus Tn mit i ≥ 1 und
c = |Ei−1 (x)|. Dann berechnet v c die Negation von v .
Fall 1: v ∈ L2i−1 , v ist also ein ODER-Gatter.
Seien v1 , . . . , vm die Eingänge von v und sei R2i−2 = L2i−2 \ {v1 , . . . , vm }
(die Menge der Eingänge von v c ).
Dann gilt:
v wertet sich zu 0 aus
Markus Lohrey (Universität Leipzig)
⇐⇒
v1 , . . . , vm werten sich zu 0 aus
⇐⇒
mindestens c Gatter aus R2i−2
werten sich zu 1 aus
⇐⇒
v c wertet sich zu 1 aus
Schaltkreiskomplexität
WS 2009/2010
178 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Fall 2: v ∈ L2i , v ist also ein UND-Gatter.
Seien v0 , v1 ∈ L2i−1 die Eingänge von v .
Dann gilt:
v c wertet sich zu 1 aus
⇐⇒
v0c oder v1c wertet sich zu 1 aus
⇐⇒
Fall 1
v0 oder v1 wertet sich zu 0 aus
⇐⇒
v wertet sich zu 0 aus
Sei Tn′ der Schaltkreis, der sich nach Schritt 2 aus Tn ergibt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
179 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Für 0 ≤ i ≤ d sei ℓi = |L2i |, d. h. ℓ0 = 2n und ℓi = s für 1 ≤ i ≤ d.
Schritt 3: Für alle 0 ≤ i < d und alle 0 ≤ c ≤ ℓi fügen wir ein Gatter hic
mit folgender Verdrahtung zu Tn′ hinzu:
(
1 falls c = n
h0c =
0 falls c 6= n
Um hic für i ≥ 1 zu definieren, benötigen wir einige Hilfsgatter:
γic ist ein Tcs -Gatter mit L2i als Menge der Eingänge.
Für alle 0 ≤ j ≤ s sei ηic,j ein Tcs -Gatter, dessen Eingänge alle Gatter
v j mit v ∈ L2i sind.
Dann ist
ℓi−1
hic
=
_
j=0
j
∧ γic ∧ ηis−c,j ).
(hi−1
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
(4)
WS 2009/2010
180 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Behauptung 2: Für alle 0 ≤ i < d und alle 0 ≤ c ≤ ℓi gilt:
hic = 1 ⇐⇒ |Ei (x)| = c.
Beweis durch Induktion über i.
IA: i = 0: Da sich in L0 genau n Eingabegatter und n negierte
Eingabegatter befinden, gilt |E0 (x)| = n und damit die Behauptung.
IS: Sei i ≥ 1.
j
Nach IH gilt für alle 0 ≤ j ≤ ℓi−1 : hi−1
= 1 ⇐⇒ |Ei−1 | = j.
Sei j = |Ei−1 |. Dann kann sich in der Disjunktion in (4) nur der Term für
j = |Ei−1 | zu 1 auswerten.
Also gilt: hic = 1 ⇐⇒ γic = ηis−c,j = 1.
Nach Behauptung 1 gilt für j = |Ei−1 |: Für alle v ∈ L2i wertet sich v j zur
Negation von v aus.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
181 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Also gilt γic = ηis−c,j = 1 genau dann, wenn sich
in L2i mindestens c Gatter zu 1 auswerten und sich
in L2i mindestens s − c Gatter zu 0 auswerten.
Dies ist äquivalent dazu, dass sich in L2i genau c Gatter zu 1 auswerten,
d. h. |Ei (x)| = c.
Sei Tn′′ der Schaltkreis, der sich nach Schritt 3 aus Tn′ ergibt.
Schritt 4: Wir fügen schließlich zu Tn′′ ein neues Ausgabegatter o hinzu.
Sei v ∈ L2d das Ausgabegatter von Tn . Dann sei
o=
s
_
c=0
c
(hd−1
∧ v c ).
Nach Behauptung 1 und 2 wertet sich damit o zur Negation von v aus.
Also akzeptiert der resultierende Schaltkreis Tn′′′ das Komplement der von
Tn (bzw. Sn ) akzeptierten Sprache.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
182 / 195
Kontextfreie Sprachen und semibeschränkte Schaltkreise
Abschluss unter Komplement
Die Schaltkreisfamilie (Tn′′′ )n≥0 hat polynomielle Größe und logarithmische
Tiefe.
Bisher hatten alle neuen UND-Gatter Eingangsgrad 2.
Beachte: Auf jedem Pfad in Tn′′′ von einem (evtl. negierten) Eingabegatter
zum Outputgatter liegen höchstens 2 Schwellenwertgatter.
Wir können daher alle Schwellenwertgatter mittels Lemma 50 eliminieren
und erhalten so eine SAC1 -Schaltkreisfamilie für das Komplement von LF .
Dies zeigt, dass SAC1 unter Komplement abgeschlossen ist.
Ist F logspace-uniform, so ist auch unsere konstruierte Schaltkreisfamilie
logspace-uniform: alle Transformationsschritte sind durch
logspace-Transducer durchführbar.
Dies zeigt, dass auch uSAC1 = LOGCFL unter Komplement abgeschlossen
ist.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
183 / 195
Polynomielle Schaltkreise
USIZEDEPTH(nO(1) , ∗, Bool) = P
Bisher haben wir Schaltkreisfamilien mit einer polynomiellen
Größenfunktion und höchstens logarithmisch wachsenden Tiefenfunktion
betrachtet.
Letztere Einschränkung wollen wir nun aufgeben, wir wollen also die
Klassen SIZEDEPTH(nO(1) , ∗, Bool) und USIZEDEPTH(nO(1) , ∗, Bool)
betrachten (für diese Klassen macht es keinen Unterschied, ob wir Bool
oder Bool2 als Basis verwenden).
Satz 51
USIZEDEPTH(nO(1) , ∗, Bool) = P (deterministische Polynomialzeit)
Beweisskizze:
USIZEDEPTH(nO(1) , ∗, Bool) ⊆ P: klar, denn wir können für eine Eingabe
x zunächst in logarithmischen Platz den Schaltkreis für Eingabelänge |x|
konstruieren, und diesen dann in Polynomialzeit bei Eingabe x auswerten.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
184 / 195
Polynomielle Schaltkreise
USIZEDEPTH(nO(1) , ∗, Bool) = P
P ⊆ USIZEDEPTH(nO(1) , ∗, Bool): Dies ist im wesentlichen der Beweis
dafür, dass das Circuit-Value Problem (Auswerten eines gegebenen
Booleschen Schaltkreis für eine gegebene Eingabebelegung) P-schwierig
ist; siehe Folien für die Vorlesung Strukturelle Komplexitätstheorie.
In diesem Beweis wird zu jeder Sprache L ∈ P eine logspace-berechenbare
Funktion f angegeben, die für eine Eingabe x einen Schaltkreis f (x)
(dessen Eingabegatter alle mit konstanten Wahrheitswerten belegt sind)
liefert mit: x ∈ L ⇐⇒ f (x) wertet sich zu 1 aus.
Macht man die n Bits in der Eingabe x ∈ {0, 1}∗ zu variablen
Eingabegattern des Schaltkreises, so erhält man einen Schaltkreis, der nur
von der Länge |x| abhängt.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
185 / 195
Polynomielle Schaltkreise
Die Klasse P/poly
Um die Klasse SIZEDEPTH(nO(1) , ∗, Bool) mittels Turingmaschinen zu
charakterisieren, benötigen wir die folgende Definition:
L ⊆ {0, 1}∗ gehört zur Klasse P/poly falls folgendes existiert:
Eine Famile (an )n≥0 von Wörtern an ∈ {0, 1}∗ , so dass ein Polynom
p(n) existiert mit |an | ≤ p(n).
Eine deterministische Polynomialzeitmaschine M mit:
∀x ∈ {0, 1}∗ : x ∈ L ⇐⇒ M akzeptiert hx, a|x| i.
Satz 52
SIZEDEPTH(nO(1) , ∗, Bool) = P/poly
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
186 / 195
Polynomielle Schaltkreise
SIZEDEPTH(n
O(1)
, ∗, Bool) = P/poly
Beweis:
SIZEDEPTH(nO(1) , ∗, Bool) ⊆ P/poly:
Sei L ∈ SIZEDEPTH(nO(1) , ∗, Bool).
Sei F = (Sn )n≥0 eine Schaltkreisfamilie über der Basis Bool mit:
(i) LF = L und (ii) sizeF ∈ nO(1) .
Sei an eine“vernünftige” Kodierung der Schaltkreises Sn als Bitstring.
Dann gilt |an | ∈ nO(1) .
Ausserdem kann eine deterministische Polynomialzeitmaschine anhand von
an den Schaltkreis Sn auf einer Eingabe x ∈ {0, 1}n auswerten.
Also gilt L ∈ P/poly.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
187 / 195
Polynomielle Schaltkreise
SIZEDEPTH(n
O(1)
, ∗, Bool) = P/poly
P/poly ⊆ SIZEDEPTH(nO(1) , ∗, Bool):
Sei L ∈ P/poly.
Also existiert eine Familie (an )n≥0 von Bitstrings, ein Polynom p(n) und
eine deterministische Polynomialzeitmaschine M mit:
(i) |an | ≤ p(n) und (ii) x ∈ L ⇐⇒ hx, a|x| i ∈ L(M).
O.B.d.A. sei |an | = p(n) für alle n ≥ 0.
Nach Satz 51 existiert eine (logspace-uniforme) Schaltkreisfamilie
F = (Sn )n≥0 mit polynomieller Größenfunktion und:
hx, a|x| i ∈ L(M) ⇐⇒ hx, a|x| i wird von S|x|+p(|x|) akzeptiert.
Wir erhalten also eine Schaltkreisfamilie mit polynomieller Größenfunktion,
welche L akzeptiert, indem wir im Schaltkreis Sn+p(n) die letzten p(n)
vielen Eingabebits mit dem Bitstring an belegen.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
188 / 195
Polynomielle Schaltkreise
Polynomielle Schaltkreise und NP
Nach Satz 51 ist P 6= NP äquivalent zu:
Vermutung
Wenn A NP-vollständig ist, dann gilt A 6∈ USIZEDEPTH(nO(1) , ∗, Bool).
Folgende stärkere Aussage wird vermutet:
Vermutung
Wenn A NP-vollständig ist, dann gilt A 6∈ SIZEDEPTH(nO(1) , ∗, Bool).
Razborov konnte 1985 eine Abschwächung dieser Vermutung für
monotone Schaltkreise (keine Negation) beweisen.
2
Sei CLIQUEn,k : {0, 1}n → {0, 1} (k ≤ n) die Boolesche Funktion, so
dass für jeden Graphen G = (V , E ) mit n Knoten gilt:
CLIQUEn,k (adj(G )) = 1 ⇐⇒ ∃U ⊆ V : |U| ≥ k ∧ ∀u, v ∈ U : (u, v ) ∈ E .
Hierbei ist adj(G ) die Adjazenzmatrix von G .
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
189 / 195
Polynomielle Schaltkreise
Polynomielle Schaltkreise und NP
Beachte: CLIQUEn,k ist eine monotone Funktion, d.h. werden Bits in der
Eingabe von 0 auf 1 gesetzt, so kann die Ausgabe nicht von 1 auf 0
wechseln.
Satz 53 (Razborov 1985)
S
V W
O(1) , ∗, {
√
n≥1 CLIQUEn, 4 n 6∈ SIZEDEPTH(n
2 , 2 })
Dieser Satz wird (manchmal) in der Vorlesung Strukturelle
Komplexitätstheorie bewiesen.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
190 / 195
Polynomielle Schaltkreise
Die Klasse BPP
Eine Sprache L gehört zur Klasse BPP, falls eine randomisierte
Turingmaschine M (siehe Folien zur Vorlesung Strukturelle
Komplexitätstheorie) mit folgenden Eigenschaften existiert:
M ist polynomiell zeitbeschränkt.
Wenn x ∈ L, dann gilt Prob[M akzeptiert x] ≥ 34 .
Wenn x 6∈ L, dann gilt Prob[M akzeptiert x] ≤
1
4
Bemerkungen:
Offensichtlich gilt P ⊆ BPP.
Es gibt durchaus Indizien für P = BPP: Impagliazzo und Wigderson
konnten P = BPP zeigen unter der Hypothese, dass es ein ε > 0 und
eine Sprache L ∈ DTIME(2O(n) ) \ SIZEDEPTH(2ǫ·n , ∗, Bool) gibt
Es ist nicht klar, wie BPP und NP zueinander liegen.
Es ist auch nicht klar, ob BPP vollständige Probleme hat.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
191 / 195
Polynomielle Schaltkreise
BPP ⊆ P/poly
Vollständige Derandomisierung geht auf Kosten von Nicht-Uniformität:
Satz 54 (Adelmann 1978)
BPP ⊆ P/poly
Beweis: Sei L ∈ BPP.
Sei M eine randomisierte Turingmaschine für L wie in der Definition von
BPP gefordert.
Fixiere eine Eingabelänge n.
Wir konstruieren einen Schaltkreis für L ∩ {0, 1}n mittels der
probabilistischen Methode:
D.h. wir konstruieren einen Schaltkreis S durch ein Zufallsexperiment und
zeigen, dass der resultierende Schaltkreis mit Wahrscheinlichkeit > 0 die
Sprache L ∩ {0, 1}n akzeptiert.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
192 / 195
Polynomielle Schaltkreise
BPP ⊆ P/poly
Das Zufallsexperiment zur Konstruktion des Schaltkreises S:
Wähle gleichverteilt und unabhängig voneinander m = 12(n + 1) viele
Bitstrings r1 , . . . , rm ∈ {0, 1}p(n) , wobei p(n) die Länge der
Zufallsstrings für M bei einer Eingabe der Länge n ist.
Konstruiere nun (durch Anwendung von Satz 51) polynomiell große
Schaltkreise S1 , . . . , Sm mit:
∀x ∈ {0, 1}n : valSi (x) = 1 ⇐⇒ M(x, ri ) = 1.
S gibt eine 1 aus, g.d.w. wenn valSi (x) = 1 für mehr als die Hälfte
aller i ∈ {1, . . . , m} gilt.
Ein Zufallststring r ∈ {0, 1}p(n) ist schlecht für x ∈ {0, 1}n , falls
M(x, r ) 6= χL (x), ansonsten ist er gut für x.
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
193 / 195
Polynomielle Schaltkreise
BPP ⊆ P/poly
Behauptung: Die Wahrscheinlichkeit, dass für alle x ∈ {0, 1}n mehr als
die Hälfte aller zufällig gewählten ri (1 ≤ i ≤ m) gut ist, ist ≥ 12 .
Für jedes x ∈ {0, 1}n ist die Wahrscheinlichkeit px , dass ein zufällig
gewähltes r ∈ {0, 1}p(n) schlecht ist, ist nach Definition von BPP
höchstens 41 .
Nun benötigen wir die Chernoff-Schranke:
Chernoff-Schranke
Seien B1 , . . . , Bm unabhängige Zufallsvariablen mit Prob[Bi = 1] = p und
Prob[Bi = 0] = 1 − p für alle 1 ≤ i ≤ m. Sei B = B1 + · · · + Bm . Dann
gilt für alle 0 ≤ θ ≤ 1:
Prob[B ≥ (1 + θ)pm] ≤ e −
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
θ2
pm
3
.
WS 2009/2010
194 / 195
Polynomielle Schaltkreise
BPP ⊆ P/poly
Fixiere eine Eingabe x ∈ {0, 1}n und wende die Chernoff-Schranke an mit:
Bi = 1 g.d.w. ri ist schlecht für x, d. h. B ist die Anzahl der für x
schlechten ri .
p = px ≤ 14 .
θ, so dass (1 + θ)pm =
Dann gilt
θ2
3p
=
(1−2p)2
12p
Prob[B ≥
≥
m
2,
1
12
d. h. θ =
1−2p
2p
und damit:
m
θ2
1
m
] ≤ e − 3 pm ≤ e − 12 = e −(n+1) < n+1 .
2
2
Dies gilt für jede Eingabe x ∈ {0, 1}n und es gibt 2n viele x ∈ {0, 1}n .
Also ist die Wahrscheinlichkeit, dass es ein x ∈ {0, 1}n gibt, für das
1
= 12 beschränkt.
mindestens die Hälfte aller ri schlecht ist, durch 2n · 2n+1
Dies beendet den Beweis der Behauptung und damit den Beweis des
Satzes von Adelmann (und damit die Vorlesung).
Markus Lohrey (Universität Leipzig)
Schaltkreiskomplexität
WS 2009/2010
195 / 195


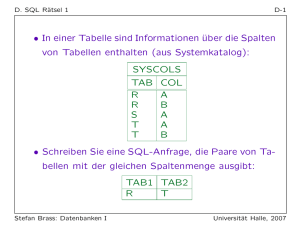







![Aufgabenblatt 9 Aufgabe 1 [Cournot–Gleichgewicht und Kooperation]](http://s1.studylibde.com/store/data/001957943_1-2e6d359103c4b453dc7370242c782f0d-300x300.png)