Herstellung mikromorpher Solarzellen - Ruhr

RUHR-UNIVERSITÄT BOCHUM
Analyse und Optimierung von
Plasmaquellen mittels Simulation:
Herstellung mikromorpher Solarzellen
Stephan Danko
Dissertation zur Erlangung des Grades eines
Doktor-Ingenieurs der Fakultät für Elektrotechnik
und Informationstechnik an der Ruhr-Universität Bochum
Bochum 2014
Dissertation eingereicht am: 9. April 2014
Tag der mündlichen Prüfung: 20. Juni 2014
Referent: Prof. Dr. Ralf Peter Brinkmann
Korreferent: Prof. Dr. Peter Awakowicz
Kurzfassung
Mit der von der neuen Bundesregierung Ende 2012 angekündigten Kürzung im Rahmen des Energie-Einspeise-Gesetzes (EEG) nimmt der Druck auf die Photovoltaikindustrie weiter zu. Insbesondere Dünnschicht-Silizium-Photovoltaikmodule haben
seit dem Preisverfall von hochreinem monokristallinem Silizium für wafer-basierte
Siliziumsolarzellen einen schweren Stand und können nur schwer mit diesen Modulen
konkurrieren. Ein entscheidender Grund dafür sind die niedrigeren Wirkungsgrade
bei zwar geringeren, aber nicht ausreichend niedrigen Kosten. Um weiter eine Rolle am Markt zu spielen, müssen die Herstellungskosten weiter gesenkt werden. In
dieser Arbeit wird die Abscheidung dünner Siliziumfilme mittels Niedertemperaturplasmen, der zentrale Produktionsschritt von Dünnschicht-Silizium-Solarzellen,
numerisch untersucht und optimiert. Dieser Schritt hat das größte Kostensenkungspotenzial bei der Fertigung solcher Solarzellen. Es besteht einerseits Bedarf an einer optimierten Materialausnutzung. Andererseits müssen höhere Abscheideraten zu
kürzeren Taktzeiten führen, die deutliche Einsparungen mit sich bringen.
Für die numerische Abbildung des Plasma-unterstützten Abscheideprozesses wird
ein allgemeingültiges globales Modell entwickelt. Mit diesem Modell können die Plasmazusammensetzung, Gasausnutzung und Abscheiderate abhängig von den Prozessparametern, dem Prozessgas und der Reaktorgeometrie in weniger als 30 s berechnet
werden.
In einem ersten Schritt erfolgt eine Validierung und Potenzialeinschätzung des globalen Modellansatzes im Vergleich mit alternativen Simulationsansätzen und experimentellen Messungen anhand einer nicht-beschichtenden Edelgasentladung (Argon).
Der simulative Vergleich bescheinigt dem entwickelten Modell quantitativ gute Er-
ii
Kurzfassung
gebnisse bei stark reduzierten Rechenzeiten. Darüber hinaus wird eine gute Übereinstimmung zwischen Simulation und Experiment erreicht.
In einem zweiten Schritt wird die beschichtende Silan-Wasserstoff-Entladung, wie sie
für die Solarzellenfertigung verwendet wird, untersucht. Die Modellergebnisse werden mit experimentellen Messungen verglichen und der Zusammenhang zwischen
Plasmaprozessbedingungen und der resultierenden Plasmazusammensetzung wird
analysiert.
Es wird eine Korrelation zwischen der Plasmazusammensetzung und der damit einhergehenden Schichteigenschaften abgeleitet. Darauf basierend erfolgt eine Optimierung des Abscheideprozesses hinsichtlich guter Schichteigenschaften bei hohen
Abscheideraten. Diese zeigt, dass ein hoher Prozessdruck zu hohen Abscheideraten
führt, wenn ausreichend Leistung zur Verfügung gestellt wird. In dem prognostizierten Prozessfenster mit einem Druck von 500 Pa, einer Leistungsdichte von 1.3 W/cm2
und einer Silankonzentration von 10 % können gute Schichten mit einer Rate von
4 nm/s abgeschieden werden. Diese Bedingungen werden im öffentlich geförderten
Projekt Quick µc-Si experimentell erfolgreich umgesetzt.
Abstract
Due to the announced cuts within the energy feed-in law by the German Government at the end of 2012, the pressure on the photovoltaics industry has increased
further. Thin-film-silicon photovoltaic modules have an especially difficult market
standing since the decline in prices of high-purity monocrystalline silicon for waferbased silicon solar cells. They can hardly compete against this technology. On one
hand, the thin film silicon solar cells have lower efficiencies in comparison to waferbased cells. On the other hand, costs of thin film cells are lower, but still not low
enough. In order to continue to play a role in the market, production costs have to
be further decreased. The deposition of thin silicon films by low-temperature plasma
processes is the main production step of thin film silicon solar cells. In the present
work, this step is studied numerically and optimized. It has the highest potential for
cost-cutting among the other production steps. Within the industry, there is a need
in optimizing the material depletion. However, higher deposition rates, that lead to
a shorter cycle time and consequently to considerable savings, must be reached.
A general global model is developed for the numerical representation of the plasmaassisted deposition process. With this model plasma composition, gas depletion, and
deposition rate can be calculated as a function of process parameter, process gas,
and reactor geometry within less than 30 s.
In the first step, a validation and interpretation of potentials of the global model
in comparison to alternative simulation methods and experimental measurements
is performed by means of an inert gas discharge (argon). The comparison reveals
favorable results within strongly reduced calculation times. Furthermore, agreement
between simulation and experiment is reached.
iii
iv
ABSTRACT
In the second step, the silane-hydrogen discharge, as used for the solar cell production, is studied. The model results are compared with experiments and the correlation between process conditions and the resulting plasma composition is analyzed.
A correlation between plasma composition and film properties is deduced. Based
thereon an optimization of the deposition process concerning good film properties
at high deposition rates is performed. Results show high deposition rates at high
process pressure while sufficient power is provided. In the process window with a
pressure of 500 Pa and a power density of 1.3 W/cm2 , a silane concentration of
10 % leads to high-quality films at a rate of 4 nm/s. These conditions are realized
successfully in experiments within the public founded project Quick µc-Si.
Inhaltsverzeichnis
Kurzfassung
i
Abstract
iii
1 Einleitung
1.1 Der globale Photovoltaikmarkt . . . . . . . . . . .
1.2 Herausforderungen von mikromorphen Solarzellen
1.3 Zielsetzung der Arbeit . . . . . . . . . . . . . . .
1.4 Simulation von Silan-Wasserstoff-Plasmen . . . .
.
.
.
.
1
1
3
4
6
.
.
.
.
.
9
9
11
15
20
21
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Technologische Grundlagen zur Abscheidung von a-Si:H/µc-Si:H
2.1 Mikromorphe Solarzellen . . . . . . . . . . . . . . . . . . . . . . .
2.1.1 Morphologie von Dünnschicht-Silizium . . . . . . . . . . .
2.1.2 Schichtwachstumsmodelle und -eigenschaften . . . . . . . .
2.1.3 Resultierende Anforderungen an die Beschichtungsquelle .
2.2 Kapazitiv gekoppelte RF-Entladungen . . . . . . . . . . . . . . .
3 Modellierung von Niedertemperaturplasmen
3.1 Transportgleichungen . . . . . . . . . . . .
3.1.1 Partikelansatz . . . . . . . . . . . .
3.1.2 Lösung der Boltzmann-Gleichung .
3.1.3 Kontinuumsbetrachtung . . . . . .
3.1.4 Drift-Diffusions-Modell . . . . . . .
3.2 Elektrostatische Näherung . . . . . . . . .
3.3 Plasmachemie . . . . . . . . . . . . . . . .
3.3.1 Argon-Chemie . . . . . . . . . . . .
3.3.2 Silan-Chemie . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
25
26
28
30
33
35
37
38
40
40
v
vi
Inhaltsverzeichnis
3.4
Simulationsumgebung . . . . . . . . . . . . .
3.4.1 Der Particle-In-Cell Code yapic . . .
3.4.2 Das Multiphysiktool CFD-ACE+ . .
3.4.3 Globale Plasmamodellierung in Form
modells . . . . . . . . . . . . . . . .
. . .
. . .
. . .
eines
. . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
Ratengleichungs. . . . . . . . . .
4 Evaluation des globalen Modells an kapazitiven Argon-Plasmen
4.1 Das automatisierte globale Modell . . . . . . . . . . . . . . . . .
4.1.1 Grundlegende Gleichungen . . . . . . . . . . . . . . . . .
4.1.2 Der Automatisierungsalgorithmus . . . . . . . . . . . . .
4.1.3 Bestimmung der EEDF . . . . . . . . . . . . . . . . . . .
4.2 Simulation von kapazitiv gekoppelten Argon-Plasmen . . . . . .
4.2.1 Simulationsgebiet und Randbedingungen . . . . . . . . .
4.2.2 Vergleich der Modellierungsansätze . . . . . . . . . . . .
4.2.3 Validierung der Referenz yapic am Experiment . . . . . .
.
.
.
.
.
.
.
.
5 Globale Modellierung von kapazitiven Silan-Wasserstoff- Plasmen
5.1 Simulationsgebiet und Randbedingungen . . . . . . . . . . . . . .
5.2 Beschreibung der Elektronen-Energie- Verteilung . . . . . . . . . .
5.3 Vergleich mit experimentellen Messungen . . . . . . . . . . . . . .
5.4 Analyse der Plasmazusammensetzung . . . . . . . . . . . . . . . .
5.5 Korrelation Prozessbedingungen - Filmeigenschaften . . . . . . . .
5.6 Optimierung von kapazitiven Quellkonzepten . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. 50
. 51
. 52
. 53
.
.
.
.
.
.
.
.
55
55
55
59
60
60
61
61
73
.
.
.
.
.
.
78
78
80
84
86
94
95
Zusammenfassung
105
Ausblick
107
Formelzeichen und Abkürzungen
109
Tabellenverzeichnis
118
Abbildungsverzeichnis
119
Literaturverzeichnis
123
1 Einleitung
Die vorliegende Dissertation wurde im Zentralbereich Forschung und Vorausentwicklung der Robert Bosch GmbH am Standord Gerlingen-Schillerhöhe in enger Zusammenarbeit mit dem Institut für Theoretische Elektrotechnik der Ruhr-Universität
Bochum durchgeführt. Durch mehrere Akquisen deckte die Robert Bosch GmbH
zwischen 2009 und 2013 die gesamte Wertschöpfungskette der kristallinen und der
Dünnschichtsiliziumphotovoltaik ab. In der Abteilung für Beschichtungstechnologien und Oberflächentechnik stellte die Entwicklung und Optimierung von Abscheideprozessen für Dünnschichtsiliziumsolarzellen eine der Hauptaktivitäten dar, in deren
Umfeld diese Arbeit angesiedelt ist.
Die Einleitung gibt einen kurzen Überblick über den globalen Photovoltaikmarkt.
Es wird auf die Herausforderungen speziell der Dünnschichtphotovoltaik basierend
auf Silizium eingegangen, zu deren Bewältigung diese Arbeit beitragen soll. Nach
der Zielsetzung der Dissertation folgt eine Zusammenfassung der vorausgegangenen
simulativen Arbeiten zur Abscheidung von Dünnschicht-Silizium.
1.1 Der globale Photovoltaikmarkt
Der Photovoltaikmarkt sieht sich derzeit sehr schweren Randbedingungen ausgesetzt: Asiatische Großunternehmen aus anderen Industrien, wie z.B. dem Displaygewerbe, führen sehr kostengünstige Auftragsfertigungen von Solarmodulen zu einem
in Europa nicht darstellbaren Preis durch. Zudem geht die Nachfrage in Folge der
Kürzungen des Energie-Einspeise-Gesetzes (EEG) nach einem Hoch in 2011 [1] stetig zurück. Trotzdem hat die Anzahl der Wettbewerber in den letzten Jahren stark
zugenommen, was aktuell zu großen Überkapazitäten führt. Alles in allem schwächt
dieses Marktumfeld die Finanzlage der Unternehmen in der gesamten Branche. Viele
2
1. EINLEITUNG
Unternehmen leiden an stetig wachsenden Liquiditätsproblemen und einige Marktaustritte wurden dadurch bereits erzwungen. Die verbleibenden Wettbewerber benötigen dringend Umsätze und sind daher bereit, Module zu niedrigsten Preisen zu
vertreiben.
Die positive Seite an diesem Preisverfall ist, dass hierdurch Photovoltaik(PV)-Strom
in Zukunft rentabel wird. So erreicht man innerhalb der nächsten Jahre bereits die
Netzparität. Es entstehen somit selbsttragende Systeme, für die keine Förderung
mehr notwendig ist. Trotzdem besteht weiterhin ein großer Bedarf an Technologien,
die es ermöglichen den PV-Strom effizient zu speichern. Bis zur Reife dieser Speichertechnologien gilt es, die von der Photovoltaik erzeugten Stromspitzen im Netz
zu verkraften, was weiterhin eine starke Abhängigkeit von politischen Randbedingungen hervorruft.
Die wichtigsten Faktoren für die Rentabilität eines PV-Unternehmens sind derzeit
sicherlich große finanzielle Rücklagen und damit eine gewisse Ausdauer in Zeiten der
Marktbereinigung. Gleichzeitig eröffnen ausreichend Mittel die Möglichkeit, über Investitionen von Preisvorteilen durch Skaleneffekte zu profitieren. Nichtsdestotrotz ist
die technologische Weiterentwicklung von Zellkonzepten einerseits und von Produktionsequipment andererseits der Schlüssel für einen langfristigen Erfolg.
Auf die Dünnschichttechnologien hat der Kostendruck in den letzten Jahren ganz
besonders zugenommen. So hatten sie 2009 den bisher größten Anteil am globalen
Photovoltaikmarkt mit knapp 20%. Im Jahr 2011 ist dieser auf 11% geschrumpft.
Vor allem bessere Verfahren zur Gewinnung von kristallinem Silizium und verbesserte Produktionstechnologien bei der Herstellung der kristallinen Siliziumzellen haben
die Kosten der sogenannten ersten Zellgeneration erheblich verringert. Dazu kommt
die höhere Effizienz dieser Zellen. Trotzdem gibt es zahlreiche Argumente für Dünnschichtsolarzellen. Die Dünnschichttechnologie, auch zweite Zellgeneration genannt,
kann generell auf flexible Substrate abgeschieden werden. Das bringt sowohl Produktionsvorteile mit sich als auch neue Anwendungsfelder. Darüber hinaus haben sich,
auch insbesondere für Dünnschicht-Silizium, die Investitionskosten im letzten Jahr
um knapp ein Viertel verringert. Der aktuelle Preis für ein Modul aus DünnschichtSilizium beträgt 0.46 e pro Wattpeak (Wp) [2] (Stand August 2013) im Vergleich
zu 0.71 e für kristalline Module [2] (Stand: Oktober 2013). Dies ist nicht zuletzt
auf die deutliche Steigerung des Wirkungsgrades von Tandemsolarzellen mit einer
1.2 HERAUSFORDERUNGEN VON MIKROMORPHEN SOLARZELLEN
3
Kombination von Schichten aus amorphem (a-Si:H) und mikrokristallinem (µc-Si:H)
Silizium zurückzuführen. So erfolgte in den zwei Jahren vor 2011 eine Steigerung auf
12.5 %, im Vergleich zu sehr geringen Steigerungen in den vorherigen fünf Jahren.
Ein entscheidender Vorteil von Silizium ist, dass dieses Material im Vergleich zu
vielen anderen für die Dünnschichttechnologie geeigneten Materialien weder toxisch
noch selten ist.
1.2 Herausforderungen von mikromorphen
Solarzellen
Bereits die ersten Schichtentwicklungen von Dünnschicht-Silizium in den sechziger
Jahren wurden mit Plasmen im Anregungsbereich von Radiofrequenzen durchgeführt [3]. Daraus wurden in den siebziger Jahren [4, 5] die ersten Solarzellen aus
amorph-hydriertem Silizium entwickelt. Der erreichte Wirkungsgrad betrug 2.4 %.
Im Laufe der letzten 30 Jahre wurde die Technologie zur industriellen Reife vorangetrieben. Die in der Tandemzelle verwendete zweite Schicht aus mikrokristallinem
Silizium wurde erstmals 1968 publiziert [6]. Trotzdem hat es bis in die 90er Jahre gedauert, bis µc-Si:H als intrinsische Schicht für Solarzellen eingesetzt werden
konnte [7–9]. Der initiale Wirkungsgrad lag bei über 7.8 % [9], wobei später ein
Rekordwert von 10.1 % für 2 µm Schichtdicke auf 1.2 cm2 Glas erreicht wurde [10].
Andererseits wurde ein stabilisierter Wirkungsgrad von 9.5 % für eine 1 cm2 Zelle
für a-Si:H erreicht [11]. Der Grund für den zeitlichen Versatz des mikrokristallinen
Materials war vor allem, dass es sich bei µc-Si:H im Gegensatz zu a-Si:H um einen
indirekten Halbleiter handelt und so dickere Schichten notwendig sind, um bei dem
niedrigeren Absorptionskoeffizienten ausreichend Licht zu absorbieren. Trotzdem ist
µc-Si:H ein vielversprechendes Material, da es u.a. keiner Degradation unterliegt.
Der Begriff mikromorph als Synonym für a-Si:H/µc-Si:H Tandemsolarzellen wurde
zum ersten mal in einer Publikation [12] der Gruppe von Prof. Arvind Shah im Jahr
1995 eingeführt. Die erste mikromorphe Solarzelle wurde vom IMT in Neuchâtel
entwickelt und erreichte schon 1997 stabilisierte Wirkungsgrade größer 10 % [13].
Abgesehen von Alternativen zum herkömmlichen Glassubstrat sind die größten Her-
4
1. EINLEITUNG
ausforderungen die Erreichung eines hohen Zellwirkungsgrades und die Minimierung
der Herstellungskosten. Letztere kann mittels Erhöhung der Produktionskapazität
erfolgen. Darüber hinaus besteht das Bestreben, den Einzelprozess zur Zellherstellung an sich zu optimieren. Hier spielen verschiedene Faktoren eine Rolle. So ist
der Wirkungsgrad bei kleineren zur Verfügung stehenden Flächen für eine maximale Rendite der entscheidende Faktor und somit der größte Preistreiber. Durch die
Preisgestaltung pro Wp fällt der hohe Aufwand für Front- und Rückglas, die Folie
zur Verkapselung und die Junction-Box bei Modulen mit mehr Leistung gleichzeitig
weniger ins Gewicht. Gleiches gilt für die Verbrauchsmaterialien wie Silangas, das
meistens in einer Mischung mit Wasserstoff den Präkursor für die plasmagestütze
chemische Abscheidung (PECVD) von Dünnschicht-Silizium darstellt und für die
Gase zur Reinigung der Beschichtungskammern wie z. B. Stickstofftrifluorid. Durch
den hohen Anteil an Maschinen- und Anlagenkosten am Modulpreis gilt es vor allem
den Durchsatz zu erhöhen. Da die Plasmabeschichtung ungefähr die Hälfte der Anlagenkosten ausmacht, besteht vor allem hier Bedarf durch verschiedene Maßnahmen
Kostensenkungen herbeizuführen. Anknüpfungsmöglichkeiten bieten hier vor allem
die Minimierung der Reinigungszeiten der Prozesskammern und die Erhöhung der
Beschichtungsraten. Vor allem die dickere mikrokristalline Schicht bietet Potential
zur Verringerung der Prozesszeiten von üblicherweise über 30 Minuten bei Schichtdicken von 1 µm und Abscheideraten von 0.5 nm/s. Die anschließende Reinigung
benötigt vergleichbare Prozesszeiten.
Für eine zunehmende Bedeutung von Dünnschicht-Silizium auf dem globalen Photovoltaikmarkt ist es also von Nöten, sowohl den Wirkungsgrad weiter voranzutreiben,
als auch den Kostenvorteil der Dünnschichttechnologie auszubauen.
1.3 Zielsetzung der Arbeit
Ein grundlegendes Verständnis der Mechanismen, die zur Abscheidung von qualitativ hochwertigem mikrokristallinem Silizium führt, ist entscheidend für die weitere
Optimierung von mikromorphen Solarzellen. Durch die zunehmende Komplexität
dieser Abscheideprozesse bringen rein empirische Weiterentwicklungen hohe Kosten
und einen großen Zeitaufwand mit sich. Anstelle dessen soll mittels Simulationen
des Plasmaprozesses ein detailliertes Verständnis erarbeitet werden. Daraus können
1.3 ZIELSETZUNG DER ARBEIT
5
Optimierungsansätze abgeleitet werden. Die vorliegende Arbeit soll einen Zusammenhang zwischen der Plasmazusammensetzung und den gewünschten Schichteigenschaften herstellen. Auf dieser Basis sollen die Prozessparameter des Plasmaverfahrens und deren Auswirkungen auf die Plasmazusammensetzung und auf Prozesszeiten analysiert und optimiert werden. Die Anzahl teurer Anlagenprototypen und
Testabscheidungen soll dadurch reduziert werden.
Die vorliegende Forschungsarbeit bedient sich im Gegensatz zu der meist ausschließlich experimentellen Plasmaprozessentwicklung simulativer Methoden. Durch Modelle sollen die komplexen Effekte im Plasma beleuchtet und die optimalen Regelparameter identifiziert werden. Hierfür sollen verschiedene Modellierungansätze
hinsichtlich der erreichbaren Ergebnisse und deren Qualität anhand einer einfacheren kapazitiv gekoppelten Argonreferenzentladung miteinander verglichen werden.
Darüber hinaus werden die zum Einsatz kommenden Modelle mittels Charakterisierungsmethoden validiert. Hier kommt die optische Emissionsspektroskopie zum
Einsatz.
Die Arbeit ist wie folgt gegliedert: Die beiden nächsten Kapitel 2 und 3 erläutern einerseits die technologischen Grundlagen zur Abscheidung von Dünnschicht-Silizium,
andererseits die Modellierungsgrundlagen. In Kapitel 2 wird der Aufbau von mikromorphen Solarzellen und die Struktur der amorphen und mikrokristallinen Siliziumschicht und dessen Wachstumsprozess erklärt. Im folgenden wird die in der Industrie
als Standard eingesetzte kapazitiv gekoppelte Plasmaquelle (CCP) zur Abscheidung
von Dünnschichtsiliziumsolarzellen und das mit der Quelle einhergehenden Plasmaregime vorgestellt.
In Kapitel 3 werden die Modelle und die darin abgebildeten plasmaphysikalischen
Effekte wie die elektrischen Felder, der Teilchentransport und die Plasmachemie skizziert. Das Kapitel schließt mit der Darstellung der verwendeten Simulationstools.
Modelle mit unterschiedlichem Detailierungsgrad ergeben unterschiedliche Ergebnisgrößen und sind verschieden anspruchsvoll was Rechenleistung und -zeit angeht. In
Kapitel 4 werden verschiedene Ansätze von einem Particle-In-Cell-Ansatz über ein
Fluid-Modell zu einem eigens entwickelten globalen Modell in einem Referenzsystem
verglichen und hinsichtlich der hiesigen Problemstellung und des Gültigkeitsbereiches bewertet.
6
1. EINLEITUNG
In Kapitel 5 kommt schließlich das globale Modell zur Abbildung von Silan-Wasserstoff-Plasmen zum Einsatz. Diese Ergebnisse wurden bereits im Artikel A global
model study of silane/hydrogen discharges veröffentlicht [14]. Die Arbeit schließt mit
einer modellbasierten Optimierung des Abscheideprozesses hinsichtlich Schichtqualität und Abscheiderate.
1.4 Simulation von Silan-Wasserstoff-Plasmen
Einen guten Überblick über verschiedene Plasmamodelle zeigt Kline auf [15]. Graves und Kushner beschreiben in [16], wie Modellierung und Simulation die Reife der
Plasmatechnologie insbesondere für die Prozessierung von Materialien der Mikroelektronik beeinflusst. Sie geben einen Überblick über verschiedene Simulationsansätze und deren Entwicklung im Laufe der Jahre. Ein weiterer Überblick über die
Plasmamodellierung geben Van Dijk et al. in [17].
Dieser Abschnitt gibt einen Überblick über simulative Arbeiten zur Abscheidung
von Dünnschicht-Silizium und grenzt die hiesige Ausführung von früheren ab. Er
fokusiert nicht auf die Beschreibung der Silan-Wasserstoff-Chemie, was Inhalt von
Kapitel 3.3.2 ist. In bisher noch geringerem jedoch nicht unherheblichem Maße profitiert auch die Photovoltaikindustrie in der Anlagen- und Prozessentwicklung von
einem zunehmenden Verständnis der physikalischen und chemischen Prozesse durch
die Simulation dieser Plasmen. Dieser Abschnitt soll hierfür einige Beispiele aufführen.
Ein entscheidender Parameter bei Plasmaprozessen ist die Elektronen-Energie-Verteilungsfunktion. Löser wie BOLSIG+ [18] ermöglichen die Berechnung des relativen
Energieeintrages in die verschiedenen chemischen Reaktionen in Silan-Wasserstoff
Plasmen als Funktion des reduzierten elektrischen Feldes und der Anregungsfrequenz. Diese Analyse wurde zur Untersuchung des Effektes der Frequenz auf die
Abscheidung von mikrokristallinem Silizium von Amanatides [19] herangezogen.
Für die Untersuchung der Plasmachemie bieten sich globale Ratengleichungsmodelle an, die eine Auskunft über die Plasmazusammensetzung, meist 0-dimensional,
1.4 SIMULATION VON SILAN-WASSERSTOFF-PLASMEN
7
geben. Solche Modelle wurden für zahlreiche elektropositive [20–24] und elektronegative Gase [25–33] entwickelt.
Kushner [34] entwickelte schon 1988 ein zeit- und ortsaufgelöstes (1d) Ratengleichungsmodell für Silan-Wasserstoff- und Silan-Argon-Gemische unter Berücksichtigung von Diffusion, Drift und der Abscheidung von Radikalen. Die Elektronenenergieverteilung wird extern berechnet. Der Druckbereich liegt in den hiesigen Untersuchungen, im Vergleich zu den relevanten Bereichen für die Siliziumabscheidung für
die Photovoltaik, bei einigen 10 Pa.
10 Jahre später veröffentlichte Fantz [35] ein ähnliches Ratengleichungsmodell für
Entladungen unterschiedlicher Silangemische (mit Argon, Helium bzw. Wasserstoff).
Die resultierenden Dichten der 19 Silan- bzw. Wasserstoffteilchen für einen Druckbereich von 2-20 Pa werden mit emissionsspektroskopischen Messungen verglichen
und zeigen gute Übereinstimmung.
Amanatides entwickelte in 2001 [36] ein Massen-Transfer-Modell für die Silan-Wasserstoff Chemie in Parallelplattenreaktoren bei einigen 100Pa mit Gasphasenkinetik, Massentransfer und Oberflächenchemie basierend auf ortsaufgelösten Messungen der SiH4 Dissoziation mittels laserinduzierter Fluoreszenz (LIF). Ein weiteres
1-dimensionales Ratengleichungsmodell für Argon-Silan-Gemische mit 54 Reaktionen wurde von Strunin [37] entwickelt. Es folgen vereinfachte globale Chemiemodelle für PV-relevante Betriebsbedingungen wie das von Strahm [38] mit vier Spezies
und komplexere ein-dimensionale Ratengleichungsmodelle [39] inklusive Konvektion, Diffusion, Drift und Abscheidung (18 Spezies, 36 Reaktionen), ähnlich dem von
Kushner in 1988 entwickelten.
Für die selbst-konsistente Bestimmung von Teilchendichten, -geschwindigkeiten und
-temperaturen im Gültigkeitsbereich der Kontinuumsmechanik kommen Fluidmodelle zum Einsatz. Einige wurden zur Abbildung von kapazitiven Silan-Wasserstoff
Plasmen aufgebaut [40–54]. Sie fokusieren vor allem auf die simulative Abschätzungen der Abscheiderate, der Plasmazusammensetzung, deren Homogenität und der
Staubbildung. Dazu lösen sie die Gleichungen zur Massen-, Impuls- und Energieerhaltung im zwei-dimensionalen Raum. Hierbei [53] werden für eine Optimierung der
Elektrodengeometrie hinsichtlich der SiH3 -Verteilung nur zwei chemische Reaktionen umgesetzt. Im Gegensatz dazu geht es bei [50] oder später in einer Erweiterung
des Modells [51] um das Verständnis der chemischen Prozesse, die dementsprechend
8
1. EINLEITUNG
mit 24 bzw. 33 Spezies und 80 bzw. 107 Gasphasenreaktionen bei Drücken zwischen
133 und 1330Pa abgebildet werden. In [52] geht es bei umgesetzten 67 Reaktionen
neben der typischen kapazitiven Entladung (CCP) auch um induktiv gekoppelte
Quellen (ICP) bzw. CCPs mit Multi-Hohlkathoden. Hierbei werden v.a. die unterschiedlichen H/SiH3 und SiH2 /SiH3 Verhältnisse analysiert. Meist kann in kapazitiven Entladungen nicht von einer Maxwell-verteilten Elektronenenergie ausgegangen
werden. Deshalb wird in einigen Arbeiten [41, 42, 44, 47, 48] zusätzlich zu den Erhaltungsgleichungen die Elektronenenergieverteilung durch eine Approximation der
Boltzmann Gleichung bestimmt.
Die vorliegende Arbeit zielt darauf ab, die Geschwindigkeit und Effizienz der globalen Modelle aus der Literatur mit Methoden höherer Ordnung zu kombinieren und
den Prozessbereich, in dem die Modelle gültig sind, zu erweitern.
2 Technologische Grundlagen zur
Abscheidung von a-Si:H/µc-Si:H
In diesem Kapitel soll der Aufbau von mikromorphen Solarzellen und der darin
gestapelten amorphen und mikrokristallinen Siliziumschichten erläutert werden. Es
werden die Wachstumsmodelle der Materialien vorgestellt und auf die daraus resultierenden Anforderungen an die Plasmaquelle eingegangen. Im Anschluss folgt eine
Vorstellung der in der Industrie zur Abscheidung von Dünnschichtsiliziumsolarzellen
als Standard eingesetzten kapazitiv gekoppelten Plasmaquelle (CCP) und des mit
der Quelle einhergehenden Plasmaregimes.
2.1 Mikromorphe Solarzellen
Um maximale Wirkungsgrade bei Dünnschichtsolarzellen zu erhalten, müssen verschiedene Absorbermaterialien zu sogenannten Stapelsolarzellen kombiniert werden.
Die Kombination aus einer Topzelle aus amorphem und einer Bottomzelle aus mikrokristallinem Silizium, wie in Abbildung 2.1 gezeigt, führt in mikromorphen Solarzellen zu einer besseren Ausnutzung des Sonnenspektrums und dadurch höheren
Wirkungsgraden. Abbildung 2.2 zeigt die Quanteneffizienz einer mikromorphen Solarzelle, zusammengesetzt aus den Quanteneffizienzen der beiden einzelnen Absorbermaterialien, in Abhängigkeit der Wellenlänge des Lichts. Mit der Quanteneffizienz
wird der Teil des Lichts benannt, der Elektronen-Loch-Paare erzeugt, die extrahiert
werden können.
Es gibt eine Vielzahl von Optimierungsmöglichkeiten in mikromorphen Solarzellen.
Grundsätzlich ist darauf zu achten, dass eine möglichst hohe Absorption des einfal-
10
2. TECHNOLOG. GRUNDL. ZUR ABSCHEIDUNG VON a-Si:H/µc-Si:H
a
b
f
TCO
Frontkontakt
Zwischenreflektor
TCO
Rückkontakt
Rückreflektor
Abb. 2.1: a) Elektronenmikroskopaufnahme eines Querschnitts durch eine mikromorphe
Solarzelle und b) schematischer Aufbau der Zelle (aus [55], mit freundlicher
Genehmigung der SPIE und von Prof. C. Ballif, Institute of Microengineering,
Ecole Polytechnique Fédérale de Lausanne).
Abb. 2.2: Quanteneffizienz einer mikromorphen Solarzelle in Abhängigkeit der Wellenlänge des Lichtes (aus der Dissertation von Berginski [56]).
2.1 MIKROMORPHE SOLARZELLEN
11
lenden Lichtes im Absorber stattfindet. Hierfür sind neben einem guten Lichteinfang hochwertige transparent leitfähige Oxidschichten (TCO) mit hoher elektrischer
Leitfähigkeit und geringer Lichtabsorption vonnöten. Durch die Kombination einer
a-Si:H und einer µc-Si:H Zelle müssen die Ströme beider Zellen zueinander abgestimmt werden (Matching). Dicke amorphe Schichten unterliegen einer erheblichen
Degradation. Um diesem Effekt vorzubeugen, kann wie in Abbildung 2.1 gezeigt,
der Strom in der a-Si:H Zelle durch eine reflektierende Zwischensicht erhöht werden. Auf diese Weise werden dünnere und stabilere amorphe Schichten ermöglicht.
Nicht zuletzt ist es wichtig, die Halbleitermaterialien an sich zu optimieren, d. h.
Fehlstellen, die zur Ladungsträgerrekombination führen, zu vermeiden und die richtige Bandlücke mittels idealer Materialmorphologie einzustellen. Dies hängt stark
von den Wachstumsprozessen von a-Si:H und µc-Si:H ab, wobei diese wiederum von
der Beschichtungsmethode beeinflusst werden. Beide Aspekte werden im Folgenden
beschrieben und insbesondere für µc-Si:H in dieser Arbeit fokussiert.
2.1.1 Morphologie von Dünnschicht-Silizium
In amorphem Silizium sind die Bausteine auf größere Entfernung gesehen in ungeordneter Verteilung und weisen lediglich submikroskopische Nahordnungsbereiche auf. Jedoch sind diese Nahordnungsbereiche denen von kristallinem Silizium
(c-Si) sehr ähnlich und besitzen nur geringe Abweichungen der Bindungslängen und
-winkel. Unter diesen Voraussetzungen ist das Bändermodell partiell anwendbar.
Die regellose Verknüpfung der Nahordnungsbereiche untereinander und die damit
einhergehenden ungesättigten Bindungen, welche besetzbare Zustände im verbotenen Band darstellen, führen im wesentlichen dazu, dass die Bandkanten nicht mehr
scharf sind [57]. Des weiteren stören die Defekte den Transport von Ladungsträgern,
indem sie als Rekombinationszentren wirken. Durch die Hydrierung und die damit
einhergehende Sättigung dieser Bindungen können die elektrischen Eigenschaften
von amorphem Silizium verbessert werden. Gewöhnlicherweise enthält das in Solarzellen eingesetzte amorphe Silizium gut 10 at. % Wasserstoff (z. B. 11.1 % in [58]).
Die bei amorphen Materialien sogenannte Beweglichkeitskante beträgt bei a-Si:H
1.6-1.9 eV, wobei durch den Einbau von Sauerstoff, Kohlenstoff, Germanium oder
Wasserstoff die Lücke beeinflusst werden kann. Die optischen Eigenschaften von
12
2. TECHNOLOG. GRUNDL. ZUR ABSCHEIDUNG VON a-Si:H/µc-Si:H
a-Si:H kommen denen eines direkten Halbleiters mit hohen optischen Absorptionskoeffizienten im sichtbaren Spektrum sehr nahe (s. Abb. 2.3). Dem zu Folge reichen
Schichten mit einer Dicke von <1 µm aus, um einen Großteil des einfallenden Lichtes mit höherer Energie als die Bandlücke zu absorbieren.
Abb. 2.3: Absorptionsspektren von a-Si:H, µc-Si:H und c-Si als Funktion der Photonenenergie (obere Skala) bzw. der Wellenlänge (aus der Dissertation von Berginski [56]).
Wie bereits erwähnt, ist das Auftreten des sogenannten Staebler-Wronski Effekts,
der das lichtinduzierte Altern durch das Aufbrechen von Siliziumbindungen und
somit die Zunahme der Defektdichte beschreibt, ein entscheidender Nachteil von
a-Si:H [59]. Die Alterung kann durch eine Temperaturbehandlung, wie in [59] beschrieben, nahezu rückgängig gemacht werden. Die Alterung nimmt mit der Schichtdicke ab. Deswegen liegt die optimale Dicke der amorphen Zelle bei rund 250 nm.
Mikrokristallines Silizium ist eine der Modifikationen von Silizium, die zwischen
der amorphen und der kristallinen Struktur einzuordnen ist und Korngrößen im
Bereich zwischen einigen 10 nm und wenigen µm aufweist. Die Korngrenzen führen ähnlich wie in der amorphen Phase zur Ausbildung von besetzbaren Zuständen
im verbotenen Band, den sogenannten tail-states. µc-Si:H ist wie c-Si ein indirekter
2.1 MIKROMORPHE SOLARZELLEN
13
Halbleiter, d. h. das Minimum des Leitungsbandes liegt nicht direkt über dem Maximum des Valenzbandes. Die Bandlücke beträgt 1.1 eV [57]. Als Folge der indirekten
Bandlücke muss für einen Bandübergang nicht nur Energie, sondern auch ein Impuls
zugeführt werden [60]. Dies bringt niedrigere optische Absorptionskoeffizienten für
sichtbares Licht mit Photonenenergien größer als 1.8 eV im Vergleich zu a-Si:H mit
sich (s. Abb. 2.3). Theoretisch wären Schichten von mehr als 3 µm nötig, um das
Sonnenlicht vollständig zu absorbieren [61]. Ab ca. 700 nm (bis 1.8 eV) liegt eine
höhere Absorption im Vergleich zu a-Si:H vor. Dieser Wellenlängenbereich macht 20
% der solaren Einstrahlungsleistung aus (Referenz-Spektrum AM1.5). Gleichzeitig
ist die elektronische Leitung bei µc-Si:H viel besser als bei a-Si:H, wodurch dickere
intrinsische Absorberschichten möglich sind. So setzt z. B. Sanyo [62] in den Tandemzellen 2 µm dicke µc-Si:H Schichten ein, die in deren PECVD Prozess bei 2.4
nm/s abgeschieden werden.
abnehmender kristalliner Volumenanteil
stationäres
Wachstum
Nukleationsschicht
~30-50 nm
Substrat
Kristallite
amorphe Bereiche
Hohlräume
Abb. 2.4: Schema für die Volumenstruktur von µc-Si:H (aus [63], mit freundlicher Genehmigung der Taylor & Francis Group, http://www.tandfonline.com).
Wie in Abbildung 2.4 gezeigt, können durch unterschiedliche Prozessbedingungen
(hier des PECVD-Prozesses) unterschiedliche Anteile der kristallinen bzw. amorphen Struktur abgeschieden werden. Bei einem hohen kristallinen Anteil sind breite
14
2. TECHNOLOG. GRUNDL. ZUR ABSCHEIDUNG VON a-Si:H/µc-Si:H
Säulen von einigen 100 nm Breite und einigen 100 nm Höhe zu sehen, die aus Kristallen von einigen nm Größe bestehen, getrennt durch Stapelfehler oder Zwillingskorngrenzen [63–65]. Die einzelnen Säulen sind durch Porositäten, sogenannte Voids,
voneinander getrennt. Im Übergangsbereich hin zu amorphem Material nimmt sowohl die Dicke als auch die Länge der Säulen und die Größe der Kristalle ab. Die
Zwischenbereiche sind mit amorphem Material gefüllt. Der Wasserstoffgehalt von
µc-Si:H liegt zwischen 3.5 at. % in sehr kristallinem und 8 at. % in sehr amorphem
Material [58].
In µc-Si:H für PV-Anwendungen sind optimalerweise zwischen 60 % und 70 % des
Materials kristallin und die restlichen 30 % bis 40 % in den Zwischenräumen sind
amorph. Man spricht vom Transitions- oder Übergangsmaterial bei idealer Materialkristallinität [66]. Ist das Material zu kristallin, nimmt der Anteil der Voids zu
und dadurch die Leitfähigkeit ab. Wie in Abbildung 2.4 gezeigt, kann µc-Si:H nicht
unmittelbar auf amorphen Grenzflächen abgeschieden werden, sondern benötigt eine Einlaufphase, in der ein Übergangsmaterial, eine sogenannte Nukleationsschicht
entsteht, die mittels geeigneter Prozessparameter möglichst dünn gehalten werden
sollte.
Zusammengefasst charakterisieren maßgeblich folgende Eigenschaften hochwertiges
mikrokristallines Silizium: Schichtkristallinität, Materialdefekte und Leitfähigkeit,
Porosität und die Materialdegradation. Die Porosität von amorphem Silizium wird
durch den Mikrostrukturfaktor R∗ beschrieben, der teilweise auch für mikrokristallines Material herangezogen wird [67]:
R∗ =
I2100
.
I2000 + I2100
(2.1)
Der Absorptionspeak I2000 repräsentiert den Anteil von SiH Molekülen, die in kompaktem Material gebunden sind. Der Peak I2100 resultiert aus SiH, das in Hohlräumen und an inneren Oberflächen gebunden ist [68]. Je kleiner der Faktor, desto höher
ist die elektrische Qualität der Schichten [69]. Je größer der Faktor, desto poröser
ist die Struktur [70].
2.1 MIKROMORPHE SOLARZELLEN
15
2.1.2 Schichtwachstumsmodelle und -eigenschaften
In Prozessen mit Silan-Wasserstoff-Gemischen entstehen allein durch Dissoziationsprozesse verschiedenste Radikale (SiH3 , SiH2 , SiH, Si, H). Wenn solche Radikale
an einer aufwachsenden Oberfläche ankommen, interagieren sie mit ihr oder werden an ihr unverändert reflektiert. Die Wahrscheinlichkeit der Interaktion wird üblicherweise mit β beschrieben. Folglich gilt für die Reflektionswahrscheinlichkeit
RRefl. = 1 − β. Es können Interaktionen verschiedener Art ablaufen. Zum einen
kann das Radikal rekombinieren (Rekombinationswahrscheinlichkeit γ) oder es verbleibt an der Oberfläche (Sticking Wahrscheinlichkeit s). Es gilt folglich, dass die
Summe dieser möglichen Oberflächeninteraktionen eins ergibt:
1 = RRefl. + γ + s,
mit
β = 1 − RRefl. = γ + s.
(2.2)
Die Werte der Wahrscheinlichkeiten für die einzelnen Radikale der hier betrachteten
Chemie werden in Kapitel 3.3.2 näher behandelt. Neben der Interaktion mit der
Oberfläche besteht für ein Radikal die Möglichkeit weiterer Gasphasenreaktionen,
höchstwahrscheinlich mit den Präkursoren SiH4 bzw. H2 . Da SiH3 keine Reaktivität
bezüglich SiH4 und H2 aufweist, die restlichen Radikale jedoch sehr hohe, ist SiH3
ein sehr langlebiges Molekül. Die übrigen Radikale sind sehr kurzlebig. Experimentelle Messungen [71] haben ergeben, dass dementsprechend SiH3 den dominanten
Schichtbildner darstellt.
Schichteigenschaften wie z.B. die Kristallinität werden einerseits durch die Zusammensetzung der Gasphase, insbesondere der Radikale, aber auch durch die Konstitution der Oberfläche bestimmt. Beide zusammen beeinflussen, welche Oberflächenreaktionen stattfinden. Vor allem der Zustand der Oberfläche beeinflusst, wohin die
mit ihr reagierenden Radikale im Festkörper diffundieren bzw. wo sie verbleiben.
Beim Wachstum von amorphem Silizium depassiviert SiH3 die mit H-Atomen
bedeckte Oberfläche und rekombiniert zu SiH4 . Treffen sich zwei SiH3 -Radikale rekombinieren die beiden unter Bildung von Si2 H6 . In beiden Fällen entstehen freie
Siliziumbindungen an der Oberfläche, die durch SiH3 Diffusion abgesättigt werden.
16
2. TECHNOLOG. GRUNDL. ZUR ABSCHEIDUNG VON a-Si:H/µc-Si:H
Zur Erklärung des Wachstumsprozesses von mikrokristallinem Silizium werden in der Literatur [71] drei Modelle herangezogen:
• Oberflächendiffusion/Verspannte Bindungen [72]
• Selektives Ätzen [73]
• Chemisches Ausheilen [74]
Im Modell der Oberflächendiffusion/verspannten Bindungen sorgen ein großer
Wasserstoffluss und exotherme Wasserstoffreaktionen für eine Begünstigung der
Oberflächendiffusion von SiH3 -Radikalen, die dementsprechend energetisch günstige
Plätze finden und sich dort unter Bildung von Kristallen abscheiden. Wachsen Keime
durch die vermehrte Diffusion zusammen, werden Spannungszustände mit verspannten Si-Si Bindungen erzeugt [75], die wiederum als Wachstumszentren agieren.
Das selektive Ätzen beschreibt die Ätzwirkung von atomarem Wasserstoff insbesondere an schwachen Siliziumbindungen in amorphen Strukturen. Diese werden
aufgetrennt und bieten neue Wachstumskeime für starke Bindungen.
Beim chemischen Ausheilen sorgen Wasserstoffatome, die tiefer in die Schicht
eindringen, für eine Absättigung und durch exotherme Reaktionen auch für eine
Ausheilung von Fehlstellen und damit für eine Kristallisierung des Materials. Es
wurden zahlreiche Experimente durchgeführt, die die hier aufgeführten Modelle belegen [71, 76].
Für alle drei Modelle ist ein hohes Verhältnis der Flüsse von atomarem Wasserstoff zu
Silanradikalen notwendig, um mikrokristallines Material abzuscheiden. Dieser atomare Wasserstoff resultiert entweder aus der Dissoziation von Silan oder Wasserstoff.
Bei geringem Wasserstoffgehalt im Gasgemisch muss folglich die Silanumsetzung sehr
effizient sein, um ausreichend H für die obigen Mechanismen bereitzustellen.
So zeigt Strahm in [38], dass unabhängig vom Ausgangsgasgemisch die Silankonzentration bei gezündetem Plasma cp (definiert als das Verhältnis des Silanpartialdruckes zum gesamten Druck pSiH4 /p) entscheidend für die resultierende Schichtkristallinität ist. Er identifiziert drei Bereiche von cp , die zu mikrokristallinem, amorphmikrokristallinem Übergangsmaterial und zu amorphem Material führen:
2.1 MIKROMORPHE SOLARZELLEN
17
• µc-Si:H : cp < 0.5 %
• µc-Si:H/a-Si:H : 0.5 % < cp < 1.2 %
• a-Si:H : cp > 1.2 %.
Zieht man die Definition der Silankonzentration im Ausgangsgasgemisch c
p0SiH4
p
(2.3)
p0SiH4 − pSiH4
p0SiH4
(2.4)
c=
und der Silanumsetzung D
D=
heran, wobei pSiH4 bzw. p0SiH4 für den Partialdruck von SiH4 bei gezündetem Plasma
bzw. im ursprünglichen Gasgemisch steht, wird der Zusammenhang zwischen cp , c
und D ersichtlich:
cp =
pSiH4
= c(1 − D).
p
(2.5)
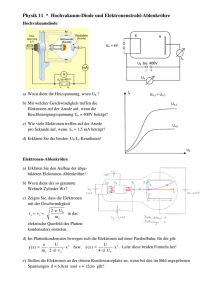
Abbildung 2.5 veranschaulicht, für welche Kombinationen aus Silankonzentration
im Ausgangsgasgemisch und Silanumsetzung die Silan-Konzentration im Plasma die
Werte 0.5 und 1.2 % einnimmt. Die Bereiche für die verschiedenen resultierenden
Phasen sind eingezeichnet. Für beliebige Plasmaprozessparameter (Leistung, Druck,
Plattenabstand und Gasfluss) ist laut Strahm also allein die Bestimmung von cp für
die Voraussage der Materialkristallinität notwendig.
Andere Autoren wie Klein [58, 77] beschreiben direkt den Zusammenhang zwischen
dem Verhältnis von Silan- zu Wasserstoffradikalen bei der Abscheidung vom gewünschten µc-Si:H/a-Si:H-Übergangsmaterial und verschiedenen Prozessbedingungen. Bei dem in diesen Arbeiten angewandten Hot-Wire-Verfahren gehen Parameter
wie Druck, Substrat-, Glühdrahttemperatur und Abscheiderate ein. Er stellt fest,
dass das benötigte Radikalverhältnis für die Abscheidung von hochwertigem mikrokristallinen Material hauptsächlich von der Substrattemperatur und der Abscheiderate abhängt. So werden bei Substrattemperaturen von 220 ◦ C und Abscheideraten
18
2. TECHNOLOG. GRUNDL. ZUR ABSCHEIDUNG VON a-Si:H/µc-Si:H
12
Silankonzentration c / %
10
8
µc−Si:H
6
cp = 1.2 %c
4
cp = 0.5 %
2
µc−Si:H/a−Si:H
a−Si:H
0
0
0.2
0.4
0.6
Silanumsetzung D / %
0.8
1
Abb. 2.5: Zusammenhang zwischen der Silankonzentration im Plasma und der Konzentration des Gasgemisches und der Umsetzung.
von rund 20 nm/s zwischen 5.2 und 7 Wasserstoffatome pro Silanradikal benötigt.
Bei einer Substrattemperatur von 450 ◦ C sind nur noch 1.8 Wasserstoffradikale pro
Silanradikal notwendig. Strahm [38] erhält über sein Plasmachemiemodell ähnliche
Verhältnisse von Wasserstoff- zu Silanradikalflüssen mit Werten von rund 12. Dingemans [78] bestimmt experimentell deutlich größere Werte von 40.
Für homogene Schichtkristallinitäten in beiden Ausdehnungen des Substrates und
über der Schichtdicke muss die Silankonzentration im Plasma über der Fläche und
der Zeit konstant sein.
Wie in Kapitel 2.1.1 erwähnt, bestimmt neben der Kristallinität vor allem die Defektdichte über die Materialqualität der Schichten in den Solarzellen. Defekte stellen
zum einen Rekombinationszentren dar und verringern so die Leitfähigkeit des Materials. Zum anderen findet an ihnen verstärkt eine Oxidation statt [79].
Auch die Defektdichte kann auf bestimmte Radikale zurückgeführt werden, die
verschiedene Oberflächenreaktionen ermöglichen. So kann sich SiH2 in alle Si-HBindungen einlagern [80], SiH3 jedoch diffundiert auf der Oberfläche und sättigt
die Fehlstellen ab [81]. Für a-Si:H wurden bei rund 250 ◦ C Substrattemperatur
2.1 MIKROMORPHE SOLARZELLEN
19
die niedrigsten Defektdichten gemessen. Diese Temperatur scheint also eine ausreichend große Diffusion zu ermöglichen, wobei die thermische Wasserstoffdepassivierung, die zu erhöhten Defektdichten führt, noch nicht stattfindet [82]. Die Radikalzusammensetzung kann über die Elektronentemperatur beschrieben werden [82,83].
SiH2 entsteht hauptsächlich über Dissoziationen von SiH4 mit Hilfe von Elektronen.
SiH3 wird durch Reaktionen von SiH4 mit atomarem Wasserstoff (s. Kapitel 3.3.2)
und durch SiH4 -Dissoziationen gebildet. Die zur Dissoziation benötigte Elektronenenergie steigt in der Reihenfolge SiH3 , SiH2 , SiH und Si an. Bei Betrachtung des
Wirkungsquerschnittes der Dissoziation zu SiH2 (in Kapitel 3.3.2, Abb. 3.6) wird
deutlich, dass dieser bis 54 eV ansteigt. Höhere Temperaturen führen folglich zu
einer verstärkten SiH2 Bildung im Verhältnis zu SiH3 . Ram [84] ermittelt bei seinen
Elektron-Zyklotron-Ressonanz-Plasmen (ECR-Plasmen) neben einem erhöhten Vorkommen von Leerstellen bei höheren Elektronentemperaturen zudem einen Anstieg
der Kristallinität.
Matsuda et al. [82] zeigen, dass insbesonders Si-H2 -Bindungen in der Schicht zu verstärkter Lichtdegradation in a-Si:H führen und folglich Defekte hervorrufen, die als
Rekombinationszentren agieren. Als Ursprung dieser Bindungen werden vor allem
kurzlebige hochreaktive Radikale wie SiH2 , SiH und Si, die nicht auf der Oberfläche
diffundieren und langkettige Silanradikale identifiziert. Die langkettigen Radikale
entstehen vor allem durch Elektronen-induzierte Dissoziation von Polymeren, die
aus der Reaktion von SiH2 mit SiH4 oder längerkettigen Molekülen hervorgehen.
Sie stellen über die Bildung von Si-H2 Konfigurationen hinaus ein Hindernis für die
SiH3 Diffusion dar.
Im Allgemeinen gilt, dass bei rund 500 K als Substrattemperatur die besten Schichten abgeschieden werden. Bei geringeren Temperaturen wird das Material hauptsächlich hinsichtlich der Kompaktheit, hervorgerufen durch die verringerte Oberflächenbeweglichkeit der Radikale, schlechter [85].
Zusätzlich zu den Radikalen haben bei der Abscheidung auch die Ionen und deren
Energieeintrag Auswirkungen auf die Schicht und deren Eigenschaften wie Kristallinität und Defektdichte (Abb. 9 in [71]). Die simulative Ermittlung der Ionenenergien
erfordert jedoch eine detaillierte Abbildung der Plasmarandschicht, die nicht Fokus
dieser Arbeit ist.
20
2. TECHNOLOG. GRUNDL. ZUR ABSCHEIDUNG VON a-Si:H/µc-Si:H
2.1.3 Resultierende Anforderungen an die
Beschichtungsquelle
Die aus den vorigen Kapiteln hervorgehenden Anforderungen an eine Abscheidung
von qualitativ hochwertigem mikrokristallinem Silizium, bei darüber hinaus minimalen Herstellkosten, sollen hier abschnittsweise zusammengefasst werden:
Die Deposition soll bei geringen Temperaturen ablaufen, da Niedertemperaturprozesse wie z.B. plasmabasierte Beschichtungsverfahren den Einsatz von kostengünstigen Substraten ermöglichen. Als Substratmaterialien kommen Glas oder flexible
Substrate aus Metall oder Kunststoff zum Einsatz. Durch die Verwendung von Substratfolien eröffnet sich die Möglichkeit von Rolle-zu-Rolle-Prozessierungen, die insbesondere durch das einfach handhabbare Handling ein großes Kostensenkungspotenzial aufweisen. Für homogene großflächige Beschichtungen eignen sich insbesondere flächige Beschichtungsquellen im Batch-Betrieb oder Linienquellen im In-LineBetrieb.
Eine einfache und kostengünstige Integrierbarkeit der Beschichtungsprozesse in den
Produktionsablauf ist notwendig. Hierbei spielen vor allem Anlagenkosten und Prozesszeiten eine große Rolle. Die Prozesszeiten bei Vakuumprozessen sind die Summe
der Pumpzeit, der eigentlichen Beschichtungszeit, abhängig von der Abscheiderate, und der anschließenden Zeit für die Reinigung der Kammer vor der nächsten
Beschichtung. Insbesondere die Reinigungsgase (NF3 , F2 ) sind sehr teuer und ermöglichen bei reduziertem Bedarf eine deutliche Senkung der Kosten.
Durch die Beschichtungsquelle müssen die zur Ausbildung qualitativ hochwertiger
Schichten benötigten Radikale, insbesondere hinsichtlich Schichtkristallinität und
Defektdichte, gebildet werden. Sie haben einen großen Einfluss auf den Wirkungsgrad der Zelle, der wiederum für die Herstellkosten entscheidend ist. Aus allen
Wachstumsmodellen in Kaptiel 2.1.2 ging hervor, dass ausreichend atomarer Wasserstoff und vor allem das Silanradikal SiH3 für eine gute Ausbildung dieser Schichteigenschaften notwendig ist.
2.2 KAPAZITIV GEKOPPELTE RF-ENTLADUNGEN
21
Die Regelbarkeit der Energieverteilung der Teilchen am Substrat bietet einen weiteren Freiheitsgrad mit dessen Hilfe Schichteigenschaften eingestellt werden können.
Des Weiteren gilt es, Staub so weit wie möglich zu vermeiden. Einerseits besteht
die Gefahr durch Staub die Schichten zu schädigen, wobei hier jedoch konstruktiv
vorgebeugt werden kann. Andererseits erhöhen sich bei Staubbildung auf alle Fälle
zwangsweise die Anlagenstandzeiten für die Reinigung.
2.2 Kapazitiv gekoppelte RF-Entladungen
Dieses Unterkapitel beschreibt das in der Industrie standardmäßig eingesetzte Verfahren für die Abscheidung von Dünnschicht-Silizium, kapazitiv gekoppelten RFEntladungen. Prinzipiell sind verschiedene Methoden wie reaktives Sputtern [86],
Photo CVD Methoden, in denen die Moleküle durch Photonen angeregt werden
[87–89], Hot wire Verfahren [77, 90] und weitere möglich. Jedoch haben vor allem
Plasmaverfahren hohes Potenzial zur homogenen Abscheidung von hochwertigem
Material auf großen Substraten. Daher wird im Folgenden ausschließlich auf kapazitiv gekoppelte PECVD-Quellen (Plasma Enhanced Chemical Vapor Deposition)
eingegangen, in denen amorphe und mikrokristalline Siliziumschichten bei niedrigen
Temperaturen aus gasförmigen Präkursoren, typischerweise aus einem Gemisch aus
Silan (SiH4 ) und Wasserstoff (H2 ), abgeschieden werden.
Abb. 2.6: Konventionelle kapazitiv gekoppelte PECVD Quelle.
22
2. TECHNOLOG. GRUNDL. ZUR ABSCHEIDUNG VON a-Si:H/µc-Si:H
Die konventionelle Methode der Plasmabeschichtung, mittels kapazitiv gekoppelter
Plasmaquelle, besteht aus zwei planparallelen Elektroden, von denen die angeregte
als Gasdusche für das Silan-Wasserstoff-Gemisch dient und auf der geerdeten das zu
beschichtende Substrat liegt (s. Schema in Abb. 2.6). Kapazitiv gekoppelte Quellen
erzeugen weniger dichte Entladungen als induktiv gekoppelte Plasmen (kurz ICP)
oder Plasmen mit Wellenheizung. Die Prozesse laufen bei einer relativ niedrigen
Gasphasentemperatur ab, da im Plasma vor allem die Ladungsträger geheizt werden und diese weniger als ein Millionstel der gesamten Teilchen darstellen. Für gute
Schichtqualitäten des mikrokristallinen Materials wird das Substrat auf rund 500 K
erhitzt [62]. Auch auf flexiblen Substraten wurden bereits erfolgreich Tandemzellen
abgeschieden. So erzielte zum Beispiel van den Donker [91] in seiner Dissertation
initiale Tandemzellwirkungsgrade von 9.4 % auf einer Aluminiumfolie, die als temporäres Superstrat dient. Nach der Prozessierung übernimmt eine Polymerfolie die
Substratfunktion und die Aluminiumfolie wird entfernt.
Kapazitive Quellen können skaliert werden und ermöglichen daher auch eine Beschichtung von sehr großen Substraten, die eine immer wichtigere Marktanforderung
darstellen. Allein elektromagnetische Effekte durch die Einkopplung von Wechselspannungen im HF- bzw. VHF-Bereich bringen Homogenitätsprobleme mit sich.
Denen kann teilweise durch konstruktive Maßnahmen entgegengewirkt werden, teilweise stellen sie prozesstechnische Grenzen dar.
Die Maschinen- und Anlagenkosten nehmen bei CCP Quellen einen Großteil der
Herstellungskosten der Tandemmodule ein. Vor allem das benötigte Matching Netzwerk für die Einkopplung der Leistung bei einem minimalen Anteil an reflektierter
Leistung trägt erheblich zu den Kosten bei.
Dadurch, dass es sich um einen Niederdruckprozess handelt, wird die Integrierbarkeit
in die Produktion im Vergleich zu einem Atmosphärendruckverfahren erschwert. Der
angewandte Druck liegt zwischen 210 und 1200 Pa, was Pumpzeiten von rund 15 Minuten mit sich bringt. Bei kapazitiven Quellen ist die Substratfläche im Verhältnis
zur restlichen Kammeroberfläche groß. Dies trägt zu einer sinnvollen Gasausnutzung bei. Darüber hinaus ist die Zusammensetzung des Plasmas in Substratnähe
sehr uniform, was wiederum zu homogenen Schichteigenschaften führt [66]. Durch
die Plasmaregime im oberen Druckbereich (um 1000 Pa) wird verstärkt Staub gebildet. Dem kann durch eine Verringerung des Plattenabstandes und folglich kürzeren
2.2. KAPAZITIV GEKOPPELTE RF-ENTLADUNGEN
23
Gasaufenthaltsdauern entgegengewirkt werden. Gleichzeitig sind die Elektroden bei
einigen Herstellern aufgestellt und um einen kleinen Winkel zur Vertikalen geneigt,
um zu verhindern, dass langkettige Moleküle auf das Substrat fallen.
Insbesondere die Anregungsfrequenz hat einen großen Einfluss auf die Abscheiderate [92]. Mit VHF-Prozessen bei 100 MHz werden Raten von 2.3 nm/s für die
Abscheidung von intrinsischem µc-Si:H erreicht [93], das als Single Junction Zelle
einen Wirkungsgrad von 9.3 % erzielt. Die Reinigung des Reaktors erfolgt üblicherweise mit NF3 , wobei hier nur zwei Drittel des teuren Reinigungsgases umgesetzt
werden. F2 erlaubt höhere Ausnutzungsgrade. Die Reinigungszeit beträgt nach der
a-Si:H Abscheidung rund fünf Minuten, nach der µc-Si:H Abscheidung 30-40 Minuten. Eine Reinigung über eine Remote-Plasmaquelle reduziert die Reinigungszeit
auf rund 15 Minuten.
Es wurde von vielen universitären Gruppen und auch in der industriellen Fertigung gezeigt, dass mit kapazitiv gekoppelten Plasmaquellen gute Schichtqualitäten
erreicht werden können [94]. Die charakteristischen Elektronen-Energie-Verteilungsfunktionen (EEDF) in kapazitiven Quellen sind also prinzipiell zur Bildung der richtigen Radikale geeignet.
Typische Plasmadichten bei CCP Quellen sind 1015 -1016 m−3 und die Elektronentemperatur beträgt 1-5 eV [95]. Ähnliche Werte werden in Simulationen ermittelt:
• ne =7×1014 m−3 , Te =4.7 eV [96]
• ne =6×1014 m−3 , Te =3 eV [47]
• ne =1.5×1015 m−3 , Te =3.3 eV [97]
Neben den Standardquellen für Silan-Wasserstoff-Entladungen gibt es inzwischen
eine Reihe leicht modifizierter CCP Quellen, von denen hier kurz einige aufgezählt
werden sollen:
• gepulste CCP-Plasmen [39]
• Quellen zur Abscheidung aus reinem Silan [98]
• Entladungen bei Zugabe von Disilan [99]
24
2. TECHNOLOG. GRUNDL. ZUR ABSCHEIDUNG VON a-Si:H/µc-Si:H
• mit DC oder LF Bias beaufschlagte Substrate [100] zur Einstellung der Energieverteilung der Ionen
• Quellen mit elektrischem Asymmetrieeffekt mittels Mehr-Frequenz-Einkopplungen [101, 102]
• Multi-Hohlkathoden in der getriebenen Elektrode zur Erhöhung der Abscheiderate (8 nm/s für die Abscheidung von mikrokristallinem Silizium) [103, 104]
• Sanyo präsentiert in [62,105] ein Gasduschenkonzept für eine CVD Quelle mit
lokal begrenztem Plasma, welches hohe Drücke und damit einhergehende hohe
Abscheideraten (2.6 nm/s) ermöglicht. Hierbei vereint die modifizierte getriebene Elektrode Gasdusche und Absaugung. Durch eine Verteilung von sowohl
Ein- als auch Auslasslöchern in der getriebenen Elektrode können stabile und
uniforme Plasmazustände bei hohem Druck (>1000 Pa) realisiert werden.
3 Modellierung von
Niedertemperaturplasmen
Die Modellierung von Niedertemperaturplasmen basiert zunächst auf der Beschreibung der Transportmechanismen der Plasmaspezies (Elektronen, Ionen und Neutralteilchen). Hierzu gehören Konvektion, Diffusion und Drift im elektrischen Feld.
Modelliert wird der Transport entweder durch die Kontinuitätsgleichungen oder die
Bewegungsgleichungen der Spezies. Außerdem werden die elektrischen Felder mit
Hilfe der Maxwell-Gleichungen elektrodynamisch oder der Poisson-Gleichung elektrostatisch beschrieben. Sie entstehen durch das äußere Anlegen von Spannungen
oder das Einkoppeln von Leistung im Zusammenspiel mit der örtlichen Verteilung
der Ladungsträger. Die Kopplung von Plasma und elektrischem Feld ist bei der
Entwicklung von selbst-konsistenten Plasmamodellen sehr herausfordernd, da der
Teilchentransport im Plasma vom elektrischen Feld abhängt und vice versa. Das
Plasma interagiert also sozusagen mit sich selbst.
In dieser Arbeit werden verschiedene Ansätze verfolgt, den Teilchentransport zu
modellieren. Sie werden zu Anfang dieses Kapitels näher erläutert, gefolgt von einer kurzen Erklärung der elektrostatischen Näherung der Maxwell Gleichungen, die
hier ausschließlich verwendet wird. Am Ende folgt eine Definition der in den Modellen verwendeten Plasmachemie, gefolgt von einem Überblick über die in der Arbeit
verwendeten Simulationsumgebungen. Für eine ausführlichere Übersicht über verschiedene Modellierungsansätze für Plasmen wird verwiesen auf [15, 17].
26
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
3.1 Transportgleichungen
Grundsätzlich ist die Beschreibung der Teilchenkinetik entscheidend für die Genauigkeit des Plasmamodells. Einen besonderen Stellenwert haben hier die Elektronen,
da sie im Falle von Argon ein 100.000 mal geringeres Gewicht haben als Ionen und
Neutralteilchen und deshalb selektiv geheizt werden. Sie erreichen sehr hohe Temperaturen von einigen Elektronenvolt und sind für die Erhaltung des Plasmas durch Ionenstoßreaktionen mit Atomen und Molekülen verantwortlich. Auch wenn die Elektronen nur einen Teil der Teilchen im Plasma repräsentieren. Dagegen liegt die Temperatur des Neutralgases und auch der Ionen, im Plasma selbst, nur wenig über der
Umgebungstemperatur. Damit sind Niedertemperatur-/Niederdruckplasmen nicht
im thermodynamischen Gleichgewicht. Je nach aufzulösenden Zeit- und Längenskalen kann der Teilchentransport auf unterschiedliche Art und Weise abgebildet werden. Im Folgenden werden mögliche Beschreibungen, nach Genauigkeit angeordnet,
erläutert. Die benötigte Rechenzeit nimmt von oben nach unten ab:
• Bewegungsgleichungen für einzelne Moleküle und Atome
• Bewegungsgleichungen für Teilchenkollektive (Particle-In-Cell Simulationen, kurz PIC)
• Beschreibung des Phasenraumes mittels Boltzmann-Gleichung
• Boltzmann-Gleichungen für einzelne Spezies nach individuellen Gesichtspunkten (Hybrid-Modelle)
• Navier-Stokes-Gleichungen in Verbindung mit einer 2-Term-Approximation
der Boltzmann-Gleichung
• Navier-Stokes-Gleichungen (Fluid-Modelle)
• Drift-Diffusions-Gleichungen
Die Lösung der Bewegungsgleichungen für einzelne Teilchen und Partikelsimulationen für Teilchenkollektive sind vor allem dann angebracht, wenn die freie Weglänge
in der Größenordnung der geometrischen Abmessungen des Problems liegt. Für höhere Drücke benötigen sie sehr viel Rechenzeit und sind daher ineffizienter.
3.1 TRANSPORTGLEICHUNGEN
27
PIC-Simulationen sind ein Ansatz, um die Beschreibung des Phasenraumes zu erhalten, in dem die Energieverteilungen aller Teilchen explizit berechnet werden. Erste
Arbeiten zur Partikelmodellierung wurden Ende der 50er und Anfang der 60er Jahre
angefertigt [106–108]. Arbeiten, die zum Verständnis von kapazitiven Plasmen beigetragen haben sind in der Literatur zu finden [109–111]. Für statistische Modelle
zur Beschreibung von Kollisionen wird verwiesen auf [112, 113].
Hybride Modelle kombinieren einen Partikelansatz für die Beschreibung des hochenergetischen Teils der Elektronenenergieverteilung mit einem Fluid-Modell für die
Elektronen im Plasmabulk. Sie kommen vor allem in Entladungen zum Einsatz, die
von Sekundärelektronenemission dominiert sind. Diese Sekundärteilchen, die durch
Ionenbeschuss aus der Kathode emittiert und durch die Randschicht beschleunigt
werden, können nicht durch ein Fluid-Modell beschrieben werden.
Im Allgemeinen kommen Hybrid-Modelle immer dann zum Einsatz, wenn die Energieverteilung nicht oder nur schwer approximiert werden kann. Dann wird eine näherungsweise Lösung der Boltzmann-Gleichung zur Bestimmung der ElektronenEnergie-Verteilungsfunktion, kurz EEDF, genutzt. Kann keine Maxwell-Verteilung
angenommen werden, weil z.B. nur der hochenergetische Anteil der Elektronen zur
Ionisation beiträgt, muss die Boltzmann-Gleichung gelöst werden. Die Lösung kann
mittels PIC-Ansatz erfolgen oder es kommen Approximationen, wie die sogenannte Zwei-Term-Näherung [96, 97, 114, 115] zum Einsatz, die jedoch, wie im folgenden
gezeigt (3.1.2), nur unter speziellen Bedingungen gültig ist.
Fluid Modelle basieren auf den Momenten der Boltzmann-Gleichung [116–118], also
der Kontinuumsmeachanik. Erste Fluid-Modelle von kapazitiven Entladungen wurden in den 80er Jahren veröffentlicht [119–122].
Die Knudsen-Zahl Kn ist ein Maß für die Notwendigkeit der statistischen Mechanik
bzw. der Möglichkeit des Einsatzes eines kontinuumsmechanischen Modells. Sie ist
definiert als das Verhältnis zwischen mittlerer freier Weglänge eines Gasmoleküls
und einer geometrischen Bezugslänge. Wie in Abbildung 3.1 gezeigt, verhalten sich
für Kn ≪ 1 die Gaspartikel wie ein Fluid und können über Kontinuumsmodelle
beschrieben werden. Wenn die Knudsen-Zahl nahe oder größer als 1 ist, muss die
kinetische Theorie von Gasen angewandt werden.
28
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
Abb. 3.1: Die Knudsen-Zahl als Charakteristikum einer Strömung (aus [123], mit
freundlicher Genehmigung der Oxford University Press).
Im Folgenden wird auf die in dieser Arbeit verwendeten Modelle eingegangen: den
Particle-In-Cell-Ansatz, die Lösung der Boltzmann-Gleichung durch Vereinfachungen und die Fluid-Approximation.
3.1.1 Partikelansatz
In PIC-Simulationen wird die Trajektorie der Teilchen durch das Lösen der Bewegungsgleichungen
~v =
∂~x
∂t
und
~a =
F~
∂~v
=
∂t
m
(3.1)
berechnet. Durch die Ladung des Teilchens wird das elektrische und magnetische
Feld durch sie beeinflusst und vice versa. Zur Minimierung der Rechenzeit wird
nicht jedes einzelne Teilchen durch eine Bewegungsgleichung abgebildet, sondern
sogenannte Superpartikel, eine Ansammlung von Einzelteilchen einer Sorte, die das
jeweilige Vielfache der Masse und Ladung repräsentieren. Neu entstandene Teilchen,
z.B. durch Kollisionen und damit einhergehenden Reaktionsmechanismen oder durch
Einströmung werden in der Simulation durch neue Superpartikel berücksichtigt, die
dem Simulationsvolumen beim Auftreten dieser Phänomene hinzugefügt werden.
Die Kollisionsrate ist die effektive Anzahl an Kollisionen eines Teilchens pro Zeit.
Sie hängt ab von deren Geschwindigkeiten und deren freien Weglängen λ:
3.1 TRANSPORTGLEICHUNGEN
29
νm =
v
.
λ
(3.2)
Kollisionen werden in PIC-Simulationen durch die Monte Carlo Methode realisiert. Sie ermittelt statistisch das Auftreten der Wahrscheinlichkeit eines Stoßes
zweier Teilchen [109, 113, 124, 125]. Aus den in der PIC-Simulation berechneten
Geschwindigkeiten der Teilchen und deren Orten geht direkt eine ortsaufgelöste
Geschwindigkeits- bzw. Energieverteilung der einzelnen Teilchensorten hervor.
Integration der Bewegungsgleichung
und Bewegung der Teilchen
Fp
Berechnung der Feldkräfte,
die auf die Teilchen wirken
Eij
vp
Δt
Fp
xp
Berechnung der Raumladungsdichte
und Stromdichte auf den Gitterpunkten
(x, v)p
(ρ, j)ij
Monte Carlo Stöße und Entfernung
der Teilchen außerhalb des Reaktors
x
E
Abb. 3.2: PIC Operationen, die in einem Zeitschritt ausgeführt werden.
Das Ablaufschema einer PIC-Simulation und der hier notwendigen Rechenoperationen ist in Abbildung 3.2 dargestellt. Die Startbedingungen definieren die anfängliche Raumladungsdichte und die Stromdichte der Ionen bzw. Elektronen. Hierauf
basierend wird mit der Monte Carlo Methode ermittelt, welche Stöße zwischen den
Teilchen stattfinden. Danach wird über die Raumladungsdichte bzw. die Teilchenpositionen das elektrische Feld berechnet und die Feldkräfte, die auf die Teilchen wirken, ermittelt. Schließlich kann durch die Integration der Bewegungsgleichung der
neue Ort der Teilchen berechnet werden. Die Zeitschrittweite unterliegt bestimmten
Stabilitätskriterien, auf die in Abschnitt 3.4.1 näher eingegangen wird.
30
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
An den Modellgrenzen können die Teilchen absorbiert bzw. reflektiert werden. Zusätzlich kann eine energieabhängige Emission von Sekundärteilchen initiiert werden.
Gängige Feldrandbedingungen, wie die von Dirichlet oder Neumann kommen zum
Einsatz. Für eine detalliertere Darstellung der Grundlagen und für weiterführende
Literatur wird auf [112, 126] verwiesen.
3.1.2 Lösung der Boltzmann-Gleichung
In Niedertemperaturplasmen absorbieren die Elektronen den größten Teil der eingekoppelten Leistung. Diese wird dann in elastischen und inelastischen Stößen mit den
restlichen Teilchen dissipiert. Durch den niedrigen Ionisationsgrad in Niedertemperaturplasmen reichen die Coulomb-Stöße nicht aus, um eine Maxwell-Verteilung der
Elektronen zu etabilieren. Sie müssen folglich kinetisch beschrieben werden. Im Gegensatz dazu absorbieren Ionen im Plasmabulk nur einen kleinen Anteil der Leistung
und stoßen überdies hinaus häufig mit dem Neutralgashintergrund. Für sie reicht
eine Fluidbeschreibung meist aus.
Die Boltzmann-Transport-Gleichung beschreibt die zeitliche Entwicklung der Verteilungsdichte der Elektronen in einem Phasenraum mit drei Raum- und drei Geschwindigkeitsrichtungen, also die Orts- und Geschwindigkeitsverteilung der Elektronen. Das Liouville-Theorem besagt:
df
= 0.
(3.3)
dt
Löst man die totale Ableitung nach partiellen auf, ergibt sich unter Berücksichtigung
der Änderung der Verteilungsfunktion durch Stoßprozesse die Boltzmann-Gleichung:
F~ ∂f
∂f
∂f
∂f df
.
=
+ ~v
+
=
dt
∂t
∂~x m ∂~v
∂t Stöβe
(3.4)
Zur Lösung mittels Zwei-Term-Näherung wird die Verteilung meist in einen isotropen f0 und einen kleinen anisotropen Anteil f1 in Feldrichtung, hier z, zerlegt:
3.1 TRANSPORTGLEICHUNGEN
31
f (~r, ~v , ψ, t) ≈ f0 (~r, |~v|, t) +
vz
f1 (~r, ~v , t),
|~v|
(3.5)
wobei
vz = |~v| cos ψ.
(3.6)
Diese Annahme gilt für hohe elastische Stoßfrequenzen im Vergleich zur Anregungsfrequenz und zur Frequenz der inelastischen Stöße. Setzt man Gleichung 3.5 in die
Gleichung 3.4 ein, so ergibt sich für die z-Richtung:
∂f0
∂f1
∂f0
∂f1
+ cos ψ
+ ~v cos ψ
+ ~v cos2 ψ
∂t
∂t
∂z
∂z
e
∂f ∂f0
e
∂ f1
f1
2
.
cos ψ =
− Ez cos ψ
− Ez
+v
m
∂v
m
v
∂v v
∂t Stöβe
(3.7)
Durch Multiplikation mit sin ψ und Integration über ψ von 0 bis π erhält man:
∂f0 v ∂f1 1 e
1 ∂
∂f0 2
.
v f1 =
+
−
Ez
∂t
3 ∂z
3 m v 2 ∂v
∂t Stöβe
(3.8)
Durch Multiplikation mit sin ψ cos ψ und der selben Integration erhält man:
∂f0
e ∂f0
∂f1
+v
− Ez
= −νm (v)f1 ,
∂t
∂z
m ∂v
mit der Stoßfrequenz νm :
νm = ng σm (v)v,
(3.9)
(3.10)
in Abhängigkeit der Gasdichte ng und des Stoßquerschnitts σm . Da für hohe Drücke
die Teilchenbewegung sehr stark stoßbestimmt ist, kann die Ortsabhängigkeit der
Verteilungsfunktion vernachlässigt werden. Folglich ist die Verteilungsfunktion nur
noch über die elektrischen Felder vom Ort abhängig. Diese Vereinfachung ist unter
der Beschreibung ‘lokale Näherung’ bekannt.
Kortshagen et al. [127] zeigten 1999 , dass die Energie-Relaxations-Länge λǫ [95]:
λǫ ≈
λm λinel
3
1/2
(3.11)
32
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
der zentrale Parameter ist, der die räumliche Inhomogenität der Energie-Verteilungsfunktion beschreibt. Hierbei steht λm mit:
λ−1
m = ng (σel + σex + σiz )
(3.12)
für die freie Weglänge der Elektronen und λinel mit:
λ−1
inel
= ng
2m
σel + σex + σiz
M
(3.13)
für die freie Weglänge der Elektronen bezüglich aller Energieverlustprozesse [95]. Für
die Gültigkeit der lokalen Näherung als Beschreibung der Elektronen im Plasmabulk
muss diese Elektronen-Energie-Relaxations-Länge im relevanten Energiebereich der
Verteilungsfunktion kleiner sein, als die Ausdehnung des Bulks. Für große λǫ , die
im gesamten relevanten Energiebereich die Bulkausdehnung überschreiten, müssen
nicht-lokale Näherungen angewandt werden, da die Ortsabhängigkeit der Verteilungsfunktion nicht mehr zu vernachlässigen ist.
Nach der Berechnung der Energie-Verteilung der Elektronen können daraus die Elektronentransportkoeffizienten wie die Elektronenmobilität µe
4πe
µe = −
3mne
Z
∞
0
v 3 dfe0
dv,
νm (v) dv
(3.14)
der Diffusionskoeffizient für die Elektronen De
4π
De =
3ne
Z
0
∞
v4
fe0 dv
νm (v)
(3.15)
und die Raten für inelastische Elektronenkollisionen kj mit Neutralteilchen j bestimmt werden. Auf die Raten wird in Kapitel 3.3 näher eingegangen.
Eine Vorgehensweise ist die der Erstellung sogenannter Zuordnungstabellen, in denen eine Reihe von reduzierten elektrischen Feldern und die zugehörigen Elektronentransport- und Ratenkoeffizienten durch die Lösung der Boltzmann-Gleichung
gelistet werden. Das reduzierte elektrische Feld E/ng ist der Quotient aus dem elektrischen Feld und der Teilchendichte des Gases. Auf diese Wertetabelle wird dann
3.1 TRANSPORTGLEICHUNGEN
33
z.B. in der Fluid-Simulation zurückgegriffen.
Das frei erhältliche Softwarepaket BOLSIG+ [18] basiert auf der in diesem Kapitel (3.1.2) eingeführten Zwei-Term-Näherung. Zur Vereinfachung der BoltzmannGleichung wird die lokale Näherung verwendet, wobei die Verteilung wahlweise vom
reduzierten elektrischen Feld oder von der mittleren Teilchenenergie abhängig ist.
Der Löser wird in [18] näher erläutert. In den hier betrachteten Wechselfeldern ermittelt er stationäre Lösungen der Boltzmann-Gleichung für Elektronen, unter Berücksichtigung von Elektronenkollisionen mit Neutralteilchen und von ElektronenElektronen-Kollisionen.
Eine andere mögliche Vereinfachung der sechs-dimensionalen Boltzmann-Gleichung
ist die Reduktion zu einer vier-dimensionalen Fokker-Planck Form mit drei Ortsund einer Energievariablen. Diese Approximation gilt für kleine freie Weglängen im
Vergleich zur Elektronen-Energie-Relaxations-Länge und wird im kommerziell erhältlichen Softwaretool CFD-ACE+ angewandt. Auch hier kommt die Zwei-TermNäherung zur Lösung zum Einsatz.
3.1.3 Kontinuumsbetrachtung
Die Erhaltungsgleichungen der Kontinuumsmechanik ergeben sich aus einer Integration der Boltzmann-Gleichung (Gleichung 3.4) [128].
Berechnet man die n-ten Momente der Boltzmann-Gleichung f (~v) gemäß:
Z
~v ...~v ...(n
v)d
T erme) f (~
3
(3.16)
~v ,
so erhält man also die Erhaltungsgleichungen unter der Annahme einer MaxwellBoltzmann-Verteilung, gemäß:
f (~v) =
Das 0-te Moment
Z
∂f
d~v +
∂t
Z
m
2πkB T
3/2
∂f
~v ·
d~v +
∂~x
e−
m~
v2
T
.
(3.17)
Z ~
F ∂f
·
d~v = 0
m ∂~v
(3.18)
34
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
ergibt nach Vereinfachung [128] die Kontinuitätsgleichung:
∂n
+ ∇ · (n~v ) = 0.
∂t
Das erste Moment
Z
Z
Z
F~ ∂f
∂f
∂f
d~v + m~v · ~v
· d~v + m~v ·
· d~v = 0
m~v ·
∂t
∂~x
m ∂~v
(3.19)
(3.20)
ergibt nach Vereinfachung [128] die Impulsbilanz:
∇p ~ nq ~
∂~v
F~
~ − ∇p + S,
~
E + ~v × B
+ (~v · ∇) ~v = n −
+S =
n
∂t
m
m
m
m
(3.21)
~ für die Streutherme durch die Kollisionen steht und durch die Impulsrelawobei S
xationszeit τm angenähert werden kann:
~ = − n~v .
S
τm
Somit ergibt sich für die Stoßrate νm :
νm =
(3.22)
1
.
τm
(3.23)
Das zweite Moment
Z
1 2 ∂f
mv
d~v +
2
∂t
Z
1 2 ∂f
mv ~v
· d~v +
2
∂x
Z
1 2 F~ ∂f 3
mv
·d v =0
2
m ∂~v
(3.24)
ergibt nach Vereinfachung [128] die Energiebilanz:
∂
nhǫi + ∇nhǫi · ~v + p∇ · ~v + ∇q − n~v · F~ = Pabs ,
∂t
(3.25)
wobei hǫi die mittlere Energie der jeweiligen Teilchensorte ist und die Leistungsdichte Pabs für die Energie steht, die von der jeweiligen Teilchensorte absorbiert wird.
Wie dieser Transfer, der von außen angelegten Leistung Pext insbesondere zu den
Elektronen im Plasma abläuft, beschreiben die Heizmechanismen. Ohmsche Heizung bedeutet in diesem Zusammenhang, dass die von den Elektronen durch das
elektrische Feld aufgenommene Energie in einem Stoßprozess in thermische Energie
umgesetzt wird. Je größer der Druck ist, desto dominanter ist die ohmsche Heizung.
3.1 TRANSPORTGLEICHUNGEN
35
Die stochastische Heizung ist ein typischer Effekt in kapazitiven RF Entladungen.
Sie tritt dadurch auf, dass Elektronen, vom Plasmabulk kommend, auf die Randschichtkante treffen, um von dort aus in den Bulk zurück reflektiert zu werden. Die
stochastische Heizung ist in Plasmen wichtig, in denen geringe Stoßraten herrschen.
Für die mathematische Beschreibung der einzelnen Terme in den Kontinuitätsgleichungen wird auf die Dokumentation der jeweiligen Software verwiesen [129].
3.1.4 Drift-Diffusions-Modell
Für die Berechnung von Strömungen mit ausreichend kleinen Knudsen-Zahlen gelten also die oben hergeleiteten Erhaltungssätze für Masse, Impuls und Energie. Zur
Herleitung der Drift-Diffusionsgleichung [130] wird letzteres vorausgesetzt. Das Umstellen der Impulserhaltung, wie hier exemplarisch für die Elektronen, ergibt:
1
1 F~
1 ∇p
1 ∂~v
+
(~v · ∇) ~v =
−
− ~v .
νm ∂t νm
νm m νm nm
(3.26)
Im Drift-Diffusions-Modell wird nun die linke Seite von Gleichung 3.26 vernachlässigt. Die Vernachlässigung des transienten Terms ist gerechtfertigt, wenn man
annimmt, dass die Impulsrelaxationszeit im Vergleich zur Anregungsfrequenz sehr
klein ist:
νRF ≪ νm ⇒
1 ∂~v
≪ ~v .
νm ∂t
(3.27)
Die Vernachlässigung des zweiten Terms bewirkt, dass die Konvektion außer Acht
gelassen und von reiner Diffusion ausgegangen wird. Dies gilt für kontinuierliche Medien (Kn ≪ 1) und geringe gerichtete Bewegungen der Teilchen (Driftgeschwindigkeit) im Vergleich zu ihrer ungeordneten Bewegung (thermische Geschwindigkeit):
1 1
1
(~v · ∇) ~v ≈ ~vth ~v ~v ≪ ~v .
νm
L
λ
(3.28)
Verwendet man nun die Definition der Stromdichte je , der Ladungsträgerbeweglichkeit µe , des elektrischen Feldes E und des idealen Gasgesetzes:
~je = −en~v ,
(3.29)
36
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
µe =
e
τm ,
me
~
~ = F,
E
e
p = nkB T,
(3.30)
(3.31)
(3.32)
so erhält man:
~
~ − µe ∇ (nkB T ) + je .
0 = µe nE
e
e
Mithilfe der Einstein-Relation:
(3.33)
µe kB T
e
(3.34)
~ = −∇Φ
E
(3.35)
De =
und des elektrischen Potentials Φ
ergibt sich schließlich die Drift-Diffusions-Gleichung:
~je = eµe n∇φ + eDe ∇n.
(3.36)
Die Gültigkeit des Drift-Diffusions-Ansatzes ist also gegeben, wenn die Stoßfrequenz
größer ist als die Anregungsfrequenz. Für Argon-Entladungen bei 13.56 MHz ist dies
für Elektronen bei einem Hintergrundgasdruck von einigen 10 Pa der Fall [131]. Für
kleinere Drücke und höhere Frequenzen wird die Trägheit der Elektronen wichtig, es
müssen also die kompletten Transportgleichungen gelöst werden. Die gleichen Voraussetzungen an die Gültigkeit des Drift-Diffusions-Ansatzes gelten für die Ionen.
Sind die Ionenkollisionen nicht dominant wie z.B. in stoßfreien Randschichten bei
Niederdruck, muss die Ionenimpulserhaltung anstelle dieses Ansatzes gelöst werden.
Die obigen Fluidgleichungen, bestehend aus Massen- (3.19), Impuls- (3.21) und Energieerhaltung (3.25), stellen kein geschlossenes Gleichungssystem dar, da die Stoßfrequenz nicht in Abhängigkeit von Dichte, mittlerer Geschwindigkeit und Energie
ausgedrückt werden kann. (Auf die Bestimmung des elektrischen Feldes wird in
Kapitel 3.2 eingegangen.) Die Bestimmung der Stoßfrequenz, die in die Transport-
3.2 ELEKTROSTATISCHE NÄHERUNG
37
und Ratenkoeffizienten eingeht, wie hier z. B. von Elektronen mit dem neutralen
Hintergrundgas, erfolgt über die Mittelung der Energieverteilung:
Z
1 ∞
νm =
ng σm (ǫ)ǫfe (ǫ)dǫ,
(3.37)
ne 0
die in reinen Fluid-Modellen, wie sie für die Ionen und das Hintergrundgas gültig
sind, meist als Maxwell-verteilt angenommen oder über die Boltzmann-Gleichung
berechnet wird.
3.2 Elektrostatische Näherung
Die Maxwell Gleichungen beschreiben die Eigenschaften der elektrischen und magnetischen Felder und erlauben die Untersuchung von Plasmen in Wechselfeldern und
die Propagation von elektromagnetischen Wellen. Sie bestehen aus den folgenden
vier partiellen Differentialgleichungen:
• Gausssches Gesetz:
~ =ρ
ǫ0 ∇ · E
(3.38)
• Gausssches Gesetz für Magnetismus:
~ =0
∇·B
(3.39)
• Faradaysches Induktionsgesetz:
~ =−
∇×E
~
∂B
∂t
(3.40)
• Amperesches Durchflutungsgesetz:
~
1
~ − ǫ0 ∂ E = ~j.
∇×B
µ0
∂t
(3.41)
In der Elektrostatik wird der Effekt der Induktion in Form der zeitlichen Ableitung
des magnetischen Feldes im Faradayschen Gesetz vernachlässigt. Gleichung 3.40 wird
zu:
38
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
~ =0
∇×E
(3.42)
und man kann ein skalares Potential einführen:
~ = −∇Φ.
E
(3.43)
In Folge vereinfachen sich die Maxwell Gleichungen zur skalaren Poisson Gleichung:
− ǫ0 ∇2 Φ = ρ = e
X
i
qi ni − ne
!
.
(3.44)
Die sogenannte elektrostatische Näherung gilt, solange nur Phänomene kleiner als
die Plasmafrequenz ωpe von Interesse sind.
3.3 Plasmachemie
Im Plasma laufen je nach Art der Gaszusammensetzung und Plasmabedingungen
verschiedene Stoßprozesse ab. Sie werden unterteilt in Ladungsaustauschstöße, elastische und inelastische Stöße (Ionisationen, Dissoziationen, Anregungen), chemische
Reaktionen und Neutralisationsreaktionen. Die Beschreibung der Stoßprozesse in
der Gasphase erfolgt am einfachsten über Reaktionsratenkoeffizienten KAB für die
miteinander stoßenden Teilchen A und B. Die Ratenkoeffizienten der chemischen
Reaktionen sind meist für einen bestimmten Temperaturbereich gültig und können
daher für eine konstante Gastemperatur in der Simulation auch als konstant angenommen werden. Für Elektronen- und Ionenstoßprozesse ist dies nicht der Fall, da
sie stark in Abhängigkeit der Temperatur der Ladungsträger variieren. Man erhält
die Koeffizienten dann aus dem Wirkungsquerschnitt des entsprechenden Stoßes σAB
durch eine Integration über die Elektronen- beziehungsweise Ionenenergieverteilung
f , abhängig davon ob es sich um eine Elektronen- oder eine Ionenstoßreaktion handelt:
KAB (T ) = hσAB vR i =
Z
∞
0
2
f vR σAB (vAB )4πvAB
dvAB .
(3.45)
Ratengleichungen beschreiben die zeitliche Änderung der Teilchendichte n von Atomen oder Molekülen:
3.3 PLASMACHEMIE
39
dn
= −nne hσm vR i
dt
(3.46)
und man erhält als Lösung der Differentialgleichung die Teilchendichte als Funktion
der Zeit:
−t
n(t) = n(t = 0)e−tne hσm vR i = n(t = 0)e τ ,
(3.47)
wobei τ für die Reaktionszeit steht.
Der Wirkungsquerschnitt σm für die Reaktionen kann sowohl theoretisch als auch
experimentell bestimmt werden, wie die zwei folgenden Beispiele zeigen. So hat Allen im Jahr 1976 [132] die Reaktionen von verschiedenen Deuterium-Molekülen mit
verschiedenen Silan-Wasserstoff-Verbindungen untersucht und die zugehörigen Kollisionsquerschnitte ermittelt. Hierzu hat er zwei Massenspektrometer und eine kollisionsfreie Reaktionskammer verwendet. Der Aufbau ermöglichte ihm die Injektion
von Ionen bestimmter Masse und einer minimalen Energie von 1 eV in die Kammer,
die den Reaktionspartner enthielt. Die in den Reaktionen produzierten Ionen wurden
bezüglich ihrer Masse analysiert und so wiederum identifiziert. Folglich konnte man
die Kollisionsquerschnitte mithilfe der Ionenströme der Edukte IE und der Produkte
IP und der Gasdichte n in der Kammer berechnen:
σ=
IP 1
,
IE nl
(3.48)
wobei l für die Länge der Kammer steht. Als Beispiel für eine theoretische Bestimmung der Wirkungsquerschnitte soll Hickman [133] herangezogen werden. Er nutzt
für die wechselseitige Neutralisierung von positiven und negativen Ionen ein komplexes Potentialmodell. Die Quellen der Ratenkoeffizienten bzw. Wirkungsquerschnitte für die in dieser Arbeit relevanten Reaktionsprozesse werden in den jeweiligen
Unterkapiteln 3.3.1 und 3.3.2 zitiert. Oberflächenreaktionen werden üblicherweise
gemäß [134, 135] mit Hilfe eines sogenannten Sticking Modells, wie in Kapitel 2.1.2
eingeführt, beschrieben. Im Folgenden wird für die in dieser Arbeit behandelten
Gase, näher auf die Wirkungsquerschnitte und die Oberflächenreaktionswahrscheinlichkeiten eingegangen.
40
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
3.3.1 Argon-Chemie
Tab. 3.1: Die in dieser Arbeit berücksichtigten Argonreaktionen.
Nr.
R1
R2
R3
R4
Reaktion
Ar + e → Ar + e
Ar + e → Ar∗ + e
Ar + e → Ar+ + 2e
Ar + Ar+ → Ar+ + Ar
Schwellenenergie (eV)
0
11.5
15.8
0
Ref. σm
[136]
[136]
[136]
[136]
Die für die Argonentladungen berücksichtigten Kollisionen beinhalten elastische Stöße der Elektronen mit dem Hintergrundgas, Ionisationsstöße, Anregungsstöße und
Ladungsaustauschstöße zwischen den Argonionen und den Hintergrundatomen (s.
Tabelle 3.1). Die Kollisionsquerschnitte stammen von Phelps [136] und sind in Abbildung 3.3 dargestellt. Was die Anregungen betrifft, werden die von Phelps für alle
Anregungsstöße zusammengefassten Querschnitte verwendet. Da der Querschnitt
für die Ladungsaustauschreaktion in einem der verwendeten Tools (CFD-ACE+)
nur über einen konstanten Wert approximiert werden kann, wird jeglicher Modellierung diese Approximation zugrunde gelegt.
3.3.2 Silan-Chemie
Die in dieser Arbeit umgesetzte Silan-Wasserstoff-Chemie basiert auf den Veröffentlichungen von Nienhuis [42, 96], De Bleecker [47] und Salabas [97]. Die Gegenüberstellung dieser Arbeiten zu Silan-Wasserstoff-Simulationen [42, 47, 96, 97] und der
darin betrachteten Reaktionen beziehungsweise Spezies soll einen Überblick über
die Unterschiede und die hier umgesetzten Ergänzungen bzw. Änderungen geben.
Nienhuis modellierte in seiner Dissertation [96] eine kapazitive Silan-WasserstoffEntladung für die Abscheidung von amorphem Silizium mit einem Fluid-Ansatz,
kombiniert mit einem Löser für die Boltzmann-Gleichung zur Berechnung der EEDF.
Die Ergebnisse wurden in folgendem Artikel veröffentlicht: [42]. Er weist explizit
3.3 PLASMACHEMIE
41
−18
σ / m2
10
−20
10
−22
10
Ionisation
elastischer Stoß
Anregung
Ladungsaustausch
−2
10
0
2
10
10
Energie / eV
4
10
Abb. 3.3: Stossquerschnitte für Argon.
auf die Wichtigkeit von Silanen höherer Ordnung, insbesondere von Disilan hin.
In einer Sensitivitätsanalyse wurden 24 Spezies, 15 Elektronenstoßreaktionen und
22 chemische Reaktionen ausfindig gemacht, um die Entladung hinreichend gut zu
beschreiben. Elastische und inelastische Stöße von Elektronen werden nur in Verbindung mit SiH4 , Si2 H6 und H2 betrachtet. Es wird auf die Bedeutung von atomarem
Wasserstoff hingewiesen, der in fast allen dieser inelastischen Stöße entsteht. Als
Dissoziationsprodukte werden neben dem atomarem Wasserstoff ausschließlich SiH3
und SiH2 betrachtet. SiH3 reagiert im Vergleich zu SiH2 nicht mit SiH4 oder H2
(siehe Tabelle 3.6) und ist daher sehr langlebig und verantwortlich für das Schichtwachstum. SiH2 ist Vorreiter für die Bildung von Silanen höherer Ordnung (siehe
Tabelle 3.6).
+
Als Ionisationsprodukte von SiH4 , Si2 H6 und H2 werden ausschließlich SiH+
2 , Si2 H4
und H+
2 betrachtet. Querschnitte, die zu anderen Ionen führen würden, werden hier
zu den Querschnitten, verantwortlich für die Bildung dieser drei Ionen, addiert.
Potzinger et al. [137] und Morrison et al. [138] konnten zeigen, dass Silan immer
zuerst dissoziiert und anschliessend ionisiert wird. Dies erklärt das Ausbleiben von
−
−
SiH+
4 -Ionen. Als negatives Ion wird nur SiH3 berücksichtigt. Si2 H5 wird mit der
Begründung vernachlässigt, dass das zugehörige Edukt Si2 H6 einen viel geringeren
Partialdruck aufweist als das Ausgangsmolekül von SiH−
3 , SiH4 . Die Bildung von
negativen Ionen ist ein typischer Effekt von Silan-Wasserstoff-Plasmen. Sie führen
42
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
zu einer elektronegativen Entladung mit einer negativen Ionendichte, die nach Nienhuis Berechnungen um einen Faktor 30 höher ist, als die Elektronendichte. Um
das Plasma aufrecht zu erhalten, muss also ausreichend ionisiert werden, d. h. es ist
ein, im Vergleich zu einer Edelgasendtladung höherer Energieeintrag notwendig.
Die Anregung des Hintergrundgases, also von SiH4 und H2 , wird allein als Energiesenke für die Elektronen simuliert. Dichten der angeregten Spezies werden nicht
berechnet. Die Anregungen von weiteren Molekülen wird wegen fehlender Querschnitte vernachlässigt.
Negative Ionen können durch das positive Plasmapotential nicht an die Reaktorwände wandern. Sie bilden entweder längerkettige Polymere oder werden neutralisiert [139]. Die Ratenkonstante für diese gegenseitige Neutralisation kann berechnet
werden [133] durch:
KN = 5.34 · 10
−13
A−0.4
m−0.5
e
ij
TGas
300
−0.5
.
(3.49)
TGas steht hier für die Gastemperatur in Kelvin (bei Nienhuis: TGas =400 K), Ae für
die Elektronenaffinität des Radikals in eV und mij ist die reduzierte Masse der beiden
+
Ionen in atomarer Masseneinheit. Aus der Neutralisation von SiH−
3 und Si2 H4 gehen
bei Nienhuis SiH3 und 2SiH2 hervor, um keine neue Spezies wie Si2 H4 einführen zu
müssen.
Größere Moleküle als Si8 H18 werden vernachlässigt. Da die Abspaltung von Wasserstoff durch Kollisionen von Silanen mit atomarem Wasserstoff wichtig sind, werden
zu allen Sin H2n+2 auch die zugehörigen Sin H2n+1 mitsimuliert.
Zwei SiH3 -Radikale reagieren bei Nienhuis zu SiH4 und SiH2 mit der Begründung,
dass Si2 H6 auch wieder in die selben Produkten zerfallen würde. Laut Perrin [140]
geschieht dies jedoch nur bei hohen Drücken.
Chemische Reaktionen von positiven Ionen mit dem Hintergrundgas werden der
Einfachheit halber nicht berücksichtigt. Die Oberflächenchemie beschreibt Nienhuis über ein sticking-Modell, durch welches die Interaktion der Radikale mit der
Grenzfläche beschrieben wird. Auf die Reaktion der Ionen und angeregten Spezies
an Oberflächen wird nicht näher eingegangen, was zu der Annahme führt, dass diese
neutralisiert beziehungsweise abgeregt werden. Die Emission von Sekundärelektronen wird vernachlässigt.
3.3 PLASMACHEMIE
43
De Bleecker erweiterte in ihrer Dissertation [47] das Chemiemodell von Nienhuis
um Reaktionen, die zur Staubbildung führen, veröffentlicht in [48]. Hierzu werden
zusätzlich bivalente Siliziummoleküle (sogenannte „Silylene “, Sin H2n ) betrachtet,
deren negative Ionen mitverantwortlich für die Bildung von langkettigen Molekülen
sind. Nienhuis hatte hier allein SiH−
3 als negatives Ion mitsimuliert, das durch dissoziatives Anlagern eines Elektrons an SiH4 entsteht. De Bleecker führt zusätzlich
dissoziatives Anlagern von Elektronen zu SiH−
2 ein.
+
+
Bei den positiven Ionen beschränkt sich De Bleecker auf SiH+
3 , Si2 H4 und H2 . De
Bleecker geht im Gegensatz zu Nienhuis von der Bildung von SiH+
3 anstelle von
+
SiH2 aus. Genauso wie bei Nienhuis werden hier die Querschnitte, die zur Bildung
anderer Ionen führen würden, zu den Querschnitten, verantwortlich für die Bildung
dieser drei Ionen, addiert. Die gleiche Näherung wird bei der Bildung von negativen
Ionen durch dissoziatives Anlagern von Elektronen an SiH4 angewandt, da die Reaktionswahrscheinlichkeiten für die Bildung von SiH− und Si− sehr gering sind.
Salabas simuliert in seiner Doktorarbeit sowohl reine Wasserstoff-, als auch SilanWasserstoff-Entladungen. Er betrachtet im Vergleich zu den anderen Arbeiten, zu+
+
+
sätzlich zum Wasserstoffion H+
2 , die Bildung von H - und H3 -Ionen [141]. H entsteht über die dissoziative Ionisation von H2 mittels Elektronenstoß und H+
3 ent+
steht über eine exotherme Ladungsaustauschreaktion von H2 mit H2 [142]. Für die
Neutralisierung der drei Wasserstoffionen kommt in dieser Arbeit auch die Rekombination mit Elektronen in Frage. Im Gegensatz zu Nienhuis und de Bleecker wird
hier zwischen der Bildung von SiH2+ und SiH3+ unterschieden.
+
Wie bei Salabas werden in der vorliegenden Arbeit die positiven Ionen H+
2 , H3 ,
+
+
SiH+
2 , SiH3 und Si2 H4 berücksichtigt. Da der dissoziative Ionisationsprozess von
Wasserstoff zu H+ einen deutlich kleineren Querschnitt aufweist als der Stoß zu H+
2,
wird dieser, wie bei Nienhuis [96] und de Bleecker [47], vernachlässigt. Die zur Ionisation, Dissoziation und Anregung benötigten Schwellenenergien sind in Tabelle 3.2
für die entsprechenden resultierenden Zustände aufgelistet.
44
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
Tab. 3.2: Schwellenenergie für die Generation von Ionen, angeregten und dissoziierten Spezies aus SiH4 , H2 und Si2 H6 .
Spezies
SiH2
SiH3
SiHv13
4
SiHv24
4
SiH∗4
SiH−
3
SiH+
2
SiH+
3
H+
2
H (b 3 Σ+
u)
N2
H
HN3
Hv01
2
Hv02
2
Hv03
2
H2 a 3 Σ+
g
H2 (B 1 Σ+
u)
1
H2 (C Πu )
H2 (c 3 Πu )
3
H2 (d
PΠu ) H2
Rydberg
HJ02
2
Si2 H+
4
SiH3
Schwellenenergie (eV)
8.3
8.3
0.27
0.113
7.8
5.7
11.9
11.9
15.4
8.9
15.
16.6
0.54
1.08
1.62
11.8
11.3
12.4
11.75
14.
Ref.
[143]
[143]
[144]
[144]
[145]
[146]
[147]
[147]
[148]
[149, 150]
[149]
[149]
[149]
[149]
[149]
[149, 150]
[149, 150]
[149, 150]
[149, 150]
[149, 150]
15.2
[149, 150]
0.044
10.2
7.
[149, 150]
[147]
[143]
3.3 PLASMACHEMIE
45
Tab. 3.3: Die in dieser Arbeit berücksichtigten elastischen Stöße und Ladungsaustauschreaktionen für Silan-Wasserstoff-Plasmen.
Nr.
Reaktion
R1
R2
R3
R4
R5
R6
R7
R8
R9
R10
R11
SiH4 + e → SiH4 + e
H2 + e → H2 + e
+
SiH−
3 + H2 → SiH3 + H2
+
SiH−
3 + H3 → SiH4 + SiH2
+
SiH−
3 + SiH2 → SiH3 + SiH2
+
SiH−
3 + SiH3 → SiH3 + SiH3
SiH+
2 + e → SiH2
+
SiH3 + e → SiH2 + H
+
H+
2 + H2 → H3 + H
H+
2 + e → H + H
+
H3 + e → H2 + H
*
Rate
[cm3 s− 1]
f (σm )
f (σm )
4.8·10−7
1.2·10−6
1.0·10−5
1.2·10−7
1.13·10−7
1.69·10−7
f (σm )
5.66·10−11
9.75·10−11
Ref.
[145], [144]
[149]
[133]
[133]
[133]
[133]
[140]
[140]
[151]∗
[140]
[140]
Exotherme Reaktion: 1.71 eV.
−18
10
−19
σ / m2
10
−20
10
−21
10
R1
R2
R9
−22
10
−2
10
0
10
Energie / eV
2
10
Abb. 3.4: Stossquerschnitte der elastischen Stöße und Ladungsaustauschstöße in
Silan-Wasserstoff-Plasmen entsprechend Tabelle 3.3.
46
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
Tab. 3.4: Die in dieser Arbeit berücksichtigten inelastischen Elektronen-SilanKollisionen.
Nr.
R12
R13
R14
R15
R16
R17
R18
R19
R20
R21
Reaktion
SiH4 + e
SiH4 + e
SiH4 + e
SiH4 + e
SiH4 + e
SiH4 + e
SiH4 + e
SiH4 + e
Si2 H6 + e
Si2 H6 + e
→
→
→
→
→
→
→
→
→
→
Ref.
2e
[147]
[144]
[144]
[145]
SiH3 + H + e
[145]
SiH2 + 2H + e
[145]
−
SiH3 + H
[146]
+
SiH2 + 2H +2e
[147]
Si2 H+
[147]
4 + 2H +2e
SiH3 + SiH2 + H + e [143]
SiH+
3 + H +
SiHv13
+e
4
SiHv24
+e
4
∗
SiH4 + e
−18
σ / m2
10
R12
R13
R14
R15
R16
R17
R18
R19
R20
R21
−20
10
−22
10
−1
10
0
10
1
10
Energie / eV
2
10
Abb. 3.5: Stossquerschnitte der inelastischen Silan-Stöße entsprechend Tabelle 3.4.
3.3 PLASMACHEMIE
47
Tab. 3.5: Die in dieser Arbeit berücksichtigten inelastischen Elektronen-WasserstoffKollisionen.
Nr.
R22
R23
R24
R25
R26
R27
R28
R29
R30
R31
R32
R33
R34
R35
Reaktion
H2 + e
H2 (b 3 Σ+
u) + e
H2 + e
H2 + e
H2 + e
H2 + e
H2 + e
H2 + e
H2 + e
H2 + e
H2 + e
H2 + e
H2 + e
H2 + e
→
→
→
→
→
→
→
→
→
→
→
→
→
→
H+
2
+ 2e
H+H+e
H2 (B 1 Σ+
u) + e
3
H2 (c Πu ) + e
H2 (a 3 Σ+
g) + e
H2 (C 1 Πu ) + e
H2 (d 3 Πu ) + e
H2 + e (Rydberg)
+e
Hv01
2
v02
H2 + e
Hv03
+e
2
HN2 + HN2 + e
HN1 + HN3 + e
HJ02
+e
2
−19
10
−20
σ / m2
10
−21
10
−22
10
−23
10
0
2
10
Ref.
[148]
[150, 152]
[149, 150]
[149, 150]
[149, 150]
[149, 150]
[149, 150]
[149, 150]
[153]
[153]
[153]
[149]
[154]
[149, 150]
R22
R23
R24
R25
R26
R27
R28
R29
R30
R31
R32
R33
R34
R35
10
Energie / eV
Abb. 3.6: Stossquerschnitte der inelastischen Wasserstoff-Stöße entsprechend Tabelle 3.5.
48
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
Zugehörig zu den Ionen werden deren Reaktionen mit Neutralteilchen, also Reaktion
9, 37 und 59 bis 64 in den Tabellen 3.3 bis 3.6, abgebildet. In diesen Tabellen sind
alle Reaktionen, unterteilt in elastische und Ladungsaustauschstöße, ElektronenSilan-Kollisionen, Elektronen-Wasserstoff-Kollisionen und chemische Reaktionen, in
denen keine Elektronen beteiligt sind, aufgelistet. In den Abbildungen 3.4 bis 3.6
sind entsprechend die dazugehörigen Wirkungsquerschnitte dargestellt. Als negatives Ion wird, gemäß der Argumentation von Nienhuis, nur SiH−
3 betrachtet. Negative
Ionen sind, aufgrund des positiven Plasmapotentials, zwischen den Randschichten
eingeschlossen. Positive Ionen erfahren in der Randschicht im Gegensatz dazu einen
Drift nach außen und prallen auf die Oberfläche. Nach Perrin [140] ist die Reaktionswahrscheinlichkeit dieser Ionen sehr hoch, da sie durch Elektronen, zum Beispiel
Auger-Elektronen, neutralisiert werden und dann über dissoziative Chemisorption
zum Schichtwachstum beitragen.
Diesbezüglich werden in den folgenden Modellen Neutralisationsreaktionen, wie Reaktion Nummer 7, 8, 10 und 11 abgebildet. Dies ermöglicht die Berechnung der
Zusammensetzung der Ionen, was nicht im Fokus von Nienhuis, de Bleecker und
Salabas stand.
Darüber hinaus werden, im Vergleich zu den drei beschriebenen Arbeiten, die Anregungsreaktionen 15, 24-29 und 33-35 hinzugefügt. Schließlich wird ein Silan-Wasserstoff-Plasma, bestehend aus 27 verschiedenen Spezies und 64 Reaktionsmechanismen
betrachtet. Einige Mechanismen sind es wert, auf ihre Besonderheiten hinzuweisen:
Die Elektronenstoßionisation von SiH4 führt zu SiH+
3 . Alle Querschnitte, die zu anderen Ionen führen, werden im Querschnitt der Ionisation zu SiH+
2 zusammengefasst.
+
Die Ionisation von Si2 H6 führt zu Si2 H4 als häufigstes Ionisationsprodukt. Die Dissoziation von Silan in Reaktion 16 und 17 führt im Verhältnis 17:83 zu SiH3 bzw.
zu SiH2 .
Anregungsstöße durch Elektronen sind wichtig, da sie für den Hauptenergieverlust
der Elektronen verantwortlich sind. Die daraus hervorgehenden angeregten Spezies
können wiederum ionisiert oder dissoziiert werden. Jedoch sind die Stoßquerschnitte
dieser Reaktionen nur selten in der Literatur zu finden. Deshalb werden angeregte
Spezies vereinfachend zu deren zugehörigen Grundzuständen aufsummiert.
Nr.
R36
R37
R38
R39
R40
R41
R42
R43-R48
R49
R50
R51
R52
R53-R57
R58
R59
R60
R61
R62
R63
R64
Reaktion
+
SiH−
3 + Si2 H4
SiH+
3 + SiH4
SiH3 + SiH3
SiH3 + H
SiH4 + H
Si2 H6 + H
Si2 H6 + H
Sin H2n+2 + H
SiH2 + H2
SiH4 + SiH2
Si2 H6 + SiH2
Si2 H6 + SiH3
Sin H2n+2 + SiH2
Si2 H5 + Si2 H5
SiH4 + H+
2
SiH4 + H+
3
SiH4 + SiH+
2
SiH4 + SiH+
2
Si2 H6 + SiH+
2
Si2 H6 + SiH+
2
→
→
→
→
→
→
→
→
→
→
→
→
→
→
→
→
→
→
→
→
Rate [cm3 s− 1]
SiH3 + 2SiH2
1.0·10−7
Si2 H+
6.0·10−11
4 + 1.5H2
SiH4 + SiH2
1.5·10−10
SiH2 + H2
8.0·10−11
SiH3 + H2
2.8·10−11 exp(-1250/TGas )
Si2 H5 + H2
0.8·10−10 exp(-1250/TGas )
SiH3 + SiH4
1.6·10−10 exp(-1250/TGas )
Sin H2n+1 + H2 (2<n<9) 2.4·10−10 exp(-1250/TGas )
SiH4
3.0·10−12 (1-(1+2.3·10−4p0 )−1 )
Si2 H6
2.0·10−10 (1-(1+0.0032p0)−1 )
Si3 H8
4.2·10−10 (1-(1+0.0033p0)−1 )
SiH4 + Si2 H5
4.1·10−10 exp(-1250/TGas )
Sin+1 H2n+4 (2<n<8)
4.2·10−10 (1-(1+0.0033p0)−1 )
Si3 H8 + SiH2
1.5·10−10
SiH+
f (σcol )
3 + H2 + H
+
SiH3 + H2 + 2H
f (σcol )
+
SiH3 + SiH3
1.1·10−9
8.2·10−10
Si2 H+
4 + H2
SiH+
1.5·10−9
3 + Si2 H5
Si2 H+
1.3·10−9
4 + SiH4
Ref.
[133]
[133]
[140]
[140]
[140]
[140]
[140]
[140]
[140]
[140]
[140]
[140]
[140]
[140]
[132]
[132]
[140]
[140]
[140]
[140]
3.3 PLASMACHEMIE
Tab. 3.6: Die in dieser Arbeit berücksichtigten chemischen Reaktionen.
49
50
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
Der Fokus dieser Arbeit besteht nicht darin, im Vergleich zu den zitierten Quellen,
zusätliche Reaktionen hinzuzufügen. Es geht vielmehr darum, chemische Reaktionen mit vorhandenen Stoßquerschnitten zur Abbildung des Abscheideprozesses von
Dünnschicht-Silizium anzuwenden.
Tab. 3.7: Im Modell berücksichtigte Oberflächenreaktionen.
Species
H
SiH2
Sin H2n+1
a
b
c
s
0
0.8
0.09 (±0.02)
0.26 (±0.05)
a
b
γ
1
0
0.16 (±0.05)
0b
Reference
a
[140]
[134]
[134]c
300 K≤ T ≤575 K
575 K≤ T ≤750 K
1≤n<9
Die Stickingkoeffizienten der Oberflächenreaktionsprozesse sind in Tabelle 3.7 zusammengefasst. Es wird davon ausgegangen, dass positive Ionen an der Oberfläche
immer mit freien Elektronen rekombinieren. Silanatome von reaktiven Silanionen
werden durch dissoziative Chemisorption abgeschieden. Der zurückgebliebene Wasserstoff wird als H2 reflektiert. Atomarer Wasserstoff unterliegt der Annahme, dass er
an der Oberfläche rekombiniert. Die Emission von Sekundärelektronen kann in dem
vorliegenden Druckregime und den darin entstehenden Entladungen im γ-Regime
vernachlässigt werden [97].
3.4 Simulationsumgebung
In dieser Arbeit kommen drei verschiedene Modellierungsansätze zum Einsatz: Ein
universitärer PIC Code, eine kommerzielle Fluid-Software und ein eigens entwickeltes globales Ratengleichungsmodell. Diese drei Tools werden im Folgenden kurz vorgestellt.
3.4 SIMULATIONSUMGEBUNG
51
3.4.1 Der Particle-In-Cell Code yapic
Der ein-dimensionale Code yapic wurde von Mussenbrock in der Programmiersprache C für die Architektur einer zentralen Recheneinheit (CPU) eines Computers entwickelt [155]. Er folgt dem klassischen, in Kapitel 3.1.1 vorgestellten, PIC-Schema
mit Monte Carlo Kollisionen. Im Code werden alle drei Geschwindigkeitskomponenten berücksichtigt. Für die zeitliche Integration der Teilchentrajektorien wird ein
leap-frog-Schema verwendet. Dieses hat, genauso wie die Lösung der Poisson Gleichung, eine Genauigkeit zweiter Ordnung.
Bei der Anwendung der PIC-Methode kommen verschiedene Stabilitätskriterien zum
Tragen [155], die in den nachfolgend gezeigten Rechnungen eingehalten werden. Sowohl die Gitterauflösung als auch die Zeitschrittweite unterliegen bestimmten Grenzen. So muss der Zeitschritt kleiner gewählt werden als die Zeit zwischen zwei Stößen
von Elektronen:
νm,e ∆t < 1
(3.50)
und kleiner als die Antwortzeit der Elektronen auf Feldänderungen, d. h.
ωpe ∆t . 0.2.
(3.51)
ωpe steht für die Elektronenplasmafrequenz und repräsentiert die Oszillation der
Elektronen bezüglich der Ionen.
Desweiteren müssen die Zeitschrittweite und die Gitterkonstante so angepasst werden, dass das Courant-Friedrichs-Lewy-Kriterium erfüllt ist, sich also ein Elektron
pro Zeitschritt nur um eine Zelle fortbewegen kann:
v∆t
. 0.4.
(3.52)
∆x
Dabei ist CFL die Courant-Zahl. Als Kriterium für die Zellgröße wird die DebyeLänge λD herangezogen, da im PIC-Schema die Kräfte zwischen Partikeln in einer
Zelle linear gegen Null gehen [126]:
CFL =
λD
& 2.
∆x
(3.53)
52
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
Die Debye-Länge ist die Länge auf welcher das elektrische Potential eines Ladungsträgers auf das Inverse der Eulerschen Zahl abfällt.
Um sicherzustellen, dass die Rechenergebnisse stationär sind, wird die Rechenzeit
der für die ambipolare Diffusion notwendigen Zeit tDa angepasst. So gilt für den
ambipolaren Diffusionskoeffizienten Da :
Da =
µ i De + µ e D i
µi
≈ Di + De ≈ µi Te
µi + µe
µe
(3.54)
unter der Annahme, dass die Beweglichkeit und die Temperatur der Elektronen viel
größer ist als die der Ionen (Te >> Ti und µe >> µi ) mit:
q
.
mνm
bei einem Plattenabstand L:
µi =
Somit erhält man für tDa
(3.55)
L2
.
(3.56)
Da
Alle PIC-Simulationen laufen mindestens für diese Anzahl von Zyklen, bevor sie als
stationär betrachtet und ausgewertet werden.
tDa =
3.4.2 Das Multiphysiktool CFD-ACE+
Die kommerzielle Software CFD-ACE+ ist ein Multiphysikprogramm mit Fokus
auf Strömungen. Es besteht aus einem Basismodul, das die Berechnung von Wärmeübertragungen und Turbulenzen ermöglicht, und Ergänzungsmodulen, wie z.B.
einem Plasmamodul.
Die Ionen und Neutralteilchen werden in diesem Modul [129, 156] durch eine Kopplung der Kontinuitäts-, der Impulserhaltungs- und der Energieerhaltungsgleichung
(Kontinuumsbetrachtung) mit der Poisson Gleichung beschrieben. Für sie wird eine
Maxwellsche Energieverteilung angenommen. Für die Elektronen kommt die Kontinuitätsgleichung und die Drift-Diffusions-Gleichung zum Einsatz. Die Mobilität
und der Diffusionskoeffizient der Elektronen werden über deren Energieverteilungsfunktion berechnet. Diese geht wiederum aus der Lösung der zeitabhängigen FokkerPlanck-Gleichung hervor und wird bezüglich der Elektronendichte aus den Fluidgleichungen normiert. Die Fokker-Planck-Gleichung wird in Abhängigkeit der totalen
3.4 SIMULATIONSUMGEBUNG
53
Energie ǫtot = u − Φ(~x) formuliert und hängt somit im Vergleich zur BoltzmannGleichung nur noch von vier Variablen, der kinetischen Energie u und den drei
Raumkoordinaten, ab. Beide Kollisionsarten, elastische und inelastische, werden bei
der Lösung berücksichtigt.
Die transiente Berechnung von Plasmaprozessen läuft in CFD-ACE+ auf zwei verschiedenen Zeitskalen ab. Der sogenannte CCP-Zeitschritt wird für die Berechnung
der schnellen Prozesse, wie die Änderung des elektrostatischen Potentials und der
Elektronendichte bzw. -temperatur, verwendet. Für die auf einer größeren Zeitskala
ablaufenden Prozesse, wie die Gasdynamik, wird ein zweiter Zeitschritt herangezogen, der drei bis vier Größenordnungen größer ist.
Die Limitierung dieser Software liegt vor allem in der zugrunde gelegten Kontinuumsbetrachtung zur Berechnung der Teilchendichten und -flüsse. Die Berechnung
der EEDF wird dadurch vereinfacht, dass nicht die volle Boltzmann-Gleichung gelöst wird. Was die Abbildung von chemischen Reaktionen betrifft, können Ladungsaustauschreaktionen nur durch einen konstanten Kollisionsquerschnitt beschrieben
werden. Für eine detailliertere Beschreibung der Software und der Annahmen zur
Lösung der Boltzmann-Gleichung wird verwiesen auf [18, 95, 157].
Durch die Lösung mehrerer gekoppelter Gleichungen muss die numerische Stabilität
gewährleistet werden. Hierfür kommen Löser mit iterativen Splitting-Verfahren zum
Einsatz, deren Parameter genau gewählt werden müssen, um eine schnelle Konvergenz der Lösung zu erzielen.
3.4.3 Globale Plasmamodellierung in Form eines
Ratengleichungsmodells
Neben dem universitären Programm yapic und dem kommerziellen Tool CFD-ACE+
wurde, wie im folgenden näher beschrieben wird (Kapitel 4.1), ein globales Ratengleichungsmodell, gekoppelt mit einer Energiegleichung, entwickelt und in Matlab
umgesetzt. Mit den Prozessbedingungen, wie der vom Plasma absorbierten Leistung,
dem Gasdruck, den Gasflüssen, der Zusammensetzung des Gases, dem Plattenabstand und der Elektronen-Energie-Verteilungsfunktion als Inputparameter, können
hiermit die einzelnen Speziesdichten im Plasma berechnet werden. Neben der Plas-
54
3. MODELLIERUNG VON NIEDERTEMPERATURPLASMEN
mazusammensetzung gehen, in einer Rechenzeit von weniger als 30 s, aus dem Ergebnis auch die Elektronentemperatur und die Teilchenflüsse und somit die Abscheideraten hervor.
Der Löser der Boltzmanngleichung für die Elektronen BOLSIG+ (s. Kapitel 3.1.2)
wird für die Bestimmung der Elektronen-Energie-Verteilungsfunktion in Form einer
Zuordnungstabelle verwendet.
4 Evaluation des globalen Modells
an kapazitiven Argon-Plasmen
Die im vorigen Kapitel beschriebenen Ansätze zur Modellierung von Niedertemperaturplasmen sollen hier anhand der simulativen Abbildung eines kapazitiv gekoppelten Plasmas miteinander verglichen werden. Für einen solchen Vergleich bietet
sich die Untersuchung einer Edelgasentladung an, die weniger rechenintensiv ist
als Silan-Wasserstoff-Entladungen und einfacher in einem Particle-In-Cell-, einem
Fluid- und einem globalen Modell umgesetzt werden kann. Deshalb kommt in diesem Kapitel, die in Abschnitt 3.3.1 eingeführte Argonchemie zum Einsatz. Ziel ist es
hier, ein breites Prozessfenster abzudecken und die drei Ansätze in diesem bezüglich
ihrer Gültigkeit zu untersuchen. Damit ermöglicht dieser Abgleich eine Bewertung
der Ansätze hinsichtlich der Abbildung von kapazitiv gekoppelten Silan-WasserstoffPlasmen für die Abscheidung von Dünnschicht-Silizium.
4.1 Das automatisierte globale Modell
Das im Rahmen dieser Arbeit entwickelte globale Modell bezieht sich auf zylindrische
Kammergeometrien mit Radius r, Plattenabstand L, Elektrodenoberfläche A = πr 2
und einem Volumen V = AL.
4.1.1 Grundlegende Gleichungen
Im Folgenden werden tiefgestellte Indizes verwendet, um die Speziesart und den
Ort zu spezifizieren. Numerische Indizes, z.B. für Summen werden hochgestellt und
mit Klammern versehen. NR ist die Anzahl der gesamten chemischen Reaktionen,
56
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
Nex die Anzal der Anregungs- und Dissoziationsreaktionen und NS die Anzahl der
Spezies. Ω ist der Satz aller betrachteten Spezies, wobei Ω+ , Ω− bzw. Ω0 für die
Untermenge der positiven und negativen Ionen bzw. der Neutralteilchen und µ+ , µ−
bzw. µ0 stellvertretend für jedes einzelne Teilchen dieses Satzes steht. Die gemittelten
Dichten der Spezies µ werden mit nµ bezeichnet und deren Masse mit mµ . Der Index
s bezieht sich auf Randschichtdichten.
Ein Satz von NR chemischen Reaktionen wird betrachtet, unter der Annahme, dass
nur Zwei-Partikel-Stöße der folgenden Form stattfinden:
M (11)
+ M (12)
→
P
τ (q) · M (q)
q≥3
M
(NR 1)
.
...
...
P (N q)
(NR 2)
(N
q)
+ M
→
τ R ·M R
(4.1)
q≥3
τ (jq) steht für den Stöchiometriefaktor der Spezies M (jq) , wobei j der Index für die
chemische Reaktion ist und q für das erste bzw. zweite Edukt (q= 1, 2) bzw. die
Produkte steht (q≥ 3). Die volumengemittelte Dichte nµ jeder Spezies µ ∈ Ω wird
durch Ratengleichungen auf Basis der chemischen Reaktionen (4.1) berechnet:
X
d
nµ =
K (j) ηµ(j) nM(j1) nM(j2) + Gµ − Sµ + Wµ ,
dt
j
(j)
(4.2)
wobei K (j) der Ratenkoeffizient der j-ten Reaktion und ηµ ein dimensionsloser Vorfaktor ist, der den Stöchiometriefaktor τ (jq) und ein Vorzeichen enthält, abhängig
davon, ob es sich um eine Teilchenvernichtung (-) oder eine Entstehung (+) handelt.
Die betrachteten Prozesse sind Ionisationen, Dissoziationen, Rekombinationen und
Ladungsaustauschreaktionen, wie in Abschnitt 3.3.2 beschrieben.
Gµ und Sµ sind Quell- bzw. Senkenterme. So wird die Gasdusche durch den Term Gµ
in der Teilchenbilanz (equation 4.2) des entsprechenden Präkursors abgebildet, der
dem eingestellten Gasfluss entspricht. Der richtige Entladungsdruck, als Summe des
Partialdrucks aller Spezies, wird durch den Senkenterm Sµ in allen Partikelbilanzen
außer der der negativen Ionen eingestellt. Wµ steht für alle Quellen und Senken an
der Kammerwand. Die Bestimmung der Ionenflüsse zur Wand für die Ionen µ ∈ Ω+
benötigt die Berechnung der Randschichtdichten ns,µ+ . Diese können über die sogenannten h-Faktoren, die das Verhältnis der Randschichtdichte zur Dichte in der
4.1 DAS AUTOMATISIERTE GLOBALE MODELL
57
Entladungsmitte beschreiben, berechnet werden:
(4.3)
hl = ns,µ+ /nµ+ .
Da sich vorige Arbeiten zur Bestimmung dieser Faktoren, wie die von Kim et al.
[31], vor allem auf sehr niedrige Druckbereiche konzentrieren, wird deren Ansatz
angepasst. Die heuristische Lösung für kollisionsfreie Entladungen:
hlp =
1
0.86
0.5
(3 + L/(2λ)) 1 + α
(4.4)
wird mit dem Ansatz basierend auf der ambipolaren Diffusion gekoppelt:
hhp =
0.86
,
0.86Lv/(2πDa)
(4.5)
so dass sich die fogende Beschreibung ergibt:
1
b
+ hlp
.
(4.6)
1+b
1+b
Diesem Ansatz zugrunde liegt die Idee, ein kollisionsloses Modell, das bei niedrigem
Druck gültig ist, mit einem Modell eines konstanten Diffusionskoeffizienten für einen
hohen Druck zu verknüpfen. Der Gewichtungsfaktor b ist dabei definiert als:
hl = hhp
b=2
λ Te
,
L Tg
(4.7)
wobei b für einen niedrigen Druck zu- und für einen hohen Druck abnimmt. Da ist
der ambipolare Diffusionskoeffizient für elektronegative und elektropositive Entladungen:
Da =
α
1
+ Ti
Te
1+α
1+α
λ
.
mµ+ utherm
(4.8)
Te , Ti und Tg sind die Elektronen-, Ionen- und Gastemperatur. λ ist die freie Weglänge, α die Elektronegativität. utherm ist die thermische Geschwindigkeit und mµ+
ist die Ionenmasse.
Das führt zu der folgenden Beschreibung des Flusses Γµ+ für jedes Ion:
Γµ+ = hl nµ+ vµ+ ,
(4.9)
58
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
wobei nµ+ die Dichte in der Entladungsmitte ist und aus der Ratengleichung 4.2
kommt und vµ+ die gewichtete Ionengeschwindigkeit ist. Letztere berücksichtigt für
jedes Ion µ+ , abhängig vom Druck, die kollisionslose Bohm-Geschwindigkeit vB,µ+
und die thermische Geschwindigkeit vtherm,µ+ in folgendem Zusammenhang:
vµ+ = vtherm,µ+
b
1
+ vB,µ+
.
1+b
1+b
(4.10)
Der Fluss der Radikale, die abgeschieden werden, wird beschrieben durch:
Γ µ0 = h
β
nvtherm .
2 (2 − β)
(4.11)
β ist die Reaktionswahrscheinlichkeit an der Oberfläche und h ist das Verhältnis der
Randschichtdichte zur Dichte in der Entladungsmitte für Neutralteilchen:
h=
1
.
1 + (Lvtherm,µ0 γDa (2 − β) /8)
(4.12)
Eine ausführlichere Erklärung des Neutralflusses und des Faktors h ist in [31] zu
finden.
Der Reaktionsratenkoeffizient K (j) der j-ten chemischen Reaktion wird aus der Literatur ermittelt oder, analog zu Gleichung 3.45, durch Integration des Wirkungsquerschnittes σ (j) bestimmt:
K
(j)
(j)
= hσ (ǫ)vR i =
Z
∞
vR σ (j) (ǫ)f (ǫ)dǫ.
(4.13)
0
Hier ist ǫ die Energie, vR die Relativgeschwindigkeit der beiden Kollisionspartner und
f die Verteilungsfunktion. Die Referenzen für die Wirkungsquerschnitte und Reaktionsraten, die für die Argon- bzw. Silan-Wasserstoff-Entladung verwendet werden
sind in Abschnitt 3.3 aufgeführt. Die Reaktionsraten werden berechnet aus dem
Produkt des Koeffizienten mit den Dichten der Reaktanten, wie in Gleichung 4.2
gezeigt.
In der Energiegleichung wird die vom Plasma absorbierte Leistung Pabs den Energieverlusten durch elastische und inelastische Stöße und durch Flüsse von ElektronenIonen-Paaren zur Wand gleichgesetzt:
4.1 DAS AUTOMATISIERTE GLOBALE MODELL
Pabs
=
V
ene
X
59
ǫc,µ Kiz,µ nµ
µ∈Ω0
+e
A X
(ǫe + ǫµ )Γµ
V µ∈Ω
(4.14)
+
!
Nex
(l)
X
K
Kel 3me
ex
ǫ(l)
(4.15)
Te +
ǫc,µ = ǫiz,µ +
ex
Kiz,µ mµ
K
iz,µ
l
Te Te
mµ
ǫe + ǫµ = 2Te +
,
(4.16)
+
ln
2
2
2πme
wobei ne die Elektronendichte in der Mitte des Reaktors repräsentiert, Pabs ist die
absorbierte Leistung und Nex ist die Anzahl der Anregungs- und Dissoziationsreaktionen. Die Einheit des Energieverlustes ǫc ist eV pro erzeugtem Elektronen-IonenPaar. ǫiz ist die Ionisationsenergie und ǫex ist die Energie für Anregungsprozesse.
Der Verlust durch Elektronenflüsse ist ǫe und durch Ionenflüsse ǫµ+ . K bezeichnet
die Ratenkonstante: Kiz für Ionisationsreaktionen, Kex für Anregungsreaktionen und
Kel für elastische Stöße. me/µ+ ist die Elektronen- bzw. Ionenmasse. Eine ausführlichere Erklärung der Energiegleichung steht in [29, 31].
Die Elektronendichte wird aus den Ionendichten unter Berücksichtigung von Quasineutralität bestimmt:
ne =
X
µ∈Ω+
nµ −
X
nµ .
(4.17)
µ∈Ω−
4.1.2 Der Automatisierungsalgorithmus
Um einen variablen Satz an Differentialgleichungen zu lösen und damit schnell und
flexibel verschiedene Gasentladungen zu untersuchen wurde ein Automatisierungsalgorithmus entwickelt. Hierin wird zuert der Vektor Ω mit allen chemischen Spezies
erzeugt. Danach transformiert der Algorithmus die chemischen Reaktionen (4.1) in
eine Matrix M. Jede Spezies µ(a) ∈ Ω, a ∈ {1, . . . , Ns } wird mit den Einträgen von
(j)
M verglichen. Dies führt zur Definition des dimensionslosen Vorfaktors ηµ(a) :
X
X
(j)
ηµ(a) := −
δ µ(a) , M (jq) +
δ µ(a) , M (jq) · τ (jq)
(4.18)
q=1,2
q≥3
60
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
mit der Kronecker Delta-Funktion δ für zwei Spezies µ1 und µ2 :
(
1 : µ1 = µ2
.
δ(µ1 , µ2 ) =
0
Nach der Generation des Satzes von Differenzialgleichungen werden diese mit einem Löser von MATLAB [158] berechnet. Die Rechenzeit beträgt weniger als 30
Sekunden für einen Prozessparametersatz.
4.1.3 Bestimmung der EEDF
Die Elektronen-Energie-Verteilungsfunktion wird entweder von einer mit BOLSIG+
berechneten Zuordnungstabelle eingelesen oder analytisch berechnet [159]:
∗
x
f (ǫ) = c1 ǫ1/2 e(−c2 ǫ ) ,
(4.19)
wobei der Parameter x∗ eine Variation zwischen Maxwell- und Druyvesteyn-Verteilungen ermöglicht. x∗ =1 ergibt eine Maxwell-Verteilung und x∗ =2 eine DruyvesteynVerteilung. c1 und c2 sind Funktionen der Elektronentemperatur [24]. f (ǫ) wird im
Folgenden definiert als EEDF und für die EEPF gilt:
EEPF = ǫ−1/2 f (ǫ).
(4.20)
4.2 Simulation von kapazitiv gekoppelten
Argon-Plasmen
Das Ziel dieser Simulationen ist es, das im vorigen Kapitel vorgestellte globale Modell an Modellen höherer Ordnung zu messen. Äquivalent zu den in Kapitel 3.1
vorgestellten Modellansätzen werden als Benchmark Particle-In-Cell Simulationen
mit dem Softwaretool yapic (s. Kapitel 3.4) und Fluid Simulationen mit und ohne
näherungsweiser Lösung der Boltzmann Gleichung herangezogen. Für die Fluidbetrachtungen kommt das kommerzielle Tool CFD-ACE+ zum Einsatz (s. Kapitel
3.4). Als Referenzsystem wird hierfür eine Argonentladung zugrunde gelegt. Diese
4.2 SIMULATION VON KAPAZITIV GEKOPPELTEN ARGON-PLASMEN
61
ist bezüglich der Chemie einfach und mit relativ geringem Rechenaufwand in allen
Ansätzen umzusetzen. Sie birgt trotzdem einige Herausforderungen, vor allem in der
Anforderung der kinetischen Beschreibung der Elektronen.
4.2.1 Simulationsgebiet und Randbedingungen
Als Prozessbedingungen gelten die in Tabelle 4.1 gelisteten Standardbedingungen
(fett gedruckt), von denen ausgehend einzelne Parameter variiert werden.
Tab. 4.1: Untersuchter Parameterbereich für den Modellvergleich an einer Argonentladung (Standardbedingungen fett).
Prozessparameter
Einheit
Bereich
Spannungsamplitude
Druck p
Plattenabstand L
Radius r
Temperatur T gas
Frequenz f
V
Pa
m
m
K
MHz
100
10-600 (100)
0.03
0.22
300
13.56
4.2.2 Vergleich der Modellierungsansätze
Bei der Interpretation der Ergebnisse soll insbesondere bewertet werden, wie verlässlich die Modelle in den Bereichen nahe der Validitätsgrenzen (s. Kapitel 3.1) des
jeweiligen Ansatzes sind.
Der PIC-Ansatzes ist die Simulation, die der Realität am nächsten kommt, da sie
den geringsten Abstraktionsgrad und die wenigsten Modellparameter aufweist. Die
Diskretisierung des Plasmas in Superpartikel ermöglicht die direkte Berechnung deren Verteilung. Der größte Nachteil dieser Methode ist, dass die Rechenzeiten für
einen großen Druck sehr lang werden.
Der Ansatz der Kontinuumsmechanik beschreibt die gemittelten Eigenschaften der
Teilchen und begrenzt durch das Kontinuumslimit den abbildbaren Knudsenbereich
nach oben.
62
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
−1
12
10
10
Elektron
Ion
Elektron
Ion
10
10
ν / 1/s
λ/m
−3
10
8
10
6
10
−5
10
4
0
10
1
2
10
10
3
10
10
0
10
1
2
10
10
p / Pa
p / Pa
(a)
(b)
3
10
Abb. 4.1: Grenzen der Kontinuumsmechanik: (a) Freie Weglänge der Elektronen und
Ionen in Abhängigkeit des Druckes, (b) Stoßrate der Elektronen und Ionen in Abhängigkeit des Druckes im Vergleich zur Anregungsfrequenz von
13.56 MHz (punktiert in rot).
Wie in Abbildung 4.1a gezeigt, ist die freie Weglänge der Elektronen erst ab p > 10 Pa
deutlich kleiner als der hier gewählte Plattenabstand von 3 cm, d. h. nur für p > 10 Pa
gilt Kn ≫ 1 und die Kontinuumsmechanik ist gültig.
Darüber hinaus setzt der Drift-Diffusions-Ansatz, wie er in CFD-ACE+ verwendet
wird, voraus, dass die Stoßrate der Teilchen größer ist als die Anregungsfrequenz (s.
Formel 3.27). So ist die Gültigkeit für Argon bei einer Frequenz von 13.56 MHz, wie
in Abbildung 4.1b gezeigt, ab einem Mindestdruck von ca. 50 Pa gegeben.
Der Boltzmann-Löser BOLSIG+, der für die Berechnung der Zuordnungstabellen
für das globale Modell eingesetzt wird, basiert auf der lokalen Näherung, d. h.
die Energie-Relaxations-Länge λepsilon muss kleiner sein, als die Ausdehnung des
Plasmas. Gemäß Gleichung 3.11 erhält man im Vergleich der Elektronen-EnergieRelaxations-Länge λǫ mit dem Plattenabstand (hier 0.03 m), dass in Argon diese
Länge für einen großen Druckbereich die Größenordnung des Plattenabstandes im
Bereich geringer Energien deutlich überschreitet.
Wie in Bild 4.2 gezeigt, gilt dies für einen Druck bis über 1000 Pa. Der Grund
4.2 SIMULATION VON KAPAZITIV GEKOPPELTEN ARGON-PLASMEN
63
4
10
λepsilon 10Pa
λinel.
100Pa
1000Pa
10Pa
λm
100Pa
1000Pa
10Pa
2
λepsilon / m
10
0
10
−2
10
100Pa
1000Pa
−4
10
−2
10
0
10
2
10
Energie / eV
4
10
6
10
Abb. 4.2: Elektronen-Energie-Relaxations-Länge nach der Definition von Gleichung
3.11 in Argonplasmen bei 10, 100 und 1000 Pa.
dafür ist, dass die Anregung von Argon erst ab einer Grenzenergie von 11.5 eV
stattfindet (s. Gleichung 3.11 und Tabelle 3.1). Folglich wird insbesondere in diesem
Kapitel im Vergleich des globalen Modells in Kombination mit BOLSIG+ (bei der,
wie in 3.4 beschrieben, die lokale Näherung zum Einsatz kommt) mit dem Fluidansatz und der Partikel-in-cell Methode ein großes Augenmerk auf die berechneten
Elektronen-Energie-Verteilungen gelegt. Auch die resultierenden Dichteprofile werden im Folgenden unter diesem Gesichtspunkt miteinander verglichen.
Der Vergleich ist folgendermaßen strukturiert: Anfänglich werden die resultierenden
EEDFs bzw. EEPFs (Elektronen-Energie-Wahrscheinlichkeitsfunktionen) aus den
Boltzmann-Lösern von CFD-ACE+ und BOLSIG+ mit yapic und einer Maxwellbzw. Druyvesteyn-Verteilung im Druckbereich von Tabelle 4.1 verglichen. Daraufhin
folgt eine Analyse der aus den verschiedenen Ansätzen resultierenden Elektronendichte bzw. -temperatur bei den selben Prozessbedingungen.
Wie in Abbildung 4.3 dargestellt, nimmt erwartungsgemäß die Anzahl hochenergetischer Elektronen in yapic für einen geringen Druck zu. Für Entladungen mit
steigendem Druck nimmt die Anzahl kontinuierlich ab. Mit zunehmendem Druck
nimmt die konvexe Form der EEPF zu, vergleichbar zu den gemessenen Werten von
Godyak et al. in [160].
64
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
0
10
10 Pa
20 Pa
50 Pa
100 Pa
300 Pa
400 Pa
500 Pa
600 Pa
−1
EEPF
bulk
/ eV
−3/2
10
−2
10
−3
10
−4
10
0
5
10
E / eV
15
20
Abb. 4.3: Elektronen-Energie-Wahrscheinlichkeitsfunktion im Plasmabulk berechnet mit yapic für verschiedene Prozessdruckwerte (p = 10-600 Pa).
Vergleicht man die EEPFs der anderen Tools bzw. der analytischen Ausdrücke mit
denen aus yapic, ergeben sich die Verteilungen aus Abbildung 4.4. Die yapic Ergebnisse verdeutlichen das zunehmende thermodynamische Nicht-Gleichgewicht der
Elektronen mit dem Druck. Für 10 Pa befinden sich einerseits die inelastischen Stöße
der Elektronen und andererseits deren Heizung in der Randschicht quasi im Gleichgewicht. Die EEPF hat einen quasi linearen Verlauf. Für zunehmenden Druck nimmt
die Energieaufnahme im hochenergetischen Bereich der Elektronen über die Randschicht ab und die Verluste durch inelastische Stöße nehmen zu. Den beiden analytischen Funktionen liegt jeweils die mittlere Energie der EEDF aus yapic zugrunde.
Wie zu erwarten ist, lassen sich diese EEDFs bzw. EEPFs nur schwer analytisch
beschreiben. Im gesamten Druckbereich liegt keine Maxwell-Verteilung vor. Speziell bezüglich der hochenergetischen Elektronen überschätzt die Maxwell-Verteilung
durchweg den Anteil dieser Teilchen. Die Druyvestyn-Verteilung unterschätzt für
einen kleinen Druck noch die maximale Energie, trifft die yapic-Verteilung dann
zwischen 20 und 50 Pa sehr gut, geht aber dann für einen hohen Druck von zu
hohen Energien aus. CFD-ACE+ bildet die Wahrscheinlichkeitsfunktion im gesamten Druckbereich qualitativ gut ab. Besonders bei geringem Druck hängt die EEPF
hauptsächlich von der totalen Energie ab. Daher hat die Berechnung mittels totaler
4.2 SIMULATION VON KAPAZITIV GEKOPPELTEN ARGON-PLASMEN
0
0
10
10
−1
−1
/ eV
−3/2
10
−2
bulk
10
−3
10
EEPF
EEPFbulk / eV
−3/2
10
−4
10
0
5
10
15
E / eV
20
−2
10
−3
10
−4
10
25
0
(a) EEPF bei 10 Pa.
0
25
20
25
−1
/ eV
−3/2
10
−2
bulk
10
−3
10
EEPF
−3/2
20
0
10
EEPFbulk / eV
10
15
E / eV
10
−1
−4
10
0
5
10
15
E / eV
20
−2
10
−3
10
−4
10
25
0
(c) EEPF bei 50 Pa.
5
10
15
E / eV
(d) EEPF bei 100 Pa.
0
0
10
10
−1
10
/ eV
−3/2
10
−2
bulk
10
−3
10
−4
10
0
600 Pa yapic
Maxwell
Druyvesteyn
BOLSIG+
ACE
−1
EEPF
−3/2
5
(b) EEPF bei 20 Pa.
10
EEPFbulk / eV
65
5
10
15
E / eV
(e) EEPF bei 300 Pa.
20
25
−2
10
−3
10
−4
10
0
5
10
15
20
25
E / eV
(f) EEPF bei 600 Pa.
Abb. 4.4: EEPF berechnet mit yapic, analytisch, BOLSIG+ und CFD-ACE+.
66
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
15
15
6
x 10
6
5
4
3
2
4
3
i
10 Pa
20 Pa
50 Pa
100 Pa
300 Pa
400 Pa
500 Pa
600 Pa
n / (1/m3)
ne / (1/m3)
5
2
1
1
0
0
x 10
0.01
0.02
0.03
0
0
0.01
0.02
0.03
L/m
L/m
(a)
(b)
Abb. 4.5: Elektronen- (a) bzw. Ionendichteprofil (b) für verschiedene Prozessdruckwerte (p = 10 − 600 Pa).
Energie in CFD-ACE+ deutliche Vorteile im Vergleich zur Berechnung in BOLSIG+.
Die Qualität der aus BOLSIG+ hervorgehenden EEPF nimmt zwar auch mit dem
Druck zu, bildet aber erst ab ca. 50 Pa die hochenergetischen Elektronen vergleichbar zu yapic ab. Ab hier wird die Vernachlässigung der Gradienten gegenüber dem
Stoßterm gültig. Die Ortsabhängigkeit wird lokal. Darüber hinaus ermöglicht die
Berücksichtigung der lokalen Temperatur über die Energiegleichung die Gültigkeit
des globalen Modells auch bei mittlerem Druck, wie im folgenden gezeigt wird.
Die Elektronendichteprofile aus yapic in Abbildung 4.5a und die entsprechenden
Ionendichteprofile in Abbildung 4.5b geben einen ersten Hinweis auf verschiedene
Heizmechanismen in den verschiedenen Druckregimen. Die Profile für Druckwerte
> 100 Pa weisen ein ausgeprägtes Maximum auf. Dieses Cosinus-Profil geht aus der
Kontinuitätsgleichung für geladene Teilchen (Gl. 3.19) unter der Annahme hervor,
dass deren Fluss durch die ambipolare Diffusion getrieben ist:
Γ = n~v = −Da ∇n.
(4.21)
Somit erhält man unter der Annahme, dass der ambipolare Diffusionskoeffizient
4.2 SIMULATION VON KAPAZITIV GEKOPPELTEN ARGON-PLASMEN
67
unabhängig vom Ort ist:
∂n
− Da ∇ 2 n = 0
∂t
(4.22)
und im stationären Zustand bei Zunahme der geladenen Teilchen durch Ionisationsprozesse:
0 = nνion + Da ∇2 n.
(4.23)
Die Lösung von Gleichung 4.23 hat die Form n(x) = n0 cos (xπ/l). Die Profile für
50 und 100 Pa sind dagegen sehr flach und weisen kein ausgeprägtes Maximum auf.
Diese flache Form kann in ähnlicher Weise analytisch hergeleitet werden, unter Berücksichtigung, dass die Geschwindigkeit der Ionen für diese Niederdruckfälle viel
größer ist als die thermische Geschwindigkeit (für eine detailierte Herleitung s. [95]).
Die Profile für p < 50 Pa zeigen eine ähnlich flache Form auf. Jedoch werden sie bei
diesem Plattenabstand so stark von den beiden Randschichten dominiert, dass ein
Maximum auftritt. Der Anstieg der Elektronendichte bis 300 Pa und der anschließende Abfall für höhere Druckwerte zeigt das nichtmonotone Verhalten von Plasmen,
ähnlich dem Verlauf der Paschenkurve. Bei allen Rechnungen wurden ausreichend
viele Zyklen berechnet, um eine stationäre ambipolare Diffusion zu gewährleisten (s.
Kapitel 3.4.1).
Die raumzeitaufgelöste Darstellung der Ionisationsevents und der Elektronenleistungsdichte in Abb. 4.6 zeigen das nicht-lokale Verhalten der Elektronen bei einem
kleinen Druck. So erfolgt die Elektronenheizung bei 10 Pa (Abb. 4.6b) weiter außen
in der Randschicht als die Ionisation (Abb. 4.6a), die weiter innen stattfindet. Hin
zu größeren Druckwerten finden Heizung und Ionisation am gleichen Ort statt, wie
in Abbildung 4.6c und d für 100 Pa und in Abbildung 4.6e und f für 600 Pa zu sehen
ist. Hier weisen die Elektronen ein lokales Verhalten auf.
Da im globalen Modell die absorbierte Leistung als Inputparameter erforderlich ist,
yapic jedoch als Randbedingung an der getriebenen Elektrode eine Spannung benötigt, wird die Leistung der stationären yapic-Rechnungen über die Felder und
Stromdichten berechnet:
68
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
IE / #
0.03
3.5
0.03
P̃e / W/m3
5000
3
2.5
0.015
1.5
L/m
L/m
0
2
0.015
−5000
1
0.5
0
0.0
ω t / 2π
0.5
0
0.0
0
(a) Ionisationsevents IE bei 10 Pa.
−10000
ω t / 2π
0.5
(b) Elektronenleistungsdichte P̃e bei 10 Pa.
0.03
0.03
4000
4
2000
0.015
2
0
L/m
L/m
3
0.015
−2000
−4000
1
0
0.0
ω t / 2π
0.5
0
0.0
0
(c) Ionisationsevents bei 100 Pa.
−6000
ω t / 2π
0.5
(d) Elektronenleistungsdichte bei 100 Pa.
0.03
0.03
500
4
0
0.015
2
L/m
L/m
3
0.015
−500
−1000
1
0
0.0
ω t / 2π
0.5
(e) Ionisationsevents bei 600 Pa.
0
0
0.0
−1500
ω t / 2π
0.5
(f) Elektronenleistungsdichte bei 600 Pa.
Abb. 4.6: Raumzeitaufgelöste Ionisationsevents (links) und Elektronenleistungsdichte (rechts) aus yapic für verschiedene Prozessdruckwerte (p = 10, 100 und
600 Pa).
4.2 SIMULATION VON KAPAZITIV GEKOPPELTEN ARGON-PLASMEN
69
−1
Pabs / W/cm2
10
−2
10
−3
10
yapic
ACE
−4
10
0
200
400
600
p / Pa
Abb. 4.7: Absorbierte Leistungsdichte in yapic und CFD-ACE+.
Pabs = πR
2
Z
L
< EeΓtot >t dx.
(4.24)
0
Diese Leistung ist in Abbildung 4.7 als Funktion des Druckes dargestellt und wird
für die Rechnungen mit dem globalen Modell verwendet. Analog zu den Dichten
der geladenen Teilchen aus Abbildung 4.5 nimmt auch die Leistung anfänglich mit
dem Druck zu und dann bei hohen Druckwerten wieder ab. Die Auswertung der absorbierten Leistung aus den Ergebnissen des kinetischen Modells von CFD-ACE+
stimmt gut mit der aus yapic überein.
Abbildung 4.8 zeigt die über dem Plattenabstand gemittelte Elektronendichte als
Funktion des Druckes. Wie schon aus den yapic Ergebnissen in Abbildung 4.5 hervorgeht, nimmt die Elektronendichte gemäß yapic für zunehmende Druckwerte bis
300 Pa zu. Dies liegt zum Einen daran, dass die eingekoppelte Leistung (s. Abbildung
4.7) zunimmt und zum Anderen, dass die Zeit zwischen zwei Stößen den Elektronen
ermöglicht, ausreichend Energie aufzunehmen. Für einen Druck größer als 300 Pa
ist die Stoßrate dann so groß, dass die Elektronen zwischen zwei Stößen nicht mehr
genug Energie für Ionisationsprozesse aufnehmen können, um den Elektronenverlust
an den Reaktorwänden zu kompensieren. Die Elektronendichte nimmt folglich für
größere Druckwerte wieder ab. Diese anfängliche Zu- und anschließende Abnahme
der Elektronendichte ergibt sich, wie in der Abbildung gezeigt, qualitativ aus allen
70
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
17
10
ne / (1/m3)
16
10
15
10
yapic
GGM (Bolsig+)
ACE
ACE Fluid
14
10
0
200
400
600
p / Pa
Abb. 4.8: Elektronendichte im Plasmabulk in Abhängigkeit des Druckes im Vergleich
zwischen yapic, CFD-ACE+ und dem globalen Modell.
vier verwendeten Ansätzen. Die kinetischen CFD-ACE+ Ergebnisse sind denen von
yapic am ähnlichsten. Das zugehörige Fluidmodell ergibt für einen Druck größer als
100 Pa Elektronendichten, die etwa um einen Faktor 2 größer sind als die des gleichen
Tools unter Verwendung des kinetischen Ansatzes. Das globale Modell unterschätzt
für niedrige Druckregime die Dichte. Die Ursache dafür liegt in der Unterschätzung
des hochenergetischen Elektronenanteils in der Energieverteilung. Für 100 Pa liegt
jedoch, dank dem lokalen Verhalten, nur noch eine Abweichung von Faktor 2.5 vor.
Für 300 Pa und mehr beträgt der Faktor für die Abweichung nur noch < 1.5.
Vergleicht man die Dichteprofile von yapic mit denen von CFD-ACE+ (Abbildung
4.9), so erhält man, abgesehen von der quantitativen Abweichung aus Abbildung
4.8, für die Druckwerte 50 und 500 Pa qualitativ übereinstimmende Profile. Die
Abweichung für 20 Pa resultiert aus der größeren Plasmadichte in CFD-ACE+, die
zu einem erhöhten Plasmapotential führt und dadurch die Dicke der Randschicht
verstärkt. Die geht mit einem stärker ausgeprägten Maximum einhergeht.
Die nicht-lokale Entladung bei einem geringen Druck (s. Abbildung 4.6) bringt eine
zusätzliche Heizung der Elektronen stochastischer Art mit sich, die für 10 und 20 Pa
zu einer Reduktion der RF-Felder, wie in Abbildung 4.10 gezeigt, führt [161].
4.2 SIMULATION VON KAPAZITIV GEKOPPELTEN ARGON-PLASMEN
71
15
10
x 10
3
ne / (1/m )
8
20 Pa yapic
50 Pa
500 Pa
20 Pa ACE
50 Pa
500 Pa
6
4
2
0
0
0.01
0.02
0.03
L/m
Abb. 4.9: Elektronendichteprofile von yapic und CFD-ACE+ im Plasmabulk im Vergleich.
4
E / (V/m)
5
x 10
10 Pa
20 Pa
50 Pa
100 Pa
300 Pa
400 Pa
500 Pa
600 Pa
0
−5
0
0.01
0.02
0.03
L/m
Abb. 4.10: Gemitteltes elektrisches Feld als Funktion des Druckes aus yapic.
72
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
−3
6
x 10
λ bzw. dRS / m
freie Weglänge der Elektronen
Randschichtdicke
4
2
0
0
200
400
600
p / Pa
Abb. 4.11: Mittlere freie Weglänge der Elektronen im Vergleich zur Randschichtdicke der Entladung in Abhängigkeit des Druckes aus yapic.
7
6
<E> / eV
5
yapic
GGM (Bolsig+)
ACE
ACE Fluid
4
3
2
1
0
100
200
300
p / Pa
400
500
600
Abb. 4.12: Mittlere Elektronenenergie im Plasmabulk in Abhängigkeit des Druckes
im Vergleich zwischen yapic, CFD-ACE+ und dem globalen Modell.
Abbildung 4.11 greift die mittlere freie Weglänge aus Abbildung 4.1a auf und stellt
sie der resultierenden, über der Periode gemittelten Randschichtdicke der Entladung
gegenüber. Der Vergleich zeigt, dass es für 10 und 20 Pa Elektronen gibt, die die
Randschicht ohne Stoß durchqueren, eine Voraussetzung für eine effektive stochastische Heizung. Diese Voraussetzung ist für höhere Druckwerte nicht mehr gegeben.
Folglich findet hier ausschließlich eine ohmsche Heizung der Elektronen statt.
4.2 SIMULATION VON KAPAZITIV GEKOPPELTEN ARGON-PLASMEN
73
Die reduzierten Felder als Folge des stochastischen Heizens der Elektronen reduzieren deren Energie im Plasmabulk. Da darüber hinaus die Stoßfrequenz proportional
zur Elektronenenergie ist, nimmt demzufolge im Bulk die ohmsche Heizung ab (s.
Formel 3.10) [161]. Dies führt zu einer zusätlichen Reduktion der Elektronenenergie
für einen kleinen Druck. Der Partikelansatz in yapic und das kinetische Modell von
CFD-ACE+ sind in der Lage diese Effekte abzubilden, wie Abbildung 4.12 zeigt.
Analog zu den gemessenen Werten von Godyak [161] nimmt die Elektronenenergie
mit dem Druck zu. Weder im Fluidansatz von CFD-ACE+, noch im globalen Modell wird die stochastische Heizung berücksichtigt. Das erklärt die mit dem Druck
abfallende mittlere Energie für diese Modelle in der selben Abbildung.
Auch wenn die Kontinuumsmechanik und der Drift-Diffusions-Ansatz erst für p >
10 Pa bzw. p > 50 Pa gültig sind, liegt zwischen dem kinetischen Ansatz von CFDACE+ und der Referenz yapic für die Elektronentemperatur und für deren Dichte
eine qualitative Übereinstimmung vor. Der quantitative Vergleich ergibt eine Abweichung der Elektronendichte von Faktor 1.44. Bezüglich der Elektronentemperatur
ergibt sich für 10 Pa ein Faktor von 1.31, der sich auf 1.05 für 600 Pa reduziert.
In den Berechnungen mittels globalem Modell unterliegt die Elektronen-EnergieVerteilung aus BOLSIG+ der lokalen Näherung, die für Argon erst bei über 1000 Pa
erfüllt ist. Nichtsdestotrotz liegen gute qualitative Übereinstimmungen in der EEDF
schon bei 50 Pa und eine gute Übereinstimmung der Elektronendichte bzw. -temperatur ab 100 Pa vor (ne : Faktor < 2.45; Te : Faktor < 1.21).
Die Gültigkeit des globalen Modells, insbesondere hinsichtlich des Inputs aus BOLSIG+, ist für reaktive Gasmischungen mit kleinen Anregungsenergien wie in SilanWasserstoff-Plasmen deutlich weniger kritisch.
4.2.3 Validierung der Referenz yapic am Experiment
Zur Validierung dieser Simulationen von Argon-Plasmen bietet sich die optische
Emissionsspektroskopie (OES) an. Sie gehört zu den wenigen nicht-invasiven Plasmadiagnostiken und benötigt darüber hinaus nur einen optischen Zugang zur Entladung. Daher ist die OES auch für industrielle Zwecke geeignet. Die sogenannte
74
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
Linien-Verhältnis Methode ermöglicht die Bestimmung der Elektronendichte und temperatur in kapazitiv gekoppelten Plasmen über die Untersuchung von zwei Linienverhältnissen des Argonplasmaspektrums. Diese Linienverhältnisse werden einerseits über ein Stoß-Strahlungsmodell, basierend auf der Arbeit von Iordanova [162],
als Funktion des Plasmaregimes, unter der Annahme einer bestimmten ElektronenEnergie-Wahrscheinlichkeitsfunktion, berechnet. Dieses Plasmaregime kann anschließend durch Vergleich der Linienverhältnisse mit experimentell ermittelten Verhältnissen bestimmt werden. Die experimentellen Untersuchungen zur Validierung werden an einer CCP Entladung bei 13.56 MHz durchgeführt. Die quadratischen Elektroden haben eine Kantenlänge von 40 cm und sind im Abstand von 1 cm angeordnet. Entladungen zwischen 20 und 420 Pa bei 300 W eingekoppelter Leistung werden
untersucht. Der Auswertung des Plasmaregimes werden verschiedene ElektronenEnergie-Verteilungen zugrunde gelegt.
Der Abgleich erfolgt der Übersicht halber nur mit dem PIC-Simulationsansatz.
Die beschriebene experimentelle Konfiguration wird analog zu Kapitel 4.2.1 und
4.2.2 im Tool yapic für verschiedene Elektrodenspannungen umgesetzt. Die Auswertung erfolgt hinsichtlich der vom Plasma absorbierten Leistung (gemäß Formel
4.24), der Elektronen-Energie-Verteilungsfunktion und der Elektronendichte bzw.
-temperatur. In den folgenden Abbildungen werden nur Simulationsergebnisse gezeigt, die mit einer absorbierten Leistung von 300 W einhergehen, analog zu der im
Experiment eingestellten Generatorleistung.
Abbildung 4.13 zeigt die zu den analysierten Druckregimen zugehörige ElektronenEnergie-Wahrscheinlichkeitsfunktion im Vergleich zu entsprechenden analytischen
Verteilungen. Es wird deutlich, dass für 60, 200 und 420 Pa weder eine Maxwellnoch eine Druyvesteyn-Verteilung die Wahrscheinlichkeitsfunktion aus yapic perfekt
abbildet. Für 100 Pa liegt eine qualitative Übereinstimmung der Maxwellverteilung
mit den PIC-Ergebnissen vor. Für die anderen Druckregime wird die analytische
Form aus Gleichung 4.19 so angepasst, dass insbesondere der Anteil der hochenergetischen Elektronen qualitativ gut abgebildet wird. So liegen für 60 Pa deutlich mehr
hochenergetische Teilchen vor, als in einer Maxwell-Verteilung. Für 200 Pa liegt eine
Verteilung vor, die zwischen einer Maxwell- und einer Druyvesteyn-Verteilung liegt.
Und für 420 Pa ist der Anteil der hochenergetischen Teilchen so gering, dass selbst
die Druyvesteyn-Funktion sie noch überschätzt.
4.2 SIMULATION VON KAPAZITIV GEKOPPELTEN ARGON-PLASMEN
0
0
10
10
60 Pa yapic
Maxwell
Druyvesteyn
x = 0.8
−1
−1
−3/2
−2
10
−3
10
−4
−2
10
−3
10
−4
10
0
100 Pa yapic
Maxwell
Druyvesteyn
10
EEPFbulk / eV
EEPF
bulk
/ eV−3/2
10
10
5
10
15
20
25
0
5
10
E / eV
0
25
0
10
200 Pa yapic
Maxwell
Druyvesteyn
x = 1.5
−1
−3
10
−4
−2
10
−3
10
−4
10
0
−1
EEPFbulk / eV
−2
10
420 Pa yapic
Maxwell
Druyvesteyn
x = 3.0
10
−3/2
10
/ eV−3/2
20
(b) EEPF bei 100 Pa.
10
bulk
15
E / eV
(a) EEPF bei 60 Pa.
EEPF
75
10
5
10
15
E / eV
(c) EEPF bei 200 Pa.
20
25
0
5
10
15
20
25
E / eV
(d) EEPF bei 420 Pa.
Abb. 4.13: EEPF, berechnet mit yapic und analytisch, für die Druckvariation, die
mittels OES charakterisiert wurde.
76
4. EVALUATION DES GLOBALEN MODELLS AN CCP Ar PLASMEN
16
7
x 10
Simulation
Exp. Maxwell
Exp. Druyvesteyn
optimierte EEDF
6
ne / (1/m3)
5
4
3
2
1
0
0
100
200
300
400
500
p / Pa
Abb. 4.14: Verlauf der experimentell ermittelten Elektronendichte als Funktion des
Druckes unter der Annahme einer Maxwell- bzw. einer DruyvesteynVerteilung. Vergleichend ist die simulativ errechnete Elektronendichte
dargestellt.
Die Abbildungen 4.14 und 4.15 zeigen die aus dem Experiment, in Verbindung mit
dem Stoß-Strahlungsmodell, ermittelten Elektronendichten bzw. -temperaturen im
Vergleich zur Simulation. Die simulierte Elektronendichte weist bei 100 Pa ein Maximum auf. Dieses Ergebnis stimmt mit den experimentellen Daten unter Annahme
einer Maxwell-verteilten Energie überein. Wie zu erwarten, führt eine Druyvesteynverteilte Elektronenenergie durch den, im Vergleich zur Maxwell-Verteilung, reduzierten Anteil an hochenergetischen Teilchen zu einer niedrigeren Elektronendichte
und dementsprechend zu einer höheren Elektronentemperatur. Berücksichtigt man
für die Auswertung der experimentell gemessenen Spektren die aus Abbildung 4.13
hervorgehenden Energieverteilungen, so erhält man sowohl für die Elektronendichte
(Abb. 4.14) als auch für die -temperatur (Abb. 4.15) eine gute Übereinstimmung zwischen Experiment und Simulation. Die leichte Überschätzung der Elektronendichte
in der Simulation resultiert hauptsächlich aus der 100 %tigen Leistungseinkopplung.
Im Experiment kommt im Gegensatz dazu nur ein Bruchteil der Generatorleistung
auch im Plasma an. Dieser Bruchteil ist nicht bekannt.
4.2 SIMULATION VON KAPAZITIV GEKOPPELTEN ARGON-PLASMEN
77
4
Te / eV
3.5
3
2.5
2
1.5
0
100
200
300
400
500
p / Pa
Abb. 4.15: Verlauf der experimentell ermittelten Elektronentemperatur Te als Funktion des Druckes unter der Annahme einer Maxwell- bzw. einer Druyvesteyn-Verteilung (Te = 2/3hǫi). Vergleichend ist die simulativ errechnete
Elektronentemperatur dargestellt.
5 Globale Modellierung von
kapazitiven Silan-WasserstoffPlasmen
5.1 Simulationsgebiet und Randbedingungen
Das in Kapitel 4.1 beschriebene globale, volumengemittelte Modell wird in diesem
Kapitel auf eine zylindrische Silan-Wasserstoff-Entladung angewandt.
Wenn keine anderen Angaben gemacht werden, wird von einer Kammer mit einem
Radius von 22 cm und einem Plattenabstand von 1 cm ausgegangen. Standardmäßig
wird mit einer eingekoppelten Leistung von 1000 W, einer einströmenden Gasmenge
von 2000 sccm und 5 % Silan gerechnet. Die Gastemperatur wird näherungsweise
der Substrattemperatur (500K) gleichgesetzt.
Tab. 5.1: Der in dieser Arbeit untersuchte Parameterbereich.
Prozessparameter
Einheit
Bereich
Absorbierte Leistung P abs
Gasfluss Φ
Druck p
Silankonzentration SC
Plattenabstand L
Radius r
Temperatur T gas
Frequenz f
W
sccm
Pa
%
m
m
K
MHz
250-2000 (1000)
480-4000 (2000)
100-1000
1-13 (5)
0.005-0.025 (0.01)
0.22
500
13.56-94.92
5.1. SIMULATIONSGEBIET UND RANDBEDINGUNGEN
79
In Tabelle 5.1 sind diese Standardbedingungen (fett) zusammen mit den untersuchten Bereichen der Betriebsbedingungen aufgelistet.
Es wird angenommen, dass die negativen Ionen im ganzen Volumen verteilt sind.
Die chemischen Reaktionen aus den Tabellen 3.3, 3.4, 3.5 und 3.6 wurden alle im globalen Modell implementiert. Eine Sensitivitätsanalyse der Silan-Wasserstoff-Chemie
wurde in [163] durchgeführt und erlaubt die Beurteilung der Wichtigkeit einzelner
Gasphasenreaktionen und somit die Bestimmung eines notwendigen Satzes von Reaktionsgleichungen, die beim jeweiligen Betriebspunkt ablaufen. Diese Analyse dient
dazu, die Rechenzeit zu optimieren, indem nur die notwendigsten Reaktionen umgesetzt werden, die in Kapitel 3.3.2 schon in reduzierter Form eingeführt wurden.
Für die Modellierung des Schichtwachstums werden die in Kapitel 2.1.2 erläuterterten und die in Tabelle 3.7 gelisteten Sticking Koeffizienten als integrale Größe
der zugrunde liegenden Prozesse verwendet. Es wird davon ausgegangen, dass die
Sticking Koeffizienten sowohl für amorphe als auch für mikrokristalline Schichten
gleichermaßen gültig sind. Von einer Modellierung von detaillierteren Modellen der
verspannten Bindungen, des selektiven Ätzens bzw. des chemischen Ausheilens (wie
in Kapitel 2.1.2 beschrieben) wird abgesehen, da gezeigt wurde, dass in der Realität
ein Zusammenspiel der genannten Modelle zum Tragen kommt.
Der Wasserstoffgehalt der Schichten variiert zwischen 1 at. % und 10 at. % und
hängt stark von der Kristallinität der Schicht ab [77]. Je amorpher die Schicht, desto mehr Wasserstoffgehalt wird gemessen. In der vorliegenden Arbeit gelangt der
Wasserstoff über die Abscheidung von Silanen in die Schicht. Dabei wird davon ausgegangen, dass 90% des Wasserstoffs der sich abscheidenden Silane zu gasförmigen
Wasserstoffmolekülen umgesetzt wird. 5% wird in Form von atomarem Wasserstoff
in die Gasphase zurückgeführt und die restlichen 5% werden abgeschieden. Eine Abscheidung von atomarem Wasserstoff aus gasförmigem, atomarem Wasserstoff wird
vernachlässigt. Auf die Beschreibung der im Modell zugrunde gelegten ElektronenEnergie-Verteilung wird im nächsten Kapitel eingegangen.
80
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
5.2 Beschreibung der Elektronen-EnergieVerteilung
Im Vergleich zu Argon-Entladungen sind Molekulargasentladungen durch die vorhandenen Anregungsstöße mit geringen Grenzenergien bezüglich der lokalen Näherung der Elektronen-Energie-Verteilung gutmütiger (s. im Vergleich Kapitel 4.2).
2
10
10Pa
100Pa
1000Pa
0
λepsilon / m
10
−2
10
−4
10
−2
10
0
10
2
10
Energie / eV
4
10
6
10
Abb. 5.1: Elektronen-Energie-Relaxations-Länge nach der Definition von Gleichung
3.11 in Silan-Wasserstoff-Plasmen bei 10, 100 und 1000 Pa.
Bild 5.1 zeigt, dass in Silan-Wasserstoff die Elektronen-Energie-Relaxationslänge im
relevanten Energiebereich bis 1000 eV schon bei Drücken ab 100 Pa kleiner ist, als
der standardmäßige Plattenabstand von 0.01 m. Nur für größere Energien, für die es
jedoch nur noch vernachlässigbar viele Elektronen gibt, nimmt die Relaxationslänge wieder zu. Somit können Entladungen mit Plattenabständen ab 0.01 m und ab
rund 100 Pa problemlos mit der lokalen Näherung abgebildet werden. Bei der Untersuchung der Silan-Wasserstoff-Entladungen in diesem Kapitel sind ausschließlich
Prozessbereiche relevant, in denen die Gültigkeit dieser Näherung gegeben ist.
5.2 BESCHREIBUNG DER ELEKTRONEN-ENERGIE- VERTEILUNG
81
0
10
f / eV−3/2
Te=5eV
SC=5%
SC=10%
SC=100%
−5
10
T =1eV
e
−10
10
0
20
40
E / eV
60
80
Abb. 5.2: Die mit BOLSIG+ berechnete Elektronen-Energie-Wahrscheinlichkeitsfunktion für das Verhältnis aus Anregungsfrequenz zu Druck von
6.55·10−15 m3 /s (100 Pa, 94.92 MHz) für verschiedene Silankonzentrationen.
0
10
f / eV−3/2
Te=5eV
SC=5%
SC=10%
SC=100%
−5
10
Te=1eV
−10
10
0
20
40
E / eV
60
80
Abb. 5.3: EEPF aus BOLSIG+ für das Verhältnis aus Anregungsfrequenz zu Gasdruck von 0.28·10−15 m3 /s (1000 Pa, 13.56 MHz) für verschiedene Silankonzentrationen.
82
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
Analog zu Kapitel 4.2.2 werden anfänglich die Energieverteilungen aus BOLSIG+
mit dem analytischen Ausdruck aus Gleichung 4.19 verglichen. Die Abbildungen 5.2
und 5.3 zeigen die EEDFs wiederum für die beiden Grenzfälle. Zum einen ist das
geringste Druckregime in Kombination mit der höchsten Frequenz, zum anderen der
größte Druck zusammen mit der kleinsten Anregungsfrequenz, jeweils bei verschiedenen Silankonzentrationen, dargestellt. Elektronentemperaturen von 1 und 5 eV
wurden hierfür verwendet. Das Auftreten von hochenergetischen Elektronen wird
durch niedrige Silankonzentrationen begünstigt. In Abbildung 5.2 wird gezeigt, dass
Silankonzentrationen von 5 and 10 % die gleichen Ergebnisse mit sich bringen. In
reinen Silanplasmen ist der Anteil der hochenergetischen Elektronen im Vergleich
dazu reduziert. Durch den Vergleich der beiden Abbildungen 5.2 und 5.3 wird deutlich, dass aus BOLSIG+ für beide Regime das exakt selbe Verhalten hervorgeht.
Aus den Abbildungen 5.4 und 5.5 wird deutlich, dass Elektronen in kapazitiv gekoppelten Entladungen nicht im Gleichgewicht sind und daher nicht durch eine MaxwellVerteilung beschrieben werden können. Da die Verteilung nicht eindeutig durch eine
analytische Funktion beschrieben werden kann, wird eine Zuordnungstabelle mit
Energie-Verteilungsfunktionen für verschiedene Temperaturen durch BOLSIG+ generiert. Diese Verteilungen werden dann im globalen Modell zur Berechnung der
Reaktionsraten verwendet.
5.2 BESCHREIBUNG DER ELEKTRONEN-ENERGIE- VERTEILUNG
83
0
10
f / eV−3/2
BOLSIG+ SC=5%
x=1.0
x=1.5
x=2.0
−5
10
−10
10
0
5
10
15
20
25
E / eV
Abb. 5.4: Die mit BOLSIG+ berechnete Elektronen-Energie-Wahrscheinlichkeitsfunktion im Vergleich zu Gleichung 4.19 für x=1, 1.5 und 2 für eine Elektronentemperatur von 1 eV.
0
10
f / eV−3/2
BOLSIG+ SC=5%
x=1.0
x=1.5
x=2.0
−5
10
−10
10
0
20
40
E / eV
60
80
Abb. 5.5: Die mit BOLSIG+ berechnete Elektronen-Energie-Wahrscheinlichkeitsfunktion im Vergleich zu Gleichung 4.19 für x=1, 1.5 und 2 für eine Elektronentemperatur von 5 eV.
84
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
5.3 Vergleich mit experimentellen Messungen
Eine genaue Charakterisierung von reaktiven Plasmen stellt immer noch eine große
Herausforderung dar. Daher gibt es nur wenig experimentelle Untersuchungen von
Silan-Wasserstoff-Plasmen. Einige wenige Gruppen haben Methoden zur Diagnose
dieser Entladungen etabliert. Für die Validierung dieses globalen Modells werden
Messungen von Strahm et al. durch FTIR Spektroskopie [38] herangezogen. Sie monitoren die Silanumsetzung D (s. Gleichung 2.4), die nicht nur für die Produktionseffizienz von Bedeutung ist, sondern auch einen guten Parameter zur Validierung
eines Chemiemodells darstellt.
Abbildung 5.6 vergleicht die Umsetzung, die aus gemessenen Silandichten resultiert,
mit den numerischen Ergebnissen des globalen Modells. Die Messungen wurden bei
den Bedingungen aus Tabelle 5.2 durchgeführt. Die experimentelle Umsetzung wird
jeweils für die Variation eines Plasmaparameters mit der simulativen verglichen. Die
Abbildung zeigt Variationen der Leistung P abs , des Gasflusses Φ, des Druckes p, der
Silankonzentration SC und des Plattenabstandes L.
D/%
100
75
50
500
1000
1500
2000
Pabs / W
(a) Absorbierte Leistung (600 Pa, 2 %, 2000 sccm, 25 mm).
D/%
100
75
50
1000
2000
Φ / sccm
3000
4000
(b) Gasfluss (2000 W, 200 Pa, 7 %, 25 mm).
5.3 VERGLEICH MIT EXPERIMENTELLEN MESSUNGEN
85
D/%
100
75
50
0
200
400
600
p / Pa
800
1.000
(c) Druck (1000 W, 2 %, 2000 sccm, 25 mm).
D/%
100
75
50
2.5
5
SC / %
7.5
10
(d) Silankonzentration (2000 W, 200 Pa, 2000 sccm, 25 mm).
D/%
100
75
Model
Exp.
50
0.01
0.015
0.02
0.025
L/m
(e) Plattenabstand (2000 W, 600 Pa, 2 %, 2000 sccm).
Abb. 5.6: Die mit dem globalen Modell berechnete Silanumsetzung im Vergleich zu
den Messungen aus [38] als Funktion der verschiedenen Prozessparameter.
Gute Übereinstimmung wird erreicht. Abweichungen treten für den niedrigen Druckbereich auf. Hier findet die Transition ins nicht-lokale Regime statt. Dies führt zu
verfälschten Elektronen-Energie-Verteilungsfunktionen aus BOLSIG+, da die EEDF
in diesem Regime stark vom Ort abhängt. Folglich werden die Reaktionsraten und
Plasmadichten im globalen Modell verfälscht.
86
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
Tab. 5.2: Der von Strahm et al. [38] durch FTIR Spektroskopie untersuchte Parameterbereich, der zum Abgleich mit dem globalen Modell herangezogen
wird.
Prozessparameter
Einheit
Bereich
Absorbierte Leistung P abs
Gasfluss Φ
Druck p
Silankonzentration SC
Plattenabstand L
W
sccm
Pa
%
m
500-2000
500-4000
75-1000
1-10
0.012-0.025
5.4 Analyse der Plasmazusammensetzung
Zur Analyse der in Kapitel 5.1 und 5.2 eingeführten Plasmaprozessbedingungen mittels globalem Modell wird die Plasmazusammensetzung untersucht. Der Verlauf der
Elektronentemperatur in Abhängigkeit des Druckes ist in Abbildung 5.7 dargestellt.
Je niedriger der Gasdruck ist, desto größer ist die freie Weglänge der Elektronen. Als
Konsequenz absorbieren die Elektronen einen großen Beitrag der Leistung, was sich
in den hohen Elektronentemperaturen zeigt. Gleichermaßen wird veranschaulicht,
dass kleine freie Weglängen zu kleinen Elektronentemperaturen führen. Durch den
elektronegativen Charakter der Entladung hängt die Elektronentemperatur auch geringfügig von der Leistung ab.
Die niedrigere mittlere Elektronenenergie ist verantwortlich für die Abnahme der
Elektronendichte für zunehmende Drücke in Abbildung 5.8. Erwartungsgemäß nimmt
die Elektronendichte mit zunehmender Leistung zu.
5.4 ANALYSE DER PLASMAZUSAMMENSETZUNG
87
3
500W
2000W
Te / (eV)
2
1
0
0
200
400
600
p / Pa
800
1000
Abb. 5.7: Elektronentemperatur als Funktion des Druckes für 500 und 2000 W absorbierte Leistung.
16
ne / (1/m3)
15
x 10
500W
1000W
1500W
2000W
10
5
0
0
200
400
600
p / Pa
800
1000
Abb. 5.8: Elektronendichte als Funktion des Druckes bei 500, 1000, 1500 und 2000 W
absorbierter Leistung.
88
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
3
5% SiH4
10% SiH4
α / (−)
2
1
0
0
200
400
600
p / Pa
800
1000
Abb. 5.9: Die Elektronegativität des Plasmas als Funktion des Druckes bei 5 und
10 % Silan.
16
2.5
x 10
1.5
3
nSiH− / (1/m3)
2
500W
1000W
1500W
2000W
1
0.5
0
200
400
600
p / Pa
800
1000
Abb. 5.10: SiH−
3 Dichte als Funktion des Druckes bei 500, 1000, 1500 und 2000 W
absorbierter Leistung.
5.4 ANALYSE DER PLASMAZUSAMMENSETZUNG
89
16
n+ / (1/m3)
15
x 10
500W
1000W
1500W
2000W
10
5
0
0
200
400
600
p / Pa
800
1000
Abb. 5.11: Kationendichte als Funktion des Druckes für 500, 1000, 1500 und 2000 W
absorbierter Leistung.
Die Elektronegativität α spiegelt wieder, ob Elektronen oder negative Ionen die dominante negative Spezies darstellen. In Abbildung 5.9 ist zu sehen, dass die Elektronegativität des Plasmas stark von der Silankonzentration und dem Druck abhängt.
SiH4 -Entladungen sind typische elektronegative Plasmen. Daher nimmt die Elektronegativität mit zunehmender Silankonzentration deutlich zu.
Elektronen lagern sich mit steigendem Druck verstärkt an Silan (Reaktion Nr. 18 in
Tabelle 3.4) an (Abbildung 5.10). Die aus dieser Reaktion resultierenden Anionen
werden durch das Plasmapotential im Bulk gehalten. Sie reagieren mit Silan, was
zum Wachstum von längerkettigen Anionen führt. Damit spielen negative Ionen eine
entscheidende Rolle bei der Staubbildung. Da einige Anionen über Reaktionen mit
positiven Ionen neutralisiert werden, wie zum Beispiel SiH−
3 (in Reaktion Nr. 3, 4,
5, 6 und 36), nimmt die Anionendichte sukzessiv mit zunehmender Moleküllänge
ab. Deshalb werden im hiesigen Modell keine Anionen, die länger als SiH−
3 sind,
abgebildet.
In Abbildung 5.11 zeigt die Kationendichte für geringe Drücke ein vergleichbares
Verhalten zur Elektronendichte, da Anionen in diesem Regime noch keine wichtige
Rolle spielen. Bei höheren Drücken dominieren die Kationen im Vergleich zu den
Elektronen, da in diesen Regimen Anionen entstehen und so einen Beitrag zur Quasineutralität leisten.
90
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
17
10
n+/− / (1/m3)
H+2
H+3
SiH+3
14
10
Si2H+4
SiH−3
e
11
10
100
500
p / Pa
1000
Abb. 5.12: Dichte der verschiedenen Ionen als Funktion des Druckes bei 1000 W
absorbierter Leistung.
+
Bei niedrigen Drücken stellen SiH+
3 und Si2 H4 die häufigsten Ionen (Abbildung
5.12). Wasserstoffionen stellen einen erheblichen Anteil der Kationen, insbesondere durch die niedrige Silankonzentration im Gasgemisch von 5 %. Da jedoch H+
2
nur durch Elektronenstoßreaktionen mit H2 und nur für Energien von mindestens
15.4 eV entsteht (s. Tabelle 3.2), kommen Wasserstoffionen insbesondere für hohe
Drücke immer weniger häufig im Vergleich zu Silanionen vor. Letztere haben eine
Ionisationsenergie von 11.9 eV. Je höher der Druck ist, desto mehr längere Silanionen werden durch Polymerisationsprozesse von Monosilanionen mit SiH4 erzeugt.
Dieser Effekt entspricht den Messergebnissen von Nunomura [164].
5.4 ANALYSE DER PLASMAZUSAMMENSETZUNG
20
91
nSiH
10
2
nSiH
3
19
nradicals / (1/m3)
10
nSi
H
nSi
H
nSi
H
nSi
H
nSi
H
nSi
H
nSi
H
2 5
3 7
18
10
4 9
5 11
17
10
6 13
7 15
16
10
0
200
400
600
p / Pa
800
8 17
1000
Abb. 5.13: Radikaldichte in Abhängigkeit des Druckes bei 1000 W absorbierter Leistung.
0.3
5% SiH4
10% SiH4
hl / (−)
0.2
0.1
0
0
200
400
600
p / Pa
800
1000
Abb. 5.14: h-Faktor (Randschichtdichte im Verhältnis zur Dichte in der Bulk-Mitte)
der Ionen in Abhängigkeit des Druckes für 5 und 10 % Silan.
92
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
0.5
hSiH
2
hSi H
0.4
h / (−)
x 2x+1
0.3
0.2
0.1
0
0
200
400
600
p / Pa
800
1000
Abb. 5.15: h-Faktor der Radikale in Abhängigkeit des Druckes.
Aus Abbildung 5.13 kann man schlußfolgern, dass die häufigsten Radikale bei hohen Drücken Si3 H7 , Si4 H9 und SiH3 sind. In Niederdruckregimen ist SiH2 wichtiger.
Das hängt direkt mit dem Sticking Koeffizienten und den Ratenkoeffizienten zusammen (s. Tabelle 3.7): SiH2 hat eine hohe Wahrscheinlichkeit in der Gasphase,
bei ausreichend hoher Stoßfrequenz, oder an der Oberfläche zu reagieren. Durch
diese Reaktionen von SiH2 werden verstärkt längerkettige Silanmoleküle bei hohen
Drücken erzeugt. Dies geht mit den Erkenntnissen in [84], [81] und [83] einher. Hier
wird das für kleine Drücke zunehmende Verhältnis von SiH2 zu SiH3 auf die höhere
Elektronentemperatur zurückgeführt (s. Kapitel 2.1.2).
Durch den sequenziellen Prozess liegt ein abnehmender Trend der Dichte hinsichtlich längeren Molekülen vor. Eine Ausnahme bilden SiH3 - und Si2 H5 -Radikale, die
mit sich selbst rekombinieren und hiermit ihre Dichten verringern.
Wie in den Gleichungen 4.9 und 4.11 gezeigt, ist der Teilchenfluss zu den Elektroden
eine Funktion deren Randschichtdichte. Diese hängt wiederum vom Ionendichteprofil
und somit vom Druckregime und der Elektronegativität der Entladung ab. Je höher
der Druck der Entladung ist, desto geringer ist das Verhältnis zwischen Randschichtund Bulk-Dichte, wie Abbildung 5.14 zeigt. Hohe Elektronegativitäten verstärken
diesen Effekt.
5.4 ANALYSE DER PLASMAZUSAMMENSETZUNG
93
Wie in Abbildung 5.15 zu sehen ist, nimmt auch die Randschichtdichte der Radikale
mit zunehmendem Druck im Vergleich zu deren Bulk-Dichte ab. Radikale mit einem
hohen Sticking Koeffizienten wie SiH2 haben folglich niedrigere Randschichtdichten
als Radikale mit einer niedrigen Wahrscheinlich einer Weiterreaktion wie Six H2x+1 .
d / (nm/s)
3
2
1
0
0
500W
1000W
1500W
2000W
200
400
600
p / Pa
800
1000
Abb. 5.16: Abscheiderate als Funktion des Druckes bei 500, 1000, 1500 und 2000 W
absorbierter Leistung.
Als Konsequenz der zunehmenden Radikaldichten bei steigendem Druck, wie in Abbildung 5.13 gezeigt, nimmt die Abscheiderate, berechnet mithilfe der Dichte von
Silizium von 2200 kg/m3 , für eine Leistung von 2000 W mit dem Druck zu (Abbildung 5.16). Für 500 und 1000 W geht für eine Druckzunahme bei > 500 Pa die Rate
wieder leicht zurück, trotz der steigenden Radikaldichten. Dieser Effekt zeigt, dass
über die Speziesdichten im Plasmabulk hinaus der Teilchentransport zum Substrat
für die Abscheideraten maßgeblich ist. Dementsprechend ist die durch Stoßprozesse
verlangsamte Diffusion hier für den Rückgang der Rate verantwortlich. Erwartungsgemäß gilt: Je höher die Leistung, desto höher ist die Rate.
Das globale Modell ermöglicht also die Analyse der Plasmazusammensetzung und
bestimmt Parameter wie die Silanausnutzung und die Abscheiderate des Prozesses
innerhalb von kurzen Rechenzeiten. Diese Features sind gut geeignet, um experimentelle Plasmaprozessentwicklungen zu beschleunigen und bieten sich für zeiteffiziente
Prozessoptimierungen an.
94
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
5.5 Korrelation Prozessbedingungen Filmeigenschaften
Für hochqualitatives mikrokristallines Material ist einerseits die richtige Morphologie, das sogenannte Übergangsmaterial, das sich zwischen amorphem und kristallinem Material einstellt, verantwortlich. Andererseits spielen Defektdichten in der
Schicht eine große Rolle. Sie agieren als Rekombinationszentren und limitieren so
den Wirkungsgrad der Zelle. Des weiteren reduziert die Staubbildung im Plasma die
Standzeiten des Equipments und birgt gleichzeitig das Risiko einer Schädigung der
Schichten.
Basierend auf den Schichtwachstumsmodellen aus Kapitel 2.1.2 werden Kriterien für
die Defektdichte und die Kristallinität des abgeschiedenen Materials eingeführt, indem Prozesse, die zu guten Solarzellen führen, simulativ abgebildet und hinsichtlich
der Plasmazusammensetzung analysiert werden. Bei konstanten Substrattemperaturen ist das Verhältnis des Flusses von atomarem Wasserstoff zum Gesamtfluss der
Radikale und des atomaren Wasserstoffs zur Wand 1/(1 + ΓRadikal /ΓH ) proportional
zur Kristallinität Xc des Materials (s. Kapitel 2.1.3). Dieses Verhältnis wird daher
als erstes Kriterium herangezogen. Darüber hinaus hängt die Dichte des abgeschiedenen Materials und damit die Inverse der Defektdichte bzw. der Schichtporosität
vom Typ der schichtbildenden Radikale ab. Wie in Kapitel 2.1.2 gezeigt, haben SiH3 Radikale größere Diffusionslängen als SiH2 und sind daher besser für das Ausheilen
von Defekten geeignet. Dementsprechend führen sie zu dichterem Material. Konsequenterweise wird das Verhältnis nSiH2 /nSiH3 als Kriterium für die Defektdichte R
herangezogen.
Die Prozessbedingungen von Gordijn et al. [165], die zu hohen Zellwirkungsgraden der hergestellten mikrokristallinen Solarzellen führen, ergeben mittels globalem
Modell die in Tabelle 5.3 gezeigten Werte für die oben definierten Kriterien. Sie definieren den Zielbereich für die im Rahmen dieser Arbeit durchgeführten Optimierung
von mikrokristallinen Solarzellen.
5.6 OPTIMIERUNG VON KAPAZITIVEN QUELLKONZEPTEN
95
Tab. 5.3: Optimierungskriterien und die zugehörigen Schichteigenschaften.
Schichteigenschaft
Kriterium
Zielbereich
Kristallinität Xc
Defektdichte R
1/(1 + ΓRadikal /ΓH )
nSiH2 /nSiH3
0.67
(0.0078)
-
0.79
0.0259
5.6 Optimierung von kapazitiven Quellkonzepten
Eine Optimierung der Prozessbedingungen aus Tabelle 5.1 soll ergeben, welche Prozesse die in Tabelle 5.3 eingeführten Kriterien erfüllen und gleichzeitig zu hohen
Abscheideraten führen. Hierzu decken 5000 Betriebspunkte diesen Bereich der Prozessbedingungen ab, die für die Abscheidung von Dünnschicht-Silizium relevant sind.
Die Verteilung der Betriebsbedingungen im Parameterraum sind das Resultat einer
statistischen Versuchsplanung mit ASCMO [166].
50
0.8
40
0.6
30
#/−
Xc = 1/(1+ΓRadikal/ΓH) / −
60
0.4
20
0.2
10
−3
10
−2
−1
10
10
R = nSiH /nSiH / −
2
0
0
10
3
Abb. 5.17: Dichteverteilung der untersuchten Prozesse im Prozessbereich von Tabelle 5.1 bezüglich der Optimierungskriterien Xc = 1/(1 + ΓRadikal /ΓH )
und R = nSiH2 /nSiH3 . Der Zielbereich ist für beide Kriterien durch die
jeweils obere und untere Grenze angegeben. Die Anzahl der Prozessbedingungen, die zu den jeweiligen Kombinationen der beiden Verhältnisse
führen, werden in der Kontur dargestellt.
96
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
In Abbildung 5.17 ist die Dichteverteilung der untersuchten Prozesse bezüglich der
Optimierungskriterien gezeigt. Die Kontur der Abbildung repräsentiert die Anzahl
der Prozesse, die zu der entsprechenden Kombination aus Kristallinität und Defektdichte führen. Der Zielbereich für beide Schichteigenschaften ist jeweils mit zwei
Linien für die obere bzw. untere Grenze markiert. Da die Defektdichte so niedrig
sein sollte wie möglich, ist die Untergrenze punktiert. Besonders der Zielbereich der
Kristallinität wird nur von wenigen Betriebspunkten erreicht. Die meisten Prozesse
im Parameterraum resultieren in geringen Defektdichten und einer wenig kristallinen
Morphologie.
Diese Kombination ist bekannt aus der Abscheidung von amorphem Silizium. Die
Zunahme der Kristallinität geht für die meisten Prozesse mit höheren Defektdichten
einher. Nur wenige Bedingungen führen zur angestrebten Kombination aus Morphologie und Mikrostruktur. Dieser trade-off ist der limitierende Faktor der Optimierung.
Unter den Bedingungen einer idealen Kombination aus Kristallinität und Mikrostruktur sind hohe Abscheideraten und eine gute Ausnutzung des Silans erwünscht. Betrachtet man nur die Bedingungen, die zu der Kombination aus gewünschter Kristallinität und Mikrostruktur führen, reduziert sich der Betriebsbereich aus Tabelle
5.3 nicht.
In Abbildung 5.18 ist in der ersten Spalte das Verhältnis 1/ (1 + ΓRadikal /ΓH ), in
Abhängigkeit der beiden restlichen Parameter dargestellt. Es repräsentiert die, bezüglich zwei Prozessparametern gemittelte Kristallinität <Xc >. Der Bereich zwischen den beiden Linien zeigt mögliche Prozessbereiche. Im jeweiligen Graphen der
zweiten Spalte ist die Standardabweichung bezüglich der Mittelung σXc relativ zum
Mittelwert < Xc > gezeigt. Sie spiegeln die Robustheit der Prozesse bei diesen Bedingungen wider. Für kleine Werte σXc / < Xc > gilt, dass der jeweilige Prozess
robust ist. Für große Werte ist er sensibel gegenüber Änderungen der Prozessparameter, über die gemittelt wurde. Die Prozessparameter Leistung und Silankonzentration betreffend, werden die Schichten im Mittel kristalliner, je niedriger die
Silankonzentration ist. Das Flussverhältnis ΓH /ΓRadikal nimmt überproportional für
abnehmende Silankonzentrationen SC zu. Für die Abhängigkeit von der absorbierten Leistung liegt ebenso ein überproportionales Verhalten vor. Je höher Pabs , desto
5.6. OPTIMIERUNG VON KAPAZITIVEN QUELLKONZEPTEN
<X >
c (Φ, p, L)
σ /<X >
/−
X
97
c (Φ, p, L)
c
/%
15
0.6
0.5
15
0.4
0.7
0.6
0 .5
0.8
0.7
0.9
2000
20
0 .4
0.8
P
0.9
abs
/W
1500
1000
20
25
0.3
0.5
0.6
500
1
5
30
0.8
0.7
30
9
13
35
40
1
5
9
SC / %
<X >
c (P
13
SC / %
, SC, L)
σ /<X >
/−
X
c (P
c
abs
/%
, SC, L)
abs
0.5
0.4
2250
10
0.3
0.5
0.6
0.7
0.8
Φ / sccm
10
10
0.6
0.7
0.8
0.3
0.4
4000
35
40
50
15
15
0.
5
0.
0.7
0.8
0.9
500
100
6
550
p / Pa
<X >
c (P
1000
, SC, Φ)
20
25
40
35
550
p / Pa
100
σ /<X >
/−
X
c (P
c
abs
25
30
30
, SC, Φ)
/%
abs
0.025
10
0.2
0.3
0.6
0.5
0.7
0.8
10
0.4
10
10
10
0.3
0.5
0.6
0.7
0.8
L/m
10
0.015
1000
10
4
0.
10
15
5
6
550
p / Pa
15
220
5
0.
0.7
8
0.
0.9
0.005
100
0.
1000
100
15
40
35
30
550
p / Pa
20
25
1000
Abb. 5.18: Links: Korelation zwischen zwei Prozessparametern und des bezüglich
der anderen Parameter gemittelten Verhältnises von 1/(1 + ΓRadikal /ΓH )
(<Xc >). Das Zielgebiet ist durch zwei Linien eingegrenzt. Rechts: Verhältnis der Standardabweichung σXc zur mittleren Kristallinität.
98
5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
kristalliner wird die Schicht. Dies stimmt mit zahlreichen experimentellen Arbeiten [167–169] überein. Mai et al. [167] haben z.B. bei konstanter Silankonzentration
und zunehmender Leistung ebenso einen Anstieg der Schichtkristallinität gemessen.
Dementsprechend wurde auch hier folglich die Silankonzentration erhöht, um wieder
im optimalen a-Si:H/µc-Si:H-Übergangsbereich anzukommen.
Es wird deutlich, dass die Mittelung für den Großteil der Kombinationen aus Pabs
und SC zu einer Streuung von 20 % führt. Nur für kleine Leistungen um 500 W
tritt eine maximale Streuung von 40 % auf.
Bezüglich der restlichen Parameter Druck, Gasfluss und Plattenabstand wird deutlich, dass Änderungen aller dieser Parameter die Kristallinität stark beeinflussen.
Insbesondere niedrige Drücke begünstigen sehr kristallines Material. Die Abhängigkeit der Kristallinität vom Gasfluss und vom Plattenabstand ist weniger stark
ausgeprägt, wobei kleine Gasflüsse tendenziell zu kristallinerem Material führen,
wie auch Mai et al. erfahren haben. Gleiches gilt für kleine Plattenabstände.
Die Streuung beträgt auch hier für den Großteil der Kombinationen maximal 20 %.
Für minimale Flüsse bzw. Plattenabstände nimmt die Streuung einen Maximalwert
von 40 % an.
Aus diesen Zusammenhängen in den Modellergebnissen kann man qualitativ schlussfolgern: Eine Erhöhung der Abscheideleistung oder des Gasflusses, z.B. mit dem Ziel
einer höheren Abscheiderate, muss mit einer Anpassung der Silankonzentration einhergehen, um Material im optimalen a-Si:H/µc-Si:H-Übergangsbereich abzuscheiden. So muss eine Erhöhung des Gasflusses mit einer Verringerung der Silankonzentration einhergehen. Eine Leistungserhöhung hingegen erfordert eine Erhöhung
der Silankonzentration. Diese Abhängigkeiten werden durch die experimentellen Erkenntnisse von Mai et al. unterstützt.
Analog zu Abbildung 5.18 zeigt Abbildung 5.19 den Zusammenhang zwischen der
bezüglich drei Parametern gemittelten Defektdichte und den zwei restlichen Prozessparametern. Wenig Defekte treten für hohe Silankonzentrationen und niedrige
Leistungen auf. Ebenso haben große Gasflüsse einen positiven Einfluss. Niedrige
Druckregime sollten vermieden werden, wenn geringe Porositäten angestrebt werden. Der Plattenabstand hat keinen großen Einfluss hinsichtlich der Defekte.
5.6. OPTIMIERUNG VON KAPAZITIVEN QUELLKONZEPTEN
<R>
(Φ, p, L)
σ /<R>
/−
R
99
(Φ, p, L)
/%
20
20
(P
, SC, L)
40
80
60
0.0
5
<R>
40
1
5
9
SC / %
60 0
8
40
13
60
9
60
5
20
20
40
80
500
1
40
20
0.1
20
20
1000
20
20
0.0
5
Pabs / W
1500
20
0.15
20
0.1
0.2
0.0
5
2000
13
SC / %
σ /<R>
/−
R
abs
(P
, SC, L)
/%
abs
4000
0.3
0.1
0.2
Φ / sccm
0.2
0.1
2250
20
20
20
0.1
0.2
0.3
0.4
0.5
500
100
40
550
p / Pa
60
550
p / Pa
<R>(P
, SC, Φ)
1000
100
σR/<R>(P
/−
, SC, Φ)
1000
/%
abs
abs
0.05
L/m
0.2
0.15
0.1
20
20
20
0.25
0.015
0.05
0
0..3
25
0.2
0.15
0.1
0.025
20
20
0.05
0.1
0.15
0.2
0.25
0.3
0.005
100
20
550
p / Pa
1000
100
60
20
40
550
p / Pa
1000
Abb. 5.19: Links: Korelation zwischen zwei Prozessparametern und des bezüglich
der anderen Parameter gemittelten Dichteverhältnises von nSiH2 /nSiH3
(<R>). Der Maximalwert ist durch eine Linie markiert. Rechts: Verhältnis der Standardabweichung σR zur mittleren Defektdichte.
100 5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
Auch hierzu können experimentelle Arbeiten genannt werden, die dieses Verhalten
belegen: [170]. So nimmt der von Pinto et al. gemessene Mikrostrukturfaktor für zunehmende Silankonzentrationen, analog zu dem hier gezeigten qualitativen Verlauf
ab. Die Mittelung der Defektdichte geht für den Großteil des Prozessbereiches auch
mit einer Standardabweichung bezogen auf den Mittelwert von rund 20 % einher.
Abbildung 5.20 zeigt die Korrelation zwischen Abscheiderate und Silanausnutzung
für jede Betriebsbedingung, die jeweils durch einen Punkt repräsentiert wird. Die
Farbe des Punktes bildet den Wert der absorbierten Leistung (Abb. 5.20a) bzw.
der Silankonzentration (Abb. 5.20b) ab. Wie zu erwarten war, gehen einerseits hohe
Abscheideraten mit hohen Silanausnutzungen einher. Andererseits führt eine hohe
Ausnutzung nicht zwingend zu hohen Raten, wenn zum Beispiel die Silankonzentration den limitierenden Faktor darstellt.
Der Einfluss der Prozessbedingungen auf die Abscheiderate ist in Abbildung 5.21
dargestellt. In dieser Abbildung sind nur Betriebspunkte gezeigt, die die Kriterien bezüglich der Schichteigenschaften erfüllen. Erwartungsgemäß sind eine hohe Silankonzentration und viel Leistung notwendig, um hohe Abscheideraten zu erreichen. Dies
wird durch experimentelle Arbeiten, wie die von Matsui [169], bestätigt. Darüber
hinaus sind hohe Drücke dienlich, jedoch muss damit eine Leistungserhöhung einhergehen. Außerdem haben geringe Plattenabstände einen positiven Einfluss auf hohe
Raten. Von der begrenzten Anzahl der Betriebspunkte und der teilweise sprunghaften Änderung der Rate kann abgeleitet werden, dass eine geringe Änderung der
Prozessbedingungen oft zu schlechten Schichteigenschaften bzw. niedrigeren Raten
führt.
Um die Bedingungen mit dem höchsten Potenzial für mikrokristalline Schichten mit
einer geringen Defektdichte im amorph-kristallinen Übergangsbereich zu finden, betrachten wir Abbildung 5.21 und wählen ein Druckregime von 500 Pa und einen
Plattenabstand von 0.008 m aus, die potentiell zu hohen Raten führen. Darüber
hinaus wurde, basierend auf Abbildung 5.18 und 5.19 ein Gasfluss von 2000 sccm
festgelegt. Eine Variation der Silankonzentration für die beiden Extrema des Leistungsbereiches der Prozessbedingungen aus Tabelle 5.1 führt zu den Ergebnissen in
Abbildung 5.22. Hier wird in jedem Punkt eine Silankonzentration zwischen 1 und
5.6. OPTIMIERUNG VON KAPAZITIVEN QUELLKONZEPTEN
5
101
2000
1800
1400
1200
2.5
1000
Pabs / W
RD / (nm/s)
1600
800
600
400
0
0
25
50
D/%
75
100
(a) Einfluss der absorbierten Leistung.
5
12
8
2.5
6
SC / %
RD / (nm/s)
10
4
2
0
0
25
50
D/%
75
100
(b) Einfluss der Silankonzentration.
Abb. 5.20: Korrelation zwischen der Abscheiderate RD und der Silanausnutzung D.
102 5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
4
2000
3.5
Pabs / W
2.5
1000
2
RD / (nm/s)
3
1500
1.5
500
1
0.5
0
0
5
10
15
SC / %
(a) Absorbierte Leistung und Silankonzentration.
4
2000
3.5
Pabs / W
2.5
1000
2
1.5
500
1
0.5
0
250
500
p / Pa
750
1000
(b) Absorbierte Leistung und Druck.
RD / (nm/s)
3
1500
5.6. OPTIMIERUNG VON KAPAZITIVEN QUELLKONZEPTEN
103
4
2000
3.5
Pabs / W
2.5
1000
2
RD / (nm/s)
3
1500
1.5
500
1
0.5
0
0.005
0.015
L/m
0.025
(c) Absorbierte Leistung und Plattenabstand.
Abb. 5.21: Einfluss der Prozessparameter auf die Abscheiderate RD für die Betriebspunkte, die die Kriterien bezüglich der Schichteigenschaften erfüllen.
15 % abgebildet, wobei die erste Silankonzentrationsvariation für 500 W und die
zweite für 2000 W durchgeführt wurde. Vergleicht man einen Prozess mit einer bestimmten Silankonzentration bei 500 W mit dem bei 2000 W, zeigt sich wieder, dass
die Abscheiderate für zunehmende Leistungen ansteigt. Gleichzeitig nimmt aber mit
zunehmender Leistung auch die Defektdichte zu. Bezüglich des Gasgemisches, kann
man hier nochmals sehen, dass die Schicht für zunehmende Silankonzentrationen
amorpher wird.
Für eine Maximierung der Abscheiderate bei den Bedingungen aus Abbildung 5.22
muss, wie in Abbildung 5.23 gezeigt, die Silankonzentration einhergehend mit der
Leistung erhöht werden. So kann eine Rate von 4 nm/s für 2000 W und 10 % Silan
erreicht werden. Diese Prozessbedingungen werden im öffentlich geförderten Projekt
Quick µc-Si [171] experimentell erfolgreich umgesetzt.
104 5. GLOBALE MODELLIERUNG VON KAPAZITIVEN SiH4 -H2 -PLASMEN
4.5
4
SC = 1−15 %
3.5
0.6
3
2.5
0.4
2000 W
2
500 W
RD / (nm/s)
1/(1+ΓRadikal/ΓH) / −
0.8
1.5
0.2
1
0.5
−3
10
−2
10
n
−1
SiH
/n
2
SiH
0
10
/−
10
3
Abb. 5.22: Resultierende Kristallinität und Defektdichte bei Variation der Silankonzentration zwischen 1 und 15 % bei 1500 und 2000 W (p = 500 Pa,
Φ = 2000 sccm, L = 0.008 m). Die dazugehörige Abscheiderate wird
durch die Farbe beschrieben.
13
5
4
SC / %
3
2
5
RD / (nm/s)
9
1
1
500
1000
1500
2000
Pabs / W
Abb. 5.23: Optimale Silankonzentration bei guter Schichtqualität und Leistungen
zwischen 500 und 2000 W für maximale Abscheideraten (p = 500 Pa,
Φ = 2000 sccm, L = 0.008 m).
Zusammenfassung
In dieser Arbeit wird die Abscheidung dünner Siliziumfilme mittels Niedertemperaturplasmen, der zentrale Produktionsschritt von Dünnschicht-Silizium-Solarzellen,
numerisch untersucht und optimiert. Dieser Schritt hat das größte Kostensenkungspotenzial bei der Fertigung solcher Solarzellen. So besteht einerseits Bedarf an einer
hohen Materialausnutzung. Andererseits werden höhere Abscheideraten angestrebt,
um kürzere Taktzeiten zu realisieren, die deutliche Einsparungen mit sich bringen.
Für die numerische Abbildung des Plasma-unterstützen Abscheideprozesses wird
ein globales Modell entwickelt. Mit diesem Modell können die Plasmazusammensetzung, Gasausnutzung und Abscheiderate abhängig von den Prozessparametern, des
Prozessgases und der Reaktorgeometrie einer kapazitiv gekoppelten Entladung in
weniger als 30 s berechnet werden. Für die Approximation der Elektronen-EnergieVerteilung werden Zuordnungstabellen verwendet, die mit dem Boltzmann-Löser
BOLSIG+ erstellt werden.
Der Vergleich der Ergebnisse des globalen Modells einer Argon-Entladung ergibt eine
gute Übereinstimmung mit alternativen Simulationsansätzen, wie einem Particle-InCell Code und einer Fluid Simulation mit kinetischer Betrachtung der Elektronen.
Auch der Abgleich zwischen Simulation und Experiment zeigt konforme Ergebnisse. Ein entscheidender Parameter des globalen Modells ist die Wahl der Elektronen-Energie-Verteilungsfunktion. Sie lässt sich bei Argon-Entladungen für Drücke
größer 100 Pa mit BOLSIG+ bestimmen. Dementsprechend gering ist hier die Abweichung zwischen global berechneter Elektronendichte bzw. -temperatur und den
PIC-Ergebnissen.
106
ZUSAMMENFASSUNG
Damit steht ein valider Ansatz für die Abbildung der reaktiven Silan-WasserstoffEntladung, in dem für die zur Abscheidung von Dünnschicht-Silizium für Solarzellen
interessanten Druckbereich, zur Verfügung. Es wird gezeigt, dass das relativ einfache
globale Modell unter Verwendung dieser Tabellen in der Lage ist, Abhängigkeiten der
Schichteigenschaften von den Prozessparametern abzubilden. Hierzu werden Korrelationen zwischen der Plasmazusammensetzung und der Mikrostruktur bzw. der
Kristallinität der Schicht aus experimentellen Prozessen guter Solarzellen abgeleitet.
Diese Kriterien werden herangezogen, um mittels Optimierungsrechnungen potenzielle Betriebsbedingungen für qualitativ hochwertige Schichten zu ermitteln. Hierdurch wird die globale Modellierung zu einer Ergänzung der experimentellen Prozessentwicklung. Sie hat das Potenzial sowohl Kosten für experimentelles Equipment
als auch Entwicklungszeiten zu reduzieren und kann im Rahmen der gezeigten Vorgehensweise auch für andere Plasmaprozesse zum Einsatz kommen. So zeigt die
Optimierung, dass ein hoher Prozessdruck zu hohen Abscheideraten führt, wenn
ausreichend Leistung zur Verfügung gestellt wird. Die resultierenden Abhängigkeiten werden durch experimentelle Arbeiten aus der Literatur bestätigt. Bei einem
Druck von 500 Pa und einer Leistungsdichte von 1.3 W/cm2 werden bei einer Silankonzentration von 10 % gute Schichten mit einer Rate von 4 nm/s abgeschieden.
Diese simulativ errechneten Prozessbedingungen werden im öffentlich geförderten
Projekt Quick µc-Si experimentell erfolgreich umgesetzt.
Ausblick
In der Zukunft werden Plasmamodelle einen zunehmenden Beitrag zur Schichtentwicklung leisten, indem sie die Anzahl der notwendigen Experimente reduzieren und
somit einerseits den Anlageninvest und andererseits die Entwicklungszeiten reduzieren. Die hier gezeigte Vorgehensweise ermöglicht den Einsatz einfacher globaler
Modelle zur Optimierung von verschiedensten Plasmaprozessen bei geringem Rechenaufwand.
Für zukünftige Arbeiten auf dem Gebiet der Modellierung von Silan-WasserstoffPlasmen zur Abscheidung von Dünnschicht-Silizium für die Photovoltaik empfiehlt
es sich, auf die Wachstumsprozesse an der Schichtoberfläche detaillierter einzugehen. Die Randschichtmodellierung repräsentiert hierfür die Schnittstelle, die die Bestimmung von Ionenenergien am Substrat ermöglicht. Sie sind mitverantwortlich
für die Entstehung von Defekten in den Siliziumschichten und haben gleichzeitig
auch einen Einfluss auf die Schichtkristallinität [172]. Langfristig sind Lösungen
wünschenswert, die eine Kopplung zwischen der Modellierung des Plasmas und der
Modellierung des Schichtwachstums, z.B. mit dem Ansatz der Molekular Dynamic
vorsehen. Desweiteren kann die Berücksichtigung der im Experiment als kritisch
bekannten Staubbildung in den Simulationen die Umsetzbarkeit der berechneten
Prozessparameter erhöhen. Ein weiterer wichtiger Aspekt bei der Abscheidung von
Dünnschicht-Silizium für Solarzellen ist die Schichthomogenität. Hierfür bieten sich
mehrdimensionale Modelle an, die die gesamte Reaktorgeometrie abbilden können.
Ein Parameter, der die Vergleichbarkeit von Simulation und Experiment entscheidend beeinflusst, ist der Anteil der Generatorleistung, die im Plasma absorbiert
wird. Die experimentelle Bestimmung des Elektrodenpotentials kann hier einerseits
zu einer Verbesserung führen. Andererseits gibt es Ansätze das externe Netzwerk
108
AUSBLICK
zwischen Generator und Plasma, bestehend aus Matchbox und Zuleitungen, mit im
Plasmamodell abzubilden.
Bezüglich des im Rahmen dieser Arbeit entwickelten globalen Modells ist es im Sinne
der Allgemeingültigkeit von Interesse, erweiterte Ansätze zur Bestimmung der Zuordnungstabellen mit den Elektronen-Energie-Verteilungen zu entwickeln. Wie gezeigt wurde, kann die Ergebnisqualität für Entladungen im geringen Druckbereich
besonders bei Gasen mit hohen Anregungsenergien durch die Anwendung der nichtlokalen Approximation zur Berechnung der EEDF weiter verbessert werden. Neben
einer erweiterten Drucksensivität kann hierdurch auch eine bessere Abhängigkeit
der EEDF von der Anregungsfrequenz abgebildet werden. So werden Optimierungen
auch bezüglich dieses Prozessparameters möglich. Die Möglichkeit der Berechnung
der Randschichtdichten für andere Plasmaquellen als für kapazitive kann darüber
hinaus die Allgemeingültigkeit des Modells erhöhen.
Formelzeichen und Abkürzungen
α
Elektronegativität des Plasmas
-
δ
Kronecker Delta-Funktion
-
ǫ
Energie
J
ǫ0
elektrische Feldkonstante
ǫµ+
Energieverlust durch Ionenflüsse zur Wand
eV
ǫc
Energieverlust pro erzeugtem Elektronen-Ionen-Paar
eV
ǫex
Anregungsenergie
eV
ǫe
Energieverlust durch Elektronenflüsse zur Wand
eV
ǫiz
Ionisationsenergie
eV
ǫtot
totale Energie
J
η
dimensionsloser Vorfaktor
-
Γ µ+
Ionenfluss für die Teilchen µ+
1/m2 s
Γtot
Summe aus Elektronen- und Ionenfluss
1/m2 s
Γ µ0
Fluss des Radikals µ0
1/m2 s
λ
freie Weglänge
m
λǫ
Energie-Relaxations-Länge
m
λD
Debye-Länge
m
8.854E-12 As/Vm
110
Formelzeichen und Abkürzungen
λinel
freie Weglänge der Elektronen für Energieverlustprozesse
m
λm
freie Weglänge der Elektronen
m
µ+
positives Teilchen
-
µ−
negatives Teilchen
-
µ0
Neutralteilchen
-
µ0
magnetische Feldkonstante
µe
Beweglichkeit der Elektronen
m2 /Vs
µi
Beweglichkeit der Ionen
m2 /Vs
νm,e
Stoßrate von Elektronen
1/s
νm
Stoßrate
1/s
νRF
Anregungsfrequenz
1/s
Ω
Satz aller betrachteten Teilchen
-
Ω+
Untermenge der positiven Ionen
-
Ω−
Untermenge der negativen Ionen
-
Ω0
Untermenge der Neutralteilchen
-
ωpe
Elektronenplasmafrequenz
φ
Elektrisches Potential
ψ
Winkel
ρ
Raumladungsdichte
C/m3
ρij
Raumladungsdichte am Gitterpunkt ij
C/m3
σ (j)
Wirkungsquerschnitt für die j-te Reaktion
12.566E-7 N/A2
1/s
V
rad
m2
Formelzeichen und Abkürzungen
111
σAB
Wirkungsquerschnitt für Stoß zwischen Teilchen A und B
m2
σel
Stoßquerschnitt für elastische Stöße
m2
σex
Stoßquerschnitt für Anregungsstöße
m2
σiz
Stoßquerschnitt für Ionisationsstöße
m2
σm
Stoßquerschnitt
m2
τ
Reaktionszeit
s
τ (jq)
Stöchiometriefaktor der j-ten Reaktion des q-ten Elements
-
τm
Impulsrelaxationszeit
s
β
Reaktionswahrscheinlichkeit an der Oberfläche
%
γ
Rekombinationswahrscheinlichkeit an der Oberfläche
%
µ
Teilchenart
µc Si:H
mikrokristallines Silizium
e
Index für Elektronen
N
Index für Neutralteilchen
j
Index bezüglich der chemischen Reaktion
q
Index bezüglich der Teilchen einer chemischen Reaktion
s
Index für Randschicht
A
Elektrodenoberfläche
a
Beschleunigung
Ae
Elektronenaffinität
B
Magnetische Feldstärke
m2
m/s2
eV
A/m
112
Formelzeichen und Abkürzungen
b
Gewichtungsfaktor
-
c
Silankonzentration im Ausgangsgasgemisch
c1
Funktionen der Elektronentemperatur
eV−3/2
c2
Funktionen der Elektronentemperatur
eV−x
cp
Silankonzentration im Plasma
%
D
Silanumsetzung
%
d
geometrische Bezugslänge
m
Da
ambipolarer Diffusionskoeffizient
m2 /s
De
Diffusionskoeffizient der Elektronen
m2 /s
Di
Diffusionskoeffizient der Ionen
m2 /s
E
Elektrische Feldstärke
V/m
e
Elementarladung
Eij
elektrische Feldstärke am Gitterpunkt ij
V/m
Ez
elektrische Feldstärke in z-Richtung
V/m
F
Kraft
f
Verteilungsfunktion
-
f0
isotroper Anteil der Verteilungsfunktion
-
f1
anisotroper Anteil der Verteilungsfunktion
-
fe0
isotroper Anteil der Verteilungsfunktion der Elektronen
-
Fp
Kraft, die auf Partikel p wirkt
Gµ
Quellterm
%
∗
C
N
N
1/m3 s
Formelzeichen und Abkürzungen
113
h
Plancksches Wirkungsquantum
6.626E-34 Js
hhp
Verhältnis Randschichtdichte - mittlere Dichte (hoher Druck)
-
hlp
Verhältnis Randschichtdichte - mittlere Dichte (geringer Druck)
-
hl
Verhältnis Randschichtdichte - mittlere Dichte
-
I2000
Absorptionspeak bei 2000 cm−1
a.u.
I2100
Absorptionspeak bei 2100 cm−1
a.u.
IE
Ionenstrom der Reaktionsedukte
A
IP
Ionenstrom der Reaktionsprodukte
A
IE
Ionisationsevents
#
j
Stromdichte
A/m2
je
Stromdichte der Elektronen
A/m2
jij
Stromdichte am Gitterpunkt ij
A/m2
K
Reaktionsratenkoeffizient
m3 /s
K (j)
Ratenkoeffizient der j-ten Reaktion
m3 /s
KAB
Ratenkoeffizient der Reaktion zwischen Teilchen A und B
m3 /s
kB
Boltzmann-Konstante
Kel
Ratenkoeffizient für elastische Stöße
m3 /s
Kex
Ratenkoeffizient für Anregungsreaktionen
m3 /s
Kiz
Ratenkoeffizient für Ionsationsreaktionen
m3 /s
kj
Reaktionsrate der j-ten Reaktion
KN
Ratenkoeffizient für Neutralisationsreaktionen
J/K
1/m3 s
m3 /s
114
Formelzeichen und Abkürzungen
Kn
Knudsen-Zahl
-
l
Länge der Kammer
m
L
Plattenabstand
m
M
Schwerteilchenmasse
kg
m
Masse
kg
M (jq)
Teilchenart der j-ten Reaktion des q-ten Elements
mµ
Masse der Teilchenart µ
kg
mµ+
Masse des Ions µ+
kg
me
Elektronenmasse
kg
mij
reduzierte Masse der Teilchen i und j
n
Teilchendichte
1/m3
nµ+
mittlere Dichte der Spezies µ+
1/m3
Nex
Anzahl der Anregungs- und Dissoziationsreaktionen
ne
Elektronendichte
1/m3
ng
Gasdichte
1/m3
nM(j1)
mittlere Dichte des ersten Elements der j-ten Reaktion
1/m3
NR
Anzahl der chemischen Reaktionen
ns,µ+
Randschichtdichte des Ions µ+
NS
Anzahl der Spezies
nµ
mittlere Speziesdichte
p
Druck
-
u
-
1/m3
1/m3
Pa
Formelzeichen und Abkürzungen
115
Pabs
absorbierte Leistung
W
Pext
externe eingekoppelte Leistung
W
pSiH4
Silanpartialdruck bei gezündetem Plasma
Pa
p0SiH4
Silanpartialdruck im ursprünglichen Gasgemisch
Pa
q
Ladung
C
QE
Quanteneffizienz
%
R
Defektdichte
r
Radius
R∗
Mikrostrukturfaktor
RRefl.
Reflektionswahrscheinlichkeit
S
Streutherm
s
sticking Koeffizient
Sµ
Senkenterm
SC
Silankonzentration
t
Zeit
s
tDa
für ambipolare Diffusion notwendige Zeit
s
Te
Elektronentemperatur
TGas
Gastemperatur
Ti
Ionentemperatur
T
Temperatur
V
Volumen
m
%
kg/m2 s
%
1/m3 s
%
eV
K
eV
K
m3
116
Formelzeichen und Abkürzungen
v
Geschwindigkeit
m/s
vs
Schwerpunktanteil der Geschwindigkeit
m/s
vµ+
gewichtete Geschwindigkeit des Ions µ+
m/s
vAB
Relativgeschiwndigkeit der Teilchen A und B
m/s
vB,µ+
Bohmgeschwindigkeit des Ions µ+
m/s
vp
Geschwindigkeit des Partikels p
m/s
vR
Relativgeschiwndigkeit
m/s
vtherm,µ+
thermische Geschwindigkeit des Ions µ+
m/s
vtherm,µ0
thermische Geschwindigkeit des Neutralteilchens µ0
m/s
vtherm
Thermischer Anteil der Geschwindigkeit
m/s
vz
Geschwindigkeit in z-Richtung
m/s
Wµ
alle Quellen und Senken an der Kammerwand
x
Ort
x∗
Parameter zwischen 0 und 1
xp
Ort von Partikel p
m
z
Raumrichtung
m
P̃e
Elektronenleistungsdichte
at. %
Atom-Prozent
a Si:H
amorphes Silizium
c-Si
kristallines Silizium
CCP
kapazitiv gekoppeltes Plasma
1/m3 s
m
-
W/m3
Formelzeichen und Abkürzungen
CFD
Computational Fluid Dynamics
CFL
Courant-Friedrichs-Lewy-Zahl
CVD
Chemical Vapour Deposition
DSMC
Direct Simulation Monte Carlo
ECR
Elektron-Zyklotron-Ressonanz
EEDF
Elektronen-Energie-Verteilungs-Funktion
EEG
Energie-Einspeise-Gesetz
EEG
Energie-Einspeise-Gesetz
EEPF
Elektronen-Energie-Wahrscheinlichkeits-Funktion
HF
High Frequency
ICP
Inductive Coupled Plasma
OES
optische Emissionsspektroskopie
PECVD
Plasma Enhanced Chemical Vapor Deposition
PIC
Particle-In-Cell
PV
Photovoltaik
RF
Radio Frequency
TCO
Transperent Conductive Oxide
VHF
Very High Frequency
117
Tabellenverzeichnis
3.1
3.2
3.3
3.4
3.5
3.6
3.7
Argonreaktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Schwellenenergie für die Generation von Ionen, angeregten und dissoziierten Spezies aus SiH4 , H2 und Si2 H6 . . . . . . . . . . . . . . .
Elastische Stöße in Silan-Wasserstoff-Plasmen . . . . . . . . . . . .
Die in dieser Arbeit berücksichtigten inelastischen Elektronen-SilanKollisionen. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Die in dieser Arbeit berücksichtigten inelastischen Elektronen-Wasserstoff-Kollisionen. . . . . . . . . . . . . . . . . . . . . . . . . . . .
Die in dieser Arbeit berücksichtigten chemischen Reaktionen. . . . .
Im Modell berücksichtigte Oberflächenreaktionen. . . . . . . . . . .
. 40
. 44
. 45
. 46
. 47
. 49
. 50
4.1
Untersuchter Parameterbereich für den Modellvergleich an einer Argonentladung (Standardbedingungen fett). . . . . . . . . . . . . . . . 61
5.1
5.2
Der in dieser Arbeit untersuchte Parameterbereich. . . . . . . . . . . 78
Der von Strahm et al. [38] durch FTIR Spektroskopie untersuchte
Parameterbereich, der zum Abgleich mit dem globalen Modell herangezogen wird. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
Optimierungskriterien und die zugehörigen Schichteigenschaften. . . . 95
5.3
Abbildungsverzeichnis
2.1
2.2
2.3
2.4
2.5
2.6
Aufbau einer mikromorphen p-i-n Solarzelle . . .
Quanteneffizienz einer mikromorphen Solarzelle .
Absorptionsspektren von a-Si:H, µc-Si:H und c-Si
Schema für die Volumenstruktur von µc-Si:H . . .
Plasma-Silan-Konzentration . . . . . . . . . . . .
Kapazitiv gekoppelte PECVD Quelle . . . . . . .
3.1
Die Knudsen-Zahl als Charakteristikum einer Strömung (aus [123],
mit freundlicher Genehmigung der Oxford University Press). . . . . .
PIC Ablaufschema . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Stossquerschnitte für Argon. . . . . . . . . . . . . . . . . . . . . . . .
Stossquerschnitte der elastischen Stöße und Ladungsaustauschstöße
in Silan-Wasserstoff-Plasmen entsprechend Tabelle 3.3. . . . . . . . .
Stossquerschnitte der inelastischen Silan-Stöße entsprechend Tabelle
3.4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Stossquerschnitte der inelastischen Wasserstoff-Stöße entsprechend Tabelle 3.5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2
3.3
3.4
3.5
3.6
4.1
4.2
4.3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
10
10
12
13
18
21
28
29
41
45
46
47
Grenzen der Kontinuumsmechanik: (a) Freie Weglänge der Elektronen und Ionen in Abhängigkeit des Druckes, (b) Stoßrate der Elektronen und Ionen in Abhängigkeit des Druckes im Vergleich zur Anregungsfrequenz von 13.56 MHz (punktiert in rot). . . . . . . . . . . . 62
Elektronen-Energie-Relaxations-Länge nach der Definition von Gleichung 3.11 in Argonplasmen bei 10, 100 und 1000 Pa. . . . . . . . . . 63
Elektronen-Energie-Wahrscheinlichkeitsfunktion im Plasmabulk berechnet mit yapic für verschiedene Prozessdruckwerte (p = 10-600 Pa). 64
120
Abbildungsverzeichnis
4.4
EEPF berechnet mit yapic, analytisch, BOLSIG+ und CFD-ACE+. . 65
4.5
Elektronen- (a) bzw. Ionendichteprofil (b) für verschiedene Prozessdruckwerte (p = 10 − 600 Pa). . . . . . . . . . . . . . . . . . . . . . . 66
4.6
Raumzeitaufgelöste Ionisationsevents (links) und Elektronenleistungsdichte (rechts) aus yapic für verschiedene Prozessdruckwerte (p =
10, 100 und 600 Pa). . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
4.7
Absorbierte Leistungsdichte in yapic und CFD-ACE+. . . . . . . . . 69
4.8
Elektronendichte im Plasmabulk in Abhängigkeit des Druckes im Vergleich zwischen yapic, CFD-ACE+ und dem globalen Modell. . . . . . 70
4.9
Elektronendichteprofile von yapic und CFD-ACE+ im Plasmabulk
im Vergleich. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
4.10 Gemitteltes elektrisches Feld als Funktion des Druckes aus yapic. . . . 71
4.11 Mittlere freie Weglänge der Elektronen im Vergleich zur Randschichtdicke der Entladung in Abhängigkeit des Druckes aus yapic. . . . . . 72
4.12 Mittlere Elektronenenergie im Plasmabulk in Abhängigkeit des Druckes
im Vergleich zwischen yapic, CFD-ACE+ und dem globalen Modell. . 72
4.13 EEPF, berechnet mit yapic und analytisch, für die Druckvariation,
die mittels OES charakterisiert wurde. . . . . . . . . . . . . . . . . . 75
4.14 Verlauf der experimentell ermittelten Elektronendichte als Funktion
des Druckes unter der Annahme einer Maxwell- bzw. einer Druyvesteyn-Verteilung. Vergleichend ist die simulativ errechnete Elektronendichte dargestellt. . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
4.15 Verlauf der experimentell ermittelten Elektronentemperatur Te als
Funktion des Druckes unter der Annahme einer Maxwell- bzw. einer
Druyvesteyn-Verteilung (Te = 2/3hǫi). Vergleichend ist die simulativ
errechnete Elektronentemperatur dargestellt. . . . . . . . . . . . . . . 77
5.1
Elektronen-Energie-Relaxations-Länge nach der Definition von Gleichung 3.11 in Silan-Wasserstoff-Plasmen bei 10, 100 und 1000 Pa. . . 80
5.2
Die mit BOLSIG+ berechnete Elektronen-Energie-Wahrscheinlichkeitsfunktion für das Verhältnis aus Anregungsfrequenz zu Druck von
6.55·10−15 m3 /s (100 Pa, 94.92 MHz) für verschiedene Silankonzentrationen. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
Abbildungsverzeichnis
121
5.3
EEPF aus BOLSIG+ für das Verhältnis aus Anregungsfrequenz zu
Gasdruck von 0.28·10−15 m3 /s (1000 Pa, 13.56 MHz) für verschiedene
Silankonzentrationen. . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
5.4
Die mit BOLSIG+ berechnete Elektronen-Energie-Wahrscheinlichkeitsfunktion im Vergleich zu Gleichung 4.19 für x=1, 1.5 und 2 für
eine Elektronentemperatur von 1 eV. . . . . . . . . . . . . . . . . . . 83
5.5
Die mit BOLSIG+ berechnete Elektronen-Energie-Wahrscheinlichkeitsfunktion im Vergleich zu Gleichung 4.19 für x=1, 1.5 und 2 für
eine Elektronentemperatur von 5 eV. . . . . . . . . . . . . . . . . . . 83
5.6
Die mit dem globalen Modell berechnete Silanumsetzung im Vergleich
zu den Messungen aus [38] als Funktion der verschiedenen Prozessparameter. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
5.7
Elektronentemperatur als Funktion des Druckes für 500 und 2000 W
absorbierte Leistung. . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
5.8
Elektronendichte als Funktion des Druckes bei 500, 1000, 1500 und
2000 W absorbierter Leistung. . . . . . . . . . . . . . . . . . . . . . . 87
5.9
Die Elektronegativität des Plasmas als Funktion des Druckes bei 5
und 10 % Silan. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
5.10 SiH−
3 Dichte als Funktion des Druckes bei 500, 1000, 1500 und 2000 W
absorbierter Leistung. . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
5.11 Kationendichte als Funktion des Druckes für 500, 1000, 1500 und
2000 W absorbierter Leistung. . . . . . . . . . . . . . . . . . . . . . . 89
5.12 Dichte der verschiedenen Ionen als Funktion des Druckes bei 1000 W
absorbierter Leistung. . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
5.13 Radikaldichte in Abhängigkeit des Druckes bei 1000 W absorbierter
Leistung. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
5.14 h-Faktor (Randschichtdichte im Verhältnis zur Dichte in der BulkMitte) der Ionen in Abhängigkeit des Druckes für 5 und 10 % Silan. . 91
5.15 h-Faktor der Radikale in Abhängigkeit des Druckes. . . . . . . . . . . 92
5.16 Abscheiderate als Funktion des Druckes bei 500, 1000, 1500 und
2000 W absorbierter Leistung. . . . . . . . . . . . . . . . . . . . . . . 93
122
Abbildungsverzeichnis
5.17 Dichteverteilung der untersuchten Prozesse im Prozessbereich von Tabelle 5.1 bezüglich der Optimierungskriterien Xc = 1/(1+ΓRadikal /ΓH )
und R = nSiH2 /nSiH3 . Der Zielbereich ist für beide Kriterien durch die
jeweils obere und untere Grenze angegeben. Die Anzahl der Prozessbedingungen, die zu den jeweiligen Kombinationen der beiden Verhältnisse führen, werden in der Kontur dargestellt. . . . . . . . . . . .
5.18 Links: Korelation zwischen zwei Prozessparametern und des bezüglich
der anderen Parameter gemittelten Verhältnises von 1/(1+ΓRadikal /ΓH )
(<Xc >). Das Zielgebiet ist durch zwei Linien eingegrenzt. Rechts:
Verhältnis der Standardabweichung σXc zur mittleren Kristallinität. .
5.19 Links: Korelation zwischen zwei Prozessparametern und des bezüglich
der anderen Parameter gemittelten Dichteverhältnises von nSiH2 /nSiH3
(<R>). Der Maximalwert ist durch eine Linie markiert. Rechts: Verhältnis der Standardabweichung σR zur mittleren Defektdichte. . . . .
5.20 Korrelation zwischen der Abscheiderate RD und der Silanausnutzung
D. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.21 Einfluss der Prozessparameter auf die Abscheiderate RD für die Betriebspunkte, die die Kriterien bezüglich der Schichteigenschaften erfüllen. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.22 Resultierende Kristallinität und Defektdichte bei Variation der Silankonzentration zwischen 1 und 15 % bei 1500 und 2000 W (p = 500 Pa,
Φ = 2000 sccm, L = 0.008 m). Die dazugehörige Abscheiderate wird
durch die Farbe beschrieben. . . . . . . . . . . . . . . . . . . . . . . .
5.23 Optimale Silankonzentration bei guter Schichtqualität und Leistungen zwischen 500 und 2000 W für maximale Abscheideraten (p =
500 Pa, Φ = 2000 sccm, L = 0.008 m). . . . . . . . . . . . . . . . . .
95
97
99
101
103
104
104
Literaturverzeichnis
[1] http://www.solarserver.de/solar-magazin/nachrichten/aktuelles/2013/kw40/ihs-photovoltaik-zubau-wird-2014-dreijahres-hoch-erreichen-wendepunkt-fuer-europa-in-sicht
.html (2013).
[2] http://www.solarserver.de/service-tools/photovoltaik preisindex.html (2013).
[3] R. Chittick, J. Alexander und H. Sterling, Journal of the Electrochemical Society 116, 77 (1969).
[4] D. Carlson und C. Wronski, Applied Physics Letters 28, 671 (1976).
[5] D. Carlson, C. Wronski, J. Pankove, P. Zanzucchi und D. Staebler, RCA review 38, 211 (1977).
[6] S. Veprek und V. Marecek, Solid-State Electronics 11, 683 (1968).
[7] A. Wang und G. Lucovsky, in Photovoltaic Specialists Conference, 1990.,
Conference Record of the Twenty First IEEE, IEEE (1990), S. 1614.
[8] G. Lucovsky, C. Wang, R. Nemanich und M. Williams, Solar Cells
30, 419 (1991).
[9] M. Faraji, S. Gokhale, S. Choudhari, M. Takwale und S. Ghaisas,
Applied Physics Letters 60, 3289 (199).
[10] K. Yamamoto, M. Toshimi, T. Suzuki, J. Tawada, T. Okamoto und
A. Nakajima, in Proc. Mater. Res. Soc. Symp. 507 (1998), S. 131.
123
124
Literaturverzeichnis
[11] J. Meier, J. Spitznagel, U. Kroll, C. Bucher, S. Fay, T. Moriarty
und A. Shah, Thin Solid Films 451, 518 (2004).
[12] J. Meier, D. Dubail, D. Fischer, J. A. Anna Selvan, N. Pellaton Vaucher, R. Platz, C. Hof, R. Flückiger, U. Kroll,
N. Wyrsch, P. Torres, H. Keppner, A. Shah und K.-D. Ufert, in Proceedings of the 13th EC Photovoltaic Solar Energy Conference (1995), S. 1445.
[13] J. Meier, S. Dubail, R. Platz, P. Torres, U. Kroll, J. Anna Selvan,
N. Pellaton Vaucher, C. Hof, D. Fischer, H. Keppner et al., Solar
Energy Materials and Solar Cells 49, 35 (1997).
[14] S. Danko, D. Bluhm, V. Bolsinger, W. Dobrygin, O. Schmidt und
R. P. Brinkmann, Plasma Sources Science and Technology 22, 055009
(2013).
[15] L. Kline und M. Kushner, Critical Reviews in Solid State and Materials
Sciences 16, 1 (1989).
[16] D. Graves und M. Kushner, Journal of Vacuum Science & Technology A:
Vacuum, Surfaces, and Films 21, S152 (2003).
[17] J. van Dijk, G. Kroesen und A. Bogaerts, Journal of Physics D: Applied
Physics 42, 190301 (2009).
[18] G. Hagelaar und L. Pitchford, Plasma Sources Science and Technology
14, 722 (2005).
[19] E. Amanatides, D. Mataras und D. Rapakoulias, Journal of Applied
Physics 90, 5799 (2001).
[20] S. Ashida, C. Lee und M. Lieberman, Journal of Vacuum Science &
Technology A: Vacuum, Surfaces, and Films 13, 2498 (1995).
[21] M. Lieberman und S. Ashida, Plasma Sources Science and Technology 5,
145 (1996).
Literaturverzeichnis
125
[22] Y. Ikeda, J. Verboncoeur, P. Christenson und C. Birdsall, Journal
of applied physics 86, 2431 (1999).
[23] Y. Hahn und S. Pearton, Korean Journal of Chemical Engineering 17, 304
(2000).
[24] J. Gudmundsson, Plasma Sources Science and Technology 10, 76 (2001).
[25] C. Lee, D. Graves, M. Lieberman und D. Hess, Journal of the Electrochemical Society 141, 1546 (1994).
[26] C. Lee und M. Lieberman, Journal of Vacuum Science & Technology A:
Vacuum, Surfaces, and Films 13, 368 (1995).
[27] Y. Lee, M. Lieberman, A. Lichtenberg, F. Bose, H. Baltes und
R. Patrick, Journal of Vacuum Science & Technology A: Vacuum, Surfaces,
and Films 15, 113 (1997).
[28] T. Kimura und K. Ohe, Plasma Sources Science and Technology 8, 553
(1999).
[29] J. Gudmundsson, Journal of Physics D: Applied Physics 35, 328 (2002).
[30] A. Efremov, G. Kim, J. Kim, A. Bogomolov und C. Kim, Microelectronic engineering 84, 136 (2007).
[31] S. Kim, M. Lieberman, A. Lichtenberg und J. Gudmundsson, Journal
of Vacuum Science & Technology A: Vacuum, Surfaces, and Films 24, 2025
(2006).
[32] D. Monahan und M. Turner, Plasma Sources Science and Technology 17,
045003 (2008).
[33] A. Hjartarson, E. Thorsteinsson und J. Gudmundsson, Plasma
Sources Science and Technology 19, 065008 (2010).
[34] M. Kushner, Journal of applied physics 63, 2532 (1988).
[35] U. Fantz, Plasma physics and controlled fusion 40, 1035 (1998).
126
Literaturverzeichnis
[36] E. Amanatides, S. Stamou und D. Mataras, Journal of Applied Physics
90, 5786 (2001).
[37] V. Strunin, A. Lyakhov, G. Khudaibergenov und V. Shkurkin, Technical Physics 47, 760 (2002).
[38] B. Strahm, A. Howling, L. Sansonnens und C. Hollenstein, Plasma
Sources Science and Technology 16, 80 (2007).
[39] D. Kim, J. Kang, A. Nasonova, K. Kim und S. Choi, Korean Journal of
Chemical Engineering 24, 154 (2007).
[40] O. Leroy, G. Gousset, L. L. Alves, J. Perrin und J. Jolly, Plasma
Sources Science and Technology 7, 348 (1998).
[41] G. Nienhuis, Plasma models for silicon deposition, Doktorarbeit (1998).
[42] G. Nienhuis, W. Goedheer, E. Hamers, W. Van Sark und J. Bezemer, Journal of Applied Physics 82, 2060 (1997).
[43] A. Salabas, G. Gousset und L. Alves, Plasma Sources Science and Technology 11, 448 (2002).
[44] A. Salabas, Fluid model for charged particle transport in capacitively coupled
radio-frequency discharges, Doktorarbeit (2003).
[45] A. Salabas, L. Marques, J. Jolly, G. Gousset und L. Alves, Journal
of applied physics 95, 4605 (2004).
[46] L. Marques, J. Jolly und L. Alves, Journal of Applied Physics 102,
063305 (2007).
[47] K. De Bleecker, Modeling of the formation and behavior of nanoparticles
in dusty plasmas, Doktorarbeit (2006).
[48] K. De Bleecker, A. Bogaerts, R. Gijbels und W. Goedheer, Physical Review E 69, 56409 (2004).
Literaturverzeichnis
127
[49] B. Lyka, E. Amanatides und D. Mataras, Japanese Journal Of Applied
Physics Part 1 Regular Papers Short Notes And Review Papers 45, 8172
(2006).
[50] B. Lykas, E. Amanatides und D. Mataras, in 19th European Photovoltaic
Solar Energy Conference, EPVSEC (2004).
[51] E. Amanatides, B. Lykas und D. Mataras, Plasma Science, IEEE Transactions on 33, 372 (2005).
[52] Joo, Thin Solid Films 519, 6892 (2011).
[53] J. Ding, Y. Zhao, N. Yuan, M. Chen, S. Wang, F. Ye und B. Kan,
Vacuum 86, 344 (2011).
[54] L. Alves und L. Marques, Plasma Physics and Controlled Fusion 54,
124012 (2012).
[55] M. Despeisse, C. Ballif, A. Feltrin, F. Meillaud, S. Fay, F. Haug,
D. Dominé, M. Python, T. Soderstrom, P. Buehlmann et al., in
Proc. of the SPIE Optics and Photonics 2009 Conference, San Diego (2009).
[56] M. Berginski, Lichtstreuende Oberflächen, Schichten und Schichtsysteme zur
Verbesserung der Lichteinkopplung in Silizium-Dünnschichtsolarzellen, Aus. 5
(Forschungszentrum Jülich, 2007).
[57] H. Blumenauer und W. Schatt, Einführung in die Werkstoffwissenschaft:
Mit 25 Tab. Von einem Autorenkollektiv]: Horst Blumenauer u. A.]. Hrsg.
Werner Schatt.-1. Aufl (Deutscher Verlag für Grundstoffindustrie, 1972).
[58] S. Klein, F. Finger, R. Carius und M. Stutzmann, Journal of applied
physics 98, 024905 (2005).
[59] D. Staebler und C. Wronski, Applied Physics Letters 31, 292 (1977).
[60] C. Kittel, Einführung in die Festkörperphysik (Oldenbourg Wissenschaftsverlag, 2005).
128
Literaturverzeichnis
[61] T. Repmann, Stapelsolarzellen aus amorphem und mikrokristallinem Silizium, Doktorarbeit (2003).
[62] Y. Aya, W. Shinohara, M. Matsumoto, K. Murata, T. Kunii, M. Nakagawa, A. Terakawa und M. Tanaka, Progress in Photovoltaics: Research and Applications (2011).
[63] L. Houben, M. Luysberg, P. Hapke, R. Carius, F. Finger und
H. Wagner, Philosophical Magazine A 77, 1447 (1998).
[64] M. Luysberg, P. Hapke, R. Carius und F. Finger, Philosophical magazine A 75, 31 (1997).
[65] E. Vallat-Sauvain, U. Kroll, J. Meier, A. Shah und J. Pohl, Journal
of Applied Physics 87, 3137 (2000).
[66] A. Smets, T. Matsui und M. Kondo, Journal of applied physics 104,
034508 (2008).
[67] R. Schropp, K. Feenstra, E. Molenbroek, H. Meiling und J. Rath,
Statistical Mechanics, Electronic, Optical and Magnetic Properties 76, 309
(1997).
[68] H. Wagner und W. Beyer, Solid state communications 48, 585 (1983).
[69] A. Mahan, P. Raboisson, D. Williamson und R. Tsu, Solar cells 21,
117 (1987).
[70] F. Finger, U. Kroll, V. Viret, A. Shah, W. Beyer, X.-M. Tang,
J. Weber, A. Howling und C. Hollenstein, Journal of applied physics
71, 5665 (1992).
[71] A. Matsuda, Journal of Non-Crystalline Solids 338, 1 (2004).
[72] A. Matsuda, Journal of non-crystalline Solids 59, 767 (1983).
[73] C. Tsai, G. Anderson, R. Thompson und B. Wacker, Journal of NonCrystalline Solids 114, 151 (1989).
Literaturverzeichnis
129
[74] K. Nakamura, K. Yoshino, S. Takeoka und I. Shimizu, Japanese Journal of Applied Physics 34, 442 (1995).
[75] H. Fujiwara, M. Kondo und A. Matsuda, Physical Review B 63, 115306
(2001).
[76] S. Guha, J. Yang, A. Banerjee, B. Yan und K. Lord, Solar energy
materials and solar cells 78, 329 (2003).
[77] S. Klein, Microcrystalline Silicon Prepared by Hot Wire CVD: Preparation
and Characterisation of Material and Solar Cells, Doktorarbeit (2003).
[78] G. Dingemans, M. Van Den Donker, D. Hrunski, A. Gordijn,
W. Kessels und M. Van De Sanden, Applied Physics Letters 93, 111914
(2008).
[79] A. C. Bronneberg, A. H. M. Smets, M. Creatore und M. C. M. Van
De Sanden, Journal of Non-Crystalline Solids 357, 884 (2011).
[80] J. Perrin und J. Non-Cryst, Abstract| PDF (457 K)| View Record in
Scopus| Cited By in Scopus (57) S. 639.
[81] M. Takai, T. Nishimoto, M. Kondo und A. Matsuda, Science and
Technology of Advanced Materials 2, 495 (2001).
[82] A. Matsuda, M. Takai, T. Nishimoto und M. Kondo, Solar energy
materials and solar cells 78, 3 (2003).
[83] T. Takeda, K. Tanaka, H. Inoue, M. Hirayama, T. Tsumori, H. Aharoni und T. Ohmi, Japanese Journal Of Applied Physics Part 1 Regular
Papers Short Notes And Review Papers 46, 2542 (2007).
[84] S. Ram, L. Kroely, S. Kasouit, P. Bulkin und P. Cabarrocas, physica status solidi (c) 7, 553 (2010).
[85] W. Beyer, Physica B: Condensed Matter 170, 105 (1991).
[86] T. Moustakas, Semiconductors and Semimetals 21, 55 (1984).
130
Literaturverzeichnis
[87] T. Saitoh, S. Muramatsu, T. Shimada und M. Migitaka, Applied Physics Letters 42, 678 (1983).
[88] T. Fuyuki, K. Du, S. Okamoto, S. Yasuda, T. Kimoto, M. Yoshimoto und H. Matsunami, Journal of applied physics 64, 2380 (1988).
[89] Y. Mishima, M. Hirose, Y. Osaka, K. Nagamine, Y. Ashida, N. Kitagawa und K. Isogaya, Japanese Journal of Applied Physics 22, L46
(1983).
[90] A. Mahan, E. Iwaniczko, B. Nelson, R. Reedy Jr, R. Crandall,
S. Guha und J. Yang, in Photovoltaic Specialists Conference, 1996., Conference Record of the Twenty Fifth IEEE, IEEE (1996), S. 1065.
[91] M. van den Donker und F. Jülich, Plasma Deposition of Microcrystalline Silicon Solar Cells: Looking Beyond the Glass (Forschungszentrum Jülich
GmbH, Zentralbibliothek, 2006).
[92] M. Fukawa, S. Suzuki, L. Guo, M. Kondo und A. Matsuda, Solar
energy materials and solar cells 66, 217 (2001).
[93] Y. Sobajima, C. Sada, A. Matsuda und H. Okamoto .
[94] A. Aberle, Thin Solid Films 517, 4706 (2009).
[95] M. Lieberman und A. Lichtenberg, Principles of plasma discharges and
materials processing (Wiley-Blackwell, 2005).
[96] G. Nienhuis, Plasma models for silicon deposition, Doktorarbeit (1998).
[97] A. Salabas, Fluid model for charged particle transport in capacitively coupled
radio-frequency discharges, Doktorarbeit (2003).
[98] M. Van den Donker, B. Rech, F. Finger, W. Kessels und M. Van de
Sanden, Applied Physics Letters 87, 263503 (2005).
[99] A. Hammad, E. Amanatides, D. Mataras und D. Rapakoulias, Thin
solid films 451, 255 (2004).
Literaturverzeichnis
131
[100] X. Zhang, F. Zhang, E. Amanatides, D. Mataras und Y. Zhao, Thin
Solid Films 516, 6912 (2008).
[101] B. Heil, U. Czarnetzki, R. Brinkmann und T. Mussenbrock, Journal
of Physics D: Applied Physics 41, 165202 (2008).
[102] D. Hrunski, F. Mootz, A. Zeuner, A. Janssen, H. Rost, R. Beckmann, S. Binder, E. Schüngel, S. Mohr, D. Luggenhölscher et al.,
Vacuum (2012).
[103] C. Niikura, N. Itagaki und A. Matsuda, Surface and Coatings Technology 201, 5463 (2007).
[104] C. Niikura, N. Itagaki und A. Matsuda, Japanese journal of applied
physics 46, 3052 (2007).
[105] W. Shinohara, Y. Aya, M. Hishida, N. Kitahara, M. Nakagawa,
A. Terakawa und M. Tanaka .
[106] P. Tien und J. Moshman, Journal of Applied Physics 27, 1067 (1956).
[107] O. Buneman, Physical Review 115, 503 (1959).
[108] C. Birdsall und W. Bridges, Journal of Applied Physics 32, 2611 (1961).
[109] C. Birdsall, Plasma Science, IEEE Transactions on 19, 65 (1991).
[110] M. Surendra und D. Graves, Plasma Science, IEEE Transactions on 19,
144 (1991).
[111] M. Turner und M. Hopkins, Physical review letters 69, 3511 (1992).
[112] J. Verboncoeur, M. Alves, V. Vahedi und C. Birdsall, J. Comput.
Phys. 1993, 104 (1993).
[113] V. Vahedi und M. Surendra, Computer Physics Communications 87, 179
(1995).
[114] T. Johnston, Physical Review 120, 1103 (1960).
132
Literaturverzeichnis
[115] I. Shkarofsky, T. Johnston, M. Bachynski und J. Hirshfield, American Journal of Physics 35, 551 (1967).
[116] J. Ingold, Physical Review A 40, 3855 (1989).
[117] A. Metze, D. Ernie und H. Oskam, Physical Review A 39, 4117 (1989).
[118] R. Porteous und D. Graves, Plasma Science, IEEE Transactions on 19,
204 (1991).
[119] D. Graves und K. Jensen, Plasma Science, IEEE Transactions on 14, 78
(1986).
[120] D. Graves, Journal of applied physics 62, 88 (1987).
[121] S. Park und D. Economou, Journal of applied physics 68, 3904 (1990).
[122] T. Makabe, N. Nakano und Y. Yamaguchi, Physical Review A 45, 2520
(1992).
[123] G. Bird, Clarendon, Oxford (1994).
[124] P. Mertmann, N. Bibinov, H. Halfmann und P. Awakowicz, Plasma
Sources Science and Technology 19, 015017 (2010).
[125] Z. Donkó, Plasma Sources Science and Technology 20, 024001 (2011).
[126] J. Verboncoeur, Plasma physics and controlled fusion 47, A231 (2005).
[127] U. Kortshagen, C. Busch und L. Tsendin, Plasma Sources Science and
Technology 5, 1 (1996).
[128] A. Keudell von, Einführung in die Plasmaphysik, Lecture notes (2005).
[129] ESI CFD Inc., CFD-ACE+ V2010.0 Modules Manual, Part 1, handbook.
[130] M. Knaipp, Modellierung von Temperatureinflüssen in Halbleiterbauelementen, Doktorarbeit, TU Wien (1998).
Literaturverzeichnis
133
[131] H. Kim, F. Iza, S. Yang, M. Radmilović-Radjenović und J. Lee,
Journal of physics D: applied physics 38, R283 (2005).
[132] W. Allen, T. Cheng und F. Lampe, J. Chem. Phys 66, 3371 (1977).
[133] A. Hickman, The Journal of Chemical Physics 70, 4872 (1979).
[134] J. Perrin, Y. Takeda, N. Hirano, Y. Takeuchi und A. Matsuda,
Surface Science 210, 114 (1989).
[135] A. Matsuda, K. Nomoto, Y. Takeuchi, A. Suzuki, A. Yuuki und
J. Perrin, Surface science 227, 50 (1990).
[136] A. Phelps, Journal of applied physics 76, 747 (1994).
[137] P. Potzinger und F. Lampe, The Journal of Physical Chemistry 73, 3912
(1969).
[138] J. Morrison und J. Traeger, International Journal of Mass Spectrometry
and Ion Physics 11, 289 (1973).
[139] K. De Bleecker, A. Bogaerts und W. Goedheer, Physical Review E
73, 26405 (2006).
[140] J. Perrin, O. Leroy und M. Bordage, Contributions to Plasma Physics
36, 3 (1996).
[141] J. Loureiro und C. Ferreira, Journal of Physics D: Applied Physics 22,
1680 (1989).
[142] L. Theard und W. Huntress Jr, The Journal of Chemical Physics 60,
2840 (1974).
[143] J. Perrin, J. Schmitt, G. De Rosny, B. Drevillon, J. Huc und
A. Lloret, Chemical Physics 73, 383 (1982).
[144] M. Kurachi und Y. Nakamura, Journal of Physics D: Applied Physics
22, 107 (1989).
134
Literaturverzeichnis
[145] The Siglo Data base, CPAT and Kinema Software, http://www.siglokinema.com.
[146] P. Haaland, The Journal of Chemical Physics 93, 4066 (1990).
[147] E. Krishnakumar und S. Srivastava, Contributions to Plasma Physics
35, 395 (1995).
[148] H. Tawara und T. Kato, Atomic Data and Nuclear Data Tables 36, 167
(1987).
[149] S. Buckman und A. Phelps, The Journal of Chemical Physics 82, 4999
(1985).
[150] http://jila.colorado.edu/text˜avp/collision_data/electronneutral/ electron.txt/.
[151] T. Tabata und T. Shirai, Atomic Data and Nuclear Data Tables 76, 1
(2000).
[152] A. Engelhardt und A. Phelps, Physical Review 131, 2115 (1963).
[153] H. Ehrhardt, L. Langhans, F. Linder und H. Taylor, Physical Review
173, 222 (1968).
[154] G. Khayrallah, Physical Review A 13, 1989 (1976).
[155] M. M. Turner, A. Derzsi, Z. Donkó, D. Eremin, S. J. Kelly,
T. Lafleur und T. Mussenbrock, Physics of Plasmas 20, 013507 (2013).
[156] R. Arslanbekov und V. Kolobov .
[157] V. I. Kolobov, Computational materials science 28, 302 (2003).
[158] MATLAB, version 7.13.0.564 (R2011b) (The MathWorks Inc., Natick,
Massachusetts, 2011).
[159] H. Amemiya, Journal of the Physical Society of Japan 66, 1335 (1997).
[160] V. Godyak und R. Piejak, Physical Review Letters 65, 996 (1990).
Literaturverzeichnis
135
[161] V. Godyak, R. Piejak und B. Alexandrovich, Plasma sources science
and technology 1, 36 (1992).
[162] S. Iordanova und I. Koleva, Spectrochimica Acta Part B: Atomic Spectroscopy 62, 344 (2007).
[163] D. Bluhm, S. Wilczek, S. Danko, O. Schmidt und R. Brinkmann, in
Proceedings of the 31st ICPIG (2013).
[164] S. Nunomura und M. Kondo, Applied Physics Letters 93, 231502 (2008).
[165] A. Gordijn, A. Pollet-Villard und F. Finger, Applied Physics Letters
98, 211501 (2011).
[166] ASCMO, version 4.1.1.380 (ETAS GmbH, Stuttgart, Germany, 2011).
[167] Y. Mai, S. Klein, R. Carius, J. Wolff, A. Lambertz, F. Finger und
X. Geng, Journal of applied physics 97, 114913 (2005).
[168] O. Vetterl, F. Finger, R. Carius, P. Hapke, L. Houben, O. Kluth,
A. Lambertz, A. Mück, B. Rech und H. Wagner, Solar Energy Materials and Solar Cells 62, 97 (2000).
[169] T. Matsui, A. Matsuda und M. Kondo, Solar energy materials and solar
cells 90, 3199 (2006).
[170] N. Pinto, M. Ficcadenti, L. Morresi, R. Murri, G. Ambrosone und
U. Coscia, Journal of applied physics 96, 7306 (2004).
[171] in BMU-Project No 0325260A.
[172] A. Verkerk, M. de Jong, J. Rath, M. Brinza, R. Schropp, W. Goedheer, V. Krzhizhanovskaya, Y. Gorbachev, K. Orlov, E. Khilkevitch et al., Materials Science and Engineering: B 159, 53 (2009).
Danksagung
Die vorliegende Arbeit wurde in der Abteilung CR/ART im Zentralbereich Forschung und Vorausentwicklung der Robert Bosch GmbH in Stuttgart im Rahmen
des öffentlich geförderten Projektes Quick µc-Si angefertigt. An dieser Stelle möchte
ich den Förderern für die Finanzierung und allen, die zum Gelingen dieser Arbeit
beigetragen haben, meinen Dank aussprechen.
Mein besonderer Dank gilt Herrn Prof. Dr. Ralf Peter Brinkmann für die wissenschaftliche Betreuung der Arbeit von Seiten der Ruhr-Universität Bochum. Trotz der
räumlichen Trennung ermöglichte er mir eine sehr gute Zusammenarbeit mit seinem
Lehrstuhl. Der konstruktive persönliche und schriftliche Austausch mit einem unerschöpflichen Fundus an thematischen und wissenschaftlichen Hinweisen haben mich
stets in neue Sphären gelenkt.
Herrn Prof. Dr. Awakowicz danke ich für die Übernahme des Koreferats und für
seinen wertvollen akademischen Rat.
Meinem Betreuer der Robert Bosch GmbH Dr. Oliver Schmidt danke ich für die tolle
Unterstützung, Motivation und die inhaltvollen und konstruktiven Diskussionen.
Bei allen weiteren Mitarbeitern und meinen engagierten Praktikanten der Abteilung CR/ART sowie der gesamten zentralen Forschung und Vorausentwicklung der
Robert Bosch GmbH möchte ich mich für die ausgezeichnete Atmosphäre, die gute
Zusammenarbeit und die zahlreichen fruchtbaren Diskussionen bedanken. Sie haben
mich vielseitig bereichert. Gleiches gilt für die Mitarbeiter der Geschäftsbereiche mit
denen ich im Austausch war und die Lehrstühle für Theoretische Elektrotechnik und
für Allgemeine Elektrotechnik und Plasmatechnik der Universität Bochum.
Nicht minder aufreibend waren die vergangenen Jahre für meine Familie, Freunde
und Begleiter, die mich in allen Phasen mit jeder möglichen Unterstützung bedacht
haben. Ihnen gilt mein besonderer Dank.
LEBENSLAUF
Stephan Danko
geb. am 11.10.1981 in Künzelsau
Beruf
seit 12/11
Entwicklungsingenieur der Robert Bosch GmbH
Zentralbereich Forschung und Vorausentwicklung, Gerlingen
Promotion
seit 12/08
Industriepromotion, Ruhr-Universität Bochum
Lehrstuhl für Theoretische Elektrotechnik
Robert Bosch GmbH
Zentralbereich Forschung und Vorausentwicklung, Gerlingen
Studium
11/07 - 05/08
Diplomarbeit
Centro Nacional de Investigaciones Metalúrgicas Madrid, E
08/04 - 09/08
Doppeldiplom - Maschinenbau
Universität Karlsruhe/INSA Lyon, F
Deutsch-Französische Hochschule (DFH)
10/02 - 10/04
Grundstudium des Maschinenbaus
Universität Karlsruhe
Schule
09/92 - 06/01
Allgemeines Abitur, Ganerben Gymnasium Künzelsau