Messen
Werbung

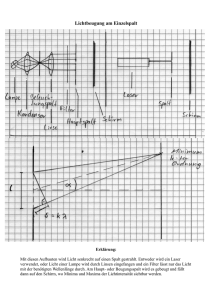
Mikroskopie 02 Auflösungsvermögen SchülerHilfen 1. Was ist das Auflösungsvermögen? Beispiel aus Google-Earth: Man kann zwar beliebig vergrößern, jedoch sind die Einzelheiten dann nicht mehr deutlich zu erkennen. Es treten nur noch „körnige“, kleinste Bildelemente auf, aus denen das Bild zusammengesetzt ist. Das Auflösungsvermögen ist bei dieser Vergrößerung nicht ausreichend genug! Beim Mikroskop: Häufig große Vergrößerung aber zu geringe Auflösung! Jeweils links: Normales Bild durch ein Mikroskop mit hoher Vergrößerung aber geringen Auflösungsvermögens Jeweils rechts: Gleiches Objekt durch Mikroskop mit großem Auflösungsvermögen. Auflösungsvermögen: Fähigkeit eines optischen Instruments, auch kleinste Strukturen des betrachteten Gegenstands deutlich darzustellen. 81941632 Rolf Piffer Seite 1 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen 2. Beugung Lässt man ebene Wasserwellen senkrecht auf einen Spalt zulaufen (Abb. rechts) , dann kann man hinter dem Spalt auch im „Schattenbereich“ Wellen erkennen. Der Effekt, dass sich Wasserwellen auch um Hindernisse herum ausbreiten können, nennt man Beugung. Dieser Effekt wird umso deutlicher, je kleiner der Spalt wird: Beugung ist eine typische Wellenerscheinung! Beleuchtet man eine Schere mit Laserlicht, tritt anstatt eines scharfen Schattens ein deutliches Beugungsmuster auf. (Quelle: D.C. Giancoli: Physik, Pearson Studium, München 2006, S. 1186) Dieses Beugungsmuster ist ein deutlicher Nachweis dafür, dass sich Licht wellenförmig ausbreitet. 81941632 Rolf Piffer Seite 2 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen Durchstrahlt man einen schmalen Spalt mit Laserlicht, kann man das folgende Beugungsbild hinter dem Spalt auf einem Schirm sehen: In der Mitte befindet sich das Hauptmaximum der Intensität (Maximum 0. Ordnung), begrenzt durch schmale Streifen von Dunkelheit (Minima der Intensität). Dann folgen weitere schwächere Maxima (Maxima 1., 2., 3. etc. Ordnung), jeweils getrennt durch Minima. Die Breite des Hauptmaximums ändert sich mit der Spaltbreite b (Quelle: http://leifi.physik.uni-muenchen.de/web_ph12/versuche/06einfachspalt/spaltbreite.htm vom 1.10.2008): => Je schmaler die Spaltblende, desto breiter das zentrale Beugungsmaximum Auch an sehr schmalen kreisförmigen Blenden tritt Beugung auf: Das „Beugungsscheibchen“ in der Mitte (Maximum 0. Ordnung) wird begrenzt durch einen dunklen Kreis mit sehr kleiner Intensität – das erste Minimum des 81941632 Rolf Piffer Seite 3 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen Intensitätsverlaufs. Bei größeren Radien (im eigentlichen Schattenbereich) sind weitere aber viel schwächere ringförmige Maxima 1., 2. etc. Ordnung zu beobachten. Derartige „Beugungsmuster“ sind von Fotographien her bekannt. Die Form der Beugung gibt sogar die Form der verwendeten Blende wieder: Versuche dazu: 1. In den Laserstrahl wird eine veränderbare Spaltblende immer schmaler gestellt. => Auf einem weit entfernten Schirm wird die Beugung durch ein immer breiteres Maximum sichtbar. 2. Kreisblenden verschiedenen Durchmessers (1,0 mm. 0,3 mm und 0,2 mm) werden in den Strahl gebracht. => Kreisförmige Beugungsmuster sind auf dem Schirm zu beobachten. 3. Mit einer Linse wird ein beleuchtetes Drahtgitter scharf auf einem Schirm abgebildet. Dann wird vor die Linse ein veränderbarer Spalt gestellt, der langsam immer enger gestellt wird. => Das Gitterbild wird bei Verengung immer unschärfer bis die Konturen der parallel zum Spalt angeordneten Drähte nicht mehr zu erkennen sind. Die Drähte senkrecht zum Spalt bleiben scharf abgebildet. 81941632 Rolf Piffer Seite 4 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen 3. Interferenz Wie kann man die Minima in den Beugungsbildern erklären? Die Wellen, die vom Spalt aus in den Raum hinter den Spalt gelangen, überlagern sich, ohne dass sich die einzelnen Wellen dadurch verändern. Trifft aber ein Wellental auf einen Wellenberg, löschen sich die Wellen gegenseitig aus. Oder allgemein gesagt: Treten genau so viele positive wie negative Werte der Wellen am Ort des Schirms auf, addieren sich diese Werte zu 0. Ein negativer Wert einer Welle liegt dann vor, wenn ihre momentane Auslenkung unterhalb der Nulllinie ist. Im nebenstehenden Beispiel sind die Werte der jeweiligen Wellen am Ort des Schirms als grüne Strecken gekennzeichnet. Es gibt genau so viele „positive“ wie „negative“ Strecken => Minimum der Intensität Diese Überlagerung von Wellen nennt man Interferenz. Bei einem Minimum liegt eine destruktive Interferenz vor. Entsprechend zu diesen Überlegungen treten auch Maxima der Intensität auf, die durch Minima begrenzt werden. Am nebenstehenden Beispiel kann man erkennen, dass sich die grünen Strecken (Werte der Auslenkung am Schirm) nicht zu Null addieren. Bei diesem Winkel zur Mittelachse liegt hier bei gleicher Spaltbreite wie oben ein Nebenmaximum vor. Maximum: konstruktive Interferenz Der Abstand zwischen benachbarten Maxima (Wellenberge) bzw. Minima (Wellentälern) der Welle heißt Wellenlänge λ. Ändert sich die Wellenlänge des Lichts, entsteht bei gleichem Spalt ein Minimum unter einem anderen Winkel als in der obigen Abbildung gezeigt. D.h. dass die Lage der Minima und Maxima auch von der Wellenlänge abhängen. 81941632 Rolf Piffer Seite 5 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen Das erste Minimum in der Intensitätsverteilung liegt dann vor, wenn die Strecke Δs bei einem Ablenkungswinkel α gerade so groß ist wie die Wellenlänge λ des Lichts. α α 2 r Aus dem rechtwinkligen Dreieck kann man erkennen, dass die Gegenkathete zum Winkel α gerade Δs und die Hypothenuse die Strecke 2r ist. • Δs Das Verhältnis von Gegenkathete zur Hypothenuse ist definiert als der Sinus des Winkels α: sin α Δs 2r oder als Bedingung für das erste Minimum bei einem Spalt der Breite 2r: sin α λ λ 0,5 2r r (1) Was kann man sich unter der Wellenlänge des Lichts vorstellen? 4. Farbe und Wellenlänge des Lichts Das weiße Licht besteht aus einem Gemisch Elektromagnetischer Wellen verschiedenster Wellenlängen. Rotes Licht hat Wellenlängen zwischen 0,65 μm und 0,70 μm (Mikrometer = 1 10-6 m). Blaues Licht liegt etwa im Bereich zwischen 0,45 μm bis 0,50 μm. Die Farbe des Lichts wird durch dessen Wellenlänge festgelegt. Blaues Licht hat eine kleinere Wellenlänge als rotes Licht. Lässt man Licht verschiedener Farbe (verschiedene Wellenlängen) durch den gleichen, sehr engen Spalt treten, kann man verschieden breite Intensitätsverteilungen 81941632 Rolf Piffer Seite 6 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen auf dem Schirm hinter dem Spalt erkennen (aus: Metzler: Physik, Schroedel-Verlag, Braunschweig 2007, S. 306): Die Breite des zentralen Beugungsbereichs ist auch abhängig von der Farbe des Lichts: Blaues Licht mit kleiner Wellenlänge hat ein schmales Hauptmaximum. Rotes Licht mit größerer Wellenlänge hat ein breiteres Hauptmaximum. 5. Zusammenfassung der Beugung von Licht an Spalten 1. Durch enge Öffnungen in einem Strahlengang verbreitert sich das Lichtbündel, so dass ein breites Hauptmaximum auf dem Bildschirm erscheint. 2. Die Minima in der Intensitätsverteilung entstehen durch destruktive Interferenz der Wellen bei bestimmten Winkeln. 3. Je kleiner die Durchtrittsöffnung ist, desto breiter ist das zentrale Intensitätsmaximum. 4. Je größer die Wellenlänge des Lichts ist, desto breiter ist das zentrale Maximum der Intensität. 81941632 Rolf Piffer Seite 7 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen 6. Beugung an Kreisblenden und Linsen Licht tritt durch eine Sammellinse mit dem Radius r und der Brennweite f. Das Beugungsscheibchen hat dann den Radius R (ist gleich dem Radius des 1. dunklen Rings) und liegt in der Brennebene. Der dunkle Ring mit dem Radius R erscheint unter dem Winkel αmin mit λ sin αmin = 0,61 • (2) r Der Faktor 0,61 tritt hier an die Stelle von 0,5 in der Formel (1) für den Spalt, da hier eine kreisförmige Blende mit dem Durchmesser 2r vorliegt. Nach der Zeichnung gilt auch: sin α min R R2 f 2 Im Allgemeinen ist R << f, so dass näherungsweise gilt: sin αmin = R/√(f2) = R/f (3) Setzt man Gleichung (2) und (3) gleich, folgt: 0,61•λ /r = R/f oder R 0,61 81941632 Rolf Piffer λf r (4) Seite 8 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen Beispiel: Wie groß ist der Radius R eines Beugungsscheibchens, für blaues Licht mit λ = 400 nm = 4 10-7 m, dem Linsenradius r = 1 cm und der Brennweite f = 10 cm? 7. Auflösungsvermögen von Linsen und Kreisblenden Tritt das Licht von zwei benachbarten punktförmigen Objekten (G1 und G2) durch eine Linse mit dem Radius 2r, so entstehen diesmal 2 Beugungsscheibchen mit gleichen Radien R in einem Abstand a auf dem Schirm: Diese Scheibchen können sich mehr oder weniger überlappen: Aus: Metzler: Physik, Schroedel-Verlag, Braunschweig 2007, S. 311 Ist der Abstand a der Maxima kleiner als der Radius R der Beugungsscheibchen (Fall a)), lassen sich die beiden Bilder nicht mehr als getrennte Bilder erkennen. Dies bestimmt den Mindestwinkel εmin, unter dem G1 und G2 vorliegen müssen, um noch als zwei getrennte Punkte identifiziert werden zu können. Je kleiner dieser Winkel werden kann, desto besser lassen sich auch feinste Strukturen des Objekts erkennen. Daher bestimmt εmin das Auflösungsvermögen einer Linse. Auflösungsvermögen A der abbildenden Linse (Kreisblende): 81941632 Rolf Piffer Seite 9 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen A = 1/ εmin Der Abstand a ist proportional zum Winkel εmin und zur Brennweite f (Strahlensatz). Damit ist: amin = εmin•f oder umgeformt εmin = amin / f (5) Setzt man (5) in die Gleichung für das Auflösungsvermögen, A = f / amin = f / R und mit der obigen Formel für den Radius R der Beugungsscheibchen: R 0,61 λf r dann folgt für das Auflösungsvermögen: A 1 r 0,61 λ (6) Beispiel.: Wie groß ist das Auflösungsvermögen des menschlichen Auges, wenn der Pupillenradius 1,5 mm, die Brennweite der Augenlinse 1,7 cm und die Wellenlänge des Lichts 600 nm beträgt und wie groß darf amin maximal werden? (für Fortgeschrittene: Der Brechungsindex des Auges ist n = 1,33) 81941632 Rolf Piffer Seite 10 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen 8. Auflösungsvermögen beim Mikroskop Die meisten Objekte, die mit einem Mikroskop beobachtet werden, leuchten nicht selbst, sondern werden durch eine Lichtquelle beleuchtet. An den kleinsten Strukturen des Objekts tritt dadurch Beugung und Interferenz auf. Jeder Punkt des Objekts beugt das Licht und es kommt zu Interferenzen, die die Minima und Nebenmaxima eines Beugungsbildes hervorrufen. In der nebenstehenden Abbildung wird ein Objekt von unten durchleuchtet. An einem beliebigen Punkt des Objekts wird das Licht wie an einem schmalen Spalt gebeugt und es entsteht ein Intensitätsmuster mit einem Hauptmaximum in der Mitte, getrennt durch einen Bereich verschwindender Intensität vom ersten Nebenmaximum. Nur ein Teil dieser Intensitätsverteilung kann in das Objektiv gelangen. In der Brennebene des Objektivs entsteht das scharfe Beugungsbild der (unendlich weit entfernten) Lichtquelle. Die Beugungsbilder –B und +B bilden das „primäre“ Bild. Das primäre Bild interessiert beim Mikroskop in der Regel nicht, da man ja ein Bild des Objekts (hier ein Strichgitter) haben möchte. Die Strahlen, die die Beugungsbilder liefern, bilden in ihrem weiteren Verlauf das gewohnte reelle Bild des Objekts (sekundäres Bild) in der Bildebene O’. 81941632 Rolf Piffer Seite 11 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen Alle Beugungsbilder werden zum Aufbau des reellen Bildes benötigt, um ein vollkommen ähnliches Bild des Objekts zu erzeugen. Jede Änderung des primären Bildes (Beugungsbilder) verfälscht das reelle Bild vom Objekt. Es genügt demnach nicht, nur das zentrale Beugungsscheibchen dieses einen Objektpunktes durch das Objektiv zu bekommen, sondern es müssen möglichst viele Maxima durch das Objektiv gelangen, um ein unverfälschtes, hoch aufgelöstes Bild zu erhalten. Versuche: a) In einen Laserstahl wird ein Strichgitter mit g =100/cm gebracht. Das Beugungsbild wird durch ein Objektiv (hier: f 150) auf eine Beugungsordnungsblende scharf abgebildet. Durch eine weitere Linse (hier: f 20) wird auf dem weit entfernten Schirm ein Abbild des Strichgitters erzeugt. Ohne Beugungsordnungsblende erscheint das Bild des Strichgitters: (Fotos der Schirmbilder aus: Arbeitsunterlagen HeNe-Laser 500 N, Firma Spindler & Hoyer KG, Göttingen; leider waren die selbst gemachten Fotos zu schlecht, da die Kamera nicht genügend Auflösung hatte, so dass man die feine Strichstruktur auf dem Foto nicht mehr sehen konnte) Die Form der Beugungsordnungsblende sieht etwa folgendermaßen aus: 81941632 Rolf Piffer Seite 12 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen b) Die Beugungsordnungsblende wird jetzt so justiert, dass nur noch das Hauptmaximum (0.ter Ordnung) durchgelassen wird: Das Bild des Strichgitters ist völlig strukturlos und enthält keine Information über das Objekt mehr. Das Bild entspricht der Abbildung der Lichtquelle, da erst durch die Beugungsmaxima höherer Ordnung Information über das Objekt geliefert wird. c) Die Beugungsordnungsblende wird jetzt so justiert, dass das Hauptmaximum (0.ter Ordnung) und die Maxima 1. Ordnung durchgelassen werden: Das Bild des Strichgitters gibt nun eine weitgehend identische Abbildung des Strichgitters, was man gut durch den Vergleich mit der Abbildung ohne Blende erkennen kann. d) Die Beugungsordnungsblende wird jetzt so justiert, dass nur die Maxima 1. Ordnung durchgelassen werden: Auch jetzt erscheint ein Bild mit einer Gitterstruktur, 81941632 Rolf Piffer Seite 13 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen jedoch ist dieses Bild nicht mehr identisch mit dem Objekt. Durch diesen Eingriff in das primäre Bild entsteht ein Abbild des Strichgitters mit größerer Strichzahl, obwohl dies gar nicht vorhanden ist. e) Die Beugungsordnungsblende wird jetzt so justiert, dass nur die Maxima 2. Ordnung durchgelassen werden: Hier tritt auch auf, dass ein Objekt vorgetäuscht wird, das wieder so gar nicht vorliegt. Das Strichgitter hat anscheinend eine noch größere Strichzahl als im Versuch d) mit ausschließlich den Maxima 1. Ordnung. Ein Beispiel aus der Praxis: Nur das zentrale Beugungsmaximum wird abgebildet: Werden zusätzlich die Maxima 1. Ordnung mit zum sekundären Bild verarbeitet, entsteht ein Bild mit höherer Auflösung: 81941632 Rolf Piffer Seite 14 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen 9. Numerische Apertur des Mikroskops Ist D der Abstand der Objektpunkte (zum Beispiel Strichabstand bzw. Gitterkonstante), dann gilt für die Ordnung m bei fester Wellenlänge λ des Lichts: sin α(m, D) = m•λ / D Ist 2u der fest vorgegebene Öffnungswinkel (siehe Zeichnung), unter dem das Objektiv vom Objekt her erscheint, dann fallen die Beugungsmaxima 1. Ordnung dann ins Objektiv, wenn gilt: sin α(1, D) = λ / D ≤ sin u oder D ≥ λ / sin u = Dmin D.h. es können nur Strukturen abgebildet werden, deren Abstand größer als Dmin ist. Die Größe 1/Dmin ist schließlich das Auflösungsvermögen des Mikroskops: A 1 D min 81941632 Rolf Piffer n sin u (7) Seite 15 von 17 Mikroskopie 02 Auflösungsvermögen SchülerHilfen Wird eine Flüssigkeit zwischen Objekt und Objektiv mit dem Brechungsindex n gebracht (Immersionsflüssigkeit), erhöht sich wegen n>1 die Auflösung. Der Faktor n•sin u wird numerische Apertur (NA) genannt. Dies kann man durch die folgenden Abbildungen verdeutlichen: Der Öffnungswinkel 2α hängt von der Entfernung zwischen Objekt und Deckglas (über dem Objekt) ab. Je kleiner der Abstand zwischen Objekt (Deckglas) und Objektiv, desto größer wird der Öffnungswinkel und es können viele Beugungsmaxima höherer Ordnung ins Objektiv gelangen. Verwendet man dazu noch eine „Immersionsflüssigkeit“ (z.B. Öl) mit möglichst hohem Brechnungsindex n zwischen Deckglas und Objektiv, dann gelangen gemäß der nebenstehenden Abbildung weitere höhere Ordnungen von Maxima ins Objektiv. Durch diese beiden Effekte wird die Auflösung des Mikroskops erhöht. Typische Objektive: 81941632 Rolf Piffer Seite 16 von 17 Billig: Mikroskopie 02 Auflösungsvermögen SchülerHilfen Apertur 0.1; Auflösung 2,75μm Hochwertig: Apertur 0,65; Auflösung 0,42μm Öl: Apertur 1,4; Auflösung 0,20μm (beide Abbildungen dieser Seit aus: Dr.H.Schlichting: Mikroskopie in der Biochemie, Vorlesungsskript) 10. Wellenlängenabhängige Auflösung beim Mikroskop Nach Gleichung (7) ist die Auflösung beim Mikroskop umso größer, je kleiner die Wellenlänge λ ist. D.h. blaues Licht ( ca. 450 nm) löst feine Strukturen besser auf als rotes (ca. 700 nm). Allerdings ist es nicht leicht, Objekte wie z.B. die abgebildete Alge zu finden, deren Strukturen genau diese Größen haben, so dass blaues Licht tatsächlich mehr Strukturen offenbart als rotes. Abbildung aus Unterrichtsmaterialien zum Testla-Projekt, Forschungszentrum DESY, Aulis Verlag 2000, S. 159: Eine Alge in 1000 facher Vergrößerung bei 458 nm (blau) und bei 680 nm /rot). Eine noch höhere Auflösung würde man erzielen, wenn man Licht noch kürzerer Wellenlänge wie z.B. Ultraviolett verwenden würde. Noch besser wären Röntgenstrahlen mit noch wesentlich kleinerer Wellenlänge, jedoch sind bei den beiden letzten Möglichkeiten die gesundheitlichen Gefährdungen durch die verwendete Strahlung viel zu groß. 81941632 Rolf Piffer Seite 17 von 17