1 Tr5gheitstensor (Fortsetzung)

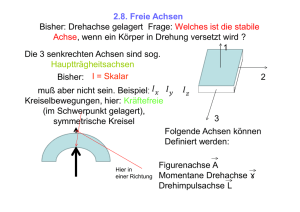
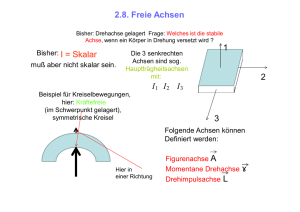
1
Trägheitstensor (Fortsetzung)
Wir verallgemeinern den in der letzten Stunde gefundenen Trägheitstensor auf den Fall einer kontinuierlichen
Massenverteilung durch die Einführung der Integration
über das Körpervolumen:
~I =
Z
0
B
(~
r) @
y2
+ z2
yx
zx
mit den Komponenten
~Ixx =
~Ixy =
Z
1
xy
xz
C
x2 + z 2
yz A dV
zy
x2 + y 2
y2 + z2
Z
(~
r) dV;
xz (~
r) dV; etc.
Wie gesehen, stellt diese Matrix einen linearen Zusammenhang zwischen Drehimpuls und Winkelgeschwindigkeit her:
~ = ~I !
L
~:
Diese Beziehung gilt in beliebigen Koordinatensystemen,
allerdings verändern sich die Komponenten von ~I und von
!
~ dabei in genau de…nierter Weise. Matrizen, die solche
physikalischen Zusammenhänge wiedergeben, nennt man
"Tensoren" (genauer Tensoren 2.Stufe, Vektoren und Skalare sind entsprechend Tensoren 1. und 0. Stufe).
Für die Rotationsenergie kann man durch komponentenweises schreiben ebenfalls einen entsprechenden Term …nden. Er lässt sich aber auch durch den Vergleich mit
der entsprechenden Beziehung bei der linearen Bewegung
motivieren, denn es gilt
1
1
1
Ekin = m 2 = m~ ~ = ~ p
~
2
2
2
und man überträgt dies zu
Erot =
1
~ =1!
!
~ L
~ ~I !
~:
2
2
Im Allgemeinen sind alle Komponenten von ~I von Null
~ in der
verschieden, d.h. insbesondere auch, dass !
~ und L
Regel nicht parallel sind. Gibt es ein Koordinatensystem
in dem ~I eine besonders einfache Form hat? Tatsächlich
teilt uns die lineare Algebra mit, dass man jeden symmetrischen Tensor, d.h. die Komponenten von ~I erfüllen
die Forderung ~Ijk = ~Ikj , durch geschickte Drehung des
Koordinatensystems auf Diagonalform bringen kann, d.h.
0
1
Ia 0 0
C
~I 0 = B
@ 0 Ib 0 A :
0 0 Ic
Die Koordinatenachsen dieses Systems werden als Hauptträgheitsachsen bezeichnet, die Komponenten Ia; Ib; und
Ic heissen Hautträgheitsmomente. Man sortiert sie nach
aufsteigender Reihenfolge
Ia
Ib
Ic :
Sind alle Hauptträgheitsmomente verschieden, handelt es
sich bei dem Körper um einen asymmetrischen Kreisel
(z.B. Quader mit drei ungleich langen Seiten), sind zwei
von ihnen gleich, spricht man von einem symmetrischen
Kreisel (z.B. Zylinder) und wenn alle drei den gleichen
Wert besitzen, ist es ein sphärischer Kreisel (Kugel, Würfel, Tetraeder, Oktaeder). Der Trägheitstensor eines sphä-
rischen Kreisels besitzt die besonders einfache Form
0
1
1 0 0
C
~I 0 = I B
@ 0 1 0 A
0 0 1
und reduziert sich damit quasi zu einem Skalar. Jeder rotationssymmetrsiche Körper ist ein symmetrischer Kreisel,
aber nicht jeder symmetrische Kreisel ist rotationssymmetrisch (z.B. eine quadratische Säule).
~ parallel:
In folgenden Spezialfällen sind !
~ und L
Rotation eines sphärischen Kreisels um eine beliebige
Achse durch den Schwerpunkt
Rotation des symmetrischen Kreisels um seine Symmetrieachse (Figurenachse) oder eine beliebige Achse
senkrecht dazu (durch den Schwerpunkt)
Rotation um eine Hautptträgheitsachse.
~ nicht parallel sind, wird die Bewegung des
Wenn !
~ und L
Körpers bei der Rotation sehr viel komplizierter.
1. freie Rotation ohne äuß
ere Kräfte (Drehmomente)
In diesem Fall ist
~ fest im Raum
die Drehimpulsachse L
die momentane Drehachse !
~ rotiert um die raum~
feste Achse von L
im Falle eines symmetrischen Kreisels rotiert die
~ . Diese Bewegung
Figurenachse ebenfalls um L
der Figurenachse wird als Nutation bezeichnet.
Wenn der Körper nicht frei rotiert sondern die Drehachse durch äuß
ere Zwangsbedingungen, z.B. in einem
Lager, stabilisiert wird, bedeutet dies, dass nun der
Drehimpuls um !
~ rotieren muss. Diese Änderung
~ muss gemäß
von L
d~
~
L=M
dt
~ , welche von den Ladurch äuß
ere Drehmomente M
gern aufzubringen sind, bewirkt werden. Solche "Unwuchten" müssen bei allen rotierenden Maschinenteilen vermieden werden, um einen schnellen Verschleiss der Lager zu unterbinden. Dazu werden die
rotierenden Teile "ausgewuchtet" (z.B. Autoräder).
Man unterscheidet zwischen der
statischen Unwucht und der
dynamischen Unwucht (Deviationsmoment)
Eine statische Unwucht wird dadurch verursacht, dass
die Drehachse nicht durch den Schwerpunkt verläuft.
In diesem Fall tritt eine Zwangskraft auf, die die
Fliehkraft
Fz = m! 2RA
aufgrund der Rotation des Schwerpunktes kompensieren muss. Die dynamischen Unwucht tritt durch
eine ungleiche Massenverteilung auf, auch wenn der
Schwerpunkt auf der Drehachse liegt:
(a) Zylindrische Welle mit Deviationsmoment bezüglich der Zylinderachse
durch zwei diametrale Nocken (b) Annulierung des Deviationsmomentes
durch zwei entgegengesetzte Nocken (E.W. Otten, Repititorium der
Experimentalphysik)
Die Kräfte Ft führen zu einem rotierenden Drehmoment, welches an der Welle angreift und unangenehme
Kräfte auf die Lager ausübt die mit dem Quadrat
der Drehzahl anwachsen. Solche Drehmomente werden als Deviationsmomente bezeichnet und können
ebenfalls durch Zusatzgewichte kompensiert werden.
2. Bewegung eines Kreisels beim Einwirken eines äuß
eren
Drehmomentes
~ weicht einer äuß
Die Drehimpulsachse L
eren Kraft
senkrecht zu dieser aus (Grund: Das verursachte
~ =~
~ und damit senkrecht
Drehmoment ist M
r F
~ ). Dies führt dazu, dass ein schief stehender
zu F
Kreisel, der nicht im Schwerpunkt unterstützt ist, im
Gravitationsfeld präzediert, d.h. seine Figurenachse
(Drehimpulsachse) beschreibt eine kreisförmige Bewegung (Präzession) um die Senkrechte (www.greiergreiner.at/hc/praezession.htm):
Beispiele: Die Erdachse führt durch die Gezeitenkräfte der Sonne eine Präzessionsbewegung mit einer
Periode von rund 26,000 Jahren aus. Die Präzessionsfrequenz des magnetischen Dipolmomentes eines
Atomkerns um die Richtung eines angelegten Magnetfeldes wird bei der kernmagnetischen Resonanzspektroskopie gemessen. Da die exakte Frequenz von
der chemischen Umgebung des Atoms abhängt, dient
diese Methode zur Strukturaufklärung komplizierter
organischer Moleküle.
Satz von Steiner
Das Trägheitsmoment eines Körpers um eine beliebige
Achse im Abstand RA vom Schwerpunkt ist gleich dem
Trägheitsmoment um eine parallele Achse durch den Schwerpunkt Is plus dem Produkt aus Masse m des Körpers
2
und RA
2:
I (RA) = Is + m RA
Aufgaben:
1. Ein senkrecht stehender starrer Stab der Länge `,
dessen Dicke gegen seine Länge zu vernachlässigen
sei, wird durch eine leichte Berührung zum Umfallen
gebracht. Berechnen Sie die Geschwindigkeit und
Beschleunigung des oberen Endes beim Aufschlag
(Hinweis: bei Drehung der Stange um den Schw1 m`2 ).
erpunkt gilt für das Trägheitsmoment I = 12
2. Berechnen Sie die Beschleunigung der Masse m2,
wenn der Radius des Rades R und dessen Masse
m ist. Die Rotation des Rades ist durch die Reibung des Seils bedingt. Die Reibung vom m1 auf
der Unterlage werde vernachlässigt. (Zahlenbeispiel:
m1 = 40 kg, m2 = 200 kg, m = 20 kg, R = 10
cm)