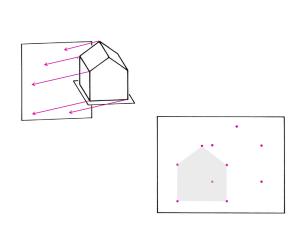
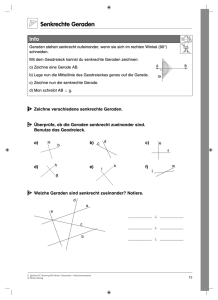
Inhalt : Das Skript erläutert Grundkenntnisse zu den
Werbung

© Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Inhalt : Das Skript erläutert Grundkenntnisse zu den Themenbereichen : . die Architekturdarstellung . Senkrechte Projektionen . Schräge Projektionen . Zentrale Projektionen der Darstellenden Geometrie und Architekturperspektive, die in den Vorlesungen vertieft und durch aktualisierte Übungen ergänzt werden. Die Überlegungen im Teil I beschränken sich auf ebenflächig begrenzte Körper und werden im Teil II durch die Themen : . Körper mit gekrümmten Flächen . Spiegelung und . Schatten, ergänzt. Die verschiedenen Themenbereiche im Skript finden Sie entweder über das Inhaltsverzeichnis (Seite 2), das alle Themen, der Seitenzahl folgend, auflistet oder über das Indexverzeichnis (Seite 89), das einzelne Stichworte des Lauftextes, in alphabetischer Reihenfolge, darstellt. Schriftart Helvetica 9 Pt normal = Lauftext Schriftart Helvetica 6 Pt normal = Bildbeschriftung. Seite. Formatleiste Schriftart Helvetica 9 Pt fett = Lauftext betont Schriftart Helvetica 9 Pt fett. rot = Link Schriftart Helvetica 9 Pt kursiv = Zitat ... Schriftart Helvetica 9 Pt kursiv. grün = Verweis 5. Auflage 2007 © Prof. Dipl.Ing. S.H. Bucher Seite Inhaltsverzeichnis © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I die Architekturdarstellung 3 die Darstellungsarten im Überblick 8 die Projektionsarten 9 Senkrechte Projektionen. allgemein 10 Kotierte Projektion 11 Zweitafelprojektion Punkt. Umklappung der Bildtafeln Punkt. Lage im Raum Punkt in der Symmetrie- und in der Koinzidenzebene Beliebige Gerade Wahrer Winkel und wahre Länge einer Geraden. Grundrißklappung Aufrißdrehung oder Mongsche Drehung Besondere Geraden Zwei beliebige Geraden Zwei sich schneidende Geraden 12 13 14 15 16 17 18 19 20 21 Allgemeine und besondere Lage einer Ebene Besondere Geraden einer Ebene. Höhenlinie, Frontlinie und Fallinien Punkt und Ebene Drei - Punkte - Ebene Abstand eines Punktes von einer Ebene Wahre Größe und Neigung des Abstandes von einer Ebene Durchstoßpunkt einer beliebigen Geraden durch eine Ebene Durchstoßpunkt einer beliebigen Geraden durch zwei Ebenen. Pendelebenenverfahren Punkt und Gerade spannen eine Ebene auf zwei sich schneidende Ebenen. Schnittgerade Wahrer Winkel zwischen zwei Ebenen Wahre Größe einer Ebene. Konstruktion mit Stützdreieck Wahre Größe einer Ebene. Konstruktion mit hilfsprojizierender Ebene 22 23 24 25 26 27 28 29 30 31 32 33 34 Der Körperschnitt des Zylinders und die Affinität Der Körperschnitt des Kegels und die Kollineation 35 36 Körperschnitt mit Hilfe der Durchstoßpunkte Körperschnitt mit Hilfe der 3. Projektion 37 38 Arten von Durchdringungen Durchdringung und Höhenebenenverfahren Durchdringung und Mantelebenenverfahren Durchdringung und Parallelebenenverfahren Durchdringung und Pendelebenenverfahren Durchdringung und Pendelebenenverfahren Durchdringung und Pendelebenenverfahren 39 40 41 42 43 44 45 Abwicklung mit Hilfe der Höhenzuordnung Abwicklung durch Grundrißklappung 46 47 Abwicklung mit Hilfe des Querschnittes Abwicklung einer Pyramide über die Spitze 48 49 Schräge Projektionen oder Axonometrien allgemein Konstruktionsverfahren. Das Einschneideverfahren Grundrißaxonometrie Grundrißaxometrie Aufrißaxonometrie Aufrißaxonometrie DIN 5 Din 5 Isometrie Isometrie Senkrechte Axonometrie. allgemein Senkrechte Axonometrie. in der Zeichenebene 50 52 54 55 56 57 58 59 60 61 62 63 Zentrale Projektionen oder Perspektiven. allgemein Zentrale Projektionen oder Perspektiven Zentralperspektive. Übereckperspektive. Perspektive bei geneigter Bildebene Begriffe Verzerrung Klappung 64 65 66 67 68 69 Elemente der Perspektive. Darstellung eines Punktes Darstellung einer Geraden. Tiefenlinie Darstellung einer im Grundriß beliebigen Geraden Darstellung einer im Raum beliebigen Geraden Die Höhenübertragung 70 71 72 73 74 Die perspektive Anlage. Grundrißanlage Bildebene und Augpunkt. Skalierung Spur und Bildebene Horizont und Spur Objektgrundriß und Augpunkt Konstruktionsverfahren. Perspektive aus zwei Rissen Zentralperspektive mit Distanzpunkten Übereckperspektive mit Meßpunkten 75 76 77 78 79 80 81 82 Seite © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Vier Aspekte 1 Die Architekturdarstellung verweist auf den Bedeutungsgehalt der Architektur selbst. " Kunst ist individuelle Wahrnehmung. Diese Wahrnehmung wandle ich ins Gefühl und verlange vom Intellekt, daß er daraus ein Werk macht. Die Zeichnung steht am Anfang der Wahrnehmung." ( Zitat P. Cezanne ) " Der Künstler ist der Schöpfer seiner selbst und seiner Umgebung. Die Zeichnung ist das unmittelbarste Medium des denkenden Handeln." ( Zitat J. Beuys ) Die Zeichnung als Instrument der Wahrnehmung von Architektur - wie Cezanne sagt - und Zeichnen als " denkendes Handeln " - wie Beuys sich ausdrückt - , sind am Werk der Architektur wesentlich beteiligt. Die Zeichnung vermag uns zu zeigen, worauf die Form verweist.Vielleicht ist es auch die Leichtigkeit der Zeichnung, die sie in besonderem Maße befähigt die Schwere der materialen Form zu erhellen. Den Zusammenhang von Zeichnung und Bedeutung in der Historie darzustellen, geht nicht aus von der Idee, nach einer umfassenden Typologie zu suchen, die sich heute verwenden ließe. Die Idee ist veranlaßt durch ein Mißfallen an der Moderne, die der Zeichnung den Charakter der Bürozeichnung gibt und sie instrumentalisiert. (Heute - wie Jean Nouvel sagt - sind die Spiele, die uns begeistern, viel weniger visueller als vielmehr geistiger Natur....????) Vielleicht vermag ein kurzer Blick auf historische Beispiele der Architekturzeichnung die geistige Natur der Architektur selbst erschließen und Hinweise geben für Darstellungsmöglichkeiten heute. Die Zeichentheorie hilft uns die Frage, was die Zeichnung kommuniziert und mit welchen Mitteln, genauer zu erläutern. Dazu eine kurze Vorbemerkung : Alle Kulturphänomene -wie die Kleidung, die Esskultur, die Sprache oder eben auch Architektur und ihre Darstellungsformen können als Zeichensysteme interpretiert werden, die mit den Begriffen der Semiotik näher erläutert sind. Die Semiotik untersucht die Entstehung, den Aufbau und die Wirkungsweise von Zeichen und Zeichenkomplexen, Teilgebiete der Semiotik sind : die Syntaktik, die Semantik und die Pragmatik. Die Syntaktik beschreibt die Zeichen und die Beziehung der Zeichen zueinander. z.B in der Architektur das Thema: Fenster und Fensterreihung. Sie ist eine formale Untersuchung, die die Analyse und den Vergleich ermöglicht. Die Semantik frägt nach dem Objektbezug des Zeichens, oder nach der Beziehung zwischen Zeichen und Bezeichnetem, also nach der Zeichenbedeutung. Die Zuordnung eines Zeichen zu seiner Bedeutung geschieht dabei aufgrund konventioneller Setzungen. z.B. die Farben der Verkehrsampel bedeuten ... Zwischen dem Ding und dem Wort, das dieses Ding repräsentiert besteht kein ursächlicher Zusammenhang. Interpretieren wir Architektur als Zeichensystem, so kann dieses je nach Bezugsebene sowohl ein geschlossenes, als auch ein offenes System darstellen. Die architektonischen Elemente oder Zeichen, wie, Fenster, Wände, Stützen, Dach, Treppe, Tür, sind dabei immer Teile eines geschlossenen Zeichensystems, da sie gewöhnlich auf ihre Gebrauchsfunktion hinweisen, also eindeutig festgelegt sind : eine Tür dient als Ein- oder Ausgang, eine Treppe verbindet zwei Ebenen, Wände oder Stützen haben tragende Funktionen. Auf der anderen Seite können jedoch architektonische Zeichen auch einem offenen System angehören, denn sie haben auch symbolische Bedeutungen, die über die reine Funktion hinausweisen und deren Gehalt in verschiedenen historischen Epochen ganz unterschiedlich sein kann. So ist die Scheintür eines ägyptischen Grabes aus dem 3. Jahrtausend v.Chr. eben nicht nur die Vortäuschung einer Tür, sondern sie symbolisiert auch die Grenze zwischen Diesseits und Jenseits und das Portal einer gotischen Kathedrale bezeichnet nicht nur einen Eingang, sondern wird zum gleichnishaften " Tor des Himmlischen Jerusalem ". die Architekturdarstellung Hinweis auf den Ort, wo diese Bilder zu sehen waren, aber weniger auf dessen Aussage.) Erst ab der Mitte des 18.Jhdts., angeregt durch die Arbeiten von Piranesi, wird die Architekturdarstellung zum Spiegel der räumlichen Konzeption der Architektur. Hatte die Barockarchitektur ein organisches Bauprinzip, das Ineinandergreifen der einzelnen Bauteile gefordert, so wird dieses Prinzip im Klassizismus durch eine blockhafte Baugliederung ersetzt. Ähnlich der Renaissancearchitektur bedient sich der Klassizismus der Sprache geometrischer Grundformen. Prägnantesten Ausdruck findet diese Verwendung einfachster geometrischer Körper in der sog. Revolutionsarchitektur, Bsp.. Steenwijk, Architektur Porträt 1583 wo diese Formen ins Monumentale und Symbolhafte Das Bild ist heute wesentlicher Teil unserer Kenntnis gesteigert werden. nicht nur der Kirche, sondern der Zeit. Das zeichneriBsp. Etienne Louis Boullee (1728-1799). Kenotaph für sche Mittel dieser Raumillusion, ist neben der Licht und Isaak Newton. 1784 Farbperspektive, die lineare Perspektive, die das Gesehene in besonderer Weise, durch den Fluchtpunkt, Bei den Entwürfen des Revolutionsarchitekten Boullee mit dem Auge des Betrachtenden verknüpft. Dabei ver- ist allerdings die Symbolik nicht mehr göttlichen Urliert die Darstellung der Kirche jede Unschuld, weil wir sprungs, sondern sie wird, der Zeit der Aufklärung und dem Blick des Betrachtenden zur rechten Säulenreihe des Rationalismus entsprechend, zum Ausdruck eines folgen, der Fluchtpunkt ist aus der Mitte gerückt und rationalen, natürlichen, vom Menschen beherrschbaren der Raum selbst in einer Übereckperspektive dargeKosmos. stellt. Das Auge das den Raum erschließt, ist innerlich nicht mehr dem Altar zugeordnet. Bsp. Claude-Nicolas Ledoux (1736-1806): Werkstatt Der Kirchenraum wird der Ort des Flaneurs. der Reifenmacher Ist das noch der Blick des andächtig Gläubigen ? Claude-Nicolas Ledoux: Haus der Flußinspektoren der Loue In Ledoux's Entwürfen für die Häuser der " Reifenma2 Die Art der Darstellung und die Art der Architekcher " und der tur sind wesensbedeutsam miteinander verknüpft. " Flußinspektoren " weisen die architektonischen Formen auf die Tätigkeiten der jeweiligen Bewohner " Die Perspektive darf, als eine jener "symbolischen hin, indem sie die Gegenstände, mit denen sich diese Formen" bezeichnet werden, durch die ein geistiger Tätigkeiten befassen, direkt abbilden. Das Haus als Bedeutungsinhalt an ein konkretes sinnliches Zeichen Zeichen stimmt mit dem was es darstellt nahezu geknüpft und in diesem Zeichen innerlich zugeeignet überein. wird, und es ist in diesem Sinne für die einzelnen Diese direkt ablesbare Ikonografie finden wir auch in Kunstepochen und Kunstgebiete wesensbedeutsam, der Architekturdarstellung. nicht nur ob sie Perspektive haben, sondern auch welche Perspektive sie haben. " ( Zitat E. Panofsky ) Von der gotischen Rißzeichnung des 13.Jhdts bis zu den barocken Idealskizzen ist die Architekturdarstellung im Wesentlichen geprägt von ihrem konstruktiven Charakter und ihrer Aufgabe als technisches Hilfsmittel. (Abgesehen vielleicht von den sog. ExpektoratioDie Pragmatik erläutert den Anwendungsbereich , den nen der Frührenaissance nach 1469, die Piero della Zusammenhang zwischen der Absicht und der Wirkung Francesca (1415.20 - 1492) zugeschrieben werden. " Prospekte einer idealen Stadt " wo Architektur - sich eines Zeichens im Gebrauch. selbst genügend, erschreckend leer und leblos, den Die niederländische Genremalerei und insbesondere die sog. Architekturporträts des 16. Jhdt. geben Anlaß Umständen des alltäglichen Lebens enthoben und zum überpersönlichen Ideal stilisiert, dargestellt ist. Die Bsp.P.Speeth, Entwurf für Totendenkmal, 1807 nach den pragmatischen Aspekten der Zeichnung zu fragen. Steenwijk ist ein Spezialist dieses Genres. Mit Vermutung Louis Vives von 1532 "... die Schönheit hoher Detailgenauigkeit stellt der Maler diesen unver- der Bilder sollte den Frauen helfen, schöne Kinder zu Durch ein starkes, dramatisches Hell/Dunkel der Zeichempfangen und zu gebären ..." gibt vielleicht einen wechselbaren Ort dar. nung ist der Vanitas - Charakter der architektonischen Seite © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Konzeption erläutert, die Bewegtheit der Zeit finden wir in der Atmosphäre des Himmels wieder ... ein Gewitter zieht auf, die leichte Untersicht der Darstellung verweist auf die Stellung des Betrachtenden gegenüber den Elementen, überall steckt ein Verweis ... Die Zeichnung ist die Projektion einer Vorstellung und wir wissen daß auch die Architektur meist Vorstellung geblieben ist. Durch das gesamte 19.Jhdt. zieht sich eine Fülle von Neo - Stilrichtungen, Neo-Gotik, Neo-Renaissance, Neo-Barock, usw., die aufgrund ihrer spezifischen Zeichenfunktionen auf ganz bestimmte Gebäudetypen angewandt werden. Besonders bei den öffentlichen Bauten entwickelte sich eine relativ einheitliche Bedeutungsdoktrin, die erklärte, welcher Stil für welchen Bautyp und für welche Funktion der richtige sei. Technisch im Wesentlichen beeinflußt durch die Ecole Bsp. die sog. Bildungsarchitektur der Wiener Ringstrade Beaux Arts, der Pariser Schule für Architektur, dient ße die Zeichnung seit 1850 der individuellen Vermittlung. Die Architekturdarstellung ist ebenso vereinbart und Die perspektive Darstellung unterstreicht die individuel- deren ästhetische Qualität wird gemessen an den le Wahrnehmung. Vorgaben der Pariser Schule. Das Hinweisen auf den Bewohner, den Besitzer, den Zweck eines Gebäudes und dessen Gebrauch ist ein Die Antwort auf das Formgebaren des 19. Jhdt. kommt Charakteristikum der repräsentativen Architektur des von Seiten der Ingineure und führte zur Entwicklung 19.Jhdts. Das Bürgertum ohne eigenen Stil, verwendet der Moderne, die im Internationalen Stil der 20er Jahre Formen und Stilmerkmale vergangener Epochen zur ihren Höhepunkt erreichte. eigenen Repräsentation. Wir sprechen vom Zeitalter des Ekklektizismus oder Historismus. Bsp. Kristallpalast London. 1851 Joseph Paxton Bsp. Eifelturm Paris 1889 Bsp. Bauhausgebäude in Dessau. 1925/26 Walter Gropius 1883 - 1969 Diese Architektur glich einem Fanal. Bsp. Perspektive Rathaus Augsburg, Theodor Fischer 1886 Bsp. Charles Garnier. Opernhaus, Paris,1861-74 Bsp. Thomas Ustick Walter. Gefängnis Moyamensing, Philadelphia, 1835 Damit schien vordergründig jeder semantische Bezug aus der Architektur verbannt. Der Beginn der Moderne zeigt aber auf der anderen Seite eine starke Sehnsucht nach inhaltichen Bezügen. Die De-Stijl Bewegung in Holland, die großen Einfluß auf die Entwicklung ausübte, versucht, vielleicht wie die Renaissance, das Universelle im Räumlichen zu erfassen. Hier tritt uns jedoch ein ganz neues, von den Naturwissenschaften geprägtes Raumgefühl gegenüber, nicht mehr der allseits geschlossene Kasten der Renaissance, sondern ein offenes, von dynamisch verbundenen Flächen erzeugtes Kontinuum, das Innen und Außen verbindet. Prägnantesten architektonischen Ausdruck findet dieses neue Raumgefühl bei Mies van der Rohe. Bsp. Deutscher Pavillon für die Weltausstellung in Barcelona. 1929 Ludwig Mies van der Rohe (1886-1868) Bsp. Theo van Doesburg 1883-1931 , und C. van Eesteren : Studie für ein Wohnhaus, 1923 Bsp. Gerrit Thomas Rietveld (1888-1964): Haus Schröder, Utrecht, 1924 Hier versteht sich Architektur in Beziehung zu einer kosmischen Ordnung, jedoch nicht als Analogie - so wie die Kuppel des Kenotaph für Isaac Newton das Universum meinte - sondern im Sinne einer realen Verbindung zum universellen Raum. Ein weiterer Kritikpunkt, ebenfalls von Jencks formuliert richtet sich gegen die univalente, die einwertige Form. Bsp. Ludwig Mies v.d. Rohe 1886 -1968. IIT-Gelände. Modell 1940-52 Bsp. Ludwig Mies v.d. Rohe 1886 -1968. Lake shore drive Apartments. Chicago 1948 - 51 Es ist besonders Mies van der Rohe, den Jencks angreift. Zitat : " Die gesamte Frage der Eignung des Dekors für einen bestimmten Bautypus, die jeder Architekt von Vitruv bis ins 19. Jhdt. diskutiert hat, ist durch Mies' Universalgrammatik und Universalmißachtung des Ortes und der Funktion ungültig geworden." Seine Kritik betrifft die gesamte Moderne und die Konsequenzen, die Jencks für die Weiterentwicklung der Architektur fordert, ist die Wiederbelebung symbolischer Bezüge der gebauten Form und eine vielfältige, vielschichtige, regional verschiedene und vom "genius loci" geprägte Sprache der Architektur. Das Team um den Amerikaner Robert Venturi. geb.1925 hat in den Büchern "Complexity and contradiction in Architecture" und "Learning from Las Vegas" ihre Vorstellungen von Architektur beschrieben. " ... ich mag eine teilweise kompromißlerische Architektur mehr als eine puristische, eine verzerrte mehr als eine stocksteife, eine vieldeutige mehr als eine artikulierte ... ich ziehe eine vermurkste Lebendigkeit einer langweiligen Einheitlichkeit vor. Dementsprechend befürworte ich den Widerspruch, ich vertrete den Vorrang des " sowohl - als - auch ". In der Architekturdarstellung der Moderne finden wir diese universelle Sicht durch die Parallelprojektion repräsentiert. Durch die Vorstellung der Parallelität der Projektionsstrahlen, wird die Bezeihung von Objekt und Abbildung eine Beziehung, die unabhängig vom betrachtenden Auge existiert. Die getuschte Bürozeichnung und die axonometrischen Darstellungsarten sind Damit plädiert Venturi für eine formale und bedeuin der Moderne - mit dem Anspruch der Allgemeingültungshafte Komplexität, für eine Architektur der Zeitigkeit - Programm. chen und Symbole, die die Postmoderne kennzeichnet. Wie Venturi bedenkt z.B. der deutsche Architekt An diesem Punkt formuliert 1961 der englische Oswald Mathias Ungers geb.1926 das Vokabular der Bsp. Corbusier, Plan Voisin für Paris, 1925 Modell Photo aus dem Dokumentarfilm "Lárchitecture Architekturhistoriker Charles Jencks (geb. 1939) den Architektur neu. Er geht in seinen theoretischen Überdàujourd`hui" 1931 Verlust der Symbolik in der Architektur, die für ihn allein legungen von der Voraussetzung aus, daß es gewisse Identifikation von Benutzer oder Betrachter mit dem architektonische Grundideen gibt, die in unterschiedIhre Elemente waren industriell gefertigt und seriell Gebauten herstellt. lichen Ausdrucksformen zu unterschiedlichen Zeiten montiert. Die emotionale Bezugnahme, die Besetzung gebauwiederkehren und ähnlich den Wortbegriffen der SpraDer Kristallpalast z.B. hatte eine Grundfläche, die ter Strukturen mit Gefühlswerten aufgrund historisch che ein Grundvokular von architektonischen Zeichen 4 mal größer als der Petersdom in Rom war. Dabei - vermittelter oder erlernter Codes sei jetzt nicht mehr bilden. Da dieses Grundvokabular elementarer Natur waren die Elemente, die sich zu dem Formnetz fügten, möglich. Es könne durch den Wegfall traditionell und ist, sind diese Ideen in allen geschichtlichen Epochen eher klein. (die größte Glasscheibe, die damals herge- regional bestimmter Architekturformen so etwas, wie gleichermaßen aufzufinden. stellt werden konnte, war 1.20 lang) das Gefühl "zu Hause zu sein" nicht mehr aufkommen. Aus diesem Grundgedanken heraus entwickelt Ungers Diese neue Architektur ohne Ornament, diese ArchiJencks hatte bei der Zeichnung die fehlende Handdie Konzeption einer " Architektur der Erinnerung ". Er tektur aus weißen Kuben, Stahl und Glas war eine schrift bemängelt. fordert bei jeder Bauaufgabe Respekt vor den kulturelPolemik gegen all das, was dem 19.Jhdt. als heilig (Bsp. In ähnlicher Weise argumentiert auch der Sozio- len Vorbildern und Rücksichtnahme auf den Geist des galt. Sie richtete sich gegen Denkmalsfunktion, gegen loge und Psychoanalytiker Alexander Mitscherlich. geb. Ortes, - er fordert eine Architektur, die sich aus dem Symbolik, gegen alle nationalen und folkloristischen 1908 in dem Buch " Die Unwirtlichkeit unserer Städte" Kontext der jeweiligen historischen Umstände erklärt. Überlieferungen. Die Form sollte pragmatisch als Pro- von 1968) Dies ist eine deutliche Absage an die Architektur des dukt einer Funktion gewertet werden. "Immer Neuen". Seite © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Die Kollonaden, das Forum, ein Atrium und die wiederholten Symmetrien zitieren die Formensprache der Villa Hadriana. Tivoli 118-134 v.Chr. Die Zeichnung besticht durch eine feine Linearität, die es vermeidet expressiv oder in irgendeiner Weise subjektiv zu sein. Die Zeichnung gibt der Erinnerung und dem Bedeutungsgehalt der Architektur Raum. Bsp. Ungers, O.M.Wettbewerbsentwurf für die Deutsche Botschaft im Vatikan (s. Josef Frank, das Haus als Weg und Platz, 1931) „Welttheater" aus Holz in Venedig 1979, ein Riesenspielzeug. Zitat aus dem Memento von Manfred Sack in DIE ZEIT Bsp. Schönstes Bauwerk des Pritzker-Preis Trägers. 38. 1997 Der wunderbar feierliche Friedhof in Modena "... Eigentlich, so dachte man einst, war Rossi ein Bsp. Das Rathaus von Borgoricco Glücksfall: Er zeichnete, er dachte über das, was er tat Bsp. Das praktischste der Iba-Wohnbau in Berlin, und was um ihn herum geschah, nach, er erkundigte Bsp. Das gelungenste das Bonnefanten-Museum in sich mit rührender, manchmal wie nach Halt suchender Maastricht. ) Beflissenheit in der Baugeschichte und ließ alles in Die Eigenwilligkeit mancher frühen Bauten vielerlei Tätigkeiten Bsp. der weiße StahlbetonWohnbau im Mailänder Viertel Gallaratese 2, ein 182 Meter langer, 12 Meter breiter, dreistöckiger Riegel, mit seinem gewaltigen Säulenentree von erschlagender Monumentalität. Nein, kein wohnliches Wohnhaus sondern abstrakte Urbanität. ist heute auf einmal weit imponierender als der Populismus seiner jüngsten Bauten, (namentlich auf der Berliner Architekturspielwiese: historistisch, knallbunt, grob - ondulierter Kleinkram. Da ist nun alles ins Gegenteil verkehrt: Turbulenz statt Strenge, Interessantheit statt Askese.) Bsp. Rossi, Aldo, Bedeutungsskizze mit Fischgrundriß 1980 zusammenfließen: als Architekt, Theoretiker, Hochschullehrer und Redakteur von Casabella. Und ziemlich plötzlich, kurz nachdem 1966 sein Buch über die „Architektur der Stadt" herausgekommen war, schwärmte die ganze, vor allem die junge Fachwelt von ihm: ein Denker! ..." Wichtig war ihm, wie man neu und zugleich in der historischen Erinnerung bauen könne, zumal da es in der Baugeschichte alles doch schon einmal und oft genug in Vollendung gegeben habe. Sein Rationalismus war nicht der der menschenfreundlichen Funktionalisten vom Neuen Bauen der zwanziger Jahre, sondern ein rigide auf die Form reduzierter, ausgenüchterter, aufs Elementare zielender Rationalismus. In seinen Entwürfen herrscht eine Leere, eine denkmalhafte symbolische Überhöhung einfacher Grundformen, die an die monumentalen Gebäude Boullees und die rätselhafte und beängstigende Welt der Bilder Giorgio de Chiricos erinnert. Wie Ungers setzt Aldo Rossi (1931 - 1997) auf die Kenntnis historischer Bezüge. Rossi, der sich selbst als Rationalist bezeichnet, bezieht sich auf eine Architekturrichtung der zwanziger und dreißiger Jahre, die ''Archittetura Razionale"in Italien, die wegen ihrer Verbindung zum italienischen Faschismus umstritten ist. Die Rationalisten forderten den Gebrauch einfachster Mittel in der Architektur, die Reduzierung der Formen auf wenige grundlegende Typen. Sie suchten nicht nach den individuellen, sondern nach d e n Formen, die sich im Laufe einer langen Geschichte als Zeichen und Ordnungsmittel eines städtischen Gefüges herausgebiltdet haben. Er überträgt eine reduzierte Typologie der Stadt auf die Typologie des Gebäudes. Rossi schreibt : " In meinen Wohnhausentwürfen beziehe ich mich auf die grundlegenden Typen des Wohnens, die sich in einem langen Prozeß gebildet haben. So ist aufgrund Bsp. Entwurf für einen Friedhof in Modena, 1971, der Analogie zur Stadt jeder Korridor eine Strasse, der Bsp. Rathaus von Mailand Muggio Hof ist ein Platz und ein Gebäude reproduziert die Orte Bsp. Massengrab eines Friedhofs San Cantaldo der Stadt." Bsp. Das berühmte schwimmende vier- und achteckige Wissenschaftler sagen, daß am Anfang das Glas war (ein unerhörtes Material, denn es ist Materie und Transparenz zugleich !), daß dann das Spiegelglas, das Plexiglas, die transparenten Kunststoffe kamen und daß wir schließlich die Bildröhre haben. Wie könnte ein Architekt von dieser Materie nicht angesprochen werden, wie er zu Zeiten des Glaspalast vom Glas gefesselt war? Was für eine Architektur und welch eine Revolution! So wird heute das Bild zum Material für Architektur. Nouvel dazu : Ich sage immer, daß sich die Architektur im Sinne der Erzeugung von Bildern nicht den unzählbaren, fabelhaften Bildern entziehen kann, die im Laufe der Jahrhunderte geschaffen wurden. Ich behaupte auch - und damit will ich meinen Beruf nicht aufgeben -, daß in der Architektur eine Tendenz zur Zweidimensionalität besteht. Dieses Spiel mit Durchlässigkeiten, mit Rastern, mit integrierenden Fassadenteilen ... Virilio ergänzt den Satz : Ja, In deiner Art zu arbeiten sehe ich Spuren dieser Die Zeichnungen Rossis - die beide Aspekte seiner Idee eines materialisierten Bildes. Du brauchst geistige Architektur beleuchten - beziehen sich auf die Tradition Bilder, um die Fassade zu erzeugen. der " pittura metaphisica ". (Vielleicht denkt Virilio an die Fassaden des Institute Er wählt meist eine perspektive Darstellung, die auf de Monde Arabe von Nuovel) den ersten Blick ein Interesse an der Raumillusion Das ist sehr erhellend: die Bilder erzeugen Architektur, weckt. Näher betrachtet ist die gesamte Figur merksie sind das bevorzugte Material der Architektur, aber würdig verwunden und durch kein übergeordnetes nicht in einer metaphorischen Art, sondern konstitutiv, Konstruktionsprinzip vereinheitlicht. Die Bildkonstrukti- also unmittelbar bedingend. on ist durch mehrere Fluchtpunkte auf verschiedenen Höhenniveaus gegeben. Nouvel : Die Architekturdarstellung steht in der Tradition der Das Programm kannst Du immer lösen; das ist ein beiZeichnung, die den Bildcharakter betont (wie die Zeich- läufiges Problem. Ich beginne zwar immer dort, aber nung der Revolutionsarchitektur) und das sichert ihr sobald ich weiß, was ich zu bearbeiten habe, ist es das eine gewisse Autonomie und künstlerische EigenwerKonzept - oder mit deinem Wort, das Bild - das die tigkeit. Form lenkt. Aber im Moment sind wir - die Architekten Inwieweit sie am Prozeß der Formfindung strukturell - dabei, nur zu stottern und zu stammeln. Du könntest beteiligt ist, steht in Frage. in meinen Arbeiten ein Dutzend Projekte finden, die die Mittel erforschen, ein Bild zum Gerinnen zu bringen und glaubwürdig zu machen; in Bezug auf ein umfas3 Die Architekturzeichnung ist selbst Material der sendes Konzept, einen Raum, eine Bedeutung. Architektur Im Augenblick verwenden wir die Bilder, ohne ihre Paul Virilio im Gespräch mit Jean Nouvel. wahren Leistungen und Anwendungen allzu gut zu kennen, ein bißchen wie die ersten Menschen, die mit Virilio : Steinen bauten! Heute steht die Frage nach den Beziehungen zwiUnter den großen Ereignissen, die dieses Jahrhundert schen Materie und Bild ! geprägt haben, war das erstaunlichste die Direktüber(gemeint ist hier das digitale Bild von Architektur) tragung der ersten Mondlandung. Wir waren dort, ohne Ist das Bild Materie? Ich bejahe die Frage. Ich würde wirklich dabei zu sein ! antworten, daß man nicht länger von Materie sprechen kann, und dabei das Bild außer acht läßt. Schon heute Virilio : ist das Bild d i e Materie des architektonischen EntGenau. Die Vorstellung ist real, wie im Kino. wurfs, morgen wird das Bild die Materie der Architektur Dazu fällt mir folgendes Beispiel ein. Ein befreundeter selbst sein. Das bedeutet nicht, daß es von BildschirRegisseur erzählte: men nur so wimmeln wird, sondern daß man sich nicht Ich sollte eine Szene drehen, in der ein Mann mit mehr mit dem Opaken und dem Transparenten - als einem Auto vorfährt und in den fünften Stock eines Differenz - zufrieden geben wird. Hauses muß, um seine Verlobte zu küssen. Er kam Seite © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I also mit dem Auto, hielt an, öffnete die Tür, stieg aus und schloß sie, ging drei Stufen hinauf, öffnete die Tür des Gebäudes, schloß sie wieder, trat ein, kam zum Aufzug, rief ihn, öffnete die Tür, schloß sie wieder, drückte auf den Knopf, fuhr in die fünfte Etage, öffnete, ging hinaus, schloß die Tür. Er klingelte, das Mädchen öffnete und sie küßten sich. Meine Frage war nun: Wo soll ich schneiden? Wo muß man schneiden, damit man das alles versteht ? Und die Antwort : Der Mann öffnet die Tür des Wagens, schließt sie wieder, aber bevor er sie zuschlägt, blickt er nach oben und zeigt so dem Zuschauer, wo seine Verlobte ist. In dem Augenblick, wo die Tür des Autos zuschlägt, öffnet sich die Wohnungstür und sie küssen sich. Gut - so werden Filme gebaut. Aber wie soll man Architektur machen ? mit den geistigen Bildern des Benutzers von Architektur ? - dimensionalen Erfahrungsraumes und gehorcht den Gesetzen der 2- Dimensionalität. Eine Architekturzeichnung ist zunächst ein Werkzeug der Verständigung. Sie soll etwas aussagen über den zu realisierenden Bau, soll bestimmte seiner Eigenschaften — Größe, Lage, Gestalt, Fügung, Material usw. beschreiben, sei es durch Ähnlichkeitsbezüge der Darstellung oder symbolische Zeichen. Im Prinzip ist sie übersetzbar in andere Maßstäbe, andere Techniken , andere Farben. Es geht bei dieser Zeichnung nicht um ihre eigene "materiale Qualität", ihr Wert liegt nicht in ihr selbst. Die in der Architekturdarstellung am häufigst verwendete Darstellungsart ist die sog. PARALLELPROJEKTION. Die Parallelprojektion hat eine hohen Abstraktiongrad, meist nur feine Linienbilder, was ihre Eindeutigkeit und hohen Wahrheitsgrad ausmacht und sie ist trotzdem von hoher räumlichen Anschaulichkeit. Der analytische Gedanke der Darstellung macht die Variation der Linie, der Fläche, der Raumform und der Farbe zu ihrem Thema. Zitat Werner Oechslin : ... Woher stammt das Mißtrauen gegen all jene Architekturzeichnurgen, die das Auge bestechen, die durch ihre farblichen Effekte auffallen, die schön sind? Gibt es über Mißfallen und Enttäuschungen hinaus grundsätzliche Einwände, die es verbieten, dieses das Auge direkt ansprechende Medium zu verwenden? Wohl kaum! Die Frage betrifft jede Architektur, deren spätere physische Präsenz nach der bildlichen Vorwegnahme des Gesamteffekts verlangt ... zum Objekt, die Bildgröße und andere Parameter. Immer läßt die Perspektive den Raum als subjektives Erlebnis, unter e i n e m Gesichtspunkt betrachtet, erscheinen. Die ursprünglichste Anwendung der Perspektive in den Theater-Prospekten von Sebastiano Serlio im 14.Jhdt. erläutert diese bestechende Wirkung. Wie Theater immer ein Hier des Ortes und ein Dort der Vorstellung beinhaltet, hat die Perspektive diese mathematische Seite der Konstruktion und diese wesentliche Seite der Illusion und Zauberei. Die Perspektive ist ein Mittel der Manipulation. Die Perspektive beschreibt allerdings nicht den Raum, der sich hinter mir schließt und nicht die Architektur als Lebensraum. Perspektive ist ein suggestiver Blick auf eine manipulierte, optische Erscheinung und der Porträt - Auftrag dieser Architekturzeichnung hindert diese bei allem illusionistischen Raffinement daran, eine gewisse Beschränktheit in Syntax und Inhalt zu überwinden: Unvermeidlich ist der dargestellte Baugegenstand im Zentrum plaziert, zeigt er sich tiefenscharf, eindeutig, realitätsträchtig, überzeugend und statisch. Immer täuscht er eine Lösung vor, darf also keine Lücken offenlassen; immer muß er posieren, darf keine störenden Ereignisse neben sich dulden. Produktive Vorstellungskraft aber wäre abhängig von genau gegensätzlichen Bildangeboten; von der Einordnung des " Projekts " in einen polyvalenten Umraum, von selektiven Betonungen oder Auslassungen, Bsp. Herzog & de Meuron, Sammlung Goetz, München 1995 Bsp. Gehry , Frank O., Skizze "Ginger und Fred", Prag 1996 frägt Virilio sich selbst und er antwortet sich auch gleich : Wir werden sparsamer mit Bildern umgehen können, weil wir mit den subjektiven und virtuellen Bildern des Benutzers bauen werden. Der angesprochene sparsamere Umgang mit Bildern geschieht ja nicht zum Nachteil des Benutzers, im Gegenteil: er bezieht seine geistigen Fähigkeiten mit ein. Man muß mit ihnen arbeiten, mit seinen Kenntnissen der Stadt, des Films, des Fernsehen ... 4 Die Architekturdarstellung ist widersprüchlich Parallelprojektion, Perspektive und Freies Zeichnen Die Architekturdarstellung ist eine Illusion des 3 Dieses "Sehen durch Papier" ist eine gedankliche Beziehung zwischen Betrachter, Objekt und Bildfläche, die unterschiedlich festgelegt, andere Arten der Darstellung ermöglicht. Die konstruktiven Vereinbarungen garantieren dabei ein hohes Maß an Verständlichkeit. Die Parallelprojektionen bezeichnen das Universelle im Räumlichen, das die Architektur unabhängig von dem betrachtenden Auge erscheinen läßt. Die Darstellung ist rekonstruierbar, berechenbar und in jeden Masstab übersetzbar. Sie stellt eine Art Denkwerkzeug dar. Peter Eisenmann sagt : "... Systematisch abgewandelt, wird eine herausgegriffene Einzelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voyeurs versetzt, der den Gestalt- Jongleur bei seiner Arbeit beobachtet. Er sieht Standbilder aus Verwandlungsproben, wobei der Probenablauf als Werk verstanden wird. Die Zeichnung hat meta - architektonische Funktion ." Bsp. Libeskind, Balmond Erweiterung des Victoria und Albert Museum, Blick in das Einganngsfoyer, London 1996 Die PERSPEKTIVE ist eine konstruktive Methode, die - dem Sehbild am ähnlichsten - räumliche Tiefe auf der Fläche des Zeichenblattes suggeriert. Die Perspektive setzt Kenntnisse ihrer Konstruktion voraus, die seit dem 15. Jhdt. im Wesentlichen vereinbart sind. Die Konstruktion der Perspektive beinhaltet die Bestimmung verschiedener Variablen, die je nach Festlegung, die Bilderscheinung und die Bildaussage verändern. Dazu gehören die Bestimmung der Aughöhe, der Distanz und der Betrachtungsrichtung Bsp. Kahn, Louis I. Konzeptskizzen für IIM in Ahmedabad, Indien vom 14.11.1962 von Simultaneität mehrerer Teilaspekte, von Sfumato und Mehrdeutigkeit der Umrisse. Naturalistische Perfektion ist eher geeignet, die imaginative Ergänzungsarbeit eines Betrachters auszuschalten. Wird er sich seiner Ausdrucksarmut gewahr, greift der Architekturporträtist entweder zur Methode dekorativer Seite © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I bis fotorealistischer Kostümierungen (Werbegrafik) oder zu diagrammatischer Aufklärungsarbeit, die sich an Intellekt und Assoziationsvermögen des Adressaten wendet, um ihn mit Hilfe unabweislicher Denkschemata von der einzig richtigen Lesart des Entwurfs zu überzeugen. Auch in einem poetisierten Rendering bleibt oberstes Ziel die Anpreisung des Projekts, selbst wenn periphere Aspekte in den Vordergrund drängen oder das Abbild in malerischer Autonomie sich zu verselbständigen scheint. Bsp. Office for Metropolitan Architecture, Rotterdam, Zaha Hadids Schwerarbeiten gegen die Schwerkraft, Tschumis und Eisenmans Geo-strips, die tropfenden Action-paintings Will Alsops. sowie die milde Malerei von Zoe Zenghelis Die Felder, in denen die Architekturzeichnung neu zu erfinden ist, sind vielfältig. Im Bereich ihrer Zeichenund Ausdrucksmittel, im Bereich der Assoziation und Sinnverwandlung, im Bereich neuer thematischer Bezüge. Wenn die Architekturzeichnung in diesem Sinne experimentell entwickelt wird, die künstlerische Zeichnung kann dabei lehrreich sein, könnte Sie konstitutioneller an Architektur beteiligt werden. Heute ist die Architekturdarstellung zum Dekorationsund Präsentationsmedium verkommen. Ein Training der eigenen Wahrnehmung, das die Aufmerksamkeit auf Sichtbares lenkt, was ich kenne aber neu sehe, könnte die Fähigkeit und vorallem die Lust zu zeichnen, beflügeln. Nennen wir es eine Schule des Sehens in der die Fragen, die sich zeichnerisch an die Architektur richten, Die Zeichnungen, mit denen versucht wird, Nicht-Deneu gestellt sind : finierbares auszudrücken: Spuren von Erinnerungen Wie schaue ich auf, in ... unter ...die Dinge ?, und Träumen des Zeichners, Rätselhaftes, nur zu Erwelchen Ausschnitt wähle ich, dem meine Aufmerkahnendes oder Gesten. Zeichnungen solcher Art sind samkeit gilt ?, nur in sehr eingeschränktem Sinne auf " Gemeintes " was sehe ich, was fühle ich, was rieche ich ?, bezogen. Sie können meist nicht in andere Techniken wieviel kann ich sehen ?, was bleibt im Dunkel ?, und Maßstäbe übersetzt werden. Sie informieren nicht, was sehe ich, was denke ich, was weiß ich ? sondern überreden oder beschwören den Betrachter. Sie führen in Wunschlandschaften, in Diskurse von offener schwebender Bedeutung, sie leben vom Zauber des Undefinierbaren, sie schließen phantastische Assoziationen und auch Sinnverwandlungen ein, sie sind nicht "brauchbar". Die Umsetzungen und Interpretationen, die aus ihnen folgen, bewegen sich auf allen möglichen Ebenen, nur nicht auf der, aus der sich die technische Machbarkeit ableiten läßt. Nennen wir es FREIES ZEICHNEN, bei dem nicht dem Abbild vorhandener oder projektierter Bauten alle Aufmerksamkeit gilt, sondern allein Bsp. Muster nach mathematischer Zufallsstruktur möglichen, konträren Gestaltungsmöglichkeiten im Sinne des Ausdrucksextrems. Die Architekturzeichnung könnte auch, wie Edgar Alan Poe in " Philosophie der Komposition " beschreibt, " ... von einer unbestimmten Unterströmung von Bedeutung getragen... " sein. Bsp. Foster, Norman aus Sketsches S.231 Seite Die Darstellungsarten im Überblick © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I senkrechte Projektionen schräge Projektionen oder Axonometrien zentrale Projektionen oder Perspektiven kotierte Projektion Grundrißaxonometrie Isometrie Zentralperspektive senkrechte Projektion Aufrißaxonometrie Senkrechte Axonometrie Übereckperspektive DIN 5 oder Ingineurprojektion Perspektive mit gekippter Bildebene Senkrechte Projektionen . Senkrechte Eintafelprojektion oder Kotierte Projektion . Senkrechte Zwei- oder Dreitafelprojektion Schräge Projektionen oder Axonometrien . Grundrißaxonometrie oder Militärprojektion . Aufrißaxonometrie oder Kavalierprojektion . DIN 5 oder Ingineurprojektion . Isometrie . Senkrechte Axonometrie Zentrale Projektionen oder Perspektiven . Zentral- oder Frontalperspektive . Übereckperspektive . Perspektive bei geneigter Bildebene Die Darstellungsarten lassen sich unterscheiden nach Masstäblichkeit und Anschaulichkeit Während die Ein- und Zweitafelprojektionen ein hohes Maß an Masstäblichkeit besitzen, verlieren die Axonometrien diese z.T zu Gunsten einer besseren Anschaulichkeit, die eine gute Vorstellung der räumlichen Situation ermöglicht. Die perspektiven Darstellungsarten erzeugen ein räumliches Bild, das unserem Sehbild am nächsten kommt. Das perspektive Bild hat einen hohes Maß an suggestiver Kraft, verliert aber gegenüber dem Orginal fast jede Masstäblichkeit. Die Darstellungsarten lassen sich nach der Art der Verwendung beurteilen. Die Ein- und Zweitafelprojektionen können als Vorlage für die Bauausführung verwendet werden, da die Maße unmittelbar dem Bild zu entnehmen sind. Die Axonometrien sind leicht zu konstruieren und ermöglichen einen guten Eindruck der räumlichen Situation. Da das axonometrische Bild mit dem Bild des Achsenkreuzes überlagert ist, kann eindeutig auf die Geometrie des Gegenstandes geschlossen werden. Axonometrien finden Verwendung im Entwurf, der Detailzeichnung, beim Thema der Variation eines Objektes und im Städtebau. Perspektive Darstellungen ermöglichen eine Vielzahl von Präsentationsformen einer räumlichen Situation. Da das perspektive Bild immer den Betrachter miteinbezieht, steht im Vordergrund der Gedanke der Illusion oder der Täuschung im Sinne des Sehbildes. Dieser kann durch entsprechende Staffagen, Licht und Schattengebung, Hintergründe, Spiegelung, farbige Ausgestaltung u.a. verstärkt werden. Seite Die Projektionsarten © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Schnittpunkt der Projektionsstrahlen im Endlichen Die Darstellungsarten lassen sich unterscheiden Die projizierenden Strahlen schneiden sich in nach der Art der Projektion. einem Punkt, dem Projektionszentrum Die Darstellende Geometrie vereinbart die = Zentralprojektion Regeln der Beziehung von räumlichen Objekten und der Zeichenebene. Das Mittel der Beziehung ist die Projektion. Beim Vorgang der Projektion werden Projektionsstrahlen durch Punkte eines räumlichen Objektes gelegt, die dann eine Bildtafel treffen und dort als Bildpunkte des Objektes erscheinen. Wir unterscheiden die Lage des Projektionszentrums und die Richtung der Projektionsstrahlen zur Bildebene. Schnittpunkt der Projektionsstrahlen im Unendlichen oder sie sind parallel zueinander = Parallelprojektion. Bei der Parallelprojektion kann noch unterschieden werden, ob die Projektionsstrahlen senkrecht auf die Bildebene treffen = senkrechte oder orthogonale Parallel projektion oder ob die Projektionsstrahlen in einem Winkel die Bildebene treffen = schräge Parallelprojektion. Seite © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Senkrechte Projektionen. allgemein Sol LeWitt geb. 1928 in Hartford, Connecticut aus der Serie "structures" 1962 - 1993 1 2 3. 1978 Baked enamel on aluminium Die Bilder räumlicher Objekte, die mit Hilfe senkrechter Projektionen entstehen, also Grundrisse, Aufrisse, Seitenrisse oder Schnitte gelten als Bilder mit hohem "Wahrheitsgrad". Sie werden als unmißverständliche Sprache von Entwerfendem und Ausführendem benützt. Sie sind immer noch das am häufigsten verwendete Medium der Architekturpräsentation. Seite 10 Kotierte Projektion © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Raumpunkt P P1 P2 Punkt Die kotierte Projektion ist hier nicht näher beschrieben, da sie auf Grund ihrer geringen Anschaulichkeit in der Architekturdarstellung eine geringe Rolle spielt. Sie wird im Ingineurwesen, wie im Strassenbau oder der Kartographie verwendet. P ( h P) Ein einfaches, räumliches Objekt am Bsp. der Würfel kann auch in einer Projektionsebene eindeutig beschrieben werden. Die Breite und die Tiefe sind bildlich dargestellt, bezogen auf eine horizontale Fläche und die Höhe ist numerisch, dem entsprechenden Punkt zugeordnet, beschrieben. Die horizontale Lage eines Punktes ist also im Bild eindeutig beschrieben, während die Höhenangabe dem Text entnommen werden muß. Dieses Höhenmaß ist in einem Höhenmasstab ( Höhenkote ) definiert. Auch andere Punkte, wie P1 und P2, erzeugen das gleiche Bild. Eindeutig ist die Lage des Punktes erst durch die Höhenangabe bestimmt, die dargestellt ist in einem Höhenmasstab. Seite 11 Zweitafelprojektion © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Koordinatenachsen z y Die Zweitafelprojektion entsteht durch senkrechte Projektion des Objektes auf zwei, oder drei senkrecht aufeinander stehende Bildebenen. Das Bild, d.h. die Projektion auf die Innenflächen eines Quaders, auf die horizontale Ebene wird als Grundriß, auf die senkrechte Bildebene von links oder von vorn betrachtet als Aufriß, von rechts betrachtet als Seitenriß, bezeichnet. Das entspricht der europäischen Sicht der Hauptrisse im Unterschied zur amerikanischen Tradition. Um alle Bilder in der Zeichenebene, die der Aufrißebene entspricht, zeigen zu können, muß die Grundrißebene und die Seitenrißebene um 90 Grad in die Zeichenebene eingeklappt werden. Dadurch erscheinen alle Bilder einander senkrecht zugeordnet. Die Richtung, Lage bzw. Höhe der Betrachtung wird, insbesondere bei Schnitten, durch Pfeile gekennzeichnet. Bei räumlich komplizierteren Objekten werden Bildebenen gewählt, die parallel zu vorhandenen Objektebenen liegen, um diese eindeutig zu beschreiben. Die Zweitafelprojektion ist die in der Architektur am häufigsten verwendete Art der Plandarstellung und findet Verwendung von der Handskizze bis zur Ausführungsdarstellung. Seite 12 Punkt. Umklappung der Bildtafeln © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Im Folgenden werden die Aufgaben - um eine räumliche Vorstellung davon zu ermöglichen - im linken Bildfeld zunächst in einer trimetrischen DarstelDreitafelprojektion lung erläutert. Im rechten Bildfeld ist dann die Aufgabe konstruktiv in der Zwei - oder Dreitafelprojektion entwickelt. Seitenriß π 3 Aufriß π 2 P''' Trimetrie Raumpunkt P'' P Das Bild des Punktes P liegt sowohl in der Grundrißebene als auch in der Aufrißebene und in der Seitenrißebene auf einer Ordnungslinie, die senkrecht auf der jeweiligen Bildtafel steht. Zur Darstellung in der Zeichenebene (entspricht der Aufrißebene) werden die Bildtafeln in diese umgeklappt. Bei der Umklappung beschreiben die Bildpunkte einen Kreisbogen, der in den Projektionen als Sehne erscheint. Die Bezeichnung der Bildpunkte: in der Grundrißebene P' in der Aufrißebene P'' in der Seitenrißebene P''' Seite 13 Punkt. Lage im Raum © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Raumpunkte Aufriß P1 im I. Quadranten P1 P2 im II. Quadranten Seitenriß P3 im III. Quadranten P3 P4 P4 Grundriß im IV. Quadranten Der Raum wird nach dem kartesischen System in vier Quadranten aufgeteilt. Die Lage eines Punktes in diesem Raum ist aus der relativen Lage seiner Bildpunkte zur Spurgeraden der Bildtafeln zu erkennen. Liegt P im 1.oder 3.Quadranten, liegen die Bildpunkte auf verschiedenen Seiten der Spurgerade. Liegt P im 2.oder 4.Quadranten, liegen die Bildpunkte auf einer Seite der Spurgerade. Seite 14 Punkt in der Symmetrie- und in der Koinzidenzebene © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Symmetrieebene Raumpunkte P1 P2 P2 P1 P3 P4 P4 Koinzidenzebene Ein Punkt P, der von der Grundrißtafel und der Aufrißtafel den gleichen Abstand hat, liegt in der winkelhalbierenden Ebene des Quadranten, in dem der Punkt sich befindet. Die winkelhalbierende Ebene des 1. und 3. Quadranten heißt Symmetrieebene. Die Bilder der Punkte dieser Ebene haben den gleichen Abstand zur Spurgeraden der Bildebenen. Die Spurgerade wird zur Symmetrieachse. P3 Die winkelhalbierende Ebene des 2. und 4. Quadranten heißt Koinzidenzebene. koinzident (lat.): zusammenfallend Die Bilder der Punkte dieser Ebene fallen in einem Punkt zusammen. Seite 15 Beliebige Gerade © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Raumpunkt Gerade Spurpunkt Spurpunkt P g S1 S2 Die Bilder der Geraden g entstehen durch die Projektion aller Punkte der Geraden auf die entsprechende Bildebene. Der Durchstoßpunkt der Geraden mit der Grundrißebene heißt Spurpunkt S1. Der Durchstoßpunkt der Geraden mit der Aufrißebene heißt Spurpunkt S2. S1 der Geraden muß an der Stelle liegen, wo das Aufrißbild der Geraden die Spurgerade der Bildtafeln schneidet, also die Höhe über dem Grundriß 0 ist. S2 der Geraden muß an der Stelle liegen, wo das Grundrißbild der Geraden die Spurgerade der Bildtafeln schneidet, also die Tiefe zum Aufriß 0 ist. Seite 16 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Raumpunkte Wahrer Winkel und wahre Länge einer Geraden. Grundrißklappung P1 P2 Eine Gerade in beliebiger Lage zu den Rissebenen erscheint in diesen verkürzt. Der wahre Winkel zu den Rissebenen erscheint ebenfalls verzerrt. Um die wahre Länge und den wahren Winkel der Gerade darstellen zu können, wird das Prinzip der Klappung oder Drehung angewendet. Wir stellen uns dazu eine senkrecht stehende Hilfsebene oder projizierende Ebene vor, am Bsp. eine senkrecht zum Grundriß stehende Hilfsebene = 1.projizierende Ebene, die die Gerade enthält. Das senkrecht stehende Dreieck wird um die Grundrisspur der Ebene in den Grundriß geklappt. Dabei wandern die Punkte, P1 und P2 der Geraden auf einem Kreisbogen, der im Grundriß als Sehne senkrecht zur Drehachse erscheint. Die Höhe der Punkte ist aus dem Aufriß in wahrer Größe bekannt. Seite 17 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Aufrißdrehung oder Mongsche Drehung 1.projizierende Ebene Gaspard Monge,1746 - 1818. Schulreformer der Revolutionszeit und Mitbegründer der späteren Ecole Polytechnique. Er entwickelte die geometrischen Gesetzmäßigkeiten der Zweitafelprojektion, die er "Geometrie Descriptive" oder "Darstellende Geometrie" nennt. Zur Bestimmung der wahren Größe und des wahren Winkels einer Geraden, kann man die projizierende Ebene, in der sich die Gerade befindet (am Bsp. die 1.projizierende Ebene), so um eine beliebige Achse drehen, daß sie parallel zu einer Bildtafel liegt. (am Bsp. parallel zur Aufrißebene). Die Strecke ist dann unverzerrt, in wahrer Größe und Neigung sichtbar. Seite 18 Besondere Geraden © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Trimetrie 2. projizierende Gerade 1.projizierende Gerade 3-Tafelprojektion Eine zu zwei Bildtafeln parallel verlaufende Eine Gerade, die senkrecht auf einer Bildebene Gerade ist sowohl Höhenlinie als auch Frontlinie steht, ist eine projizierende Gerade. Ihr Bild in dieser Ebene ist ein Punkt. Sie wird als Hauptlinie bezeichnet. Senkrecht auf Grundriß = 1.projizierende Gerade Eine Gerade deren Punkte den gleichen Abstand Eine Gerade, deren Punkte den gleichen Abzur Aufrißebene haben, ist eine Frontlinie. stand zur Grundrißebene haben, ist eine Höhenlinie. Senkrecht auf Aufriß = 2. projizierende Gerade Seite 19 Zwei beliebige Geraden © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I P1 P2 Raumpunkte Geraden g1 g2 Zwei Geraden g 1 und g 2 verlaufen beliebig im Raum. s.S.16: Beliebige Gerade Sie haben keinen gemeinsamen Punkt, d.h. sie schneiden sich nicht und sie bilden keine gemeinsame Ebene. Im Grund- und im Aufriß schneiden sich zwar die jeweiligen Bilder der Geraden, die Schnittpunkte liegen aber nicht auf einem gemeinsamen Ordner. D.h. die Geraden haben keinen Punkt im Raum gemeinsam. Zur Bestimmung der Sichtbarkeit: . ausgehend von dem scheinbaren Schnittpunkt im Grundriß, was liegt auf dem Ordner darüber ? und . ausgehend von dem scheinbaren Schnittpunkt im Aufriß, was liegt auf dem Ordner davor ? Seite 20 Zwei sich schneidende Geraden © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Punkt Spuren der Ebene P s1 s2 2 Geraden verlaufen so im Raum, daß sie sich in einem Punkt P schneiden. Zwischen den Geraden spannt sich eine Ebene auf. Liegt eine Gerade in einer Ebene, so liegen ihre Spurpunkte auf den Spuren ( s1 und s2 ) der Ebene. Die Spuren der Ebene in den Bildtafeln erhält man, indem jeweils die beiden Durchstoßpunkte der Geraden in den Bildtafeln miteinander verbunden werden. s. S. 16: Beliebige Gerade Seite 21 Allgemeine und besondere Lage einer Ebene © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Trimetrie 2 -Tafelprojektion doppeltprojizierende Ebene Beide Spuren stehen senkrecht auf der x- Achse und erscheinen in der 2 - Tafelprojektion als durchlaufende Linie. Trimetrie 2 -Tafelprojektion Eine Ebene schneidet die Grundrißebene in der Grundrisspur und die Aufrißebene in der Aufrisspur. allgemeine Lage Die Spuren treffen in schiefen Winkeln die x- Achse. grundrißprojizierende oder erstprojizierende Ebene Die Ebene steht senkrecht auf der Grundrißebene. Die Aufrisspur schneidet die x- Achse in einem rechten Winkel. aufrißprojizierende oder zweitprojizierende Ebene Die Ebene steht senkrecht auf der Aufrißebene. Die Grundrisspur schneidet die x- Achse in einem rechten Winkel. schneidet die Ebene die Tafeln in der x- Achse fallen dort beide Spuren zusammen. Aus dem Bild in der 2 - Tafelprojektion ist die Lage der Ebene nicht ersichtlich. beide Spuren verlaufen parallel zur x- Achse Höhenebene Die Ebene verläuft parallel zur Grundrißebene. Die Aufrisspur verläuft parallel zur x- Achse. Frontebene Die Ebene verläuft parallel zur Aufrißebene. Die Grundrisspur verläuft parallel zur x- Achse. Seite 22 Besondere Geraden einer Ebene. Höhenlinie, Frontlinie und Fallinien © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I v2 h2 v1 h1 Höhenlinie einer Ebene Die Höhenlinie h1 h2 ... einer Ebene ist der Ort von Punkten gleicher Höhe. Die Grundrisspur der Ebene ist die Höhenlinie mit der Höhe 0. Alle anderen Höhenlinien verlaufen dazu parallel im Grundriß und erscheinen im Aufriß als Horizontale. v1 f1 h1 Frontlinie einer Ebene Die Frontlinie v1 v2 ... einer Ebene ist der Ort von Punkten mit gleichem Abstand zur Aufrißebene. Die Aufrisspur der Ebene ist die Frontlinie mit dem Abstand 0. Alle anderen Frontlinien verlaufen dazu parallel im Aufriß und erscheinen im Grundriß als Parallele zur x- Achse. Fallinie erster Ordnung f1 f2 ... stehen im rechten Winkel zu den Höhenlinien h1 h2 ... der Ebene. Ebenso die Bilder im Grundriß. Ihre wahren Neigungen entsprechen dem Gefälle der Ebene. v1 Fallinie zweiter Ordnung stehen im rechten Winkel zu den Frontlinien v1 v2 ... der Ebene. Ebenso die Bilder im Aufriß. Ihre Neigungen entsprechen dem wahren Winkel von Ebene und Aufrißebene. Für Konstruktionen mit Ebenen sind die spurparallelen Hauptlinien und die spurnormalen Fallinien (d.h. die Fallinien erster Ordnung) von besonderer Bedeutung. Seite 23 Punkt und Ebene © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I v1 h1 Raumpunkt P Gegeben ist eine Ebene E in allgemeiner Lage und ein Punkt P. Der Punkt liegt dann in der Ebene, wenn Höhenlinie h1 oder Frontlinie v1 durch den Punkt P parallel zu den Spuren der Ebene E sind. oder : Ist weder Front- noch Höhenlinie eines Punktes parallel zu den Spuren der Ebene, liegt der Punkt nicht in der entsprechenden Ebene. zur Konstruktion in den Tafeln : . Höhenlinie durch P im Aufriß zeichnen. . Das Bild der Höhenlinie im Grundriß ist parallel zur Spur der Ebene. d.h. der Punkt P ist ein Punkt der Ebene oder: . Frontlinie durch P im Grundriß zeichnen. . Das Bild der Frontlinie im Aufriß ist parallel zur Spur der Ebene. d.h. der Punkt P ist ein Punkt der Ebene Seite 24 Drei - Punkte - Ebene © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Raumpunkte P1 P2 P2 P3 Durch drei im Raum liegende Punkte P1, P2 und P3 wird eine Ebene E aufgespannt. Die Spuren der Ebene findet man, indem die Punkte untereinander verbunden werden. Die Durchstoßpunkte dieser Verbindungsgeraden durch die Bildtafeln sind die Punkte der Spuren der gesuchten Ebene in den Bildtafeln. Konstruktionsschritte : Im Aufriß : Die Verbindung der Punkte P1 P2 im Aufriß auf die x - Achse verlängert, ergibt die 0 - Höhe der entsprechenden Geraden im Grundriß = Spurpunkt der gesuchten Spur der Ebene im Grundriß. Die Verbindung der Punkte P1 P3 im Aufriß auf die x - Achse verlängert, ergibt die 0 - Höhe der entsprechenden Geraden im Grundriß = ein weiterer Spurpunkt der gesuchten Spur der Ebene im Grundriß. 2 Punkte definieren die Spur der gesuchten Ebene im Grundriß Im Grundriß : Die Verbindung der Punkte P3 P2 im Grundriß auf die x - Achse verlängert ergibt die 0 - Tiefe der entsprechenden Geraden im Aufriß = Spurpunkt der gesuchten Spur der Ebene im Aufriß. Die Verbindung der Punkte P3 P1 im Grundriß auf die x - Achse verlängert ergibt die 0 - Tiefe der entsprechenden Geraden im Aufriß = ein weiterer Spurpunkt der gesuchten Spur der Ebene im Aufriß. 2 Punkte definieren die Spur der gesuchten Ebene im Aufriß. Damit ist die Ebene eindeutig definiert. Seite 25 Abstand eines Punktes von einer Ebene © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Raumpunkt P Raumpunkt P Punkt P liegt außerhalb der Ebene. Gesucht ist der Abstand des Punktes von der Ebene. Eine Ebene durch den Punkt P, die erstprojizierende Ebene, bildet mit der gegebenen Ebene eine Schnittfläche (schraffiert), die sich im Aufriß darstellen läßt. Der Abstand ist die kürzeste Verbindung Das Aufrißbild des Abstandes (durch Aufrißdes Punktes zur Ebene. punkt, senkrecht zur Aufrisspur) ergibt mit dem Die Abstandsgerade steht in zwei beliebigen Aufrißbild der Schnittfläche geschnitten, den Richtungen senkrecht auf der Ebene. gesuchten Aufrißpunkt des kürzesten Abstandes. zur Konstruktion in den Tafeln : Zur Konstruktion des Abstandes legt man auf Grund o.g. Bedingungen zwei Ebenen durch P, die jeweils senkrecht auf der Ebene stehen. Dazu wählt man die Ebenen, die sowohl im Grundriß wie auch im Aufriß die Spuren der Ebene unter einem rechten Winkel schneiden. Die gleiche Konstruktion gilt für das Grundrißbild des Abstandes. Seite 26 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Punkt Wahre Größe und Neigung des Abstandes von einer Ebene P Entsprechend der Konstruktion s.S. 26: Abstand eines Punktes von einer Ebene ist der Abstand des Punktes P zur Ebene gegeben. Die Hilfsebene (schraffiert), die unter der Abstandsgeraden senkrecht auf der Grundrißebene steht, wird um ihre Grundrißspur in die Grundrißebene geklapt. In der Umklapung wird im Grundriß die wahre Größe der Hilfsebene und die wahre Größe und Neigung des Abstandes zur Ebene sichtbar. s.S. 17: Grundrißklappung zur Konstruktion in den Tafeln: Der Radius der Drehung erscheint in der Grundrißebene als Sehne senkrecht zur Drehachse. Die Drehachse entspricht dem Grundrißbild der Abstandsgeraden. Die Höhen der Hilfszebene sind aus dem Aufriß in wahrer Größe bekannt. Seite 27 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Gerade Durchstoßpunkt Durchstoßpunkt einer beliebigen Geraden durch eine Ebene g S In Grundrißrichtung der Geraden stellen wir uns eine Senkrechte 1. projizierende Hilfsebene vor, die die Gerade g enthält. Die Hilfsebene entspricht einer 1. projizierenden Ebene. Die Hilfsebene mit der gegebenen, schrägen Ebene geschnitten ergibt im Aufrißbid die Schnittgerade beider Ebenen. Der Schnittpunkt dieser Schnittgeraden mit dem Aufrißbild der Geraden g stellt den Durchstoßpunkt im Aufriß dar, der senkrecht dem Raumbild, bzw. dem Grundrißbild, der gegebenen Geraden zugeordnet werden kann. Seite 28 Durchstoßpunkt einer beliebigen Geraden durch zwei Ebenen. Pendelebenenverfahren © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I S A Gerade g P1 P2 B Wenn die Durchstoßpunkte einer Geraden durch zwei Oberflächen, am Bsp. zwei Deckflächen der Pyramide, gefunden werden soll, so kann dies mit einer 1. projizierenden Ebene s.S. 28: Durchstoßpunkt einer beliebigen Geraden durch eine Ebene oder wie hier beschrieben mit dem Pendelebenenverfahren konstruiert werden. Die Pendelebene ist eine Ebene, die sowohl die Gerade als auch die Spitze S der Pyramide beinhaltet. Auf der Geraden werden zwei, beliebige Punkte A und B, außerhalb der möglichen Durchdringungspunkte mit den Deckflächen, gewählt. Diese Punkte mit der Spitze verbunden, ergeben im Aufriß das Bild der Pendelebene, das dem Grundriß zugeordnet das Bild der Pendelebene im Grundriß ergibt. Die gefundene Grundrisspur der Pendelebene schneidet die Grundrisspuren der Deckfächen in den Punkten P1 und P2. Werden P1 und P2 mit der Pyramidenspitze S verbunden, findet man als Schnittpunkte mit der Geraden die Durchstoßpunkte der Geraden durch die Deckflächen der Pyramide. Seite 29 Punkt und Gerade spannen eine Ebene auf © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Gerade Raumpunkt g P Zwischen einem Punkt P und einer Geraden g spannt sich eine Ebene E auf. Die Spuren der Ebene E erhält man, indem die Durchstoßpunkte der Geraden g durch die Bildtafeln mit P verbunden werden. ( Mit der gegebenen Geraden wird die Ebene also durch zwei weitere Geraden definiert.) . Die Durchstoßpunkte dieser Verbindungsgeraden durch die Bildtafeln und die Durchstoßpunkte der Geraden durch die Bildtafeln, sind Punkte der Spuren der Ebene E. Zur Konstruktion in der Zwei-Tafelprojektion müssen die Durchstoßpunkte der Gerade g und die Durchstoßpunkte der Verbindungsgeraden durch die Bildtafeln bestimmt werden. Seite 30 zwei sich schneidende Ebenen. Schnittgerade © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I S2 S2 S2 S1 S1 S1 zwei sich schneidende Ebenen, gegeneinander zwei sich schneidende Ebenen, nach rechts geneigt. geneigt. zwei sich schneidende Ebenen, nach rechts geneigt. zwei sich schneidende Ebenen, nach rechts geneigt. Spuren der Ebenen parallel im Grundriß. Spuren der Ebenen parallel im Aufriß. Zwei sich schneidende Ebenen haben eine gemeinsame Schnittgerade. Die Schnittpunkte der Spuren zweier Ebenen, S1 und S2 sind Punkte der gemeinsamen Schnittgeraden. Seite 31 Wahrer Winkel zwischen zwei Ebenen © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I B C A D Zwei sich schneidende Ebenen sind durch ihre Spuren gegeben. Gesucht ist der wahre Winkel zwischen den Ebenen. Konstruktionsschritte : Zunächst wird die Schnittgerade konstruiert. s.S. 31: Zwei sich schneidende Ebenen Dann wird, von einem beliebigen Punkt aus (am Bsp. Punkt A) eine Normalebene errichtet, in der der wahre Winkel der gegeneinander geneigten Ebenen liegt. Die Grundrisspur der Normalebene schneidet die Spuren der Ebenen in Punkt A und B und das Grundrißbild der Schnittgeraden in einem rechten Winkel in Punkt C. Die Grundrisspur erscheint in wahrer Größe. Die Höhe der Normalebene von dem Punkt C aus, steht senkrecht zu der Schnittgerade und kann im Grundriß als Senkrechte auf die eingeklappte Schnittgerade s.S.17:Wahrer Winkel und wahre Länge einer Geraden. Grundrißklappung sichtbar gemacht werden. Auf das Bild der geklappten Richtung der Höhe (senkrecht auf C) eingedreht, ergibt sich Punkt D und mit A und B verbunden die wahre Größe der Normalebene in der die Dreiecksseiten AD und BD den wahren Winkel der sich schneidenden Ebenen einschließen. Seite 32 Wahre Größe einer Ebene. Konstruktion mit Stützdreieck © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I B A C Eine beliebig im Raum liegende Ebene erscheint dann in wahrer Größe, wenn sie zu einer der Bildtafeln parallel gedreht wird. Konstruktionsschritte : am Bsp. für Punkt C beschrieben. 1 Wahl der Höhenlinie durch den Punkt A (im Aufriß festlegen), entspricht der Vorstellung einer Drehachse der Ebene, um die gedreht, die Ebene in wahrer Größe (grundrißparallel) erscheint. . Der Drehradius des Punktes C ist . die Hypotenuse des Stützdreieckes von dem . die Kathete im Grundriß und . die Höhe im Aufriß gegeben ist. 2 Jeder Punkt beschreibt dabei einen Kreisbogen, der senkrecht zur Drehachse steht, und dessen Mitte darauf liegt. Der Radius ist der Abstand des Punktes von der Drehachse. entsprechend Punkt B. Seite 33 Wahre Größe einer Ebene. Konstruktion mit hilfsprojizierender Ebene © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I B A C Konstruktionsschritte : 1 Wahl der Höhenlinie durch den Punkt A, entspricht der Vorstellung einer Drehachse der Ebene, um die gedreht, die Ebene in wahrer Größe (grundrißparallel) erscheint. 2 Jeder Punkt beschreibt dabei einen Kreisbogen, der senkrecht zur Drehachse steht, und dessen Mitte darauf liegt. Der Radius ist der Abstand des Punktes von der Drehachse. 3 In der , die senkrecht zur Drehachse steht, erscheint die Ebene, bzw. das Dreieck als Gerade. 4 Durch Drehung in die, dem Grundriß parallele Ebene, erhält man die wahren Größen der Abstände der Punkte B und C zur Drehachse. Seite 34 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Der Körperschnitt des Zylinders und die Affinität Projektionsstrahlen Affinitätsachse Mit der Affinität ist der Zusammenhang zweier Flächen beschrieben, die in zwei sich schneidenden Ebenen liegen. Da die konstruktive Beziehung beider Ebenen, die einem geraden Prisma oder einem geraden Zylinder zugeordnet sind, beschrieben wird, ist hier ein Zusammenhang beschrieben, der generell die konstruktive Beziehung von Objekt und Bild in der Parallelprojektion verständlich machen kann. Die Mantellinien des Prismas oder des Zylinders entsprechen dabei der Vorstellung der parallelen Projektionsstrahlen, die in der Schräge liegende Schnittebene dem Objekt, und die in der Grundrißebene, die der Bildebene entspricht, liegende Fläche, dem Bild. Die geometrischen Beziehungen beider Flächen werden so beschrieben: Die Affinität ist gegeben durch die Richtung der Projektionsstrahlen und durch mindestens ein entsprechendes Punktepaar des Objektes und des Bildes. . jedem Punkt des Objektes ist auf dem Projektionsstrahl ein Bildpunkt zugeordnet. . die Verbindungslinien Orginalpunkte und Bildpunkte sind zueinander parallel. . einander entsprechende Geraden sind sich affin zugeordnet, d.h. sie schneiden sich auf der Affinitätsachse. . Teilverhältnisse einer Strecke bleiben erhalten. In ähnlicher Weise beschreibt die Kollineation den Zusammenhang zweier Flächen in der Perspektive. s.S.36: Kollineation In der 2 - Tafelprojektion kann der Zusammenhang von Objekt, Bild und wahrer Größe des Objektes erläutert werden. Seite 35 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Kollineationszentrum Der Körperschnitt des Kegels und die Kollineation S Kollineationsachse Mit der Kollineation ist der Zusammenhang zweier Flächen beschrieben, die in zwei sich schneidenden Ebenen (schräge Ebene und Grundrißebene) liegen. Da die konstruktive Beziehung beider Ebenen, die einer geraden Pyramide oder einem geraden Kegel zugeordnet sind, beschrieben wird, ist hier ein Vorgang beschrieben, der generell die konstruktive Beziehung von Objekt und Bild in der Perspektive verständlich machen kann. Der Kegel entspricht dabei der Vorstellung des Sehkegels, die in der Schräge liegende Schnit- tebene dem Objekt, und die in der Grundrißebene, die der Bildebene entspricht, liegende Fläche, dem Bild. . einander entsprechende Geraden schneiden sich in der Kollineationsachse. . das Teilverhältnis einer Strecke durch einen Punkt verändert sich im Allgemeinen. s.S. 35: Affinität Die geometrischen Beziehungen beider Flächen werden so beschrieben: Die perspektive Kollineation ist gegeben durch In der 2 - Tafelprojektion kann der Zusammendas Kollineationszentrum S, die hang von Objekt, Bild und wahrer Größe des Kollineationsachse und durch mindestens ein Objektes erläutert werden. entsprechendes Punktepaar. . jedem Punkt des Objektes ist auf dem Kollineationsstrahl ein Bildpunkt zugeordnet. Seite 36 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Körperschnitt mit Hilfe der Durchstoßpunkte Die Schnittfläche von schrägem Prisma und schräger Ebene wird punktweise ermittelt. Dazu werden, ausgehend vom Grundrißbild, alle Durchstoßpunkte der Körperkanten des Prismas mit der schrägen Ebene dargestellt. s.S. 28: Durchstoßpunkt einer beliebigen Geraden durch eine Ebene Die Verbindung der Durchstoßpunkte miteinander ergibt das Bild der Schnittfläche im Aufriß und im Grundriß. Die wahre Größe der Schnittfläche ist über die Vorstellung der affinen Beziehung von Schnittfläche, wie sie im Grundriß gegeben ist und der, um die Affinitätsache in den Grundriß eingeklappten Fläche (= wahre Größe der Fläche) konstruierbar. Zuvor aber ist die wahre Höhe eines Punktes der Schnittfläche zu bestimmen s.S.26: Abstand eines Punktes von einer Ebene und in die Ausklappung zu übernehmen. Seite 37 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Körperschnitt mit Hilfe der 3. Projektion Die 3.Projektion ergibt sich aus der Vorstellung einer 1.projizierenden Ebene, die senkrecht zur Grundrisspur der schrägen Ebene steht. In den Grundriß geklappt, ergibt sich das Bild der Pyramide und der Spur der schrägen Ebene in dieser Projektion (die Höhen sind dem Aufriß zu entnehmen). Die Schnittpunkte der Pyramide mit der schrägen Ebene, die in dieser Projektion als Linie erscheint,können dem Grundriß senkrecht zugeordnet werden und ergeben dort, auf den entsprechenden Körperkanten, das Bild der Schnittfläche im Grundriß. Die Grundrißpunkte senkrecht dem Aufriß zugeordnet ergeben das Bild der Schnittfläche im Aufriß. Die wahre Größe der Schnittfläche ist mit Hilfe der Zusammenschau von Grundrißbild und Bild der Schnittfläche in der 3.Projektion ermittelt. Dazu wird das Bild der Schnittfläche in der 3.Projektion um den Drehpunkt in den Grundriß geklappt und senkrecht den entsprechenden, im Grundriß gegebenen, Punkten der Schnittfläche zugeordnet. Seite 38 Arten von Durchdringungen © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Wir unterscheiden drei Arten der Durchdringung zweier Körper (am Bsp. die Durchdringung zweier Prismen). Berührung Bei der Berührung schneiden sich die Achsen der Körper. Es entstehen zwei sich schneidende Schnittflächen. Verzapfung Bei der Verzapfung schneiden sich die Achsen der Körper nicht. Es entsteht eine geschlossene Schnittfläche. Durchbohrung Bei der Durchbohrung können sich die Achsen der Körper schneiden. Es entstehen zwei Schnittflächen. Seite 39 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Durchdringung und Höhenebenenverfahren Je nach Art der Körper und nach den Bildern in den Rissen sind bei Durchdringungen verschiedene Konstruktionsverfahren zu wählen. wir unterscheiden das : Höhenebenen-, Mantelebenen-, Parallelebenen- und Pendelebenenverfahren. Die Durchbohrung von Prisma und Pyramide wird mit Hilfe des Höhenebenenverfahrens konstruiert. Dabei legt man in Höhe der aufrißprojizierenden Körperkanten des Prismas Höhenebenen, deren Schnittflächen mit der Pyramide im Grundriß dargestellt werden können. Die Schnittpunkte der aufrißprojizierenden Körperkanten des Prismas mit den Höhenebenen sind Punkte der Schnittebene. Seite 40 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Durchdringung und Mantelebenenverfahren A H B G C D F E Die Durchdringung von Prisma und Pyramide wird mit Hilfe des Mantelebenenverfahrens konstruiert. Dies gilt für die Punkte A,C und E. Die Aufrißpunkte F und H können direkt und die Punkte B und D über den Seitenriß als Punkte der Durchdringungskurve im Grundriß dargestellt werden. Seite 41 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Punkt P Durchdringung und Parallelebenenverfahren A Gegeben sind zwei, sich durchdringende Prismen im Grund- und Aufriß. Gesucht ist die Durchdringung und die Abwicklung des durchdrungenen Prismas. Konstruktionsschritte : 1. Bei der Aufgabe wird, um die Durchdringung zu bestimmen, eine Ebene gewählt, die parallel zu beiden Prismen liegt. Die Spur dieser Ebene im Grundriß kann mit Hilfe der Konstruktion zweier sich schneidender Geraden bestimmt werden.Dazu muß eine Kante des Prismas parallel durch einen beliebigen Punkt des anderen Prismas ( am Bsp. Punkt P ) verschoben werden. Im Aufriß ist der Durchstoßpunkt dieser Geraden mit der Höhe 0 gegeben, der dem Grundrißbild zugeordnet werden kann. Damit ist die Spur s der Ebene gegeben. 2. Die gefundene Ebene wird mit der Grundris- spur parallel durch den Grundrisspunkt A des einen Prismas verschoben. Mit dem anderen Prisma geschnitten ergeben sich Mantellinien und die Durchdringungspunkte mit der Kante über dem entsprechenden Grundrißpunkt.Die Durchdringungspunkte im Aufriß erhält man durch senkrechte Zuordnung. 3. Die Konstruktion wird für die anderen Punkte des einen Prismas wiederholt. Dadurch sind alle Durchstoßpunkte des einen Prismas mit dem anderen gegeben. 4. Für zwei Körperkanten des anderen Prismas sind ebenfalls die Durchstoßpunkte mit der gleichen Konstruktion zu bestimmen.Dadurch sind die Bilder beider Durchdringungsflächen gegeben. Seite 42 Durchdringung und Pendelebenenverfahren © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Wie bei der Frage, welche Durchstoßpunkte hat eine beliebige Gerade mit einer Pyramide, s.S. 29: Durchstoßpunkt einer beliebigen Geraden durch zwei Ebenen. Pendelebenenverfahren Durchtsoßpunkt der Pendelachse S2 ist bei folgendem Beispiel das Pendelebenenverfahren auf die Frage der Durchdringung zweier Pyramiden angewandt. Eine Körperkante der einen Pyramide entspricht einer beliebigen Gerade, deren Durchdringungspunkte mit der anderen Pyramide zu konstruieren sind. Alle Durchdringungspunkte aller Körperkanten ergeben die geschlossene Schnittfläche der Verzapfung von Pyramide und Pyramide. Die Basisdreiecke der Pyramiden liegen im Grundriß und in einer schrägen Ebene, deren Spuren im Grund- und Aufriß bestimmt werden Können. Die Pendelachse ist durch die Verbindung beider Pyramidenspitzen P1 und P2 gegeben und durch die Durchstoßpunkte S1 im Grundriß und S2 in der schrägen Ebene. Für die Durchstoßpunkte der Körperkante BP2 durch die Deckflächen der Pyramide konstruieren wir eine Pendelebene, die wir durch die Pendelachse und den Punkt B festlegen. Die Grundrisspur dieser Pendelebene mit dem Basisdreieck der Pyramide geschnitten ergibt die Punkte T1 und T2, die mit der Pyramidenspitze P1 verbunden, die Durchstoßpunkte 1 und 2 der Körperkante mit der Pyramide ergeben. Analog sind die anderen Durchstoßpunkte zu konstruieren. B P1 A 1 2 P2 T1 T2 S1 Seite 43 Durchdringung und Pendelebenenverfahren © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I S2 B C A F E S1 P2 P1 D Konstruktionsschritte in der 2-Tafelprojektion: Gesucht sind zunächst die Spuren der Ebene, die durch das Basisdreieck ABC der Pyramide gegeben sind. Die Verlängerung der Geraden BC auf die x - Achse im Aufriß ergibt im Grundriß den Durchstoßpunkt D der Geraden = ein Spurpunkt. Die Verbindungsgerade P1 und P2 im Grundriß schneidet die gegebene Spur der Ebene, die Ebenso findet man durch die Verlängerung der das Basisdreieck ABC bestimmt. Geraden BA einen weiteren Spurpunkt E. Die Schnittfläche einer auf dieser VerbindungsDurch beide Spurpunkte E und D ist die Grund- gerade senkrecht stehenden Ebene mit der risspur der Ebene ABC gegeben. durch die Spuren gegebenen schrägen Ebene, Ausgehend von der Grundrißgeraden BA findet ist im Aufriß darzustellen. Die Verbindungsgeman im Aufriß den Spurpunkt F. Mit dem Schnitt- rade der Pyramidenspitzen mit dem Bild der punkt der Grundrisspur mit der x - Achse ist da- Schnittgeraden im Aufriß geschnitten, ergibt den mit auch die Aufrisspur der Ebene ABC gegeben. Durchstoßpunkt S2. Im nächsten Schritt gehen wir von der Gerade Die Höhe 0 der Verbindungsgeraden im Aufriß aus, die durch die Spitzen P1 und P2 der Pyradem Grundrißbild zugeordnet, ergibt den Durchmiden gegeben ist. Gesucht sind die Durchstoß- stoßpunkt S1. punkte dieser im Grundriß und in der durch das Basisdreieck ABC bestimmten Ebene. Seite 44 Durchdringung und Pendelebenenverfahren © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I S2 P1 B 8 C P2 7 6 5 S1 S1 T1 T2 1 P1 Mit der Pendelachse S2, P1 und P2 und dem ordnung sind die entsprechenden Aufrisspunkte Punkt B der einen Pyramide ist die Pendelebene festzulegen. durch B gegeben. Die Grundrisspur der Pendelebene schneidet das Grundrissdreieck der anderen Pyramide in den Punkten T1 und T2, diese Punkte mit der Pyramidenspitze P1 verbunden ergeben auf der Geraden B P2 zwei Durchstosspunkte 1 und 2 der gesuchten Schnittkurve im Grundriss. Durch senkrechte Zu- Analog dem vorhergehenden Beispiel mit der Konstruktion der Pendelebene durch den Punkt B ist in gleicher Weise mit dem Punkt C eine Pendelebene bestimmt und die Durchstoßpunkte 3 und 4 der Körperkante der einen mit der anderen Pyramide festgelegt. Ausgehend von der Grundrisspur der Pendelebene durch D und durch E sind im Aufriß die Durchstosspunkte 5 und 6 und 7 und 8 gegeben. Dadurch ist die Durchdringungskurve durch 8 Durchstosspunkte gegeben. Die Pendelebene durch den Punkt A ergibt im Grundriß k e i n e Durchstosspunkte. Seite 45 Abwicklung mit Hilfe der Höhenzuordnung © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Deckfläche A ausgehend von Punkt A 1 2 3 Seitenflächen 4 Grundfläche Die Abwicklungen von ebenflächigen Körpern mit mehrfach geknickten oder gefalteten Flächen werden in der Architektur für die Herstellung von Dächern, Faltwerken und vielen Einzelelementen verwendet. Vorallem im Modellbau sind Abwicklungen von großem Interesse, weil der in der Fläche abgewickelte Körper - gegenüber der Konstruktionszeichnung eventuell vergrößert - dort ausgeschnitten und in den Raum gefaltet werden kann. Um die Abwicklung eines Körpers zeichnen zu können, sind die wahren Größen der Teilflächen des Körpers zu definieren. Für den Modellbau ist darauf achten, daß die Flächen möglichst zusammenhängend in der Abwicklung dargestellt sind. Die Längen der Geraden der Grundrißfläche sind Am Beispiel ist die Schnittfläche des schräganim Uhrzeigersinn ( ausgehend von Punkt A ) auf geschnittenen Prismas mit Hilfe der 3. Projektion eine Waagrechte zu übertragen. ermittelt. In den Grundriß geklappt, ist die wahre Die wahren Höhen können auf Senkrechte über Größe dieser dargestellt. den entsprechenden Eckpunkten zugeordnet Die Grundrißfläche des Prismas ist bereits werden. gegeben. Die Grundfläche und die Deckfläche finden wir durch Zirkelschläge um die entsprechenden Die wahren Größen der Körperkanten sind im Punkte mit den gegebenen Längen. Aufriß gegeben. Seite 46 Abwicklung durch Grundrißklappung © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Am Beispiel wird die Schnittfläche des schrägangeschnittenen Prismas in der 3.Projektion ermittelt. In den Grundriß geklappt ist die wahre Größe dieser gegeben. Die Grundrißfläche ist bereits in wahrer Größe gegeben. Die wahren Größen der senkrechten Deckflächen des Prismenstumpfes sind gegeben, wenn man sich vorstellt, daß jede Fläche um die entsprechende Grundrisspur in den Grundriß geklappt wird. Dabei wandern die Punkte der Flächen, deren Höhen im Aufriß gegeben sind auf Kreisbögen, die in der Projektion als Linien, senkrecht zur Drehachse erscheinen. Der Abwicklung ist noch die wahre Größe der Schnittfläche zuzuordnen. Seite 47 Abwicklung mit Hilfe des Querschnittes © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I A Die Querschnittfläche wird in den Grundriß geFür die Abwicklung wird eine 1.projizierende klappt in wahrer Größe dargestellt. Ebene parallel zu den Kanten des Prismas gewählt. In der Ebene erscheint der Querschnitt des Körpers als Gerade und die Körperkanten in wahrer Größe. Für die Konstruktion der wahren Größe der Deckfläche s.S. 33: Wahre Größe einer Ebene. Konstruktion mit Stützdreieck. Die wahren Breiten der Querschnittfläche sind auf eine Waagrechte (ausgehend von A) angetragen und über und unterhalb der Eckpunkte sind die wahren Längen der entsprechenden Körperkanten des Prismas übertragen. Die Bodenfläche kann wie die Deckfläche mit dem Zirkel an die entsprechenden Kanten angetragen werden. Hier nicht darbestellt. Zur Abwicklung : Seite 48 Abwicklung einer Pyramide über die Spitze © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Pyramidenspitze S Gegeben ist eine regelmäßige Pyramide in den Tafeln und eine schräge, 2. - projizierende Fläche. Gesucht ist die Schnittfläche und die Abwicklung des Pyramidenstumpfes. Die Schnittfläche im Grundriß ist aus der Darstellung im Aufriß und im Seitenriß gegeben. Die wahre Größe der Schnittfläche ist durch Grundrißdrehung gegeben. Die wahren Größen der Körperkanten des Prismas sind im Aufriß durch die Mongsche Drehung gegeben. Zur Abwicklung werden ausgehend von der Pyramidenspitze S die wahren Längen der Pyramidenkanten durch einen Kreisbogen dargestellt. Auf den Kreisbogen werden die wahren Längen der Grundrißfigur übertragen. Damit sind die Deckflächen der Pyramide in wahrer Größe gegeben. Von der Spitze aus sind dann die wahren Längen bis zu dem Pyramidenstupf darzustellen und die Grundrißfläche und die Schnittfläche in wahrer Größe an die entsprechenden Punkte zu übertragen. Seite 49 Schräge Projektionen oder Axonometrien allgemein © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Darstellung eines Würfels in Grundrißaxonometrie Aufrißaxonometrie DIN 5 Isometrie senkrechter Axonometrie Axonometrische Darstellungen prägen die Architekturzeichnung des 20. Jahrhunderts. Das Bauhaus beschränkt sich fast ausschließlich auf diese Art der Darstellung. Die getuschte Bürozeichnung wird "Programm" und die Axonometrie zu der Ausdrucksform. Durch die parallele Projektion ist ein Verfahren gegeben, das die Zeichnung unabhängig vom Betrachter in einem selbst bestimmten, virtuellen System erscheinen läßt und die Konzeption der Architektur betont. Die Zeichnung hat in diesem Sinne "metaarchi- tektonische Funktion". z.B. Peter Eisenman benutzt die axonometrische Darstellung als eine Art "Denkwerkzeug", er weist ihr architektur - theoretische Aufgaben zu. Zitat : " ... systematisch abgewandelt, wird eine Einzelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voyeurs versetzt, der den Gestalt - Jongleur bei seiner Arbeit beobachtet ... " Seite 50 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Beispiel 1 Projektionsstrahl Beispiel 2 Projektionsstrahl Objektpunkt P Objektpunkt Bildpunkt P P Bildpunkt kein räumliches Bild entsteht. Nach der Festlegung ist jedem Objektpunkt ein Bildpunkt eindeutig zugeordnet und das axonometrische Bild ist geraden- und parallelentreu, d.h Geraden von Objekt und Bild entsprechen sich und parallele Objektgeraden bleiben parallele Bildgeraden. Veränderung der Lage des Objektes zur Bildebene als Veränderung Das axonometrische Bild eines räumlichen Ob- der Winkel der Koordinatenachsen zueinanjektes entsteht durch schräge Parallelprojektion der und in eine schräge Bildebene. - als Veränderung der Objektlängen im Verhälts.S. 9: Die Projektionsarten nis zu den Bildlängen = Verkürzungsverhältnisse. Der Winkel der einfallenden Projektionsstrahvgl. Beispiel 1 und Beispiel 2 len und die Lage des Objektes zur Bildebene In der Bildebene, die der frei gewählten, schrä- . Die Winkel der Koordinatenachsen und können frei gewählt werden. gen Ebene entspricht und in der die Projektion . Die Verkürzungsverhältnisse Ausnahme: des Objektes, auf Grund o.g. Bedingungen werden im Weiteren unabhängig voneinander Die Richtung der Projektionsstrahlen darf zu keierscheint, erscheint die Veränderung des Winin der Bildebene festgelegt. ner Objektfläche senkrecht verlaufen, da sonst kels der einfallenden Projektionsstrahlen und die Sie bestimmen im ursprünglichen Koordinaten- P raum die Drehung der Bildebene und die Richtung der Projektionsstrahlen. Sie bestimmen auch die Art der Axonometrie. Wir unterscheiden die allgemeine Axonometrie, die die Wahl der Variablen freistellt und die Arten der Axonometrie, die durch Konventionen festgelegt sind ( wie die Grundrißaxonometrie, die Aufrißaxonometrie, die Isometrie und die DIN 5). Welche Art der Axonometrie verwendet werden soll, kann nur im Zusammenhang von Anschaulichkeit der Zeichnung und Verwendungszweck entschieden werden. Seite 51 Konstruktionsverfahren. Das Einschneideverfahren © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I In der Bildebene. Festlegung der Koordinatenachsen und der Rissachsen Zuordnung der -in den Rissen- gegebenen Objektpunkte, in die -durch die Vorgaben der Trimetrie- festgelegte Bildebene. z z Horizontale y y x x Wegen der seitenrichtigen Zuordnung sind die Bilder der gegebenen Risse über die Spurrichtung gespiegelt. Mit dem Einschneideverfahren können schräge Projektionen oder Axonometrien auf der Grundlage gegebener Risse konstruiert werden. Die Bilder der Rissachsen sind den gewählten Koordinatenachsen zugeordnet. Das axonometrische Bild eines Punktes entsteht, wenn die Bilder des Punktes, wie sie in den Zunächst werden die Winkel der Koordinaten- Rissen gegeben sind, durch Ordner, die jeweils achsen zur Horizontale festgelegt. parallel zu den Fluchten sind, einander zugeordDie z - Achse bleibt senkrecht , die Drehung von net werden. x- und y-Achse oder die Winkel zu der horizonta- Das axonometrische Bild des Objektes ist durch len Linie sind frei wählbar. Zuordnung aller Punkte gegeben. Dadurch sind die Spuren und die in die Zeichenebene geklappten Bilder der KoordinatenDurch die Drehung eines Risses sind die Verflächen gegeben (Konstruktion mit Hilfe des kürzungsverhältnisse zweier KoordinatenrichThaleskreises). Die zugeordneten Risse sind so tungen und die Drehung des zweiten Risses in die Zeichenebene zu legen, daß der 0- Punkt gegeben, was wiederum die Verkürzung der des Risses in der Flucht der Achse liegt, die im dritten Koordinatenachse bestimmt. entsprechenden Riss senkrecht steht. Konstruktionsmöglichkeiten Gesucht : Winkel der Koordinatenachsen: x - Achse 31 Grad und y - Achse 17 Grad x.y.z und Objektgrundriß Aufriß zur Horizontale x.y.z und Objektseitenriß Grundriß Verkürzungsverhältnisse: x.y.z und Objektaufriß Grundriß x : y : z = 0,91 : 0,71 : 0,81 x.y.z und Objektgrundriß Seitenriß x.y.z und Objektaufriß Seitenriß Wir unterscheiden : x.y.z und Objektseitenriß Aufriß - trimetrische Darstellungen mit 3 verschiedenen x.z und Objektgrundriß und Seitenriß y Verkürzungsverhältnissen y.z und Objektgrundriß und Aufriß x - dimetrische Darstellungen mit 2 verschiedenen Verkürzungsverhältnissen und Die Koordinatenachsen und die Verkürzungsver- - isometrische Darstellungen mit gleichen Verkürhältnisse entsprechen im Bildbeispiel der Trime- zungsverhältnissen trie, die in dem vorliegenden Skript wegen ihrer hoher Anschaulichkeit häufig verwendet ist. trimetrische Axonometrie Gegeben : Seite 52 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I ZIG - ZAG von Gerrit Thomas Rietveld. Bildvorgabe Gegeben ist im Grund- und Aufriß der Stuhl: Modell: Zig - Zag Designer: Gerrit Thomas Rietveld Jahr: !934 Material: Buche natur, unpoliert oder naturfarbig poliert Maße: s. Zeichnung Hersteller: Cassina, Mailand Gesucht ist dessen Darstellung in den verschiedenen Axonometrieen. Vergleichen Sie die Bildwirkung des Objektes in den Darstellungsarten. Seite 53 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I z Grundrißaxonometrie Horizontale x y Grundriß Bei der Grundrißaxonometrie liegt die Bildebene parallel zur Grundrißebene des Objektes. Dadurch bleiben die Maße und Winkel des Objektgrundrisses oder aller dazu parallelen Ebenen bei der Abbildung erhalten. Die Projektionsstrahlen werden meist so gewählt, daß die Höhen um die Hälfte verkürzt erscheinen. Grundrißaxonometrie Winkel der Koordinatenachsen: x - Achse 30 Grad zur Horizontale Verkürzungsverhältnisse: x : y : z = 1 : 1 : 0.5 Die Grundrißaxonometrie ergibt eine starke Aufsicht des Objektes. Geeignet für größere und im Grundriß komplizierte Objekte (Leitungspläne, Lagepläne). Seite 54 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Grundrißaxonometrie Aufrißaxonometrie DIN 5 Grundrißaxometrie Isometrie Die Darstellung des Stuhles in der Grundrißaxonometrie Seite 55 Aufrißaxonometrie © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I z Aufriß x Horizontale y Bei der Aufrißaxonometrie liegt die Bildebene parallel zur Aufrißebene des Objektes. Dadurch bleiben die Maße und Winkel der Aufrißebene des Objektes, oder die der dazu parallelen Ebenen, bei der Abbildung erhalten. Alle anderen Ebenen erscheinen durch die schräge Projektion, je nach Richtung der Projektionsstrahlen, verzerrt. Die Projektionsstrahlen werden meist so gewählt, daß die Tiefen um die Hälfte verkürzt erschei- nen. Aufrißaxonometrie Winkel der Koordinatenachsen: y - Achse 45 Grad zur Horizontale Verkürzungsverhältnisse: x : y : z = 1 : 0.5 : 1 Die Aufrißaxonometrie ist eine einfache Darstellung mit guter Anschaulichkeit, allerdings mit geringer Tiefenwirkung. Seite 56 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Grundrißaxonometrie Aufrißaxonometrie DIN 5 Aufrißaxonometrie Isometrie Die Darstellung des Stuhles in der Aufrißaxonometrie Seite 57 DIN 5 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I z Horizontale y x Anschauliche Axonometrien entstehen, wenn die Bildebene und die Drehung der Rissachsen so gewählt werden, daß nur zwei verschiedene Verkürzungen entstehen = dimetrische Axonometrie. Das ist der Fall, wenn die Öffnungswinkel der Koordinatenachsen in der Bildebene 131,5 Grad, 131,5 Grad und 97 Grad und die damit gegebenen Verkürzungen 0,94 : 0,47 : 0,94 betragen. Die in der DIN angegebenen Winkel und Verkürzungen sind Näherungswerte. DIN 5 Winkel der Koordinatenachsen: y - Achse 7 Grad zur Horizontale und x - Achse 42 Grad zur Horizontale Verkürzungsverhältnisse: x : y : z = 1 : 0.5 : 1 Seite 58 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Grundrißaxonometrie Aufrißaxonometrie DIN 5 Din 5 Isometrie Die Darstellung des Stuhles in der DIN 5 Seite 59 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Isometrie z Horizontale y x Die Bildebene und die Drehung der Rissachsen wird so gewählt, daß alle Achsen in gleichem Maße verkürzt werden = isometrische Axonometrie. Das ist der Fall, wenn alle von den Achsen eingeschlossenen Winkel gleich groß sind, also 120 Grad.Das Spurendreieck der Bildebene wird gleichseitig. Die Verkürzung beträgt jeweils 2/3 oder 0.8165. In der Regel werden die achsenparallelen Kanten jedoch unverkürzt dargestellt. Isometrie Winkel der Koordinatenachsen: x - Achse 30 Grad zur Horizontale y - Achse 30 Grad zur Horizontale Verkürzungen: x:y:z=1:1:1 Seite 60 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Grundrißaxonometrie Aufrißaxonometrie DIN 5 Isometrie Isometrie Gesucht ist die Darstellung des Stuhles in der Isometrie Seite 61 Senkrechte Axonometrie. allgemein © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I z Die senkrechte oder orthogonale Axonometrie ermöglicht eine sehr gute Anschaulichkeit. Die Konstruktion ist im Verhältnis zu den anderen Axonometrien allerdings aufwendig. Konstruktionsschritte : In dem von den Achsen x, y und z gebildeten Raum, liegt eine beliebige Ebene. Die Achsen werden in senkrechter Richtung auf diese Ebene projiziert. Man erhält innerhalb des Spurendreiecks die Achsen x y und z der senkrechten Axonometrie. Um einen Körper abbilden zu können, werden die Bildtafeln des gefundenen Spurendreiecks in die Bildebenen eingedreht.Die Bildebenen liegen dabei in der durch das Spurendreieck gebildeten Ebene. Dabei wandern die Punkte, z.B. der 0 - Punkt auf einem Kreisbogen, der senkrecht zur Drehachse steht. Drehachse ist die jeweilige Spur. Der geometrische Ort ist der Thaleskreis über der Spur in der Fläche des Spurendreiecks. Bei der Eindrehung der Bildtafel (Bsp. Grundrißfläche) wandern die, in ihr enthaltenen, Punkte und Strecken ebenfalls in die eingedrehte Bildtafel. Das Bild der einzudrehenden Bildtafel ist affin zu dem Bild der eingedrehten Bildtafel. Die Affinitätsrichtung (Zuordnungsrichtung) ist durch die Zuordnung von 0 - Punkt und eingedrehtem Nullpunkt gegeben. y x Seite 62 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Senkrechte Axonometrie. in der Zeichenebene Die im Raum (Trimetrie) erläuterten Zusammenhänge der konstruktiven Bedingungen der senkrechten Axonometrie, werden bei der Anwendung in der, dem Spurendreieck entsprechenden, projizierten Ansicht sichtbar. Konstruktionsschritte : Festlegung eines beliebigen Dreieckes Die Achsen innerhalb des gegebenen Dreieckes, die zu den Koordinatenachsen der senkrechten Axonometrie werden, stehen senkrecht auf der jeweils gegenüberliegenden Seite. Der O-Punkt der ausgedrehten Bildtafel ( kann für den Grund- Auf- und Seitenriß gelten ) ist durch die Senkrechte zur jeweiligen Spur und durch den Thaleskreis über dieser bestimmt. Der in den Bildtafeln gegebene Grund- und Aufriß (am Bsp. ist ein Würfel im Grund- und Aufriß gegeben ) ist dann, mit Hilfe der zu den Spuren senkrechten Zuordnung in das Bild der senkrechten Axonometrie zu übertragen. Dabei geht man vom Grundriß in das Bild, vom Bild zum Auriß, wo die gegebenen Höhen ergänzt werden und vom Aufriß zurück in das Bild. Die Zuordnungsrichtung steht senkrecht auf der jeweiligen Spur. Seite 63 Zentrale Projektionen oder Perspektiven. allgemein © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Hisao Suzuki Architekturfotografie Philologische Fakultät von Albert Noguerol und Pilar Diez. Santiago de Compostela. Haupttreppe. 1991 " ... woher stammt das Mißtrauen gegen jene Architekturzeichnungen, die das Auge bestechen, die durch farbliche Effekte auffallen, die schön sind ? Gibt es über Mißfallen und Enttäuschungen hinaus grundsätzliche Einwände, die es verbieten, dieses das Auge direkt ansprechende Medium zu verwenden ? Die Perspektive ? ... " Zitat W. Oechslin in Daidalos 1989 Seite 64 Zentrale Projektionen oder Perspektiven © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Bildebene Augpunkt Bild Die Perspektive erreicht ein hohes Maß an Anschaulichkeit. Die Aufgabe der Perspektive wäre erfüllt, wenn das perspektive Bild den gleichen, optischen Eindruck, wie die Betrachtung des Orginales hervorrufen würde. Aus der Kenntnis aber weniger Tatsachen, daß sich die Vorstellung des Raumes hinter dem Betrachter schließt, Raum entscheidend durch die Augbewegung und die Eigenbewegung des Betrachters, durch akustische und ander Phänomene bestimmt ist, wird deutlich, wie grundsätzlich Ob- verschieden die Bildwahrnehmung von Raum und die Raumwahrnehmung tatsächlich sind. Sieht man von diesen Phänomenen ab, so entsteht mit Hilfe der perspektiven Konstruktion ein erstaunlich naturnahes Bild. dem Orginalpunkt zusammenfällt. Werden nun nach und nach alle Punkte des Gegenstandes mit dem Sehstrahl abgetastet, so entsteht auf der Bildebene ein Bild, dessen Form mit dem Gegenstand identisch erscheint. Der beschriebene Vorgang entspricht einer ProDabei gehen wir von einem fixierten, einäugigen jektion. Die Sehstrahlen entsprechen den ProjekAugpunkt aus und stellen uns zwischen Betrach- tionsstrahlen die ausgehend vom Augpunkt, dem ter und Objekt eine Ebene, die sog. Bildebene Projektionszentrum, auf der Bildebene Bildpunkte vor. Fixiert der Betrachter einen Objektpunkt, so erzeugen.Perspektive Bilder entstehen durch durchstößt der Sehstrahl die Bildebene an einem Zentralprojektion. Punkt, der aus der Sicht des Betrachters mit Seite 65 Zentralperspektive. Übereckperspektive. Perspektive bei geneigter Bildebene © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Zentralperspektive Wir unterscheiden drei Arten der Perspektive. Übereckperspektive Bei der Zentralperspektive verlaufen zwei Richtungen des abzubildenden orthogonalen Körpers parallel zur Bildebene ( am Bsp. die Breite und die Höhe ), die Kanten dieser Richtung haben ihren Fluchtpunkt im Unendlichen, d.h die Bilder dieser Kanten bleiben parallel. Für die dritte Richtung ( am Bsp. die Tiefe ) ergibt sich ein im Endlich liegender Fluchtpunkt, der zentrale Fluchtpunkt. Perspektive bei geneigter Bildebene Bei der Übereckperspektive verläuft eine Richtung des abzubildenden orthogonalen Körpers parallel zur Bildebene ( am Bsp. die Höhe ), die Bilder dieser Kanten bleiben parallel. Für die anderen zwei rechtwinklig aufeinanderstehenden Richtungen ergeben sich 2 Fluchtpunkte. daher Perspektive mit 2 Fluchtpunkten oder Übereckperspektive. Bei der Perspektive bei geneigter Bildebene verlaufen die Kanten des Würfels in drei rechtwinklig aufeinanderstehenden Richtungen. Alle Kanten einer Richtung verlaufen parallel und haben einen gemeinsamen Fluchtpunkt. Drei Richtungen definieren 3 verschiedene Fluchtpunkte bei allgemeiner Lage eines orthogonalen Körpers in der Perspektive. Seite 66 Begriffe © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Objekt hinter der Bildebene Hauptpunkt Objekt in der Bildebene Objekt vor der Bildebene H Hauptsehstrahl Augpunkt Spur s Das abzubildende Objekt. In der zeichnerischen Perspektive ist es sinnvoll Objekte darzustellen, die linear begrenzt, meist rechtwinklig und gleichmäßig sind. Bildebene strahl gegeben ist, verändert sich die Größe des perspektiven Bildes (Skalierung). Die Schnittspur mit der Bildebne ist die punkten. Die zur Grundrißebene und zur BildeSpur s. In ihr fallen Objektpunkte und Bildpunkte bene parallele Ebene, in der die Distanz, der zusammen. Augpunkt und der Hauptpunkt liegen heißt SaDer Hauptsehstrahl steht senkrecht zur Bildebne gittalebene. Die zur Bildebene parallele Ebene, und durchstößt diese im Hauptpunkt H. Durch Die Horizontebene in der Augpunkt und Distanz liegen, heißt VerDer Augpunkt die Veränderung des Abstandes von Augpunkt liegt parallel zur Standebene, enthält den Augschwindugnsebene. In ihr liegende Objektpunkt oder das Projektionszentrum liegt auf einer Senk- zu Standebene, der durch die Distanz gegeben punkt und beschreibt als Schnittspur mit der haben ihr Bild im Unendlichen.Um die räumliche rechten (Distanz) über dem Standpunkt in der ist, entstehen verschieden Objektansichten im Bildebene den Horizont. Vorstellung der perspektiven Anlage zeichnerisch Horizontebene. Seine Lage ist entscheidend für perspektiven Bild (Froschperspektive, Normalperdarstellen zu können, werden die Stand- und die das perspektive Bild. Der Augpunkt bestimmt die spektive oder Vogelperspektive). Die Bildebene Horizontebne in die Bildebene engeklappt. Richtung des, von ihm ausgehenden wird im Allgemeinen senkrecht zur Standebene Sehstrahlenbündels. Die Standebene angenommen. Auf ihr entsteht das perspektive s.S. 69: Klappung Durch die Veränderung des Abstandes von entspricht der Grundrißebene, in der die räumli- Bild als Durchdringung der Projektionsstrahlen Augpunkt zu Bildebene, der durch den Hauptseh- che Lage des Objektes beschrieben ist. zwischen Projektionszentrum und den ObjektSeite 67 Verzerrung © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I 45 Grad Winkelabweichung entspricht einer Verzerrung von 100 % 30 Grad Winkelabweichung entspricht einer Verzerrung von 33 % 15 Grad Winkelabweichung entspricht einer Verzerrung von 7% Bildebene Bildkugel entspricht der kugelförmig gekrümmten Netzhaut Die Verschiedenheit des Sehens von der perspektiven Konstruktion, am Bsp. die Abweichung der gekrümmten Netzhaut zur ebenen Projektionsfläche der Bildebene, führt dazu, daß perspektive Bilder verzerrt erscheinen. Dabei nimmt die Verzerrung der abgebildeten Objektelemente mit dem Abstand zum Hauptpunkt zu. Die Verzerrung entspricht dem Tangens - Quadrat der Winkelabweichung vom Hauptsehstrahl. Um bei der Perspektive anschauliche Bilder zu bekommen, sollte der Sehwinkel bei Aussenraumperspektiven nicht größer als 60 Grad, bei Innenraumperspektiven nicht größer als 90 Grad sein, d.h. ein abzubildendes Objekt sollte innerhalb eines Sehkegels liegen, der sich 60 bzw. 90 Grad öffnet. Die Achse dieses Kegels ist der Hauptsehstrahl. Seite 68 Klappung © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Horizont Spur. Bildebene eingeklappter Augpunkt Die Standebene und die Horizontebene stehen senkrecht auf der Bildebene. Beim Zeichnen entspricht das Zeichenblatt der Bildebene. Voraussetzung ist, daß die Horizontebene und die Standebene in die Bildebene = Zeichenebene eingeklappt werden. Klappachse für beide Ebenen ist die jeweilige Spur mit der Bildebene. Die Verschwindungsebene geht durch den Augpunkt, steht senkrecht auf der Standebene und liegt parallel zur Bildebene. Bei der Klappung erscheint die Verschwindungsebene als Spur mit der Bildebene = Verschschwindungsgerade. Objektpunkte, die hinter der Verschwindungsebene liegen, können nicht gesehen werden. eingeklappter Standort auf Verschwindungsgerade Seite 69 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Elemente der Perspektive. Darstellung eines Punktes Horizont Bildebene = Spur Objektpunkt Bildpunkt P P geklappter Grundrißpunkt P perspektiver Bildpunkt Grundrißpunkt P Augpunkt Punkt P liegt in der Grundrißebene. Der Projektionsstrahl, ausgehend vom Augpunkt, geht durch den Objektpunkt P in der Grundrißebene und schneidet die Bildebene im Bildpunkt P. Konstruktion : Augpunkt - Grundriß - perspektives Bild Bei der Klappung des Grundrißpunktes und des Augpunktes in die Bildebene erscheint auch der geklappte Sehstrahl, als verlängerte Verbindung des Bildpunktes P, des geklappten Grundriß- und des Augpunktes. Seite 70 Darstellung einer Geraden. Tiefenlinie © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Hauptpunkt H Spurpunkt Grunndrißpunkt Bildpunkt Spurpunkte S n der Tiefenlinien S P P Die vom Augpunkt ausgehenden Projektionsstrahlen gehen durch beliebige Punkte der Grundrißgeraden g. Die Durchstoßpunkte dieser Projektionsstrahlen durch die Bildebene sind die Bildpunkte der Geraden. durch den Augpunkt parallel zur Geraden. Der Durchstoßpunkt dieses Projektionsstrahles durch die Bildebene ist das Bild des unendlich fernen Punktes der Geraden oder der Fluchtpunkt der Geraden. Zur Bestimmung der Bildgeraden im Grundriß dienen 2 Überlegungen: . Der Spurpunkt S der Geraden ist sowohl Grundrißpunktbwie auch Punkt der Bildebene, d.h. Bildpunkt. . Lassen wir einen Punkt der Geraden g ins Unendliche wandern, so wird der Projektionsstrahl Durch die Bestimmung des Spurpunktes der Geraden und des Fluchtpunktes ist die Gerade eindeutig definiert. Der Fluchtpunkt entspricht am Bsp. dem Hauptpunkt, also dem Durchstoßpunkt des Hauptsehstrahles durch die Bildebene. Eine Gerade die senkrecht zur Bildebene läuft und parallel zur Grundrißebene, heißt Tiefenlinie. Alle Tiefenlinien haben den Hauptpunkt als Fluchtpunkt. Seite 71 Darstellung einer im Grundriß beliebigen Geraden © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Fluchtpunkt Fluchtpunkt Fluchtpunkt F Gegeben ist eine beliebige Gerade im Grundriß. Mit Hilfe des Spurpunktes und des Fluchtpunktes der Geraden finden wir das perspektive Bild . Der Spurpunkt ist der Durchstoßpunkt der Gerade mit der Bildebene. Der Fluchtpunkt F ist der Durchstoßpunkt des Projektionstrahls zum unendlich fernen Punkt dieser Geraden durch die Bildebene. Dieser Projektionsstrahl ist parallel zur gegebenen Geraden und liegt in der Horizontebene. Der Fluchtpunkt liegt auf dem Horizont. F1 F2 Auf dem Horizont liegen alle Fluchtpunkte ( F1 F2 ... Fn ) der Geraden, die in der Grundrißebene oder in Ebenen parallel zur Grundrißebene liegen. Parallele Geraden haben dengleichen Fluchtpunkt. Seite 72 Darstellung einer im Raum beliebigen Geraden © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I RF Rampenfluchtpunkt RF (O) F Horizontalfluchtpunkt Spurpunkt Punkt der Geraden F S2 S P (P) S1 P O Gegeben ist eine beliebige Gerade durch einen Punkt P und den Spurpunkt S. Parallelverschoben durch den Augpunkt finden wir als Schnittpunkt mit der Bildebene den Rampenfluchtpunkt RF dieser Richtung. Die Gerade g und ihr Grundrißbild spannen eine Ebene auf, die senkrecht zur Standebene steht. Ebenso die durch den Augpunkt parallel verschobene Gerade und ihr Bild in der Horizontebene. Die Schnittgeraden dieser Ebenen mit der Bildebene sind Senkrechte. Der Fluchtpunkt der beliebigen Richtung = Rampenfluchtpunkt liegt also senkrecht über dem Horizontalfluchtpunkt des Grundrißbildes dieser Richtung. Das perspekive Bild der Geraden ist gegeben durch ihren Spurpunkt in der Bildebene und den Rampenfluchtpunkt (und das perspektive Bild des Punktes P). Konstruktion aus dem Grundriß : Durch Eindrehen des Grundrißbildes der Geraden g um den Spurpunkt S1 auf die Spur erhält man den Punkt (P). In (P) kann man den wahren Winkel der Neigung antragen und erhält als Schnittpunkt mit der Senkrechten über S1 den Spurpunkt der geneigten Geraden S2. Durch Eindrehen des Augpunktes um F erhält man (O) auf dem Horizont. In (O) kann man den wahren Winkel der Neigung antragen und erhält als Schnittpunkt mit der Senkrechten über F den Fluchtpunkt der geneigten Geraden = Rampenfluchtpunkt. Die Verbindung Rampenfluchtpunkt und Spurpunkt der geneigten Geraden ist das gesuchte perspektive Bild der beliebigen Geraden. Seite 73 Die Höhenübertragung © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I F Horizont Bildebene = Spur Fluchtpunkt F Gerade g Spurpunkt S Grundrißpunkt Bildpunkt P Grundrißpunkt P Die Gerade g verläuft parallel zur Grundrißebene und hat zu ihr einen gewissen Abstand ( Höhenlinie ). Sie hat wie ihr Bild in der Grundrißebene den gleichen Fluchtpunkt F. Die perspektive Grundrißrichtung ist durch die Verbindung SF gegeben. P Die Höhe der Geraden über dem Grundriß erscheint in der Bildebene in wahrer Größe. Durch die Höhe und durch den Fluchtpunkt ist das perspektive Bild der Höhenlinie gegeben. In einem beliebigen Grundrißpunkt P läßt sich jetzt, nachdem der Punkt im perspektiven Bild gefunden ist (Standort - Grundriß - perspektives Bild) die entsprechende perspektive Höhe darstellen. Seite 74 Die perspektive Anlage. Grundrißanlage © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I F=H F1 F2 Horizont Spur Bildebene Augpunkt Die Anlage des Objektgrundrisses zur perspektiven Anlage, die durch Augpunkt, Bildebene, Spur und Horizont gegeben ist bedingt die Art des perspektiven Bildes. Die Hauptgrundrißrichtungen des Objektes liegen in beliebigem Winkel zur Bildebene = Übereckperspektive. Hauptgrundrißrichtungen bestimmen F1 und F2. Zwei Hauptgrundrißrichtungen liegen parallel zur Bildebene = Zentralperspektive. Fluchtpunkt F entspricht dem Hauptpunkt H. Seite 75 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Bildebene und Augpunkt. Skalierung Horizont Spur Bildebene Augpunkt Je weiter sich die Bildebene vom Augpunkt entfernt, desto größer wird die Schnittfläche der Bildebene mit dem Sehkegel oder anders ausgedrückt das perspektive Bild des Objektes - bei gleichem Abstand von Augpunkt zu Objektgrundriß. Bildskalierung =Vergrößerung oder Verkleinerung des Bildes Seite 76 Spur und Bildebene © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Horizont Horizont Spur Spur = Bildebene Bildebene Augpunkt Augpunkt Im allgemeinen wird, wie in den vorhergehenden Darstellungen , der Grundriß vom perspektiven Bild getrennt, d.h. die Bildebene in einer freien Distanz zur Spur gewählt. Dies gilt insbesondere für kompliziertere, perspektive Bilder, weil dadurch eine gewisse Übersichtlichkeit gewährleistet ist. Bei einfachen, räumlichen Vorgaben, kann der Grundriß sich mit dem perspektiven Bild überlagern, d.h. die Bildebene mit der Spur zusammenfallen. Dies bedeutet eine Vereinfachung der Konstruktion, weil der Zusammenhang von Grundriß und perspektivem Bild direkt dargestellt werden kann und nicht durch eine senkrechte Zuordung über die Bildebene. Bei gleichem perspektiven Bild bedeutet dies aber eine andere Entfernung des Augpunktes zum Grundriß. Seite 77 Horizont und Spur © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Horizont Horizont Spur Spur Bildebene Bildebene Augpunkt Augpunkt Die Lage des Horizontes zur Spur oder die Lage der Aughöhe zur Standebene bedingt die Art der Ansicht des Objektes. Wir unterscheiden Normal- Vogel- oder Froscchperspektive. Bei einer Normalperspektive wird masstäblich eine Aughöhe von etwa 1.50 - 1.70 m über der Standebene angenommen. Bei Frosch- oder Vogelperspektive kommt das perspektive Bild schnell an den Rand des Sehkreises. Um Verzerrungen zu vermeiden kann die Bildebene gekippt werden. s.S.8 Perspektive mit gekippter Bildebene Seite 78 Objektgrundriß und Augpunkt © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Horizont Horizont Spur Spur Bildebene Bildebene Augpunkt Augpunkt Der Abstand des Augpunktes zum Objekt bestimmt den Bildausschnitt des perspektiven Bildes. Dabei ist bei freier Wahl des Abstandes auf mögliche Verzerrungen zu achten. s.S.68: Verzerrung Seite 79 Konstruktionsverfahren. Perspektive aus zwei Rissen © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Seitenriß dem Grundriß zugeornet Seitenriß dem Grundriß zugeornet Horizont Horizont Spur Spur Bildebene Bildebene Grundriß Grundriß Augpunkt Augpunkt Perspektive Bilder können - wie bisher - ohne Seitenriß konstruiert werden, wenn die Bildebene den Grundriß schneidet und ausreichend Höhenangaben bekannt sind. Die Höhenangaben erscheinen in der Bildebene in wahrer Größe und können direkt ins perspektive Bild übernommen werden. = Perspektive aus dem Grundriß Perspektive Bilder können konstruiert werden, wenn die perspektive Anlage ( d.h. die Zusammenschau von Augpunkt, Bildebene, Horizont, Spur und Objekt ) im Grund - und zugeordnet im Seitenriß gegeben ist. Die perspektiven Bilder der Punkte ergeben sich, wenn die Grunrißpunkte vom Augpunkt im Grundriß in die Bildebene projiziert, den Seitenrißpunkten vom Augpunkt im Seitenriß in die entsprechende Bildebene projiziert, einander senkrecht zugeordnet werden. Seite 80 Zentralperspektive mit Distanzpunkten © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Horizont Spur Bildebene Augpunkt Bei diesem Verfahren kann das perspektive Bild ohne Vorgabe von Rissen konstruiert. ist auch der Ort der Fluchtpunkte aller Geraden, die im 45 Grad Winkel die Bildebene treffen. Bei der Bestimmung einer Größe des QuadraZuerst wird der Distanzkreis um den gewählten tes, in wahrer Größe in der Bildebene oder nach Hauptpunkt gezeichnet. freier Wahl vor oder hinter der Bildebene parallel Der Radius entspricht dem Abstand Augpunkt zu oder senkrecht zu ihr, ist das perspektive Bild Bildebene. des Quadrates durch die horizontalen oder vertiDer Distanzkreis entspricht der Schnittfläche kalen Distanzpunkte gegeben. eines 90 Grad - Sehkegels mit der Bildebene. Die Mittelachse dem Hauptsehstrahl. Alle Mantellinien des Sehkegels treffen im 45 Grad Winkel die Bildebene, d.h. der Distanzkreis Seite 81 Übereckperspektive mit Meßpunkten © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I D M Horizont M Spur Horizont Spur P (P) Bildebene Augpunkt Im Grundriß : Der Fluchtpunkt M ist durch Parallelverschiebung der Richtung der Zuordnung durch den Ohne Zuhilfenahme des Grundrisses ist der Gesucht ist das perspektive Bild eines Punktes Augpunkt als Schnitt mit der Bildebene gegeben. Meßpunkt M im perspektiven Bild durch die P, der auf einer bereits dargestellten Tiefenlinie Eindrehung des vertikalen Distanzpunktes D um liegt. Der Abstand zur Bildebene ist gegeben. den Fluchtpunkt links auf den Horizont gegeben. Entsprechend wird für die Tiefenlinien, die nach Durch horizontale Drehung um den Durchstoßrechts laufen, der Distanzpunkt D um den Fluchtpunkt mit der Bildebene erscheint der Abstand punkt rechts auf den Horizont eingedreht. in der Bildebene. Der Richtung dieser Zuordnung = Verbindung Anwendungsbereich ist die perspektive RekonPunkt P und dem eingedrehten Punkt (P), ist struktion der Fotografie. ein Fluchtpunkt M auf dem Horizont zugeordnet, dem sogenannten Meßpunkt. Im perspektiven Bild : Seite 82 Geometrische Grundkonstruktionen © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Strecken Senkrechte im Punkt A Kreisbogen mit r um A schlagen. Um B und C Kreisbögen mit Radius BC. AD senkrecht auf BC. Senkrechte im Punkt B Um B, C und D Kreisbögen mit r schlagen. Die Verlängerung von CD über D hinaus schneidet den Kreis umd D in E. BE ist in B senkrecht auf AB. D Strecke AB teilen AC unter beliebigem Winkel zu AB. AC (z.B. in drei gleich lange Teilstrecken) teilen. C mit B verbinden und Parallelen zu BC durch D und E ziehen. Goldener Schnitt Senkrechte in B zeichnen und AB/2 abtragen. C und A verbinden. Kreisbogen um C mit Radius BC schneidet AC in D. Kreisbogen um A mit Radius AD schneidet AB in E. Es verhält sich a : b = b : c . Der Goldene Schnitt a : b etwa 1000 : 618 = 1 : 0,618 E C D C D D E B A C Strecke AB halbieren und Mittelsenkrechte auf AB Um A und B Kreisbögen mit r (r= größer als AB/2) schlagen. CD ist Mittelsenkrechte und halbiert AB. A C B A A B E B Lot auf Gerade BC Um A, B und C Kreisbögen mit r schlagen. AD ist senkrecht auf BC. Parallele zu AB durch C Um D ( auf AB beliebiger Punkt ), C und E Kreisbögen mit Radius CD schlagen. C mit F verbinden. Die Gerade durch CD und F ist parallel zu AB. A Winkel Halbieren eines Winkels Um A, B und C Kreisbögen mit r schlagen. AD halbiert den Winkel CAB. C B A B C C F D C D A A D E B B D Seite 83 Geometrische Grundkonstruktionen © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Winkel ohne Scheitel halbieren Parallele zu g 1 schneidet g 2 in S. Um S Kreisbogen mit r schlagen. A mit B verbinden und bis C verlängern. Mittelsenkrechte auf AC ist die Winkelhalbierende. Winkel übertragen Um A und D Kreisbögen mit r schlagen. Schenkelneigung BC abgreifen und Kreisbogen mit Radius BC um E schlagen. DF entspricht AC. C Kreise Tangente an Kreis von einem Punkt aus P mit M verbinden und über MP Thaleskreis zeichnen. Verbindung AP = Tangente an Kreis von P aus. Kreismittelpunkt Zwei nichtparallele Kreissehnen zeichnen. Die Mittelsenkrechten dieser schneiden sich im Kreismittelpunkt. F A g2 M M S B A B D E P C g1 Rechten Winkel dritteln Um A, B und C gleichgroße Kreisbögen schlagen. AD und AE dritteln den rechten Winkel Winkel von 30 Grad und 60 Grad konstruieren Tangente in einem Punkt des Kreises Um A, B und C Kreisbögen mit gleichem Radius Punkt P mit M verbinden. Auf MP in P Senkrechschlagen. AC ist Schenkel zu Winkel CAB, AD ist te zeichnen = Tangente. Schenkel zu Winkel DAB. Umkreis eines Dreiecks Der Schnittpunkt der Mittelsenkrechten zweier Dreiecksseiten = M. A C C D D M M P E A A B B Seite 84 Geometrische Grundkonstruktionen © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Innkreis eines Dreiecks Der Schnittpunkt der Winkelhalbierenden = M Regelmäßige Vielecke 5 - 10 - ... Eck MC halbieren und von E mit Radius EB Punkt F darstellen. BF entspricht der Länge der Fünfeckseite. Gleichseitiges Dreieck Kreisbogen mit r um D. 7 Eck Um A Kreisbogen mit r. BC/2 = 1/7 des Kreisumfanges. B M F E M B A D Abwicklung des Kreisumfanges Auf Waagrechte durch M Durchmesser d abtragen. Um A Kreisbogen mit d/2. Die Verbindung CB verlängern auf Senkrechte über D = E. DE entspricht 1/12 des Kreisumfanges. C 4 - 8 - ... Eck Punkte A, B, C, D zu einem Quadrat verbinden. Die Teilung der Quadratseiten ergibt das 8 - Eck... 6 - 12 - ... Eck Radius r von A aus auf Kreis abtragen. Radius r von B aus auf Kreis abtragen B A B E B 9 Eck Um A und B mit d C und D darstellen. AB in neun Teile teilen. Von C und D aus durch die geradzahligen Teilpunkte 2, 4, 6, und 8 auf den Kreis verbinden ergibt die Kreisteilpunkte. A D M C A M C A D C D B D Seite 85 © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Geometrische Grundkonstruktionen 11 Eck AB in 11 Teile teilen. Über A und über C hinaus verlängern um 1/11 Teil der Strecke AB. Die Verbindung EF ergibt den Schnittpunkt G mit dem Kreis. Die Verbindung GD entspricht 1/11 des Kreises. D ist der 3. Teilpunkt. F C G E A D M B Seite 86 Literaturliste © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Darstellende Geometrie Klix. Nickel VEB Fachbuchverlag Leipzig 1990 Darstellende Geometrie Fucke, Kirch, Nickel Verlag Harri Deutsch, Frankfurt 1989 Darstellende Geometrie für konstruierende Berufe Meyer. Heisig. Weber. Hohmann Schroedel.Gehlen Verlag 1975 Darstellende Geometrie W.Noli. Teil 1.2 und 3. Selbstverlag. Gießen 1985 Darstellende Geometrie Teil 1 und 2. Pumann. Pumann Verlag. Coburg Darstellende Geometrie Walter Wunderlich. Verlag Bibliografisches Institut. Mannheim. 1984 Darstellende Geometrie Band 1 und 2. Fritz Reutter. Verlag G. Braun. Karlsruhe. 1988 Anschauliche Geometrie Hilbert. Cohn Vossen Springer Verlag 2. Auflage 1996 ARCH + 137 Anfänge moderner Raumkonzeption Juni 1997 Darstellende Geometrie Prof. Arno Bonanni. Skriptum des Fachgebietes für Architekturdarstellung und -gestaltung der TU Berlin. Berlin. 1985 Darstellende Geometrie W.Noli. Selbstverlag. Gießen. 1989 Darstellende Geometrie für konstruierende Berufe Meyer. Heisig. Weber. Hohmann Schroedel.Gehlen Verlag 1975 Baugeometrie Darstellende Geometrie als Zeichen- und Konstruktionshilfe für Architekten und Bauingenieure I,II Entwerfen und Darstellen Brauner, Heinrich, Kickinger, Walter Die Zeichnung als Mittel des architektonischen Wiesbaden, Berlin 1977 Entwurfs Roland Knauer Darstellende Geometrie Ernst und Sohn-Verlag. 1991 Hochschulwissen in Einzeldarstellungen Graf, Barner Heidelberg 1973 Faszination des Scheins 500 Jahre Geschichte der Perspektive. Otto Patzelt Verlag für Bauwesen GmbH. Berlin 1991 Geometrische Grundlagen der Architekturdarstellung Cornelie Leopold Kohlhammer. Architektur 1999 Geometrie der Architekturzeichnung Einführung in Axonometrie und Perspektive. T. Hilpert Vieweg Verlag Braunschweig 1988 Grundlehre Geometrie Begriffe, Lehrsätze, Grundkonstruktionen. Kürpig. Niewiadomski Vieweg Verlag Braunschweig 1992 Grundlagen der Darstellung Perspektive und perspektives Zeichnen. 2 Bände. Vorlesungsskript der TU München. Prof. Wienands Lehre der Perspektive und ihre Anwendung R.Schmidt. Augustus Verlag. Augsburg 1991 Perspektiven. Projektionen Grundlagen - Anwendungsbeispiele - Übungen Andreas Wieser. Werner Verlag 97 Perspektive Schritt für Schritt. R.Schmidt, Bauverlag 1988 Perspektive und Axonometrie R.Thomae, Kohlhammer 1976 Perspektive MPZ - München 1989 Zeichnen und Darstellende Geometrie K. Henke Universität Stuttgart. Institut für Entwerfen und Konstruieren. Vorlesungsskript. 1994 Zirkel und Lineal Kulturgeschichte des konstruktiven Zeichnens. Jörg Sellenriek Callwey. München 1987 Seite 87 Symbole © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I Punkte Punkt im Grundriß Punkt im Aufriß Punkt im Seitenriß Schnittpunkt, Durchstoßpunkt, Spurpunkt Mittelpunkt Brennpunkt. Fluchtpunkt Augpunkt P 1, P 2, P 3, ... A, B, C, ... P' P '' P ''' S M F 0.0 Geraden Strecken kartesische Koordinaten Spurgeraden Höhenlinien Frontlinien Fallinien g 1, g 2, g 3 ... AB, AC, BC ... x, y, z s 1, s 2, s 3 ... h 1, h 2, h 3 ... v 1, v 2, v 3 ... f 1, f 2, f 3 ... Ebenen Grundriß Aufriß Seitenriß E 1, E 2, E 3 ... π1 π2 π3 Polygone ABC, ABCD ... Länge l Höhe h Radius r Parallele || Winkel α,β,γ 90 Grad - Winkel Linienarten Körperkanten sichtbar Körperkanten sichtbar Körperkanten unsichtbar Körperkanten unsichtbar Konstruktionslinien Konstruktionslinien Ergebnislinien sichtbar Ergebnislinien unsichtbar schwarz. voll 0,25 schwarz. voll 0,15 schwarz. gepunktet 0,35 schwarz. gepunktet 0,25 grün. voll 0,15 grün. gepunktet 0,25 rot. voll 0.15 rot. gepunktet 0.25 Ebenenarten herausgehobene Ebene schraffiert. schwarz Schlagschattenebene gefüllt. rot Körperschattenebene gefüllt. grün Seite 88 Index © Hochschule München. Architektur Fakultät. Darstellende Geometrie und Architekturperspektive. Teil I A Abwicklung 46 Abwicklung durch Grundrißklappung 47 Abwicklung einer Pyramide über die Spitze 49 Abwicklung mit Hilfe der Höhenzuordnung 46 Abwicklung mit Hilfe des Querschnittes 48 Abwicklung des Kreisumfanges 85 Affinität 35 Aufrißaxonometrie 8, 56 Aufrißdrehung 18 Augpunkt 67, 76 Axonometrien 8, 50 Aufrißdrehung oder Mongsche Drehung 18 Beliebige Gerade 16 Besondere Geraden 19 Frontlinie 19 Hauptlinie 19 Höhenlinie 19 projizierende Gerade 19 Wahrer Winkel und wahre Länge 17 Zwei beliebige Geraden 20 Zwei sich schneidende Geraden 21 Gleichseitiges Dreieck 85 Goldener Schnitt 83 Grundrißaxonometrie 8, 54 B H Beliebige Gerade 16 Besondere Geraden 19 Bildebene 67, 76 Bildtafeln 13 Hauptlinie 19 Hauptpunkt 67 Hauptsehstrahl 67 Höhenebenenverfahren 40 Höhenlinie 23 Höhenübertragung 74 Horizont 67 Horizontebene 67 D dimetrische Axonometrie 58 dimetrische Darstellungen 52 DIN 5 8, 58 Distanzpunkte 81 Durchdringungen 39 Höhenebenenverfahren 40 Mantelebenenverfahren 41 Parallelebenenverfahren 42 Pendelebenenverfahren 43, 44, 45 Durchstoßpunkt 28 Durchstoßpunkt einer beliebigen Geraden durch eine 28 Durchstoßpunkt einer beliebigen Geraden durch zwei 29 Körperschnitt mit Hilfe der Durchstoßpunkte 37 I Ingineurprojektion 8 Inhaltsverzeichnis 2 Innkreis eines Dreiecks 85 Isometrie 60 isometrische Darstellungen 52 K Koinzidenzebene 15 Kollineation 36 Koordinatenachsen 51 E Körper 37 Ebene 22 Abwicklung durch Grundrißklappung 47 Abstand eines Punktes von einer Ebene 26 Abwicklung einer Pyramide über die Spitze 49 Besondere Geraden einer Ebene 23 Abwicklung mit Hilfe der Höhenzuordnung 46 Fallinien 23 Abwicklung mit Hilfe des Querschnittes 48 Frontlinie 23 Arten von Durchdringungen 39 Höhenlinie 23 Durchdringung und Höhenebenenverfahren 40 Drei - Punkte - Ebene 25 Durchdringung und Mantelebenenverfahren 41 Durchstoßpunkt einer beliebigen Geraden durch eine 28 Durchdringung und Parallelebenenverfahren 42 Durchstoßpunkt einer beliebigen Geraden durch zwei 29 Durchdringung und Pendelebenenverfahren 43, 44, 45 Pendelebenenverfahren 29 Körperschnitt mit Hilfe der 3. Projektion 38 Punkt und Ebene 24 Körperschnitt mit Hilfe der Durchstoßpunkte 37 Punkt und Gerade spannen eine Ebene auf 30 kotierte Projektion 8, 11 Wahre Größe einer Ebene 33 Kreise 84 Konstruktion mit hilfsprojizierender Ebene 34 Konstruktion mit Stützdreieck 33 L Wahre Größe und Neigung des Abstandes von einer Linienarten 88 Eb 27 Literaturliste 87 Wahrer Winkel zwischen zwei Ebenen 32 Lot 83 Ebenenarten 88 Einschneideverfahren 52 F Fallinie 23 Frontlinie 19, 23 G Gerade 16 M Mantelebenenverfahrens 41 Mittelsenkrechte 83 Mongsche Drehung 18 N Normalebene 32 P Parallele 83 Parallelprojektion 9 Pendelebenenverfahren 29 Perspektive 64 Begriffe 67 Die Höhenübertragung 74 Die perspektive Anlage 75 Bildebene und Augpunkt 76 Grundrißanlage 75 Horizont und Spur 78 Objektgrundriß und Augpunkt 79 Skalierung 76 Spur und Bildebene 77 Elemente der Perspektive 70 Darstellung einer Geraden 71 Darstellung einer im Grundriß beliebigen Geraden 72 Darstellung einer im Raum beliebigen Geraden 73 Darstellung eines Punktes 70 Klappung 69 Konstruktionsverfahren 80 Perspektive aus dem Grundriß 80 Perspektive aus zwei Rissen 80 Übereckperspektive mit Meßpunkten 82 Zentralperspektive mit Distanzpunkten 81 Perspektive bei geneigter Bildebene 66 Übereckperspektive 66 Verzerrung 68 Zentrale Projektionen 65 Zentralperspektive 66 Projektionsstrahlen 9 projizierende Ebene 18 projizierende Gerade 19 Punkt 13 in der Symmetrie- und in der Koinzidenzebene 15 Lage im Raum 14 Umklappung der Bildtafeln 13 trimetrische Axonometrie 52 trimetrische Darstellungen 52 U Übereckperspektive 8, 66 Umkreis eines Dreiecks 84 V Verkürzungsverhältnisse 51 Verschschwindungsgerade 69 Vielecke 85 W Winkel 83 Winkel ohne Scheitel halbieren 84 Winkel von 30 Grad und 60 Grad konstruieren 84 Z Zeichenebene 69 Zentrale Projektionen 8, 64 Zentralperspektive 8, 66 Zentralprojektion 9 ZIG - ZAG 53 Zweitafelprojektion 12 R Rampenfluchtpunkt 73 Rechten Winkel dritteln 84 Regelmäßige Vielecke 85 S Schräge Projektionen 50 Senkrechte 83 Senkrechte Axonometrie 62 senkrechte Projektionen 8 Senkrechte Projektionen allgemein 10 Spur 67, 77 Spurgeraden 14 Standebene 67 Strecken 83 Symbole 88 Symmetrieebene 15 T Tangente 84 Tiefenlinie 71 Seite 89