DAP2¨Ubung – Blatt 13 - Chair 11: ALGORITHM ENGINEERING

Fakultät für Informatik
Lehrstuhl 11 / Algorithm Engineering
Prof. Dr. Petra Mutzel
Carsten Gutwenger, André Gronemeier, Anna-Lena Lamprecht,
Tobias Marschall, Hubert Wagner, Hoi-Ming Wong
Sommersemester 2008
DAP2 Übung – Blatt 13
Ausgabe: 3. Juli — Abgabe: 10. Juli
Globalübung: Fr. 18. Juli
Aufgabe 13.1 (4 Punkte) Beschreibe eine Implementierung des Algorithmus von Prim für den
Fall, dass der Graph G = (V, E) als Adjazenzmatrix dargestellt wird. Deine Implementierung
soll eine Laufzeit von O(|V |2 ) haben. Begründe die Laufzeit deiner Implementierung.
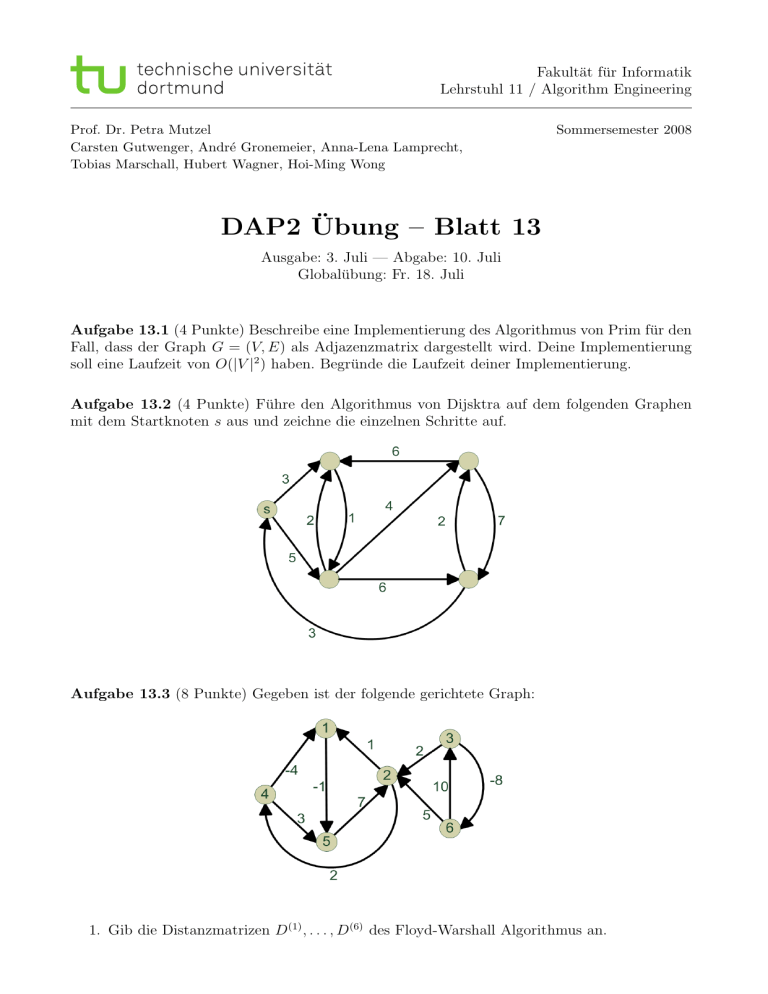
Aufgabe 13.2 (4 Punkte) Führe den Algorithmus von Dijsktra auf dem folgenden Graphen
mit dem Startknoten s aus und zeichne die einzelnen Schritte auf.
Aufgabe 13.3 (8 Punkte) Gegeben ist der folgende gerichtete Graph:
1. Gib die Distanzmatrizen D(1) , . . . , D(6) des Floyd-Warshall Algorithmus an.
2. Der transitive Abschluss eines gerichteten Graphen G = (V, E) ist durch den gerichteten
Graphen G+ = (V, E + ) mit
E + = {(u, v) : es existiert ein Pfad von Knoten u nach Knoten v in G mit u 6= v}
definiert.
Zeichne den Graphen G+ . Gib einen einfachen Algorithmus an, der für dünne Graphen
(|E| in O(V )) ein besseres Laufzeitverhalten hat als der Algorithmus von Floyd-Warshall.
Begründe warum dein Algorithmus in diesem Falle schneller ist.
Aufgabe 13.4 (4 Punkte) Wir wollen in einem gerichteten Graphen mit Hilfe von Dijkstras
Algorithmus einen kürzesten Pfad P von Knoten s nach Knoten t berechnen. Wann können
wir erkennen, dass der Algorithmus den Pfad P schon berechnet hat, so dass wir zwecks Zeiteinsparung frühzeitig abbrechen können?
Bonusaufgabe 13.5 (4 Bonuspunkte) Ein negativer Kreis ist ein Kreis mit gewichteten Kanten, so dass die Summe der Gewichte negativ ist. Erläutere wie man mit dem Algorithmus von
Floyd-Warshall festellen kann, ob ein gerichteter Graph ohne Schleifen einen negativen Kreis
enthält oder nicht.
Bona sort!
– das DAP2-Team