11. ¨Ubungsblatt zu Algorithmen I im SS 2015
Werbung

KIT
Jun.-Prof. Henning Meyerhenke, Jun.-Prof. Dennis Hofheinz
Institut für Theoretische Informatik
Christian Staudt, Christoph Striecks
11. Übungsblatt zu Algorithmen I im SS 2015
https://crypto.iti.kit.edu/algo-sose15
{staudt,striecks}@kit.edu
Aufgabe 1
(Bellman-Ford-Algorithmus, 2 + 1 Punkte)
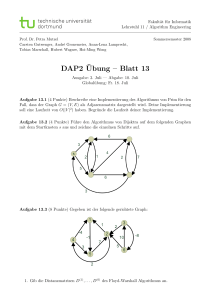
Gegeben sei der unten abgebildete gerichtete Graph mit Kantengewichten. Auf diesem Graph soll der
Bellman-Ford-Algorithmus mit a als Startknoten ausgeführt werden.
a) Tragen Sie in jeden Knoten jeweils die kürzeste Distanz von a zu diesem Knoten ein. (In der
unteren Hälfte jedes Knotens wurde dafür Platz gelassen.)
b) Zeichnen Sie den vom Bellman-Ford-Algorithmus berechneten Baum kürzester Wege in den
Graphen ein.
b
d
−1
1
3
1
−1
a
2
f
3
1 5
2
4
c
e
−1
3
Aufgabe 2
(Jarnı́k-Prims und Kruskals Algorithmus, 2 + 2 Punkte)
Berechnen Sie einen Minimum Spanning Tree (MST) des angegebenen Graphen mit dem Algorithmus
von Jarnı́k-Prim und dem Algorithmus von Kruskal. Geben Sie jeweils die Kanten des MST in
der Reihenfolge an, in der sie der Algorithmus auswählt. Um Eindeutigkeit herzustellen, verwenden
Sie Knoten 8 als Startknoten von Jarnı́k-Prim und wählen Sie in beiden Algorithmen bei gleichen
Kantengewichten stehts diejenige Kante aus, die die kleinste Endknotennummer von allen vier Knoten
besitzt.
5
8
1
7
7
4
11
6
9
6
5
6
4
7
2
5
8
2
7
8
10
3
3
8
4
3
3
7
5
7
4
1
1
9
2
5
12
Aufgabe 3
(Minimum Spanning Tree (MST), 5 + 2 Punkte)
Wir betrachten beliebige zusammenhängende ungerichtete Graphen G = (V, E) mit V = {1, . . . , n},
n ∈ N, und Kantengewichten aus {1, 3}. Sei G in Form eines Adjazenzfeldes gegeben.
a) Geben Sie einen Algorithmus an, der in Zeit O(|E|) einen MST von G berechnet.
b) Argumentieren Sie kurz, warum Ihr Algorithmus aus Teilaufgabe a) das gewünschte Laufzeitverhalten aufweist.
Ausgabe: Mittwoch, 1.7.2014
Abgabe: Freitag, 10.7.2014, 12:45 im Briefkasten im Untergeschoss von Gebäude 50.34
2