Heimübungen zur Vorlesung Datenstrukturen und Algorithmen SS

Robert Elsässer
u.v.a.
Paderborn, den 18. Juni 2009
Heimübungen zur Vorlesung
Datenstrukturen und Algorithmen
SS 2009
Blatt 10
AUFGABE 1:
Eine Kante e ∈ E eines zusammenhängenden, ungerichteten Graphen G = (V, E) heißt
Brückenkante, falls der Graph G0 = (V, E \ e), der durch das Entfernen der Kante e aus
G entsteht, nicht mehr zusammenhängend ist. Abbildung 1 stellt einen Graphen mit einer
Brückenkante dar.
Abbildung 1: Ein ungerichteter Graph mit einer Brückenkante e
Geben Sie einen Algorithmus in Pseudocode an, der in Laufzeit O(|V |·|E|+|E|2 ) entscheidet,
ob ein ungerichteter Graph G (gegeben als Adjazenzliste) eine Brückenkante besitzt oder
nicht. Zeigen Sie, dass ihr Algorithmus korrekt arbeitet sowie die Laufzeitschranke einhält.
AUFGABE 2:
Gegeben sei ein gerichteter, gewichteter Graph G = (V, E) durch eine Liste von Elementen
die wie folgt zu betrachten sind:
Für einen Eintrag der Form (xy, a) gilt: Es gibt in G eine gerichtete Kante von x nach y mit
Kantengewicht a.
L = (sb, 5), (sa, 10), (sf, 5), (bf, 6), (ba, 3), (be, 5), (bc, 5), (f s, 2), (f e, 4), (ca, 3),
(ce, 2), (cd, 5), (df, 1), (de, 1), (ef, 1), (ec, 1), (af, 1), (ae, 2)
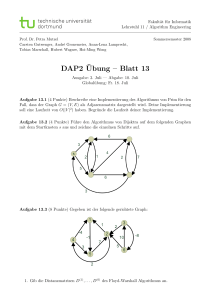
a) Zeichnen Sie den Graphen G und geben Sie zusätzlich dessen Darstellung als Adjazenzmatrix an.
b) Aus der Vorlesung ist Ihnen der Algorithmus von Dijkstra (SSSP) bekannt um kürzeste Wege zu berechnen. Mit jedem Schleifendurchlauf wird in diesem Algorithmus der
kürzeste Weg δ(s, u) vom Startknoten s zu einem Knoten u ∈ V berechnet. Führen Sie
auf dem Graphen G, mit Startknoten s, den Algorithmus von Dijkstra aus und notieren
Sie ihre Zwischenschritte wie folgt: Geben Sie am Ende jedes Schleifendurchlaufs die
Menge S an, den soeben berechneten, kürzesten Weg δ(s, u), sowie eine Tabelle in der
jedem Knoten v ∈ V \ S die aktuelle Distanz d[v] zum Startknoten zugewiesen wird
(vergleiche hierzu auch Tabelle 1) .
Tabelle 1:
Q\S
d[v]
c) Angenommen alle Kantengewichte des Graphen G wären genau 1. Beschreiben Sie einen
Algorithmus (kein Pseudocode nötig) der das Problem Single Source Shortest Path auf
dem veränderten Graphen G in Zeit O(|V | + |E|) löst.
AUFGABE 3:
Sei G = (V, E) ein gerichteter Graph. Ein Kreis K in G heißt Eulerkreis, wenn K jede Kante
aus E genau einmal enthält. Einzelne Knoten können in K mehrfach vorkommen.
Entwerfen Sie einen Algorithmus in Pseudocode, der in Zeit O(|V | + |E|) feststellt, ob es
in einem gerichteten, zusammenhängendem Graphen G = (V, E) einen Eulerkreis gibt oder
nicht. Zeigen Sie, dass ihr Algorithmus korrekt arbeitet sowie die Laufzeitschranke einhält.
AUFGABE 4:
Gegeben sei ein ungerichteter, gewichteter Graph G = (V, E). Entwickeln Sie einen Algorithmus, der von einem Startknoten s ∈ V zu jedem anderen Knoten v ∈ V \ {s} in G den
kürzesten und leichtesten Weg findet. Der leichteste Weg zwischen zwei Knoten s und v ist
der Weg mit den wenigsten Kanten.
In unserem Fall suchen wir zunächst alle kürzesten Wege zu einem Zielknoten v. Unter
all diesen Wegen suchen wir nun den, der die wenigsten Kanten aufweist. Das Kriterium
“kürzester Weg” ist das notwendige und das “leichtester Weg” das hinreichende Kriterium.
Diese Aufgabe sollen Sie nun in Java programmieren. Gehen Sie dazu auf die DuA-Webseite
für dieses Semester und laden Sie sich dort das Java-Framework herunter. Dieses besteht
aus einem Graphen-Generator und einer visuellen Anzeige mit der Sie ihren Algorithmus auf
Korrektheit prüfen können.
Implementieren Sie Ihren Algorithmus entweder in die dafür vorgesehene Klasse oder in eine
eigene Ihrer Wahl und schicken Sie ihre Implementierung (nur Ihre selbstgeschriebenen JavaKlassen ohne das Gesamtframework) als .zip-Datei bis nächsten Donnerstag, den 25. Juni
2009 bis 13 Uhr an die EMail-Adresse funsheep (at) upb (punkt) de.