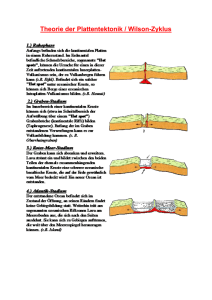
Geophysik für Geologen
Werbung

K. Bahr: Geophysik für Geologen 1. Die Kontinentalverschiebungstheorie 1.1 Wegeners Argumente: Schelflinien und Fossilien 1.2 Gegenargumente: Scherwellen und „fehlende Physik“ 2. Die geowissenschaftliche Revolution von 1963 2.1 Paläomagnetismus vor und nach dem magnetic cleaning 2.2 Umkehrungen des Magnetfeldes und seafloor spreading 2.3 Rekonstruktion der Plattenbewegungen 3. Konvektion 3.1 Wärmetransport und Rayleighzahl 3.2 Der Maxwell’sche Modellkörper 4. Von der Konvektion zur Plattentektonik 4.1 Konvektionsgetriebene Plattentektonik 4.2 Plattengetriebene Konvektion 4.3 Die Plume-Hypothese 5. Plattentektonik und Subduktion 5.1 Ozeanische Lithosphäre und Inselbögen 5.2 Gebirgsbildung I : Der aktive Kontinentalrand 5.3 Gebirgsbildung II: Kontinent-Kontinent-Kollisionen 5.4 Zusammenfassung: Der Wilson-Zyklus 6. Subduktion und Erdbeben 6.1 Der Modellkörper von Saint-Venant 6.2Die Benioff-Zonen 6.3Magnitude, Energie und Zerstörung 7. Erdbeben und Seismologie 8. Seismologie und Anisotropie 8.1 SKS Splitting 9. Anisotropie und lattice-preferred orientation (LPO) 9.1 Kristallographie und seismische Anisotropie von Olivin 9.2 Mantelfluss, Relativbewegungen und LPO 10. LPO und Wasser im Erdmantel 10.1 Subduktion als Transportprozess für Wasser: Das 10.2 Wasserstoff-Diffusivität in Olivin 10 Be - Experiment 11 Geophysik und geophysikalische Exploration: Zusammenfassung 1. Die Kontinentalverschiebungstheorie Die Kontinentalverschiebungstheorie war sozusagen der Vorläufer der Plattentektonik. Die Theorie nahm horizontale Bewegungen der Kontinente über (vergangene) geologische Zeiten an, so wie die Plattentektonik. Im Gegensatz zur Plattentektonik machte diese Theorie aber keine (oder zumindest keine korrekte) Aussage über die physikalischen Mechanismen, die zu diesen Horizontalbewegungen führen. Das 1. Kapitel ist offensichtlich teilweise wissenschaftshistorisch – eigentlich die Domäne der Emeriti. Motivation: Warum in einer ansonsten modernen, den heutigen Stand eines Teilgebiets der Geophysik wiedergebenden Vorlesung ein historisches Kapitel? Die Vorlesung richtet sich vor allem an Studenten des 7. Semesters, die vorher physikalische Fakten gelernt haben – Aussagen waren entweder wahr oder falsch, allenfalls traten sogenannte Dualismen auf – zwei wahre Aussagen widersprechen sich nur scheinbar, wie etwa der Teilchen-Welle Dualismus der QM oder der FestFlüssig-Dualismus der Rheologie des Erdmantels. Im folgenden Semester werden diese Studenten (hoffentlich) Mitglieder von Arbeitsgruppen der Göttinger Physik sein, und deshalb an der Forschung beteiligt: Sie werden sich mit Naturerscheinungen befassen, bei denen zwischen ‚wahr‘ und ‚falsch‘ noch nicht unterschieden werden kann. Die ersten beiden Kapitel werden an wenigen Beispielen aus der Geophysik zeigen, dass sich jede heute ‚wissenschaftlich gesicherte‘ Aussage irgendwann einmal in dem gleichen Schwebezustand zwischen ‚wahr‘ und falsch befand. 1.1.Wegeners Argumente: Schelflinien und Fossilien Problem bei der historischen Sichtweise: Wann soll man anfangen? Es hat vor Wegener ‚globale‘ Theorien der Gebirgsentstehung gegeben, etwa die Schrumpfungstheorie von E. Suess in ‚Das Antlitz der Erde‘ (1884-1903). Das die Umrisse von Südamerika und Afrika zu einander passen, fiel bereits Snyder-Pellegrini (1859) auf. Der Meteorologe und Geophysiker Alfred Wegener (1880-1930) veröffentlichte 1912, 1915 und 1922 in ‚Über die Entstehung der Kontinente und Ozeane‘ die Theorie der Kontinentalverschiebung. Seine Argumente: 1. Schelflinien. Die heutigen Küstenlinien von Nord- und Südamerika einerseits und Europa und Afrika andererseits passen nicht so gut zusammen. Die Übereinstimmung wird viel besser, wenn man statt der Küstenlinien (dem heutigen NN) die Schelflinien (Übergang vom Randmeer zur Tiefsee) nimmt – dann gehören Randmeere wie zB die südliche Nordsee zum Kontinent. 2. Identische Geologien in heute getrennten Kontinenten. Beispiele: 1) Die kambrischen (?) Sedimente in Schottland und Nordirland / in New Brunswick 2) die gleichen flood basalts am Ostrand Südamerika und in Westafrika (NB: stehen im verdacht, Überreste eines starken Anstiegs der Fördermenge des (heutigen) Tristan da Cunha hot spots zu sein – Zusammenhang mit dem Aufbruch von Godwanaland? 3) sehr ähnliche Sedimente im Norden und Süden der Neuseeländische Südinsel - heutige Erklärung: Transform-Störung mit horizontaler Plattenbewegung 3. Ähnliche Fossilienfunde in heute getrennten Kontinenten, z.B. die kambrischen Trilobiten, von denen es zwei unterscheidbare Gruppen gibt: Eine ‚europäische‘ Gruppe mit Fundorten fast überall in Nordeuropa und in New Brunswick, und eine ‚amerikanische‘ Gruppe mit Fundorten im östlichen Noramerika und in Nordirland und Schottland. Heutige Erklärung (im Rahmen der Plattentektonik): Bei der Schliessung des Atlantiks vor (?) 150 Mio Jahren wurden die ‚MiniTerraene New Brunswick und Nordirland und Schottland zwischen Europa und Nordamerika ‚ausgetauscht‘. Wegen der später folgenden Gegenargumente: Auch Fossilien von Landtieren, etwa dem Reptil Lystrosaurus in Südafrika, Australien und Antarktika. Heutige Erklärung: Das war Godwanaland. Später stellte die Paläoklimatologie ein weiteres Argument, welches Wegener noch nicht kannte, bereit: Die Vereisung Indiens im Perm. Paläo-Vereisungen lassen sich anhand der ‚Schleifspuren‘, die das Eis bei seiner Ausbreitung hinterlässt, identifizieren (Beispiel Finnland während der letzten Eiszeiten). Genau solche Spuren waren in Indien gefunden worden. Wenn Indien zur Zeit ihrer Entstehung, genau wie jetzt, in der Nähe des Äquators war, muss der gesamte Planet vereist gewesen sein, denn nördlich und südlich des Äquators kann es ja nur noch kälter gewesen sein. Was ist dann mit dem Leben passiert? Als physikalischen Mechanismus für die Horizontalbewegung nahm Wegener die Eötvös-Kraft an – gravitative Anziehung durch den Äquatorwulst. Die Existenz dieser Kraft wurde allgemein akzeptiert, schliesslich waren horizontale Gravitationskräfte im Zusammenhang mit der Isostasie schon Mitte des 19. Jahrhunderts gemessen worden. Wiederholung: Was ist Isostasie? Über einer geschichteten Erde zeigt das der Richtung der Gravitationskraft folgenden Lot senkrecht nach unten – zum Erdmittelpunkt hin. Neben einen Gebirge erwartet man eine zusätzliche horizontale Komponente wegen der Anziehung durch die Masse des Gebirges. Isostasie bezeichnet die Entdeckung, dass bei Messungen der Lotabweichung (hor:vert) eine geringere horizontale Gravitationkraft gefunden wurde, als sie für ein Gebirge mit der Dichte des Erdmantels erwartet wird. Das Gebirge hat also eine geringere Dichte als der Mantel, und darüber hinaus eine in den Mantel hineinreichende ‚Gebirgswurzel‘ von ebenfalls geringere Dichte. Hier, bei der Isostasie, taucht zum ersten Mal die Modellvorstellung von den auf und in dem schweren Mantel ‚schwimmenden‘ leichten Kontinenten auf (Airy, 1855; Pratt, 1855). 1.2.Gegenargumente: Scherwellen und „fehlende Physik“ Die Frage, ob die Eötvös-Kraft oder andere horizontale Gravitationskräfte gross genug sind, um Kontinente zu bewegen, wurde von Lambert (1921) so umformuliert: Das hängt von der Viskosität des Mantelmaterials ab. Das stärkste Argument gegen die Kontinentalverschiebungstheorie kam nun aus der Geophysik: Nach dem Seismologen Jeffrey (1925) ist Viskosität nur für eine Flüssigkeit definiert, und Flüssigkeiten leiten keine Scherwellen – weil der Schermodul und deshalb die Scherwellengeschwindigkeit v s vp (K 4 ) 3 verschwinden (im Gegensatz zur Geschwindigkeit von Kompressionswellen, in die auch der für eine Flüssigkeit definierte Kompressionsmodul K eingeht. Aus der Seismologie war aber bekannt, dass sich im Mantel der Erde (im Gegensatz zum flüssigen äusseren Kern) Scherwellen ausbreiten können. (Wir wissen heute, dass für die Ausbreitung von Scherwellen die Viskosiät nur einen Grenzwert überschreiten muss, der vom Schermodul und der Periode abhängt – Überschlagsrechnung: der Schermodul des Mantels ergibt sich zu 1011 Pa , für eine Periode von 20 s ergibt sich ein Grenzwert von 2 *1012 Pa * s , der um viele Grössenordnungen unter der tatsächlichen Viskosität des Mantels, 10 20..10 21 Pa * s liegt.) Nachdem das Konzept der Viskosität ‚falsch‘ war, wurde die zur Verschiebung der Kontinente benötigte Kraft unendlich gross. Das geophysikalische Argument gegen die Kontinentalverschiebungstheorie war also, dass es keine physikalische Kraft dafür gibt. Allerdings waren die meisten Geowissenschaftler in der 1. Hälfte des 20. Jahrhunderts keine Geophysiker, sondern Geologen. (Die rasante Ausweitung des Arbeitsgebietes Geophysik in der 2. Hälfte des 20. Jahrhunderts ist einerseits mit der hier erzählten Geschichte und andererseits mit der massiven Nachfrage nach Erdöl und der angewandten Exploration verknüpft). Die in der Geology noch des frühen 20. Jahrhunderts vorherrschende Denkrichtung war der Uniformitarismus, der schon im ausgehenden 18. Jahrhundert von Lyell in Edinburgh gelehrt wurde: Frühere geologische Prozesse liefen so wie die heutigen ab, es gibt keine Katastrophen oder Umbrüche, die Gegenwart ist der Schlüssel zum Verständnis der Vergangenheit. Wenn (aus dieser Richtung gesehen) die Kontinentalverschiebungstheorie ‚stimmt‘, dann hat sich, z.B., die Lage der Kontinente relativ zu den Klimazonen verändert, und schon deswegen könnte die Gegenwart nicht mehr der Schlüssel zur Vergangenheit sein.. Man kann noch fragen, was sich diese Geologen ausgedacht haben, um Wegeners ‚Daten‘, etwa die ähnlichen Fossilien in heute getrennten Kontinenten, mit einer alternativen Theorie zu interpretieren – etwa die versunkenen Kontinente. Da diese aber isostatisch nicht zu halten waren und das Versinken genau diejenige Katastrophe darstellte, die der Uniformitarismus zu vermeiden hatte, wurden die versunkenen Kontinente durch schmale Landbrücken ersetzt, auf denen jene Tiere, deren Überreste heute auf dem ‚falschen‘ Kontinent liegen, den Ozean überqueren können. Das wirkt vielleicht aus heutiger Sicht lächerlich, aber die so operierenden Geologen versuchten, ein Gedankengebäude zu retten, das lange Zeit funktioniert hatte. Den Mantel flüssig zu machen, war noch abstruser als die versunkenen Kontinente. 2. Die geowissenschaftliche Revolution von 1963 Geophysikalische Argumente hatten die Anerkennung der Kontinentalverschiebungstheorie in der 1. Hälfte des 20. Jahrhunderts behindert, und geophysikalische Argumente sollten ihr schliesslich zum Durchbruch verhelfen. Während jedoch die Gegenargumente aus der Seismologie kamen – einer arrivierten Wissenschaft, die das Wissen über den Aufbau des Erdkörpers entscheidend vermehrt hatte, kamen die Pro-Argumente aus dem Paläomagnetismus. Dieser Zweig der Geophysik, der die remanente Magnetisierung von Gesteinen untersucht, wurde von den meisten Geowissenschaftlern überhaupt erst anlässlich dieses Eintretens für die Kontinentalverschiebungstheorie wahrgenommen. 2.1 Paläomagnetismus vor und nach dem magnetic cleaning Das Magnetfeld der Erde sieht, wenn es in grosser Entfernung von den Quellen im äusseren Kern der Erde betrachtet wird, fast aus wie ein Dipolfeld. Wenn die Ursache des Feldes untersucht werden soll, etwa mit Dynamotheorie, gilt dies so nicht: An der Kern-Mantel-Grenze haben alle Terme in der Entwicklung des Magnetfeldpotentials nach Kugelflächenfunktionen etwa die gleiche Energiedichte, und der Dipolterm hat nur noch eine leichte Dominanz gegenüber dem Quadrupol-, Oktupolterm etc. Dass sich an der Erdoberfläche ein dominanter Dipolterm ergibt, liegt nur an der geometrischen 3 Abschwächung, die für den Dipol BOberfl / BKern rK 3 berträgt, für den Quradupolterm jedoch rE rK 4 4 usw. Im Aussenraum kommt zusätzlich die Deformation durch den Sonnenwind hinzu. An der rE Erdoberfläche kann das Erdmagnetfeld aber durch ein Dipolfeld mit den Komponenten 2 0 M cos M sin Br und B 0 in Kugelkoordinaten (r , , ) angenähert werden. Creer , 3 4 r 4 r 3 Irving und Runcorn (1954) erkannten, dass zwischen der Kobreite eines Ortes an der Erdoberfläche und der Inklination I arctan Br der Zusammenhang tan 2 cot I bestehen sollte, wenn der B scheinbare Dipol parallel zur Rotationsachse ausgerichtet ist. Für das Folgende ist zunächst wichtig, dass die remanente Magnetisierung eines Materials, genau wie die magnetische Kraftflussdichte, ein Vektor ist. Wiederholung: Was ist remanente Magnetisierung? Eine Magnetisierung die bleibt, auch wenn das äussere Magnetfeld, welches sie verursacht hat, wieder abgeschaltet (oder umgepolt) ist. Für die remanente Magnetisierung von Gesteinen ist eine spezielle Spielart des Ferromagnetismus verantwortlich. – Ferromagnetische Materialien haben ein magnetisches Moment wegen Elektronenspins, die nicht von einander unabhängig sind. Weil Elektronen identische Teilchen sind, genügen sie gewissen quantenmechanischen Regeln, die die klass. Elektrodynamik nicht kennt, Effekt: Die Momente ‚benachbarter‘ Elektronen werden parallel ausgerichtet und es entsteht eine spontane Magnetisierung. Bei den Antiferromagnetika (Beispiel: Hämatit Fe 2 O3 ) sind die Elektronenspins paarweise antiparallel ausgerichtet, so dass sich keine makroskopische Magnetisierung ergibt. In Ferrimagnetika (Beispiel Magnetit Fe3O4 ) gibt es ebenfalls eine antiparallele Ausrichtung von Elektronenspins, aber diesmal mit unterschiedlichen magnetischen Momenten, so dass eine makroskopische Magnetisierung bleibt. Wiederholung: Antiferro- und Ferrimagnetismus auf der atomaren Ebene: Eisen hat die Elektronenkonfiguration 1s 2 2s 2 2 p 6 3s 2 6 p 6 3d 6 4s 2 . Fe 2 Ionen haben zwei 4-s Elektronen verloren, d.h. in der äussersten ‚Schale‘ sind sechs 3-d Elektronen, deren Spinanordnung ist, es verbleiben 4 Bohrsche Magneton. Fe 3 Ionen haben zusätzlich ein 3-d Valenzelektron verloren, die Spinanordnung ist und es bleiben 5 Magneton. Magnetische Mineralien sind Oxyde von Eisen, mit Vorzeichenwechsel des Spin in benachbarten Ionen. Verbleibt ein resultierendes magnetisches Moment? Beim Hämatit Fe 23 O32 nein, beim Magnetit Fe 2 Fe 23 O42 ja. Paläomagnetismus begann mit der Entdeckung, dass die Inklination der remanenten Magnetisierung von Gesteinen an vielen Fundorten der Regel tan 2 cot I nicht folgt. Also musste nach der Aufprägung der remanenten Magnetisierung – z.B. durch Abkühlung von Lava unter die CurieTemperatur des ferrimagnetischen Materials - entweder der Dipol seine Orientierung verändert haben, oder die erstarrte Lava hat sich in dieser Zeit im Magnetfeld der Erde bewegt. Um diese Frage zu beantworten, wurde zunächst die Beobachtungsgrösse apparent polar wander path definiert, sie besteht aus einer Folge von virtuellen geomagnetischen Polen (VGP), abgeleitet von magnetithaltigen Gesteinsproben aus der gleichen geologischen Einheit, aber mit unterschiedlichen Abkühlungsaltern. Ein virtueller geomagnetischer Pol ist etwa der Durchstosspunkt der Dipolachse durch die Erdoberfläche, und in einem 2D Schnitt durch die Erde ergibt sich die Kobreite dieses VGP aus der Diskrepanz zwischen der tatsächlichen Kobreite eines Probenfundortes und der aus der Inklination der Remanenz vorhersagten Kobreite. Nebenbemerkung. Die dritte Komponente des Magnetfeldes eines achsenparallelen Dipols ist B 0 , wegen der Rotationssymmetrie. Man kann also mit dieser Methode nicht auf West-Ost-Bewegungen schliessen. Zwar weißt die remanente Magnetisierung von Gesteinsproben neben der Inklination auch eine Deklination auf, aber diese ist ein Hinweis auf Drehbewegungen der Lithosphärenplatte des Probenfundortes seit der Abkühlung (falls man die Bewegung dieser Platte überhaupt akzeptiert). Der einfache 2D Schnitt durch den Planeten ist dann durch etwas sphärische Trigonometrie zu ersetzen. Um zwischen den beiden oben erwähnten Alternativen – Bewegung des Dipols oder Bewegung der magnetitisierten Probe- zu unterscheiden, werteten Creer, Irving und Runcorn schliesslich die apparent polar wander paths von unterschiedlichen Lithosphärenplatten (damals hiessen diese einfach noch Erdteile) aus: ergibt sich für verschiedene Erdteile dieselbe scheinbare Polwanderungskurve, dann ist dies ein starker Hinweis auf eine tatsächliche Polbewegung (oder eine gemeinsame Bewegung aller Platten relativ zur Rotationsachse). Creer, Irving und Runcorn erhielten aber sehr unterschiedliche Polwanderungskurven für verschiedene Kontinente, und dies war der erste geophysikalische Nachweis von Relativbewegungen der Platten zu einander. Allerdings war die Durchschlagskraft des Arguments begrenzt durch das begrenzte Auflösungsvermögen paläomagnetischer Messungen: Jede einzelne Probe konnte nach der Aufprägung der remanenten Magnetisierung durch tektonische Prozesse ‚gekippt‘ (um eine horizontale Achse verdreht) werden, wodurch die Inklination der Probe verfälscht wird. Man führt deshalb eine statistische Mittelung über unterschiedliche Proben aus der gleichen geologischen Einheit (etwa gleiches Abkühlungsalter) durch; und erhält neben einem Mittelwert für die Lage des VGP auch ein Varianz-Mass für eine gewisse Trefferwahrscheinlichkeit: Der ‚wahre‘ VGP liegt mit dieser Wahrscheinlichkeit innerhalb eines Kegels mit dem halben Öffnungswinkel , und 20 würde (in mittleren Breiten) auf eine Ungenauigkeit der zu bestimmenden Kobreite von 2*10° führen. Während dieses Problem durch eine Mittelung über genügend viele Proben verringert werden kann, erfordert die sogenannte viskose Remanenz zusätzliche Labortechniken: Die natürliche remanente Magnetisierung NRM besteht neben der Thermoremanenz TRM – sozusagen das Nutzsignal des Paläomagnetismus – auch aus dieser VRM, eine langsamen magnetischen Nachwirkung, die dadurch entsteht, das die magnetisierbare Probe auch nach der Abkühlung noch dem Magnetfeld der Erde ausgesetzt ist, u.U. mit anderen Richtungen als zur Zeit der Abkühlung. Magnetic cleaning bezeichnet die Entfernung dieses Störsignals vor der paläomagnetischen Auswertung, durch schrittweise Abmagnetisierung der Probe (As-Zijderveld, 1958), entweder durch Erhitzen bis fast zur Curietemperatur, oder durch eine Wechselfeldentmagnetisierung. Deklination und Inklination der Probe während der Abmagnetisierung werden in Zijderveld-Diagrammen dargestellt, als Richtung der ‚sauberen‘ TRM werden D und I kurz vor dem Verschwinden der Remanenz angenommen. Zwar machte das magnetic cleaning die paläomagnetischen Daten konsistenter, aber die Zweifler wiesen darauf hin, dass die Dipolhypothese der Paläomagnetismus letztendlich nicht beweisbar ist. Diese Hypothese besagt, dass der scheinbare Dipol, über kurze geologische Zeiträume (100000a) gemittelt, stets parallel zur Rotationsachse ausgerichtet ist; nur wenn dies stimmt, kann die Nord-SüdPosition der Probe während der Abkühlung aus tan I 2 cot bestimmt werden. Die zeitliche Mittelung ist notwendig, weil wegen der Säkularvariation des erdmagnetischen Hauptfeldes die Dipolachse häufig gerade nicht genau parallel zur Rotationsachse ausgerichtet ist – z.Z. ist der Dipol um 11° gegen die Rotationsachse verdreht. Bei der Arbeit im Gelände werde Proben mit nur etwa dem gleichen Abkühlungsalter (z.B. aus verschiedenen Lavaströmen des gleichen Vulkans) genommen werden und die Säkularvariation dadurch herausgemittelt. Für die letzten 100000 Jahre ist die Dipolhypothese bewiesen (in dieser Zeit haben sich die Platten nur um wenige km bewegt, d.h. die für verschiedene Zeitpunkte innerhalb der letzten 100000 a gefundenen VGP sind wirklich geomagnetische Pole infolge der Säkularvariation, sie gruppieren sich tatsächlich um den geographischen Nord- bzw. Südpol). Da für ältere geologische Zeiten zwischen Platten- und Dipolbewegungen nicht so einfach unterschieden werden kann, ist man dort auf Plausibilitätsbetrachtungen angewiesen: 1) In der zur Beschreibung des Geschwindigkeitsfeldes im flüssigen äusseren Erdkern modifizierten Navier-Stokes-Gleichung überwiegen zwei Terme: der Coriolis- und der Lorentzterm, und sie sind etwa gleich gross (während z.B. Trägheitskräfte gegenüber Corioliskräften vernachlässigbar sind), also spielt die Rotation ber der Aufrechterhaltung des Magnetfeldes eine Rolle. 2) Die starken Magnetfelder von Jupiter und Saturn haben auch Dipolterme, die einen etwa zur Rotationsachse parallelen Dipol beschreiben (Uranus und Neptun aber nicht....) 2.2 Umkehrungen des Magnetfeldes und seafloor spreading Seit Brunhes (1906) wurden auch Proben mit inverser Magnetisierung gefunden (d.h. D und I sind gegenüber den zum Fundort gehörenden Werten um 180° verdreht). Nach der Entdeckung der Selbstumkehr der remanenten Magnetisierung (Néel, 1948) wurde etwa 10 Jahre über die Alternativen „Selbstumkehr der remanenten Magnetisierung der Proben“ oder „Feldumkehr des erdmagnetischen Hauptfeldes“ gestritten. Entschieden wurde die Frage mit Hilfe der Magnetostratigraphie, der Ableitung einer zeitlichen Folge von Umpolungen aus der Analyse von magnetisierten Sedimenten. Weil dabei für ganz verschiedene Testgebiete dieselbe Umpolungsfolge herauskam, wurde die Feldumkehr akzeptiert. Wir wissen heute, dass die Umpolungsfolge fraktal ist: Wenn die Epochen gleicher Polarität, die sog. Chrons, in Grössenklassen eingeteilt werden, dann führt die Darstellung von log(Anzahl pro Klasse) als Funktion von log(Länge der chrons dieser Klasse) auf eine Gerade mit negativer Steigung. Für die Plattentektonik wurde diese fraktale Umpolungsfolge wichtig, nachdem Mason (1958) bei der Auswertung der magnetischen Daten eines Forschungschiffes, das vor der Küste von Oregon gemessen hatte, magnetische Streifenmuster entdeckte: Offenbar hat die ozeanische Kruste eine remanente Magnetisierung, die streifenweise der heutigen und der entgegengesetzten Polarität des Erdmagnetfeldes entspricht. Diese magnetischen Streifenmuster wurden in den folgenden Jahren überall in der ozeanischen Kruste entdeckt. Vine und Matthew (1963) zeigten schliesslich, dass die Ortsfolge, die sich aus einem Schnitt senkrecht zu den Streifenmuster von Mason ergibt, mit der Zeitfolge der Magnetostratigraphie korreliert, wenn sich zwei ozeanische Platten mit v 3cm / a von einem mittelozeanischen Rücken wegbewegen. Wenn dort Lava austritt und bei der Abkühlung unter die Curie-Temperatur eine remanente Magnetisierung in Richtung des dann existierenden äusseren Feldes erfährt, dann folgt aus der Kombination von zeitlicher Feldumkehr und Plattenbewegung die räumliche Folge von remanenten Magnetisierungen der ozeanischen Kruste mit der heutigen bzw. der dazu inversen Richtung. Die Arbeit von Vine und Matthew (1963) entschied also die bei Fragen „Selbstumkehr oder Feldumkehr“ und „Horizontale Plattenbewegung – ja oder nein?“ gleichzeitig zu Gunsten der Feldumkehr und der Plattenbewegung. Historische Randbemerkung: Vine & Matthews (1963) waren nicht die ersten. 1962 hatte Lawrence Morley eine Arbeit mit der gleichen Hypothese bei ‚Journal of Geophysical Research‘ eingereicht, die aber abgelehnt wurde mit der Begründung, die Hypothese würde nur einen guten Party-Gag hergeben. 2.3 Rekonstruktion der Plattenbewegungen Wegen der o.g. Nebenbemerkung zu B 0 können aus einer Folge von VGPs einer Platte mit verschiedenen Abkühlungsaltern nicht die Positionen der Platte zu diesen Zeiten bestimmt werden. Die Informationen reichen lediglich, um die Paläobreiten sowie die Verdrehungen der Platten (relativ zur heutigen Lage) anzugeben. Zusätzliche Informationen: Zwei Kontinentalplatten können nicht zur gleichen Zeit am gleichen Ort gewesen sein. Ausserdem lässt sich u.U.aus den Streifenmuster der letzten maximal 250 Millionen Jahre die Bewegungsrichtung (nämlich senkrecht zu den Streifen) rekonstruieren (Nebenbemerkung: Ältere ozeanische Kruste gibt es nicht mehr, weil die bereits wieder subduziert worden ist. Wenn VGPs von heute verschiedenen Platten vor einem geologischen Alter plötzlich zusammengehen, ist dies ein Hinweis auf das ‚Zerbrechen‘ ein Paläoplatte – z.B. der Zerfall von Godwanaland vor 200 Millionen Jahren zu Afrika, Südamerika, Indien, Antarktika und Australien. Wenn VGPs nach einem geologischen Alter zusammengehen, ist dies ein Hinweis auf Kontinententstehung durch das ‚Zusammenbacken‘ von sogenannten Teraenen, also streifenförmige Mini-Kontinente – z.B. die Entstehung Mitteleuropas aus Rhenoherzynikum, Saxothuringikum und Moldanubikum. Merken sollte man sich Während des Perm (225 Millionen Jahre) hingen fast alle Platten zusammen, Superkontinent Pangaea Während des Trias (200 Millionen Jahre) 2 Superkontinente: Laurasia (Nordamerika, Europa, Asien ohne Indien) und Godwanaland (Südamerika, Afrika, Antarktika, Australien, Indien und Neuseeland) Schliessung des Iapetus Ozeanes (Protoatlantik) von 160 Millionen Jahren, dabei Austausch von Mikroterraenen: Heutiges Schottland, Nordirland vor dieser Schliessung mit Nordamerika verbunden; gleichzeitig war New Brunswick vor der Schliessung mit ‚Avalonia‘ (=England, Nordfrankreich) verbunden. Fast-Schliessung der Tethys (Rest-Tethys = heutiges Mittelmeer) seit 180 Millionen Jahren (Trias) und Subduktion der europäischen unter die afrikanische Platte; in der Folge alpine Gebirgsbildung mit Höhepunkt im Tertiär. Indien bewegte sich in nur 60 Millionen Jahren 60 Breitengerade nordwärts: mittlere Plattengeschwindigkeit 11 cm/Jahr – Beginn der Himalya-Faltung seitdem. 3. Konvektion Konvektion ist Wärmetransport durch Materialtransport. Dass dieser Prozess für grossräumige Bewegungen von Mantelmaterial verantwortlich sein kann und deshalb u.U. die antreibenden Kräfte der ‚Kontinentalverschiebungstheorie‘ bereitstellt, hat Holmes (1931, 1933) als erster vorgeschlagen, während Haskell (19737) die Viskosität des Erdmantels mit Hilfe der nacheiszeitlichen Hebung Skandinaviens bestimmt hat. Das Ergebnis war, dass die Viskosität mit 10 20 Pa * s noch um Grössenordnungen unter der Grenz-Viskosität liegt, bei der Konvektion einsetzt. Die meisten Geowissenschaftler der 30 er Jahre des letzten Jahrhunderts waren hiervon nicht beeindruckt – in der traditionellen Geologie kommt das Konzept der Viskosität nicht vor. Die harten paläomagnetischen Daten, die schliesslich tatsächliche Plattenverschiebungen nachwiesen, waren ja auch erst in der 50er und 60er Jahren gefunden worden – warum so spät? Die wichtigsten Daten kamen vom Ozeanboden (s. Kap. 2), der erst dann technisch zugänglich war. Das Modell von der Konvektion im Kochtopf, bei der die Herdplatte den heissen Erdkern und die Suppe den konvektierenden Mantel symbolisiert, ist zu einfach: Der Mantel selbst enthält zusätzlich Energiequellen (radioaktives Material), und auf dem beweglichen (viskosen) Teil des Mantel befindet sich die in einzelne Platten zerfallene, spröde Lithosphäre. 3.0 Der adiabatische Temperaturgradient, oder Konvektion aus der Sicht eines kleinen Massenelements Eine notwendige Bedingung für das Auftreten von Konvektion in einer Flüssigkeit ist ein Temperaturgradient (o.E. in vertikaler Richtung). Wenn ein Massenelement ein wenig nach oben verschoben wird, adiabatisch (dh ohne Wärmeaustausch mit seiner Umgebung), wird es wegen des geringeren Druckes kühler. Wenn seine neue Temperatur gerade die Umgebungstemperatur ist, dann heisst der in dem Medium auftretende Temperaturgradient adiabatisch. Bei einem geringeren Temperaturgradienten ist das Massenelement jetzt kühler und dichter als seine Umgebung, und sinkt wider nach unten – da wir an infinitesimal kleine Verschiebungen denken, passiert in Wirklichkeit gar nichts, das Medium ist stabil geschichtet und Konvektion findet nicht statt. Wenn der tatsächliche Temperaturgradient aber höher als der adiabatische ist, dann ist das Massenelement oben heisser und weniger dicht als seine Umgebung, und es wird auftriebsbedingt weiter aufsteigen. Das Medium ist dann unstabil, und spontane Konvektion tritt auf (nach F. Stacy p. 303). 3.1 Wärmetransport und Rayleighzahl In einer von unten geheizten Flüssigkeitsschicht wird die Wärme mit Konduktion (Wärmeleitung) und Konvektion nach oben transportiert. Welcher dieser beiden Prozesse dominiert, hängt von der dimensionslosen Rayleighzahl Ra gTh 3 die sich beim Übergang von der Navier-Stokes- und derWärmeleitungsgleichung auf dimensionslose Variable ergibt. ( Dichte der Flüssigkeit, g Schwerebeschleunigung, Koeffizient der thermischen Ausdehnung, T Temperaturdifferenz zwischen unten und oben, h Mächtigkeit der Schicht, Temperaturleitfähigkeit und Viskosität der Flüssigkeit). Offenbar stehen die die Konvektion unterstützenden Parameter im Zähler von Ra . Die h 3 Abhängigkeit gilt streng nur für die hier benutzte für zweidimensionale Geometrie, für die jetzt folgende Überschlagsrechnung ist dies aber ausreichend. Es lässt sich zeigen (Übung in GA Kap.5), dass im einfachsten zweidimensionalen Modell die Konvektion einsetzt, wenn Ra 1000 . Mit 4000kg / m3 , g 10m / s 2 , 2 1 kg 6 6 m 3 *10 , T 3000K , h 2.9 *10 m, 10 , 10 21 K s m*s 6 23 erhalten wir für den Erdmantel Ra 8.6 *10 und Pr 2.5 *10 . 5 Mit zunehmenderRayleighzahl haben wir zunächst nur Konduktion, dann immer schneller rotierende, zunächst aber noch stationäre Konvektionszellen, und schliesslich turbulente Konvektion, bei der diese Konvektionszellen ihre Lage, Grösse und Form chaotisch verändern. Ist Mantelkonvektion chaotisch? Eine analytische Lösung für den zeitlichen Verlauf des Geschwindigkeitsfeldes in der Flüssigkeit gelingt nur, wenn das sich aus der Navier-Stokes- und Wärmeleitungsgleichung ergebene Gleichungssystem (3.14, 3.15) stark vereinfacht wird, dann ergeben sich als Lösung für die o.g. schwach überkritische Rayleighzahl stationäre Konvektionswalzen. Lorenz (1963) hat für eine etwas weniger starke Vereinfachung ein System von drei nichtlinearen Differentialgleichungen angegeben, deren Lösung nur noch numerisch möglich ist; der zeitliche Verlauf des Geschwindigkeitsfeldes ist hier bereits chaotisch (D. Turcotte, Fractals and Chaos in Geology and Geophysics, 2nd edition, Cambridge University Press 1997). Die numerische Lösung von noch komplizierteren (und realistischeren) Gleichungssystemen ist eine Aufgabe der -> Geodynamik. Wenn die untersuchten Systeme chaotisch sind, hängt der zeitliche Verlauf sehr stark von winzigen Änderungen der Anfangsbedingungen ab. Es ist also nicht möglich, den tatsächlichen Verlauf der im Mantel stattfindenden Konvektion zu simulieren; stattdessen erhält die Geodynamik simulierte Systeme, die bestimmte statistische Eigenschaften der natürlichen Konvektion reproduzieren können – etwa die mittlere Verteilung der auftretenden Geschwindigkeiten, wie sie vom Paläomagnetismus und aus GPS Messungen bekannt sind. Nebenbemerkung. Konvektion haben wir auch im flüssigen äusseren Kern der Erde, dort ist die Viskosität um 20 Grössenordnungen geringer als im Erdmantel und die Raleighzahl entsprechend grösser. Typische Geschwindigkeitsfelder haben dann, gegenüber einigen cm/jahr (s. Kap 2), Amplituden von 20 km/Jahr, dies ist an der Säkularvariation des Erdmagnetfeldes direkt ablesbar. Gebremst wird die Kern-Konvektion auch nur kaum durch die Viskosität, sondern durch die Rückwirkung des Erdmagnetfeldes auf das Geschwindigkeitsfeld im äusseren Kern.(Erinnerung: Für das ‚Monitoring‘ von Plattenbewegungen mit Hilfe des Paläomagnetismus ist die Säkularvariation ein Störsignal, dass durch Variation des Abkühlungsalters der untersuchten Proben über Zeiträume, die gross im Vergleich zur Säkularvariation (1000 Jahre), aber klein im Vergleich zu geologischen Zeiträumen (während derer sich die Platten nennenswert bewegen, 10 7 Jahre) herausgemittelt werden muss). 3.2 Der Maxwell’sche Modellkörper In Kap. 1.2 hatten wir bereits gesehen, dass die Konzepte ‚Viskosität‘ und und Scherwellenausbreitung sich nicht widersprechen müssen: Damit sich Scherwellen ausbreiten können, muss die Viskosität nur deutlich grösser sein als das Produkt von Umgebungsdruck und Eigenperiode, und für seismische Wellen mit der Periode 20 s ergab sich ein Grenzwert, der 8-9 Grössenordnungen unter der tatsächlichen Mantelviskosität lag. Auch für die tiefsten Eigenschwingungen der Erde mit Perioden um 3200s ist der Mantel ‚fest‘. Dagegen würde das o.g. Kriterium für Schwingungen mit der Periode 108 Jahre 3 *1015 s - etwa die Dauer eines overturns bei der Mantelkonvektion - nicht mehr reichen; auf dieser Zeitskala ist der Mantel also flüssig. Genaueres in ‚Rheologie der Erde‘ ! Anschaulich beschrieben wird dieses Verhalten durch den Maxwell’schen rheologischen Modellkörper, der aus einer Reihenschaltung des Hooke’schen (‚Feder‘) und des Newton’schen (‚Spritze‘ oder ‚Stossdämpfer‘) Modellkörpers besteht – er reagiert auf kurzzeitige Kräfte elastisch und auf langsame viskos. Eine Flüssigkeit heisst ‚Newton’sche Füssigkeit (Newtonian viscous fluid), wenn der Zusammenhang zwischen Druck (oder Spannung) und Veformungsrate linear ist, d.h. wenn t die Viskosität in t nicht vom Druck abhängt. Dies ist streng nicht der Fall, weil Viskosität innere Reibung beschreibt, die auf thermische Dissipation führt (irgendwo muss die bei dieser Reibung freiwerdende Energie schliesslich hin), und die Verformung ist natürlich auch temperaturabhängig. Für einfache geodynamische Modellrechnungen wird die Newton’sche Flüssigkeit dennoch benutzt. (Im Gegensatz zum Modellkörper mit Reihenschaltung von ‚Feder‘ und ‚Spritze‘ ist der andere, der aus einer Parallelschaltung der beiden o.g. Teile besteht, millionfach technisch realisiert – in Autos.) 4. Von der Konvektion zur Plattentektonik Wenn wir jetzt noch einige Lithosphärenplatten auf die Konvektionszellen packen, haben wir eine ‚Plattentektonik‘ , in der (im Gegensatz zur Kontinentalverschiebungstheorie) die Konvektion der verantwortliche physikalische Mechanismus ist. Wieder ist das Modell noch zu einfach: Während in den ersten Modellen die Lithosphärenplatten nur passive ‚Reiter‘ auf den Konvektionszellen waren, haben wir jetzt Hinweise darauf, dass die Bewegung dieser Platten selbst – etwa das Eintauchen eines subduzierten Slabs in den Mantel - eine der die Konvektion treibenden Kräfte ist. Bisher gar nicht verstanden ist die Koexistenz von Konvektionszellen und sogenannten Plumes, unter denen man sich ‚schnelle‘ Aufströme von heissem Material vorstellt. Einige Wissenschaftler glauben, dass solche Plumes für das Auseinanderbrechen der alten Superkontinente verantwortlich sind. So ist etwa der jetzige Hotspot Tristan da Cunha ein Überbleibsel von einem Plume, der 200 Millionen Jahren eine besonders hohe Förderleistung hatte und sich zudem genau unter Südamerika und Afrika befand (damals als Teil von Godwanaland zusammenhängend). 4.1 Plattenbewegungen ‚Lithosphäre‘ bezeichnet die Kruste und den obersten Teil des Mantels der Erde, der soweit abgekühlt und ‚versteift‘ ist, dass in ihm keine Bewegungen mehr stattfinden können – die Lithosphäre kann also nur ‚als Ganzes‘ der Konvektionsbewegung folgen. Da diese aber an unterschiedlichen Stellen unterschiedliche Richtungen annimmt, zerbricht die Lithosphäre zu Lithosphärenplatten, deren Kollision zu Subduktion und deren Auseinanderdriften zu mittelozeanischen Rücken führen. Es gibt zwei grundsätzlich unterschiedliche ‚Sorten‘ von Lithosphäre, die kontinentale und die ozeanische. Altersbestimmung mit Hilfe der Radioaktivität: Während kontinentale Lithosphäre bis zu 3.5 Milliarden Jahre alt sein kann, hat man keine ozeanische L., die älter als 250 Millionen Jahre alt ist , gefunden – warum? Diese Zeit ergibt sich als Verhältnis von der Grösse der grössten (pazifischen) Platte zur mittleren Driftgeschwindigkeit, wie sie historisch mit seafloor spreading (s. Kap 2.2) und heute mit dem global positioning system GPS gefunden wird. Dies ist gar nicht so unproblematisch, denn relativ zu was soll man eigentlich die Bewegung messen? Mehr dazu in Kap. 4.3 beim hot spot reference frame Mehr zu den Wechselwirkungen zwischen den verschiedenen Lithosphären in Kap. 5. Die Annahme einer ‚steifen‘ oder spröden Lithosphäre, die unter zu starken Spannungen zerbricht (anstatt sich plastisch zu verformen) ist auf einer planetaren Längenskala zulässig; wenn man dagegen Viskosität und Schermodul innerhalb der Lithosphäre betrachtet (-> Rheologie der Erde), ist dies nicht richtig, weil in der unteren Kruste auch plastisches Fliessen auftritt. Eine Übersicht über die heutigen Platten: (Jeder kennt:) AN, Antarktika; AU, Australia; EU, Eurasia, NA North America; NB Nubia (d.h.Afrika); PA, Pacific; SA, South America (Wer diese Vorlesung gehört hat, sollte noch diese kennen:) AR, Arabia; B, Borneo; CA, Caribbean; CO, Cocos; IN, India; JF, Juan de Fuca; NZ, Nazca; SC,Scotia Sea; SM, Somalia (Bei der 3. Gruppe sind die Grenzen nicht so klar und zT nicht durch Subduktion oder mittelozeanischen Rücken, sondern durch starke Seismizität definiert) CL, Caroline; I, Indo-China, NC North China; OK Okhotsk; Y, Yangtze Wir nehmen die Vorstellung der realexistierenden Platten zum Anlass, drei verschiedenen Szenarien von Platten-Relativbewegungen zu definieren: ridge – die Platten bewegen sich auseinander (mittelozeanischer Rücken, z.B. mid atlantic ridge und east pacific rise), trench – die Platten bewegen sich gegeneinander, so dass eine abtauchen muss (Tiefseegraben, z.B. Tonga-Fidji oder Mariannen), und transforms – die Platten verschieben sich horizontal gegen einander (Transformstörung, z.B. SüdNeuseeland). Die Kinematik der Platten beschreiben wir zunächst, unter der Annahme, dass die Erde eine Scheibe ist, mit Euler Polen (dieses Konzept lässt sich dann gut auf eine kugelförmige Erde übertragen, s.u.). Kinematik bedeutet Beschreibung der Bewegungen, jedoch (im Gegensatz zur Dynamik) nicht eine Suche nach den Ursachen der Bewegung – die Einordnung dieser Kinematik in 4.1 ist also etwas zufällig, aber wir können einige der hier eingeführten Begriffe am Ende von Kap. 4.2, wo wir zwischen den beiden Szenarios ‚konvektionsgetriebene Plattentektonik‘ und ‚Plattengetriebene Konvektion‘ unterscheiden wollen, ganz gut gebrauchen. Die einfachste Plattenbewegung auf einer platten Erde ist eine kreisförmige Platte, die um ihren Mittelpunkt rotiert. Dieser Mittelpunkt ist ihr Euler Pol, und der gesamte Rand der Platte ist eine Transformstörung, längs derer die kreisförmige Platte sich relativ zu einer anderen, sie umgebenden Platte bewegt. Eine etwa realistischere Plattenbewegung entsteht, wenn sich anstelle eines Vollkreises nur ein Kreissegment verdreht, und der Euler Pol jetzt wieder der Punkt ist, um den sich die Platte dreht, dieser Pol möge aber ausserhalb des Kreissegments liegen (Zeichnung!) Wenn das Kreissegment wie ein Tortenstück aussieht, haben wir am äusseren und am inneren Kreisausschnitt wieder Transformstörungen, an einer radialen Plattengrenze ein rift und an der anderen einen trench. Wenn wir keine Kreisbewegung, sondern eine einfache lineare horizontale Verschiebung wollen, muss der Abstand der Platte zu ihrem Euler Pol unendlich sein. Diese letzte Bedingung zeigt schon eines der Probleme mit der Erde als Scheibe! Beim Übergang zu einer kugelförmigen Erde entspricht dem Euler Pol im Unendlichen jetzt ein solcher im Pol im Abstand von 90° (auf einem Grosskreis), und der linearen Verschiebung entspricht eine Verschiebung längs eines Grosskreises. Vom Euler Pol aus gesehen ist diese Verschiebung aber eine Drehbewegung! Jede Plattenbewegung auf der Kugeloberfläche kann und muss als Drehbewegung verstanden werden. Den Euler Pol findet man, wie bei der ebenen Erde, indem man an mindestens zwei Stellen einer Transformstörung je eine zur TS senkrechte Linie (eine Art Radiusvektor in Bezug auf den Euler Pol) konstruiert, der EP ist der Schnittpunkt diese Linien. Beim Vergleich des Tortenstück-Modells (mit gebogenen Transformstörungen und zu denen senkrecht senkrechten rifts) mit realen Daten (sehr gut: der mittelatlantische Rücken im Südatlantik!) müssen wir das Bild von den kreisförmigen Transformstörungen noch dahingehend abgeändert, dass die Transformstörungen von kurzen, aber wieder auf ihnen senkrechten, rifts unterbrochen werden. Der im Grossen Nord-Süd verlaufende mittelatlantische Rücken setzt sich also aus vielen kleinen TS und rifts zusammen, weil Plattentektonik auf einer Kugeloberfläche nur Drehbewegungen zulässt. – Beim Finden des Euler Pols muss noch zwischen scheinbarem und wahren Trend der Transformstörungen unterschieden werden, letzteren findet man durch der Verschieben der TS längs der rifts, so dass sich wieder ein durchgehendes Kreisstück ergibt. Zwei weitere Methoden, den Euler Pol zu finden: 1) slip vectors, mit denen die Ausbreitungsrichtung von an Transformstörungen entstandenen S Wellen (und damit die Richtung der transform) gefunden wird. 2) Mit Hilfe des seafloor spreading (Kap. 2.2) wird die lineare Plattengeschwindigkeit (z.B. in mm/jahr) als Funktion des Abstandes vom (angenommenen) Euler Pol gemessen (Zeichnung); für ein ridge entlang eines Grosskreises mit zwei Euler Polen im Abstand von 180° ergibt dies eine Sinuskurve mit v 0 an den EP und v vmax in der Mitte, nur für einen falsch angenommen Euler Pol verschiebt sich dieses Maximum. Jetzt wird auch klar, warum Plattenbewegungen nicht wirklich in mm/jahr, sondern in °/my (Grad pro Millionen Jahren) angegeben werden. 4.2 Plattengetriebene Konvektion Im Modell der konvektionsgetriebenen Plattentektonik hat die Plattenbewegung keine Rückwirkung auf das Geschwindigkeitsfeld, d.h. auf die Bewegung des Mantelmaterials. Zumindest 3 Mechanismen für eine solche Rückwirkung sind aber vorstellbar: 1) slab pull: der bei der Subduktion in den Mantel abtauchende Teil ozeanischer Lithosphäre ist kühler und deshalb dichter als der umgebende Mantel, er ‚fällt‘ in diesen; der Vorgang stellt Bewegungsenergie zur Unterstützung der Konvektion bereit. Quantitative Abschätzung: Ein Slab (=subduzierende Platte) der Mächtigkeit d und Breite W möge bis zur Tiefe D in den Mantel mit einem Temperaturunterschied T zwischen z=0 und z=D eintauchen. Seine Dichteanomalie (bei einem mittleren Temperaturunterschied T / 2 zum umgebenen Mantel) und sein Volumen sind T und dWD; die (nach unten gerichtete) Auftriebskraft ist also FB ( T / 2)dWDg . Diese ‚negative‘ Auftrieb wird durch viskose Reibung kompensiert, die zugehörige Kraft kann, wie im Laborversuch, als proportional zur Viskosität , Fläche DW und Plattengeschwindigkeit v so wie umgekehrt proportional zur ‚Mächtigkeit der Flüssigkeits-Schicht‘ angenommen werden. Als Mächtigkeit wählen wir die halbe Länge L/2 der Platte – in der Annahme, dass L auch die (horizontale) Grösse einer Konvektionszelle ist und dass die Flüssigkeit zwischen der Subduktionszone und einem hypothetischen Fixpunkt in der Mitte der Konvektionszelle geschert vDW wird: FV L/2 Aus der Gleichsetzung FB FV ergibt sich die Geschwindigkeit des abtauchenden slabs v TdLg 4 Wir übernehmen 2 1 6 m , 10 , 4000kg / m , g 10m / s , 3 *10 K s aus Kap. 3, aber T 1400K (Temperaturunterschied nicht für den ganzen Mantel, sondern nur 3 2 5 zwischen ‚unten‘ und ‚oben‘ bezüglich des abtauchenden slabs) und 10 22 kg , und setzen m*s noch L 3 *10 6 m , und wählen als Mächtigkeit des slabs d=30000m, und erhalten v 3 *10 9 m / s 0.1m / Jahr . 2) ridge push: Die ozeanische Platte verjüngt sich – nicht nur in bezug auf ihr Alter, sondern auch in bezug auf ihre Mächtigkeit, zum Mittelozeanischen Rücken hin. Dort entsteht also eine Art schräger Rampe, auf der die Platte herunterrutscht – auch dieser Vorgang stellt Bewegungsenergie zur Unterstützung der Konvektion bereit. 3) Durchgang der subduzierenden Platten durch Phasengrenzen im oberen Mantel. Phasengrenzen (PG) wurden wegen des sprunghaften Anstiegs der seismischen Geschwindigkeiten zuerst mit seismologischen Methoden gefunden. An der PG in 410 km Tiefe ändert sich die Kristallstruktur des Olivins (Mg , Fe) 2 SiO4 , aus dem der obere Mantel grösstenteils besteht, vom Olivingitter zum sog. Spinellgitter (dichtere Kugelpackung. Das Material ist weiterhin Olivin, der Name des Kristallgitters ist von dem Halbedelstein Spinell entlehnt, der das gleiche Gitter hat. Diese Phasengrenze ist physikalisch, nicht chemisch, weil die Komposition des Materials sich nicht ändert). An der PG in 660 km Tiefe ändert sich auch die chemische Komposition, und unterhalb haben wir anstelle des Olivins Perovskit (Mg , Fe) SiO3 und Magnesiowüstit (Mg , Fe)O . Die Phasengrenze in 410 km Tiefe ist exotherm – dies bedeutet, dass sie im p-T Diagramm durch eine monoton steigende Funktion dargestellt wird (positiver Clayperon slope): Zu einer niedrigeren Temperatur gehört, an der PG, ein niedrigerer Druck. Ein abtauchende, kalte Platte (jawohl, sie ist auch nach 100 Millionen Jahren noch kälter als der sie umgebende Mantel – wer es nicht glaubt, berechne bitte die Abkühlzeit bei der geothermischen Diffusion, in Abhängigkeit von der Grösse des zu kühlenden Körpers) verringert also den Druck an der PG, so dass sich die dichtere, unter der PG befindliche Hochdruckphase scheinbar der Platte ‚entgegenwölbt‘ und eine positive Dichteanomalie erzeugt, die zu einem zusätzlichen gravitativen Zug nach untern führt – dies ist vermutlich ein effektiverer slab pull als der unter 1) genannte Mechanismus. Dagegen ist die Phasengrenze in 660 km Tiefe endotherm und der Clayperon slope ist negativ: Alle o.g. Argumente drehen sich jetzt um diese PG ‚behindert‘ das Eintauchen der Platte in den unteren Mantel. Nb. Jetzt kann man sich natürlich fragen, ob die subduzierenden Platten es überhaupt bis in den unteren Mantel ‚schaffen‘. Viele Studien in seismischer Tomographie in den 90er Jahren fanden Übereste von ozeanischen Platten, die entweder horizontal an der 660 km PG ‚entlangschrammen‘ oder aber in den unteren Mantel vordringen. Die o.g. Frage ist wegen des geringen räumlichen Auflösungsvermögens von seismischer Tomographie in diesen Tiefen nur schwer zu beantworten – als wahrscheinlichst Antwort gilt heute ‚es gibt beide Szenarien‘. Bis jetzt haben wir 3 mögliche Rückwirkungen der Plattentektonik auf das Geschwindigkeitsfeld im Erdmantel kennengelernt, so dass „plattengetriebene Konvektion“ gegenüber „Konvektionsgetriebener Plattentektonik“ zumindest möglich erscheint. Können wir das ‚Funktionieren‘ beider Szenarios in Bezug auf ihre Vorhersagen zum Auftreten von ridges, transforms und trenches, wie in 4.1 eingeführt, gegen einander abwägen? Ja, nämlich anhand von 1) Ridge offsets, also der Beobachtung, dass wir anstelle langer ridges Transformstörungen haben, die von kurzen, aber wieder auf ihnen senkrechten, rifts unterbrochen werden. Im Bild der konvektionsgetriebenen Plattentektonik sollten wir stattdessen lange ridges sehen, die genau über den Aufströmen zwischen den Konvektionszellen liegen. Das 2. Szenario erklärt das Auftreten der ridge offsets besser, weil ein grossräumiger mittelozeanischer Rücken wie der atlantische (der in Wirklichkeit aus kurzen ridges und transforms besteht), nicht notwendig der Grenze zwischen zwei Konvektionszellen folgen muss – nur die transforms geben die tatsächliche Richtung desMantelflusses an. 2) Jumping ridges, also die Beobachtung, dass ridges in Zeitabständen von wenigen Millionen Jahren ihre Lage und Richtung ändern können. Der jüngere ridge ist dabei senkrechter zur Richtung des spreadings als der ältere. Im 1. Szenario brauchen wir zur Erklärung schnelle Änderungen der Lage von kleinräumigen Konvektionszellen, im 2 .Szenario dagegen nur langsame Änderungen der Konvektionsbewegung, auf die die ozeanische Lithosphäre mit der Ausbildung neuer Risse (cracks) reagiert. (Nach Cox & Heart – ist das wirklich überzeugend? Weiss doch keiner, wie chaotisch und auch kleinräumig die Konvektion wirklich ist....) 3) Ridge meets trench – was passiert eigentlich, wenn ein mittelozeanischer Rücken subduziert wird? Wenn, wie im 1. Szenario, ridges bzw. trenches genau über Auf- bzw. Abströmen von Mantel liegen, dann müsste jetzt die Konvektion selbst behindert werden, weil Auf- und Abstrom zusammenkommen und sich auslöschen. Im 2. Szenario wird nur die Platte zwischen ridge und trench verschluckt. 4.3 Die Plume-Hypothese Die meisten Vulkane auf der Erde sind durch Subduktion entstanden und befinden sich in unmittelbarer Nähe (max. 200 km) von Subduktionszonen – verkürzt dargestellt transportiert die Subduktion u.a. junge ozeanische Sedimente in den Mantel, und das darin enthaltene Wasser verringert die Schmelztemperatur und macht Schmelzen wahrscheinlicher als anderswo – Genaueres siehe Kap. 5. Es gibt aber auch 50 – 100 (diese Zahl wird später diskutiert) Intraplattenvulkane, deren Entstehung nicht mit den in 4.1 und 4.2 diskutierten Konvektionsmechanismen verknüpft zu sein scheint – ein Musterbeispiel ist Hawaii. Die Lage dieser Vulkane korreliert keineswegs mit den Plattengrenzen, aber ‚etwas‘ mit langwelligen Geodanomalien, die durch räumliche Temperaturvariationen im unteren Mantel entstehen. Die attraktivste Hypothese zur Entstehung dieser Intraplattenvulkane ist die von Wilson, dass sie Oberflächensignaturen von an der Kern-Mantelgrenze aufsteigenden Aufströmen verringerter Viskosität, sogenannter ‚Plumes‘ sind. Zur Unterscheidung von den ‚echten‘ Vulkanen wurden sie auch hotspots genannt. In den guten alten Zeiten (also bis etwa 1998) glaubten die meisten Geowissenschaftler, dass die Plumes fest an der Kern-Mantelgrenze ‚kleben‘ und die durch Konvektion verursachten Horizontalbewegungen nicht oder nur mit sehr viel geringerer Geschwindigkeit mitmachen; während die vertikale Geschwindigkeitskomponente des PlumeMaterials wegen der verringerten Viskosität um eine Grössenordnung höher ist als die der Plattenbewegungen – etwa 1m/a. Da wir an der Erdoberfläche nicht die Kernmantelgrenze, sondern die sich bewegenden Platten sehen, bot die Vorstellung von den stationären Plumes die Möglichkeit, einen festen Bezugsrahmen, den hot spot refence frame zu definieren, relativ zu dem sich das Mantelmaterial und die Platten bewegen. Die zunächst recht spekulative Hypothese hatte schnell Unterstützung der Geochemiker, die die chemische Komposition und vor allem Isotopenverhältnisse von Erdmaterialien untersuchen: Die chemische Zusammensetzung von Laven aus den hotspots und von Laven aus mittelozeanischen Rücken (MORB – mid ocean ridge basalt) erwies sich als unterschiedlich – ein Hinweis darauf, dass diese verschiedenen Vulkane aus verschiedenen Reservoiren gespeist werden, wenn auch kein Nachweis, dass die Plumes von der Kern-Mantelgrenze kommen. Schliesslich gibt es aber geochemische Hinweise darauf, dass das Material in den Plumes Überreste ozeanischer Kruste enthält, dies wäre dann eine Unterstützung der Hypothese von den bis in den untersten Mantel abgetauchten subduzierten Platten. Insgesamt kann als eine der stärksten Aussagen der Geophysik gelten, dass – infolge der Konvektion – das Material im Mantel vermischt wird; und als die wohl stärkste Aussage der Geochemie, dass bestimmte Reservoire gerade nicht vermischt werden. Die Vorstellung von den ortsfesten hotspots war nie ganz unangezweifelt: Wenn sie streng richtig wäre, müssten die anderen hotspots mit Vulkanen in der pazifischen Platte – z.B. Marquesa, Pitcairn und die Osterinseln – infolge der Plattenbewegung sea mount chains von der gleichen Form wie die Hawaii-Emporer chain produziert haben. Steinberger und O’Connell (1998) zeigten mit geodynamischen Modellrechnungen, dass die Konvektion die Plume-Aufströme verbiegen und ‚zerreissen‘ kann. Schliesslich sollen zusammen mit den Plumes noch die flood basalts erwähnt werden. Diese wirken zunächst wie (geologisch alte) Oberflächensignaturen von Plumes, nur mit einer um 10 4...108 höheren Förderrate an basaltischem Magma. Ein typisches Beispiel sin die indischen Deccan flood basalts, die heute als eine (auf einer geologischen Zeitskala) kurzfristige Erhöhung der Fördermenge des heute unter Reunion befindlichen hotspots vor 65 Millionen Jahren interpretiert werden. Da dieses Alter genau mit der Kreide-Trias Grenze zusammenfällt, wird der ‚Super-Vulkanausbruch‘ von einigen Autoren für das Massensterben am Ende der Kreidezeit verantwortlich gemacht. Genauso bekannt ist die Theorie, die einen gleichalten Asteroidenimpakt bei Chixilub (Yukatan) dafür verantwortlich macht (Alvarez et al. 1980, 1984). Für den Einfluss der flood basalts auf die Evolution spricht, dass etwa zeitgleich mit allen Massensterben (mass extinction events) der letzten 250 Millionen Jahre flood basalts aufgetreten sind (Courtillot, 1994, 2002). 5 Plattentektonik und Subduktion Subduktion ozeanischer Kruste an trenches (Tiefseegräben) war in der Kinematischen Betrachtung der Plattentektonik als Methode, Lithosphäre zu verschlucken, eingeführt worden – an rifts wird dagegen neue ozeanische Lithosphäre gebildet. Subduktion passiert auch, wenn ozeanische auf kontinentale Lithosphäre trifft, und in diesem Fall wird die dünnere ozeanische Lithosphäre unter die mächtigere kontinentale Lithosphäre subduziert. (Achtung: Es ist nicht wirklich die grössere Mächtigkeit, sondern die geringere Dichte, die die kontinentale Lithosphäre oben hält; dagegen unterstützt der Dichteüberschuss der abtauchenden, gegenüber dem umgebenen Mantel kühleren ozeanische Lithoshäre ihre Subduktion – Kap. 4.2) Die Frage, warum ozeanische Lithosphäre dünner ist als kontinentale, führt natürlich gleich auf die nächste Frage nach der Entstehung dieser beiden Lithosphärenarten, oder, noch fundamentaler: Warum gibt es überhaupt zwei grundsätzlich unterschiedliche Typen von Lithosphäre- mit Altersbandbreiten von 0-250 Millionen Jahren für die ozeanische, aber 0 – 3.5 Milliarden jahre für die kontinentale Lithosphäre? Und was passiert, wenn zwei Abschnitte kontinentaler Lithosphäre auf einander treffen? 5.1 Ozeanische Lithosphäre und Inselbögen Ozeanische Lithosphäre entsteht an mittelozeanischen Rücken (da diese nicht notwendig in der Mitte eines Ozeanes sein müssen – Beispiel East Pacific Rise – ist der Begriff ungeschickt, besser ridge, spreading center), wenn mid ocean ridge basalts (MORB) an die Oberfläche gelangen und abkühlen (hier wird die Diskussion der Frage vermieden, aus welcher Tiefe diese basaltische Lava kommt, und ob der Prozess Teil einer Konvektionszelle ist, s. 4.1 und 4.2). Die Mächtigkeit der Ozeanischen Lithosphäre ist über die thermische Diffusion direkt an ihr Abkühlungsalter und dieses, wie unter dem Stichwort seafloor spreading erklärt, an die Entfernung vom spreading center geknüpft: Solange die Plattengeschwindigkeit unverändert bleibt, gibt es eine lineare Beziehung zwischen dieser Entfernung und dem Alter, und dieses Alter ist wiederum mit der Eindringtiefe der geothermischen Diffussion verknüpft, wie wir es in 3.1 für die kennengelernt haben. Wenn wir also das Abkühlalter in horizontaler und die Eindringtiefe in vertikaler Richtung auftragen, ergibt sich eine liegende Parabel, die gerade die Mächtigkeit der (abgekühlten) ozeanischen Lithosphäre als Funktion des Abstandes vom ridge oder spreading center beschreibt. Wenn zwei ozeanische Lithosphärenabschnitte auf einander treffen, wird einer subduziert. Die Form dieser Subduktionszone im Kartenbild (Ansicht von oben) kann ein Bogen sein (Beispiel Aleutenbogen), dessen Krümmungsradius vom Abtauchwinkel abhängt. Weil Subduktion ein effektiver Transportprozess für (in Seesedimenten eingeschlossenes) Wasser ist, transportiert die Subduktion Wasser in den Mantel. Weil Wasser die Schmelztemperatur senkt, ist in etwa 100-150 km Tiefe die Schmelztemperatur in der Umgebung der abtauchenden Platte mit der tatsächlichen Temperatur (1000 °K) vergleichbar, so dass eine – vermutlich wässrige – Schmelze entsteht. (Einschub: Was ist Schmelztemperatur?) Diese ist für den Inselbogenmagmatismus verantwortlich: ‚Hinter‘ der Subduktionsfront entsteht eine ebenfalls bogenförmige Vulkankette, wobei der Abstand wieder vom Abtauchwinkel der subduzierenden Platte abhängt – bei 45° also 100-150 km. Beispiele für oz-oz Subduktion mit Inselbögen am Westrand der Pazifischen Platte sind Tonga, Neue Hebriden, Solomon-I., Mariannen, Kurilen, Aleuten, ausserdem Sunda-Banda südlich der Borneo Platte, sowie die kleinen Antillen und der Ostrand von Scotia Sea im Atlantik. 5.2 Gebirgsbildung I : Der aktive Kontinentalrand Wenn ozeanische Lithosphäre unter kontinentale subduziert, entsteht ein aktiver Kontinentalrand (was ist ein passiver KR?). Das Zusammenspiel von Subduktion und Magmatismus ist hier zunächst ähnlich wie bei der Kollision zweier ozeanischer Lithosphärenabschnitte; und 100 –150 km hinter der Subduktionsfront haben wir wieder Vulkanismus. Die geochemische Zusammensetzung der Schmelzen ist aber anders und sehr viel variabler als beim Inselbogenvulkanismus, ausserdem sind die Laven im Vulkanismus an aktiven Kontinentalränder reich an Silikaten. Dies und die grössere Variationsbreite der geochemischen Zusammensetzung kann zumindest qualitativ mit der Perkolation durch die kontinentale Kruste erklärt werden, bei der die Schmelze chemisch mit Krustenmaterial reagiert. Anders als bei der oz-oz Kollision verdickt sich die ‚obere‘ Platte (d.h. die kontinentale Lithosphäre wird über der Subduktion noch mächtiger). Die möglichen Gründe: Kompression in Richtung der Kollision, Anreicherung der Kruste durch Schmelzen, die nicht vollständig an die Erdoberfläche vordringen, und schliesslich Isostasie: Die beiden erstgenannten Mechanismen führen auf Gebirgsbildung, also entsteht wegen des unter 1.1 beschriebenen isostatischen Ausgleichs auch eine Gebirgswurzel (hist: Tatsächlich wurde die Isostasie zuerst am Beispiel eines aktiven Kontinentalrandes - Anden - quantitativ beschrieben (Airy, 1855; Pratt, 1855) der freilich damals nicht als solcher erkannt wurde). Mit geophysikalischer Exploration der Kruste wurde lange versucht(bis 1995?), Schmelzen in der Kruste zu erkennen – besonders mit Seismologie (Abschwächung der Amplituden seismischer Wellen durch Schmelzen) und Elektromagnetischer Tiefenforschung (Erhöhung der elektrischen Leitfähigkeit durch Schmelzen). Können aktive Kontinentalränder zur Entstehung kontinentaler Lithosphäre beitragen? Ein möglicher Mechanismus ist die Akkretion von von Mikrokontinenten (Terraenen‘), welche in die subduzierte ozeanische Lithosphäre eingechlossen sind, durch die kontinentale Platte. Zwar sind in der ‚jetzigen‘ geodynamischen Situation nur wenige solcher Mikrokontinente bekannt (Japan, Neuseeland), aber eine geologische Karte Nordamerikas zeigt, dass dieser Mechanismus für Bildung des Westteils Nordamerikas mit verantwortlich war. Auch Mitteleuropa.... Beispiele für aktive Kontinentalränder sind grosse Teile der amerikanischen Westküste: Cascaden, Mittelamerika, Anden; sowie Alaska (östlich des oz-oz Aleutenbogens). Schliesslich gibt es den aktiven Kontinentalrändern verwandte Subduktionssysteme unter den Kontinentalen Mikroplatten Japan, Neuseeland, Sumatra (westlich des oz-oz Inselbogens Sunda-Banda) und Agäis. 5.3 Gebirgsbildung II: Kontinent-Kontinent-Kollisionen Es gibt nur wenige Beispiele rezenter Kontinent-Kontinent Kollisionen, daher schwierig, allgemeine Regeln zu formulieren. Vermutlich keine Subduktion – soweit (zB mit seism. Methoden) Subduktionszonen sichtbar, enthalten diese vermutlich ozeanische Teile einer Lithosphärenplatte, die subduziert wurden, bevor der kontinentale Teil kam.- Beispiel: nach Süden abtauchende Krustenwurzeln unter den Alpen – Kollision der Europäischen mit der Nubischen Platte, Schliessung der Thetys, deren ozeanische Lithosphäre vorher subduziert wurde (ein kleiner Teil davon ist aber noch da, im Mittelmeer, aber vermutlich auch in den Kalkalpen) Wenn kein Material subduziert wird, was passiert dann damit? Es wird in die für den isostatischen Ausgleich notwendige Gebirgswurzel eingebaut. Beispiele für Kontinent-Kontinent Kollisionen sind das Himalaya und die Alpen. 5.4 Zusammenfassung: Der Wilson-Zyklus Wilson (1966) schlug ein Model zyklischer Kontinentalverschiebung vor, dabei war das Öffnen und Schließen des Atlantischen Ozeans das Vorbild. Der Wilson-Zyklus beginnt mit dem Aufbrechen eines Kontinents längs eines rift valley (‚gegenwärtiges’ Beispiel: Kenia Rift). Der 2. Schritt ist die Bildung eines ridge oder spreading center (Beispiel: Rotes Meer) und der 3. Schritt die Bildung eines Ozeanes (Beispiel: Atlantik) mit zunächst passiven Kontinentalrändern. Die ozeanische Lithosphäre wird an den Rändern immer mächtiger, im 4. Schritt ‚sinkt’ sie und wird unter den Kontinentalrand subduziert, der dabei zum aktiven Kontinentalrand wird. Die gesamte ozeanische Lithosphäre zwischen ridge und aktivem Kontinentalrand wird subuziert, bis das ridge selbst subduziert wird (Schritt 5, Beispiel: die Juan de Fuca ridge wird unter die nordamerikanische Westküste subduziert). Danach wird die restliche ozeanische Lithosphäre subduziert, und die beiden ursprünglich auf zwei ‚gegenüberliegenden’ Seiten des Ozeanes gelegenen Kontinente stoßen zusammen (Schritt 6, Beispiel: Himalya) 6 Subduktion und Erdbeben Erdbeben entstehen, wenn sprödes Material einem plötzlichen Druck ausgesetzt wird, oder eine vorhandene Spannung plötzlich weggenommen wird. Das erste Beispiel beschreibt die Situation in der aktiven Seismik (Gestein wird mit Hammer oder Sprengstoff erschüttert), das zweite Beispiel beschreibt die Entstehung von Erdbeben an Transformstörungen und Subduktionszonen, wo durch die Relativbewegungen von Platten gegeneinander Spannungen aufgebaut werden, denen das Material irgendwann nicht mehr standhält. Die zeitliche Festlegung ‚irgendwann‘ soll keine postmoderne Beliebigkeit in die Argumentation einführen, sie weißt vielmehr auf die Hypothese hin, dass die zeitliche Abfolge von Erdbeben ein chaotischer Prozess und prinzipiell nicht vorhersagbar ist. Keine Hypothese mehr, sondern eine schon vor der Beschreibung vieler natürlicher Geometrien durch Fraktale in den 1980er Jahren bekannte Tatsache ist die empirisch gefundene Häufigkeitsverteilung der Erdbeben in Abhängigkeit von ihrer Magnitude – heute ein Musterbeispiel für eine fraktale Verteilung in der Geophysik. 6.1 Der Modellkörper von Saint-Venant Rheologische Modellkörper sind uns in Kap. 1-3 begegnet; zur Erklärung von Erdbeben an Subduktionszonen kommt hier der Modellkörper von Saint-Venant hinzu. Er besteht aus einem Schiebeblock über einer planen (oder rauhen) Oberfläche, der, solange er noch in Ruhe ist, einer ihn verschiebenen Kraft eine Haftreibung entgegensetzt; wenn er erst einmal in Bewegung ist, wird diese Haftreibung durch eine geringere Gleitreibung ersetzt. Ein Spielzeugmodell zur Erklärung periodisch wiederkehrender Erdbeben ist die Reihenschaltung des Saint-Venant Körpers mit der Hooke’schen Feder, an der ein velocity driver mit konstanter Geschwindigkeit zieht. Dieses Modell enthält die Relativbewegung der Platten zueinander, den Aufbau einer Spannung in einem elastischen Medium sowie den spröden Bruch, wenn diese Spannung zu gross wird. Es ist anschaulich, dass in diesem einfachsten Modell die zeitliche Abfolge von ‚ruhendem‘ und ‚sich bewegenden‘ Schiebeblock periodisch ist (Rechnung in Turcotte 1997). Dagegen können bereits zwei mit einer weiteren Hooke’schen Feder gekoppelte Schiebeblöcke (Zeichnung) chaotisches Verhalten zeigen, wenn das Verhältnis der Federkonstanten in einer bestimmten Bandbreite ist (Rechnung in Turcotte 1997; was ist chaotisches Verhalten genau? Die Observablen – in diesem Fall die Auslenkungen der beiden Blöcke – spannen einen – in diesem Fall zweidimensionalen – Phasenraum auf. Bei periodischem Verhalten ergibt sich eine stets wiederkehrende Trajektorie in diesem Phasenraum, bei chaotischem Verhalten wird ein nichtverschwindener Anteil des Volumens – in diesem Fall eine Fläche – des Phasenraumes abgedeckt). Natürlich beschreibt auch das Modell von zwei gekoppelten Schiebeblöcken das Verhalten von Platten an Subduktionszonen nicht. Dieses Modell transportiert nur den folgenden Gedankengang: Wenn schon ein so stark vereinfachtes Modell auf einen chaotischen zeitlichen Verlauf führt, dann ist ein solcher Verlauf bei einem realistischeren und sehr viel komplizierteren Modell (wir denken an eine Reihen- und Parallelschaltung von vielen Schiebeblöcken mit unterschiedlichen Feder’konstanten‘, die ausserdem noch nach jeder Bewegung ihren Elastitizitätsmodul ändern mögen....) wahrscheinlich. 6.2 Die Benioff-Zonen Lange bevor Erdbeben als Folgeerscheinungen von Versetzungen an abtauchenden Platten verstanden waren, hatte H. Benioff die Lage und Tiefe von Erdbebenherden bestimmt (Nomenklatur: Epizentrum = Projektion der Herdposition auf die Erdoberfläche, Hypozentrum = Herposition incl. Tiefenangabe): Für einen Vertikalschnitt in einer bestimmten Richtung – mit unserem heutigen Wissen: senkrecht zur Subduktionsfront - ergab die gleichzeitige Auftragung vieler Hypozentren eine schräg in den Mantel zeigenden Linie, mit Tiefen bis maximal 670 km. Während das einzelne Erdbeben kaum vorhersagbar ist (Kap. 6.1), kann die Wahrscheinlichkeit für das Auftreten von Erdbeben über einer bestimmten Magnitude innerhalb langer Zeiträume recht gut angegeben werden. Wenn N die Häufigkeit von Erdbeben mit Oberflächenmagnituden grösser M s ist, ergibt sich die Verteilung log N const b * M s (6.7) Weil M s auch ein logarithmisches Mass ist, ist (6.7) eine fraktale Verteilung (1. Was ist eine fraktale Verteilung 2. Gibt es andere fraktale Verteilungen in der Geophysik?). Beispiel: Im Zeitraum 19181955 gab es 10 Erdbeben mit M s 8.6 , 84 Beben mit M s 7.9 und 868 Beben mit M s 7.0 . Ein globaler Mittelwert für b ist 1, mit Abweichungen zu kleineren b in Gebieten mit hohen mechanischen Spannungen, tiefen Erdbeben und kontinentalen Riftsystemen (-> Bevorzugung starker Beben gegenüber der globalen Verteilung). 7 Erdbeben und Seismologie korrigiert 19.11.08 Die Gesetze der Optik über Reflexion und Brechung lassen sich weitgehend auf Schallwellen übertragen, wenn wir ‚Lichtgeschwindigkeit’ durch ‚Schallgeschwindigkeit’ und ‚optischer dichter’ durch ‚langsamer’ (Medium mit geringerer Schallgeschwindigkeit) ersetzen. Der gebogene Verlauf von Erdbeben’strahlen’ im Erdmantel entsteht durch eine kontinuierliche Zunahme der Schallgeschwindigkeit mit der Tiefe. Außerdem gibt es Diskontinuitäten in 410 und 660 km Tiefe sowie an der Kern-Mantelgrenze in 2900 km Tiefe und zwischen dem äußeren und dem inneren Kern; an diesen Diskontinuitäten ändert sich die Schallgeschwindigkeit sprunghaft und es treten Reflexionen auf. Die Analogie zur Optik ist nicht perfekt: Zusätzlich zu Transversalwellen (das Material schwingt senkrecht zur Ausbreitungsrichtung, so wie das elektrische und das magnetische Feld von Lichtwellen) treten Kompressionswellen auf, bei denen das Material in Ausbreitungsrichtung schwingt. Diese Wellen können Flüssigkeiten durchdringen, während Scherwellen die Rückstellkräfte im Kristallgitter brauchen. Mit der Koexistenz von Kompressions- und Scherwellen, die in der Geophysik wegen der unterschiedlichen Schallgeschwindigkeiten (s. 7.8, 7.9) auch als p- und s-Wellen (primäre, sekundäre Ankunft der Welle beim Seismographen) wurde der flüssige äußere Erdkern entdeckt. Das gleichzeitige Auftreten beider Wellenarten im Mantel hatte zu einer langen Diskussion über die ‚Flüssigkeit’ des Mantels geführt (s. Kap. 1 und 3.2). Erdbeben mit Magnituden über 4 stellen so viel Energie bereit, dass die Erdbebenwellen den gesamten Erdkörper durchlaufen und danach immer noch aufgezeichnet werden können. In allen einführenden Darstellungen der Geophysik wird beschrieben, wie in den ersten Jahrzehnten des 20. Jahrhundert der schalenförmige Aufbau des Erdkörpers mit Raumwellen (zusammenfassende Bezeichnung von P- und S-Wellen, im Gegensatz zu Oberflächenwellen) gefunden wurde. Für unser Thema ‚Plattentektonik’ ist jedoch nicht dieser schalenförmige Aufbau, sondern Abweichungen davon interessant – diese Abweichungen werden durch langsame Strömungen im Mantel, abtauchende ‚slabs’, Plumes usw. erzeugt. Hier haben vor allem Untersuchungen von Oberflächenwellen (Abschnitt 7.2) und die seismische Tomographie (Abschnitt 7.4) Beiträge geliefert. Für den Physiker ist zunächst die Ableitung der Wellengleichung interessant, oder die Antwort auf die Frage ‚Was breitet sich mit Schallgeschwindigkeit aus?’. 8 Seismologie und Anisotropie So wie wir im letzten Kapitel – mit einigen Modifikationen und Einschränkungen – von der Optik zur Seismologie gelangt sind, so können wir jetzt den Begriff der Polarisation auf seismische Scherwellen übertragen. 8.1 SKS splitting SKS ist eine Welle, die als P-Welle durch den Kern gegangen ist und etwa senkrecht (‚von unten’) einfällt. Wenn diese Welle eine Zone azimuthaler seismischer Anisotropie (anisotrop bezüglich der seismischen Geschwindigkeiten v sx , v sy in x, y-Richtung) durchlaufen hat, dann kommen anstatt einer S-Welle zwei unterschiedlich polarisierte Scherwellen mit unterschiedlichen Geschwindigkeiten und deshalb unterschiedlichen Ankunftszeiten an. Es sind Laufzeitunterschiede t 1s gemessen worden, aus ihnen lassen sich mit Modellannahmen v über das Ausmass der Anisotropie ( z.B. sx 1.03) Aussagen zur Mächtigkeit der anisotropen v sy Schicht gewinnen – oder umgekehrt lässt sich aus einer Annahme über die Mächtigkeit eine Aussage über die Anisotropie gewinnen. Im Gegensatz zur Mächtigkeit kann aber die absolute Tiefe der anisotropen Schicht aus diesen Daten nicht bestimmt werden. Als Ursache dieser azimuthalen Anisotropie kommen in Betracht: a) in einer Richtung ausgerichtete Risse aligned cracks die mit Flüssigkeit (Wasser, Schmelzen) gefüllt sind. b) eine Anisotropie der Schallgeschindigkeit in Kristallen. So ist z.B. die Geschwindigkeit v s längs der a-Achse von Olivin um 10% höher als längs der anderen Achsen. Die Interpretation der seismischen Anisotropie mit Möglichkeit b) setzt voraus, das viele Kristalle die gleiche Orientierung haben, und Mantelfluss ist eine mögliche Ursache für eine solche lattice preferred orientation von Olivinkristllen. 9. Anisotropie und lattice – preferred orientation Seit Ende der 70er Jahre gab es Studien über seismische Anisotropie im obersten Mantel; trotz aller Probleme mit horizontalem / vertikalen Auflösungsvermögen ergab sich bei den meisten Arbeiten eine ‚schnelle Richtung’ (R. mit der höheren Schallgeschwindigkeit) in Richtung der Plattenbewegung. Allerdings kann die Richtung der heutigen Plattenbewegung erst seit ca 1990 wirklich genau mit GPS (global positioning system) bestimmt werden, davor war man z.T. auf die zeitliche Extrapolation paläomagnetischer Daten angewiesen. Zwar ist aus Labormessungen der Schallgeschwindigkeit in Einkristallen – z.B. von Olivin - bekannt, dass diese anisotrop bezüglich der seismischen Geschwindigkeiten sind, aber in einem homogenen Mantel würden man eine regellose Verteilung der Kristalle und deshalb keine makroskopische (mit Seismologie messbare) Anisotropie erwarten. Azimuthale seismische Anisotropie unter Kontinenten: Daten von Vinnik et al(1992, 1994), Montaigner (1979), Debayle & Kennett (2000) u.a Laufzeitunterschiede von 0.5-1.5 s Erklärung I. Anisotropie in der Lithosphäre, als Überbleibsel der Orogenese (Warum? Zur Orogenese, z.B. bei Kontinent – Kontinent Kollisionen, gehören tektonische Kräfte Vorzugsrichtungen) Erklärung II. Anisotropie unter der Lithosphäre durch lattice – preffered orientation (LPO) von Olivinkristallen, verursacht durch die gegenwärtige Plattenbewegung Erklärung III. Anisotropie unter der Lithosphäre wegen Mantelfluss bei Topographie an der Lithosphärenunterkante, oder kleinräumiger Konvektion. c b a II, III nur möglich weil a) v p a v p b aus Labormessungen 4.8 km / s 4.6 km / s und weil b) LPO unter Scher Stress im Labor nachgewiesen (Folie) bei beidem a) seismischer Anisotropie und b) LPO ist der Zusammenhang zwischen Labor-Skala (10-9 m3) und Seismologie-Skala (> 109 m3) problematisch: Nur bei wirklich homogenen Materialien darf man den bei einer kleinräumigen Messung bestimmten physikalischen Parameter unverändert für ein grosses Volumen übernehmen. Bei heterogenen Materialen (und ein Gemisch von anisotropen Kristallen ist heterogen) kommt eine Korrektur hinzu, die sogenannte Skalierung. Auf diese Skalierung kommen wir im Anschluss an die Messungen der elektrischen Leitfähigkeit zurück. Wenn das Skalierungsproblem gelöst würde, dann würde mit Seismologie ein Werkzeug zur Kartierung des Mantelflusses zur Verfügung stehen, wenn es die in Kapitel 8 angesprochenen Probleme des Auflösungsvermögens (bei SKS vertikal, bei Oberflächenwellen horizontal) nicht gäbe….. Warum ist eine räumlich hochauflösende Kartierung des Mantelflusses wünschenwertig? Kann man zwischen Szenario II und III unterscheiden (?) Wenn Szenario II, kann dann hochauflösende Kartierung des Mantelflusses auch zwischen 4.1 – 4.3, nämlich konvektionsgetriebener Plattentektonik, plattengetriebener Konvektion und Plumes unterscheiden? Gibt es eine andere geophysikalische Explorationsmethode, die Mantelfluss mit höherer räumlicher Auflösung kartieren kann? 10. LPO und Wasser im Erdmantel 10.1 Subduktion als Transportprozess für Wasser Dass Subduktion überhaupt ein Transportprozess ist, haben Morris et al. (Nature, Vol 344, (1990) nachgewiesen: Sie fanden dass Beryllium – Isotop 10Be in Laven von Inselbögen. 10 Be ist ein radioaktiv Isotop mit T1/2 = 1.5 106 y, das in der Atmosphäre durch die kosmische Höhenstrahlung gebildet wird und dann erst in den Ozean und schließlich in Sedimente am Ozeanboden Eingang findet. Damit überhaupt trotz der kurzen Halbwertszeit etwas 10Be wieder im back-arc-Vulkanismus hoch kommt, muss die subduzierte Platte etwa mit der Geschwindigkeit v Δx T1 2 10 cm/y in den Mantel tauchen. Subduktion mit der Geschwindigkeit der ozeanischen Platten wie aus Paläomagnetismus bekannt. ... Den größten Wasseranteil in der subduzierten ozeanischen Kruste hat die ca 1 km mächtige Sedimentesbedeckung mit Porositäten um 50% 1 km2 ozeanische Kruste enthält 0.5 km3 Wasser! In 106 Jahren werden bei v 10 cm/y pro km Subduktionsfront: 100 km2 ozeanische Kruste subduziert, die bis zu 50 km3 Wasser transportieren. Zwar wird der größte Teil davon bereits wieder unter dem Akkretionsprisma herausgequetscht, aber ein Teil des Wassers gelangt in ca 100 km Tiefe und ist dort m Vulkanismus beteiligt: Wasser verringert die Schmelztemperatur (Harris 1972). Metamorphosen wie Harzburgit Serpentinit oder Basalt Amphibolit, bei denen Wasser oder OHGruppen in die Kristallstruktur der gesteinsbildenden Mineralien eingebaut wird, erlauben einem Teil des Wassers, mit dem slab bis in den mittleren Mantel zu kommen. Granit, SiO2 : Hinweis auf Sauerstoff im Mantel 10.2 Wasserstoff – Diffusivität in Olivin Diffusion allgemein: Transport von ‚Teilchen’ wegen eines Konzentrationsgefälles 1. Ficksches Gesetz J n D grad n m2 D Diffusionskoeffizient s Änderung der Teilchenzahldichte in einem Volumen n d i v J 2. Ficksches Gesetz n D div grad n D 2 n = Diffusionsgleichung (Kap 3: Diffusionsgleichung für Temperaturfeld) Der Diffusionskoeffizient gibt also an, wie schnell sich ‚Teilchen’ bewegen. Beispiel für Teilchendiffusion: Bewegung von H Ionen in Olivinkristallen. Olivinkristalle sind anisotropbezüglich der Diffusionskoeffizienten, Da 40 Dc (Mackwell + Kohlstedt JGR 1990) Weil die Anisotropie des Olivins bezüglich der Diffusionskoeffizienten sich über die NernstEinstein-Gleichung unmittelbar in eine Anisotropie der elektrischen Leitfähigkeit umrechnen lässt, ist die Magnetotellurik zu derjenigen Explorationsmethode geworden, mit der sich die Richtungen der LPO im Mantel am genauesten bestimmen lassen. 11. Plattentektonik und geophysikalische Exploration: Zusammenfassung Explorationstechniken zur Erkundung der Plattentektonik (PT) Paläomagnetismus: indirekte Positions-Bestimmung. relativ zum Dipolfeld, auf großen (geologischen) Zeitskalen + findet die ‚Lage’ (nur ) und Orientierung der kontinentalen Platten zu geologischen Zeiten bis ca 500.000.000 Jahren + PT ‚bewiesen’ - nur ‚geodätische Information, kein Beitrag zur Suche nach Antriebsmechanismus der PT Global Positioning System GPS: direkte Bestimmung der jetzigen Position der kontinentalen Anteile der Platten relativ zu Erde/Satellit im 2-Körper-Problem + findet die jetzigen Plattengeschwindigkeiten - nur geodätische Information wie beim Paläomagnetismus Seismologie: 3D Bild des Erdinneren bezüglich v p , v s + findet Heterogenitäten (seismische Tomographie) - bei LPO entweder keine Tiefenauflösung (SKS – Splitting) oder geringe horizontale Auflösung (Anisotropie aus Oberflächenwellen) o Aussagekraft im unteren Mantel beschränkt: räumliche Auflösung ~ 1000 km >> Mächtigkeit der subduzierten slabs Elektromagnetische Tiefenforschung: 3D Bild bezüglich - findet Heterogenitäten mit geringerer Auflösung als seismische Tomographie (weil Diffusionsgleichung statt Wellengleichung) + bei LPO gleichseitig horizontale und Tiefenauflösung o Starke Sensitivität bezüglich Komposition (Wasser, Schmelzen) hat Vorteile (findet geringe Mengen Wasser ....) und Nachteile (Ambiguität bei der Interpretation) Aussagekraft im unteren Mantel ist Null Geochemie: Unterschiedliche Komposition der Schmelzen aus 1) mittelozeanischen Rücken 2) Inselbogenvulkane 3) hot spots