Optik 2017-03
Werbung
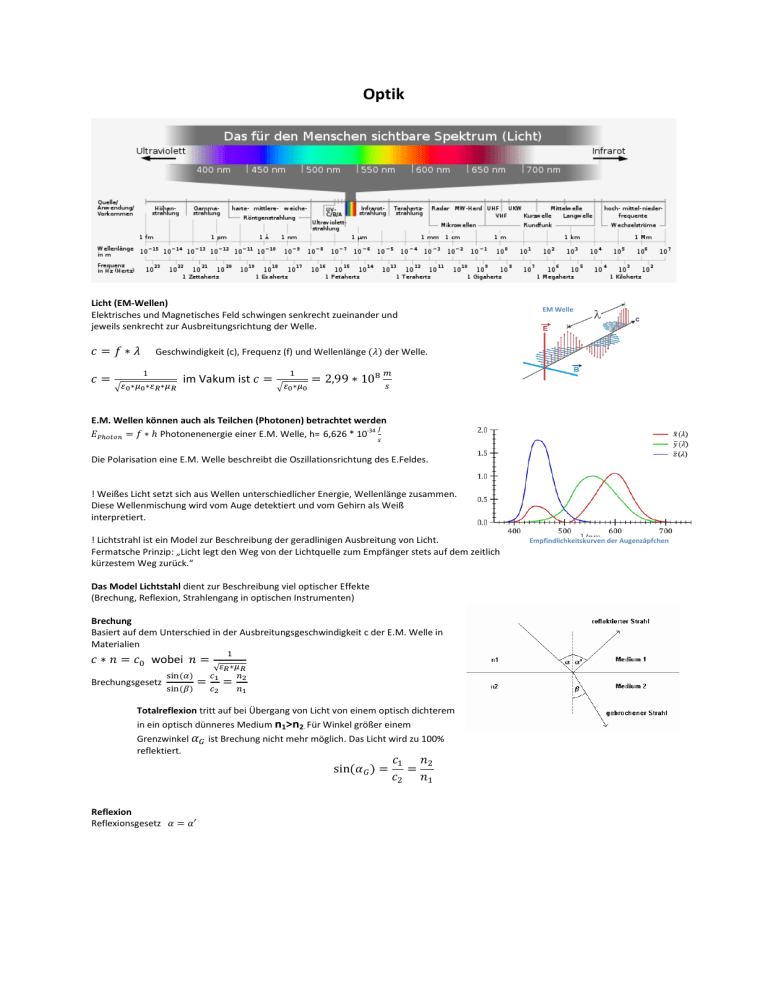
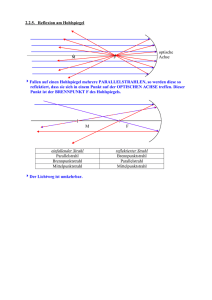
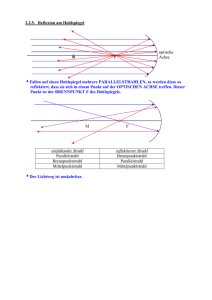
Optik Licht (EM-Wellen) Elektrisches und Magnetisches Feld schwingen senkrecht zueinander und jeweils senkrecht zur Ausbreitungsrichtung der Welle. 𝑐 =𝑓∗𝜆 𝑐= EM Welle Geschwindigkeit (c), Frequenz (f) und Wellenlänge (𝜆) der Welle. 1 √𝜀0 ∗𝜇0 ∗𝜀𝑅 ∗𝜇𝑅 im Vakum ist 𝑐 = 1 √𝜀0 ∗𝜇0 = 2,99 ∗ 108 𝑚 𝑠 E.M. Wellen können auch als Teilchen (Photonen) betrachtet werden 𝐽 𝐸𝑃ℎ𝑜𝑡𝑜𝑛 = 𝑓 ∗ ℎ Photonenenergie einer E.M. Welle, h= 6,626 * 10-34 𝑠 Die Polarisation eine E.M. Welle beschreibt die Oszillationsrichtung des E.Feldes. ! Weißes Licht setzt sich aus Wellen unterschiedlicher Energie, Wellenlänge zusammen. Diese Wellenmischung wird vom Auge detektiert und vom Gehirn als Weiß interpretiert. ! Lichtstrahl ist ein Model zur Beschreibung der geradlinigen Ausbreitung von Licht. Fermatsche Prinzip: „Licht legt den Weg von der Lichtquelle zum Empfänger stets auf dem zeitlich kürzestem Weg zurück.“ Das Model Lichtstahl dient zur Beschreibung viel optischer Effekte (Brechung, Reflexion, Strahlengang in optischen Instrumenten) Brechung Basiert auf dem Unterschied in der Ausbreitungsgeschwindigkeit c der E.M. Welle in Materialien 𝑐 ∗ 𝑛 = 𝑐0 wobei 𝑛 = Brechungsgesetz sin(𝛼) sin(𝛽) = 1 √𝜀𝑅 ∗𝜇𝑅 𝑐1 𝑛2 𝑐2 = 𝑛1 Totalreflexion tritt auf bei Übergang von Licht von einem optisch dichterem in ein optisch dünneres Medium n1>n2. Für Winkel größer einem Grenzwinkel 𝛼𝐺 ist Brechung nicht mehr möglich. Das Licht wird zu 100% reflektiert. sin(𝛼𝐺 ) = Reflexion Reflexionsgesetz 𝛼 = 𝛼′ 𝑐1 𝑛2 = 𝑐2 𝑛1 Empfindlichkeitskurven der Augenzäpfchen Linsen: Wichtige Strahlen in Linsen Mittelpunktstrahl Parallelstrahl Brennpunktstrahl Mittelpunktstrahl Brennpunktstrahl Parallelstrahl Linsenprofile Strahlgang Streulinse Strahlgang Sammellinse Optische Instrumente: Lupe, Gegenstand innerhalb der Sammellinsen Brennweite virtuell vergrößertes Bild Mikroskop, Gegenstand ist nah und befindet sich zwischen einfacher und doppelter Brennweite des Objektivs reelles Zwischenbild. Das Orkular wird so positioniert, dass diese Zwischenbild sich kurz innerhalb des Orkular-Brennweite befindet. Das Orkular erzeugt ein vergrößertes zwischen Bild wie eine Lupe. Teleskop, Gegenstand ist fern(unendlich) das Objektivs erzeugt ein reelles Zwischenbild in der -Brennweite. Das Orkular vergrößert dieses zwischen Bild wie eine Lupe. Bessel-Verfahren zur Bestimmung der Brennweite einer Linse Ordnet man Gegenstand und Bildschirm so an, dass ihr fester Abstand d mindestens 4-mal die Linsenbrennweite beträgt, so kann mit einer Sammellinse an zwei Positionen zwischen Gegenstand und Bild eine Abbildung erzeugt werden. Die Positionen der Linse befinden sich im Abstand e. Mit der Linse in Stellung I erhält man eine vergrößerte, in Stellung II eine verkleinerte Abbildung des Gegenstandes. Die Brennweite f der Linse kann wie folgt bestimmt werden. f d 2 e2 4d Beugung Licht wird an Ecken und Kanten gebeugt. Das Huygenssches Prinzip besagt das hinter Abschattung Kugelwellen entstehen. Wellenfront und Kohärenz Zur Lateralen Beschreibung der E.M. Wellen eins eines Lichtstrahls nutz man den Begriff Wellenfront. Eine Wellenfront stellt eine Ebene/Fläche gleicher Phase der E.W. dar. Kohärenz beschreibt über welche zeitliche Dauer und welchen geometrischen Abstand die Wellenfronten den Abstand der Wellenlänge 𝜆 konstant einhalten. Die Kohärenzlängen von thermischen Strahlern (Sonne, Lampe) beträgt~ 10-6m. Die Kohärenzlänge von Lasern bis zu mehreren km. Interferenz Ist die ungestörte Überlagerung (Superposition) von E.M. Wellen. Die Gesamtamplitude an ein Ort ergibt sich aus der Summe der Amplituden der interferierenden Wellen. Die interferierenden Wellen müssen zueinander kohärent sein. Die bekanntest Interferenzerscheinungen entstehen bei der Überlagerung der Kugelwellen die durch einen Spalt, Doppelspalt und ein Interferenzgitter entstehen. α sn en Ein kohärenter Lichtstrahl, der ein Gitter bzw. einen Doppelspalt passiert deren Spaltabstände b betragen erzeugt auf einen Schirm ein Interferenz Bild. Die Interferenz-Maxima auf diesem Schirm entstehen an Position bei denen der optische Weg 𝒆𝒏 (Gitter, Spalt bis zum Schirm) für die interferierenden Wellen sich genau um ein ganzzahliges Vielfaches n ihrer Welllängen 𝝀 unterscheidet. Je nach Anzahl n unterscheidet man diese Maxima in n-te Ordnungen. Die 0te-Ordnung erscheint mittig auf dem Schirm. Höhere Ordnungen werden im Abstand sn zur 0ten-Ordnung auf dem Schirm abgebildet. 𝑛∗𝜆 𝑠𝑛 = sin(𝛼) = 𝑏 𝑒𝑛