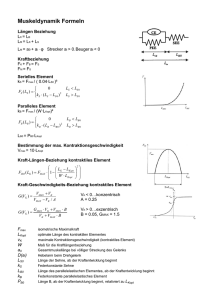
Die Reaktionsgeschwindigkeit

Die Reaktionsgeschwindigkeit
Die grundlegende Größe, mit der in der Kinetik gearbeitet wird, ist die
Reaktionsgeschwindigkeit. Sie gibt an, wie viele Teilchen pro Zeit in einer chemischen
Reaktion umgesetzt werden. Diese Geschwindigkeit hängt dabei von vielen Faktoren ab. Je
nach zugrunde liegendem Modell gibt es unterschiedliche Möglichkeiten, die
Reaktionsgeschwindigkeit zu betrachten.
Ein wichtiger Faktor, der zu berücksichtigen ist, ist die Konzentration der vorliegenden
Stoffe. Je mehr Teilchen in einem Volumen vorliegen, desto mehr Kollisionen werden pro
Zeiteinheit vorkommen. Da eine Reaktion aber nur stattfinden kann, wenn zwei Teilchen
miteinander kollidieren, steigt die Reaktionsgeschwindigkeit mit der Konzentration der
Edukte.
Wenn eine Reaktion folgenden Typs vorliegt
so gilt für die Hinreaktion das Geschwindigkeitsgesetz
wobei vR die Reaktionsgeschwindigkeit, ( − ∆cA) die Abnahme der Konzentration des Stoffes
A und ∆t die verstrichene Zeit ist. Diese Reaktionsgeschwindigkeit ist die
Durchschnittsgeschwindigkeit der Reaktion, da einzelne Moleküle unterschiedliche lange
Zeitintervalle benötigen, bevor sie in ein Reaktionsereignis eintreten.
Da die Abnahme der Edukte der Zunahme der Produkte entsprechen muss, gilt außerdem
Dieses stark vereinfachte Modell bedarf noch einiger Verfeinerungen bezüglich:
•
•
•
•
•
•
•
•
der Aktivität, also die effektive Konzentration
der Menge der Edukte im Verhältnis zu der Menge der Produkte und gegebenenfalls
des Lösungsmittels
der Temperatur
der Stoßenergie
der Anwesenheit von Katalysatoren
der Reaktionen mit auftretenden Gasen vom Partialdruck
der Ausrichtung großer Reaktionspartner (Enzyme, Katalysatoroberfläche) beim
Zusammenstoß
des Zerteilungsgrades
Die Reaktionsordnung
Für jede Reaktion lässt sich eine Reaktionsgleichung formulieren, die beschreibt, wie viele
Edukt-Teilchen miteinander reagieren, um eine bestimmte Anzahl Produkt-Teilchen zu
bilden.
Läge etwa folgende Reaktionsgleichung vor
würde dies bedeuten, dass zwei Teilchen A mit einem Teilchen B, einem Teilchen C und
einem Teilchen D kollidieren müssten, um das Produkt E zu bilden.
Jedoch ist die Wahrscheinlichkeit, dass fünf Teilchen gleichzeitig und zudem mit
ausreichender Energie kollidieren, äußerst gering.
Viel wahrscheinlicher ist, dass zunächst zwei oder drei Teilchen zusammen treffen, ein
Zwischenprodukt bilden, dieses Zwischenprodukt kollidiert dann mit weiteren Teilchen
gegebenenfalls unter Bildung weiterer Zwischenprodukte und zuletzt bildet sich das Produkt
E, hier ein Beispiel:
Die Zerlegung der Gesamtreaktion in einzelne Schritte, in Elementarreaktionen, und deren
Untersuchung zeigt, wie die Reaktion genau abläuft.
Experimentell oder auf der Grundlage modellhafter Annahmen kann ermittelt werden, wie die
Reaktionsgeschwindigkeiten der Elementarreaktionen von den jeweiligen Konzentrationen
der Komponenten A, B, C und D abhängen.
Die Abhängigkeit der Reaktionsgeschwindigkeit vom Exponenten mit dem die Konzentration
eines bestimmten Reaktanden in das Geschwindigkeitsgesetz eingeht, wird als
Reaktionsordnung in Bezug auf diesen Reaktanden bezeichnet.
Die Gesamtordnung einer Reaktion ist die Summe der Reaktionsordnungen aller an ihr
beteiligten Reaktanden.
Die drei häufigsten, weil wahrscheinlichsten, Reaktionsordnungen
Reaktio
sind:
Reaktionen nullter Ordnung
Derartige Reaktionen sind unabhängig von der
der Konzentration der Reaktanden, hier ist die
Reaktionsgeschwindigkeit also konstant. Dies kann z. B. der Fall sein, wenn es sich um
lichtabhängige Reaktionen handelt (dann ist der Faktor k von der Lichtintensität abhängig)
wobei
v – Reaktionsgeschwindigkeit
CA(t) – Konzentration des Stoffes A zum Zeitpunkt t
t – Zeit
k – Geschwindigkeitskoeffizient
Beispiele sind photochemische Reaktionen oder katalytische Reaktionen.
Integration beider Seiten ergibt:
Zu Beginn der Reaktion (t = 0 ) ist die Konzentration des Reaktanten [A]0. Dementsprechend
gilt für die Integrationskonstante C = [A]0
Somit resultiert die integrierte Form des Zeitgesetzes:
Diee Auftragung von [A] gegen t liefert eine Gerade mit der Steigung -k.
Reaktionen erster Ordnung
Hier handelt es sich um katalytische oder radioaktive Zerfallsprozesse. Die
Reaktionsgeschwindigkeit ist nur von der Konzentration des zerfallenden Stoffes abhängig.
integriert
mit
[A]t – Konzentration von A zur Zeit t
[A]0 – Anfangskonzentration von A
Umformung des Geschwindigkeitsgesetzes ergibt
Gleichung (2) stellt die differentielle Form des Zeitgesetzes dar Durch Integration dieser
Gleichung und Bestimmung der Integrationskonstanten C erhält man das entsprechende
Zeitgesetz in integrierter Form.
Integration der Gleichung (2) gibt:
Die Integrationskonstante C kann anhand der Integrationsgrenzen bestimmt werden. Zu
Beginn der Reaktion (t = 0) ist [A]0 die Konzentration von A. Für ln[A]0 ergibt sich:
Deshalb:
Es folgt damit:
Eine Auftragung von ln[A] oder ln[A] / [A]0 gegen die Zeit t ergibt eine Gerade mit
der Steigung -k. Bei einer Reaktion erster Ordnung sollten die entsprechenden
Messpunkte bis zu einem Reaktionsumsatz von 80-90% auf dieser Geraden liegen.
Gleichung (6) kann auch wie folgt formuliert werden:
Dies bedeutet, dass die Konzentration von A exponentiell mit der Zeit abnimmt.
Die Geschwindigkeitskonstante k läßt sich auch aus der Halbwertszeit t1/2 ermitteln. Unter der
Halbwertszeit versteht man die Zeit, in der die Hälfte der ursprünglichen Konzentration des
Reaktanten A verbraucht ist ==> [A] = 1/2 [A]0 .
Es gilt entsprechend Gleichung (6)::
Reaktionen zweiter Ordnung
In diesem Falle reagieren zwei Edukte zu einem oder mehreren Produkten. Die
Reaktionsgeschwindigkeit ist abhängig von den Konzentrationen der Ausgangsstoffe.
oder bei nur einem Stoff
Trennung der Variablen und Integration ergeben:
Für die Konzentration von A zu Beginn der Reaktion t = 0 wird A0 gesetzt. Die
Integrationskonstante C hat folglich den Wert 1 / [A]0.
Somit ergibt sich die integrierte Form des Zeitgesetzes mit
Eine Auftragung von 1 / [A] gegen die gegen die Zeit t ergibt
gibt eine Gerade mit der
Steigung k. Bei einer Reaktion zweiter Ordnung (Konzentrationen der
Reaktionspartner identisch) sollten die entsprechenden Messpunkte bis zu einem
Reaktionsumsatz von 50% auf dieser Geraden liegen.
Sofern [A]0 and [B]0 unterschiedlich sind, führt man zweckmäßig die Umsatzvariable x ein.
Für Gleichung (1) ergibt sich:
wobei [A]0 - x = [A], [B]0 - x = [B] und x die Abnahme von A und B darstellt.
Nach Trennung der Variablen und Partialbruchzerlegung läßt sich Gleichung (5) integrieren
wobei C die Integrationskonstante darstellt.
Unter der Voraussetzung dass x = 0, sofern t = 0 wird der Wert für C erhalten
und Gleichung (6) wird zu
Eine Auftragung von
gegen t ergibt eine Gerade mit der Steigung ([A]0 - [B]0) k.
Gleichung (8) kann auch, wie folgt formuliert werden
Allerdings gibt es einen Sonderfall, bei dem einer der Reaktanden in einem sehr hohen
Überschuss vorliegt, so dass die Konzentrationsänderung über die Zeit der Reaktion
verschwindend gering ist. Das ist zum Beispiel der Fall, wenn Wasser sowohl
Reaktionspartner als auch das Lösungsmittel darstellt (z. B. bei einer Esterhydrolyse). In
diesem Fall folgt die Reaktionsgeschwindigkeit den Gesetzmäßigkeiten einer Reaktion erster
Ordnung. Da es sich aber trotzdem um eine bimolekulare Reaktion handelt, spricht man von
Reaktionen pseudoerster Ordnung (oder scheinbar erster Ordnung).
Ein weiterer Sonderfall ergibt sich, wenn experimentell eine Reaktion 0. Ordnung gemessen
wird (obwohl eine Reaktion höherer Ordnung vorliegt). Dann spricht man von einer Reaktion
scheinbar nullter Ordnung. Dies kann insbesondere bei katalytischen Prozessen der Fall sein
(wie z. B. der Enzymkatalyse oder der katalytischen Hydrierung von Ethen) wenn der
limitierende Faktor die Anzahl „Plätze“ am Katalysator sind und nicht wie oft die Moleküle
zusammenprallen (da dann die direkte Elementarreaktion so gut wie keine Rolle mehr spielt).
Gleichgewichtsreaktionen
Viele Reaktionen sind Gleichgewichtsreaktionen bei denen das gebildete Produkt wieder zum
Edukt zurück reagieren kann.
Die Änderung der Konzentration A ist in diesem Fall bestimmt durch die
Differenzialgleichung
mit den Reaktionsparametern kab der Reaktion
und kba der Rückreaktion
.
Es ergibt sich daraus das folgendes Geschwindigkeitsgesetz:
Geschwindigkeitsgesetz
Zusammenfassung
Differentielles Integriertes Linearer
Reaktionsordnun
Zeitgesetz
Plot
Zeitgesetz
g
Steigung
Einheiten der
der
Geschwindigkeitskonstant
Geraden
e
0
- d[A] / dt = [A] = [A]0 [A]
k
kt
gegen t
-k
mol · L-11 · s-1
1
- d[A] / dt = [A] = [A]0 e ln[A]
- kt
k [A]
gegen t
-k
s-1
2
- d[A] / dt = 1 / [A] = 1 / 1 / [A]
k [A]2
[A]0 + kt gegen t
k
L · mol-11 · s-1
Temperaturabhängigkeit der Reaktionsgeschwindigkeit
RGT-Regel (Reaktionsgeschwindigkeit
sgeschwindigkeit-Temperatur-Regel):
Regel): Wird die Temperatur für eine
chemische Reaktion um 10 K erhöht, dann erhöht sich die Reaktionsgeschwindigkeit um das
2- bis 4-fache
fache (für eine Reaktion mit einer Aktivierungsenergie um die 50 kJ/mol!)
Mathematisch und physikalisch
sikalisch wird dies mit dem Ansatz von Arrhenius begründet. Nach
diesem kann die Temperaturabhängigkeit der Reaktionsgeschwindigkeit mit einer
Exponentialfunktion beschrieben
en werden. Wie oben schon beschrieben lautet die
Bestimmungsgleichung für eine Reaktion zweiter Ordnung:
Die Temperaturabhängigkeit ist in dem so genannten Geschwindigkeitskoeffizienten
enthalten, denn es gilt hier die Arrhenius-Gleichung.
Arrhenius
. Der Geschwindigkeitskoeffizient k ist
nur dann eine Konstante, solange die Temperatur nicht verändert wird und kann dann auch als
Geschwindigkeitskonstante bezeichnet werden.
we
Überblick über die wichtigsten Formeln der Reaktionskinetik
Berechnung der MomentanMomentan Berechnung der
Reaktionstyp
geschwindigkeit v
Halbwertszeit
0. Ordnung
1. Ordnung
2. Ordnung
•
0. Ordnung:
•
1. Ordnung:
•
2. Ordnung:
In allen Fällen erhält man k aus der Steigung der entstehenden Graphen. Je mehr Messpunkte
Mes
man hat, desto genauer wird das Ergebnis.
Arrhenius
Arrhenius-Gleichung
Es ist eine bekannte Tatsache, dass die Geschwindigkeit einer
chemischen Reaktion im allgemeinen mit steigender Temperatur
zunimmt. Die quantitative Beziehung zwischen
Reaktionsgeschwindigkeit und Temperatur wird durch die
Arrhenius
Arrhenius-Gleichung
beschrieben:
Svante Arrhenius
Ea = Aktivierungsenergie
R = 8.314 J/mol·K
T = absolute Temperatur in Kelvin
A = präexponentieller Faktor oder Häufigkeitsfaktor
A = p · Z, wobei Z die Stoßzahl ist und p einen sterischen Faktor
darstellt.
Z erweist sich als nur schwach abhängig von der
Reaktionstemperatur.
Somit stellt der Häufigkeitsfaktor für die entsprechende Reaktion
eine Konstante dar.
Die Arrhenius-Gleichung basiert auf der Stoßtheorie, wonach die
Reaktanten sowohl in der korrekten Orientierung als auch mit der
nötigen kinetischen Energie zusammenstoßen müssen, damit sie in die
Produkte umgewandelt werden.
Logarithmiert man beide Seiten der Gleichung (1), so erhält man
Die Auftragung von lnk gegen 1/T liefert eine Gerade
mit der allgemeinen Gleichung y = -mx + b, wobei
x = 1/T
y = lnk
m = - Ea / R
b = lnA
Die Aktivierungsenergie Ea lässt sich aus der Steigung
m der Geraden ermitteln: Ea = -m · R
Die Aktivierungsenergie wird in Veröffentlichungen
auf eine Kommastelle angegeben. Bei der Angabe der
lnA-Werte sind 2 Dezimalen statthaft.
Bestimmung von Ea
Um die Aktivierungsenergie möglichst exakt zu
bestimmen sollte das entsprechende Experiment bei
mindestens drei verschiedenen Reaktionstemperaturen
durchgeführt werden. Die Temperaturintervalle sollten
mindestens 5°C betragen.
"Zweipunktegleichung"
Rein rechnerisch läßt sich die Aktivierungsenergie einer gegebenen Reaktion anhand der
experimentellen Daten bestimmen, die man bei zwei verschiedenen Reaktionstemperaturen
gewonnen hat.
Es gilt
bei T1:
bei T2:
Subtraktion der Gleichung (4) von Gleichung (3) führt zu
Unformen obiger Gleichung und Auflösen nach Ea gibt
Enzymkinetik
Michaelis-Menten
Menten-Theorie
Die Michaelis-Menten-Theorie legt den Grundstein für die Enzymkinetik. Hier wurde das
theoretische Rüstzeug erarbeitet, Enzyme nicht nur hinsichtlich
hinsichtlic ihrer Aktivität zu
charakterisieren, sondern auch die Stoffmenge (Konzentration) zu finden, welche eine den
Gegebenheiten angepasste Umwandlung ermöglicht.
ermöglicht
Im Allgemeinen sind Enzyme in der Lage, schwankende Substrat-Konzentrationen
Konzentrationen
auszugleichen, d. h. ein Fließgleichgewicht („steady state“) dadurch einzustellen, dass sie ihre
Tätigkeit dem Angebot anpassen.
Im Gegensatz zur Kinetik chemischer Reaktionen gibt es in der Enzymkinetik das Phänomen
der Sättigung:: bei sehr hohen Substratkonzentrationen kann die Umsatzgeschwindigkeit v
nicht weiter gesteigert werden d. h. es wird ein Wert Vmax erreicht.
Theoretische Begründung
Als Biokatalysatoren bilden Enzyme E mit ihrem Substrat S einen Komplex ES (Enzym(Enzym
Substrat-Komplex),
Komplex), aus dem heraus sich die Reaktion zum Produkt P vollzieht:
k1 und k'1 sind die Geschwindigkeitskonstanten für die Assoziation
Assoziation von E und S bzw. die
Dissoziation des Enzym-Substrat-Komplexes
Komplexes ES. k2 und k'2 sind die entsprechenden
Konstanten für die Reaktion zum Produkt bzw. die Rückreaktion zum Substrat. Diese
Rückreaktion findet unter den Bedingungen der Enzymkinetik, d.
d h. unmittelbar nach
Mischung der Komponenten E und S, noch nicht statt.
statt. Ferner wird die Umwandlung von ES
zu EP (und nicht die spontanee Freisetzung von P) gemessen, so dass die folgende
Vereinfachung gerechtfertigt ist:
Hierin ist k2 ein Maß der maximalen Reaktionsgeschwindigkeit bei Substratsättigung ( Vmax),
auch Wechselzahl,, molekulare Aktivität, „turnover number“ oder kcat genannt (kcat = Vmax /
[E0]). Die Michaeliskonstante,, die Substratkonzentration, die bei der Halbsättigung vorliegt
(die Umsatzgeschwindigkeit also v = Vmax/2 beträgt), ergibt sich zu
(Michaelis-Menten-Fall,
Fall, gegeben wenn k2<< k-1) oder allgemeiner zu
Situation [Zerfallswege von ES/Bildungsweg von ES] für den Fall, dass k2
(Briggs-Haldane-Situation
gegenüber k1 nicht vernachlässigt werden kann)
Sättigungsverlauf: eine
Hyperbel zwischen Km und
Vmax
Sättigungshyperbel
Km entspricht 1/2 Vmax
igungsfunktion eines “Michaelis-Menten
“Michaelis Menten Enzyms” lässt sich unter Verwendung der
Die Sättigungsfunktion
Parameter Km und Vmax wie folgt formulieren:
formulieren
Dies ist die Michaelis-Menten
Menten Beziehung,
Beziehung d. h. die Gleichung einer Hyperbel mit den
folgenden in der Abbildung gezeigten Eigenschaften:
•
Ihre Asymptoten entsprechen den Werten Vmax (realer Ast) und Km (imaginärer Ast,
gestrichelt);
•
•
•
Gleicht die Substratkonzentration [S] dem Km-Wert, so liegt die Hälfte des
ursprünglich vorhandenen Enzyms [Eo] in Form des Enzym-Substrat-Komplexes [ES]
vor, die andere Hälfte ist frei [E].
Da die Sättigung asymptotisch angenähert wird, sind hierzu Substratkonzentrationen
erforderlich, die mehr als dem zehnfachen Km-Wert entsprechen. Im Umkehrschluss
gilt: Hat man für ein Enzym eine Sättigungshyperbel gemessen, d. h. die
Umsatzgeschwindigkeit v als Funktion der Substratkonzentration [S] bestimmt, so
lassen sich daraus Vmax (die Aktivität) und Km (die reziproke Affinität) ableiten. Ein
relativ neues, einfaches und doch präzises Verfahren zu diesem Zweck ist die direktlineare Auftragung (Enzymkinetik).
Inhibitoren, darunter wichtige Medikamente und Gifte, ändern die Eigenschaften von
Enzymen und können mit den hier eingeführten Methoden näher charakterisiert und in
ihrer Wirkungsweise besser verstanden werden:
•
•
•
„kompetitive“ Inhibitoren erhöhen den Km-Wert, verändern Vmax jedoch nicht
„unkompetitive“ Inhibitoren erhöhen ebenfalls den Km-Wert, senken zudem
aber Vmax
„nichtkompetitive“ Inhibitoren senken Vmax, verändern den Km-Wert aber
nicht
Enzymkinetik
Die Enzymkinetik ist ein Teilgebiet der biophysikalischen Chemie. Sie beschreibt, wie
schnell enzymkatalysierte chemische Reaktionen verlaufen. Die Enzymkinetik findet breite
Anwendung in Biologie und Medizin, da auch biologische Substrate (Reaktionspartner) –
darunter solche, die im Menschen auftreten – untersucht werden. Ein Hauptziel der
Enzymkinetik ist die Beschreibung der Konzentrationsabhängigkeit der
Reaktionsgeschwindigkeit mit geeigneten Formeln, sowie die Bestimmung der dazugehörigen
Parameter für ein bestimmtes Protein. Da Enzyme dazu dienen, Reaktionen zu beschleunigen
und zu lenken, ist die enzymkinetische Analyse zum Verständnis von Enzymfunktionen
unerlässlich.
Die Bindungsreaktion kann nach dem Massenwirkungsgesetz beschrieben werden, sie wird
charakterisiert durch Dissoziationskonstante Kd = k − 1 / k + 1. Dabei ist Kd diejenige
Konzentration des Substrates, bei der (in Abwesenheit der Umsetzung zu Produkt) die Hälfte
aller Enzymmoleküle Substrat gebunden haben. Sie ist umgekehrt proportional zur Affinität
des Enzymes für das Substrat.
Die Umsetzung des Enzym-Substrat-Komplexes zu Enzym und Produkt wird bestimmt durch
eine Geschwindigkeitskonstante 1. Ordnung, kcat. Die tatsächliche Geschwindigkeit der
enzymatischen Reaktion ergibt sich zu v = kcat * [ES]. Allerdings vermindert die
Zerfallsreaktion die Konzentration von [ES], es ist deshalb erforderlich, diese statt mit Kd mit
zu berechnen. Dann ergibt sich[1]
Dies ist die Gleichung einer Hyperbel, sie nähert sich für unendlich hohe
Substratkonzentrationen, wenn alle Enzymmoleküle Substrat gebunden haben, einem
Grenzwert
an. Die Konzentration bei der die
Reaktionsgeschwindigkeit gerade die Hälfte des Maximalwertes erreicht, ist die MichaelisKonstante Km. Zur Bestimmung von Vmax und Km aus Meßreihen von v und [S] dienen
computergestützte Verfahren wie die nichtlineare Regressionsanalyse (Simplex- oder
Levenberg-Marquardt-Verfahren). Graphische Extrapolationsverfahren (Linearisierungen)
wie etwa die doppelt-reziproke Auftragung nach Lineweaver und Burk sollten dafür nicht
verwendet werden, da sie zu ungenau sind. Sie eignet sich jedoch sehr gut zur Präsentation
der Ergebnisse enzymkinetischer Versuche, weil das menschliche Auge Abweichungen von
einer Gerade leichter erkennen kann als die von einer Kurve.
Direkt-lineare Auftragung
Wenig bekannt ist die Tatsache, dass sich enzymkinetische
enzymkinetische Parameter bequem und präzise
direkt aus einer Sättigungshyperbel gemäß der Abbildung herleiten lassen („direkt-lineare
(„direkt
Auftragung“ auch „Cornish-Bowden
Bowden-Diagramm“
Diagramm“ genannt). In dieser Hyperbel ist die
enzymatische Umsatzgeschwindigkeit v (Y-Achse)
(Y
als Funktion der Substratkonzentration [S]
dargestellt.
Für die direkt-lineare
lineare Auftragung überträgt man die Anfangsgeschwindigkeiten des
enzymatischen Umsatzes direkt in das v-[S]-Diagramm.
v
Die [S]-Werte sind vor
Versuchsbeginn bekannt (eingestellte Substratkonzentrationen);
Substratkonzentrationen); während der Versuchsreihe
ist dann der Ordinatenwert für v (die Anfangsgeschwindigkeit) nachzutragen. Im Gegensatz
zu normalen Auftragungen werden die Messwerte also nicht als Punkte dargestellt, sondern in
Form von Linien, die sich im günstigsten
stigsten Fall in einem gemeinsamen Punkt schneiden, aus
dessen Koordinatenwerten Km und Vmax folgen. Die katalytische Effizienz folgt übrigens aus
der Steigung der Tangente an den Ursprung: Vmax/Km; daraus ergibt sich kcat/Km.
Die Fehlerbehandlung wird im direkt-linearen
direkt linearen Plot weitgehend vereinfacht: die Linien im
zweiten Quadranten werden mehr oder weniger um einen Punkt streuen. Mittelwertsbildung
gibt dann die wahrscheinlichen Werte für die Parameter Km und Vmax. Bei Inspektion der
Streubreite der Messpunkte können Ausreißer leicht
leic identifiziert und sogenannte Mediane
abgelesen werden.
Linearisierungsverfahren
Linearisierungsverfahren wurden in der Vergangenheit sehr
sehr häufig für die schnelle grafische
Bestimmung der wichtigen Kinetikparameter Km und Vmax verwendet. Sie sind zwar
einprägsam und verbreitet, führen jedoch zu einer teils erheblichen Verfälschung des
Ergebnisses durch Messfehler und sind zur Fehlerbetrachtung
Fehlerbetrachtung mehr oder weniger ungeeignet.
Mittlerweile hat die Ermittlung der Michaelis-Menten-Parameter
Michaelis
Parameter durch nichtlineare
Regression stark an Bedeutung gewonnen, die zu deutlich genaueren Ergebnissen führt.
Lineweaver-Burke-Diagramm
Lineweaver-Burk-Diagramm
Diagramm (doppelt-reziproke
(doppelt
Auftragung)
1/v als Funktion von 1/[S].
zur Datenrepräsentation meist verwendet, zur Auswertung jedoch am wenigsten verlässlich.
Kleine Fehler in v ergeben bei kleinen [S]-Werten
[S] Werten eine große Abweichung in 1/v, bei großen
[S]-Werten ist diese eher zu vernachlässigen.
Eadie-Hofstee-Diagramm
Das Eadie-Hofstee-Diagramm nimmt eine Mittelstellung ein. Hierbei wird v über (v/[S])
aufgetragen.
Eine Umformung der Michaelis-Menten-Gleichung ergibt die folgende Gleichung:
Aus dem Diagramm lassen sich vmax als Y-Achsenabschnitt und Km als negative Steigung der
Regressionsgeraden ableiten.
Der Fehler wächst mit v/[S]. Da v bei beiden Koordinaten eingeht, konvergieren alle
Abweichungen zum Ursprung.
Scatchard-Diagramm
Das Scatchard-Diagramm
v/[S] als Funktion von v.
gleicht dem vorigen (Achsen sind vertauscht) und wird zumeist zur Repräsentation von
Bindungsmessungen (anstelle enzymkinetischer Daten) angewendet. Scatchard- und EadieHofstee-Diagramme gelten als die besten Werkzeuge zur Diagnose kooperativer Phänomene.
Im Falle negativer Kooperativität oder nicht-identischer, isolierter Bindungsplätze entsteht ein
konkaver Verlauf mit linearem Endast. Die Steigungen entsprechen hier den Affinitäten (Kd
beziehungsweise Km) und die Gesamtzahl der Bindungsplätze (aktiven Zentren) ist aus dem
Schnittpunkt mit der x-Achse abzulesen.
Hill-Diagramm
Graphische Methode, vorrangig für die Bestimmung eines kooperativen Bindungsvorganges
für ein Protein (Enzym). Gebunden werden Substrate S (bzw. Liganden L) Die Graphik setzt
Kenntnis von Vmax (beziehungsweise n) voraus. Die Auftragung von
log v/(Vmax-v) als Funktion von log [S] beziehungsweise
log r/(n-r) als Funktion von log [L]
ist eine Gerade der Steigung 1 (nH = 1), wenn die Bindungsplätze voneinander unabhängig
sind. Bei kooperativen Systemen kann die Steigung am Nullpunkt (der Hill-Koeffizient nH)
theoretisch der Zahl der Untereinheiten (n) gleichen, wird aber praktisch darunter bleiben.
Falls die individuellen Km-(Kd-)Werte nicht durch Tangenten an die 45°- Ausläufer der Kurve
extrapolierbar sind, ist nH ein Ersatzmaß der Kooperativität einzusetzen; nur für nH = 1 gleicht
der Nulldurchgang ln Km (beziehungsweise ln Kd). Für Hämoglobin (n = 4), das als
klassisches, hochkooperatives Protein gilt, wurde nH zu 2,8-2,9 bestimmt.
Inhibitoren
Viele Therapeutika und Gifte sind Hemmstoffe (Inhibitoren) von Enzymen. Aus diesem
Grunde ist der Aufklärung des Wirkungsmechanismus immer eine besondere Bedeutung
zugekommen. Die Nomenklatur der Hemmtypen wurde von W.W. Cleland 1963 auf eine
systematische Grundlage gestellt, leider werden in vielen Lehrbüchern immer noch Begriffe
abweichend verwendet.
Hier sollte allerdings beachtet werden, dass sich klassische Analysen auf reversibel bindende
Stoffe beschränken. Irreversible Bindung einer Substanz an ein Enzym führt zur
Inaktivierung, nicht zur Hemmung.
Abgeleitet aus der Michaelis-Menten-Gleichung (v = Vmax x [S] / (Km + [S]) stellt sich die
allgemeine Inhibitionsgleichung wie folgt dar:
Danach kann das Verhältnis des Ki-Wertes
-Wertes (Dissoziationskonstante des Komplexes EI) und
des Kii-Wertes
Wertes (Dissoziationskonstante des Komplexes EIS) zur Ableitung des
Inhibitionstyps dienen:
Kompetitiv
Inhibitor und Substrat schließen sich gegenseitig von der Bindung an das Enzym aus. Dies
bedeutet jedoch nicht notwendigerweise,
notwendigerweise, dass der Inhibitor an der gleichen Bindungsstelle
bindet wie das Substrat. Auch wenn die Bindung von Substrat bzw. Inhibitor zu
Konformationsänderung im Enzym führen, welche die Bindungsstelle für den jeweils anderen
blockieren, ist die Hemmung kompetitiv.
kompetitiv. Wenn Substrat und Inhibitor allerdings die gleiche
Bindungsstelle haben, dann ist der Hemmtyp notwendig kompetitiv.
Bei der Kompetitiven Hemmung kann der Inhibitor durch Substrat aus dem Enzym verdrängt
werden, Vmax ändert sich also nicht. Allerdings wird für jede gewünschte Geschwindigkeit
eine höhere [S] benötigt, die scheinbare Km wird also mit steigender [I] höher. Im
Lineweaver-Burk-Diagramm führt dies zu einer Schar von Geraden, die einen gemeinsamen
Schnittpunkt auf der y-Achse (1 / Vmax) haben.
Unkompetitiv
Der Inhibitor bindet nicht an das freie Enzym, sondern an den ES-Komplex. Höhere
Konzentrationen des Substrates können daher den Hemmstoff nicht vom Enzym verdrängen,
sondern führen zu vermehrter Bindung. Umgekehrt vermindert Bindung des Hemmstoffes die
Konzentration von ES, nach dem Prinzip von Le Chatelier muss sich also zusätzliches ES aus
E und S bilden: Die scheinbare Km vermindert sich, die Affinität des Enzymes für das Substrat
steigt mit steigender [I]. Gleichzeitig nimmt natürlich Vmax ab. Im Lineweaver-BurkDiagramm finden wir eine Schar paralleler Geraden.
Nicht-kompetitiv
Der Inhibitor kann sowohl an E als auch an ES binden. Im einfachsten Fall ist dabei Ki = Kii,
d.h. das die Substratbindung die Affinität des Enzymes für den Inhibitor nicht verändert, etwa
durch Konformationsänderung. Dann folgt natürlich auch, dass die Bindung des Inhibitors die
Affinität des Enzymes für das Substrat nicht ändert und Ks = Kss. Wegen des Zusammenhangs
zwischen Ks und Km ändert die Bindung von Inhibitor also auch nicht Km.
Es lässt sich nun zeigen (durch Substitution und Eliminierung aus den Definitionen von
Ki,Kii,Ks und Kss), dass Ki / Kii = Ks / Kss. Wenn also Ki < Kii, dann folgt Ks < Kss und die
scheinbare Km steigt mit [I]. Falls andererseits Ki > Kii, dann folgt Ks > Kss und die scheinbare
Km sinkt mit steigendem [I].
Die nicht-kompetitive Hemmung führt im Lineweaver-Burk-Diagramm zu einer Schar von
Geraden mit gemeinsamen Schnittpunkt links von der y-Achse, der Schnittpunkt liegt auf der
x-Achse wenn Ki = Kii, er liegt über der x-Achse falls Ki < Kii und unter der x-Achse falls Ki >
Kii.