Muskeldynamik Formeln
Werbung
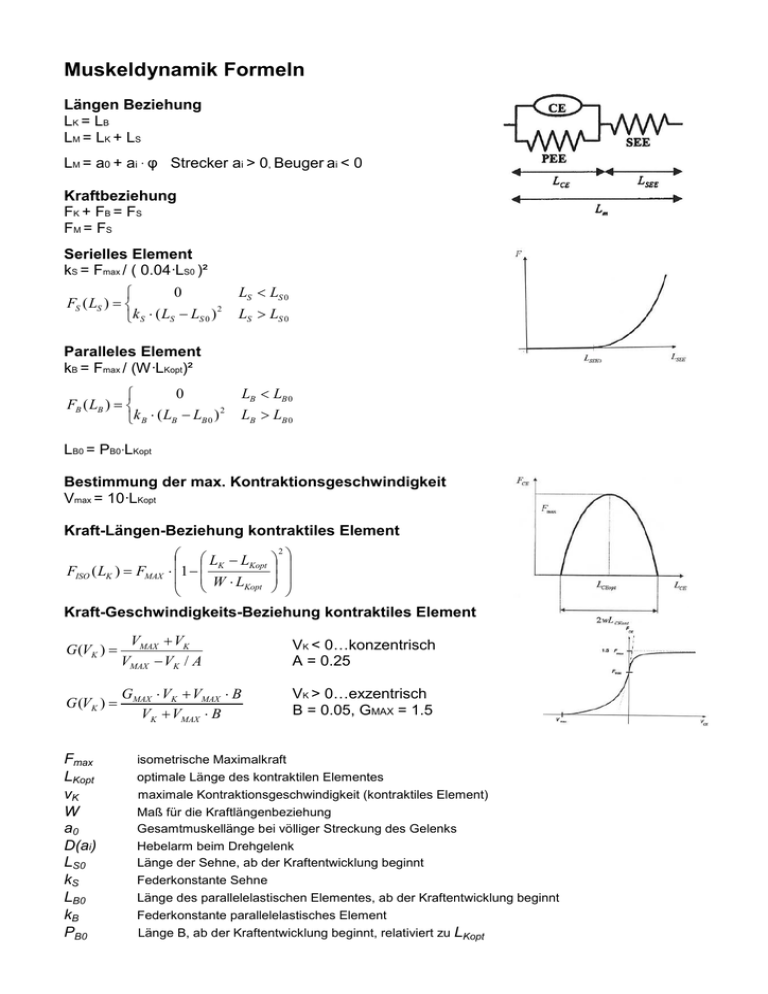
Muskeldynamik Formeln Längen Beziehung LK = LB LM = LK + LS LM = a0 + ai · φ Strecker ai > 0, Beuger ai < 0 Kraftbeziehung FK + FB = FS FM = FS Serielles Element kS = Fmax / ( 0.04·LS0 )² 0 FS ( LS ) = 2 k S ⋅ ( LS − LS 0 ) LS < LS 0 LS > LS 0 Paralleles Element kB = Fmax / (W·LKopt)² 0 FB ( LB ) = 2 k B ⋅ ( LB − LB 0 ) LB < LB 0 LB > LB 0 LB0 = PB0·LKopt Bestimmung der max. Kontraktionsgeschwindigkeit Vmax = 10·LKopt Kraft-Längen-Beziehung kontraktiles Element L − L 2 Kopt FISO ( LK ) = FMAX ⋅ 1 − K W ⋅L Kopt Kraft-Geschwindigkeits-Beziehung kontraktiles Element G (VK ) = VMAX + VK VMAX − VK / A VK < 0…konzentrisch A = 0.25 G (VK ) = GMAX ⋅ VK + VMAX ⋅ B VK + VMAX ⋅ B VK > 0…exzentrisch B = 0.05, GMAX = 1.5 Fmax LKopt vK W a0 D(ai) LS0 kS LB0 kB PB0 isometrische Maximalkraft optimale Länge des kontraktilen Elementes maximale Kontraktionsgeschwindigkeit (kontraktiles Element) Maß für die Kraftlängenbeziehung Gesamtmuskellänge bei völliger Streckung des Gelenks Hebelarm beim Drehgelenk Länge der Sehne, ab der Kraftentwicklung beginnt Federkonstante Sehne Länge des parallelelastischen Elementes, ab der Kraftentwicklung beginnt Federkonstante parallelelastisches Element Länge B, ab der Kraftentwicklung beginnt, relativiert zu LKopt Simulation Formeln 2D Bewegungsgleichungen M · a = S Fi I · α = S Ti 3D Bewegungsgleichungen M · v′ = S Fi I·w′ + w × (I·w) = S Ti M x v a Fi Masse Position Geschwindigkeit Beschleunigung Kräfte Gesamtmasse I φ w α Ti M = ∫ ρ dV ≈ ∑ mi xs = Trägheitsmoment i V Schwerpunkt Trägheitsmoment Drehwinkel Winkelgeschwindigkeit Winkelbeschleunigung Drehmomente 1 1 ρ x dV ≈ ∫ MV M I = ∫ ρ r 2 dV ≈ ∑ mi ri 2 i V ∑m i xi relativer Schwerpunkt η= i xs L Kräfte FW = m·g FF = µ·FN FD = ½·ρ·CD·A·v2 FA = ½·ρ·CL·A·v2 FM = ½·ρ·CM·A·r·ω×v Gewichtskraft Reibungskraft Luftwiderstand Luftauftrieb Magnus Kraft Eindringwiderstand Schnee Hypoplastisch Abscherwiderstand Schnee Hangabtreibende Kraft Normalkraft Laterale Kraft FP = H·V FP = H·V·f(ε) V = L·e2/2·tan θ ε = e/emax 0 ε − f 1 f (ε ) = f − f 2 1 1 FS = p*·e·L FH = m·g·sinα FN = m·g·cosα FL = m·v2/r – m·g·sinα·cosβ Mathematische Formeln Interpolation y (t ) = y1 + Ableitung y2 − y1 ⋅ (t − t1 ) t2 − t1 y' ≈ y2 − y1 y (t + ∆t ) − y (t ) ≈ t2 − t1 ∆t Lösen von Bewegungsgleichungen x′′=f(x,x’) bzw. a = f(x,v) x′ = v xneu = x + ∆t · v v′ = a = f(x,v) vneu = v + ∆t · a = v + ∆t · f(x,v) ε < f1 f1 ≤ ε ≤ f 2 f2 < ε