Rechenbeispiele

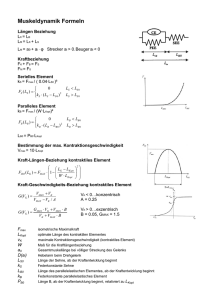
Zusammenfassung Muskelformeln
Längen Beziehung
LCE = LPEE
LM = LCE + LSEE
LM = a0 + ai · φ
Strecker ai > 0, Beuger ai < 0
Kraftbeziehung
FCE + FPEE = FSEE
FM = FSEE
Serielles Element
kSEE = Fmax / ( 0.04 · LSEEslack )²
Paralleles Element
kPEE = Fmax / (W · LCEopt)²
LPEEslack = PEEslack · LCEopt
FMAX bei der Länge LPEE = ( PEEslack + W ) · LCEopt
Bestimmung der max. Kontraktionsgeschwindigkeit
Vmax = 10 · LCEopt /t t…für t wird 1s verwendet
Kraft-Längen-Beziehung kontraktiles Element
Kraft-Geschwindigkeits-Beziehung kontraktiles Element
vMAX  vCE
G (vCE ) 
…VCE < 0…konzentrisch A = 0.25
vMAX  vCE / A
G (vCE ) 
GMAX  vCE  vMAX  B
vCE  vMAX  B
…VCE > 0…exzentrisch
B = 0.05, GMAX = 1.5
CE
PEE
SEE
Kontraktiles Element
Parallelelastisches Element
Seriellelastisches Element
M
L
Muskel
Länge
a0
ai
φ
vCE
Länge Muskel bei neutraler Position des Modells
Hebelarm zum Drehpunkt des Gelenks
Winkel vom Gelenk
Kontraktionsgeschwindigkeit des kontraktilen Elements
k
Federkonstante
slack entspannt, locker
LSEEslack Länge Sehne, ab der die Kraftentwicklung beginnt
LCEopt Länge des kontraktilen Elements, bei der die höchste isometrische Kraft wirkt
W
Konstante (einheitslos), über welchen Längenbereich kann das kontraktile Element
eine Kraft erzeugen (Maximale Längenbereich, in dem der Muskel eine Kraft
erzeugen kann in Relation zur optimalen Muskellänge)
G(vCE) Verhältnis der Kraft bei einer Kontraktionsgeschwindigkeit zur isometrischen
Maximalkraft
A
Konstante für den konzentrischen Fall
B
Konstante für den exzentrischen Fall
Bewegungsgleichung
Beispiel Fallschirmspringer:
Stellen Sie die Newton’schen Bewegungsgleichungen für einen Fallschirmspringer auf.
Modellieren Sie dazu den Fallschirmspringer als einen einzelnen starren Körper.
Rotationskräfte und der aerodynamische Auftrieb können vernachlässigt werden. Geben Sie
Bezeichnung und SI Einheiten zu den Symbolen an!
a. Welche Kräfte greifen an
b. Wie lauten die Newton’schen Bewegungsgleichungen
a) Gewichtskraft: Fg = - m g, Luftwiderstand Fd = ½ ρ Cd A v2
b) m a = Fg + Fd, a = v′, v = x′
Bezeichnung und Einheiten zu allen Symbolen
Beispiel Gummiseil und Luftreibung:
Tragen Sie die fehlenden Grundeinheiten ein und berechnen Sie die Beschleunigung für
die zwei Längen l0 = 30m und l1 = 100m bei folgenden Angaben:
Vereinfachung: Gummiseil ist masselos
m = 80 kg, s0 (Ausgangslänge) = 50 m, cwA = 0,4_____, ρ = 1 _______, k = 20_________
v0 = 20________
Fges = FGew – FFed - FLuftw (Jene Kräfte, welche nach unten wirken, werden als positiv
angenommen)
Durch umformen erhält man die folgenden Formeln:
v0 = 10m/s² – 1/(160kg) * 0.4m² * 1 kg/m³ * 400m²/s² = 9 m/s²
s0 < sE
v1 = - 20/80 * (100 – 50) + 10m/s² – 1/(160kg) * 0.4m² * 1 kg/m³ * 400m²/s² = 9 m/s² =
= -12.5 + 9 = 3.5 m/s²
s0 > sE
Beispiel Fallschirmspringer:
Die Bewegungsgleichung eines Fallschirmspringers lautet:
m · a = F = +FG – FL = m · g - ½ ·  · CDA · v2
Zum Zeitpunkt des Öffnens des Fallschirms beträgt die Höhe 1200 m und die
Fallgeschwindigkeit 50 m/s. Die Masse des Fallschirmspringers samt Schirm ist 100 kg, die
Luftdichte 1.1 kg und der Luftwiderstandsbeiwert CD = 0.7. Der Durchmesser des voll
geöffneten Schirms beträgt 4 m.
Wie groß ist die Höhe und die Fallgeschwindigkeit nach 0.2 s. Integrieren Sie dazu die
Bewegungsgleichung mit einem Zeitschritt von t = 0.1 s, also t = 0, t = 0.1 und t = 0.2.
m · a = m · g - ½ ·  · CDA · v2
a = g - ½ ·  · CDA · v2 / m
A = (D/2)² · Pi = 12.56 m²
a = g - c · v2
c = ½ ·  · CDA / m = 0.0484
v-neu = v + a · t
h-neu = h + v · t
t
h
v
a
0.0
0.1
0.2
1200
1195
1188
-50.0
-38.9
-28.4
-111
-63.3
-41.5
Die Höhe beträgt 1188 m und die Fallgeschwindigkeit 28.4 m/s.
Muskelmodellierung
Beispiel Kraft Längen Beziehung:
Fmax,iso = 8000 N; LCEopt = 0.15 m; LSEEslack = 0.2 m;
a0 = 0.3 m; a1 = 0,05 m
Berechnen Sie die Kraft der Kniestrecker für einen Kniewinkel von 150° (sehr stark gebeugt
im Kniegelenk, 0° = gestreckt) für W= 0.6 und W = 1.2.
Die Dehnung der Sehne kann vernachlässigt werden.
Lges = A0 + Dknee · (Kniew. · π /180) = 0,3 + 0,05 · 2,61 = 0,43 m
LCE = Lges - Lslack= 0,43 - 0,2 = 0,23m
F = Fmax [1- ((LCE - LCEOpt) / (W*LCEopt))²]
= 8000 [1-((0,23-0,15) / (0,6* 0,15))²] =
= 8000 [1 – (0,08/0,09)²] = 8000 [1 – (0.8888)²]= 8000 [1 – 0.81]= 1520 N
= 8000 [1 – (0,08/0,18)²] = 8000 [1 – (0,4444)²]= 8000 [1 – 0.19]= 6419 N
Beispiel Muskelverkürzungsgeschwindigkeit:
Ein Muskel erzeugt isometrisch eine Kraft von 5 kN und hat eine maximale
Verkürzungsgeschwindigkeit von 1 m/s. Bei welcher Kontraktionsgeschwindigkeit erzeugt
der Muskel die höchste Leistung (Genauigkeit 0.1 m/s)?
vMAX  vCE
G (vCE ) 

vMAX  vCE / A
F = Fiso * ( vmax + vce ) / ( vmax – vce * 4 ) =
Achtung auf die Vorzeichen bei der Geschwindigkeit:
Setzt man z.B. positive Werte für vce ein, würden sich Kraftwerte ergeben, welche größer als
die isometrische Maximalkraft wären. (für v = 0.1m/s: 5 kN * 1,1/0,6= 9.16 kN)
v = -0.1 m/s: 5kN * 0.9/1.4 = 3.21 kN
P = F * v = 321 W
-0.2 m/s:
* 0.8/1.8 = 2.22 kN
= 444 W
-0.3
0.7/2.2 = 1.59 kN
= 477 W
-0.4
0.79 kN
= 307 W
Beispiel Muskelmodellierung kombiniert mit biomechanischen Grundlagen:
Eine Person erreicht beim Sprung aus der tiefen Hocke (Kniewinkel 40°,
Kniewinkel gestreckt 180°) eine vertikale Sprunghöhe von 50 cm. Der
vertikale Beschleunigungsweg des Körperschwerpunktes beträgt dabei 60 cm.
a) Berechnen Sie die vertikale Absprunggeschwindigkeit!
b) Berechnen Sie die durchschnittliche äußere Gesamtkraft!
c) Berechnen Sie die durchschnittliche Muskelkraft (aF = 0.2 m)!
d) Berechnen Sie die durchschnittliche Leistung unter der Annahme, dass die
Beschleunigung konstant ist!
e) Wie groß muss die isometrische Maximalkraft mindestens sein, um diese Leistung
erbringen zu können (die Kraft-Längen Beziehung kann vernachlässigt werden)?
Verwenden Sie dafür die durchschnittliche Muskelkontraktionsgeschwindigkeit.
(Falls Sie einen Punkt nicht lösen können, schätzen sie die Lösung und rechnen Sie die
anderen Punkte weiter.)
gegeben:
Masse m = 80 kg
Muskellänge a0 = 0.20 m
Normalabstand Muskelwirkungslinie zu Kniedrehpunkt a4 = 0.05 m
LSEEslack = 0.16 m
W = 1.2
LCEopt = 0.08 m
vmax = 1.2 m/s
A = 0.25
vA = √2gh = 3.16 m/s …Absprunggeschwindigkeit
Δt = Δs / vm = 0.6 / 1.58 =0.38 s
…
am = Δv / Δt = 3.16 / 0.38 = 8,31 m/s²
Zeit für die Absprungbewegung (Beginn
Absprung bis zum Loslösen vom Boden
durchschnittliche Beschleunigung während der
Absprungbewegung
Fges= m · (g + am) = 80 kg · (10 + 8.31) m/s² = 1465 N
FM = Fges · aF / a4 = 5861 N
aF Normalabstand Gesamtkraft zu Kniegelenk
P = Fges · vm = Fges · (vA/2) = 1412 N · 1.58 m/s = 2230 W
vM = w · a4 = (140° ∙ π / 180) / 0.38 s · 0.05m =
vM durchschnittliche Muskelkontraktionsgeschw.
= 3.6 rad/s · 0.05m = 0.18 m/s
F max  FCE
v MAX  vCE / A
v MAX  vCE
= 5861 ∙ (1,2 + 0.18 ∙ 4) / (1,2 – 0.18) = 11 032 N
Beispiel: Kraftlängenbeziehung Muskel kombiniert mit biomechanischen Grundlagen
Körpergewicht [kg]
70
Zusatzgewicht [kg]
100
55
Sprunggelenkswinkel [°]
Kniewinkel [°]
30
Hüftwinkel [°]
55
F
[cm]
gegeben:
Muskellänge a0 = 0.2 m
Knieradius a4 = 0.05 m
LSEEslack = 0.16 m
W = 1.2
LCEopt = 0.09 m
gesucht:
a) LM und LCE
b) Wie groß muss die max. isometrische Kraft der Kniestrecker sein, damit die Person die
Position halten kann?
FM = Fges · aF / a4 = 1700 · 0.15/0.05 = 5100 N (Kraft für beide Kniestrecker, linke und rechte
Seite)
 FM,li = FM,re = 2550 N
LM = a0 + a4 · φ = 0.2 + 0.05 · 150° · π/180 = 0.33 m
LCE = LM – LSEE = 0.33 - 0.16 = 0.17 m
 Fmax = FISO / […] = FISO /[1- (0.06/0.108)²] = FISO / 0.7 = 2550 N / 0.7 = 3642 N
Beispiel Muskelmodellierung kombiniert mit biomechanischen Grundlagen
Folgende Angaben gelten für ein Krafttrainingsgerät:
Masse Gewicht: 100 kg
Radius Drehscheibe: 10 cm
1.) Welche maximale Kraft benötigt der Kniestrecker bei einem gestreckten und bei einem
90° gebeugten Knie, um das Gewicht isometrisch zu halten?
2.) Welche isometrische Maximalkraft wird bei einem 90° gebeugten Knie benötigt, wenn die
Drehgeschwindigkeit des Hebels 20 Grad/s beträgt?
LCEopt = 0.15m; LSlack = 0.2m ; a0 = 0.3 m; aknie = 0.05 m; W= 0.6; vmax = 1.2 m/s
Drehscheibe
B
Seil
Gewicht
A
FM = Fgew · rScheibe / aknie = 1000 N · 0.1 / 0.05 = 2000 N
Lges,0° = LM = a0 + ai · φ
= a0 + aknie · (φ · π /180) = 0,3 + 0,05 · 0 = 0,3 m
Lges,90° = 0.3 + 0.05 · 90 · π /180 = 0.378 m
LCE = Lges – Lslack= 0.3 m – 0.2 m = 0.1 m
 Fmax = FISO / […] = FISO /[1- (-0.05/0.09)²] = FISO / 0.7 = 2000 N / 0.7 = 2857 N
vM = w · a4 = (20°/s ∙ π / 180) · 0.05m = 0.017m/s
F max  FCE
v MAX  vCE / A
v MAX  vCE
vM Muskelkontraktionsgeschw.
= 2857 · (1.2 + 0.017 · 4) / (1.2 – 0.017) = 3062 N
Beispiel Tennis
Berechnen Sie die translatorische und die rotatorische Energie direkt nach dem 1. Service (v=
200 km/h, w = 3000 rpm, m = 0.06kg und I = 0.00044 kgm²)?
ET = mv²/2 = 0.06 (200/3.6)² /2 = 92.6 Nm
ER = Iw²/2 = 0.004 (3000 2PI /60)² /2 = 2.14 Nm
Freischneiden von Kräften
a) Zeichnen Sie alle Kräfte beim Skifahrer A ein und beschriften Sie diese!
b) Erklären Sie den Bewegungsablauf für den Fall, dass der Skifahrer B die Ski nicht
aufgekantet hat mit Hilfe von physikalischen Argumenten!
Fall A: Ski vom Fahrer B ist nicht aufgekantet
Wenn sich die Skischaufel des Fahrers B auf dem Ski A befindet, so ist die
Normalkraft zwischen den Ski relativ gering. Da auch der Reibungskoeffizient zwischen Ski
A und Ski B gering ist, wird das Drehmoment im Sprunggelenk kaum erhöht und der Ski B
behält seine Bewegungsrichtung bei. Befindet sich der Skifahrer B über dem Ski A so erhöht
sich die Reibungskraft zwischen Ski A und Schnee um ca. zwei Drittel und die Reibungskraft
zwischen Ski A und Ski B ist mindestens so groß wie die Reibungskraft zwischen Ski und
Schnee. Daraus folgt, dass sich die gesamte Reibungskraft um ca. 160 bis 200% erhöht und
dementsprechend sich auch das Drehmoment im Sprunggelenk um diesen Wert erhöht.
Dadurch besteht die Möglichkeit eines Sturzes nach vorne vom Skifahrer A.
Beispiel Ringturnen: Freischneiden und Muskelmodellierung
l1
Abb. 1 zeigt eine Positionen beim Ringturnen
gegeben:
l
Masse Turner m = 60 kg
Muskellänge a0 = 0.20 m
Schulterradius a3 = 0.06 m
Abstand Schulter Ringe l1 = 0.3 m
LSEEslack = 0.15 m
W = 1.2
LCEopt = 0.084 m
gesucht:
a) LM und LCE
b) Wie groß muss die max. isometrische Kraft der Schulteradduktoren sein, damit die Person
die Position halten kann?
FM = Fges * l / a3 = 300 * 0.3/0.06 = 1500 N
LM = a0 + a3 · φ = 0.2 + 0.06 * 90° *Pi/180 = 0.294 m
LCE = LM – LSEE = 0.294 - 0.15 = 0.144 m
= …= …0.642  Fmax = 1500N / 0.642 = 2333N
Beispiel Liegestütz
Welcher Unterschied besteht bezüglich des Drehmomentes in der Schulter bei der
abgebildeten Position mit und ohne Reibungskraft? Zeichnen Sie zur Begründung die
wirkenden Kräfte ein!
KSP
KSP
Beispiel Krafttraining:
Welche Drehmomente wirken in der Schulter und im Ellbogen bei der Abb. 1 und Abb. 3?
Die Hantel hat eine Masse von 30 kg. Die Länge des Ober- und Unterarms beträgt 40 cm (vgl.
Abb. b). Welche Muskelkraft muss wirken, dass bei Abb. a die Hantel in dieser Position
gehalten werden kann (Muskelarm vom m. biceps beträgt 4 cm) ?
Schulter
Hantel
45°
45°
40
cm
45°
40
cm
Ellbogen
Abb. 1
Abb. 2
Abb. 3
l1 = 0.4m * cos(45°) = 0.28m
Abb. 1) ME = MS = l1 * FH = 0.28 m * 300 N = 84Nm
Abb. 3) ME = 84Nm; MS = 0
Fb = ME / lM = 300 * 0.4 / 0.04m = 3000N
Beispiel Krafttraining
Zeichnen Sie den Momentenverlauf vom abgebildeten Krafttrainingsgerät von A nach
B!
Drehmoment
B
A
A
B
Theoriefragen
Beispiel Bewegungsgleichungen
Geben Sie die fünf Schritte für das Erstellen der Bewegungsgleichung kurz an (max. 8 Wörter
pro Schritt)! Beschreiben Sie die ersten drei Schritte genauer für ein Federpendel!
1. Freischneiden
FG … Gewichtskraft
Dynamischer Fall: FG ≠ FF
2. Äußere Kräfte definieren Gewichtskraft FG = m • g
Federkraft
FF = k • Δy
3.Beschleunigungskraft berechen Fa = ∑F
Summe aller Kräfte ergibt die Beschleunigungskraft
Fa
= (-) FF + FG m • a = - k (y – yF) + m g
4. Kräftegleichung nach a bzw. y‘‘ auflösen
5. Schritt: a, v und s schrittweise berechnen
FF … Federkraft
FF = k • (y – yF)