Kinetik isolierter und gereinigter Enzyme zum Verständnis ihrer

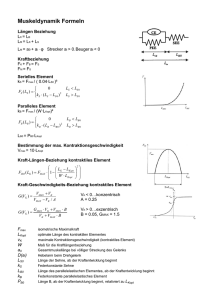
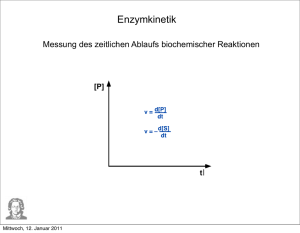
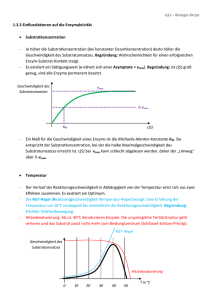
Kinetik isolierter und gereinigter Enzyme zum
Verständnis ihrer Reaktionsmechanismen
unkatalysierte Reaktion
enzymatische Reaktion
⇒
V = k[S]
V0 = k[S]
⇓
⇒
k1
k2
k3
E + S ↔ ES ↔ EP → E + P
k-2
k-1
V0 = k3[EP]
allgemeine Reaktionsgeschwindigkeit-Gleichung
V0 = kkat[Zg]
Zg = geschwindigkeitbestimmendes
Zwischenprodukt
kkat = GeschwindigkeitsKonstante der
Gesamptreaktion
Bei mehrfasigen enzymatischen Reaktionen stellt ein dynamisches Gleichgewicht
zwischen der Entstehung und der Weiteränderung des Geschwindigkeit-bestimmenden
Zwischenprodukts ein (Fliessgleichgewicht, steady state): [Zg] = konst; V = konst = V0
Die Michaelis-Menten-Kinetik
Vmax[S]
V0 = -------------Km + [S]
Michaelis-Menten-Gleichung
k1
k2
E + S ↔ ES → E + P,
k-1
wenn
k-1 + k2
Km = -----------k1
ist
V0 = Wmax/2 ⇒
Km = [SVmax/2]
Km >> [S]
⇒
Vmax
V0 = ------- [S]
Km
Km << [S]
⇒
V0 = Vmax
Mit Ausnahme regulatorischer
Enzyme gehorchen Enzyme der
Michaelis-Menten-Kinetik
Die doppelt-reziproke Transformation der Michaelismenten-Gleichung (Lineweaver-Burk-Diagramm)
Michaelis⇐ MentenGleichung
inverse Form
der Michaelis⇐ MentenGleichung
⇑
Lineweaver-Burk-Gleichung
Das Lineweaver-Burk Diagramm kann bei Analyse enzymkinetischer Probleme,
z.B. bei Unterscheidung der drei Arten von Enzym-Hemmung, verwerdet werden
Die wichtigsten kinetischen Parameter
V0 = kkat[Zg]
⇐ allgemeine Reaktionsgeschwindigkeit-Gleichung
V0 = Vmax
Bei grossem
⇐ Substratsüberschuss
[Zg] = [Et]
Vmax = kkat[Et]
V0
Vmax[S]
= -------------Km + [S]
kkat[Et][S]
V0 = ---------------Km + [S]
V0(Km + [S])
kkat = -----------------[Et][S]
wenn [S] << Km
Km + [S] = Km
kkat
V0
------ = ---------Km
[Et ][S]
Michaelis⇐ MentenGleichung
Vergleichs-Parameter
⇑
⇓
Wechselzahlen (turnover numbers)
Untersciedliche Wege der bimolekularen
enzymatischen Reaktionen
Hexokinase
ATP + D-Glucose → → ADP + D-Glucose-6-phosphat
E’ ~ persistent verändertes Enzym
Die doppeltreziproke Darstellung
(Lineweaver-Burk-Diagram) von
Ergebnissen kinetischer Untersuchungen hilft
bei Ermittlung unterschiedlicher Aspekten des
Mechanismus enzymatischer Reaktionen.
Reversible, kompetitve Enzym-Inhibition (-Hemmunng)
Vmax[S]
V0 = --------------αKm + [S]
wenn αKm << [S], ist V0 = Vmax
⇐ umgestaltete Michaelis-Menten-Gleichung
umgestaltete Lineweaver-Burk-Gleichung ⇒
Einige Medikamente sind Inhibitoren
αKm
Km
α = ------- : ----Vmax
Vmax
Reversible, unkompetitive Enzym-Inhibition (-Hemmung)
Vmax[S]
V0 = ----------------Km + α’[S]
wenn
Km << α’[S],
ist
V0 = Vmax/ α’
⇐ umgestaltete Michaelis-Menten-Gleichung
umgestaltete Lineweaver-Burk-Gleichung ⇒
α’
1
α’ = ------- : -----Vmax Vmax
Reversible, gemischte Enzym-Inhibition (-Hemmung)
Vmax[S]
V0 = ------------------αKm + α’[S]
wenn αKm << α’[S], ist
V0 = Vmax/ α’
⇐ umgestaltete Michaelis-Menten-Gleichung
umgestaltete Lineweaver-Burk-Gleichung ⇒
Irreversible Enzym-Inhibition
Chymotrypsin + Diisopropylfluorophosphat
Ein Selbstmord-Inhibitor ist ein modifiziertes Substrat, das
zuerst reversibel und kompetitiv in dem aktiven Zentrum des
Enzyms gebunden wird. Der entstehende Enzym-InhibitorKomplex kann danach durch den normalen enzymatischen
Mechanismus in das normale Produkt und eine sehr
reaktionsfähige Verbindung überführt werden, die sich kovalent
und irreversibel an eine essenzielle funktionelle Gruppe des
aktiven Zentrums bindet oder sie zerstört.
Die Wirkungsweise einiger neuen Arzneimittel berucht sich an
Selbstmord Inhibition.
Abhängigkeit der Enzymaktivität vom pH-Wert
(pH-Optimum)
Der Grund für die pH-Abhängigkeit der Enzyme ist, dass Seitenketten
einiger Aminosäureresten in ihren aktiven Zentren schwache Säuren oder
Basen von unterschiedlichem pH-Optimum sind. Diese Seitenketten
dissoziieren bei unterschiedlichen pH-Werten in unterschiedlichem Mass.
Dies beeinflusst die räumliche Anordnung der funktionellen Gruppen in dem
aktiven Zentrum des Enzyms, und dadurch seine katalytische Aktivität.