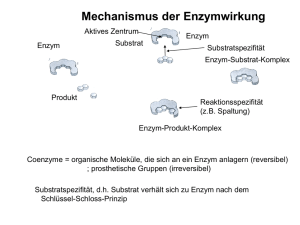
Versuch 5: Enzyme (Alkalische Phosphatase)

Versuch 5: Enzyme (Alkalische Phosphatase)
(V10 6.03.2012)
Lernziele:
1) Reaktionsgeschwindigkeit, Aktivierungsenergie, chemisches Gleichgewicht;
2) Was tun Katalysatoren und Enzyme,
3) Michaelis-Menten Gleichung, Lineweaver-Burk-Diagramm,
4) Kompetitive Hemmung, allosterische Regulation, pH-Optimum.
Hintergrund:
1) Katalysatoren:
Enzyme sind biologische Katalysatoren. Als solche beschleunigen sie die Geschwindigkeit
chemischer Reaktionen – oftmals um ein Zigtausendfaches, sodass man Enzyme in solchen
Fällen ruhig als Ein/Aus-Schalter einer Reaktion betrachten kann. Die enzymatische
Aktivität wird durch viele Faktoren reguliert, z.B. der chemisch-physikalischen Umgebung
(pH-Wert, Temperatur, Ionen, etc.), der Verfügbarkeit von Substrat, der Anwesenheit von
bereits gebildetem Produkt, oft auch durch spezifische regulatorische Moleküle, und nicht
zuletzt durch die Konzentration des Enzyms selbst. Die Geschwindigkeit der katalysierten
Reaktion wird dadurch kontinuierlich regelbar, und das Enzym funktioniert dann wie der
Lautstärkeregler an Ihrer Stereoanlage.
Damit ein Molekül eine chemische Reaktion eingehen kann, muss es eine bestimmte
innere Mindestenergie annehmen, die sogenannte „Aktivierungsenergie“. Eine Substanz ist
umso stabiler, je größer die Differenz ihrer inneren Energie und der Aktivierungsenergie
ist (deshalb lagern wir empfindliche Lebensmittel im Kühlschrank). Die chemische
Reaktion kann also beschleunigt werden, indem man der Verbindung Energie zuführt, z.B.
durch Erhitzen. Dadurch erhöht sich die Chance eines individuellen Moleküls, die
Aktivierungsenergie zu erreichen und damit die Reaktion einzugehen. Auch Enzyme
beschleunigen die Reaktion, indem sie die Differenz zwischen innerer Energie des
Substrats und der Aktivierungsenergie verringern. Die zugrunde liegenden molekularen
Mechanismen sind außerordentlich vielfältig und einfallsreich. Durch die Bindung an ein
Enzymmolekül kann ein Teil der inneren Energie des Enzyms auf das Substrat übertragen
werden, oder das Enzym stabilisiert einen Übergangszustand bzw. ein Zwischenprodukt
der Reaktion, was formal einer Herabsetzung der Aktivierungs-Energie gleichkommt.
2) Das Michaelis-Menten Diagramm:
In Ihrem ersten Experiment werden Sie eine enzymatisch katalysierte Reaktion
durchführen und mehrmals, bei immer höheren Substrat-Konzentrationen, wiederholen.
Dabei werden Sie feststellen, dass eine Erhöhung des Substratangebots zunächst annähernd
proportional zu einer gesteigerten Geschwindigkeit in der Bildung des Reaktionsproduktes
führt. Mit zunehmender Substratkonzentration wird dieser Effekt immer bescheidener, bis
schließlich eine weitere Substraterhöhung keine weitere Beschleunigung mehr bewirkt.
Der Grund dafür ist, dass Substratmoleküle nur dann reagieren können, wenn sie an ein
Enzymmolekül gebunden haben. Da die Anzahl der verfügbaren Enzymmoleküle in allen
Ihren Ansätzen die gleiche war, tritt mit steigender Substratkonzentration eine zunehmende
Absättigung der Enzymmoleküle ein, sodass für weiteres Substrat zunehmend weniger
freie Enzymmoleküle zur Verfügung stehen, bis letztlich alle vorhandenen Enzymmoleküle
zu jedem Zeitpunkt ein Substratmolekül gebunden haben. Die Reaktion läuft dann mit,
unter den gegebenen Rahmenbedingungen, maximal möglicher Geschwindigkeit.
Wenn Sie in einem Diagramm die gemessenen Geschwindigkeiten (v) gegen die
jeweiligen Substratkonzentrationen (S) auftragen, erhalten Sie eine nach rechts hin immer
flacher
verlaufende
Kurve,
die
sich
asymptotisch
der
maximal
möglichen
Reaktionsgeschwindigkeit (Vmax) annähert. Sie erinnern sich, dass Vmax dann erreicht wird,
wenn alle Enzymmoleküle jederzeit Substrat gebunden haben. Daraus folgt, dass bei halbmaximaler Geschwindigkeit nur 50% aller Enzymmoleküle Substrat gebunden haben.
Wenn Sie in Ihrer Kurve diesen Punkt suchen, können Sie die dafür erforderliche
Substratkonzentration auf der x-Achse ablesen. Hätten Sie nun Gelegenheit, mehrere
Enzyme zu untersuchen, dann könnten Sie vielleicht feststellen, dass diese Kurve mal
steiler, mal flacher ausfallen. Entsprechend würde die Substratkonzentration, die zum
Erreichen der halb-maximalen Geschwindigkeit erforderlich ist, mal geringer, mal höher
sein. Dieses Verhalten reflektiert die Festigkeit („Affinität“), mit der Enzym und Substrat
einander binden. Die Substratkonzentration, die zum Erreichen der halb-maximalen
Geschwindigkeit, also zur Besetzung von 50% aller vorhandenen Enzymmoleküle
erforderlich ist, wird damit zu einer wichtigen Kennzahl eines Enzym-Substrat-Paares.
Diese Kennzahl heißt die Michaelis-Menten Konstante („Km“).
Maud Menten hat in ihrer Dissertation bei Leonor Michaelis 1913 ein mathematisches
Modell für dieses Verhalten formuliert. Versuchen Sie doch einmal, die zugrunde
liegenden Überlegungen dieser Theorie nachzuvollziehen. Sie sind in jedem BasisLehrbuch der Biochemie besser und ausführlicher beschrieben, als es in diesem Rahmen
hier möglich wäre. Sie werden dann sehen, warum die Kurve, die Sie in Ihren eigenen
Experimenten erhalten haben eine Parabel der Form v = Vmax  S / (Km + S) ergeben
musste.
3) Lineweaver-Burk Darstellung:
Wenn Sie nun aus denselben Messwerten die Kehrwerte (1/v) bilden und gegen die
Kehrwerte der dazugehörigen Substratkonzentrationen (1/S) auftragen, dann geschieht
etwas Sonderbares: anstelle einer gekrümmten Kurve erhalten Sie eine Gerade, die links
der y-Achse die x-Achse schneidet. Dieser Schnittpunkt repräsentiert den negativen
Kehrwert von Km. Der Schnittpunkt der Gerade mit der y-Achse bildet den Kehrwert der
Maximalgeschwindigkeit ab (warum?). Wenn Sie die obige Michaelis-Menten Gleichung
nach 1/v auflösen, erhalten Sie die entsprechende Geradengleichung. Dieses sogenannte
Lineweaver-Burk Diagramm hat einige Vorteile, z.B. den, dass eine Gerade bereits durch
zwei Punkte definiert ist, und nicht erst unzählige Wiederholungen des Experiments
durchgeführt werden müssen, um Vmax zu bestimmen. Außerdem ist aus der
asymptotischen Annäherung der Kurve Vmax ohnehin nur näherungsweise zu bestimmen.
Der Nachteil der Lineweaver-Burk Darstellung ist, dass kleine (und deshalb ungenaue)
Messwerte zu großen Kehrwerten führen und deshalb relativ kleine Fehler zu großen
Ungenauigkeiten führen. Später entwickelte Linearisierungsverfahren umgehen dieses
Problem. Aber das geht über unseren Erstkontakt mit Enzymen klar hinaus.
Aus Vmax lässt sich bei bekannter Enzymkonzentration die sogenannte Wechselzahl kcat
(„turnover number“) berechnen: kcat = Vmax/[E]. Sie gibt an, wieviele Substratmoleküle
pro Sekunde von einem Enzymmolekül umgesetzt werden. Ein weiterer wichtiger
Parameter für ein gegebenes Enzym-Substratpaar ist die katalytische Effizienz, der
Quotient kcat/Km. Manche Enzyme setzen ihre natürlichen Substrate so schnell um, dass die
Reaktion nur noch von der Substratdiffusion zum aktiven Zentrum abhängt und somit das
physikalische Limit von kcat/Km erreicht wird, welches bei 108 - 109 M-1 s-1 liegt.
Links das Michaelis-Menten-Diagramm, rechts die Lineweaver-Burk-Auftragung derselben Daten.
4) Kompetitive Inhibition:
Zu den vielen Verbindungen, die eine Enzymreaktion beeinflussen können zählen oft auch
solche, die eine gewisse strukturelle Ähnlichkeit mit dem Substrat aufweisen. Solche
Verbindungen können zwar an das katalytische Zentrum des Enzyms binden, werden aber
dort keine (oder eine andere) chemische Reaktion eingehen. Ihre Besetzung des
katalytischen
Zentrums
verhindert
natürlich
die
gleichzeitige
Bindung
eines
Substratmoleküls. Allerdings kann sie durch einen entsprechenden Überschuss an Substrat
kompensiert werden. Da beide Verbindungen um die Bindungsstelle am Enzym im
Wettstreit liegen, nennt man solche Substanzen „kompetitive Inhibitoren“. Die Stärke des
hemmenden Effekts hängt ab von der Konzentration und (verständlicherweise) der
Affinität des Inhibitors zum Enzym. Einen kompetitiven Inhibitor kann man an einer
scheinbaren
Erhöhung
des
Km-Wertes
erkennen
(warum?).
Die
erreichbare
Maximalgeschwindigkeit bleibt jedoch auch in Anwesenheit eines kompetitiven Inhibitors
gleich (warum?).
Mathematisch ergibt sich diese Erhöhung aus dem Term Km' = Km  (1 + I/Ki). Warum das
so ist würde hier zu weit führen, aber Sie brauchen diese Beziehung in Ihrem nächsten
Experiment, um die Affinität des Inhibitors zu berechnen. Sie werden in Ihren
Experimenten Gelegenheit haben, die Funktionsweise von alkalischer Phosphatase (AP) zu
untersuchen. AP katalysiert die Hydrolyse von Phosphorsäureestern, also die Abspaltung
von anorganischem Phosphat aus einer Vielzahl von organischen Verbindungen, z.B.
phosphorylierten
Aminosäure-Seitenketten
in
Proteinen,
den
5’-Enden
von
Nukleinsäurefragmenten, ATP, etc., ja sogar von Verbindungen, die in der Natur gar nicht
vorkommen. Das dabei anfallende Phosphat, das eben noch Teil des Substratmoleküls war,
hat selbst eine gewisse Affinität zum katalytischen Zentrum des Enzyms und wirkt damit
als kompetitiver Inhibitor. Wie Sie diese messen können, entnehmen Sie der
Arbeitsanleitung in Teil B2 weiter unten. Wenn Sie Ihre Messreihe in einem Puffer
wiederholen, der Phosphationen enthält, dann verändert sich das Aussehen der MichaelisMenten Kurve und die Gerade im Lineweaver-Burk Diagramm (wie werden sie im
Vergleich zur ungehemmten Reaktion aussehen?)
5) Nicht-kompetitive Inhibition:
Alkalische Phosphatase hat zwei Bindungsstellen für Zn2+ und eine für Mg2+ Ionen. An das
Polypeptid gebunden, erhöhen diese Ionen die enzymatische Aktivität ganz entscheidend.
Sie sind damit gute Beispiele für allosterische Aktivatoren. Zweiwertige Kationen werden
durch geeignete Chelatoren (woher kommt dieser Name?) stark gebunden. Die Zugabe von
Ethylendiamin-Tetraessigsäure (EDTA) zum Reaktionsansatz wird dazu führen, dass ein
Großteil der Ionen vom Enzym abgezogen und an EDTA gebunden wird. In Ihrem
Experiment
C
können
Sie
beobachten,
welchen
Einfluss
das
auf
die
Reaktionsgeschwindigkeit hat, und dass sich dieser Effekt durch Zugabe von ZnCl2 im
Überschuss wieder kompensieren lässt.
Es gibt natürlich auch allosterische Inhibitoren. Da diese, wie der Begriff „allosterisch“
nahe legt, außerhalb des katalytischen Zentrums binden, können sie nicht durch erhöhte
Substratkonzentration aus dem Enzym verdrängt werden. Deshalb ändert sich bei
allosterischen Hemmungen auch der Km-Wert nicht. Da solche Inhibitoren aber generell
die Aktivität des Enzyms beeinträchtigen, wirkt das so als wäre weniger Enzym
vorhanden. Dadurch verringert sich die maximal mögliche Reaktionsgeschwindigkeit (wie
würden Michaelis-Menten und Lineweaver-Burk Diagramme dann aussehen?).
Bevor es los geht noch ein paar Details zum experimentellen System, mit dem Sie arbeiten
werden: „Alkalische Phosphatase“ wird so genannt, weil ihr Aktivitätsoptimum im
alkalischen pH-Bereich liegt. Als Testsubstrat verwenden wir p-Nitrophenylphosphat. Die
Abspaltung des Phosphatrests führt zur Bildung eines p-Nitrophenolat-Anions, das eine
charakteristische gelbe Farbe zeigt, anhand derer wir die Konzentration des
Reaktionsprodukts photometrisch messen können.
Ihre Experimente:
Experiment A:
Aufgabe: Bestimmung des pH-Optimums von AP
Der pH-Bereich, in dem alkalische Phosphatase ihre maximale Aktivität zeigt wird
gemessen, indem man Puffer verschiedener pH-Werte verwendet. Dazu wird unter
Substratsättigung des Enzyms die maximale Reaktionsgeschwindigkeit (Vmax) bestimmt.
Durchführung:
Der Testansatz enthält:
800 µl 0.1 M Glycin-NaOH Puffer (6 Ansätze mit jeweils unterschiedlichem pH-Wert)
80 µl p-Nitrophenylphosphat (0.01 mol/l)
80 µl dest. Wasser
40 µl Enzym
Es stehen Glycinpuffer mit sechs verschiedenen pH-Werten zur Verfügung.
1) Pipettieren Sie alle angegebenen Lösungen, mit Ausnahme des Enzyms (!), in der
angegebenen Reihenfolge in saubere, trockene Küvetten.
2) Stellen Sie die Wellenlänge des Photometers auf 405 nm.
3) Stellen Sie die Küvette #1 in das Photometer und gleichen Sie es durch Drücken der
"Set Ref"-Taste auf Null ab.
4) Nehmen Sie die Küvette aus dem Photometer, geben Sie die Enzymlösung zu und
verschließen Sie die Küvette mit einem Stück Parafilm. Mischen Sie den Ansatz und
starten Sie dabei gleichzeitig die Stoppuhr.
5) Stellen Sie die Küvette in das Photometer zurück und notieren Sie die Absorption bei t1
= 20 sec und bei t2 = 80 sec.
6) Wiederholen Sie dieselbe Vorgangsweise mit den anderen Küvetten.
pH-Wert
E (405 nm) 20 sec
E (405 nm) 80 sec
∆E/min
Das gebildete gelbe p-Nitrophenolat ist ein Produkt der enzymatischen Katalyse. Je mehr
davon gebildet wird, desto gelber wird die Lösung und desto größer wird der Wert für ∆E.
In einem Diagramm werden die Reaktionsgeschwindigkeiten (als ∆E/min, y-Achse) gegen
die pH-Werte (x-Achse) aufgetragen. Die höchste Reaktionsgeschwindigkeit ∆E/min tritt
beim optimalen pH-Wert auf.
Ergebnis: pH-Optimum = ……….
Experiment B:
Aufgaben:
1) Bestimmung des Km-Wertes von alkalischer Phosphatase.
2) Bestimmung der Wechselzahl kcat
3) Berechnung der katalytischen Effizienz kcat/Km
4) Bestimmung von Km' in Anwesenheit von 0.5 mM Phosphat als
kompetitivem Inhibitor.
5) Berechnung der Inhibitor-Affinität (Ki).
Durchführung:
B.1. Bestimmung der Michaelis-Konstante Km und der Wechselzahl von AP
Pipettieren Sie alle angegebenen Lösungen, mit Ausnahme des Enzyms (!) in saubere,
trockene Küvetten und führen Sie die Messung wie in Experiment A beschrieben durch.
Küvetten #
1
2
3
4
5
Glycin-Puffer, pH 9.6 (µl)
800
800
800
800
800
0.01 M pNPP (µl)
10
20
40
80
160
H2O (µl)
150
140
120
80
-
Enzymlösung (µl)
40
40
40
40
40
Aus der Absorption E bzw. deren Änderung ∆E bei 405 nm kann man die Konzentration
des Produktes p-Nitrophenolat bestimmen. Man muß dazu nur die Schichtdicke d der
Küvette (1 cm) und den molaren Extinktionskoeffizienten ε von p-Nitrophenolat (ε =
18000 L  mol-1  cm-1) kennen, dann kann man mit Hilfe des Lambert-Beer-Gesetzes (E =
ε  c  d) die Konzentration c berechnen. Lassen Sie sich durch diese Gleichungen und
Koeffizienten nicht einschüchtern. Eigentlich handelt es sich dabei nur um eine
Schlussrechnung, und ε gibt nur an, wie hoch die Absorption einer 1 M Lösung wäre. Die
wenig anschauliche Dimension von ε ergibt sich dabei aus dem Umstand, dass die
Absorption eine dimensionslose Größe ist und die Konzentration mol/L (mol  L-1) im
Nenner steht, die Schichtdicke d ebenso. Formen Sie also die obige Gleichung nach c um
und setzen Sie die gemessene Absorption für E ein, dann erhalten Sie die Konzentration
des Reaktionsproduktes.
Die Reaktionsgeschwindigkeit wird ausgedrückt als Konzentrationsänderung pro
Zeiteinheit, z.B. µmol  L-1  min-1 oder, was das gleiche ist, µM/min.
Ergebnisse der Messungen:
Küvetten #
1
2
3
4
5
E (405 nm) t = 20 sec
E (405 nm) t = 80 sec
∆E/min
v (µM/min)
1/v (min/µM)
[pNPP] (µM)
1/[pNPP] (L/µmol)
E = Absorption (= Extinktion), ∆E = Änderung der Absorption, v = Geschwindigkeit, [pNPP] =
Ausgangskonzentration vom Substrat p-Nitrophenylphosphat (zu berechnen aus Konzentration und
Volumen der Stammlösung und Volumen des Gesamtansatzes).
Zeichnen Sie nun aus Ihren Ergebnissen ein Michaelis-Menten- und ein Lineweaver-BurkDiagramm und ermitteln Sie aus beiden Darstellungen Km und Vmax (welche Diagrammform eignet sich dazu besser?) Vermeiden Sie bei der Erstellung Ihrer Diagramme Zahlen
mit allzuvielen Nullen vor oder hinter dem Komma. Dafür gibt es die entsprechenden
Vorsätze m (10-3), µ (10-6), n (10-9) etc., bzw. Zusätze wie „ 10-3“, etc.
Als absoluter Wert ist Vmax wenig aussagekräftig und eignet sich nur für den Vergleich
verschiedener Proben untereinander. Wenn man aber die Konzentration der reinen
Enzymmoleküle im Ansatz kennt, kann man über Vmax berechnen, wie viele Moleküle
Substrat ein Molekül Enzym pro Sekunde umsetzen kann. Dieser Wert heißt die
„Wechselzahl“ und ist ein weiteres wichtiges Charakteristikum eines Enzym/SubstratPaares. Vmax ergibt sich dann aus Wechselzahl und Konzentration des Enzyms im Ansatz
(kcat = Vmax/[E]). Alkalische Phosphatase hat ein Molekulargewicht von 69 kDa. Nehmen
Sie an, die Enzym-Stammlösung, die Sie erhalten haben, hätte eine Konzentration von
33 µg/ml, und berechnen Sie damit aus der von Ihnen ermittelten Vmax die Wechselzahl für
AP. Berücksichtigen Sie dabei, dass kcat mit der Einheit „pro Sekunde“ also s-1 angegeben
wird. Der Quotient aus kcat und Km beschreibt die katalytische Effizienz, die hier für die
Alkalische Phosphatase und das Substrat p-Nitrophenylphosphat gilt. Als Einheit wird
hierfür M-1 s-1 verwendet.
Ergebnis:
Km
= ……….
Vmax
= ……….
kcat
= ……….
kcat/Km = ……….
B.2 Bestimmung von Km' und Vmax in Gegenwart von anorganischem Phosphat
und Berechnung der Inhibitorkonstante Ki für Phosphat
Der Versuch wird genauso durchgeführt wie Versuch B.1, nur enthält diesmal der
Glycinpuffer 0.5 mM Phosphat als kompetitiven Inhibitor.
Pipettierschema:
Küvetten #
1
2
3
4
5
800
800
800
800
800
0.01 M pNPP (µl)
10
20
40
80
160
H2O (µl)
150
140
120
80
-
Enzymlösung (µl)
40
40
40
40
40
Glycin-Puffer, pH 9.6 mit 0.5
mM Phosphat (µl)
Ergebnisse der Messungen:
Küvetten #
1
2
3
4
5
E (405 nm) t = 20 sec
E (405 nm) t = 80 sec
∆E/min
v (µM/min)
1/v (min/µM)
[pNPP] (µM)
1/[pNPP] (L/µmol)
Zeichnen Sie Ihre Messwerte in die Diagramme von Experiment A1 ein und bestimmen
Sie auch für den neuen Versuch Km und Vmax. Welchen Einfluss hat anorganisches
Phosphat auf die Reaktionskinetik im Michaelis-Menten Diagramm, bzw. in der
Umformung nach Lineweaver-Burk? Wie würde das mit einem allosterischen Inhibitor
aussehen?
Ergebnisse: Versuch #
1
Phosphatkonzentration (in der Küvette) (mM)
0
2
Km (µM)
Vmax (µM/min)
Die Inhibitorkonstante Ki beschreibt die Affinität eines Inhibitors zum Enzym.
Ki lässt sich berechnen nach der Gleichung: Km' = Km  (1 + I/Ki). [I] ist dabei die
Inhibitorkonzentration. Formen Sie diese Gleichung so um, dass Sie I isolieren können.
Ergebnis: Ki = …………..
Experiment C:
Die allosterische Regulation der alkalischen Phosphatase wird untersucht, indem zunächst
durch EDTA Zink entzogen und dann durch Zugabe von weiterem Zink der EDTA-Effekt
wieder aufgehoben und überkompensiert wird. Alkalische Phosphatase benötigt
zweiwertige Kationen (Zn, Mg), um aktiv zu sein. EDTA entzieht dem Enzym diese Ionen,
was den Verlust eines allosterischen Aktivators bedeutet. Durch Zugabe von Zink kann der
EDTA-Effekt wieder aufgehoben werden.
Aufgabe: Inaktivierung der AP durch EDTA und Reaktivierung durch Zink.
Durchführung:
Der Standardansatz enthält: 800 µl 0.1 M Glycin-NaOH Puffer, pH 9.6
80 µl 0.01 mol/l p-Nitrophenylphosphat
80 µl dest. Wasser
40 µl Enzym
Pipettieren Sie die Lösungen in der angegebenen Reihenfolge in eine Küvette. Nach
Zugabe des Enzyms wird sofort gemischt und bei 405 nm im Photometer abgeglichen.
Sobald die Geräteanzeige 0.000 erscheint, lesen Sie 3 Minuten lang alle 30 sec die
Extinktion ab und notieren Sie die Werte. Mit einem zweiten Ansatz wird so verfahren,
dass 20 µl EDTA-Lösung zugegeben werden und erst nach 3 min Inkubation das Substrat
p-Nitrophenylphosphat. Messen Sie für 3 min die Extinktion wie zuvor und geben Sie
danach demselben Ansatz 50 µl ZnCl2-Lösung zu. Mischen Sie den Ansatz schnell und
lesen Sie die Extinktion für weitere 3 min alle 30 sec ab. Zur Auswertung erstellen Sie ein
Diagramm, in dem Sie die Absorptionswerte beider Ansätze gegen die Zeit auftragen.
Zeit (sec)
0
30
E Ansatz 1
60
90
120
150
150
E Ansatz 2 (EDTA)
E Ansatz 2 + ZnCl2
Material-Liste:
Geräte:
Kolbenhub-Pipetten, einstellbar für Maximalvolumina von 1000, 200 und 20 µl
Eppendorfgefäße (1.5 ml) mit Haltern
Photometer (405 nm) und Küvetten
180
Stoppuhr
Lösungen:
Glycin-NaOH Puffer, pH 9.6 (0.1 mol/l) (MW = 75.07 g/mol)
p-Nitrophenylphosphat (0.01 mol/l) (Na-Salz, MW = 371 g/mol)
Alkalische Phosphatase, 1000 U/ml, 10 mg/ml, mit 1x CIAP-Puffer 1:300 verdünnt
Glycin-NaOH Puffer, pH 9.6 (0.1 mol/l) mit 0.5 mmol/l Dinatriumhydrogen-Phosphat)
Glycin-NaOH Puffer, pH 8.0 (0.1 mol/l)
Glycin-NaOH Puffer, pH 8.8 (0.1 mol/l)
Glycin-NaOH Puffer, pH 9.2 (0.1 mol/l)
Glycin-NaOH Puffer, pH 9.6 (0.1 mol/l)
Glycin-NaOH Puffer, pH 10.0 (0.1 mol/l)
Glycin-NaOH Puffer, pH 10.4 (0.1 mol/l)
EDTA (Ethylendiamintetraacetat) (0.1 mol/l)
ZnCl2-Lösung (0.1 mol/l)