Reaktionskinetik – Katalyse

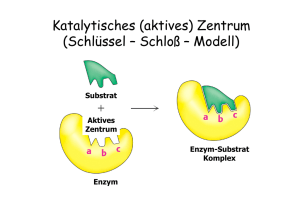
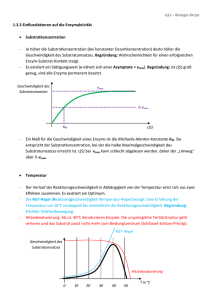
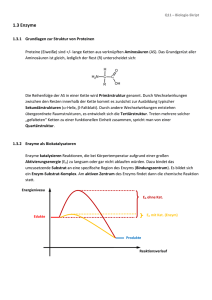
Reaktionskinetik
–
Katalyse
Katalysatoren beschleunigen chemische Reaktionen, ohne das Gleichgewicht
zu beeinflussen. Sie beeinflussen nur die Aktivierungsenergie
Katalyse
Katalysatoren beeinflussen den Reaktionsweg (Mechanismus),
nicht aber die Nettoreaktion und Größen selbiger (∆ usw.)
 Absenken der Aktivierungsenergie
 Reaktion läuft deutlich schneller ab
 KEINE Änderung der GG-Konstanten!
Die Reaktion muss nicht über den
“ganzen Berg”
Alter Katalysator (alter Bahntunnel) –
geringe Absenkung der Akt-Energie
Neuer Katalysator (NEAT-Tunnel):
Größere Absenkung der Akt-Energie
Erstfeld und Bellinziona bleiben auf
gleicher Höhe! Nur Zeit wird verändert!
Katalyse
Auf eine Reaktion angewendet:
Der geschwindigkeitsbestimmende Schritt wird im alternativen
Reaktionsweg umgangen
Unkatalysierte Reaktion:
Ea = 76 kJ/mol
Epot
Nicht beschleunigt
mit I2 als Katalysator:
Ea = 57 kJ/mol
Um Faktor 2000 beschleunigt
2 H2O2  2 H2O + O2
mit Katalase als Katalysator:
Ea = 8 kJ/mol
Um Faktor 1015 beschleunigt
Rn
(Zersetzung von Wasserstoffperoxid)
Katalyse
Arten der Katalyse:
Homogene Katalyse:
Katalysator befindet sich in gleichem
Phase wie die Reaktanden
(z.B. I2 o. Enzyme bei H2O2 Zersetzung)
Heterogene Katalyse:
Katalysator befindet sich in einer
anderen Phase als die Reaktanden
(öfters Metalle oder Oxide (Pd, Pt Y2O5)
Homogene Katalyse: HBr katalysiert auch die Zersetzung von H2O2
Reaktion verläuft vermutlich über ein vorgelagertes Gleichgewicht.
Beobachtetes Geschwindigkeitsgesetz:
(Bsp für eine Säurekatalyse)
Säure- und Basenkatalyse
Säurekatalyse:
Zentraler Schritt ist die Übertragung eines Protons auf das Substrat
X + HA
HX+ + A-
HX+
Produkte
z.B. Esterhydrolyse, Keto-Enol Tautomerie
Basenkatalyse:
Zentraler Schritt ist die Übertragung eines Protons vom Substrat
XH + B
X-
X- + BH+
Produkte
z.B. Claisenkondensation, Aldolkondensation
Enzymkatalyse
Enzyme sind meist hochspezifische homogene Biokatalysatoren mit
hoher katalytischer Aktivität. Damit gibt es meist schnelle mit keinen
Nebenreaktionen
Aktives Zentrum zur
Bindung von Substraten
Polypeptid (Protein  Enzym) oder
katalytisch aktive RNA ( Ribozym) oder
Protein/RNA Komplex (z.B. Ribosom)
Spezifisches
Substrat – sehr
selektive nichtkovalente WW (HBrücken, VdW,…)
Enzym (E) + Substrat (S)
Enzym-Substrat-Komplex
(ES)
Enzymkatalyse
Enzyme haben regulierbare Aktivität über:
a) Feedback:
Enzym wird durch Endprodukt einer katalytischen
Kette herunter reguliert (reversible Produkthemmung)
b) Regulation:
Ein Stoff (z.B. Ca2+) bindet an das Enzym und verändert
die Konformation, so dass es aktiv wird. Oftmals aktiviert
dieser Komplex das nächste Enzym (Regulatorprotein)
c) Modifikation: Kovalente Veränderung mit neuen funktionellen Gruppen
(z.B. Phosphorylierung)
d) Proteolyse:
Das aktive Enzym wird durch die Abspaltung eines
Peptidstückchens erzeugt (z.B. Trypsin)
Katalase
Trypsin
Amylase
Enzymkatalyse
Modellvorstellungen: Schlüssel-Schloss-Prinzip
(E.Fischer, 1890)
3D-Struktur des Substrats und
des aktiven Zentrums passen
perfekt zueinander
Adsoption von Substrat an die Oberfläche:
Geringe cS dann ist
Hohe cS dann ist
Reaktionsgeschwindigkeit v
Besser: Induktiver Fit (Enzym passt sich an Substrat an)
Konzentration [S]
Michaelis-Menden-Modell
Enzym und Substrat stehen mit Enzym-Substrat Komplex im Gleichgewicht
Kinetik mit
vorgelagertem Gleichgewicht
E+S
k1
k’-1
ES
k2
E+P
Wie bei anderen Reaktionen, ist
nun ein Ausdruck für die
Reaktionsgeschwindigkeit gesucht
- in Abhängigkeit von cE und cS
Produktbildender Schritt wird
als irreversibel angenommen
v = k2 cES
cES = ?
Michaelis-Menten-Modell
Wichtige Annahmen zur Herleitung der Formel:
Enzym-Substrat-Komplex
liegt quasistationär vor
Michaelis-MentenKonstante:
Damit ergibt sich für cES
Falls
≪
dann gilt
,
Also: Geschwindigkeiten
Komplexbildung = Komplexzerfall
dcES
0
dt
K M
cES 
k 1  k 2
k1
Resultierende Einheit: mol/l
c E , 0 cS , 0
cS , 0  K M
≪
,
v  k 2 cE ,0  vmax
Michaelis-Menten-Gleichung:
v  vmax
v  k 2 cE , 0
cS , 0
cS , 0  K M
Alle Bindungsstellen mit
Substrat gesättigt
cS , 0
cS , 0  K M
Michaelis-Menten-Modell
Michaelis-Menten-Gleichung:
Bei cS,0 = KM gilt:
v
vmax
2
v  vmax
vmax
cS , 0
cS , 0  K M
Wie werden
und KM bestimmt?
1
Lineweaver-Burk-Auftragung
KM 1
1
1


v vmax vmax cS
1
1
Alternativ (seltener):
Eadie-Hofstee-Auftragung
v  vmax  K M
v
cS
Michaelis-Menten-Modell
Bedeutung von KM und vmax
Wenn KM = cS
Substratkonzentration, bei der die
Hälfte der aktiven Zentren besetzt ist
Wenn k2 ≪k-1
KM ist die GG-Konstante für die
Dissoziation des ES-Komplexes
Typische Werte für KM
TON = “turnover number”
(Katalysevorgänge
pro Sekunde)
Bsp: Carboanhydrase:
CO2 + H20  HCO3- + H+
Katalytische Effizienz 
mit
KM ist meist 10-1 bis 10-7 M
,
Typische Zahlenwerte: 100 – 105 s-1
Bei
8 ∗
10
und 6 ∗ 10
perfekte Diffusionskontrolle 
direkter Umsatz! 108 – 109
∗