% Datei rhub_PIDuM20
Werbung

R. Kessler, D:\75884983.doc, S. 1/5
Hubschrauber mit Simulink und mit Matlab
Datei hub_60.mdl
Kessler, Nov. 05
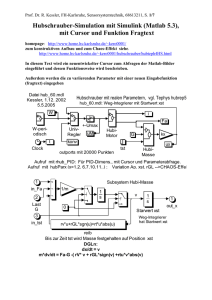
Hubschrauber mit realen Parametern, vgl. Tephys hubrep5.txt
hub_60.mdl: Weg-Integrierer mit Startwert xst
W
i
Fa
W-periodisch
UnivRegler
t
Clock
+-Umax
HubiMotor
uM
G
kx
konv
ux
tst
outports mit 20000 Punkten
HubiMasse
Für PID: Aufruf mit rhub_PIDuM20 rhub_PID
Für Chaos-Effekt: Aufruf mit hubParx (x=1,2, 6,7,10,11..) ; Variation Ap, xst, rGL
clear;vmax=1;Ap=20;Td=0.7;Ti=5;konv=1;kW=1;MATL=1;dtM=0.01;cur=0;bild=8;rhub_PIDuM20
bild 8,Ap=20,Td=0.7,konv=1,kW=1,Ti=5,vmax=1, mitMatlab: dt=0.01
10
W
ux
uM/10
Fa
8
6
Fa
4
uM/10
2
0
W,ux
-2
0
5
10
15
20
25
30
35
40
45
50
% Datei rhub_PIDuM20.m Simulink und wahlweise auch reines Matlab
% wahlweise mit Cursor (bei Simulink)
% Aus rhub_PIDuM2.m entstanden, aber hier ohne Abfrage mit fragtext
%clear;vmax=1;Ap=20;Td=0.7;Ti=5;konv=1;kW=1;MATL=1;dtM=0.01;cur=0;bild=8;rhub_PIDuM20
% R. Kessler FH-Karlsruhe, 5.5.2005 und Okt. 2008
% Variation der PID-Parameter TD, Ti, vmax, kon um "optimale"
% PID-Dimensionierung zu erhalten
%
format compact; % verhindert unnötigen Zeilenvorschub
% Werte der Parameter, soweit nicht im Aufruf enthalten:
f=0.04; % Frequenz der Führgröße,
Wmax=2;
tW = 0.1;
% vmax= 20;
dt = 0.0100; kg = 0.02102;
R = 3.53;
imax= 2.5;
J = 6.0274E-5; tst = 1.00000;
R. Kessler, D:\75884983.doc, S. 2/5
xst = 0;
kx = 14;
% Ti = 4000;
konv =
0;
% Td = 0;
kW = 1;
% Ap = 20;
rGL = 0.10000; % entspricht dem Experiment
Umax = 15.00000; Umin= -15;
eta = 0; % bei eta =0 hat der Propeller rückwärts keinen Auftrieb
ka = 2.46E-6; % für Auftriebskraft Fa
G = 0.20000; % Gewichtskraft (ist erforderlich bei eta =0, weil
% Hubi bei Rückwärts-Drehrichtung keinen Auftrieb hat
rv = 0;
rt = 0;
m = 1.92700; % Masse
tmax = 50.0;
% Gute Werte: Ap=20; Td=1; konv=0; Ti=10; vmax=1; kW=0.9;
% Gute Werte: Ap=20; Td=0.7; konv=0; Ti=7; vmax=1; kW=0.9;
if bild==1, hub_60 ; end; % Simulink-Schaltung auf Bildschirm
sim('hub_60'); % Simulation ausführen
figure(bild); clf reset; % ruft Figur bild auf und löscht Inhalt
set(0,'DefaultLineLineWidth', 1.5); % Kurven dick
plot(t,W, t,ux,'m', t, uM/10+4,'k', t,Fa+6,'r' ); grid on;
% Achsen zeichnen und beschriften:
hold on;
set(0,'DefaultLineLineWidth', 1); % Kurven dünn
plot([0,max(t)],[0,0],'k',[0,max(t)],[4,4],'k',[0,max(t)],[6,6],'k' );
set(0,'DefaultLineLineWidth', 1.5); % Kurven dick
text(max(t),0,' W,ux');
text(max(t),4,' uM/10');
text(max(t),6,' Fa');
axis([0,tmax,-3,10 ]); % sorgt für vorgegebene Achsenbereiche
legend('W','ux','uM/10','Fa');
Sbild = ['bild ',num2str(bild)];
S1=[',Ap='num2str(Ap)];S2=[',Td='num2str(Td)];
S3=[',konv='num2str(konv)];S4=[',kW='num2str(kW)];
S5=[',Ti='num2str(Ti)];S6=[',vmax='num2str(vmax)];
Titext= [Sbild, [S1,S2,S3,S4,S5,S6] ]; title(Titext);
% Cursor:
if cur>0
%///// Start Cursor: //////
tc= t; yc= [W'; ux'; uM'/10; Fa']; % Wichtig: die Vektoren transponiert übergeben
ofsc= [0, 0 ,4,6]; % Wichtig: die Grafik-Offsets wie im plot-Befehl
Stry=[' Zeit W
ux
uM/10, FA']; % Tabellenkopf
tab=1; while 1 Simcurs2; end; %///// Ende Cursor: //////
end;
% Wahlwiese mit reinem Matlab rechnen
if MATL>0
disp('anschliessend mit Matlab: Taste'); pause;
hubmat_60_2;
end;
*******************************************************************
% Datei hubmat_60_2.m R. Kessler März 2006, Oktober 2008
% wie Simulink-Modell hub_60.mdl, aber hier mit "reinem Matlab" statt Simulink
% wird von rhub_PIDuM20.m gemeinsam mit dem Simulink-Modell aufgerufen
format compact;
N=floor(tmax/dtM); %Deklarieren der Speicherwerte.
% Wichtig,sonst Rechenzeit riesig,
% Rechenzeit steigt etwa quadratisch an mit Anzahl Rechenpunkte
tp=zeros(1,N); Wp=tp; uMp=tp; Fap=tp; uxp=tp; wp=tp;
% Startwerte:
x=0; v=0; W=0; int=0; w=0; Fa=0; WXalt=0;
R. Kessler, D:\75884983.doc, S. 3/5
t=0; k=0;
tic; % Start Stoppuhr
% Numerisches Lösen der DGLn, vgl. Simulink
% Algorithmus ähnlich "Euler", aber anders als bei Euler werden hier immer
% die "aktualisierten" Werte benutzt, bei Euler werden dagegen erst beim
% nächsten Schleifendurchlauf die neuen Werte benutzt.
while t < tmax
W0=Wmax*sign(sin(2*pi*f*t)); % Sollwert Rechteckfunktion
st= (W0-W)/tW; % Steigung Sollwert
if st> vmax st= vmax; end;
if st<- vmax st= -vmax; end;
W=W+st*dtM; % W= Sollwert, anstiegsbegrenzt auf +- vmax
if t < tst x=xst; v=0; end; % für t<tst ist x=xst und v=0; tst= Startzeit
if t>= tst x=x+v*dtM; end; % x = Posisiton der Masse
if t>= tst v=v+(-G+Fa-rv*v-rGL*sign(v)-rt*v*abs(v))*dtM/m;end; % v =Geschwind.
% 3 Arten Reibung: viskos (rv), Gleitreibung (rGL), turbulente Reibung (rt)
% G=Gweicht, Fa= Aufrirebskraft infolge Propeller
ux=kx*x; % ux = Regelgröße
int=int+(W-ux)*dtM/Ti; % I-Anteil des Reglers
DA=Td*((konv>0)* (W-ux-WXalt)/dtM -(konv <=0) * kx*v ); % D-Anteil des Reglers
WXalt=W-ux;
uM=Ap*(kW*W-ux +DA +int); % uM = Ausgang des Reglers, noch unbegrenzt
if uM >Umax uM=Umax; end; if uM <-Umax uM=-Umax; end;
% uM = Motorspannung, begrenzt auf +- Umax
i = (uM - kg*w)/R; if i> imax i=imax;end; if i< -imax i=-imax;end; % i =Strom
w = w+ ((i - 2.219*Fa)*kg )*dtM/J; % w = Winkelgeschwindigkeit Propeller
Fa= ka*w*abs(w) *( (w>0)+eta *(w<0) ) ; % Auftriebskraft des Propellers
k=k+1;
% Speichern der Plotwerte (Index p)
%tp=zeros(0,N); Wp=tp; uMp=tp; Fap=tp; uxp=tp; wp=tp;
%if k==1 size(Wp),size(uMp),size(Fap),size(uxp), end;
tp(k)=t; Wp(k)=W; uMp(k)=uM; Fap(k)=Fa; uxp(k)=ux;
t=t+dtM;
end; % while t < tmax
toc; % toc= Rechenzeit
MATbild = bild+20; figure(MATbild); clf reset;
plot(tp,Wp, tp,uxp,'m', tp, uMp/10+4,'k', tp,Fap+6,'r' ); grid on;
% Achsen dünn zeichnen und beschriften:
hold on;
set(0,'DefaultLineLineWidth', 1); % Kurven dünn
plot([0,max(tp)],[0,0],'k',[0,max(t)],[4,4],'k',[0,max(t)],[6,6],'k' );
set(0,'DefaultLineLineWidth', 1.5); % Kurven dick
text(max(tp),0,' W,ux');
text(max(tp),4,' uM/10');
text(max(tp),6,' Fa');
axis([0,tmax,-3,10 ]); % sorgt für vorgegebene Achsenbereiche
legend('W','ux','uM/10','Fa');
Sbild = ['bild ',num2str(bild)];
Titext= [Sbild, S1,S2,S3,S4,S5,S6,[', mitMatlab: dt=',num2str(dtM)] ];
title(Titext);
% Ende Datei hubmat_60_2.m
*******************************************************************
% Datei SimCurs2.m Zeitcursor für Matlab-Bilder
% R. Kessler FH-Karlsruhe, 23.10.2003, Endfassúng 12.5.2004, 5.5.2005
%
% Cursor-Abfrage mit linker Maustaste,
% Ende mit rechter Maustaste (oder Esc)
%
% Zeit-Cursor: wird aufgerufen von "beliebigem" Programm
R. Kessler, D:\75884983.doc, S. 4/5
% übergabewerte:
% xVektor tc, DatenMatrix yc, OffsetVektor ofsc, string Tabellenkopf
% Bei Simulink sind die to workspace Felder Spaltenvektoren,
% also müssen die to workspace-Vektoren transponiert übertragen werden
axen=axis; % V = AXIS returns a row vector containing the scaling
% for the current plot.
ystep = 0.06 * ( axen(4)-axen(3) ); % ySchrittweite der Tabelle
ystep = 0.04 * ( axen(4)-axen(3) ); % ySchrittweite der Tabelle
ytext = 0.93* (axen(4)-axen(3)) + axen(3); % y-Position Tabelle neu 4.5.05
ytext = 0.98* (axen(4)-axen(3)) + axen(3); % y-Position Tabelle neu 5.5.05
xtext = 0.1 * (axen(2)-axen(1));
[zeil,spalt]=size(yc); % zeil = Anzahl Zeilen, spalt=Anzahl Spalten
kzeil=1:zeil; % Vektor
clear Zeittab; % Zunächst Löschen, damit bei Mehrfach-Aufruf
% dieses Cursorprogramms die Tabelle leer ist !!
N=0; weiter=1;
xlabel('
');
xlabel('Cursorwerte in Tabelle schreiben? linke Maus, Ende Esc od. rechte Maus')
disp('------------------------------------------------------------------')
while weiter > 0 %N < 10 % maximal N-1 Cursor-Klicks möglich
[Xcurs,Ycurs,button]= ginput(1); % Fadenkreuz will 1 Taste
if button ==1 % linke Maustaste hat die Nummer 1,rechte die Nummer 3
% Abfangen Klicken ausserhalb zulässigem x-y-Bereich:
N=N+1; % oben nach hier verlegt
OK=1;
if ( Xcurs < min(tc)), OK =-1; N=N-1; end;
if ( Xcurs > max(tc)), OK =-1; N=N-1; end;
if ( Ycurs < axen(3)), OK =-1; N=N-1; end;
if ( Ycurs > axen(4)), OK =-1; N=N-1; end;
if OK >0 % wenn im zulässigen Zeitbereich geklickt wurde
if N == 1,
text(xtext,ytext,['Nr ',Stry]); % Tabellenkopf aufs Bild schreiben
end; % if N == 1
% Kurvenzeichen unter die Kopfzeile plotten:
KZ= ['s', 'o', '<' ,'^', '<','>' ,'+', 'x'];
hold on;
for kzeil =1:zeil
plot(xtext/5 +xtext+ xtext+kzeil*xtext,ytext-1*ystep,[KZ(kzeil)] );
end; % kzeil ...
[wert,NrX]= min( abs( Xcurs- tc) ); % Finden des Zeitwertes
zeit= tc(NrX);
Zeittab(N,1)= zeit; % 1. Spalte der Zeit-Tabelle
for ktab=1:zeil
Zeittab(N,ktab+1)= yc(ktab, NrX) ;
end; % ktab...
% Zeile N der Tabelle aufs Bild schreiben:
text(xtext/5 +xtext,ytext - (N+1)*ystep,...
[num2str(N),' ',num2str(Zeittab(N,1:1+zeil),3)]);
% Jetzt vertikale Linien bei den selektierten Zeiten:
hold on;
Lix(N,:)= [tc(NrX),tc(NrX)];
y_li_max=max(ytext,0.9*axen(4));
y_li_max=max(ytext,0.8*axen(4));
Liy=[0.9*axen(3),y_li_max];
plot(Lix(N,:),Liy,':m'); hold on; % Vertikale punktierte Linien
for kzeil =1:zeil,
% Kurvenzeichen KZ an den Cursor-Klick-Stellen
plot(Lix(N,:), yc(kzeil,(NrX))+ofsc(kzeil),KZ(kzeil));
R. Kessler, D:\75884983.doc, S. 5/5
end; % kzeil..
hold off
end; % if OK > 0
end; % if button ==1
% Taste Esc oder rechte Maustaste zum Beenden des Cursors:
if (button== 27)| (button == 3) weiter= 0; % Ende Cursor
% Jetzt Tabelle auf Bildschirm schreiben:
if (tab > 0) & (N > 1)
disp(Stry); % Tabellenkopfauf Bildschirm schreiben
disp( Zeittab(:,:) );
end; % if (tab...
break, % Cursor beenden
end; % if button == 27 oder 3,
end;% while weiter > 0 while N < 10
xlabel('
')
break; % Rückkehr zur Aufrufstelle
% Hinweis:
% Die Tabelle im Bild ist eine Datei mit Namen Zeittab.
% Speichern der Tabelle mit dem neuem Namen Zeittab1:
%
save Zeittab1 Zeittab - ascii ;
% Laden der Tabelle:
%
Tab1=load('Zeittab1'), sie heißt jetzt Tab1
% Ende Matlab-Datei SimCurs2.m