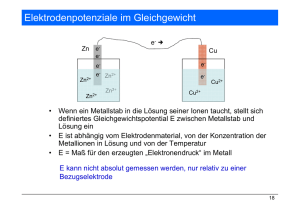
Galvanische Zellen - Willem H. Koppenol

Galvanische Zellen
Wir kehren zurück zum Beginn der Elektrochemie und sehen uns die Konstruktion von
Alessandro Volta näher an. Die galvanische Zelle müsste eigentlich voltasche Zelle heissen,
wenn man die (oben geschilderte) Entwicklungsgeschichte betrachtet. Was geschieht hier
eigentlich? Da wir am einen Ende einer Volt-Säule einen Elektronenüberschuss erzeugen
(Minus-Pol) und am andern ein Defizit (Plus-Pol), muss eine Elektronen verschiebende
chemische Reaktion ablaufen, also eine Redoxreaktion. Wie wir schon wissen, muss diese aus
zwei Teilreaktionen, einer Reduktion und einer Oxidation, bestehen. Die klassische Volta-
Säule besteht aus einem Stapel alternierender Zink- und Kupferplättchen, die paarweise durch
mit neutralem oder saurem Elektrolyt getränkten Filz- oder Kartonplättchen getrennt sind:
_
+
In der Abbildung sind je zwei Kupferplatten (braunrot) und Zinkplatten (grau) durch
Elektrolyt (farblos) getrennt. Es handelt sich um zwei in Serie geschaltete galvanische
Elemente, jedes besteht aus Zn-Platte, Elektrolyt-Filz und Cu-Platte. Der interne Kontakt wird
direkt zwischen Kupfer- und Zinkplatte hergestellt, man könnte hier auch auftrennen und
einen Draht einsetzen. Volta stellte fest, dass die Zinkplatten korrodiert werden und an
Gewicht verlieren, während die Kupferplatten höchstens blanker werden, ohne Masse
abzugeben.
Zn
→
Zn2+ + 2 e–
erklärt die Beobachtung am Zinkplättchen. Am Kupfer gibt es mehrere Möglichkeiten: Falls
das Kupfer noch passiviert war (zu Voltas Zeit sehr wahrscheinlich), trug es eine Schicht aus
Cu2O. Damit
Cu2O + 2 H+ + 2 e– →
2 Cu + H2O
O 2 + 4 H + + 4 e–
2 H2O
Die Volta-Säule funktioniert aber auch mit blanken Cu-Platten:
→
Es handelt sich also um einen Vorläufer der heute noch gebräuchlichen Zink-Luft Batterie.
Wir können das etwas eleganter aufbauen, indem wir eine Vorrichtung wie bei der
Elektrolyse benutzen. Um präzise Aussagen zu erhalten, muss man zwischen den beiden
1
Räumen um die Elektroden noch eine Barriere gegen völlig freie Diffusion einfügen, damit
keine rasche Durchmischung des Elektrolyten aus den beiden Zonen stattfindet.
U
+
Cu
_
Membran oder
Diaphragma
Cu
2+
SO42-
Zn
Zn2+
SO42-
Bei der abgebildeten galvanischen Zelle handelt es sich um ein so genanntes Daniell-Element,
einer verbesserten Version der Volta-Säule. Sie war eine Zeit lang die Standard-Stromquelle
für Telegraphen, als es noch keine Dynamos gab. So wie sie hier beschaltet ist, liefert sie
allerdings keinen Strom. Ein Voltmeter, wie das Spannungsmessgerät genannt wird, hat
theoretisch (und heute auch beinahe praktisch) einen unendlichen elektrischen Widerstand.
Die Spannung kommt durch eine Ladungsverschiebung zustande, die dadurch verursacht
wird, dass Zn eigentlich als Zn2+ in Lösung gehen möchte, während Cu2+ sich unter
Elektronenaufnahme als Cu absetzen will. Zu einem winzigen Teil geschieht das auch, damit
akkumulieren sich elektrische Ladungen auf den Elektroden, bis die Reaktion zum Stillstand
durch Anwachsen der elektrischen Feldstärke kommt, also Gleichgewicht herrscht. Dies ist
wieder ein dynamisches Gleichgewicht, ist es erreicht, so ist die Austauschgeschwindigkeit
zwischen Metall und Metallkationen auf beiden Seiten gleich schnell. Die Richtung der
Ladungsverschiebung und ihr Ausmass werden durch die Austrittsarbeiten der beiden Metalle
festgelegt. Die Austrittsarbeit ist die Energie, die benötigt wird, um Elektronen aus dem
2
Metall herauszulösen. Sie ist um so grösser, je elektronegativer das Metall ist. Am leichtesten
treten Elektronen aus Alkalimetallen aus, sie sind stark reduzierend, und entsprechend wenig
oxidierend sind ihre Kationen. Weiter rechts im Periodensystem findet man die Edelmetalle,
die eine hohe Austrittsarbeit aufweisen und deren Kationen kräftig oxidierend wirken. Die
Spannung, die man am Voltmeter misst, ist deshalb eigentlich ein Mass dafür, wie „gerne“ die
Reaktion ablaufen würde, bei der die ganze Zinkelektrode aufgelöst und gleichviel Kupfer (in
Mol) auf die andere Elektrode abgeschieden wird. Den Wert der Spannung nennt man
Potentialdifferenz ∆E. Ein Potential selbst wäre der Wert der Spannung einer der
Teilreaktionen (Halbzellenreaktionen) gegenüber einem Referenzwert. Ein historischer
Begriff für diese Spannung ist „elektromotorische Kraft“ (EMK). ∆E drückt direkt aus,
wieviel Energie frei würde, wenn wir die Reaktion durch Kurzschliessen des Voltmeters bis
ins finale Gleichgewicht laufen liessen. Weil keine Wärme beim Messen von ∆E frei wird, ist
∆E direkt ein Mass für das ∆G der Reaktion, die bei Kurzschluss eintreten würde.
∆G = –nF∆E
wobei n für die Zahl der pro Atom oder Molekül transferierten Elektronen und F für ein Mol
Elementarladungen steht. Dass der Ausdruck ein Energiemass ist, kann einfach gezeigt
dQ
werden: P = UI = U
, damit W = U ∫ I(t) dt = UQ . nF ist eine Ladungsmenge, ∆E ist eine
dt
0
t
Spannung. Weil ∆G° = –RT lnK ist, muss auch der Konzentrationsausdruck des
Massenwirkungsgesetzes mit ∆E°, der Potentialdifferenz unter Standardbedingungen,
verknüpft sein: ∆E° =
RT
ln K . Die Konzentrationsabhängigkeit von ∆G, falls nicht finales
nF
Gleichgewicht herrscht, ist ∆G = ∆G° + RT lnκ. κ ist ein Ausdruck analog zum MWG der
entsprechenden Reaktion, enthält aber die Konzentrationen zur Zeit der Messung und nicht
die des Gleichgewichts. In der Thermodynamik-Literatur wird statt κ oft Q als Symbol
verwendet, was im Zusammenhang mit der Elektrochemie zu Verwechslung mit der
Ladungsmenge führen kann. Im finalen Gleichgewicht ist ∆G = 0, also 0 = ∆G° + RT lnκ,
womit lnK = lnκ, da ∆G° = –RT lnK. Unsere Bruttoreaktion im Daniell-Element ist
Cu2+ + Zn
⇀
↽
Cu + Zn2+
also κ =
Zusammengefasst: –RT lnK + RT lnκ = –nF∆E oder
∆E =
[Zn 2+ ]
.
[Cu 2+ ]
RT
RT
RT
RT 1
RT 1
ln K −
ln κ =
ln K +
ln = ∆E° +
ln
nF
nF
nF
nF κ
nF κ
3
Dies ist die Gleichung von Otto Nernst. Sie dient dazu, die Konzentrationsabhängigkeit der
EMK zu beschreiben. Für das Daniell-Element
RT [Cu 2+ ]
∆E = ∆E° +
ln
mit n = 2.
nF [Zn 2+ ]
Leider ist ∆E eine Spannung, also ein U-Wert. Um Potentiale zu erhalten, mit denen man
rechnen und vergleichen kann, muss man ein Bezugsystem definieren, weil es gemäss der
speziellen Relativitätstheorie keine absoluten Bezugspunkte geben kann. Physiker definieren
die Erde als Bezug für elektrische Potentialmessung (oder irgendein passendes lokales
System), für die Chemie ist es sinnvoller, eine bestimmte Halbzellenreaktion zu wählen.
Dabei hat man sich für
2 H + + 2 e–
⇀ H2
↽
entschieden. Das ist eine „schöne“ Wahl, weil das Element Nr. 1 als Standard dient. Praktisch
gesehen ist es eher ein Desaster, weil die Halbzelle schwierig zu handhaben ist. Unsere
Potentiale müssen für festgelegte Standardbedingungen gelten, d.h. Konzentrationen und
Partialdrucke müssen für die Messung fixiert werden. Das ist für das System H+/H2 alles
andere als einfach, weil p H 2 = 101.3kPa und [H+] = 1 M erfüllt sein müssen. Zudem ist H2 ein
explosionsgefährlicher Stoff. Nichtsdestotrotz ist das Halbzellen-System
Pt | H2 | H+ || die Normalwasserstoff-Elektrode (Normal Hydrogen Electrode NHE)
der Standard mit E° ≡ 0 V bei [H+] = 1 M , p H 2 = 101.3kPa und T = 298.15 K (25 °C).
Die gezeigte Notation ist eine praktische Konvention. Der senkrechte Strich | steht für eine
Phasengrenze, der senkrechte Doppelstrich || für eine Diffusionsbarriere. Das nächste Bild
zeigt die Messung des Elektrodenpotentials bei Standardbedingungen für die Halbzelle
Cu | Cu2+ ||
des Daniell-Elements. Die gesamte „Kette“ wird als
Pt | H2 | H+ || Cu2+ | Cu
notiert. Als Anion in den Halbzellen wird oft Chlorid verwendet, weil es die Einstellung der
Potentiale beschleunigt, d.h. als Katalysator wirkt. Als solcher beeinflusst es
thermodynamische Kennwerte wie ∆E nicht. Bildet Cl– jedoch Komplexe mit Metallionen,
muss es vermieden werden, weil die Komplexbildung die Thermodynamik ändert. Diese
Einflüsse werden wir im nächsten Kapitel ausführlich besprechen.
Weil in der gezeigten Anordnung [H+] = 1 M und [Cu2+] = 1 M ist der Nernst-Ausdruck für
die Bruttoreaktion
⇀ Cu + 2 H+
Cu2+ + H2 ↽
∆E = ∆E° +
RT [Cu 2+ ]
ln
= ∆E°
2 F [H + ]2
4
U
H2
101.3 kPa
Diaphragma
Pt
Cu
KCl
Lösung
[H+]
1M
NHE
[Cu2+]
1M
Vergleichs-Halbzelle
0
. Auf diese Weise lassen sich beliebige
Weil aber E 0H+ / H ≡ 0 V ist ∆E 0 = E Cu
2+
/Cu
2
Redoxgleichgewichte vermessen. Auch Systeme ohne feste Metallkomponenten sind
zugänglich. Fe3+/Fe2+ können mittels einer Pt-Elektrode gemessen werden. Erforderlich ist
[Fe3+] = [Fe2+] = [H+] = 1 M in der Halbzelle. Man kann sich die Abtastung durch das Pt so
vorstellen, dass die Elektronen beim Austausch zwischen Fe3+ und Fe2+ zum Teil über das
Metall transferiert werden und die Elektrode so die Ladungen „fühlt“. Die Sammlung der
Potentiale bei Standardbedingungen wird „Elektrochemische Spannungsreihe“ genannt. Die
offizielle Bezeichnung der Potentiale selbst ist „Standard-Elektrodenpotential“. Ältere
sinngemässe Bezeichnungen sind „Normalpotential“und „Standard-Reduktionspotential“.
Alle diese Potentiale sind der Reduktionsreaktion der Halbzelle zugeordnet:
⇀ Red
Ox + n e– ↽
Es gibt ältere Tabellen mit Standard-Oxidationspotentialen, diese haben einfach das inverse
Vorzeichen. Die Bezeichnung „Redoxpotential“ ist unsinnig und wird oft in der Biochemie
verwendet. Gemeint sind in der Regel Standard-Elektrodenpotentiale. Für das Daniell-
5
Element findet man E 0Cu 2+ /Cu = +0.34 V und E 0Zn 2+ / Zn = −0.76 V . Somit beträgt
∆E° = 0.34 V - (–0.76 V) = 1.10 V, falls die Konzentrationen 1 M sind.
E
+0.34 V
0.000 V
+ 1.10 V
- 0.76 V
Für andere Konzentrationen muss man
∆E = E 0Cu 2+ /Cu − E 0Zn 2+ /Zn +
RT [Cu 2+ ]
ln
2 F [Zn 2+ ]
mit der Nernst-Gleichung rechnen. Nernst-Gleichungen kann man auch für Halbzellen
schreiben und sie nachher zu den Gesamtzellen durch Differenzbildung kombinieren. Für die
NHE lautet die Gleichung
E = E 0H+ /H +
2
RT [H + ]2
ln
2F
pH2
in der konventionellen Richtung der Reduktion. In dieser Schreibweise steht im
konzentrationsabhängigen Term die oxidierte Form immer im Zähler und die reduzierte im
Nenner. Eventuelle „Hilfsreagenzien“ wie H+ oder OH– müssen ebenfalls in der Gleichung
stehen, sie beeinflussen das Potential erheblich. H2O wird nicht notiert, seine
Überschusskonzentration ist stets so hoch, dass es in die Konstanten integriert wird (hier in
E°). Das gilt nicht in nichtwässriger Lösung, in der früher erwähnten Karl-Fischer Reaktion
von SO2 zu SO3 in methanolischer Lösung als Beispiel ist H2O natürlich ein limitierender
Faktor.
Alternative Referenzsysteme
Die Wahrscheinlichkeit, dass man in seinem Chemikerleben eine leibhaftige NHE zu Gesicht
bekommt, ist recht klein. Trotzdem kann man ab und zu in Verlegenheit kommen, ein
6
Potential zu messen. Dazu verwendet man ein „Referenzelektrode“ als zweite Halbzelle.
Diese zeichnet sich dadurch aus, dass sie unter auch misslichen Umständen i.A. ein stabiles
Potential relativ zur NHE aufweist. Es existierten einige Varianten, doch unter diesen hat sich
die Silber/Silberchlorid-Elektrode klar durchgesetzt und ist für wässrige Lösung praktisch
alleine gebräuchlich. Für Messungen in organischen Lösungsmitteln verwendet man das
Ferrocenium/Ferrocen System Fe(cp)2+/Fe(cp)2 mit Pt-Abgriff.
Die Silber/Silberchlorid-Elektrode (Ag/AgCl) beruht auf dem Löslichkeitsprodukt des AgCl,
das die [Ag+] über einen weiten Bereich von Bedingungen fast konstant hält. Das Ausgangs-
Redoxpaar ist
⇀ Ag
Ag+ + e– ↽
E 0Ag + / Ag = +0.800 V
Mit K so (AgCl) = [Ag + ][Cl− ] = 10−10 M 2 kann man [Ag+] in der Nernst-Gleichung
substituieren: E = E 0Ag + /Ag +
RT
ln[Ag + ]
F
→
E = E 0Ag + /Ag +
K
RT
ln so−
F
[Cl ]
Wenn man [Cl–] konstant macht, indem man gesättigte KCl (ca. 3 M) verwendet, hat man ein
äusserst stabiles Potential von +0.200 V. Schema:
Ag | AgCl | KCl ||
Eine ältere, in der Literatur noch oft zu findende Referenzhalbzelle ist die so genannte
Kalomel-Elektrode. Kalomel ist Hg2Cl2, ein schwerlösliches Salz des Hg22+ Ions. „Kalomel“
heisst „schönes Schwarz“, obwohl der frisch hergestellte Stoff rein weiss ist. Licht oder Alkali
lösen aber eine Disproportionierungsreaktion aus:
Hg2Cl2
→
Hg + HgCl2
Weil das Quecksilber dabei fein verteilt abgeschieden wird, erscheint die Substanz dann
schwarz. Das AgCl der Silber/Silberchlorid-Elektrode unterliegt ebenfalls der Photolyse,
womit die Packung der Elektrode nach einiger Zeit braun erscheint, weil Ag ausgeschieden
wird. In beiden Fällen wird die Funktion nicht beeinträchtigt, weil die Umsetzung durch Licht
nur an der Oberfläche geschieht. Der grösste Teil der Masse bleibt immer noch das
potentialbestimmende Metallsalz. Die Kalomel-Elektrode wird beschrieben als
Pt | Hg | Hg2Cl2 | KCl ||
Ein Pt-Draht taucht in flüssiges Hg-Metall, das mit einer KCl-Lösung (gesättigt), die die
Hg2Cl2-Suspension enthält, kontaktiert ist. Im Gegensatz zur Ag/AgCl-Elektrode gibt es hier
2 Flüssigkeiten, was die Handlichkeit einschränkt.
7