Elektrodenpotenziale im Gleichgewicht

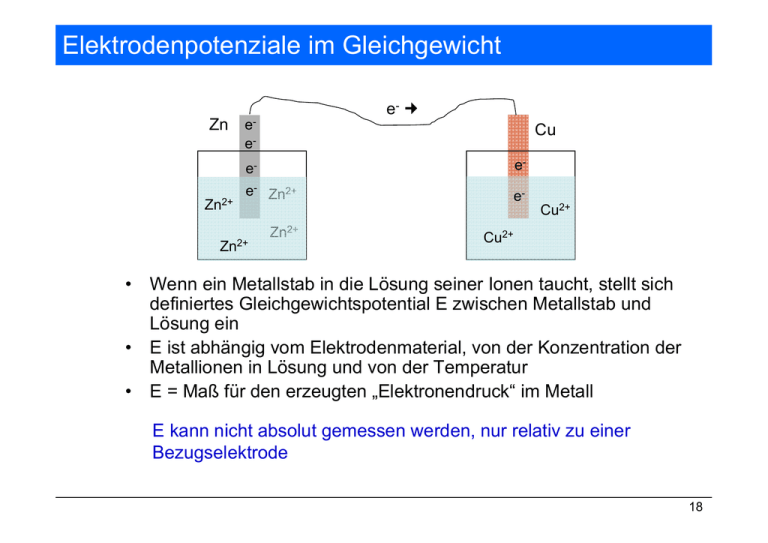
Elektrodenpotenziale im Gleichgewicht
e- „
Zn e-
Cu
e-
Zn2+
e-
e-
e- Zn2+
e-
Zn2+
•
•
•
Zn2+
Cu2+
Cu2+
Wenn ein Metallstab in die Lösung seiner Ionen taucht, stellt sich
definiertes Gleichgewichtspotential E zwischen Metallstab und
Lösung ein
E ist abhängig vom Elektrodenmaterial, von der Konzentration der
Metallionen in Lösung und von der Temperatur
E = Maß für den erzeugten „Elektronendruck“ im Metall
E kann nicht absolut gemessen werden, nur relativ zu einer
Bezugselektrode
18
Die Normal-Wasserstoffelektrode
Normalpotenzial
(oder Standardpotenzial)
Standardpotenziale anderer Elektroden werden auf die StandardWasserstoffelektrode bezogen
19
Die Normal-Wasserstoffelektrode als Bezugselektrode
Kupfer ist edel, Zink ist unedel
-
+
+
-
ECu0 = + 0.34 V
EZn0 = - 0.76 V
Cu2+ + 2 e- „ Cu
H 2 „ 2 H + + 2 e-
Zn „ Zn2+ + 2 e2 H + + 2 e- „ H 2
positives Vorzeichen:
Reduktion von Cu2+ bevorzugt
negatives Vorzeichen
Oxidation von Zn bevorzugt
20
Elektrochemische Spannungsreihe
Ordnung der Redox-Paare nach
steigendem Reduktionspotential
Je positiver E0, desto stärker ist
die Reduktion bevorzugt
Bezugselektrode
21
Die Elektromotorische Kraft (EMK)
EMK = elektrisches Potential einer galvanischen Zelle (in Volt)
• Je stärker die Tendenz zum Ablaufen der Redox-Reaktion, desto
größer ist EMK
• Die EMK einer beliebigen galvanischen Zelle lässt sich aus den
Standardreduktionspotentialen errechnen:
EMK = ΔE0 = E0 (Kathode) – E0 (Anode)
Anode
Kathode
EMK = ΔE0 = 0,35 V – (-0,76 V) = 1,11 V
Redoxreaktionen laufen nur dann freiwillig ab, wenn EMK = ΔE0 > 0
22
Freie Reaktionsenthalpie und EMK (Standardpotential)
Die freie molare Standardreaktionsenthalpie ist ein Maß für die maximale
elektrische Energie, die ein galvanisches Element unter Standard-Bedingungen
abgeben kann:
ΔG0 = -z x F x ΔE0
z…. Anzahl der ausgetauschten Elektronen
F….Faraday-Konstante (elektrische Ladung von 1 mol
Elektronen 96485 C/mol)
ΔE..EMK (Zellpotenzial, Zellspannung)
Standardbedingungen: 25 °C (oder 298 K), effektive Konzentration (Aktivität) von
gelösten Stoffen = 1mol/l, von reinen Stoffen = 1, Partialdruck von Gasen = 1,013
bar
Berechnung von Gleichgewichtskonstanten bei Redoxreaktionen:
ΔG0 = -z x F x ΔE0
ΔE0 =
2,303 RT
zxF
lgK oder
ΔG0 = - RT lnK = - 2,303 RT lgK
ΔE0 =
0,059 V
z
lg K
Zusammenhang von
Gleichgewichtskonstante
und EMK im
Standardzustand
Freiwilliger Ablauf einer Reaktion „ ΔG negativ, ΔE positiv
23
Verschiedene Einheiten für R
24
Konzentrationsabhängigkeit des Potenzials
Wenn nicht alle beteiligten Stoffe die Standardkonzentration von 1 mo/l
aufweisen, gilt für eine beliebige Reaktion:
aA+bB„cC+dD
ΔG =
ΔG0
+ RT lnK
a…Aktivität (≈ Konzentration)
mit K = MWG =
ac(C) x ad(D)
aa(A) x ab(B)
ΔG = -z x F x ΔE
NERNST´sche Gleichung
ΔE = ΔE0 -
RT
zxF
lnK
ΔE = ΔE0 -
0,059V
lgK
zxF
Δ
Δ
z
25
NERNST´sche Gleichung für Halbzellen
Wenn die Nernstsche Gleichung für Halbzellen verwendet wird, ist
das Vorzeichen zu beachten!!
E = E0 -
2,303 RT
zxF
lgK
allgemeine Form
0,059 [OX ]
E=E +
lg
[RED]
z
0
+
0,059
E = E0 -
z
lgK
für 25 °C
0,059 [RED ]
E=E −
lg
[OX ]
z
0
-
Achtung !
Vorzeichen
Für Gase gilt [Red] = pGas/1,013 bar
26
Übung
•
Wie groß ist das Potential des Redoxsystems Zn2+/Zn, wenn die
Konzentration der Lösung 0,1 mol/l bzw. 0,01 mol/l beträgt?
E0 = -0,76 V
•
Welches Potential hat die folgende Zelle
Sn | Sn2+ (1,0 mol/l) || Pb2+ (0,001 mol/l) | Pb
Sn
e- „
Pb
Sn2+
Sn2+
E0 = -0,136 V
Pb2+
Pb2+
E0 = -0,126 V
27
pH-Abhängigkeit von Reduktionspotentialen
• Wenn H+ oder OH- Ionen an der Reaktion beteiligt sind, ist das
Reduktionspotential vom pH-Wert abhängig.
• Häufig gilt:
Oxidationsmittel sind in saurer Lösung stärker wirksam
Reduktionsmittel sind in basischer Lösung stärker wirksam
Beispiel:
Wie groß ist das Reduktionspotential einer Permanganatlösung mit
c(MnO4-) = 0,1 mol/l, die Mn2+ Ionen mit c(Mn2+) = 0,001 mo/l enthält,
bei pH = 1 und pH = 5 ?
28
Quantitative Beschreibung von Redoxgleichgewichten
Im Gleichgewicht gilt:
E1 =
=
E1 = E2
Umrechnen auf
dekadischen Logarithmus,
T = 298 K:
= E2
(E20 – E10)
31
Beispiel Cu2+ | Cu || Zn | Zn2+
Zn
+
Cu2+
Cu
E10 (Zn2+/Zn) = -0,76 V
+
Zn2+
E20 (Cu2+/Cu) = + 0,34 V
2
[ Zn 2+ ]
(0,34 + 0,76)
= lg
= lg K = 37
2+
0,059 V
[Cu ]
K = 1037
32
Redoxtitrationen – Permanganometrie I
Verfahren, z. B. zur quantitativen Bestimmung von
Oxalsäure, Ca2+ (nach vorheriger Umsetzung zu Calciumoxalat) oder Fe2+
Die Titration erfolgt im sauren Medium:
MnO4- + 8 H+ + 5 e- „ Mn2+ + 4 H2O
1
1
c( KMnO4 ) = c( KMnO4 )
5
5
KMnO4-Lösungen sind nicht titerbeständig (Titer = Äquivalentkonzentration)
„ Genaue Ermittlung der Äquivalentkonzentration (Faktorbestimmung) durch
Titration gegen NaC2O4 oder Oxalsäure nötig
beständig, „Urtiter“
1
c
(
KMnO4 ) = 0,1 mol /l
Man titriert mit einer Lösung der Äquivalentkonzentration
5
33
Redoxtitrationen – Permanganometrie II
Titration einer Lösung von Na2C2O4 mit der KMnO4-Lösung:
Ermittlung des Titers der KMnO4-Lösung:
1
c( KMnO4 ) = 0,102 mol ⋅ l −1
5
Äquivalenzpunkt: beginnende Eigenfärbung der Lösung (rosa)
Bestimmung von Ca2+
• Fällung von Ca2+ als (NH4)C2O4 aus ammoniakalischer Lösung
• Filtrieren, waschen, in verdünnter H2SO4 auflösen
• mit KMnO4 titrieren
34
Praktikumsrelevante Themen
Komplexgleichgewichte
•
•
•
Definitionen
Nomenklatur
Komplexometrie
37
Aufbau von Komplexverbindungen
Komplex
=
Koordinationszentrum
Metallatom oder –ion
+
Ligandenhülle
Ionen oder Moleküle
Koordinationszahl (KZ) = Anzahl der vom Koordinationszentrum
chemisch gebundenen Liganden
Koordinationszentrum
Ligand
Komplex
KZ
Al3+
F-
[AlF6]3-
6
Fe3+
H 2O
[Fe(H2O)6]3+
6
Ni0
CO
Ni(CO)4
4
Ag+
CN-
[Ag(CN)2]-
2
38
Besondere Eigenschaften von Komplexen
(Chelateffekt)
39
Wichtige Koordinationszahlen
KZ 2
bei einwertigen Kationen (Ag+, Cu+, Au+) und Hg2+, linear
[NC – Ag – CN]-
KZ 4
[H3N – Ag – NH3]+
[Cl – Ag – CN]-
Hauptgruppenelemente AlCl4-, BeF4-, BH4d0 und d10 [VO4]3- [MnO4]- [ZnCl4]- [Cu(CN)4]3d-Elemente mit wenigen d-Elektronen
[MnO4]2- [FeO4]2 [FeCl4]-
KZ 6
alle Übergangsmetalle bilden
oktaedrische Komplexe
H3 N
NH3
Cu2+
NH3
NH3
40
Liganden
Einzähnige Liganden
Ffluoro
Clchloro
CNcyano
OHhydroxo
H 2O
aqua
NH3
ammin
CO
carbonyl
Mehrzähnige (Chelat-)Liganden
Ethylendiamin (en, 2-zähnig)
Ethylendiamintetraessigsäure
(EDTA, 6-zähnig)
Porphyrin (4-zähnig)
41
Benennung von Komplexen I
Erst das Kation, dann das Anion
Schema für kationische Komplexe: [Cr(H2O)6]Cl3
Hexa
aqua
chrom
(III)
Anzahl der
Liganden
ƒ
ƒ
ƒ
ƒ
ƒ
Ligand
Koordinationszentrum
-
chlorid
Oxidationszahl
Anion
Anzahl der Liganden durch griech. Vorsilben angegeben (mono, di, tri,
tetra, penta hexa....)
wenn der Ligandenname selbst Zahlworte enthält (z. B. ethylendiammin)
werden die Vorsilben „bis“, „tris“, „tetrakis“.... verwendet
Eine römische Ziffer oder 0 in runden Klammern nach dem Zentralion
gibt dessen Oxidationsstufe an
Anionische Liganden enden auf „o“
Bei verschiedenen Liganden ist die Reihenfolge: negativ – neutral –
positiv
[Pt(en)2Cl2]Br2
Dichloro-bis(ethylendiamin)-platin(IV)-bromid
42
Benennung von Komplexen II
Schema für anionische Komplexe: K4[Fe(CN)6]
Hexa
Kalium cyano
ferr
Kation
Anzahl der
Liganden
Ligand
Koordinationszentrum
at
(III)
at
Oxidationszahl
Beispiele
K2[PtCl4]
Kalium-tetrachloroplatinat(II)
Na[Al(OH)4]
Natrium-tetrahydroxoaluminat(III)
(NH4)[Cu(CN)4]
Ammonium-tetracyanocuprat(II)
Kationische Komplexe
[Cu(NH3)4]SO4
Tetraamminkupfer(II)-sulfat
[Pt(NH3)3Cl3]Cl
Trichlorotriamminplatin-(IV)-chlorid
[Ni(CO)4]
Tetracarbonylnickel(0)
43
Stabilität von Komplexen
Beschreibung durch das MWG:
Je größer K, desto stabiler der Komplex
44
Der Chelateffekt
4 Teilchen
„
7 Teilchen
Ni2+
[Ni(NH3)6]2+ + 3 en x
Κ = 108.6 l6 mol-6
+ 6 NH3
Κ = 1018.3 l3 mol-3
Gibbs-Helmholtz-Gleichung
ΔRG = ΔRH - Tx ΔRS
ΔRG freie Reaktionsenthalpie
ΔS >>>>> 0
ΔRH Reaktionsenthalpie
ΔRS Reaktionsentropie (Maß für die Unordnung)
Chelateffekt = Entropieeffekt. ΔRG < 0 wenn ΔRS >> 0
45
Komplexometrie
•
Quantitative Bestimmung von Metallkationen durch Komplexbildung
mit Chelate
Wichtige Chelatbildner:
(oder –acetat EDTA)
bilden sehr stabile, wasserlösliche Komplexe mit fast allen Kationen
„ Grundlage für die Bestimmung der Wasserhärte
46
Metallindikator
Farbwechsel durch pH-Änderung und Komplexbildung
1) Zugabe des Indikators, Komplex mit Ca2+ und Mg2+ entsteht
weinrot/purpur
2) Verdrängung des Indikators durch EDTA (= H2Y2-)
blau
47
Komplexometrische Bestimmung der Wasserhärte I
48
Bestimmung der Gesamtwasserhärte
Gesamthärte = Calciumhärte + Magnesiumhärte
Da bei der Reaktion Protonen freigesetzt werden, muß der pH-Wert der Lösung durch Zusatz
einer Pufferlösung (NH4+/NH3-Puffer) bei pH 10 konstant gehalten werden. Bei pH > 12 fällt
Mg2+ als Mg(OH)2 aus.
1 ml EDTA-Lösung (c = 0,01 mol/l) = 0,01 mmol Ca2+ = 0,56 mg CaO
Bei Titration mit EDTA-Lösung der Konzentration c = 0,02 mol/l errechnet sich die
Gesamthärte wie folgt:
49
Bestimmung der Kalkhärte
50