1 Zur Einf uhrung - Experimental Atomic Physics at Frankfurt University

1
Impulsraum-Imaging von atomarer
Mehrteilchenreaktionsdynamik
Ein U berblick
Inhaltsverzeichnis
1 Zur Einfuhrung
2 Zur technischen Realisierung
3 Ausgewahlte Ergebnisse
1
3
6
3.1 Photo- und Comptoneekt . . . . . . . . . . . . . . . . . . . . . . 6
3.2 Photodoppelionisation . . . . . . . . . . . . . . . . . . . . . . . . 9
3.3 Wechselwirkung mit geladenen Teilchen . . . . . . . . . . . . . . . 16
4 Ausblick
23
1 Zur Einfuhrung
Einige ihrer groten Triumphe feierte die Quantenmechanik bei der Beschreibung
stationarer Einteilchensysteme. Fur Energieeigenwerte, der zentralen Megroe
stationarer Systeme, besteht fur Wenigteilchensysteme eine beeindruckende U bereinstimmung zwischen experimentellem Befund und theoretischer Vorhersage. Im
Gegensatz hierzu bereitet die Behandlung echter dynamischer Mehrteilchensyteme, d.h. solcher, die sich nicht auf eektive Einteilchenprobleme reduzieren
lassen, noch heute grote Schwierigkeiten. Systeme, die alleine von der Coulombwechselwirkung bestimmt werden, bieten hier ein besonders vielversprechendes
Forschungsobjekt. Die Wechselwirkung gilt als vollstandig bekannt und ist so
einfach, da sich die Schwierigkeiten, die aus korrelierter Mehrteilchendynamik
resultieren, eindeutig isolieren lassen. Gleichzeitig ist korrelierte Mehrteilchendynamik von Coulombsystemen von zentraler Bedeutung fur unsere makroskopische
Welt. Sie liegt nicht nur Festkorpereekten, wie etwa der Supraleitung zugrunde,
sondern ist der innere Antrieb fur chemische Reaktionen bis hin zur Selbstorgani-

1 ZUR EINFUHRUNG
2
sation des Lebens. Die praktische Wichtigkeit dieser Probleme steht in unbefriedigendem Kontrast zu unserem Wissenstand auf diesem Gebiet. Selbst so scheinbar
einfache Probleme wie die Promotion eines einzelnen Elektrons ins Kontinuum
in einem quasiadiabatischen Sto (z.B. 5 keV p ! He) oder die Emission von
zwei Elektronen durch Absorbtion oder Compton Streuung eines einzelnen Photons bei He oder H2, den einfachsten Zweielektronensystemen, sind noch nicht
befriedigend gelost.
Ein wesentliches Hemmnis fur den Fortschritt des Verstehens der Mehrteilchenreaktionsdynamik war uber lange Zeit das Fehlen ezienter und hochauosender experimenteller Techniken, die es erlauben, den Endzustand von atomaren Reaktionen vollstandig zu vermessen. Eine direkte U bertragung der in
Kern- und Hochenergiephysik entwickelten Vielteilchennachweissysteme scheitert
an den vergleichsweise winzigen Energien der Teilchen (typisch eV - milli eV fur
Ionen und 1-100 eV fur Elektronen). Von diesen Teilchen lat sich nur einmalig
ihr Ort, aber niemals eine Spur oder ihre Energie aus der Pulshohe eines Detektors messen. Daher wurden in der Atomphysik weitgehend elektrostatische oder
magnetische Spektrometer verwendet, die alle einen kleinen Eintrittsschlitz fur
die Energie- bzw. Winkelanalyse benotigen. Dadurch decken solche traditionellen
Elektronenspektrometer nur einen extrem kleinen Nachweisraumwinkel ab. Das
macht den koinzidenten Nachweis von auch nur zwei Teilchen aus einer Reaktion
schwierig und macht es praktisch unmoglich, den gesamten Endzustandsimpulsraum aller Teilchen zu vermessen. So liegt auch nur fur Einfachionisation durch
Elektronensto (sogenannte (e,2e) Experimente) systematischeres Datenmatial
vor. In jungster Zeit gelangen ahnliche Experimente zur Photodoppelionisation
von atomaren Systemen. Diese Experimente sind 'kinematisch vollstandig', d.h.
sie bestimmen fur die Reaktionen, deren Endprodukte in Ihren (kleinen) Nachweisraumwinkel fallen, die Impulsvektoren aller Teilchen. Ihnen ist jedoch nur ein
winziger Unterraum des korrelierten Endzustandes der Reaktion zuganglich.
Die in dieser Arbeit vorgestellte Technik der "Cold Target Recoil Ion Momentum Spectroscopy\(COLTRIMS) bietet einen grundlegend neuen experimentellen
Zugang zur Untersuchung atomarer und molekularer Reaktionen. Sie ist eine Abbildungstechnik, die traditionelle Spektrometer durch ein Vielteilchenmikroskop
fur den Impulsraum ersetzt. So wie herkommliche Mikroskope Bilder im Ortsraum
liefern, bildet diese Technik den korrelierten Endzustandsimpulsraum aller Fragmente einer atomaren Reaktion ab. Dadurch entstehen vieldimensionale Bilder,
die direkt das Quadrat der Endzustandswellenfunktion einer Reaktion im Im-
2 ZUR TECHNISCHEN REALISIERUNG
3
pulsraum reprasentieren. Solche vollstandig dierentiellen Wirkungsquerschnitte
bieten den prazisesten Test theoretischer Vorhersagen, der moglich ist. Da die
Messung fur jede einzelne Storeaktion die Impulse aller Teilchen registriert, lat
sich die Reaktion nachtraglich in der Computeranalyse der Datenfelder unter jedem beliebigen Blickwinkel betrachten, z.B. konnen die Impulsverteilungen in beliebigen kollektiven Koordinaten (z.B. Jakobi-Koordinaten) betrachtet oder auch
auf beliebige Impulsunterraume projeziert werden. Solche umfassenden Moglichkeiten des Darstellungs-, Perspektiv- und Koordinatenwechsels sind fur die experimentelle Atomphysik volliges Neuland. Sie erlauben in vielen Fallen direkt die
einer Reaktion zugrunde liegenden Mechanismen sichtbar zu machen.
Mit dieser neuen Technik wurden in den letzten 5 Jahren eine Vielzahl grundlegender Experimente der atomaren Stophysik durchgefuhrt. Die Experimente umfassen Beispiele aus der gesamten Bandbreite der Wechselwirkung ionisierender Strahlung mit Atomen: Ionisation durch keV [1] uber MeV Protonen
[2, 3], bis GeV U92+ [4, 5, 6, 7], Ionisation durch Antiprotonen [8] und Elektronen [9, 10, 11], Reaktionen wie Einfach- [12, 13] oder Doppelelektroneneinfang [14], Aufklarung korrelierter Zweielektronen Prozesse von Elektronen zweier
Stopartner [15, 16, 17, 18] oder innerhalb eines Atomes [19], Einfach- und Doppelionisation durch Absorbtion oder Comptonstreuung [20, 21, 22, 23] von linear
polarisierten Photonen von der Schwellenenergie [24, 25, 26, 27, 28, 29] bis zu 100
keV [23], Doppelphotoionisation mit zircular polarisiertem Licht [30] und Doppelphotoionisation von ausgerichteten H2-Molekulen [31]. Fur eine umfassende
Darstellung dieser Ergebnisse verweisen wir auf den beiliegenden U bersichtsartikel [32]. Nach einer kurzen Diskussion der grundlegenden technischen Aspekte
des Vielteilchenimpulsmikroskopes in Kapitel 2 stellen wir in Kapitel 3 einige ausgewahlte Beispiele dieser Ergebnisse dar. Ziel ist es, dabei examplarisch aufzuzeigen, wie sich Mehrteilchendynamik in den neuartigen vollstandig dierentiellen
Impulsraummessungen aufklaren lat.
2 Zur technischen Realisierung
Der typische Impulstransfer in atomaren Reaktionen liegt im Bereich weniger
atomarer Einheiten (a.u.). Eine a.u. entspricht dem mittleren Impuls eines Elektrons im Grundzustand des Wasserstoatoms. Wahrend die Impulse der entstehenden Ionen und Elektronen typischerweise von vergleichbarer Groe sind,
entsprechen diese Impulse fur die Ruckstoionen aufgrund ihrer groen Masse
2 ZUR TECHNISCHEN REALISIERUNG
4
nur Energien im bis milli eV Bereich. Dadurch entzogen sich Ruckstoionenimpulse fur lange Zeit der Messung. Nach vereinzelten Versuchen der Messung
der Emissionsrichtung solcher Ionen aus peripheren Stoen seit den 60er Jahren [33, 34, 35, 36, 37, 38] gelang Ullrich und Schmidt-Bocking [39] unter Verwendung eines warmen statischen Gastargets die erste Messung des Tranversalimpulses von Neon Ionen aus 340 MeV U32+ ! Ne Stoen an der GSI in
Darmstadt. Es folgten Messungen ebenfalls mit einem statischen aber auf 30 K
gekuhlten Gastarget zur Untersuchung des Transversalimpulsaustausches in p-He
Stoen [40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50]. In diesen ersten Spektrometern wurden die transversalen Ionenimpulse uber die Flugzeit in einem feldfreien
Raum bestimmt. Man erreichte eine Auosung von einigen a.u.. Eine vergleichbare Auosung bei zusatzlicher Messung des longitudinalen Ruckstoionenimpulses
wurde mittels eines eusiven Gasstrahltargets durch die Projektion der Ionen
auf einen ortsempndlichen Detektor erreicht [51, 52]. Den Durchbruch brachte
schlielich der Einsatz von U berschallgasstrahlen als Target [9, 53, 15, 7, 12, 54].
Die interne Temperatur solcher U berschallgasstrahlen liegt bei unter 0.1 K. Damit wurden Impulsauosungen fur die Ruckstoionenimpulsmessung von typisch
0.05 a.u. moglich, was einer Ruckstoionenenergie von 5 eV entspricht. Durch
die Kreuzung des U berschallgasstrahls mit dem Projektilstrahl von Photonen,
Elektronen oder Ionen erhalt man ein sehr scharf begrenztes Reaktionsvolumen
von typisch 0.1-1 mm3. Die hierin in Einzelstoen erzeugten Ionen lassen sich mit
schwachen elektrischen Feldern mit 4-Raumwinkel auf einen ortsauosenden Detektor projezieren. Aus der Messung der Flugzeit und des Auftreortes erhalt man
mit hoher Auosung den Startimpuls der Ionen. Durch Einsatz elektrostatischer
Linsen wird die Auosung weitgehend unabhangig von der Groe des Reaktionsvolumens. Ionen mit gleichem Impuls lassen sich in Orts- und Flugzeitrichtung
unabhangig von Ihrem Startort auf einen Punkt fokussieren [55]. Das elektrische
Feld, das die Ionen auf einen Detektor projeziert, beschleunigt die Elektronen in
die entgegengesetzte Richtung, wo sie von eine zweiten ortsauosenden Detektor nachgewiesen werden. Auch hier lat sich der Impulsvektor mit sehr guter
Auosung aus Flugzeit und Auftreort berrechnen. Um auch hoherenergetische
Elektronen mit 4-Raumwinkel auf den Detektor abzubilden, kann einem Vorschlag von Moshammer et al. folgend, dem elektrischen Feld ein homogenes magnetisches Feld uberlagert werden [56, 57]. Rustet man diese Impulsmikroskope
mit neu entwickelten, schnellen, multihitfahigen Delay-Line-Detektoren [58, 59]
aus, so lassen sich auf dem Ionen- und dem Elektronendetektor jeweils mehre-
2 ZUR TECHNISCHEN REALISIERUNG
5
 die Flugzeitmessungen konnen
re Teilchen aus einer Reaktion nachweisen. Uber
alle nachgewiesenen Teilchen eindeutig einem Ereignis zugeordnet werden. Fur
weitere technische Details von COLTRIMS verweisen wir auf Kapitel 3 des beiliegenden U bersichtartikels. In der Messung konnen so die Impulse des Ions und
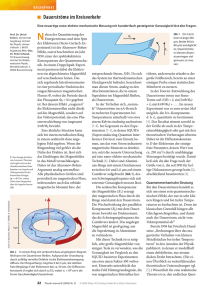
Abbildung 1: Typisches Beispiel fur ein COLTRIMSpektrometer. Auf 30K vorgekuhltes Helium Gas expandiert durch eine Duse von 30m Durchmesser ins
Vakuum. Dabei bildet sich ein intern kalter U berschallgasstrahl aus. Durch einen
Skimmer gelangt der Kern dieses Strahles in die Streukammer. Der Gasstrahl
wird mit dem Projektilstrahl von Ionen, Elektronen oder Photonen gekreuzt.
Elektrostatische und in manchen Fallen magnetische Felder projezieren die Ionen
(nach rechts) auf einen und die Elektronen (nach links) auf einen gegenuberliegenden ortsauosenden Channelplatedetektor. Aus Auftreort und Flugzeit wird
der Startimpulsvektor der Teilchen berrechnet. Target und Projektilstrahlintensitaten sind so gewahlt, da Einzelstobedingungen vorliegen und die Flugzeitmessungen eine eindeutige Zuordnung der registrierten Teilchen zu einem Reaktionsereignis zulassen.

3 AUSGEWAHLTE
ERGEBNISSE
6
eines oder mehrerer Elektronen sowie Ladungszusstand und Streuwinkel des Projektils fur jede Reaktion koinzident gemessen werden. Die Impulse aller Teilchen
im Eingangs- und Endkanal einer Reaktion sind durch Impuls- und Energieerhaltung miteinander verknupft. Daher kann fur eine kinematisch vollstandige
Messung ein Teilchen im Endkanal unbeobachtet bleiben. Sein Impuls kann unter
Verwendung der Erhaltungssatze aus den gemessenen Impulsen aller anderen berrechnet werden. In vielen Fallen kann daher darauf verzichtet werden, die Streuung des Projektils zu detektieren, ohne dadurch Information zu verlieren. Dies ist
von besonderer Bedeutung, da die Impulsauosung der Messung dadurch in erster
Ordnung unabhangig von der Qualitat des Projektilstrahls wird. Ein schnelles geladenes Projektil erfahrt in den meisten atomaren Stoen nur einen im Vergleich
zu seinem Anfangsimpuls winzigen Impulsubertrag. Indem man Ruckstoionenund Elektronenimpulse mit, kann man mit sonst unerreichbarer Genauigkeit
die Projektilimpulsanderung bestimmen. Einfachstes Beispiel hierfur ist eine Reaktion in der nur ein Elektron vom Target ins Projektil transferiert wird. Da
im Endzustand nur zwei Teilchen vorliegen und kein freies Elektron emittiert
wird, mu also jede Impulsanderung des Projektils exakt durch den Impuls des
Ruckstoiones kompensiert werden. Damit sind Streuwinkel und Ruckstoionentransverslimpuls sowie Projektilimpulsverlust und Ruckstoionenlongitudinalimpuls entgegengesetzt gleich. Eine Auosung von 0.05 a.u. im Ruckstoionenimpuls
fuhrt damit fur die Bestimmung der Ablenkung eines 10 MeV/u Uran Projektils
zu einer Genauigkeit von 10,8 rad, was einer Auslenkung von 1 mm uber 100 km
sowie einer Energieverlustauosung von E=E = 10,8 entspricht.
3 Ausgewahlte Ergebnisse
3.1 Photo- und Comptoneekt
Einer der strukturell einfachsten und fundamentalsten Wechselwirkungsprozesse
mit einem Atom ist die Ionisation durch einzelne Photonen. Dabei kann das
Photon entweder absorbiert (Photoeekt [60]) oder inelastisch gestreut werden
(Comptonstreuung [61]). Am Beispiel der Heliumeinfachionisation:
+ He ! He1+ + e,
+ He ! He1+ + e, + 0
(1)
(2)
sollen diese beiden Prozesse diskutiert werden. Sie unterscheiden sich grund-

3 AUSGEWAHLTE
ERGEBNISSE
7
legend in ihren Impuls- und Energiebilanzen. Bei der Photoabsorbtion wird Energie, Impuls und Drehimpuls des Photons vollstandig vom Atom aufgenommen.
Der Impuls des Photons (k = E =c) ist dabei meist klein gegen den Impuls
des emittierten Elektrons (fur E =80 eV betragt er z.B. k =0.02 a.u. im Vergleich zum Impuls eines Elektrons aus Reaktion (1) von ke=2 a.u.). Daraus folgt,
da bei Photoabsorbtion Elektron und Ruckstoion mit entgegengesetzt gleichem
Impuls emittiert werden (fur eine detailierte Analyse der Impulsbilanzen siehe
[26] und Kapitel 3 des folgenden U bersichtsartikels [32]). Aufgrund des Massenverhaltnisses tragt das Elektron jedoch den Hauptanteil der Energie. Im Gegensatz hierzu konnte Compton Streuung auch an einem freien Elektron stattnden.
Sie erfordert hinreichend hohe Photonenimpulse (Energien), damit das Photon
bei einer inelastischen Streuung hinreichend Energie zur U berwindung der Bindungsenergie ubertragen kann. Der Atomkern spielt bei beiden Prozessen eine
sehr unterschiedliche Rolle. Bei der Comptonstreuung ist er nur unbeteiligter Zuschauer, der keinen Impulsubertrag erhalt, bei der Photoabsorbtion kompensiert
er den Elektronenimpuls. Dieses grundlegende Charakteristikum von Photo- und
Comptoneekt konnten mit COLTRIMS erstmals direkt sichtbar gemacht werden
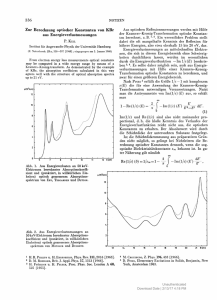
[21, 25]. Abbildung 2 zeigt die gemessene Impulsverteilung von He1+-Ruckstoionen die von 80 eV und 9 keV Photonen erzeugt wurden. Dargestellt ist die Impulsebene senkrecht zur Ausbreitungsrichtung des Photons. Das Licht ist linear
polarisiert, die Polarisationsachse ist horizontal. Bei 80 eV tritt keine Comptonstreuung auf, die Impulsvektoren der Ruckstoionen liegen auf Kugelschalen (fester Impulsbetrag) um den Ursprung. Die auerste Schale entspricht He1+-Ionen
im Grundzustand, die inneren Kreise resultieren von He1+-Ionen in angeregten
Zustanden. Die Winkelabhangigkeit der Grundzustandsionen zeigt eine Dipolverteilung. Fur die angeregten Zustande kann der Drehimpuls des Photons auch vom
Ion aufgenommen werden, soda hier auch Elektronen entlang der Polarisationsrichtung emittiert werden. Bei 9 keV tritt zusatzlich zu den Ruckstoionen aus
der Photoabsorbtion ein groer Anteil von Ionen mit Impulsen nahe Null auf. Sie
resultieren von Comptonstreuung. Die Impulsverteilung dieser Ionen spiegelt die
Impulsverteilung im Anfangszustand wieder (ein Spiegelbild des Comptonprols
der Elektronen).
Photo- und Comptoneekt werden durch Einteilchenoperatoren beschrieben.
Zweielektronenprozesse wie etwa Einfachionisation plus Anregung oder Doppelionisation, die durch diese Wechselwirkungsprozesse induziert werden, sind daher
immer Folge von Elektron-Elektron-Korrelation. Alleine die sehr globale Groe
counts
2
8
10 4
1
He
1+
kyrec (a.u.)

3 AUSGEWAHLTE
ERGEBNISSE
10 3
0
-1
10 2
-2
-2
-1
0
1
2
kzrec (a.u.)
-20
k
yr
0
ec (
a.u
.)
20
20
0
a.u.)
k zrec (
-20
Abbildung 2: Impulsverteilungen von He1+-Ruckstoionen erzeugt durch Photonen einer Energie E = 80eV (links) und E 9keV (rechts). Die dargestellte
Impulsebene ist senkrecht zur Ausbreitungsrichtung der Photonen (x-Richtung),
der elektrische Feldvektor des linear polarisierten Lichtes liegt horizontal. Die linke Abbildung zeigt alle Ionen deren Impulskomponente krx in Photonenrichtung
im Interval ,0:1 < krx < 0:1 liegt, dir rechte Abbildung ist uber alle Impulse krx
Integriert. Der auere Ring auf der linken Seite resultiert von He1+ Ruckstoionen im Grundzustand, die inneren Ringe von angeregten Ionen. Die ringformige
Struktur auf der rechten Seite bei groen Impulsen resultiert vom Photoeekt,
die scharfe Nadel bei Impuls Null vom Comptoneekt. (Die Daten bei E = 80eV
wurden gemessen an der Advanced Light Source des Lawrence Berkeley National
Laboratories [25]. Die Daten bei E = 9keV wurden am HASYLAB am DESY
gemessen [21]).
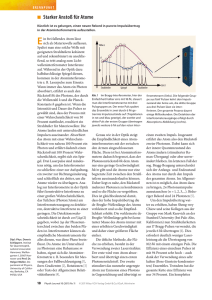
des Verhaltnisses R der Querschnitte von Doppel- zu Einfachionisation ist daher
schon ein interessantes Ma fur Korrelationseekte. Dieses Verhaltnis steigt fur
den Photoeekt an der Doppelionisationschwelle zunachst entsprechend E1exc:025 mit
der U berschuenergie Eexc, die beiden Elektronen im Kontinuum zur Verfugung
steht an und erreicht ein Maximum von R=3.6% bei Eexc 120 eV . Im Grenzwert hoher Energien geht R nicht gegen Null, sondern fallt auf einen konstanten Wert R1. Mittels COLTRIMS konnte fur niedrige Photonenenergien gezeigt

3 AUSGEWAHLTE
ERGEBNISSE
9
werden, da die bis dahin vorliegenden Messwerte fur R etwa 25% zu hoch waren [25]. Die Impulsmessung jedes einzelnen Ions erlaubt es, erstmalig und im
Gegensatz zu herkommlichen Ladungszustandsmessungen, alle in der Literatur
diskutierten Quellen moglicher systematischer Fehler auszuschlieen. Die neuen
Werte sind in hervorragender U bereinstimmung mit allen neueren theoretischen
Ergebnissen [62, 63, 64, 65]. Fur hohe Photonenenergien konnten, wie in Abbildung (2b) gezeigt, erstmals die Beitrage von Photo- und Comptoneekt separat
gemessen werden. Fur den Photoeekt wurde der schon 1967 [66] vorhergesagte Wert von 1.67% (COLTRIMS Experiment: Rp1=1.720:12%) hervorragend
bestatigt [21, 20]. Fur den Comptoneekt liegt RC1 =0.980.09% [23] deutlich
tiefer und zeigt eine uberraschende und signikante Abweichung von den theoretischen Vorhersagen von RC1 =0.8% [67, 68, 69]. Der Limes hoher Photonenenergien entspricht physikalisch dem instantanen entfernen eines Elektrons aus
dem Helium Grundzustand. Die korrelierte Zweielektronenwellenfunktion relaxiert daraufhin auf die Eigenzustande des wasserstoahnlichen He1+ (sudden approximation, shake-o Proze). Relaxation und primare Einfachionisation sind
in diesem Limes unabhangig voneinander. Der Unterschied zwischen Comptonund Photoeekt bei der Emission des primaren Elektrons wird in Abbildung (2b)
deutlich. Der Photoeekt 'schneidet' selektiv den Teil der Wellenfunktion heraus,
in dem ein Elektron und der Kern einen groen, genau zur Photonenenergie passenden, Impuls haben. Im Ortsraum entspricht das sehr kernnahen Elektronen.
Der Comptoneekt dagegen ist nicht impulsselektiv. Entsprechend probt Doppelionisation nach Compton- und Photoeekt die korrelierte Helium Wellenfunktion
in unterschiedlichen Bereichen des Phasenraumes. Eine weitere Aufklarung des
Relaxationsprozesses sowie der noch bestehenden Diskrepanzen zwischen Theorie
und Experiment bezuglich RC1 kann man von schon begonnenen Messungen der
Impulsverteilung der langsamen Relaxationselektronen erwarten.
3.2 Photodoppelionisation
Fur die Doppelionisation durch Photoeekt,
+ He ! He2+ + 2e,
(3)
bei niedrigen Photonenenergieen gelangen fur He 1993 [70] die erste Messung
der Winkelkorrelation zwischen den beiden Elektronen. Hier und in spateren
Messungen [71, 72, 73, 74, 75, 76, 77]. wurden jeweils unter bestimmnten Winkeln und Energien beide Elektronen mit traditionellen Elektronenspektrometern

3 AUSGEWAHLTE
ERGEBNISSE
10
nachgewiesen. Mittels COLTRIMS konnte dann, ohne Beschrankung auf Winkel
und Energien der Dreiteilchenendzustand vollstandig im Impuls aller Teilchen
vermessen werden. Abbildung 3 zeigt die Impulsverteilungen eines (beliebigen)
der beiden Elektronen (ke) und die des He2+ Ruckstoiones (krec) im Vergleich.
Wahrend die Elektronenimpulsverteilung im wesentlichen isotrop im Winkel ist,
zeigt die Impulsverteilung des Kernes eine deutliche Dipolcharakteristik. Dieser
Unterschied legt ein einfaches physikalisches Bild eines Zweistufenprozesses nahe.
In einem ersten Schritt wird das Photon, dessen Wechselwirkung mit dem Atom
in erster Naherung durch den Dipoloperator beschrieben wird, von einem Ladungsdipol absorbiert. Im Atom ist der Kern immer der positive Pol des Dipols.
Den negativen Pol bildet, je nach Naherung, ein Elektron oder der Ladungsschwerpunkt der beiden Elektronen. Der Drehimpuls des absorbierten Photons
spiegelt sich in der Winkelverteilung der Fragmente des Ladungsdipols. Die beobachtete dipolartige Emissionscharakteristik des Kernes resultiert aus diesem
ersten Schritt. Fur den zweiten Schritt wurden zwei Varianten vorgeschlagen.
Wenn man animmt, da zunachst nur ein Elektron am Absorbtionproze beteiligt ist, so mu in einem zweiten Schritt eine Elektron-Elektron-Wechselwirkung
stattnden, um zur Doppelionisation zu fuhren [78, 79]. Im zweiten Modellfall, in
dem der Ladungsschwerpunkt des 'Dielektrons' am primaren Absorbtionsproze
beteiligt ist, bricht in einem zweiten Schritt dieses 'Dielektrons' im Kontinuum
auf [80, 81]. In beiden Fallen ist es der zweite Schritt, der die Dipolcharakteristik
in der Impulsverteilung des Elektrons verwischt.
Bei geringen U berschuenergien, d.h. nahe an der Schwelle, wird die Energieabhangigkeit des Doppelphotoionisationsquerschnittes durch das zweite Modell
sehr gut beschrieben. Man betrachtet den Proze hierzu anstelle in den Impulskoordinaten der beiden Elektronen k1 und k2 in Jakobikoordinaten kr = k1 + k2
und kR = 21 (k1 , k2). kr = ,krec ist dabei der Impuls des 'Dielektrons' der
vom He2+ Kern kompensiert wird, kR ist der Relativimpuls der beiden Elektronen und beschreibt die Aufbruchbewegung des 'Dielektrons'. Diese Koordinatentransformation lat sich als einen aufschlureichen Wechsel der Perspektive
interpretieren. Die Beschreibung in den elektronischen Koordinaten k1 und k2
enspricht dem Bild zweier Elektronen, die dem Einzentrencoulombpotential des
Kernes entkommen. Die Beschreibung in Jakobikoordinaten [80] entspricht dagegen der Vorstellung eines Kerns (mit Impuls ,kr), der sich im 'molekularen'
Zweizentrencoulombpotential [82] des Elektronenpaares bewegt, das selbst wieder
mit Impuls kR aufbricht. Die vollstandige Messung des Endzustandsimpulsrau-

3 AUSGEWAHLTE
ERGEBNISSE
y momentum (a.u.)
0
5
10
ion momentum
15
20
11
25 0
(a)
10
20
30
electron momentum
40
50
(b)
0.2
0
-0.2
-0.2
0
0.2
ion z momentum (a.u.)
-0.2
0
0.2
electron z momentum (a.u.)
Abbildung 3: Impulsverteilungen von He2+-Ruckstoionen (links) und Elektronen
(rechts) fur + He ! He2+ + 2e, . Die Photonenenergie ist 1 eV uber de Doppelionisationsschwelle. Die z und y Komponenten der Impulse sind aufgetragen. Die
Polarisationsrichtung des linear polarisierten Lichtes ist z, die Ausbreitungsrichtung x. Es sind nur Ereignisse mit -0.1< krx;ex <0.1 a.u dargestellt. Der auere
Kreis zeigt den aufgrund der Photonenergie maximal moglichen Impuls der Teilchen, der innere Kreis in (a) zeigt den Ruckstoionenimpuls fur den Fall, da ein
Elektron die gesamte Energie aufnimmt (aus [24]).
mes mit COLTRIMS erlaubt erstmals den Doppelphotoionisationsproze auch
experimentell in Jakobikoordinaten zu untersuchen (Abbildung 4).
Eine theoretische Analyse der Doppelphotoionisation an der Schwelle in
Wannier-Theorie in vierter Ordnung [83, 80, 81, 24, 84, 85, 86] liefert zwei Losungen fur das Dreiteilchenkontinuum. Die beiden theoretisch moglichen Kontinuumzustande unterscheiden sich in der Quantenzahl K der Projektion des Drehimpulses auf die Achse, die beide Elektronen verbindet, d.h. auf die Richtung
von kR. Der Vergleich mit dem Experiment zeigt eindeutig, da fast ausschlielich der Zustand mit K=1 bevolkert wird (Abbildung 4). Nahe an der Schwelle
wird also das Ruckstoion mit groer Wahrscheinlichkeit in Richtung des elek-

3 AUSGEWAHLTE
ERGEBNISSE
12
trischen Feldvektors des Lichtes emittiert, das Elektronenpaar bricht senkrecht
hierzu auf. Dadurch entkommt der He2+ Kern dem von den beiden Elektronen gebildeten Zweizentrensattelpotential senkrecht zur interelektronischen Achse. Ein
sehr ahnliches Emissionsmuster zeigt sich auch noch 20 eV uber der Schwelle [28].
Die Impulsvektoren aller drei freien Teilchen nach der Doppelphotoionisation
liegen aufgrund der Impulserhaltung in einer Ebene (der kleine Photonenimpuls
wird hierbei vernachlassigt). Um die Korrelation der Elektronen aufgrund der
langreichweitigen Coulombwechselwirkung im Endzustand sichtbar zu machen,
ist es hilfreich, die Impulsverteilung der beiden Elektronen in dieser Ebene zu
betrachten und uber alle Orientierungen des Polarisationsvektors zu dieser Ebene zu integrieren (Abbildung 5). Die Elektron-Elektron-Abstoung fuhrt dazu,
da die beiden Elektronen bevorzugt in die entgegengesetzte Halbebene emittiert werden. Da beide Elektronen durch Absorbtion eines Photons aus dem
He-Grundzustand emittiert wurden, mu die Zweielektronenwellenfunktion im
Kontinuum 1P0-Symmetrie aufweisen. Als ungerade Wellenfunktion mu sie eine
Nullstelle fur k1 = ,k2, d.h. fur Emission beider Elektronen mit gleicher Energie in entgegengestzte Richtung haben (siehe hierzu auch [87, 70, 88, 89]). Fur 1
und 20 eV U berschuenergie ist diese Nullstelle deutlich sichtbar. Bei der niedrigen Photonenergie erstreckt sie sich auch auf ungleiche Energieaufteilung (siehe
hierzu auch [75, 90]).
Die volle komplizierte Struktur des Zweielektronenkontinuums wird sichtbar,
wenn man im Laborsystem die Emissionscharakteristik eines Elektrons fur festgehaltene Energie und Polarwinkel des anderen Elektrons zur Polarisationsachse
auftragt (siehe Abbildung 6). Die Verteilungen sind wieder von der ElektronElektron-Abstoung und den Symmetriebedingungen eines 1P0 Zustandes bestimmt. Der mit dem blauen Gitter angedeutete Kegel zeigt eine Knotenache
der Kontinuumswellenfunktion. Eine ausfuhrliche Diskussion dieser Auswahlregeln ndet sich in [88].
Mit den COLTRIMS-Messungen wurden erstmals solche Verteilungen fur alle
Energieaufteilungen zwischen den Elektronen und alle Polar- und Azimuthalwinkel zuganglich. Von groer Bedeutung fur den Vergleich mit den theoretischen
Vorhersagen ist, da nicht nur die Form, sondern auch der Absolutwert der vielfachdierentiellen Wirkungsquerschnitte gemessen wurde. In vielen Fallen unterscheiden sich die Rechnungen wesentlich mehr in der Absoluthohe als in der From
(siehe hierzu von theoretischer Seite [92, 93, 94]. und von experimenteller Seite
[90, 72]). Fur eine detaillierte Analyse der Verteilungen und Vergleiche mit theo-
y momentum (a.u.)
y momentum (a.u.)
y momentum (a.u.)

3 AUSGEWAHLTE
ERGEBNISSE
kr
13
kR
0.2
0
-0.2
ε
kr (K=0)
kR (K=0)
kr (K=1)
kR (K=1)
0.2
0
-0.2
0.2
0
-0.2
-0.2
0
0.2
z momentum (a.u.)
-0.2
0
0.2
z momentum (a.u.)
Abbildung 4: Vergleich der experimentellen Verteilungen der Jakobiimpulse
kr = k1 + k2 = ,krec und kR = 21 (k1 , k2) fur + He ! He2+ + 2e, , mit Eigenzustanden in Wannier-Theorie (in 4ter Ordung des Sattelpunktspotentiales)
[80, 81], mit der Projektion K=1 und K=0 des Gesamtdrehimpulses auf die interleketronische Achse kR. Die Polarisationsrichtung des Lichtes ist horizontal. Die
Kreise zeigen die aufgrund der Photonenergie maximal moglichen Impulse. Die
Photonenenergie ist 1 eV uber der Doppelionisationsschwelle von Helium (aus
[24]).
retischen Vorhersagen verweisen wir auf [90, 70, 71, 72, 73, 74, 75, 76, 77, 95, 96,
97, 93, 98, 92, 93, 94].
Wird die Doppelionisation des Heliums durch zirkular anstelle von linear po-

3 AUSGEWAHLTE
ERGEBNISSE
e2 momentum perpendicular to e1 (a.u.)
10
15
20
25
30
35
14
40 0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25
20 eV above threshold
1 eV above threshold
0.2
0
e1
e1
-0.2
node
-0.2
0
0.2
e2 momentum parallel to e1 (a.u.)
-1
0
1
e2 momentum parallel to e1 (a.u.)
Abbildung 5: Impulsverteilung der Elektronen in der Ebene, die durch die Impulse
der beiden Elektronen (und des Ions) aufgespannt wird fur + He ! He2+ +2e,.
Eines der Elektronen wird entlang der positiven x-Achse emittiert, die Impulsverteilung des zweiten ist aufgetragen. Die Daten sind uber alle Orientierungen
der Polarisationsachse integriert. Die Verteilung ist durch die Elektron-ElektronAbstoung und die 1P0-Symmetrie der Zweielektronenwellenfunktion (Nullstelle
bei k1 = ,k2) dominiert. Die aueren Kreise zeigen die aufgrund der Photonenergie maximal moglichen Impulse, die inneren Kreise zeigen die Impulse bei
gleicher Energieaufteilung zwischen den beiden Elektronen (aus [91]).
larisiertem Licht induziert, so andern sich die Impulsverteilungen erheblich. Zirkular polarisiertes Licht fuhrt eine Handigkeit in den Anfangszustand ein. Eine
Abhangikeit des dierentiellen Photoionisationsquerschnittes von der Chiralitat
des Lichtes (zirkularer Dichroismus) ist fur magnetische Festkorper und chirale Molekule seit langem bekannt (siehe etwa [99]). Im Falle Helium wird ein
solcher Eekt nur dadurch moglich, da im Endzustand zwei Elektronen unterschiedlicher Energie und die Photonenrichtung ein Dreibein mit unterscheidbaren
Schenkel aufspannen konnen und der Zustand somit eine denierte Handigkeit
haben kann [100, 101, 77, 30]. Hierzu mussen die Elektronen aufgrund ihrer Ener-

3 AUSGEWAHLTE
ERGEBNISSE
15
Abbildung 6: Emissionscharakteristik der Elektronen nach Photodoppelionisation
von Helium durch linear polarisiertes Licht bei einer Photonenenergie von 85 eV.
Aufgetragen ist der vierfachdierentielle Querschnitt d4=d#1d#2d1,2dE1. Das
erste Elektron wurde mit einer Energie von 0:1eV < E1 < 1eV untern einem
Polarwinkel von #1 (in Richtung des engen violetten Konus) emittiert. Der gelbe
Pfeil zeigt die Richtung der Polarisation. Der durch das blaue Netz angedeutete
Konus zeigt die Flache einer Nullstelle bei #1 = ,#2, die fur gleiche Energieaufteilung aus der 1P0-Symmetrie des Zustandes resultiert (aus [91]).
gie unterscheidbar sein und die Photonenrichtung darf nicht in einer Ebene mit
den beiden Elektronenimpulsvektoren liegen. Abbildung 7 zeigt die Starke dieses Eektes. Die Symmetrie der Impulsverteilungen gegenuber Spiegelung an der
x-Achse, die fur linear polarisiertes Licht in Abbildung 5 sichtbar ist, wird gebrochen. Eine Inversion des Drehsinnes des Lichtes fuhrt zu einer Spiegelung der
Impulsverteilungen.
Fur linear polarisiertes Licht, wo die Form der Verteilungen oft schon aus
der Symmetrie des 1P0-Endzustandes bestimmt ist, konnen die Daten auch
in der absoluten Hohe von aufwendigen Close-Coupling-Rechnungen befriedigend beschrieben werden [102, 29]. Ansatze innerhalb des Wannier-Modells
[83, 80, 81, 24, 84, 85, 86] oder solche, die das Dipolmatrixelement direkt berechnen [90, 95, 96, 97, 93], beschreiben in vielen Fallen ebenfalls die Daten sehr
gut. Fur zirkular polarisiertes Licht hingegen ist die U bereinstimmung zwischen
Theorie und Experiment jedoch so schlecht [30], da selbst das scheinbar so einfache Probleme der Emission von zwei Elektronen durch Wechselwirkung mit
einem Photon heute noch nicht als gelost betrachtet werden kann. Mit COLTRIMS steht ein leistungsfahiges Verfahren zur Verfugung, den Fortschritt auf

3 AUSGEWAHLTE
ERGEBNISSE
electron2 σ
1
16
electron2 σ
+
-
ky2 [a.u.]
0.5
k1
0
k1
-0.5
max
max
k2
-1
-1
-0.5
k2
photon
0
kx2 [a.u.]
0.5
1
-1
-0.5
photon
0
0.5
1
kx2 [a.u.]
Abbildung 7: Emissionscharakteristik der Elektronen nach Photodoppelionisation von Helium durch rechts bzw. links zirkular polarisiertes Licht bei einer
Photonenenergie von 99 eV. Gezeigt ist die Impulsebene senkrecht zur Ausbreitungsrichtung des Lichtes. Der Impulsvektor k1 des schnelleren der beiden Elektronen ist entlang der x-Achse durch den Pfeil angedeutet. Die Impulsverteilung
des langsameren Elektron ist aufgetragen. Die Kreise zeigen die aufgrund der
Photonenergie maximal moglichen Impulse des langsamen Elektrons.
diesem Gebiet durch Experimente weiter voranzutreiben. Insbesondere Mehrelektronenubergange in Molekulen [31, 103], bei hoheren Photonenenergien, bei denen
andere Reaktionsmechanismen dominieren, sowie Untersuchungen mit zirkular
polarisiertem Licht und zu Mehrelektronenubergangen nach Comptonstreuung
bieten ein vielversprechendes Feld fur die Zukunft.
3.3 Wechselwirkung mit geladenen Teilchen
Die Untersuchungen von Ionisationsprozessen durch Ionensto sind komplementar zu den oben geschilderten Untersuchungen mit Photonen. Wahrend der
Photoeekt fast ausschlielich Dipolubergange induziert, steht in einem Ionensto
sehr viel Drehimpuls aus der Projektilbewegung zur Verfugung. Ein interessantes

3 AUSGEWAHLTE
ERGEBNISSE
17
Bindeglied von seiten der Photoionisation bietet hier die Comptonstreuung, die
ebenfalls im wesentlichen hohere Multipolubergange induziert [104, 105, 106, 107].
Von der Ionenstoseite bildet der Limes hoher Geschwindigkeiten einen U bergang zur Photoionisation. Schon 1934 haben Weizsacker und Williams gezeigt
[108, 109], da die Ionisation durch geladene Teilchen bei hohen Geschwindigkeiten durch die Wechselwirkung mit einem Feld virtueller Photonen beschrieben
werden kann. In COLTRIMS Experimenten bei GSI konnte dies eindrucksvoll de-
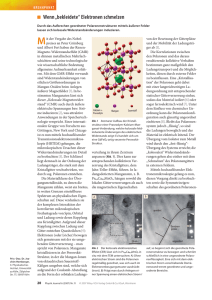
Abbildung 8: Projektion der Impulsverteilungen von Elektronen und He1+-Ruckstoionen aus der Reaktion 1 GeV/u U92+ + He ! He1+ + e, + U 92+ auf die
Streuebene deniert durch Strahl und Ruckstoion. Die x-Achse ist parallel zum
Projektilimpuls (in postiver x-Richtung), die y-Achse parallel zum Ruckstoionentransversalimpuls im Endzustand. Die Farbskala zeigt den Logarithmus des
doppeltdierentiellen Wirkungsqueschnitts d2=(dkx dkk) (aus [4]).
monstriert werden [7, 110, 6, 5, 4, 111, 112, 113]. Fur 1 GeV U92+ ! He wurden
fur die Einfachionisation die Impulse der Elektronen in Koinzidenz mit denen der
Ruckstoionen gemessen. Unter Ausnutzung des Impuls- und Energieerhaltungssatzes lat sich damit auch der Impulsubertrag auf das Projektil bestimmen.

3 AUSGEWAHLTE
ERGEBNISSE
18
Die Experimente zeigen, da das relativistische Projektil nur Energie, aber, wie
ein Photon, fast keinen Impuls ubertragt. Das Atom fragmentiert hauptsachlich
senkrecht zur Strahlachse. Ruckstoion und Elektron werden mit entgegengesetzt gleichem Impuls emittiert. Dieses Fragmentationsmuster kann erfolgreich
im Modell der Absorbtion eines Photons aus dem virtuellen Photonenfeld des
Projektils beschrieben werden [4, 113, 114]. Eine vollstandige Fragmentation eines Mehrelektronentargets im kurzen (10,18 s) und intensiven (1019 W/cm2) Feld
virtueller Photonen bietet einen neuartigen und vielversprechenden Zugang zu
einer Impulspektroskopie von korrelierten, gebundenen Mehrelektronensystemen
[4, 5, 113, 114].
kx (a.u.)
0
1
50
100
150
200
250
0 25 50 75 100 125 150 175 2000
recoil
50 100 150 200 250 300 350
electron
0
projectile
-1
-1
0
1
kzrec (a.u.)
-1
0
1
kze (a.u.)
-1
0
1
kzpro (a.u.)
Abbildung 9: Projektion des Impulsubertrages auf Ruckstoion, Elektron und
Projektil, auf die Ebene, die vom Projektilstrahl und dem gestreuten Projektil deniert wird, fur die Reaktion 1 MeV/u p + He ! He1+ + e, + p. Die +kz
Achse ist parallel zur Strahlrichtung, das Projektil wird in positive kx Richtung
nach oben gestreut. Die Farbskale zeigt (linear) den doppeldierentiellen Wirkungsquerschnitt d2=(dkxdkz ). Der Kreisauschnitt im mittleren Bild, zeigt die
Impulse eines binaren Projektil Elektron Stoes (aus [3]).
Bei niedrig geladenen Projektilen mittlerer Energie dominieren hingegen vollig
andere Impulaustauschprozesse und Ionisationsmechanismen. Solche Untersuchungen wurden mit COLTRIMS am van-de-Gra-Beschleuniger des Instituts
fur Kernphysik der Universitat Frankfurt druchgefuhrt [40, 15, 12, 2, 19, 14, 3,

3 AUSGEWAHLTE
ERGEBNISSE
19
54, 55]. Sie wurden erganzt durch das erste Experiment zum Impulsaustausch
in (Antiproton!He)-Stoen am CERN [8, 115]. Abbildung 9 zeigt, da bei
(1 MeV p! He)-Stoen die Einfachionisation durch eine Streuung des Projektils
am Elektron und am Kern dominiert wird. Elektron und Ion erhalten ihren Transversalnimpuls im Endkanal aus einem Impulstransfer vom Projektil. In longitudinaler Richtung dagegen wird sowohl von Protonen als auch von Antiprotonen
praktisch kein Impuls auf das Ion ubertragen [2, 3, 115, 8].
Durch ahnliche COLTRIMS-Impulsraummessungen konnten bei vergleichbaren Projektilgeschwindigkeiten zwei interessante dynamisch korrelierte Zweilektronenprozesse aufgeklart werden [15, 17, 18, 19, 55, 116]. Hierbei konnte die
Streuung zweier Elektronen, die entweder je eines am Projektil und am Target
[15, 17, 18] oder im anderen Fall beide am Target gebunden waren, direkt beobachtet werden. Der zweite Proze einer Elektron-Elektron-Streuung in einem
Atom, der danach zum Einfang eines Elektrons in Projektil und zur Emisssion
des anderen fuhrt, wird von keiner heute existierenden Theorie hinreichend beschrieben. Der totale Querschnitt fur diesen Proze wird um eine Groenordnung
unterschatzt und die Impulsverteilungen werden ungenugend wiedergegeben.
Geht man schlielich zu Projektilgeschwindigkeiten, die kleiner sind als die
mittlere Geschwindigkeit der gebundenen Targetelektronen, so wird die Ionisation durch einen binaren Impulsubertrag zwischen Projektil und Targetelektron
sehr unwahrscheinlich, bzw. kinematisch unmoglich. Entsprechend fallt der Ionisationsquerschnitt stark ab. Bei diesen Geschwindigkeiten dominiert der Einfang eines Elektrons in einen gebundenen Zustand des Projektils bei weitem
uber die Elektronenemission ins Kontinuum. Dieser unwahrscheinliche Proze der
Ionisation bei langsamen Stoen konnte mit COLTRIMS erstmals kinematisch
vollstandig untersucht werden. Abbildung 10 zeigt die Impulsaustauschprozesse
am Beispiel der Reaktion 15keV p + He ! p + He1+ + e,.
In diesen langsamen Stoen wird fast kein Impuls auf die Elektronen ubertragen, dagegen dominiert der Impulsaustausch zwischen Projektil und Targetkern bei weitem. Da die Projektilgeschwindigkeit kleiner oder vergleichbar mit
der mittleren Elektronengeschwindigkeit ist, hat die elektronische Wellenfunktion hinreichend Zeit, sich auf das zeitabhangige Zweizentrenpotential von Projektil und Target einzustellen. Fur kurze Zeit wirkt das Elektron als Bindeglied zwischen den beiden Kernen und hilft so, Vorwartsimpuls vom Projektil
auf den Targetkern zu ubertragen. Der Longitudinalimpuls, den das Ruckstoion aufnimmt, wird entsprechend dem Projektil entzogen. Das Elektron rela-

3 AUSGEWAHLTE
ERGEBNISSE
20
40
60
80
100 120 0
100
200
300
400
500
600
0
20
40
60
80
100 120
kx (a.u.)
0
20
5
recoil
electron
projectile
0
-5
-2
0
2
kzrec (a.u.)
-2
0
2
kze (a.u.)
-2
0
2
kzpro (a.u.)
Abbildung 10: 15 keV/u p+He ! He1+ +e, +p. Projektion des Impulsubertrages
auf Ruckstoion, Elektron und Projektil, auf die Ebene, die vom Projektilstrahl
und dem gestreuten Ruckstoion deniert wird. Die +kz Achse ist parallel zur
Strahlrichtung, das Ruckstoion wird in negative x Richtung gestreut. Die Farbskale zeigt (linear) den doppeldierentiellen Wirkungsquerschnitt d2=(dkxdkz )
(nach [117]).
xiert dann in den meisten Fallen in einen gebundenen Zustand von Projektil
oder Target und "strandet\[118, 119, 120] nur in seltenen Fallen im Kontinuum. Die COLTRIMS-Messung gibt nun erstmals Abbilder des Quadrates der
Wellenfunktion dieser Kontinuumselektronen im Impulsraum fur gleichzeitig gemessene Streuebene und Stoparameter der Kernbewegung [1]. Man ndet, da

3 AUSGEWAHLTE
ERGEBNISSE
21
die Elektronen hauptsachlich in der Streubene, die durch die Strahlrichtung und
den Impuls des Ruckstoiones im Endzustand deniert ist, emittiert werden. Abbildung 11 zeigt die Impulsverteilungen der Elektronen in der Streuebene der
Kerne fur Einfachionisation von Helium durch 5-15 keV Protonen. Die Projektilbewegung verlauft von links nach rechts, das Projektil wird nach oben gestreut,
das Ruckstoion entsprechend nach unten emittiert. Aufgetragen sind auf die
Projektilgeschwindigkeit normierte Elektronengeschwindigkeiten. Targetzentrierte Elektronen nden sich bei (0,0), Elektronen, die sich mit dem Projektil mitbewegen, bei (1,0), und der Sattelpunkt des Zweizentrenpotentiales bendet sich
bei (0.5,0). Man ndet eine starke Stoparameterabhangigkeit der Elektronenemission. Bei engen Stoen werden im Wesentlichen targetzentrierte Elektronen
emittiert. Im Bereich mittlerer Stoparameter, die den groten Beitrag zum totalen Ionisationsquerschnitt liefern, zeigt sich eine hufeisenformige Verteilung mit
einem Minimum auf dem Sattel. Bei groen Stoparametern ndet sich ein Maximum der Verteilung auf dem Sattel. Die Verteilungen zeigen zudem eine sehr
starke Abhangigkeit von der Projektilgeschwindigkeit. Zwischen 5 und 15 keV
oszilliert die Elektronenimpulsverteilung von Emission in Richtung des gestreuten Projektils uber eine symmetrische hufeisenformige Verteilung bei 10 keV zu
einer Emission weg vom gestreuten Projektil. Macek und Ovchinnikov haben
als Erklarung hierfur eine Interferenz zwischen zwei Serien von quasimolekularen
U bergangen vorgeschlagen. Eine dieser Serien hat als ersten Schritt eine Kopplung mit Drehimpuls Null, die zweite eine mit Drehimpulsubertrag h [121].
10 keV p-He
p⊥rec=1-5 a.u.
10 keV p-He
p⊥rec=0.2-1 a.u.
10 keV p-He
1
vze/vp
(c)
(b)
(a)

3 AUSGEWAHLTE
ERGEBNISSE
0.5
0
-0.5
0.5
0
-0.5
0.5
0
-0.5
0.5
p⊥rec=5-10 a.u.
0
18
16
14
12
10
8
6
4
2
0
50
40
30
20
10
0
20
18
16
14
12
10
8
6
4
2
0
0.5
0
-0.5
0.5
0
-0.5
0.5
0
-0.5
5 keV
10 keV p-He
0
15 keV p-He
-0.5
0.5
(d)
(e)
(f)
1
vxe/vp
14
12
10
8
6
4
2
0
50
40
30
20
10
0
80
70
60
50
40
30
20
10
0
22
Abbildung 11: Geschwindigkeitsverteilungen von Elektronen aus der Reaktion 5 , 15keV p + He ! p + He1+ + e,. Dagestellt ist die Streuebene der beiden Kerne. Das Projektil bewegt sich in positive z-Richtung und wird nach
oben gestreut, das He1+-Ruckstoion entsprechend nach unten emittiert. Die Geschwindigkeiten der Elektronen wurden auf die jeweilige Projektilgeschwindigkeit normiert. Elektronen, die am Target ruhen, nden sich entsprechend bei
(0,0), solche die mit dem Projektil mitiegen bei (1,0). Der Sattelpunkt des
(p-He)1+-Zweizentrenpotentials bendet sich bei (0.5,0). Die linke Spalte zeigt
die Stoparameterabhangigkeit bei 10 keV, die rechte Spalte zeigt die Geschwindigkeitsabhangigkeit. In der linken Spalte nimmt der Stoparameter von oben
nach unten ab. Der zugehorige transversale Impulsubertrag ist im Bild notiert.
In der rechten Spalte liegt fur 10 keV der Transversalimpulsubertrag im Intervall
k?rec = 1-5 a.u.. Fur die anderen Projektilgeschindigkeiten wurden die Grenzen
des Intervalls mit 1/vpro skaliert, um in etwa den gleichen Stoparameterbereich
abzudecken. Abbildung (b) und (e) sind identisch (teilweise aus [1]).
-0.5
vxe/vp
vxe/vp
vxe/vp
vxe/vp
vxe/vp
vxe/vp
4 AUSBLICK
23
4 Ausblick
Vieldimensionale Impulsraumbilder atomarer Reaktionen, die mit COLTRIMS
erstmalig zuganglich wurden, bieten einen sehr direkten Zugang zur Dynamik
von Mehrteilchenprozessen. Die Technik liefert in einem doppelten Sinne kinematisch vollstandige Abbilder des Endzustandes der untersuchten Reaktion. Einmal
werden, wenn ein Ionisationsereignis registriert wird, die Impulse aller Teilchen
bestimmt. Mit Ausnahme des Spins wird dadurch uber keine Observable integriert. Zum anderen wird der vollstandige Vielteilchenimpulsraum abgedeckt,
d.h. es werden nicht nur in einem kleine Ausschnitt alle Teilchen beobachtet,
sondern alle Richtungen und alle Impulse aller Teilchen gleichzeitig detektiert

(4-Raumwinkel). Dadurch erhalt man einen vollstandigen Uberblick
uber die
Reaktion. Nicht der Experimentator entscheidet vor dem Experiment welchen
Ausschnitt der Reaktion er betrachtet, sondern er beobachtet den Endzustandsimpulsraum als Ganzes und der physikalische Proze bestimmt uber die Wahrscheinlichkeitsverteilung der Ereignisse in diesem Raum. Damit lassen sich zum
Einen theoretische Vorhersagen auf breiter Basis prazise testen. Gleichzeitig kann
man aber auch nach dem Experiment am Rechner an den Daten Koordinatentransformationen und Integrationen uber beliebige Unterraume durchfuhren, um
nach Koordinatenystemen und Perspektiven auf den Proze suchen, unter denen
die zugrundeliegende Physik moglichst deutlich und verstandlich wird. Fur die
Separation von Compton- und Photoeekt (Abbildung 2) sowie zur Trennung
von Elektron-Elektron-Streuungen [15, 17, 19] genugt es z.B. nur die Impulsverteilung der Ruckstoionen zu betrachten. Fur Photodoppelionisation, um ein
anderes Beispiel zu nennen, ist es aufschlureich, den Proze in (kollektiven) Jakobikoordinaten zu betrachten. Fur Ionisation durch geladene Teilchen ist, wie
gezeigt, eine Betrachtung in karthesischen Impulskoordinaten (anstelle der sonst
ublichen winkeldierentiellen Energieverteilungen) hilfreich.
Um diese Experimente moglich zu machen, wurden technisch wie konzeptionell fur die Atomphysik neue Wege beschritten. Eine Kombination aus lokalisierten kalten dunnen Gastargets, elektrischen und magnetischen Abbildungsfeldern
und schnellen, multihitfahigen Detektoren bilden ein Vielteilchenimpulsmikroskop, das bisher unerreichte Auosung mit 4-Raumwinkel fur den Teilchennachweis kombiniert. Die weiteren Anwendungen ebenso wie die naheliegenden Weiterentwicklungen dieser Technik sind vielfaltig. Zahlreiche korrelierte Zwei- und
Mehrelektronenprozesse wie etwa resonanter Einfang und Ionisation (RTE), Doppelionisation nach Comptonstreuung, Doppelelektronentransfer im Limit hoher
LITERATUR
24
Geschwindigkeiten, Vielfachionisation in relativistischen Stoen und Mehrfachionisation in kurzen, intensiven Laserpulsen konnen erstmals vielfachdierentiell
untersucht werden. Die Untersuchung von Molekulfragmentation durch langsame
hochgeladene Ionen oder durch Synchrotronstrahlung bietet eine Verbindung zur
chemischen Dynamik und zur Strukturuntersuchungen. Die Verwendung von lasergekuhlten und laserpraparierten Targets anstelle von U beschallstrahlen wird
nicht nur einen groen Fortschritt im Auosungsvermogen bringen, sondern auch
spinausgerichtete und vielfachangeregte Target zuganglich machen. Eine Implementierung in Speicherringe ist bei GSI, am TSR und am Cryring in Stockholm
in Arbeit. Die koinzidente Messung von Elektronen- und Ruckstoionenimpulsen
nach dem -Zerfall lat extrem genau Messungen der Winkelkorrelation zwischen
Neutrino und Elektron zu und erlaubt fur die Zukunft vielleicht eine Messung
der Neutrinomasse fur bestimmte einzelne Zerfalle. Eine U bertragung der Abbildungstechnik auf die Elektronen- und Ionenemission von Festkorperoberachen
ist moglich. Das Potential dieser neuen Impulsraummikroskope reicht damit weit
uber die atomare Stophysik in andere Zweige von Physik, Chemie und anderen
Naturwissenschaften.
Literatur
[1] R. Dorner, H. Khemliche, M.H. Prior, C.L. Cocke, J.A. Gary, R.E. Olson,
V. Mergel, J. Ullrich und H. Schmidt-Bocking. Phys. Rev. Lett, 77:4520,
1996.
[2] R. Dorner, V. Mergel, L. Zhaoyuan, J. Ullrich, L. Spielberger, R.E. Olson,
and H. Schmidt-Bocking. J. Phys, B28:435, 1995.
[3] Th. Weber. Diplomarbeti, Universitat Frankfurt 1998.
[4] R. Moshammer, J. Ullrich, W. Schmitt, H. Kollmus, A. Cassimi, R. Dorner,
R. Dreizler, O. Jagutzki, S. Keller, H.-J. Ludde, R. Mann, V. Mergel, R.E.
Olson, T. Prinz, H.Schmidt-Bocking und L Spielberger. Phys. Rev. Lett,
79:3621, 1997.
[5] R. Moshammer, J. Ullrich, H. Kollmus, W. Schmitt, M. Unverzagt, O. Jagutzki, V. Mergel, H. Schmidt-Bocking, R. Mann, C.J. Woods und R.E.
Olson. Phys. Rev. Lett, 77:1242, 1996.
LITERATUR
25
[6] M. Unverzagt, R. Moshammer, W. Schmitt, R.E. Olson, P. Jardin, V. Mergel, J. Ullrich und H. Schmidt-Bocking. Phys. Rev. Lett, 76:1043, 1996.
[7] R. Moshammer, J. Ullrich, M. Unverzagt, W. Schmidt, P. Jardin, R.E.
Olson, R. Mann, R. Dorner, V. Mergel, U. Buck und H. Schmidt-Bocking.
Phys. Rev. Lett, 73:3371, 1994.
[8] Kh. Khayyat, Th. Weber, R. Dorner, M. Achler, V. Mergel, L. Spielberger,
O. Jagutzki, U. Meyer, J. Ullrich, R. Moshammer, H. Knudsen, U. Mikkelsen, P. Aggerholm, V.D. Roderiguez, S.F.C. O'Rourke, S.P. Moeller, R.E.
Olson, P. Fainstein, J.H. McGuire und H. Schmidt-Bcking. Phys. Rev. Lett,
:eingereicht zur Veroentlichung, 1998.
[9] O. Jagutzki. Dissertation, Universitat Frankfurt 1994.
[10] O. Jagutzki, L. Spielberger, R. Dorner, S. Nuttgens, V. Mergel, H. SchmidtBocking, J. Ullrich, R.E. Olson und U. Buck. Zeitschrift fur Physik, D36:5,
1996.
[11] L. Spielberger, O. Jagutzki, R. Dorner, K. Froschauer, A. Gensmantel,
H. Schmidt-Bocking, J. Ullrich und U. Buck. In C T. Whelan et.al., editor,
,,(e,2e) and related processes", pages 119{129. Kluwer Academic Publishers, 1993.
[12] V. Mergel, R. Dorner, J. Ullrich, O. Jagutzki, S. Lencinas, S. Nuttgens,
L. Spielberger, M. Unverzagt, C.L. Cocke, R.E. Olson, M. Schulz, U. Buck,
E. Zanger, W. Theisinger, M. Isser, S. Geis und H. Schmidt-Bocking. Phys.
Rev. Lett, 74, 1995.
[13] V. Mergel, R. Dorner, J. Ullrich, O. Jagutzki, S. Lencinas, S. Nuttgens,
L. Spielberger, M. Unverzagt, C.L. Cocke, R.E. Olson, M. Schulz, U. Buck
und H. Schmidt-Bocking. Nucl. Instr. Meth., B96:593, 1995.
[14] R. Dorner, V. Mergel, L. Spielberger, O. Jagutzki, H. Schmidt-Bocking und
J. Ullrich. Phys. Rev., A57:312, 1998.
[15] R. Dorner, V. Mergel, R. Ali, U. Buck, C.L. Cocke, K. Froschauer, O. Jagutzki, S. Lencinas, W.E. Meyerhof, S. Nuttgens, R.E. Olson, H. SchmidtBocking, L. Spielberger, K. Tokesi, J. Ullrich, M. Unverzagt W. Wu. Phys.
Rev. Lett, 72:3166, 1994.
LITERATUR
26
[16] R. Dorner, V. Mergel, L. Spielberger, O. Jagutzki, S. Nuttgens, M. Unverzagt und H. Schmidt-Bocking. Nucl. Instr. Meth., B98:367, 1995.
[17] W. Wu, R. Ali, C.L. Cocke, V. Frohne, J.P. Giese, B. Walch, K.L. Wong,
R. Dorner, V. Mergel, H. Schmidt-Bocking und W.E. Meyerhof. Phys. Rev.
Lett, 72:3170, 1994.
[18] W. Wu, K.L. Wong, E.C. Montenegro, R. Ali, C.Y Chen, C.L Cocke,
R. Dorner, V. Frohne, J.P Giese, V. Mergel, W.E. Meyerhof, M. Raphaelian, H. Schmidt-Bocking und B. Walch. Phys. Rev., A55:2771, 1997.
[19] V. Mergel, R. Dorner, M. Achler, Kh. Khayyat, S. Lencinas, J. Euler,
O. Jagutzki, S. Nuttgens, M. Unverzagt, L. Spielberger, W. Wu, R. Ali,
J. Ullrich, H. Cederquist, A. Salin, R.E. Olson, Dz. Belkic, C.L. Cocke und
H. Schmidt-Bocking. Phys. Rev. Lett, 79:387, 1997.
[20] L. Spielberger. Dissertation, Universitat Frankfurt, 1997. ISBN 3{8265{
2607{4. Shaker Verlag, Aachen, 1997.
[21] L. Spielberger, O. Jagutzki, R. Dorner, J. Ullrich, U. Meyer, V. Mergel,
M. Unverzagt, M. Damrau, T. Vogt, I. Ali, Kh. Khayyat, D. Bahr, H.G.
Schmidt, R. Frahm und H. Schmidt-Bocking. Phys. Rev. Lett., 74:4615,
1995.
[22] L. Spielberger, O. Jagutzki, B. Krassig, U. Meyer, Kh. Khayyat, V. Mergel,
Th. Tschentscher, Th. Buslaps, H. Brauning, R. Dorner, T. Vogt, M. Achler,
J. Ullrich, D.S. Gemmel und H. Schmidt-Bocking. Phys. Rev. Lett., 76:4685,
1996.
[23] A. Muthig und L. Spielberger Private Mitteilung.
[24] R. Dorner, J. Feagin, C.L. Cocke, H. Brauning, O. Jagutzki, M. Jung,
E.P. Kanter, H. Khemliche, S. Kravis, V. Mergel, M.H. Prior, H. SchmidtBocking, L. Spielberger, J. Ullrich, M. Unverzagt und T. Vogt. Phys. Rev.
Lett., 77:1024, 1996. see also erratum in Phys. Rev. Lett. 78. 2031 (1997).
[25] R. Dorner, T. Vogt, V. Mergel, H. Khemliche, S. Kravis, C.L. Cocke, J. Ullrich, M. Unverzagt, L. Spielberger, M. Damrau, O. Jagutzki, I. Ali, B. Weaver, K. Ullmann, C.C. Hsu, M. Jung, E.P. Kanter, B. Sonntag, M.H. Prior,
E. Rotenberg, J. Denlinger, T. Warwick, S.T. Manson und H. SchmidtBocking. Phys. Rev. Lett., 76:2654, 1996.
LITERATUR
27
[26] T. Vogt. Diplomarbeit, Universitat Frankfurt, 1995.
[27] T. Vogt, R. Dorner, O. Jagutzki, C.L. Cocke, J. Feagin, M. Jung, E.P. Kanter, H. Khemliche, S. Kravis, V. Mergel, L. Spielberger, J. Ullrich, M. Unverzagt, H. Brauning, U. Meyer und H. Schmidt-Bocking. in: Proceedings
of the Euroconference Ionization and Coincidence Spectroscopy ed.: C.T.
Whelan and H.R.J. Walters, Plenum, 1997.
[28] H.P Brauning, R. Dorner, C.L. Cocke, M.H. Prior, B. Krassig, A. BrauningDemian, K. Carnes, S. Dreuil, V. Mergel, P. Richard, J. Ullrich und
H. Schmidt-Bocking. J. Phys., B30:L649, 1997.
[29] H.P Brauning, R. Dorner, C.L. Cocke, M.H. Prior, B. Krassig, A.S. Kheifets, I. Bray, A. Brauning-Demian, K. Carnes, S. Dreuil, V. Mergel,
P. Richard, J. Ullrich und H. Schmidt-Bocking. J. Phys., eingereicht zur
Veroentlichung, 1998.
[30] V.Mergel, M. Achler, R. Dorner, Kh. Khayyat, T. Kambara, Y. Awaya,
V. Zoran, B. Nystrom, L.Spielberger, J.H. McGuire, J. Feagin, J. Berakdar
und H. Schmidt-Bocking. Phys. Rev. Lett., :im Druck, 1998.
[31] R. Dorner, H. Brauning, O. Jagutzki, V. Mergel, M. Achler, R. Moshammer,
J. Feagin, A. Brauning-Demian, L. Spielberger, J.H. McGuire, M.H. Prior,
N. Berrah, J. Bozek, C.L. Cocke und H. Schmidt-Bocking. Phys. Rev. Lett.,
eingereicht zur Veroentlichung, 1998.
[32] R. Dorner, V. Mergel, O. Jagutzki, L. Spielberger, J. Ullrich, R. Moshammer, und H. Schmidt-Bocking. Physics Reports, auf dem Wege der
Veroentlichung, 1998.
[33] J.W. McConkey, A. Crowe und M.A. Hender. Phys. Rev. Lett, 29:1, 1972.
[34] L.J. Puckett und D.W. Martin. Phys. Rev., A5:1432, 1976.
[35] W. Steckelmacher, R. Strong und M.W. Lucas. J. Phys, B11:1553, 1978.
[36] J.C. Levin, R.T. Short, O.S. Elston, J.P. Gibbons, I.A. Sellin und
H. Schmidt-Bocking. Phys. Rev., A36:1649, 1987.
[37] J.P. Grandin, D. Hennecart, X. Husson, D. Lecler, I. Lesteven-Vaisse und
D. Lis. Europhys. Lett., 6:683, 1988.
LITERATUR
28
[38] C.E. Gonzales Lepra, M. Breinig, J. Burgdorfer, R. DeSerio, S.B. Elston,
J.P. Gibbons, H.P. Hulskotter, L.Liljeby, R.T. Short und C.R. Vane. Nucl.
Instr. Meth., B24/25:316, 1987.
[39] J. Ullrich und H. Schmidt-Bocking. Physics Letters A, 125:193, 1987.
[40] R. Dorner, J. Ullrich, H. Schmidt-Bocking und R.E. Olson. Phys. Rev. Lett,
63:147, 1989.
[41] R. Dorner, J. Ullrich, O. Jagutzki, S. Lencinas, A. Gensmantel und
H. Schmidt-Bocking. In W.R. MacGillivray, I.E. McCarthy und M.C. Standage, editors, Electronic and Atomic Collisions, Invited Papers of the ICPEAC XVII, Seite 351. Adam Hilger, 1991.
[42] R. Dorner, J. Ullrich, O. Jagutzki, S. Lencinas, H. Schmidt-Bocking und
R.E. Olson. Z.Phys., D21:57, 1991.
[43] R. Dorner, J. Ullrich, R.E. Olson, O. Jagutzki und H. Schmidt-Bocking.
Phys. Rev., A47:3845, 1993.
[44] J. Ullrich, R. Dorner, R.E. Olson und H. Schmidt-Bocking. In A. Dalgarno,
R.S. Freund, P.M. Koch, M.S. Lubell und T.B. Lucatorto, editors, The
Physics of Electronic and Atomic Collisions, Invited Papers of the ICPEAC
XVI, Seite 372. AIP, 1989.
[45] J. Ullrich, R. Dorner, S. Lencinas, O. Jagutzki, H. Schmidt-Bocking und
U. Buck. Nucl. Instr. Meth., B61:415, 1991.
[46] J. Ullrich, R. Dorner, O. Jagutzki, S. Lencinas, A. Gensmantel, E. Forberich, K. Ullmann, R.E. Olson und H. Schmidt-Bocking. In SHIM, Book of
Invited Talks, 1992.
[47] C. Meng, R.E. Olson, R. Dorner, J.Ullrich und H. Schmidt-Bocking. J.
Phys, B26:3387, 1993.
[48] A. Gensmantel, J. Ullrich, R. Dorner, R.E. Olson, K. Ullmann, E. Forberich,
S. Lencinas und H. Schmidt-Bocking. Phys. Rev., A45:4572, 1992.
[49] E. Forberich, R. Dorner, J. Ullrich, R.E. Olson, K. Ullmann und A. Gensmantel. J. Phys, B24:3613, 1991.
LITERATUR
29
[50] S. Lencinas, J. Ullrich, R. Dorner, R.E. Olson W. Wol, L. Spielberger,
S. Hagmann, M. Horbatsch, C.L. Cocke und H. Schmidt-Bocking. J. Phys,
B27:287, 1994.
[51] R. Ali, V. Frohne, C.L. Cocke, M. Stockli, S. Cheng und M.L.A. Raphaelian.
Phys. Rev. Lett, 69:2491, 1992.
[52] V. Frohne, S. Cheng, R. Ali, M. Raphaelian, C.L. Cocke und R.E. Olson.
Phys. Rev. Lett, 71:696, 1993.
[53] P. Jardin, J.P. Grandin, A. Cassimi, J.P. Lemoigne, A. Gosseling, X. Husson, D. Hennecart und A. Lepoutre. In AIP Conference Proceedings No
274, Seite 291. AIP, 1993.
[54] V. Mergel. Diplomarbeit Universitat Frankfurt, 1994.
[55] V. Mergel. Dissertation, Universitat Frankfurt. ISBN 3{8265{2067{X. Shaker Verlag, 1996.
[56] R. Moshammer, M. Unverzagt, W. Schmitt, J. Ullrich und H. SchmidtBocking. Nucl. Instr. Meth., B 108:425, 1996.
[57] H.Kollmus, W. Schmitt, R. Moshammer, M. Unverzagt und J. Ullrich. Nucl.
Instr. Meth., B124:377, 1987.
[58] O. Jagutzki. private communication, .
[59] V. Mergel, O. Jagutzki, L. Spielberger, K. Ullmann-Peger, R. Dorner und
H. Schmidt-Bocking. Conference Proceedings of the MRS 1997, , 1997.
[60] A. Einstein. Ann. d. Phys., 17:132, 1905.
[61] A.H. Compton. Phys. Rev., 21:484, 1923.
[62] J.Z. Tang und I. Shimamura. Phys. Rev., A52:1, 1995.
[63] M. Pont und R. Shakeshaft. Phys. Rev., A51:494, 1995.
[64] K.W. Meyer, J.L. Bohn, C.H. Green und B.D. Esry. J. Phys., B30:L641,
1997.
[65] A. Kheifets und I. Bray. Phys. Rev., A57:2590, 1998.
LITERATUR
30
[66] F.W. Byron und C.J. Joachain. Phys. Rev., 164:1, 1967.
[67] L.R. Andersson und J. Burgdorfer. Phys. Rev., A50:R2810, 1994.
[68] T. Suric, K. Pisk, B.A. Logan und R.H. Pratt. Phys. Rev. Lett., 73:790,
1994.
[69] M.A. Kornberg und J.E. Miraglia. Phys. Rev., A53:R3709, 1996.
[70] O. Schwarzkopf, B. Krassig, J. Elmiger und V. Schmidt. Phys. Rev. Lett.,
70:3008, 1993.
[71] O. Schwarzkopf, B. Krassig, V. Schmidt, F. Maulbetsch und J. Briggs. J.
Phys., B27:L347{50, 1994.
[72] O. Schwarzkopf und V. Schmidt. J. Phys., B28:2847, 1995.
[73] A. Huetz, P. Lablanquie, L. Andric, P. Selles und J. Mazeau. J. Phys.,
B27:L13, 1994.
[74] G. Dawber, L. Avaldi, A.G. McConkey, H. Rojas, M.A. MacDonald und
G.C. King. J. Phys., B28:L271, 1995.
[75] P. Lablanquie, J. Mazeau, L. Andric, P. Selles und A. Huetz. Phys. Rev.
Lett., 74:2192, 1995.
[76] J. Viefhaus, L. Avaldi, F. Heiser, R. Hentges, O. Gessner, A. Rudel, M. Wiedenhoft, K. Wielczek und U. Becker. J. Phys., B29:L729, 1996.
[77] J. Viefhaus, L. Avaldi, G. Snell, M. Wiedenhoft, R. Hentges, A. Rudel,
F. Schafer, D. Menke, U. Heinzmann, A. Engelns, J. Berakdar, H. Klar
und U. Becker. Phys. Rev. Lett., 77:3975, 1996.
[78] J.A.R. Samson. Phys. Rev. Lett., 65:2863, 1990.
[79] Ken-ichi Hino, T. Ishihara, F. Shimizu, N. Toshima und J.H. McGuire.
Phys. Rev., A48:1271, 1993.
[80] J.M. Feagin. J. Phys., B28:1495, 1995.
[81] J.M. Feagin. J. Phys., B29:l551, 1996.
[82] J.M. Feagin und J.S. Briggs. Phys. Rev. Lett., 57:984, 1986.
LITERATUR
31
[83] G.H. Wannier. Phys. Rev., 90:817, 1953.
[84] A.K. Kazanski und V.N. Ostrovsky. Phys. Rev., A51:3698, 1995.
[85] A.K. Kazanski und V.N. Ostrovsky. J. Phys., B27:447, 1994.
[86] A.K. Kazanski und V.N. Ostrovsky. J. Phys., B28:1453, 1995.
[87] A. Huetz, P. Selles, D. Waymel und J. Mazeau. J. Phys., B24:1917, 1991.
[88] F. Maulbetsch und J.S. Briggs. J. Phys., B28:551, 1995.
[89] L. Malegat, P. Selles und A. Huetz. J. Phys., B30:251, 1997.
[90] R. Dorner, H. Brauning, J.M. Feagin, V. Mergel, O. Jagutzki, L. Spielberger, T. Vogt, H. Khemliche, M.H. Prior, J. Ullrich, C.L. Cocke und
H. Schmidt-Bocking. Phys. Rev., A57:1074, 1998.
[91] R. Dorner, V. Mergel, H. Brauning, M. Achler, T. Weber, Kh. Khayyat,
O. Jagutzki, L. Spielberger, J. Ullrich, R. Moshammer, Y. Azuma, M.H.
Prior, C.L. cocke und H. Schmidt-Bocking. Atomic processes in Plasmas,
AIP conference proceedings: im Druck, 1998. Editoren: E. Oks, M. Pindzola.
[92] M. Pont, R. Shakeshaft, F. Maulbetsch und J.S. Briggs. Phys. Rev.,
A53:3671, 1996.
[93] F. Maulbetsch, M. Pont, J.S. Briggs und R. Shakeshaft. J. Phys., B28:L341,
1995.
[94] S.P. Lucey, J. Rasch, C.T. Wheelan und H.R.J. Walters. J. Phys., B31:1237,
1998.
[95] F. Maulbetsch und J.S. Briggs. J. Phys., B26:1679, 1993.
[96] F. Maulbetsch und J.S. Briggs. J. Phys., B26:L647, 1993.
[97] F. Maulbetsch und J.S. Briggs. J. Phys., B26:L647, 1994.
[98] M. Pont und R. Shakeshaft. Phys. Rev., A51:R2676, 1995.
[99] G. Schonhense und J. Hormes. VuV and Soft X-Ray Photoionization, Ed.:
U. Becker and D.A. Shirley, Plenum Press, New York, 1996, :607, 1996.
LITERATUR
32
[100] J. Berakdar und H. Klar. Phys. Rev. Lett., 69:1175, 1992.
[101] J. Berakdar, H. Klar, A. Huetz und P. Selles. J. Phys., B26:1463, 1993.
[102] M. Pont und R. Shakeshaft. Phys. Rev., A54:1448, 1996.
[103] T.J. Reddish, J.P. wightman, M.A. MacDonald und S. Cvejanovic. Phys.
Rev. Lett., 79:2438, 1997.
[104] L.R. Andersson und J. Burgdorfer. Phys. Rev. Lett., 71:50, 1993.
[105] L.R. Andersson und J. Burgdorfer. The Physics of Electronic and Atomic Collisions, AIP conference proceedings 295:836, 1993. Editoren: T.
Andersen, B. Fastrup, F. Folkmann, H. Knudsen, N. Andersen.
[106] L.R. Andersson und J. Burgdorfer. Phys. Rev., A50:R2810, 1994.
[107] J. Burgdorfer, L.R. Andersson, J.H. McGuire und T. Ishihara. Phys. Rev.,
A50:349, 1994.
[108] C.F. von Weizacker. 88:612, 1934.
[109] E.J. Williams. Phys. Rev., 45:729, 1934.
[110] R. Moshammer, J. Ullrich, M. Unverzagt, W. Schmitt, P. Jardin, R.E.
Olson, R. Dorner, V. Mergel und H. Schmidt-Bocking. Nucl. Instr. Meth.,
B107:62, 1996.
[111] R. Moshammer, J. Ullrich, H. Kollmus, W. Schmitt, M. Unverzagt,
H.Schmidt-Bocking, C.J. Wood und R.E. Olson. Phys. Rev., A56:1351,
1997.
[112] S.F.C. ORourke, R. Moshammer und J. Ullrich. J. Phys, B30:5281, 1997.
[113] S. Keller, H.J. Ludde und R. Dreizler. Phys. Rev., A55:4215, 1997.
[114] J. Ullrich, R. Moshammer und R. Dorner. Physikalische Blatter, 54:140,
1998.
[115] Kh. Khayyat. Dissertation, Universitat Frankfurt, 1998.
[116] V. Mergel, R. Dorner und H. Schmidt-Bocking. Physikalische Blatter, eingereicht zur Veroentlichung.
LITERATUR
33
[117] R. Dorner, V. Mergel, L. Spielberger, M. Achler, Kh. Khayyat, T. Vogt,
H. Brauning, O. Jagutzki, T. Weber, J. Ullrich, R. Moshammer, M. Unverzagt, W. Schmitt, H. Khemliche, M.H. Prior, C.L. Cocke, J. Feagin, R.E.
Olson und H. Schmidt-Bocking. Nucl. Instr. Meth., B127:225{31, 1997.
[118] R.E. Olson. Phys. Rev., A27:1871, 1983.
[119] R.E. Olson, A.E. Wetmore und M.L. McKenzie. J. Phys, B19:L629, 1986.
[120] R.E. Olson. J. Phys, B20:L809, 1987.
[121] J. Macek und S. Yu. Ovchinnikov. Phys. Rev. Lett, 80:2298, 1998.