Mathematik f ¨ur Informatiker II

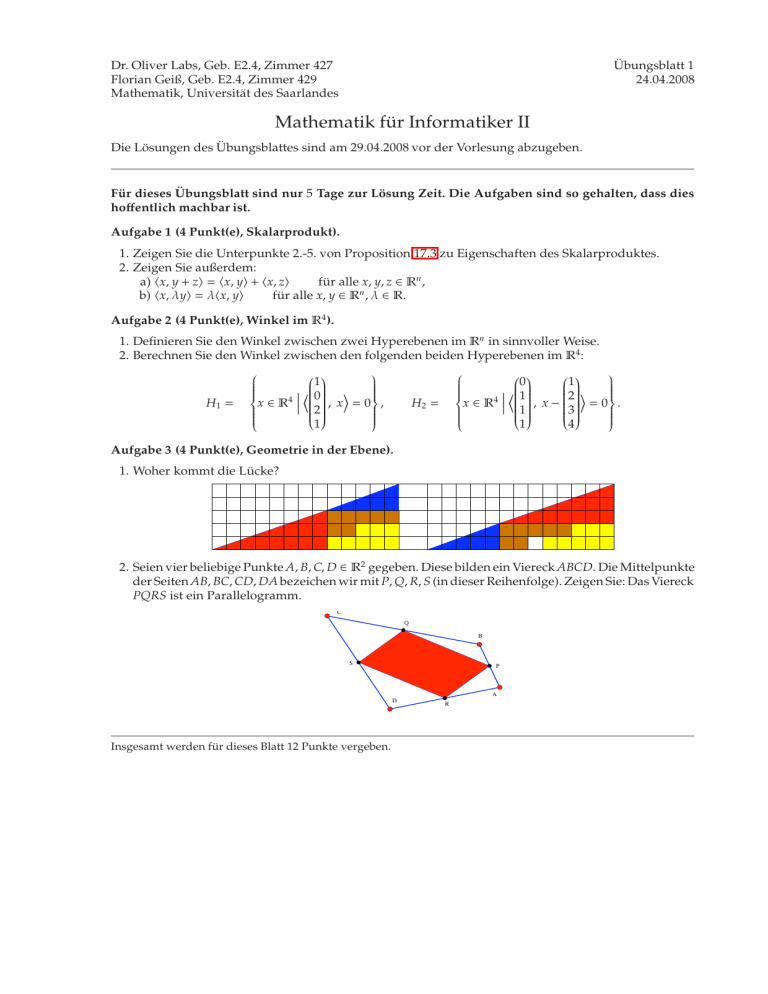
Dr. Oliver Labs, Geb. E2.4, Zimmer 427
Florian Geiß, Geb. E2.4, Zimmer 429
Mathematik, Universität des Saarlandes
Übungsblatt 1
24.04.2008
Mathematik für Informatiker II
Die Lösungen des Übungsblattes sind am 29.04.2008 vor der Vorlesung abzugeben.
Für dieses Übungsblatt sind nur 5 Tage zur Lösung Zeit. Die Aufgaben sind so gehalten, dass dies
hoffentlich machbar ist.
Aufgabe 1 (4 Punkt(e), Skalarprodukt).
1. Zeigen Sie die Unterpunkte 2.-5. von Proposition 17.3 zu Eigenschaften des Skalarproduktes.
2. Zeigen Sie außerdem:
a) !x, y + z" = !x, y" + !x, z"
für alle x, y, z ∈ Rn ,
b) !x, λy" = λ!x, y"
für alle x, y ∈ Rn , λ ∈ R.
Aufgabe 2 (4 Punkt(e), Winkel im R4 ).
1. Definieren Sie den Winkel zwischen zwei Hyperebenen im Rn in sinnvoller Weise.
2. Berechnen Sie den Winkel zwischen den folgenden beiden Hyperebenen im R4 :




 
 
 




1
0
1














%% &  %% & 




2



0
1










4 %  
4 %  


x
∈
R
x
∈
R
H1 = 
,
H
=
,
x
=
0
,
x
−
.
=
0









2
%
%
2
1
3











 
 
 












1
1
4
Aufgabe 3 (4 Punkt(e), Geometrie in der Ebene).
1. Woher kommt die Lücke?
2. Seien vier beliebige Punkte A, B, C, D ∈ R2 gegeben. Diese bilden ein Viereck ABCD. Die Mittelpunkte
der Seiten AB, BC, CD, DA bezeichen wir mit P, Q, R, S (in dieser Reihenfolge). Zeigen Sie: Das Viereck
PQRS ist ein Parallelogramm.
C
Q
B
S
P
A
D
Insgesamt werden für dieses Blatt 12 Punkte vergeben.
R