Modellierung und Herstellung kapazitiver Mikrofone in - E

Marc Füldner
Modellierung und Herstellung kapazitiver
Mikrofone in BiCMOS-Technologie
Dissertation
München, 2004
Modellierung und Herstellung kapazitiver
Mikrofone in BiCMOS-Technologie
Der Technischen Fakultät der
Universität Erlangen-Nürnberg
zur Erlangung des Grades
DOKTOR-INGENIEUR
vorgelegt von
Marc Füldner
München – 2004
Als Dissertation genehmigt von
der Technischen Fakultät der
Universität Erlangen-Nürnberg
Tag der Einreichung: 7.11.2003
Tag der Promotion: 11.2.2004
Dekan: Prof. Dr. rer. nat. Albrecht Winnacker
Berichterstatter:
Prof. Dr.-Ing. Reinhard Lerch
Prof. Dr. rer. nat. Gerhard M. Sessler
Kurzfassung
In Produkten wie Mobiltelefonen, Hörgeräten, Camcordern oder PDA’s werden in großen
Stückzahlen Elekret-Kondensatormikrofone eingesetzt. Diese verwenden überwiegend
fluorierte Polymere als Material für die Elektretschicht. Aufgrund der eingeschränkten
Temperaturstabilität der Elektretfolien werden Elektret-Mikrofone manuell gelötet.
Demgegenüber erfüllen mikromechanische Silizium-Mikrofone in SMD (Surface Mounted
Device)-Gehäusen die Temperaturanforderungen automatisierter Montagelinien und erlauben
daher die kostengünstige Leiterplattenbestückung mit Reflow-Lötprozessen. Weitere Vorteile
von Silizium-Mikrofonen liegen in einer geringen Baugröße, einer geringen
Exemplarstreuung, einer niedrigen Körperschallempfindlichkeit, einer kostengünstigen
Massenfertigung und der Möglichkeit zur Schaltungsintegration.
Die vorliegende Arbeit stellt die Modellierung und Herstellung von kapazitiven SiliziumMikrofonen vor, die mit den Verfahren einer BiCMOS (Bipolar Complementary MetalOxide-Semiconductor)-Technologie prozessiert werden.
Die Modellierung des Mikrofons ist für die Optimierung von Prozess und Design
unerlässlich, da die Herstellung und Prüfung zeit- und kostenintensiv ist. Das entwickelte
Systemmodell basiert auf einem elektrischen Ersatzschaltbild und beinhaltet erstmals die
Nichtlinearität der Verformungsversteifung und die mechanische Nachgiebigkeit von
Membranen mit Federstrukturen und Korrugationen, die mit der Methode der FinitenElemente untersucht werden. Die sehr gute Übereinstimmung zwischen experimentellen
Ergebnissen und Simulationen zu den Membran-Nachgiebigkeiten, den Empfindlichkeiten,
dem Rauschen, der Strömungsdämpfung und dem akustischen Kurzschluss demonstriert die
Gültigkeit der aufgestellten Modelle. Damit steht der Entwicklung ein Simulationswerkzeug
zur Verfügung, das eine Optimierung und produktspezifische Entwicklung der Mikrofone
ermöglicht.
Ein neu entwickelter Mikrofonprozess verwendet erstmals die monokristalline
Siliziumschicht eines SOI (Silicon On Insulator)-Wafers als spannungsfreie Membran
zusammen mit einer epitaktisch gewachsenen Silizium-Gegenelektrode. Beeinträchtigt durch
thermische Spannungen in der Membranaufhängung erreichen die Mikrofone bei einer
Vorspannung von 1 V und einer Membranfläche von 1 mm2 Empfindlichkeiten bis zu
2.4 mV/Pa und einen äquivalenten Rauschschallpegel von 40 dB(A).
Weitere Silizium-Mikrofone verwenden eine abgeschiedene polykristalline Siliziumschicht
als Membran. Zur Verbesserung der mechanischen Empfindlichkeit werden fortgeschrittene
Membrandesigns mit Federstrukturen und Korrugationen eingesetzt. Darüber hinaus
verringert eine neue Technologie zur Perforation der Gegenelektrode die akustische
Dämpfung und erhöht die akustische Bandbreite der Mikrofone. Mit einer Vorspannung von
3 V werden Empfindlichkeiten deutlich über 10 mV/Pa bei einem Nutzband von 20 Hz –
10 kHz und ein äquivalenter Rauschschallpegel von 27 dB(A) erreicht. Bezüglich dieser
elektroakustischen
Eigenschaften
eignen
sich
die
Silizium-Mikrofone
für
Telekommunikationsanwendungen.
Abstract
In most microphone applications like mobile phones, hearing aids, camcorders or personal
digital assistants electret condenser microphones (ECMs) are installed in high-volume. Recent
ECMs use fluorinated polymers as material for the electret foil. Because of the limited
temperature resistance of the electret foils, ECMs are soldered by hand.
In contrast to standard ECMs, micromachined silicon microphones packaged as surface
mounted devices fulfil the temperature requirements of automated assembly lines with
reduced costs of placing on a printed circuit board. Further advantages of silicon microphones
are small size, good reproducibility, low sensitivity to vibration, low-cost batch fabrication
and the ability to integrate electronic circuits.
This work presents modelling and fabrication of silicon condenser microphones in BiCMOS
(Bipolar Complementary Metal-Oxide-Semiconductor) technology.
Modelling of silicon microphones for process and design optimization is essential since
fabrication and testing are time consuming and cost-intensive. The developed system model
of microphones is based on an equivalent network diagram including the non-linear stressstiffening effect and the mechanical compliance of diaphragms with springs and corrugations
analysed by finite element simulations. A very good agreement between experimental and
simulation results of the membrane compliance, sensitivity, noise, acoustical damping and
acoustical bypass demonstrates the validity of the model. Thus, the presented system model of
silicon microphones can be used for optimization and design-to-product development.
A new process for the fabrication of silicon microphones uses SOI (Silicon On Insulator)
wafers to provide a monocrystalline silicon diaphragm with low stress and a silicon epitaxy to
form the counter electrode. Suffering from thermal stress of the membrane support, a
microphone sensitivity up to 2.4 mV/Pa and an equivalent noise level of 40 dB(A) is achieved
with a 1 mm2 diaphragm and a bias voltage of 1 V.
In an alternative fabrication approach, the diaphragm is made of deposited polysilicon. To
improve the mechanical compliance, advanced membrane designs with spring and corrugation
structures are implemented. Furthermore, acoustical damping and microphone bandwidth are
improved by a new perforation technology of the back electrode. Sensitivities above
10 mV/Pa, a flat frequency response from 20 Hz to 10 kHz and an equivalent noise level of
27 dB(A) are achieved for bias voltages of 3 V. Regarding their electro-acoustical
performance, the silicon microphones are applicable for telecommunication applications.
Vorwort
Herrn Prof. Dr.-Ing. Reinhard Lerch vom Lehrstuhl für Sensorik der Universität ErlangenNürnberg danke ich ganz herzlich für die fachliche Betreuung und die freundliche
Unterstützung des Vorhabens, diese Promotion in Kooperation mit der Infineon Technologies
AG in München durchzuführen.
Herrn Prof. Dr. rer. nat. Gerhard M. Sessler danke ich für die Übernahme des Koreferats und
dem dieser Arbeit entgegen gebrachtem Interesse.
Herzlich bedanken möchte ich mich bei Herrn Dr. Robert Aigner für die großzügige
Unterstützung der Arbeit bei Infineon Technologies, die fachlichen Anregungen und die
Freiheit zum selbstständigen Arbeiten.
Besonderen Dank gilt Herrn Dr. Alfons Dehé für die freundschaftliche Betreuung und den
zahlreichen technischen Diskussionen, die wesentlich zum Gelingen der Arbeit beigetragen
haben.
Meinen Kollegen aus der Mikrosystemtechnik-Abteilung, insbesondere Herrn Stefan Barzen
und Herrn Michael Brauer, möchte ich für die Zusammenarbeit und das angenehme
Arbeitsklima danken.
Meinen Doktorandenkameraden Herrn Torsten Reimann, Herrn Marc Strasser, Herrn Martin
Handtmann, Herrn Gernot Fattinger und Herrn Dr. Florian Plötz ist es zu verdanken, dass mir
die letzten Jahre auch außerhalb der Arbeitszeit viel Freude bereitet haben.
Meinen Eltern, die mir mein Studium und damit diese Promotion ermöglichten, gilt mein
ganz besonderer Dank. Die moralische Unterstützung meiner Frau Eva hat mich immer
wieder motiviert und durch schwierige Phasen gebracht.
München, im September 2003
Marc Füldner
Inhaltsverzeichnis
Inhaltsverzeichnis
SYMBOLVERZEICHNIS
IV
KAPITEL 1
1
EINLEITUNG
1
1.1
1
Motivation
1.2
Stand der Technik
1.2.1
Konventionelle Mikrofone
1.2.2
Silizium-Mikrofone
3
3
3
1.3
Ziele und Lösungsvorschläge der Arbeit
7
1.4
Inhalt und Aufbau der Arbeit
8
KAPITEL 2
9
HERSTELLUNG VON SILIZIUM-MIKROFONEN IN BICMOS-TECHNOLOGIE
9
2.1
Konzeption der Mikrofonherstellung
2.1.1
Mikrofonempfindlichkeit und Kollapsspannung
2.1.2
Mechanische Membrannachgiebigkeit
2.1.3
Mechanische Schichtspannung
9
9
11
12
2.2
Kapazitives Mikrofon mit SOI-Sensormembran und epitaktischer Silizum-Gegenelektrode
2.2.1
Mikrofonaufbau
2.2.2
Herstellungsprozess
15
15
16
2.3
Kapazitives Mikrofon mit polykristalliner Siliziummembran und epitaktischer SilizumGegenelektrode
21
2.4
Kapazitives Mikrofon mit polykristalliner Siliziummembran und Gegenelektrode
2.4.1
Mikrofonaufbau
2.4.2
Integrierte Herstellung einer hochperforierten Gegenelektrode
2.4.3
Herstellung von Membranen mit hoher mechanischer Nachgiebigkeit
22
23
24
26
2.5
30
Zusammenfassung
KAPITEL 3
31
NUMERISCHE SIMULATIONEN ZUM MECHANISCHEN VERHALTEN VON
MIKROFONMEMBRANEN
31
3.1
Zielsetzung und Simulationsablauf
31
3.2
Quadratische und kreisförmige Membranen
3.2.1
Quadratische Membranen
3.2.2
Kreisförmige Membranen
3.2.3
Ableitung einer erweiterten Beziehung zur nichtlinearen Membran-Nachgiebigkeit
32
32
35
36
3.3
38
Feder-Membranen
I
Inhaltsverzeichnis
3.3.1
3.3.2
3.3.3
3.3.4
3.3.5
Spannungsfreie Feder-Membran
Feder-Membran mit Schichtspannung
Modellierung von Feder-Membranen
Einfluss von Spannungsgradienten auf das mechanische Verhalten von Feder-Membranen
Diskussion der Simulationsergebnisse
3.4
Korrugierte Membranen
3.4.1
Analytische Berechnung eines Korrugationsbalkens
3.4.2
Spannungszustand einer Korrugationsmembran
3.4.3
Durchbiegung bei Druckbelastung
3.4.4
Modellierung der Nachgiebigkeit von Korrugationsmembranen
3.4.5
Schwankung der Membrannachgiebigkeit bei Fertigungstoleranzen
3.4.6
Diskussion der Simulationsergebnisse
38
39
41
43
46
46
47
49
50
50
52
53
KAPITEL 4
54
MODELLIERUNG VON KAPAZITIVEN SILIZIUM-MIKROFONEN
54
4.1
Modellbildung
54
4.2
Konzentrierte Netzwerkelemente im kapazitiven Mikrofon
4.2.1
Akustische Federelemente
4.2.2
Akustische Widerstandselemente
4.2.3
Akustische Massenelemente
4.2.4
Mechanische Elemente
4.2.5
Strahlungsimpedanz
57
57
57
59
59
61
4.3
Netzwerkmodellierung und Simulation von Mikrofonen
4.3.1
Mechanisch-akustisches Netzwerkmodell
4.3.2
Analytische Berechnung der Mikrofon-Nachgiebigkeit
4.3.3
Simulationen zur Mikrofon-Nachgiebigkeit
4.3.4
Dynamische Bandbreite und Perforationsdesign
4.3.5
Analytische Berechnung des akustischen Eigenrauschens
4.3.6
Simulationen zum akustischen Eigenrauschen
61
62
63
64
66
70
72
4.4
Kapazitive Wandlung in einer Niederfrequenz-Schaltung
4.4.1
Ruhekapazität und Perforationsdesign
4.4.2
Elektrostatische Membrananziehung
4.4.3
Kapazitives Wandlerverhalten
74
75
77
78
4.5
Impedanzwandlerschaltung
4.5.1
Analytische Berechnung der Spannungsverstärkung und Ausgangsimpedanz
4.5.2
Simulationen zur Spannungsverstärkung und Ausgangsimpedanz
4.5.3
Analytische Berechnung der Rauschspannungsdichte
4.5.4
Simulationen zur Rauschspannungsdichte
79
80
80
81
85
4.6
Simulationen zum Gesamtsystem aus Mikrofon mit Beschaltung
4.6.1
Empfindlichkeit und Rauschen
4.6.2
Signal/Rauschabstand
87
88
89
4.7
93
Zusammenfassung
KAPITEL 5
94
ANGEWANDTE EXPERIMENTELLE UNTERSUCHUNGSMETHODEN
94
5.1
II
Interferometrische Messung
94
Inhaltsverzeichnis
5.2
Eigenfrequenzanalyse
95
5.3
Kapazitätsmessung
96
5.4
Messung der Mikrofonempfindlichkeit und Rauschspannung
96
KAPITEL 6
98
MESSERGEBNISSE ZU MIKROFONEN MIT EPITAKTISCHER SILIZIUMGEGENELEKTRODE
98
6.1
Oberflächenanalyse von Membran und Gegenelektrode
99
6.2
Eigenfrequenz und mechanische Nachgiebigkeit von Membran und Rückseitenplatte
101
6.3
Mikrofon-Kapazität und Kollapsspannung
103
6.4
Impedanzwandlerschaltung und Messaufbau
103
6.5
Mikrofon-Empfindlichkeiten
105
6.6
Rauschen der Mikrofone
108
6.7
Zusammenfassung der Messergebnisse
109
KAPITEL 7
110
MESSERGEBNISSE ZU MIKROFONEN MIT POLYKRISTALLINER
SILIZIUMMEMBRAN UND GEGENELEKTRODE
110
7.1
Eigenfrequenzanalyse zur Untersuchung der mechanischen Nachgiebigkeit
7.1.1
Eigenfrequenz und Nachgiebigkeit von Feder-Membranen
7.1.2
Eigenfrequenz und Nachgiebigkeit von Membranen mit Korrugationen
7.1.3
Dotierstoff-abhängige Schichtspannung von Membranen
111
111
112
114
7.2
115
Statische Randverbiegung bei Feder-Membranen aufgrund von Spannungsgradienten
7.3
Elektroakustische Empfindlichkeit von Silizium-Mikrofonen
7.3.1
Empfindlichkeit von Mikrofonen mit Kreis-, Netz- und Korrugationsmembran
7.3.2
Einfluss der Strömungsdämpfung auf das Tiefpass-Verhalten der Empfindlichkeit
7.3.3
Einfluss des Gehäusevolumens auf das Hochpass-Verhalten der Empfindlichkeit
116
116
117
118
7.4
Elektrisches und akustisches Rauschen
119
7.5
Zusammenfassung der Messergebnisse
120
KAPITEL 8
121
ZUSAMMENFASSUNG UND AUSBLICK
121
LITERATURVERZEICHNIS
125
III
Symbolverzeichnis
Symbolverzeichnis
Lateinische Buchstaben
a
ah
A
ADC
Ajfet
b
bc
c
C
C0
Ca
Cbp
Cgs
Cgd
Ch
Cin
Cgap
Cp
Cm
Cm,Feder
Cm,c
Cm,q
Cm,k
CMembran
CMikrofon
CPlatte
Csolid
CV
dh
D
dh
e
E
f
fFeder
fo
fu
gm
hc
F
Fe
Fm
gm
I
IV
Kantenlänge
Kantenlänge Perforationsloch
Fläche
Transformationsfunktion Gleichspannungsschaltung
Spannungsverstärkung Impedanzwandlerschaltung
Breite
Breite einer Korrugation
Schallgeschwindigkeit
Kapazität
aktive Mikrofon-Kapazität
akustische Nachgiebigkeit der Membran
akustische Nachgiebigkeit der Rückseitenplatte
Sperrschichtkapazität Gate-Source
Sperrschichtkapazität Gate-Drain
Kapazität eines Kondensatorsegments mit Perforationsloch
Volumennachgiebigkeit Chipvolumen
akustische Nachgiebigkeit des Kondensatorspaltes
parasitäre Kapazität
mechanische Membran-Nachgiebigkeit
Nachgiebigkeit Feder-Membran
Nachgiebigkeit Korrugationsmembran
Nachgiebigkeit quadratische Membran
Nachgiebigkeit Kreismembran
Nachgiebigkeit einer zugbelasteten Membran ohne Biegesteifigkeit
mechanische Mikrofon-Nachgiebigkeit
Nachgiebigkeit einer rein biegesteifen Platte
Kapazität eines unperforierten Plattenkondensators
Hohlraumnachgiebigkeit Gehäuse
Abstand zwischen Perforationslöchern
Plattensteifigkeit
Abstand zwischen Perforationsöffnungen
Elementarladung
Elastizitätsmodul
Frequenz
Federmembran-Faktor, Erhöhung der Nachgiebigkeit
obere Grenzfrequenz
untere Grenzfrequenz
Transistorsteilheit
Korrugationshöhe
Kraft
elektro statische Kraft an der Membran
mechanische Rückstellkraft der Membran
Transistorsteilheit
Strom
Symbolverzeichnis
Ids
Ig
k
keff
Kf
Km
LE
LSystem
m
Mbp
Min
Mm
Mp
Mrad
Mvent
N
Nc
Np
Nu
p
Q
q
R
Rs
Rg
r
rh
rmono
rpoly
R
R0
Rg
Rgap
Rin
Rp
Rrad
Rs
Rvent
S
SSystem
t
tbp
tdia
T
u
v
U
U0
Ubat
Up
V
Kanalstrom
Gatestrom
Federkonstante, Boltzmann-Konstante
effektive Federkonstante einer Membran
Funkelrauschfaktor
Korrekturterm zur Berücksichtigung der Spannungsversteifung
Eigengeräuschpegel
äquivalenter Rauschschallpegel von Mikrofon und Schaltung
Masse
dynamische Masse der Rückseitenplatte
akustische Masse der Gehäuseöffnung
dynamische Masse der Membran
akustische Masse der Perforationslöcher
Massenbelastung der Strahlungsimpedanz
akustische Masse im Ventilationspfad
Dichte des Mikrofonrauschens, auch: Anzahl Federstrukturen
Korrugationsanzahl
Rauschdruckdichte an der Membran
Rauschspannungsdichte am Lastwiderstand
Schalldruck
Ladung
Volumenstrom, Fluss
Widerstand
Lastwiderstand
Ladewiderstand
Entfernung von der Membranmitte
Radius Perforationsloch
Wachstumsrate von monokristallinem Silizium
Wachstumsrate von Polysilizium
Membranradius
innerer Membranradius
Ladewiderstand
akustischer Widerstand der Querströmung im Kondensatorspalt
Strömungswiderstand durch Gehäusewand
Strömungswiderstand durch Perforationslöcher
Strahlungswiderstand
Lastwiderstand
Strömungswiderstand im Ventilationspfad
elektroakustische Mikrofon-Empfindlichkeit
elektroakustische Empfindlichkeit von Mikrofon und Schaltung
Dicke
Dicke Rückseitenplatte
Dicke Membran
Temperatur
Signalspannung
Schnelle, Geschwindigkeit
Spannung
Vorspannung an der Mikrofonkapazität
Batterie- bzw. Betriebsspannung
Kollapsspannung
Volumen
V
Symbolverzeichnis
Vds
Vgs
Vt
VMikrofon
w
wc
W
WI
Wp
Wq
xeff
x0
x0‘
Drain-Source Spannung
Gate-Source Spannung
Pinch-off Spannung
Übertragungsfunktion vom Eingangsdruck auf den Druck an der Membran
Membranauslenkung
Weite einer Korrugation
Rauschdichte einer Rauschquelle
Rauschstromdichte einer Rauschquelle
Rauschdruckdichte der Rauschquelle
Rauschflussdichte der Rauschquelle
mittlere Auslenkung der Membran
Kondensatorspalthöhe in Ruhelage
elektrostatische Membranauslenkung
Griechische Buchstaben
ε0
εx, εy, εz
η
ν
ρ
ρh
σ
σcorr
σ0
Σ
VI
Dielektrizitätskonstante von Luft
Dehnungen
Viskosität
Querkontraktionszahl
Dichte
Perforationsflächendichte
mechanische Membranspannung
Membranspannung einer Korrugationsmembran
intrinsische Schichtspannung
Spannungsgradient
Einleitung
Kapitel 1
Einleitung
1.1
Motivation
Mikrofone werden in großen Stückzahlen in verschiedenen Produkten eingesetzt.
Umsatzstärkster Anwendungsbereich ist die Telekommunikation mit Mobiltelefonen,
Telefonanlagen, Freisprecheinrichtungen und Anrufbeantwortern. Daneben kommen
Mikrofone im Multimediabereich (PCs, Camcorder, Diktiergeräte, Handhelds) und in der
Consumerelektronik zum Einsatz. In dem überwiegenden Teil der heutigen Produkte werden
Elektret-Mikrofone verwendet. Diese arbeiten nach dem kapazitiven Wandlerprinzip, bei dem
eine schwingungsfähige Membran und eine starre Elektrode einen Kondensator bilden. Die
vom Schalldruck ausgelenkte Membran führt zu einer Kapazitätsänderung und erzeugt bei
konstanter Kondensatorladung eine Wechselspannung. Die Verwendung einer permanent
polarisierten Elektretschicht zur Speicherung der Kondensatorladung macht prinzipiell keine
externe Speisespannung notwendig. Da häufig in die Mikrofonkapsel ein Vorverstärker
hybrid eingebaut wird, der die hohe Quellimpedanz des Mikrofons in eine für die weitere
Signalverarbeitung günstige Ausgangsimpedanz transformiert, muss zu dessen Betrieb eine
Gleichspannung zur Verfügung gestellt werden. Die Elektret-Mikrofone aus den genannten
Produktbereichen besitzen eine gute Aufnahmequalität bei niedrigen Herstellungskosten.
Nachteilig ist der irreversible Verlust von Elektretladung bei rauen Umgebungseinflüssen wie
hoher Temperatur und Luftfeuchtigkeit und die damit verbundene unvorhersehbare Drift in
der
Mikrofonempfindlichkeit.
Im
Zusammenhang
mit
der
eingeschränkten
Temperaturstabilität (<80° C) sind die relativ hohen Bestückungskosten von ElektretMikrofonen zu nennen, die manuell gelötet oder über aufwändige Federkonstruktionen
kontaktiert werden müssen.
Auch in Hörgeräten der Medizintechnik werden Elektret-Mikrofone verwendet. Sie stellen die
höchsten Ansprüche an den Signal-Rauschabstand, die Miniaturisierung und die
Langzeitstabilität. Insbesondere bei Array-Anwendungen zur Erzielung einer Richtwirkung ist
eine geringe Exemplarstreuung und eine zeitlich konstante Mikrofonempfindlichkeit
notwendig. Diese Anforderungen führen zu erhöhten Herstellungs- und Gehäusekosten von
Elektret-Mikrofonen für Hörgeräteanwendungen.
Die Kondensatormikrofone der Studio- und Messtechnik bestehen aus einer
schwingungsfähigen Elektrode aus hochwertigem Metall, z.B. einer Stahl-Nickel-Legierung,
und einer zweiten Metallplatte, die die Gegenelektrode bildet. Kondensatormikrofone besitzen
die höchste Aufnahmequalität, sind allerdings aufgrund der aufwändigen Montage
kostenintensiv und benötigen eine hohe Speisespannung (~50-200 V).
Die Anforderungen an eine neue Generation von Mikrofonen sind nach diesen Betrachtungen
sehr hoch. Sie sollten bei einer hohen Aufnahmequalität mit einer geringen
Versorgungsspannung auskommen und preiswert in der Herstellung und beim Einbau in das
Produkt sein. Weitere wichtige Merkmale sind geringe Exemplarstreuungen, ein hoher Grad
an Miniaturisierung und die Widerstandsfähigkeit gegenüber äußeren Einflüssen wie Hitze,
1
Einleitung
Feuchtigkeit oder Erschütterung. Die Methoden der Mikromechanik erscheinen aussichtsreich
diese Anforderungen zu erfüllen und darüber hinaus zusätzliche Vorteile zu generieren. In der
Mikromechanik wird die hoch entwickelte Silizium-Planartechnologie der Mikroelektronik
zusammen mit speziellen Fertigungsverfahren der Volumen- und Oberflächenmikromechanik
zur Erzeugung mikromechanischer Strukturen verwendet.
Am deutlichsten zeigen sich die Möglichkeiten der Mikromechanik in der Miniaturisierung
solcher Silizium-Mikrofone. Ein miniaturisiertes Mikrofon mit integriertem Impedanzwandler
und einem Gehäuse von der Größe des Siliziumchips ermöglicht die störungsfreie Aufnahme
des Schallfeldes bis in den oberen Audio-Frequenzbereich. Aus kommerzieller Sicht führt die
Miniaturisierung zu großen Stückzahlen pro Wafer und damit zu niedrigen Stückkosten. Mit
Silizium-Mikrofonen ist man außerdem in der Lage, Gehäusetechnologien und
Aufbautechniken der Mikroelektronik zu verwenden, so dass beispielsweise kompakte SMD
(surface mount devices)- Bauteile realisiert werden können [Bev99]. Solche SMD-Mikrofone
ermöglichen, auch wegen ihrer hohen Temperaturstabilität, eine automatisierte
Leiterplattenbestückung mit Standard-Equipment bei niedrigen Kosten. Neben den
kommerziellen Vorteilen weisen miniaturisierte Silizium-Mikrofone verbesserte
Eigenschaften auf. Durch die Miniaturisierung und die Verwendung dünner Schichten besitzt
die Mikrofon-Membran eine sehr geringe Masse und ist daher unempfindlich gegenüber
Erschütterungen. Diese geringe Körperschallempfindlichkeit ist bei Kfz-Anwendungen, bei
Hörgeräten oder im Umfeld von vibrierenden Maschinen von Interesse. Hinsichtlich der
mechanischen Empfindlichkeit der Membran ist eine Verkleinerung der Membranfläche
ungünstig. Dennoch können hohe mechanische Empfindlichkeiten durch die gleichzeitige
Anwendung von mikromechanischen Schichten zur Realisierung extrem dünner Membranen
erzielt werden. Da die Spalthöhe bei kapazitiven Silizium-Mikrofonen ebenfalls durch eine
dünne Schicht erzeugt wird, kommt das Mikrofon mit einer niedrigen Versorgungsspannung
aus. Die dünnen Schichten und ihre lateralen Dimensionen im Mikrofon werden durch die
bekannten Prozesse der Schichttechnik, Lithographie und Ätztechnik sehr genau und
reproduzierbar gefertigt. Die damit verbundene niedrige Exemplarstreuung der SiliziumMikrofone ist speziell für eine optimale Richtwirkung von Mikrofon-Arrays bedeutend.
Anwendungsbeispiele sind Freisprechanlagen im Automobil oder Hörgeräte.
Neben den genannten Vorteilen gegenüber konventionellen Mikrofonen eröffnen sich für
Silizium-Mikrofone neue Anwendungsbereiche. Die hohe Temperaturstabilität des Mikrofons
erlaubt einen Einbau in temperaturkritische Bereiche, wie der Konsole im Automobil. Großes
Potenzial liegt in einer Integration der Signalverarbeitung auf dem Mikrofonchip. Eine
monolithische Integration führt zu einer weiteren Miniaturisierung und Kostenreduktion, da
die hybride Montage der elektronischen Bauteile entfällt. Aufgrund der kurzen Signalwege
besitzt ein integriertes Mikrofon eine verbesserte elektromagnetische Verträglichkeit. Auch
die Entwicklung von intelligenten Mikrofonen ist denkbar. Diese „smarten“ Mikrofone
könnten beispielsweise eine Selbstkalibrierung durchführen und Störgeräusche wie Echo oder
Husten „on-chip“ filtern.
Mikromechanisch gefertigte Silizium-Mikrofone besitzen also die Leistungsfähigkeit,
konventionelle Mikrofone in vielen Anwendungsbereichen zu ersetzen und neue Produkte zu
ermöglichen. Trotz intensiver Entwicklungsarbeiten und einer Vielzahl von verschiedenen
Mikrofonbauformen ist eine kommerziell nutzbare Massenfertigung von empfindlichen
Silizium-Mikrofonen bis heute nicht gelungen.
2
Einleitung
1.2
Stand der Technik
1.2.1 Konventionelle Mikrofone
Konventionelle Mikrofone nutzen unterschiedliche physikalische Effekte zur Wandlung des
Schalldruckes in ein elektrisches Signal. Tabelle 1.1 zeigt die relative Häufigkeit eines
Wandlerprinzips für verschiedene Anwendungsbereiche. Aufbau und Funktionsweise solcher
Mikrofone werden in [Ler93] und [Ros88] behandelt.
Anwendungsbereich
Wandlerprinzip
Multimedia und
Consumerelektronik
Telekommunikation
Hörgeräte
Messtechnik
Studiotechnik
Elektret
++
+
++
+
+
++
+
Ο
+
Kondensator
elektrodynamisch
Ο
+
piezoelektrisch
Ο
+
Ο
Ο
Tabelle 1.1: Konventionelle Mikrofone und deren Anwendungsbereiche (++ =häufige
Verwendung, Ο =seltene Verwendung) [Ler93].
Der Vergleich der konventionellen Mikrofone verdeutlicht die Dominanz von ElektretMikrofonen, die in praktisch allen Produkten eingesetzt werden. Diese Bedeutung verdanken
sie ihrer hohen Aufnahmequalität und den gut entwickelten Verfahren zu ihrer Herstellung
[Yas94]. In modernen Elektret-Mikrofonen besteht die schallempfindliche Membran aus einer
dünnen Metallplatte oder einer metallisierten Kunststofffolie. Um nicht die mechanischen
Eigenschaften der Membran zu beinträchtigen, wird die durch ein Koronaverfahren
permanent polarisierte Elektretschicht auf die metallische Gegenelektrode aufgeklebt. Als
Elektretmaterial haben sich fluorierte Polymere wie TeflonTM bewährt, die eine relativ gute
Ladungsspeicherung aufweisen [Ses87].
1.2.2 Silizium-Mikrofone
Mikromechanische Silizium-Mikrofone werden seit vielen Jahren in unterschiedlichen
Bauformen untersucht. Einen sehr guten Überblick über Silizium-Mikrofone bis 1996 geben
die Veröffentlichungen von Scheeper et al. [Schee94] und Sessler [Ses91, Ses96]. Im
Folgenden werden in kurzer Form die Entwicklungen auf dem Gebiet der Silizium-Mikrofone
anhand wichtiger Kenngrößen diskutiert. Dabei bezieht sich die elektroakustische
Empfindlichkeit auf eine Frequenz von 1 kHz. Der äquivalente Rauschschallpegel gibt,
bezogen auf die Hörschelle des menschlichen Ohres von 2⋅10-5 Pa, das Verhältnis der
Rauschspannung im Nutzband zur Empfindlichkeit in Dezibel an. Er entspricht dem
Schallpegel, der nötig wäre, ein dem Rauschen von Mikrofon und Verstärker entsprechendes
Signal zu erzeugen. Der äquivalente Rauschschallpegel wird häufig in dB(A) angegeben. Die
A-Bewertung ist eine Filterfunktion, die das menschliche Hörempfinden nachbildet
(DIN45633). Die obere Grenzfrequenz soll die Frequenz bezeichnen, bei der die
Empfindlichkeit um 3 dB von der Empfindlichkeit bei 1 kHz abweicht.
3
Einleitung
Elektret-Mikrofone
Die Detektion der Schallwelle über eine Kapazitätsänderung ist das am häufigsten
angewandte Wandlerprinzip bei Silizium-Mikrofonen. Die Vorteile der kapazitiven Wandler
liegen bei einer hohen Empfindlichkeit mit niedrigem Eigenrauschen, einem geringen
Leistungsverbrauch und einer geringen Temperaturempfindlichkeit. Das bereits bei den
konventionellen Mikrofonen sehr erfolgreiche Konzept der Elektret-Mikrofone, die
Kondensatorladung permanent in einem Dielektrikum zu speichern, wird auch bei SiliziumMikrofonen verfolgt (Tabelle 1.2).
Anstelle von TeflonTM bei konventionellen Mikrofonen wird bei Silizium-Mikrofonen häufig
Siliziumdioxid (Si02) als Elektret-Material verwendet. Gründe für den Ersatz des Polymeres
sind die schlechte Schichthaftung und die Schwierigkeit, Teflon mit Standardprozessen zu
strukturieren. Eine hohe Temperaturstabilität bei gleichzeitig guter Empfindlichkeit zeigen
spannungskompensierte Schichtsysteme aus Siliziumnitrid (Si3N4) und Siliziumdioxid
[Thie99]. Sehr gute Empfindlichkeiten werden mit MylarTM als Membranmaterial erreicht
[Spre89, Mur89]. Die Kunststofffolie eignet sich allerdings nicht für die Integration in eine
mikromechanische Fertigung, da der Kunststoff nicht mit den hohen Prozesstemperaturen der
Abscheideverfahren kompatibel ist
Autor
Empfindlichkeit
Rauschschallpegel
obere Grenzfrequenz
Jahr
Elektret/MembranMaterial
[mV/Pa]
[dB(A)]
[kHz]
[Hsi99]
Teflon/Si3N4
45
<30
3
[Thie99]
Si02/Si3N4
5.3
32
15
[Mur89]
Si02/Mylar
8
30
> 15
[Spre89]
Si02/Mylar
25
> 15
Tabelle 1.2: Mikromechanische Elektret-Mikrofone.
Kondensator-Mikrofone
Verzichtet man auf die permanente Polarisation der Elektretschicht, ist man nicht auf spezielle
Materialen zur Ladungsspeicherung und dem Prozess der Aufladung angewiesen und erreicht
einen höheren Integrationsgrad mit bestehenden Fertigungstechnologien der Mikroelektronik.
Ein wesentlicher Nachteil ist, dass der Mikrofonkondensator durch eine externe
Spannungsquelle aufgeladen werden muss. Darüber hinaus wird man das hohe elektrische
Feld im Elektret-Mikrofon selbst durch eine hohe Spannung oder einen dünnen
Kondensatorspalt nicht erreichen, so dass für eine vergleichbare Empfindlichkeit wesentlich
empfindlichere Membranen benötigt werden. Auf dem Gebiet der kapazitiven Mikrofone mit
externer Spannungsversorgung, die im Folgenden Kondensator-Mikrofone genannt werden,
wurden die zahlreichsten Anstrengungen zur Entwicklung empfindlicher Silizium-Mikrofone
unternommen. Bereits in älteren Veröffentlichungen findet man Mikrofone mit guten
Empfindlichkeiten bis zu 3 mV/Pa, doch benötigten diese noch hohe Versorgungsspannungen
über 16 V [Hoh83, Hoh89, Kueh92, Bour92, Schee92, Berg94]. Abbildung 1.1 gibt einen
Überblick der jüngsten Arbeiten auf dem Gebiet der mikromechanischen KondensatorMikrofone. Da das Rauschen und daher der äquivalente Rauschschallpegel stark von der
Qualität der elektrischen Verstärkerschaltung abhängt und Angaben zum Eigenrauschen der
Mikrofone selten sind, werden die Mikrofone anhand ihrer Empfindlichkeit und der dazu
benötigten Betriebsspannung charakterisiert.
4
Einleitung
22
Hörgeräte
Empfindlichkeit [mV/Pa]
20
18
16
[Berg94]
14
[Romb00]
[Bern96]
[Schaf98]
12
Telekom.
[Kab99]
10
[Ning95]
8
[Zou97]
[Hsu98]
[Scheep94]
6
4
2
[Muel00]
[Tor99]
[Kron01]
0
11
10
9
8
7
6
5
4
3
2
1
0
Betriebsspannung [V]
Abbildung 1.1: Mikromechanische Kondensator-Mikrofone.
Die umrandeten Gebiete geben die typischen Einsatzbereiche von heutigen ElektretMikrofonen in Hörgeraten (---) und in der Telekommunikation (___) wider. Keines der
mikromechanisch gefertigten Silizium-Mikrofone erfüllt die Anforderungen der
Hörgeräteindustrie mit Empfindlichkeiten von 20-25 mV/Pa bei 1.3 V und einem maximalen
Rauschpegel von 25 dB(A) [SAT01, Know01]. Hervorzuheben sind die Arbeiten von
Knowles Electronics IC Group [Schaf98] und Microtronic A/S [Rom00], mit einem bereits
1997 von J. Bay beschrieben Mikrofon [Bay97]. Die vorgestellten Mikrofone sind bezüglich
Empfindlichkeit, Rauschschallpegel und Versorgungsspannung mit konventionellen ElektretMikrofonen in Telekommunikationsanwendungen vergleichbar (ca. 10 mV/Pa, 30 dB(A),
Versorgungsspannung 1-3 V [Prim02]). Das Mikrofon von [Schaf98] benötigt dazu einen
Ring-Oszillator, der die Versorgungsspannung auf 12 V hochtransformiert. In Hinblick auf
einen geringen Leistungsverbrauch für mobile Anwendungen ist dieser Ansatz ungünstig.
Piezoresistive Mikrofone
Ein piezoresistives Mikrofon besteht aus einer dünnen Membran, die bei Schalldruck eine
mechanische Biegespannung aufbaut. Die mechanische Spannung wird anhand einer
elektrischen Widerstandsänderung einer auf der Membran liegenden Struktur aus
piezoresistivem Material gemessen. Die Piezowiderstände werden vorteilhaft in einer
Wheatstoneschen Brückenkonfiguration auf der Membran platziert [Schel98]. Aufgrund des
einfachen Aufbaus können piezoresistive Mikrofone problemlos monolithisch integriert
werden. Piezoresistive Mikrofone erreichen trotz hoher Betriebsspannungen nur geringe
Empfindlichkeiten, und die Möglichkeit zur Steigerung der Empfindlichkeit beschränkt sich
im Wesentlichen auf eine Vergrößerung der Membran [Schee94]. Die besten von R. Schellin
[Schel98] veröffentlichten piezoresistiven Mikrofone besitzen geringe Empfindlichkeiten bis
zu 0.45 mV/Pa, wobei eine Brückenspannung von 12 V benötigt wird.
Piezoelektrische Mikrofone
Piezoelektrische Mikrofone haben den Vorteil, keine äußere Spannungsversorgung zu
benötigen. Die mechanische Spannung einer ausgelenkten Membran bei Schallanregung
erzeugt an einer Sandwichstruktur aus zwei Elektroden und einer piezoelektrischen Schicht
eine elektrische Spannung. Bei vergleichbarer Bandbreite sind die erreichten
5
Einleitung
Empfindlichkeiten deutlich niedriger als die von kapazitiven Mikrofonen [Niu01, Schel98,
Rie93]. Die hohe Empfindlichkeit von Lee et al. [Lee98] wird auf Kosten einer mechanischen
Resonanzfrequenz der Membran im zu übertragenden Frequenzbereich erzielt.
„Feld-Effekt-Transistor“ Mikrofone
Einen sehr innovativen Ansatz beschreibt W. Kühnel [Kueh91, Kueh92]. Das Mikrofon
besteht wie ein kapazitives Mikrofon aus einer beweglichen Membran und einer starren
Gegenelektrode. In die Membran ist das Gate eines Feld-Effekt-Transistors integriert.
Getrennt durch den Spaltabstand befindet sich der Transistorkanal mit Source und Drain in
der Gegenelektrode. Ändert sich die Höhe des Kondensatorspaltes durch eine
Membranschwingung, dann moduliert das elektrische Feld zwischen Gate und Source den
Drain-Strom. Die Ausgangsimpedanz dieser FET-Mikrofone ist konzeptbedingt niedrig, da
der Impedanzwandler in Form des Feld-Effekt Transistors bereits integriert ist. Der
äquivalente Rauschschallpegel ist aufgrund des für Feld-Effekt Transistoren typischen KanalSchrotrauschens vergleichsweise hoch.
Optische Mikrofone
Bei optischen Mikrofonen wird die Phasen- oder Intensitätsänderung einer durch die
Mikrofonanordnung laufenden Lichtwelle detektiert. Die Notwendigkeit, eine Lichtquelle und
ein Interferometer zur Messung der Phasenverschiebung bzw. ein Detektor zur
Intensitätsmessung bereitzustellen, verhindert eine breite Anwendung von optischen
Mikrofonen. Dennoch könnten sie aufgrund ihres guten Signal-Rausch-Verhältnisses und
ihrer elektromagnetischen Verträglichkeit in speziellen Anwendungen eingesetzt werden.
Auch für zukünftige optische Systeme, bei der eine Transformation in elektrische Signale
nicht notwendig ist, bieten sich optische Mikrofone an.
Tabelle 1.3 gibt einen Überblick über die Ergebnisse von nicht-kapazitiven SiliziumMikrofonen.
Empfindlichkeit [mV/Pa]
/ Vorspannung [V]
Rauschschallpegel
[dB(A)]
Grenzfrequenz
[kHz]
43
15
Wandlerprinzip
Autor
Jahr
piezoresistiv
[Schel98]
0.45 / 12
piezoresistiv
[Shep99]
0.02 / 10
piezoelektrisch
[Lee98]
30 / *
piezoelektrisch
[Niu01]]
0.52 / *
piezoelektrisch
[Schel98]
0.21 / *
55
≈ 15
piezoelektrisch
[Rie93]
0.92 / *
57
18
Feld-Effekt
[Kueh92]
5 / 30
58
17
Feld-Effekt
[Graf93]
6 / 15
62
7
optisch
[Schn94]
[Schel98]
(59 mrad/Pa)
46
5
optisch
[Plis94]
(100 mrad/Pa)
optisch
[Hall01]
1.8
4
7
23
>> 20
Tabelle 1.3: Nicht-kapazitive Silizium-Mikrofone (*=keine Vorspannung notwendig).
6
Einleitung
1.3
Ziele und Lösungsvorschläge der Arbeit
Ziele
In den vorhergehenden Abschnitten wurden die Vorteile und Möglichkeiten von
mikromechanischen Silizium-Mikrofonen gegenüber den etablierten Mikrofonen in
konventioneller Fertigung dargelegt. Unter den Silizium-Mikrofonen herrschen die
kapazitiven Wandler aufgrund ihrer guten Eigenschaften vor. Um die Vorteile der
Siliziumtechnologie wie Massenfertigung, Miniaturisierung, Kostenreduktion, Integration von
Sensorelement und Schaltung, Reproduzierbarkeit und Qualitätskontrolle konsequent zu
nutzen, wird eine monolithische Ein-Chip Lösung angestrebt. Diese stellt gleichzeitig die
höchsten Anforderungen an die Prozess- und Designentwicklung. So war zu Beginn der
Arbeit trotz intensiver Forschungsarbeiten nur ein mikromechanisches Mikrofon bekannt, das
die Grundvoraussetzungen für eine Anwendung im Telekommunikationsbereich erreicht. Eine
kommerzielle Umsetzung von Silizium-Mikrofonen ist bis heute nicht gelungen.
Im Rahmen dieser Arbeit sollte daher ein kapazitives Silizium-Mikrofon entwickelt werden,
das bei einer geringen Versorgungsspannung eine hohe Empfindlichkeit mit niedrigem
Eigenrauschen aufweist. Die Prozessierung sollte innerhalb der Fertigungsumgebung des
Halbleiterunternehmens Infineon Technologies AG mit den zur Verfügung stehenden
Verfahren einer Standard BiCMOS (Bipolar Complementary Metal-Oxide-Semiconductor)Technologie gelingen.
Die Modellierung des Mikrofons ist für die Optimierung und Abstimmung von Prozess und
Design unerlässlich, da die Herstellung und Prüfung zeit- und kostenintensiv ist. Die aus der
Literatur bekannten Modelle sind zum Teil unvollständig oder können auf die entwickelten
Mikrofone nicht angewendet werden. Aus diesem Grund bestand ein weiteres Ziel dieser
Arbeit darin, ein kompaktes Modell der neuartigen Silizium-Mikrofone aufzustellen. Eine
große Bedeutung kommt der Verifizierung der Simulationsergebnisse zu. Erst durch die
experimentelle Überprüfung der aufgestellten Modelle sind verlässliche Vorhersagen zur
Entwurfsverbesserung möglich. In der Literatur werden überwiegend entweder Simulationen
oder Messungen vorgestellt. Ein wesentliches Ziel bestand daher in der experimentellen
Untersuchung der Mikrofone und dem Vergleich mit den Simulationsergebnissen der in
dieser Arbeit aufgestellten Modelle.
Lösungsvorschläge
In dieser Arbeit werden verschiedene Konzepte zur Realisierung empfindlicher Mikrofone
verfolgt. In einem neu entwickelten Ein-Chip Mikrofonprozess wird erstmals die SiliziumGegenelektrode durch eine kombinierte Gasphasenabscheidung und Epitaxie gebildet.
Dadurch erzielt man eine planare Waferoberfläche mit monokristallinen Siliziumbereichen,
die sich für eine anschließende Schaltungsintegration eignen. Ein neuartiger Aspekt ist die
Verwendung von SOI (silicon on insulator)-Wafern als Ausgangsmaterial. Die
monokristalline Siliziumschicht wird als stressfreie Platte mit hoher mechanischer
Empfindlichkeit verwendet, und die Siliziumdioxidschicht dient als zuverlässiger Stopp der
Ätzung der Waferrückseite. Auf der Basis dieses neuen Mikrofonprozesses werden alternativ
Mikrofone auf einem Standard-Siliziumwafer mit abgeschiedener Siliziumdioxid- und
Polysiliziumschicht prozessiert. Zur Verbesserung der Empfindlichkeit wurden Mikrofone
mit Membranen entworfen, die an Balkenstrukturen befestigt werden. Weitere Arbeiten zur
Entwicklung von empfindlichen Silizium-Mikrofonen wurden an einem zu Beginn der Arbeit
zur Verfügung stehenden Mikrofonprozess durchgeführt. Dieses Mikrofon verwendet eine
abgeschiedene polykristalline Siliziumschicht als Membran. Die Arbeiten konzentrierten sich
7
Einleitung
auf die Verbesserung der mechanischen Empfindlichkeit der Membran durch fortgeschrittene
Membrandesigns und einer Verringerung der akustischen Dämpfung durch eine neue
Technologie zur Perforation der Gegenelektrode.
Die Modellierung der Mikrofone basiert auf einem elektrischen Ersatzschaltbild mit
mechanischen und akustischen Elementen. Es nutzt die formalen Entsprechungen zwischen
den mechanisch-akustischen Gleichungssystemen und dem elektrischen Gleichungssystem.
Fragestellungen, die nicht analytisch behandelt werden können, werden mit der Methode der
Finiten-Elemente numerisch simuliert. Aus den Simulationsergebnissen werden Beziehungen
abgeleitet, die in das Netzwerkmodell integriert werden. Das mechanisch-akustische
Mikrofonmodell wird schließlich in einem Schaltungssimulator umgesetzt und mit der
Simulation der elektrischen Beschaltung ergänzt. Dieses Gesamtmodell ermöglicht eine
effiziente Simulation des kompletten Signalweges ausgehend von der Schallquelle bis zum
elektrischen Ausgangssignal. Dasselbe Modell liefert das akustische Eigenrauschen des
Mikrofons und das elektrische Rauschen der Beschaltung. Die hergestellten SiliziumMikrofone mit zahlreichen Prozessparameter- und Designvariationen ermöglichen eine mit
dieser Vielfalt noch nicht durchgeführte experimentelle Überprüfung der aufgestellten
Modelle.
1.4
Inhalt und Aufbau der Arbeit
Kapitel 2 behandelt die Herstellung der mikromechanischen Silizium-Mikrofone. Einleitend
werden die für das Mikrofonverhalten relevanten Prozess- und Designparameter und die
technologisch bedingten Möglichkeiten und Einschränkungen diskutiert. Neben der
Beschreibung der entwickelten Mikrofonherstellungsprozesse wird auf spezielle
Designvariationen eingegangen.
Das dritte Kapitel widmet sich der numerischen Simulation. Mit Hilfe der Methode der
finiten Elemente wird das mechanische Verhalten verschiedener Mikrofonmembranen
untersucht. Ziel der Simulationen ist die Ableitung einfacher algebraischer Ausdrücke zur
Integration in ein Netzwerkmodell des Mikrofons.
In Kapitel 4 wird das Netzwerkmodell des Systems, bestehend aus Mikrofon, umgebender
Luft und elektrischer Beschaltung, mit mechanischen, akustischen und elektrischen
Elementen und deren Verknüpfung dargestellt. Auf Basis dieses Systemmodells werden
Simulationen zur frequenzabhängigen Mikrofonempfindlichkeit, dem Übertragungsverhalten
der Schaltung und dem akustischen und elektrischen Rauschen durchgeführt.
Die zur Charakterisierung der entwickelten Mikrofone angewandten Messaufbauten werden
in Kapitel 5 beschrieben.
In Kapitel 6 und Kapitel 7 werden jeweils die gewonnenen Messergebnisse zu den zwei
Mikrofon-Technologien vorgestellt. Anhand der Messergebnisse wird das in Kapitel 4
aufgestellte Mikrofon-Gesamtmodell experimentell überprüft.
Das achte Kapitel fasst die wichtigsten Resultate dieser Arbeit zusammen. Die Arbeit
schließt mit einem Ausblick auf noch ausstehende Arbeiten zur Weiterentwicklung der
kapazitiven Silizium-Mikrofone.
8
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Kapitel 2
Herstellung von Silizium-Mikrofonen in BiCMOSTechnologie
Die in dieser Arbeit entwickelten Silizium-Mikrofone wurden mit Ausnahme weniger
mikromechanischer Prozesse in der 6“ (150 mm)-Fertigungsumgebung der Infineon
Technologies AG am Standort München-Perlach hergestellt. Eine Randbedingung bei der
Prozessentwicklung war daher die Verwendung von Materialen und Verfahren einer
Standard-BiCMOS-Technologie.
Zu Beginn werden im Abschnitt 2.1 mit Hilfe analytischer Gleichungen Konzepte zur
Mikrofonherstellung abgeleitet. In Abschnitt 2.2 wird ein eigenständig entwickelter, neuer
Prozess zur Herstellung kapazitiver Ein-Chip Silizium-Mikrofone vorgestellt. Das besondere
Merkmal dieser auf SOI (Silicon On Insulator)- Wafern hergestellten Mikrofone ist die aus
einer dünnen monokristallinen Siliziummembran und einer dicken Epitaxie-Gegenelektrode
bestehende Sensorkapazität. Mit einem modifizierten Prozess wurden Mikrofone auf 6“Siliziumwafern hergestellt, deren Membranen aus polykristallinen Silizium bestehen und zur
Erhöhung der mechanischen Nachgiebigkeit mit Schlitzen versehen werden (Abschnitt 2.3).
Weitere Untersuchungen wurden an gleichartigen Mikrofonen durchgeführt, bei denen die
Membran ebenfalls aus einer abgeschiedenen polykristallinen Siliziumschicht gebildet wird.
Der Aufbau dieser Mikrofone wird in Abschnitt 2.4 vorgestellt. Der Schwerpunkt der
Arbeiten lag in der Weiterentwicklung der mechanischen Empfindlichkeit von
Siliziummembranen und der Herstellung einer perforierten Gegenelektrode mit niedrigem
Strömungswiderstand.
2.1
Konzeption der Mikrofonherstellung
Die hohen Anforderungen an die Herstellung von Silizium-Mikrofonen verdeutlicht die
notwendige Empfindlichkeit zur Detektion der Druckänderungen von etwa 10-4-10 Pa
verglichen mit einem Drucksensor, der statische Drücke von 105 Pa misst. Ausgangspunkt der
Überlegungen ist eine analytische Beziehung für die elektrische Empfindlichkeit eines
kapazitiven Mikrofons. Mit ihrer Hilfe werden die Möglichkeiten einer Optimierung der
Mikrofonempfindlichkeit abgeleitet und in Bezug auf Verfahren und Materialen der SiliziumTechnologie diskutiert.
2.1.1 Mikrofonempfindlichkeit und Kollapsspannung
In Niederfrequenz-Schaltung wird die Mikrofonkapazität durch eine Vorspannung U0 über
einen hochohmigen Widerstand aufgeladen. Bei konstanter Ladung ist die durch den
Schalldruck verursachte Kapazitätsänderung einer Wechselspannung u~ proportional. Unter
der Näherung einer im Verhältnis zum Spaltabstand kleinen Membranauslenkung setzt sich
die Mikrofonempfindlichkeit S aus einem von der elektrischen Feldstärke abhängigen Anteil
9
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
U0/x0 [V/m], mit dem Spaltabstand x0 der Mikrofonkapazität C und der Vorspannung U0, und
der mechanischen Nachgiebigkeit der Membran Cm [m/Pa] zusammen
S=
U dC
U ∫∫ w( p ~ , x, y ) ⋅dxdy
U
u~
=− 0 ⋅
≈− 0 ⋅
≡ − 0 ⋅ Cm .
p~
p~ C
x0
x0
p ~ ⋅ ∫∫ dxdy
(2.1)
p~ bezeichnet den Schalldruck, u~ die Signalspannung und w(p~,x,y) die Druck- und
ortsabhängige Membranauslenkung. Die mechanische Nachgiebigkeit Cm beschreibt eine
effektive Auslenkung bei Druckbelastung, bei der die tatsächliche Durchbiegung der
Membran in eine translatorische, kolbenartige Verschiebung mit dem selben Volumen
umgerechnet wird.
Die Vorspannung U0 an der Mikrofonkapazität ist vom Betrag her durch die sogenannte
Kollapsspannung Up (Snap-in/Pull-In Voltage) beschränkt, bei der die elektrostatische Kraft
zwischen der Membran und der Gegenelektrode die mechanische Rückstellkraft der Membran
überwiegt (vgl. 4.4.2)
8 ⋅ x0
27 ⋅ ε 0 ⋅ C m
3
Up =
.
(2.2)
Für einen stabilen Betrieb des Mikrofons darf daher die Vorspannung an der
Mikrofonkapazität nur einen Bruchteil α von der Kollapsspannung betragen. Mit dieser
Nebenbedingung und den Gleichungen (2.1) und (2.2) kann die Mikrofonempfindlichkeit als
Sα =
U0
8 ⋅ x0 ⋅ C m
8 ⋅ x0 ⋅ C m
⋅
≡α ⋅
Up
27 ⋅ ε 0
27 ⋅ ε 0
(2.3)
formuliert werden. Die Wahl des Stabilitätsfaktors α=U0/Up<1 wird von den Anforderungen
an die Linearität, den maximal zu detektierenden Schalldruck und Prozessschwankungen
abhängen. Im Unterschied zu der suggerierten Annahme aus Gleichung (2.1), die
Empfindlichkeit würde mit einem kleinen Spaltabstand optimiert, nimmt die Empfindlichkeit
Sα mit dem Spaltabstand x0 zu, da die Kollapsspannung mit der Spalthöhe überproportional
steigt und entsprechend die Vorspannung erhöht werden könnte. Allerdings bestehen
prozesstechnische Schwierigkeiten bei der Herstellung großer Spaltabstände (vgl. 2.4.2).
Hinzu kommt, dass die Vorspannung durch die zur Verfügung stehende Betriebsspannung der
Anwendung beschränkt ist. In Abbildung 2.1 ist die maximal erreichbare
Mikrofonempfindlichkeit unter der Nebenbedingung U0≤Ubat mit einer typischen
Batteriespannung eines Mobiltelefons von Ubat=2 V und einem Stabilitätsfaktor von 0.6, d.h.
U0≤0.6⋅Up, dargestellt.
10
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
20.00 - 25.00
15.00 - 20.00
10.00 - 15.00
5.00 - 10.00
- 5.00
20
U0=Ubat
15
10
25
5
22
19
0
16
C
m
[n
m
13
/P
a]
Empfindlichkeit [mV/Pa]
25
U0<Ubat
10
7
4
11
1.2
1.4
1.6
1.8
Sp
2
2.2
and
bst
a
t
l
a
2.4
]
[µm
Abbildung 2.1: Maximale Mikrofonempfindlichkeit in Abhängigkeit von der mechanischen
Nachgiebigkeit Cm und dem Spaltabstand x0 (Ubat=2 V, α=0.6).
Die Erhöhung des Spaltabstandes ist abhängig von der mechanischen Nachgiebigkeit
vorteilhaft, solange die Vorspannung ebenfalls erhöht werden kann und nicht durch die
Betriebspannung beschränkt wird. Bei einer höheren mechanischen Empfindlichkeit kann die
Vorspannung niedriger gewählt werden, so dass die Beschränkung einer maximalen
Vorspannung erst bei größeren Spaltabständen eintritt. Während es für den Spaltabstand eine
optimale Höhe bei gegebenen Cm, α und Ubat gibt, führt die Erhöhung der mechanischen
Nachgiebigkeit zu einer hohen Mikrofonempfindlichkeit bei gleichzeitig niedriger
Versorgungsspannung. Sie ist daher die wichtigste Designgröße und wird im Folgenden näher
untersucht.
2.1.2 Mechanische Membrannachgiebigkeit
Für eine quadratische Membran ist nach [Hoh86] die mechanische Membran-Nachgiebigkeit
bei idealen Einspannbedingungen näherungsweise durch




w( p ~ , x, y ) ⋅dxdy
a
1
∫∫


≈
⋅
≡
2

30 ⋅ σ ⋅ t
7.3 ⋅ E ⋅ t
p ~ ⋅ ∫∫ dxdy


+
1
2
2
 (1 − υ ) ⋅ σ ⋅ a

2
C m,q
(2.4)
gegeben. Der Gültigkeitsbereich der Gleichung wird näher in Kapitel 3 untersucht.
11
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Danach stehen fünf Parameter zur Optimierung der mechanischen Nachgiebigkeit zur
Verfügung:
•
•
•
die geometrischen Abmessungen des Mikrofons mit der Kantenlänge a und der Dicke t,
das Elastizitätsmodul E und die Querkontraktionszahl ν und
die mechanische Schichtspannung σ des Membranmaterials.
Die Membrandicke sollte im Verhältnis zur Membrankantenlänge möglichst klein sein. Im
Prinzip können mit der Silizium-Planartechnologie Schichten von wenigen Nanometern
Dicke realisiert werden. Da jedoch bei sehr dünnen Schichten bereits geringfügige
Prozessschwankungen der Abscheideverfahren die Reproduzierbarkeit der Membrandicken
und damit der Mikrofonempfindlichkeit beeinträchtigen, ist man bei der Wahl der
Schichtdicke eingeschränkt. Die dominierende Größe ist die Kantenlänge der
Mikrofonmembran, die quadratisch in die mechanische Nachgiebigkeit eingeht. Sie kann aus
technologischer Sicht nahezu beliebig und sehr reproduzierbar durch die Photo- und
Ätztechnik hergestellt werden. Mit der Membranfläche nimmt die Fläche der Gegenelektrode
und die Schwierigkeit, eine ebene und starre Gegenelektrode zu prozessieren, zu. Zudem wird
aus kommerzieller Sicht eine möglichst kleine pro Mikrofon beanspruchte Waferfläche
angestrebt. Die Wahl der Prozess- und Designparameter zur Herstellung mikromechanischer
Mikrofone sollte daher neben funktionellen Ansprüchen wie Empfindlichkeit und
Reproduzierbarkeit auch wirtschaftliche Aspekte berücksichtigen und hängt entscheidend von
der zur Verfügung stehenden Fertigungstechnologie ab. Dies gilt insbesondere für die
Einschränkung auf wenige Silizium-kompatible Membranmaterialen, womit die
Materialkonstanten des Elastizitätsmodul und der Querkontraktionszahl festgelegt werden.
Die mechanische Schichtspannung des Membranmaterials hingegen kann sich in einem
weiten Wertebereich bewegen.
2.1.3 Mechanische Schichtspannung
Im Hinblick auf eine hohe mechanische Nachgiebigkeit ist eine stressfreie Platte ideal. Dann
resultiert die mechanische Rückstellkraft nur aus der inneren Biegesteifigkeit. Ist dieser
Spezialfall gegeben, spricht man von einer Platte. Bei einer reinen Membran wird das
Auslenkungsverhalten von tangential zur Ebene wirkenden Zugspannungen bestimmt. In
dieser Arbeit soll für den allgemeinen Fall einer Überlagerung von Biege- und
Zugspannungen der Begriff der Membran verwendet werden.
Bei bereits relativ niedrigen Zugspannungen fällt die mechanische Nachgiebigkeit stark ab.
Diesen Sachverhalt verdeutlicht die Abbildung 2.2, in der die mechanische Nachgiebigkeit
einer Siliziummembran nach Gleichung (2.4) in Abhängigkeit der mechanischen
Zugspannung für Kantenlängen von 600 µm bis 1200 µm dargestellt ist.
12
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Nachgiebigkeit Cm,q [nm/Pa]
100
10
1
a=1200 µm
a=1000 µm
a=800 µm
a=600 µm
0.1
0.01
0.1
1
Zugspannung [MPa]
10
100
Abbildung 2.2: Mechanische Nachgiebigkeit Cm,q [nm/Pa] einer quadratischen
Siliziummembran mit Zugspannung für verschiedene Kantenlängen a (Dicke 1 µm).
Das Verhältnis von Membrandicke zu Membrankantenlänge ist bei Silizium-Mikrofonen
typischerweise kleiner als 1:500, so dass bei einem Elastizitätsmodul von Silizium mit 1.62
GPa bereits bei Zugspannungen von 1.62 GPa/5002≈0.65 MPa die Schichtspannung über die
Biegesteifigkeit dominiert und die mechanische Nachgiebigkeit mit der Spannung umgekehrt
proportional abnimmt. Die mechanische Spannung σ in einer Membran setzt sich aus
mehreren Anteilen zusammen
σ = σ ex + σ th + σ d + σ i .
(2.5)
Von außen auf die Membran wirkende Spannungen, die beispielsweise nach der Montage des
Mikrofonchips vom Gehäuse oder Kleber ausgehen können, werden in einem externen
Spannungsbeitrag σex zusammengefasst. Eine thermische Spannung σth entsteht, wenn sich
beim Abkühlen von der Abscheidetemperatur die Membranschicht und das Substrat aufgrund
unterschiedlicher thermischer Ausdehnungskoeffizienten verschieden stark zusammenziehen.
Dotierstoffatome, die durch Diffusion oder Implantation in das Material eingebracht werden,
tragen eine von der Konzentration abhängige Dotierstoff-induzierte Spannung σd zur
Gesamtspannung bei. Die Ursache ist der unterschiedliche Ionenradius von Silizium und dem
Dotierstoff. Der intrinsische Stress σi fasst sämtliche Spannungsbeiträge zusammen, die
während der Abscheidung im Material entstehen. Dazu gehören Spannungen die bei der
Ausbildung von Korngrenzen, Veränderungen der inneren Bindungen und der Kristallstruktur
und durch die Abgabe von Fremdatomen entstehen [Elb98]. Die intrinsische Spannung hängt
daher stark vom jeweiligen Material, den speziellen Abscheidebedingungen und
nachträglichen Temperungen ab. Aus der Literatur sind verschiedene Silizium-kompatible
Membranmaterialen zur Herstellung von Mikrofonen bekannt:
•
•
•
•
Metall/Siliziumnitrid-Schichtsysteme [Schee94, Kron01],
Polysilizium [Hsu98, Tor99],
Polysilizium/Siliziumnitrid-Schichtsysteme [Zou97, Mueh00],
und monokristallines Silizium [Berg94, Kab99, Bour92].
13
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Siliziumnitrid (Si3N4) und Polysilizium werden nach dem CVD (Chemical Vapour
Deposition)-Verfahren abgeschieden, bei dem das erforderliche Prozessgas über Konvektion
und Diffusion zur heißen Substratoberfläche gelangt und als ein Reaktionsprodukt die
gewünschte Schicht entsteht. Unter den CVD-Verfahren hat sich die thermisch aktivierte
Abscheidung bei niedrigem Druck (Low Pressure Chemical Vapour Deposition, LPCVD)
bewährt, da diese reaktionsbestimmte Gasphasenabscheidung eine konforme
Schichtbedeckung liefert [Wid96].
Siliziumnitrid
LPCVD-Siliziumnitrid erfährt während der Abscheidung bei 700–850° C eine Schrumpfung
des Volumens, die auf eine Umwandlung der Atomverbindungen zurückzuführen ist. Die
dadurch verursachte intrinsische Zugspannung überwiegt gegenüber dem kompressiven
Spannungsbeitrag der thermischen Spannung und führt zu einer sehr hohen Zugspannung von
etwa 1 GPa [Stad92, Kap00]. Die Zugspannung wird durch nachträgliches Tempern noch
weiter erhöht. Eine deutliche Verringerung der Zugspannung wird durch ein optimiertes
Verhältnis der Prozessgase Dichlorsilan und Ammoniak erreicht [Kron01].
Polysilizium
Die Abscheidung von Polysilizium unterhalb einer Temperatur von 600° C erfolgt in einer
amorphen Form, die wegen dem im Vergleich zu monokristallinen Silizium kleinen
thermischen Ausdehnungskoeffizienten eine thermische Druckspannung entstehen lässt. Die
Umwandlung von der amorphen zur polykristallinen Struktur findet bei Temperaturen
oberhalb von etwa 550° C statt. Mit dieser Umwandlung verdichtet sich das Volumen der
Siliziumschicht und erzeugt eine intrinsische Zugspannung, die die thermische
Druckspannung überkompensiert. Eine Verringerung der Zugspannung kann durch eine
Dotierung mit Phosphor-Ionen und einer Rekristallisation bei Temperaturen über 750° C
erzielt werden [Elb97, Tork99]. Oberhalb der Löslichkeitsgrenze von Phosphor in Silizium
findet eine Dotierstoffsegregation in den Korngrenzen statt, die eine Diffusion von
Siliziumatomen über die Korngrenzen erleichtert und das Kornwachstum begünstigt [Wad78].
Über der Grenztemperatur von 600° C wird Silizium unmittelbar polykristallin
abgeschiedenen. Die Ausbildung von Kristalliten mit zwischengelagerten Siliziumatomen
erzeugt eine Druckspannung in der Schicht. Sie eignet sich aufgrund der Gefahr einer
Plattenbeulung nicht als Mikrofonmembran. Die Druckspannung in der Polysiliziumschicht
kann aber in einer Anordnung aus zwei Schichten dazu verwendet werden, die Zugspannung
einer Siliziumnitrid-Schicht zu kompensieren. Durch eine Anpassung der Schichtdicken kann
so die effektive Membranspannung eingestellt werden.
Monokristallines Silizium
Hervorragende Spannungseigenschaften besitzt niedrigdotiertes monokristallines Silizium, da
es nahezu keine thermische, intrinsische oder Dotierstoff-induzierte Schichtspannung
aufweist. Eine monokristalline Kristallstruktur kann nicht durch eine Abscheidung erzeugt
werden, so dass Mikrofonmembranen aus dem Silizium-Substrat strukturiert werden müssen.
Die erreichte Schichtspannung der aus der Literatur bekannten Membranen bzw.
Membransysteme liegt typischerweise bei mehreren 10 MPa, so dass in Einklang mit
Abbildung 2.2 die Empfindlichkeit der Mikrofone relativ gering ist bzw. große
Membranflächen benötigt werden [Mueh00]. Die Motivation bestand daher darin, alternative
Prozesse und Designs zur Herstellung von Silizium-Mikrofonen zu entwickeln, die bei
kleinen Membranflächen eine hohe Empfindlichkeit aufweisen.
14
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
2.2
Kapazitives Mikrofon mit SOI-Sensormembran und epitaktischer SilizumGegenelektrode
Im vorhergehenden Abschnitt wurde erläutert, dass sich monokristalline Schichten besonders
gut für empfindliche Membranen eignen. Die Schwierigkeit besteht darin, eine dünne
monokristalline Siliziummembran in reproduzierbarer Weise zu strukturieren. Wird ein
zeitkontrollierter anisotroper Rückseitenprozess ohne chemischen Ätzstopp verwendet um
einen Siliziumwafer bis zur gewünschten Membrandicke zu dünnen, dann wirkt sich die
Dickenschwankung des Siliziumwafers direkt auf die Membrandicke aus [Berg94]. Für die
Produktion in hohen Stückzahlen ohne aufwändiges Anpassen der Empfindlichkeit
(Matching) ist ein verlässlicher Ätzstopp zur Erzeugung dünner, reproduzierbarer Membranen
erforderlich. Ein bekanntes Verfahren nutzt die gute Selektivität einer EDP (EthlylendiaminPyrocatechol)-Ätzlösung zu p+-dotiertem Silizium aus [Kab99]. Der wesentliche Nachteil bei
diesem Verfahren liegt in der hohen Dotierstoffkonzentration, die für den elektrochemischen
Ätzstopp notwendig ist und eine Dotierstoff-induzierte Spannung in der Membran generiert.
Der Vorteil einer monokristallinen Siliziummembran mit geringer Schichtspannung ist nicht
mehr gegeben [Bour92].
Ein neuartiger Ansatz in dieser Arbeit ist der Einsatz von SOI-Wafern zur Herstellung von
Silizium-Mikrofonen. Die Besonderheit von SOI-Wafern ist die dünne monokristalline
Siliziumschicht, die durch eine Isolationsschicht von dem Trägersubstrat elektrisch getrennt
ist. Bevor der Herstellungsprozess beschrieben wird, soll zunächst zur Erläuterung der
Neuerungen und Vorteile der Aufbau der entwickelte Mikrofone beschrieben werden. Dem
folgt die Beschreibung der Prozessfolge (2.2.2).
2.2.1 Mikrofonaufbau
Abbildung 2.3 stellt schematisch das kapazitive Ein-Chip Silizium-Mikrofon dar. Zur
Verdeutlichung des inneren Aufbaus ist der Mikrofonchip in der Mitte aufgeschnitten.
Abbildung 2.3: Schematischer Aufbau des kapazitives Mikrofons mit SOI-Membran.
15
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Die schwingungsfähige Membran besteht aus der monokristallinen Siliziumschicht eines SOIWafers. Die elektrische Kontaktierung der Membran erfolgt über eine „Insel“ in der
Gegenelektrode, die durch tiefe, Oxid-gefüllte Gräben isoliert ist. Da die zwischen dem
Silizium-Substrat und der SOI-Membran gelagerte Siliziumdioxidschicht (buried oxide) im
Prozess als zuverlässiger Stopp der Ätzung der Waferrückseite dient, kann im Gegensatz zu
dem Verfahren mit einem elektrochemischen p+-Ätzstopp die SOI-Schicht vergleichsweise
niedrig dotiert werden. Nach den Überlegungen des letzten Abschnittes sollte die
monokristalline, schwach dotierte SOI-Membran nahezu frei von mechanischen Spannungen
sein und daher eine hohe mechanische Nachgiebigkeit besitzen. Die quadratische Form der
Mikrofonkapazität resultiert aus der von der Kristallebene abhängigen Rückseitenätzung. Für
den statischen Druckausgleich wird in die Membran eine kleine Öffnung eingebracht.
Im Mikrofonbereich bildet eine Silizium-Epitaxie eine polykristalline SiliziumGegenelektrode, die mit Perforationslöchern versehen wird. Diese ermöglichen es der Luft,
aus dem schmalen Kondensatorspalt zu entweichen und die vom Luftpolster auf die
Sensormembran ausgeübte Rückstellkraft zu reduzieren. Außerdem befinden sich an der
Unterseite der Gegenelektrode schmale Noppen, die bei ungewolltem kurzfristigen Kontakt
der Membran mit der Gegenelektrode die Berührungsfläche und so die Haftkraft verringern.
In den Randbereichen des Mikrofonchips erzeugt die Epitaxie erhöhte Gebiete mit
monokristallinem Silizium. Im Vergleich zu bekannten Ein-Chip Mikrofonprozessen hat der
Epitaxieprozess den Vorteil, neben einer dicken und daher stabilen Gegenelektrode
gleichzeitig eine planare monokristalline Waferoberfläche bereitzustellen, die sich zur
weiteren Prozessierung, etwa der Integration von mikroelektronischen Schaltungen, eignet.
2.2.2 Herstellungsprozess
Verschiedene Verfahren zur Herstellung einer monokristallinen Siliziumschicht auf einer
Isolationsschicht, meistens Siliziumdioxid, sind bekannt [Col91]. In dieser Arbeit wurden
nach dem BESOI (Bonded Etched-Back Silicon On Insulator)-Verfahren hergestellte SOIWafer verwendet. Bei diesen werden zwei oxidierte Siliziumwafer bei hoher Temperatur
aufeinander gebondet. Einer der beiden Wafer wird anschließend durch Polieren und
kontrolliertes Rückätzen auf die Zieldicke der Siliziumschicht gedünnt. Die von dem
Hersteller „Shin-Etsu“ gelieferten SOI-Wafer besitzen eine einen Mikrometer dünne
Siliziumschicht auf Siliziumdioxid (Dicke 1µm) und p-dotiertes Siliziumsubstrat (Dicke
625 µm) mit einer kristallographischen <100>-Ebene als Scheibenoberfläche. Die in der
Abbildung 2.4 dargestellten und im folgenden beschriebenen Prozessschritte zur Herstellung
der Silizium-Mikrofone wurden in einer 6“ Fertigungslinie der Infineon Technologies AG in
München durchgeführt. Die Techniken der Silizium-Planartechnologie (Schicht-, Photo-,
Ätz-, Dotier- und Reinigungstechnik) sollen hier nicht im Detail beschrieben werden. Sie
werden in der Literatur ausführlich behandelt [Schu91, Wid96].
Der Herstellungsprozess beginnt mit einer Implantation von Phosphor-Ionen mit geringer
Dosis (1013 cm-2 bei 130 keV) in die SOI-Schicht. Die geringe Dosis soll eine ausreichende
elektrische Leitfähigkeit gewährleisten und gleichzeitig die Kristallstruktur und die
Spannungseigenschaften nicht beeinträchtigen. Die notwendige Aktivierung der Dotieratome
erfolgt bei den hohen Temperaturen der folgenden Schichtabscheidungen. Die Erzeugung von
Strukturen im Mikrometerbereich bedient sich der bekannten lithographischen Technik. Dazu
wird eine dünne Photoresistschicht auf den Wafer aufgeschleudert. Bei Belichtung mit
ultraviolettem Licht erfährt ein Positivphotoresist eine photochemische Umwandlung und
kann chemisch entfernt werden. Die erste Phototechnik im Mikrofonprozess dient der
Strukturierung der Membran mit kleinen Öffnungen zum statischen Druckausgleich im
16
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Mikrofonbetrieb. In den photoresistfreien Bereichen wird die Silizium- und
Siliziumdioxidschicht mit einem anisotropen chemisch-physikalischen Trockenätzprozess
entfernt (Abbildung 2.4, b). Die Photoresistmaske wird nicht weiter benötigt und wird
nasschemisch beseitigt. Im nächsten Prozessschritt wird ein insgesamt 1.2 µm dickes CVDSiO2 nach dem TEOS (Tetra-Ethyl-Ortho-Silicate)- Verfahren in zwei Schritten mit jeweils
0.6 µm Schichtdicke abgeschieden. Das anschließende Tempern bei 900° C verdichtet das
Siliziumdioxid und führt zu einer Schrumpfung der Schichtdicke um ca. 5%. Mit Hilfe einer
Photo- und Ätztechnik werden in die erste Oxidschicht eine Vielzahl kleiner Vertiefungen im
Membranbereich erzeugt (c). Diese bilden im späteren Prozessverlauf schmale Noppen
(bumps) an der Unterseite der Gegenelektrode. Das abgeschiedene Siliziumdioxid dient
lediglich als Abstandshalter zwischen den Elektroden und wird am Ende des
Mikrofonprozesses nasschemisch entfernt, um den luftgefüllten Kondensatorspalt zu bilden.
Man bezeichnet es daher auch als Opferoxid (sacrifical oxide). Auf das Opferoxid wird
ebenfalls aus der Gasphase eine 400 nm dünne Polysiliziumschicht abgeschieden (d). Diese
deckt das Oxid ab und bildet den Untergrund für die noch folgende Epitaxie der
Gegenelektrode. Man spricht daher auch von einem „polyseed layer“. Nun wird durch eine
Phototechnik mit anschließendem Trockenätzen der gesamte Schichtstapel außerhalb des
Mikrofonbereichs bis zum Siliziumsubstrat rückgeätzt. Eine Kombination aus Abscheidung
und Trockenätzung bildet eine Stufe aus Polysilizium (spacer) an den Strukturkanten und
bedeckt offene Oxidbereiche (e). Im nächsten Schritt werden zur Verbesserung der
elektrischen Kontakte Phoshor-Ionen mit einer hohen Dosis (1016 cm-2) implantiert. Die im
Kristall entstandenen Implantationsschäden werden durch eine Temperung in inerter
Atmosphäre ausgeheilt. Es folgt der Prozess der Silizium-Epitaxie. Unter einer Epitaxie
versteht man das monokristalline Aufwachsen einer Schicht, in diesem Fall eine
Siliziumschicht, auf einem monokristallinen Untergrund. Siliziumepitaxieschichten werden
mit dem CVD-Verfahren bei Temperaturen von 1100° C erzeugt, bei denen das Silizium aus
der Gasphase die Kristallorientierung des Siliziumsubstrats annehmen kann. Dies gilt für die
Außengebiete, in denen das Siliziumsubstrat den Untergrund bildet. Dagegen verursacht das
polykristalline Silizium der Polyseed-Schicht im Mikrofonbereich eine ebenfalls
polykristalline Struktur, die sowohl vertikal als auch von der Stirnfläche des Schichtstapels
ausgehend lateral aufwächst. Das polykristalline Silizium breitet sich daher mit der
Schichtdicke in den Außenbereich aus (f). Aufgrund der langsameren Wachstumsrate von
Polysilizium im Vergleich zu monokristallinen Silizium kommt es mit zunehmender
Schichtdicke zu einem Ausgleich der Oberflächentopographie. Das Verhältnis der
Wachstumsrate von Polysilizium und Silizium wurde experimentell zu rpoly/rmono= 0.68
bestimmt. Damit reduziert sich bei Anwendung einer 7 µm dicken Epitaxieschicht die
anfängliche Stufenhöhe des Schichtstapels im Mikrofonbereich von 3.5 µm auf ca. 1.3 µm.
Durch chemisch unterstütztes mechanisches Polieren (CMP, chemical mechanical polishing)
kann die Topographie und Oberflächenrauhigkeit der Polysilizium-Gebiete weiter verbessert
werden. Beim CMP-Verfahren wird die rotierende Waferoberfläche mit einem elastischen
Pad und einem aus Polierkörnern und aktiven chemischen Zusätzen bestehenden Poliermittel
planarisiert. In der Gegenelektrode erzeugt eine anisotrope Silizium-Trockenätzung die
Perforationslöcher und die lateralen Isolationsgräben, die anschließend mit einem CVDSiliziumdioxid und Borphosphorglas (BPSG, bor phosphorous silicat glass) verschlossen
werden (g). Die Anreicherung des Siliziumdioxids mit Bor (Massenanteil 4%) setzt die
Fließtemperatur herab, so dass mit einer Temperung bei 900° C die Oberfläche weiter
planarisiert wird. Da zur Maskierung der tiefen Silizium-Trockenätzung eine Lackschicht
nicht ausreicht, wird zunächst die Struktur der Perforation in eine Siliziumdioxid-Hartmaske
übertragen, die zur Erhöhung der Widerstandsfähigkeit bei 900° C ausgehärtet wird. Nach
dem Rückätzen aller bisher abgeschiedener Schichten auf der Waferrückseite wird eine 100
nm dicke Si3N4 (Siliziumnitrid)-Schicht abgeschiedenen, so dass sich auf der Rückseite
17
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
lediglich die Siliziumnitrid-Schicht befindet. Sie dient als Hartmaske für die
Rückseitenätzung und wird auf der Wafervorderseite gleich wieder entfernt. Mit der
Aluminium-Metallisierung und dem Aufbringen einer Lackmaske zum Schutz gegen die
Opferschichtätzungen endet die Prozessierung in Silizium-Planartechnik (h). Die Volumenund Oberflächenmikromechanik (bulk/surface micromaching) beginnt mit einer
Rückseitenlithographie zur Strukturierung der Siliziumnitrid-Hartmaske. Im nicht-maskierten
Bereich ätzt eine Kaliumhydroxid (KOH)-Lösung in Richtung der <100>-Kristallebene
schneller als die <111>-Ebene und erzeugt die charakteristischen V-förmigen Ätzgruben in
der Waferrückseite. Dieses anisotrope Ätzverhalten wird auf die von der kristallographischen
Ebene abhängige Bindungsenergie eines Siliziumatoms zurückgeführt [Heu89].
Experimentell wurde mit der verwendeten KOH-Lösung bei 60° C ein Ätzratenverhältnis von
35:1 ermittelt. Die Wafervorderseite wird während der Ätzung mit einer speziellen Halterung
durch einen Vakuumring geschützt. Die Ätzung wird bis zum Erreichen der
Siliziumdioxidschicht und dem Öffnen der Membranfläche fortgesetzt (i). In einem letzten
nasschemischen Ätzprozess mit gepufferter Flusssäure wird die Mikrofonkapazität vom Oxid
befreit und in Propanol und Aceton gespült (j). Zur Vermeidung von Kapillarkräften und
einem irreversiblem Verkleben der frei beweglichen Strukturen wird das Verfahren der
Kritischen-Punkt-Trocknung angewendet, bei dem ein direkter Übergang von flüssiger zu
gasförmiger Phase verhindert wird [Mul93].
18
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Abbildung 2.4: Herstellungsprozess eines Silizium-Mikrofons mit spannungsarmer Membran
auf SOI-Material und epitaktischer Gegenelektrode (nicht maßstabsgetreu).
Die Vorderseite eines gefertigten Mikrofons und ein Ausschnitt von der Waferrückseite mit
einem Feld von vier Mikrofonen wurde mit einem Lichtmikroskop aufgenommen (Abbildung
2.5). Zur Charakterisierung der entwickelten Mikrofone wurde die besonders stark in die
Mikrofonempfindlichkeit eingehende Kantenlänge der Membran von 400-1800 µm variiert.
19
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
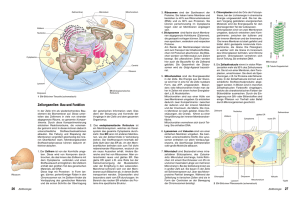
Abbildung 2.5: Mikroskopaufnahme der Mikrofonvorderseite mit Blick auf die perforierte
Gegenelektrode (links) und der Waferrückseite mit Membranen unterschiedlicher
Kantenlänge (rechts).
Die Aufnahme von der Vorderseite (links) zeigt die perforierte Gegenelektrode und die
Aluminium-Leiterbahnen zur Kontaktierung der Mikrofonkapazität. Die Membranleiterbahn
wird durch die Gegenelektrode geführt und ist lateral durch einen mit Oxid gefüllten
Isolationsgraben isoliert. In einer Gegenelektrode mit einer Fläche von (0.8 mm)2 befinden
sich circa 40000 Löcher und nehmen 14% der Gesamtfläche ein. Sie werden von der
lichtmikroskopischen Aufnahme nicht aufgelöst. In der rechten Aufnahme von der
Waferrückseite erkennt man die KOH-Ätzgruben, deren Flanken von den kristallographischen
<111>-Ebenen gebildet werden. Im Membranbereich kann ohne eine akustische oder
elektrische Last eine statische Auslenkung beobachtet werden. Auf dieses Phänomen wird bei
den Messungen der statischen Membranauslenkung mit einem Interferometer näher
eingegangen.
Zur Auflösung der vertikalen Strukturgrößen im Mikrometerbereich wird ein
Rastelektronenmikroskop (REM) verwendet. Die Abbildung 2.6 zeigt zwei Querschnitte
durch die Mitte und den Rand der Mikrofonkapazität.
Abbildung 2.6: REM-Aufnahmen der Mikrofonkapazität (links) und dem Randbereich des
Mikrofons mit dem Übergang von Polysilizium zu epitaktischen Silizium (rechts).
20
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Die Mikrofone werden vor der KOH-Rückseitenätzung und der Opferschichtätzung
untersucht, damit das Brechen der Probe nicht die empfindlichen Strukturen zerstört. Die
gebrochene Probe wurde kurz mit Flusssäure behandelt, die das vergrabene Siliziumdioxid
und das Opferoxid im Spalt rückätzt. In der linken Aufnahme ist deutlich die dünne
monokristalline SOI-Membran (1 µm) und die dicke polykristalline Gegenelektrode (6 µm)
zu erkennen. Die Löcher in der Gegenelektrode besitzen nominell eine Kantenlänge von 1.5
µm und sind periodisch in einem Abstand von 4 µm angeordnet. Die vom Design
vorgesehene quadratische Form der Löcher wird durch die eingeschränkte Auflösung der
Fototechnik und den Ätzprozessen abgerundet. In der rechten Aufnahme mit einem
Querschnitt aus dem Randbereich des Mikrofons erkennt man an der Kristallstruktur des
Siliziums den Übergang von Polysilizium im Gegenelektrodenbereich zu monokristallinem
Silizium der Epitaxie im Außenbereich. Der gemessene Winkel von 53° zwischen der
schrägen Grenzfläche und der <100>-Kristallebene stimmt sehr gut mit dem erwarteten
Winkel von arctan(rmono/rpoly)=55.8° überein. Die verbleibende Stufe am Mikrofonrand
verläuft sehr flach und beträgt lediglich 1.5 µm. Die ovalen dunklen Bereiche sind Artefakte
der Probenpräparation und kennzeichnen Gebiete mit hoher Dotierstoffkonzentration.
2.3
Kapazitives Mikrofon mit polykristalliner
epitaktischer Silizum-Gegenelektrode
Siliziummembran
und
SOI-Wafer sind wegen der aufwändigen Herstellung deutlich teurer als StandardSiliziumwafer. Die nach dem BESOI-Verfahren realisierten SOI-Schichten besitzen darüber
hinaus eine relativ hohe Schichtdickenschwankung im Vergleich zu CVD-Schichten. Es
wurden daher Mikrofone mit dem zuvor beschriebenen Prozess auf Standard-Siliziumwafern
hergestellt und untersucht. Das mittige, vergrabene Siliziumdioxid des SOI-Wafers wird
durch ein thermisch verdichtetes CVD-SiO2 ersetzt, und an die Stelle der SOI-Schicht tritt
eine CVD-Polysiliziumschicht. Aufgrund der konformen Schichtabscheidung und der
geringen Oberflächenrauhigkeit wurde ein amorphes LPCVD-Polysilizium bei einer
Abscheidetemperatur von 560° C verwendet. Die Umwandlung zur polykristallinen Struktur
erfolgt durch einen mehrstufigen Heizprozess bei 550-700° C. Der Mikrofonprozess muss
durch die Substitution des Ausgangsmaterials nur geringfügig modifiziert werden.
Insbesondere bestehen weiterhin die Vorteile der Gegenelektroden-Epitaxie.
Zur Erhöhung der mechanischen Nachgiebigkeit der unter Zugspannung stehenden
Polysilizium-Membranen wurden diese derart strukturiert, dass sie nicht am gesamten Rand,
sondern nur an schmalen Balkenstrukturen aufgehängt sind. Zu diesem Zweck werden
schmale Schlitze in die Membran geätzt. Abbildung 2.7 zeigt zwei Varianten von geschlitzten
Membranen.
21
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Abbildung 2.7: Geschlitzte Membranen aus Polysilizium. Die schraffierte Fläche
verdeutlicht die Stützstellenbereiche der Biegebalken.
Mit jeweils vier langen Schlitzen in der Membran werden vier symmetrisch angeordnete
Biegebalken und ein großflächiger Membranbereich gebildet. Die Biegebalken des Designs
auf der linken Seite der Abbildung weisen eine Breite von ca. 55 µm und eine Länge von
170 µm auf. Die Biegebalken des zweiten Designs auf der rechten Seite sind mit 110 µm
doppelt so breit, dafür aber mit etwa 700 µm deutlich länger und daher sehr empfindlich. Zur
Verdeutlichung der Stützstellenbereiche werden diese durch eine schraffierte Fläche
gekennzeichnet. Im Vergleich zu geschlossen eingespannten Membranen besitzen die mit
Schlitzen versehenen Membranen eine geringere Biegesteifigkeit bei gleicher
Membranfläche.
Die Aufnahmen zeigen die frei beweglichen Membranen nach dem Ätzen des Opferoxides.
Die Interferenzstreifen in den Bereichen der Biegebalken deuten wieder auf eine statische
Membranauslenkung hin, wie sie durch eine auf die Membran wirkende Druckspannung
verursacht wird.
2.4
Kapazitives Mikrofon
Gegenelektrode
mit
polykristalliner
Siliziummembran
und
In diesem Abschnitt wird ein kapazitives Ein-Chip Silizium-Mikrofon vorgestellt, das
ebenfalls eine Membran aus polykristallinem Silizium aufweist und auf StandardSiliziumwafern hergestellt wird. Zur Erläuterung der Unterschiede zu den zuvor
beschriebenen Mikrofonen wird zunächst der Mikrofonaufbau vorgestellt (2.4.1).
Anschließend werden zwei wichtige Gesichtspunkte bei der Prozessentwicklung eingehender
behandelt: die integrierte Herstellung einer Gegenelektrode mit weiten Perforationslöchern
zur Reduzierung des akustischen Strömungswiderstandes (2.4.2) und die Entwicklung von
empfindlichen Membranen (2.4.3).
22
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
2.4.1 Mikrofonaufbau
Eine schematische Darstellung des Mikrofons zeigt die Abbildung 2.8. Der deutlichste
Unterschied im Mikrofonaufbau liegt in der vertauschten Position der beiden Elektroden, bei
dem die Membran über der Gegenelektrode angeordnet ist. Die Funktionsweise des
kapazitiven Wandlers wird dadurch nicht beeinflusst.
Abbildung 2.8: Schematische Darstellung des kapazitiven Silizium-Mikrofons mit
polykristalliner Siliziummembran und Gegenelektrode (nicht maßstabsgetreu).
Die Membran wird aus einer Polysiliziumschicht gebildet, die unter einer hohen Zugspannung
steht. Es sind daher zusätzliche Maßnahmen zur Erhöhung der Empfindlichkeit notwendig,
auf die im Abschnitt 2.4.3 eingegangen wird. Die Gegenelektrode besteht aus einer dünnen
n+-Polysiliziumschicht, die durch eine Siliziumnitridschicht vom Untergrund elektrisch
isoliert wird. Die erforderliche mechanische Steifigkeit der Rückseitenplatte stellt eine auf
dem Silizium-Substrat epitaktisch gewachsene Siliziumschicht bereit. Diese bildet aufgrund
der vom Substrat verschiedenen Dotierstoffkonzentration zugleich einen elektrochemischen
Ätzstopp für die Rückseitenätzung mit einer HF/HNO3-Lösung [Mee71]. Das anisotrope
Ätzverfahren bedingt die zirkulare Form der Mikrofonkapazität. Die dicke Rückseitenplatte
erzeugt keine eigene Topographie, da die Epitaxie zu ihrer Herstellung ganzflächig
aufgewachsen wird. Nicht dargestellt ist der in die monokristalline Silizium-Epitaxieschicht
integrierte Sperrschicht-Feldeffekttransistors (JFET, Junction Field-Effect Transistor), der mit
Polysiliziumwiderständen eine Impedanzwandlerschaltung auf dem Mikrofonchip bildet.
Die tiefe Ätzung der Perforationslöcher in der Rückseitenplatte steht am Anfang des
Mikrofonprozesses. Vor der weiteren Prozessierung müssen die Perforationslöcher möglichst
eben mit einer Schichtabscheidung aufgefüllt und verschlossen werden. Im nächsten
Abschnitt soll auf diesen Aspekt der Mikrofonherstellung näher eingegangen werden.
23
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
2.4.2 Integrierte Herstellung einer hochperforierten Gegenelektrode
Das Luftpolster im Kondensatorspalt wirkt wie ein Federelement, das eine Rückstellkraft auf
die Membran ausübt. Daher müssen in der Gegenelektrode Ausstrommöglichkeiten für die
Luft vorgesehen werden. Im einfachsten Fall werden in der Gegenelektrode
Perforationslöcher durch eine anisotrope Ätzung erzeugt, die zur weiteren Prozessierung mit
einer abgeschiedenen Schicht verschlossen werden. Diese Schicht bildet einen Teil der
Opferschicht, die den Kondensatorspalt definiert. In Abbildung 2.9 ist die Prozessfolge zur
Erzeugung einer freistehenden Membran und einer perforierten Gegenelektrode vereinfacht
dargestellt. Zunächst wird die Isolationsschicht aus Siliziumnitrid und das Polysilizium der
Gegenelektrode abgeschieden (a). In den Schichtstapel werden die Perforationsöffnungen bis
zum Silizium-Substrat anisotrop geätzt (b). Als Hartmaske dient ein Siliziumdioxid, das nach
der Ätzung entfernt wird. Zum vollständigen Ausfüllen der Perforationsöffnungen ist ein
abgeschiedenes Siliziumdioxid nötig, dessen Schichtdicke mindestens die Hälfte der lateralen
Abmessung einer Perforationsöffnung beträgt. Dickere Oxidschichten vergrößern den
Spaltabstand (c). Die elektrochemische Ätzung des Silizium-Substrates mit der EpitaxieGrenzfläche als Ätzstopp und die Opferschichtätzung stellen die Membran und
Rückseitenplatte fertig (d).
Abbildung 2.9: Herkömmliche Herstellung eines Perforationsloches in der Gegenelektrode
mit Hilfe der Opferschicht-Technik (nicht maßstabsgetreu).
Als Füll- und Opferschicht wurde ein LPCVD-TEOS-Siliziumdioxid verwendet. Der
reaktionsbestimmte Niederdruckprozess liefert eine gute Kantenbedeckung zur Auskleidung
der Perforationslöcher. Probleme bei der geschilderten Prozessierung treten bei dicken
Siliziumdioxidschichten auf. Der im Vergleich zu Silizium deutlich niedrigere thermische
Ausdehnungskoeffizient von Siliziumdioxid führt in der Siliziumdioxidschicht zu einer
Druckspannung [Kap00]. Insbesondere bei mit Oxid gefüllten Löchern kommt es zu
erheblichen Stresskonzentrationen in der Perforationsinnenwand und Oberfläche [Hu91], die
tiefe Risse im Siliziumsubstrat erzeugen können. Eine weitere technologisch bedingte
Beschränkung der Opferschichtdicke resultiert aus der zunehmenden Stufenhöhe der OxidStützstellenbereiche der Membran und den damit zusammenhängenden Schwierigkeiten einer
konformen Belackung mit Photoresist bei folgenden Fototechniken.
Mit der Schichtdicke vom Siliziumdioxid ist auch die Weite einer Perforationsöffnung
beschränkt, da sie maximal das Doppelte der Schichtdicke betragen darf. Der akustische
Strömungswiderstand einer Perforationsöffnung hängt nach dem Hagen-Poiseuilleschen
24
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Gesetz einer laminaren Rohrströmung mit der vierten Potenz vom Durchmesser bzw. der
Kantenlänge ab. Das bedeutet, dass selbst bei einer großen Anzahl von Perforationslöchern
die technologisch eingeschränkte Weite der Öffnung zu einem hohen Strömungswiderstand
führt und das dynamische Verhalten des Mikrofons beeinträchtigt. Eine Verbesserung ist mit
schlitzförmigen Perforationen zu erreichen, deren Schlitzbreite aber nicht deren Schlitzlänge
beschränkt ist.
Aufgrund dieser Problematik wurde ein neuer Prozess zur Herstellung einer gelochten
Gegenelektrode entwickelt, bei dem die Perforationsweite die doppelte Opferschichtdicke
übersteigen kann. Der in der Abbildung 2.10 vorgestellte Prozess kann in den
Mikrofonprozess vollständig integriert werden, da am Ende eine ebene Oberfläche
sichergestellt ist.
Abbildung 2.10: Integrationsfähiger Prozess zur Herstellung weiter Perforationsöffnungen in
der Rückseitenplatte.
Zunächst wird das Polysilizium der gewünschten Perforationsanordnung und -weite
entsprechend strukturiert (a). Darüber wird eine Siliziumdioxid-Schicht abgeschieden, in die
eine schmale Öffnung geätzt wird (b). Mit Hilfe dieser Hartmaske wird ein tiefes Loch in dem
Epitaxie-Silizium erzeugt (c). Anschließend wird mit einer isotropen Siliziumätzung das
Perforationsloch bis zur Ätzkante der Polysilizium-Gegenelektrode aufgeweitet (d). Durch
diese Prozessführung wird ein nahezu beliebig weites Perforationsloch im Silizium erzeugt,
das dennoch eine schmale Öffnung auf der Waferoberfläche besitzt. Diese Öffnung kann nun
mit einer verhältnismäßig dünnen Siliziumdioxidschicht verschlossen werden (e). Wie zuvor
wird der Kondensatorspalt nach der Abscheidung der Membran (f) durch die Rückseiten- und
Opferschichtätzung freigestellt (g,h).
Da die Öffnung der Hartmaske von der Perforationsweite unabhängig ist, schlägt sich bei dem
hier vorgestellten Prozess die technologische Einschränkung für die Dicke der
Siliziumdioxidschicht nicht auf die Weite der Perforation nieder. Einige wichtige Stationen
25
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
der technologischen Umsetzung zeigt die Bildfolge der Abbildung 2.11. Die Kennzeichnung
der REM-Aufnahmen lehnt sich an die der schematischen Querschnitte aus Abbildung 2.10
an.
c
e
d
g
Abbildung 2.11: Raster-Elektronen-Mikroskopaufnahmen
Perforationsöffnungen in der Rückseitenplatte.
der
Prozessierung
weiter
Die Aufnahmen zeigen die Prozessschritte der anisotropen Ätzung in das Silizium (c), der
isotropen Ätzung zur Aufweitung der Perforation (d), des Verschließens mit einer
Siliziumdioxidschicht (e) und der elektrochemischen Ätzung von der Waferrückseite (g).
2.4.3 Herstellung von Membranen mit hoher mechanischer Nachgiebigkeit
Amorph abgeschiedenes Polysilizium steht nach einer Kristallisation unter einer hohen
Zugspannung von bis zu 360 MPa [Kap00]. Mit dieser Zugspannung erhält man bei einer
1 µm dicken Membran mit 1 mm2 Membranfläche eine für typische Mikrofonanwendungen
um zwei Größenordnungen zu geringe mechanische Nachgiebigkeit von etwa 0.1 nm/Pa. Zur
Erhöhung der Empfindlichkeit von polykristallinen Siliziummembranen wurden zwei
voneinander unabhängig einsetzbare Maßnahmen ergriffen:
•
•
Reduzierung der mechanischen Zugspannung
Rekristallisation
Einsatz von fortschrittlichen Membrandesigns
durch
eine
Dotierstoff-induzierte
Reduktion von Schichtspannung durch Dotierung und Tempern
Die endgültige Schichtspannung im Polysilizium hängt vom Prozessablauf und einer Vielzahl
von Parametern ab: der Abscheidetemperatur, der in-situ Dotierung [Bieb95],
Kristallisationen, Dotierung durch Implantation oder Diffusion [Elb97] und weiteren
Temperungen zur Spannungsrelaxation dotierter Schichten [Schei96]. Eine Optimierung der
26
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
mechanischen Schichtspannung muss daher jeweils spezifisch auf den Abscheide- und
Gesamtprozess abgestimmt erfolgen.
Abbildung 2.12 zeigt den Einfluss der Dotierstoffkonzentration von implantierten PhosphorIonen auf die Schichtspannung von Polysilizium (Dicke 0.4 µm). Das Polysilizium wurde in
amorpher Form abgeschieden, kristallisiert und nach der Dotierung für weitere 60 min bei
900° C getempert. Die Schichtspannung wurde über die Durchbiegung der Substratscheibe
gemessen. Der Biegeradius ist umgekehrt proportional zur Schichtspannung und hängt sonst
nur von Materialkonstanten des Substrates und dem Dickenverhältnis von Substrat und
Schicht ab.
150
125
Schichtspannung [MPa]
100
75
Zugspannung
50
25
0
0.1
1
10
100
-25
-50
Druckspannung
-75
-100
15
Implantationsdosis [10
-2
cm ]
Abbildung 2.12: Dotierstoffabhängigkeit der mechanischen Spannung einer PolysiliziumMembran bei Implantation von Phosphor-Ionen und anschließender Temperung.
Mit der Konzentration der Phosphor-Dotierung nimmt die intrinsische Zugspannung ab. In
Einklang mit dem Modell einer durch Phosphor-Ionen in den Korngrenzen begünstigten
Rekristallisation ist ein gewisse Dotierstoffkonzentration notwendig. Bei einer Konzentration
über 3-5⋅1020 cm-3 herrscht sogar eine Druckspannung in der Polysiliziumschicht. Vermutlich
basiert diese auf den im Vergleich zu Silizium größeren Ionenradius von Phosphor als
Element der 5. Hauptgruppe [Orp91]. Der Übergang von einer Zug- zu einer Druckspannung
erfolgt relativ abrupt. Da eine Druckspannung in einer Mikrofonmembran in jedem Fall
ausgeschlossen werden muss, wird man in der Praxis aufgrund von Prozessschwankungen
eine vollständig spannungsfreie Membranschicht aus Polysilizium nicht reproduzierbar
herstellen können.
Feder-Membranen
Zur Einhaltung von Fertigungstoleranzen wird man eine Zugspannung in der PolysiliziumMembran von einigen 10 MPa einstellen. Stattdessen wird die mechanische Nachgiebigkeit
durch den Einsatz von fortschrittlichen Membrandesigns weiter erhöht. Dazu wurde das
Konzept der geschlitzten Membranen aus Kapitel 2.3 weiterentwickelt, bei denen die
Membranfläche an schmalen Balkenstrukturen befestigt ist. Die folgende Abbildung zeigt die
27
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Layouts und Mikroskopaufnahmen von drei realisierten Varianten solcher im Folgenden als
„Feder-Membranen“ bezeichneten Mikrofonmembranen.
Abbildung 2.13: An Biegebalken befestigte Mikrofonmembranen.
Der Vorteil einer geringeren Biegesteifigkeit einer Feder-Membran ist derselbe wie bei einer
geschlitzten Membran. Im Unterschied zu den geschlitzten Membranen wird der gesamte
mechanisch und elektrisch inaktive Membranbereich entfernt, so dass nur konkave
Membranränder vorliegen. Ein konkaver Membranrand neigt weniger zu einer Verbiegung
bei einem vertikalen Spannungsgradienten entlang der Schichtdicke. Die offenen Flächen in
der Membran können weiterhin dazu verwendet werden, einen akustischen Kurzschluss bei
tiefen Frequenzen zu bewirken. Dies gelingt über den gezielten Einsatz von
Perforationslöchern in diesen Bereichen, deren gesamter Strömungswiderstand mit der
Membrannachgiebigkeit eine untere Grenzfrequenz für die Mikrofonempfindlichkeit
definieren. Die dynamische Begrenzung der Mikrofonempfindlichkeit ist beispielsweise zur
Dämpfung von niederfrequenten Störsignalen in KFZ-Anwendungen interessant. Ein weiterer
Vorteil von Balken-Membranen liegt in der reduzierten parasitären Randkapazität, die sich
aus der Stützfläche der Membran, dem Randoxid und der dem Silizium-Substrat
zusammensetzt. Eine reduzierte parasitäre Kapazität erhöht die relative Kapazitätsänderung
und damit das elektrische Ausgangssignal.
Die genannten Vorteile treten besonders deutlich hervor, wenn wenige schmale Biegebalken
verwendet werden. Damit wächst allerdings die Anfälligkeit gegenüber einen
Spannungsgradienten in der Membran, der zu einer Randverbiegung führen kann. Diese
Problematik ist qualitativ bei der Balken-Membran mit vier Stützstellen zu erkennen, bei der
trotz der konkaven Form eine Randverbiegung zu beobachten ist (Abbildung 2.13, Mitte).
28
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Korrugierte Membranen
Bei einer korrugierten Membran wird in Form einer Stufe ein Federelement in einer
geschlossenen Membran realisiert. Diese Membranbereiche können sich unter den Einfluss
einer Zugspannung lateral ausdehnen und daher die Spannung teilweise aufnehmen. Den
Nachteil von frei beweglichen Membranrändern, wie sie bei den Feder-Membranen auftreten,
besitzen diese Membranen nicht. Die Abbildung 2.14 zeigt eine Mikroskopaufnahme einer
korrugierten Membran mit einem schematischen Querschnitt durch die Mikrofonkapazität.
Die Korrugationen verursachen keinen Mehraufwand in der Prozessierung, da sie mit einer
Fototechnik zusammen mit den Bumps in der Membran hergestellt werden. Die
Korrugationen werden erzeugt, indem vor der Membranabscheidung eine Vertiefung in das
Opferoxid geätzt wird. Da die Ätzung nicht vollständig anisotrop ist, sind die
Korrugationswände leicht angewinkelt. Die Tiefe der Ätzung definiert daher die Höhe der
Korrugation und kann nur einen Bruchteil der Opferschichtdicke betragen. Eine Korrugation
verringert den Abstand zwischen der Membran und Gegenelektrode. Außerdem können in
den Bereichen der Korrugationen keine Bumps platziert werden. Um die Gefahr eines
Kontaktes durch Feuchtigkeit (Sticking) und Spannung (Snap Down) nicht zu erhöhen,
werden die Korrugationen vorteilhaft in der Nähe der Einspannung in die Membran
eingebracht, wo die Membranauslenkung am geringsten ist. Diese Einschränkung wirkt sich
auf die Breite, dem Abstand und der Anzahl der Korrugationen aus.
Abbildung 2.14: Fotographie, REM-Querschnitt und Skizze einer geschlossenen Membran
mit Korrugationen.
Die mechanische Nachgiebigkeit der Membran kann durch die Anzahl der ringförmig
angeordneten Korrugationsringe im Randbereich eingestellt werden. Zur Untersuchung der
Abhängigkeit zwischen Korrugationsanzahl und Nachgiebigkeit wurden Membranen mit 4
bzw. 8 Korrugationen hergestellt. Die reine Biegesteifigkeit einer korrugierten Membran ist
im Vergleich zur einfachen geschlossenen Membran größer. Dieser Effekt ist in der Praxis
nicht zu beobachten, da der Relaxationseffekt der Zugspannung überwiegt. Numerische
Simulationen zum mechanischen Verhalten korrugierter Membranen werden im dritten
Kapitel behandelt. Die Aufnahme der Abbildung 2.15 zeigt ein Membrandesign, das die
Vorteile von Feder- und Korrugationsmembranen kombiniert. In eine Feder-Membran mit
reduzierter parasitärer Randkapazität und Biegesteifigkeit werden zusätzlich Korrugationen
zur Spannungsrelaxation eingebracht. Der enge Krümmungsradius zwischen zwei
Biegebalken verhindert Randverbiegungen aufgrund von Spannungsgradienten.
29
Herstellung von Silizium-Mikrofonen in BiCMOS-Technologie
Abbildung 2.15: An Biegebalken aufgehängte Membran mit Korrugationen.
2.5
Zusammenfassung
Anhand analytischer Gleichungen wurde der Einfluss verschiedener Prozessparameter auf die
Mikrofonempfindlichkeit und Kollapsspannung geschlossener Membranen diskutiert. Sie
verdeutlichen, dass die Miniaturisierung von Silizium-Mikrofonen eine niedrige mechanische
Spannung in der Membran erfordert. In dem neuen entwickelten Mikrofonprozess wird eine
niedrigdotierte, monokristalline Siliziumschicht eines SOI-Wafers verwendet. Ein alternativer
Ansatz zur Herstellung empfindlicher Silizium-Mikrofone ist der Einsatz von Membranen mit
Federstrukturen. Diese Mikrofone werden auf Standard-Siliziumwafern mit einer
polykristallinen Silizium-Membran unter Zugspannung hergestellt.
Die Luftkompression im schmalen Kondensatorspalt eines Silizium-Mikrofons begrenzt die
dynamische Bandbreite der Empfindlichkeit. Die mit dem präsentierten Prozess integriert
hergestellten weiten Perforationsöffnungen in der Rückseitenplatte mit einem geringen
akustischen Widerstand sorgen bei sehr empfindlichen Mikrofonen für eine ausreichende
Entdämpfung.
30
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
Kapitel 3
Numerische Simulationen zum mechanischen Verhalten
von Mikrofonmembranen
Die Grundlage jeder Modellierung und Simulation bildet das Differential-Algebraische
Gleichungssystem des physikalischen Systems mit den kontinuierlichen Feldgrößen. In der
Strukturmechanik treten jedoch häufig Systeme auf, die nicht analytisch zu berechnen sind.
Eine numerische Näherungslösung ist mit der Finite-Elemente-Methode (FEM) möglich
[Bath90], bei der das Kontinuum in eine endliche Anzahl von Gebieten, den finiten
Elementen, unterteilt wird. Mit der Methode der Finiten-Elemente können auch irreguläre
Strukturen mit nahezu beliebiger Genauigkeit, die mit der Feinheit der Diskretisierung und
der Ordnung der Ansatzfunktionen zunimmt, simuliert werden.
Die Membran als akustisch-mechanischer Wandler bildet das Herzstück des kapazitiven
Mikrofons. Die Kenntnis des elastischen Verhaltens der Membran ist für eine erfolgreiche
Modellierung des Mikrofons ausschlaggebend. Da nur für einfache Membranformen
analytische Näherungslösungen zum Spannungs-Verformungszustand und zur mechanischen
Nachgiebigkeit existieren, werden die verschiedenen Mikrofonmembranen mit einem FiniteElemente-Programm simuliert. In Abschnitt 3.1 wird zunächst die Zielsetzung und der
generelle Simulationsablauf der numerischen Analysen beschrieben. Anschließend wird auf
die einzelnen Membrantypen eingegangen: quadratische und kreisförmige geschlossene
Membranen (3.2), Feder-Membranen (3.3) und korrugierte Membranen (3.4).
3.1
Zielsetzung und Simulationsablauf
In den folgenden Abschnitten wird das mechanische Verhalten der Mikrofonmembranen
numerisch mit der Methode der finiten Elemente untersucht. Die Ergebnisse dienen dazu, den
Einsatzbereich bekannter Näherungslösungen zu erweitern bzw. neue Beziehungen
abzuleiten. Im Einzelnen wird der Spannungszustand der Membran, die statische
Membranverbiegung ohne Druckbelastung und die Auslenkung der Membran bei einem
äußeren Druck simuliert.
Vor der Simulation wird ein der Problemstellung angepasster Elementtyp ausgewählt, der bei
minimalem Rechenaufwand zuverlässige Ergebnisse liefert. In einem ersten
Simulationsschritt wird eine Zugspannung durch eine thermische Kontraktion in der
Membran eingebracht. Für den ebenen Spannungszustand, d.h. unter der Annahme, dass in
Richtung der Membrandicke keine Spannung wirkt (σz=0), gilt für die Dehnungen in der
homogenen isotropen Membran
1
⋅ (σ x − υ ⋅ σ y ) = α ⋅ ∆T ,
E
1
ε y = ⋅ (σ y − υ ⋅ σ x ) = α ⋅ ∆T .
E
εx =
(3.1)
(3.2)
31
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
Der thermische Ausdehnungskoeffizient α wird derart gewählt, dass die gewünschte
mechanische Spannung bei einer Temperaturlast ∆T erzeugt wird. Durch Umformen erhält
man den Zusammenhang zwischen dem Ausdehnungskoeffizienten und der mechanischen
Spannung σ (=σx=σy)
α=
σ ⋅ (1 − ν )
E
⋅
1
.
∆T
(3.3)
Es soll betont werden, dass es sich nicht um eine Simulation der Temperaturabhängigkeit
handelt, sondern α lediglich zur Spannungserzeugung eingeführt wird. Die
Temperaturdifferenz kann im Prinzip beliebig gewählt werden, z.B. ∆T=-1° K für eine
Zugspannung. Nach dieser Temperaturlast kann der Spannungszustand der Membran und eine
eventuell hervorgerufene statische Verbiegung der Membran untersucht werden.
Im zweiten Simulationsschritt wird die vorgespannte Membran mit einem homogenen
statischen Druck belastet. Aus den simulierten Elementverschiebungen wi wird schließlich die
mechanische Nachgiebigkeit durch Aufsummierung berechnet
∑w ⋅ A
=
p⋅∑ A
i
Cm
i
i
.
(3.4)
i
i
Darin ist Ai die Fläche des Elementes i mit der Verschiebung wi. Die Größe der mechanischen
Nachgiebigkeit ist von besonderer Bedeutung für die Simulation der Empfindlichkeit von
kapazitiven Mikrofonen. In Kapitel 4 wird gezeigt, dass die Definition (3.4) bei einem
kapazitiven Wandler zweckmäßig ist, wenn die Auslenkung im Vergleich zur
Kondensatorspalthöhe klein ist. Die gewonnenen Simulationsergebnisse zur
Membrannachgiebigkeit können dann in parametrisierter Form als konzentriertes Element in
das Netzwerkmodell des Mikrofons eingehen.
3.2
Quadratische und kreisförmige Membranen
Für die mechanische Nachgiebigkeit von quadratischen und kreisförmigen Membranen
existieren Nährungslösungen, die mit Hilfe von FEM-Analysen bewertet werden sollen (3.2.1,
3.2.2). Auf Basis der Simulationsergebnisse wird eine verbesserte Näherungslösung
angegeben, die bei Nichtlinearitäten geringere Simulationsfehler liefert (3.2.3).
3.2.1 Quadratische Membranen
Die Durchbiegung einer Mikrofonmembran unter Druckbelastung hängt von der inneren
Biegesteifigkeit und der mechanischen Schichtspannung ab. Eine geschlossene analytische
Lösung der partiellen Differentialgleichung einer quadratischen Membran existiert nicht. Eine
näherungsweise Berechnung wurde von [Hoh86] durchgeführt. Zunächst wird das
mechanische Verhalten einer Platte, d.h. bei einer vernachlässigbaren Schichtspannung
gegenüber der inneren Biegesteifigkeit, über die Minimierung der kinetischen und
potentiellen Energie nach dem Rayleigh-Verfahren berechnet. In der gleichen Weise kann der
Fall einer vernachlässigbaren Biegesteifigkeit behandelt werden. Die häufig verwendete
kosinusförmige Ansatzfunktion gibt die tatsächliche Biegeform nicht akkurat wieder
32
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
([Pan90]) und wurde von [Mai95] erweitert. Die Rechnungen führen zu Lösungen für die
Auslenkungsfunktionen einer reinen Platte oder reinen Membran, aus denen durch Integration
über die Membranfläche effektive mechanische Nachgiebigkeiten CPlatte und CMembran, für
beide Spezialfälle abgeleitet werden. Mit diesen ist eine asymptotisch gute Näherung für den
allgemeinen Fall durch die Addition der Plattensteifigkeit 1/CPlatte und der
„Spannungssteifigkeit“ 1/CMembran möglich und führt zur mechanischen Nachgiebigkeit einer
quadratischen Membran Cm,q
C m ,q ≈
C Platte ⋅ C Membran
C Platte + C Membran




a2
1


=
⋅
2
 .
28.6 ⋅ σ ⋅ t
7.7 ⋅ E ⋅ t

+ 1 
2
2
 (1 − υ ) ⋅ σ ⋅ a

(3.5)
Zur Beurteilung dieser Näherungslösung wurden nichtlineare FEM-Simulationen einer
quadratischen Membran durchgeführt. Da die Membranen erheblich dünner als lang und eben
sind, können zur Verkürzung der Rechenzeit Schalenelemente verwendet werden. Bei einem
Schalenelement handelt es sich um ein aus dem dreidimensionalen Kontinuum degeneriertes
Element mit der Dicke als Parameter. Schalenelemente setzen voraus, dass Spannungen
entlang der Membrandicke vernachlässigt werden können und dass Teilchen, die ursprünglich
eine senkrechte Gerade auf der Mittelfläche bildeten, auf einer Geraden bleiben. Die Qualität
der Simulationsergebnisse wird durch eine Erhöhung der Elementordnung und der
Elementanzahl kontrolliert. Verwendet werden Elemente mit vier und acht Knoten pro
Element, d.h. mit linearen oder quadratischen Ansatzfunktionen. Jeder Knoten besitzt sechs
Freiheitsgrade: drei Verschiebungsfreiheitsgrade für die Lage der Knoten im Raum und drei
Rotationsfreiheitsgrade zur Bestimmung der Verdrehung der Normalen auf den Knoten
gegenüber der Elementmittelfläche. Die Schalenelemente unterstützen geometrische
Nichtlinearitäten, die bei mechanischen Spannungen (stress stiffening) und großen
Verformungen (large deformation) auftreten.
Abbildung 3.1 vergleicht die mechanische Nachgiebigkeit einer quadratischen Membran nach
Finite-Elemente-Simulationen mit den Erwartungswerten der Gleichung (3.5). Der
Simulationsparameter ist die Zugspannung σ, die für zwei Kantenlängen (a=600, 1000 µm)
von 10 kPa bis 1 GPa variiert wird. Die Membran bestehe aus einer Siliziumschicht mit einem
Elastizitätsmodul E von 1.62⋅1011 MPa, einer Querkontraktionszahl von 0.26 und einer Dicke
von t=1 µm.
33
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
100
30
Abweichung zwischen
Näherung und Simulation [%]
Nachgiebigkeit Cm,q [nm/Pa]
FEM (lineare Ansatzfkt., 6.400 Elemente)
a=1000 µm
10
a=600 µm
1
0.1
FEM-Simulation
FEM (quadratische Ansatzfkt., 14.400 Elemente)
25
20
a=600 µm
15
a=1000 µm
10
5
Nichtlinearität durch
Spannungsversteifung
0
analytische Näherung Gl. (3.5)
0.01
0.01
0.1
1
10
100
Zugspannung σ [MPa]
1000
-5
0.01
0.1
1
10
100
1000
Zugspannung σ [MPa]
Abbildung 3.1: Nachgiebigkeit quadratischer Membranen nach der analytischen Näherung
und numerischen Simulationen.
Im linken Graphen ist die mit der Zugspannung abnehmende mechanische Nachgiebigkeit
dargestellt. Die Übereinstimmung zwischen der Näherung und den FEM-Simulationen ist für
beide Kantenlängen relativ gut, wobei die Näherung im mittleren Spannungsbereich eine
weichere Membran beschreibt. Im rechten Graphen ist die relative Abweichung zwischen
beiden Lösungen in Abhängigkeit von der Zugspannung aufgetragen, die aus der
Nichtlinearität der Spannungsversteifung resultiert. Ist die Zugspannung vergleichbar mit der
Biegespannung, gilt also CPlatte≈CMembran, weicht die tatsächliche Auslenkungsfunktion von
den Spezialfällen einer reinen Platte bzw. Membran ab, so dass die Annahme einer linearen
Superposition beider Rückstellkräfte in Gleichung (3.5) zu dem beobachteten Fehler führt.
Eine Erhöhung der Ordnung der Ansatzfunktion und der Anzahl der Elemente verändert die
Ergebnisse der FEM-Simulation nur geringfügig, so dass von einem geringen
Diskretisierungsfehler ausgegangen werden kann.
Eine weitere Nichtlinearität tritt bei großen Verformungen auf. Bei Membranen macht sich
diese geometrische Nichtlinearität bemerkbar, wenn die Membranauslenkung Werte in der
Größenordnung der Membrandicke annimmt [Timo59]. Dann erzeugt die Auslenkung
zusätzliche innere Spannungen in der Membran, die zu einer Versteifung führen. Die
Verformungsversteifung demonstriert die Simulation einer 400 nm dicken Membran in
Abbildung 3.2. Die Kantenlänge der Membran beträgt 1000 µm.
Im Gegensatz zur Simulation einer 1 µm dicken Membran beobachtet man bei einer 0.4 µm
dicken Membran eine hohe Abweichung zwischen der analytischen Näherung und der
nichtlinearen FEM-Simulation im Bereich niedriger Zugspannungen. Die FEM-Simulationen
liefern deutlich niedrigere mechanische Nachgiebigkeiten, die auf die Berücksichtigung der
Verformungsversteifung zurückzuführen sind. Wird der Effekt der Verformungsversteifung in
der Simulation bewusst deaktiviert, dann stimmt die Näherungslösung im Rahmen des Fehlers
der Spannungsversteifung mit der Simulation überein (gestrichelte Linie).
34
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
1000
Abweichung zwischen
Näherung und Simulation [%]
Nachgiebigkeit Cm,q [nm/Pa]
t=0.4 µm
100
t=1 µm
10
analytische Näherung Gl. (3.5)
FEM ohne Verformungsversteifung
nichtlineare FEM
1
0.01
0.1
1
10
Zugspannung σ [MPa]
70
nichtlineare FEM
65
FEM ohne Verformungsversteifung
60
55
Nichtlinearität durch
50
Verformungsversteifung
45
40
35
30
25
t=0.4 µm
t=1 µm
20
15
10
5
0
-5
0.01
0.1
1
10
100
1000
Zugspannung σ [MPa]
Abbildung 3.2: Nichtlineare Verformungsversteifung bei großen Auslenkungen und dünnen
Membranen.
3.2.2 Kreisförmige Membranen
Die partielle Platten-Differentialgleichung mit intrinsischer Eigenspannung kann für eine
kreisförmige Membran geschlossen gelöst werden. Die Lösung ist bereits für diesen einfachen
Fall kompliziert [Timo59]. Eine Näherung ist wieder durch die Superposition der getrennten
Lösungen einer Platte und einer Membran ohne Biegespannungen möglich. Analog zu
Gleichung (3.6) erhält man einen Ausdruck für die Nachgiebigkeit einer kreisförmigen
Membran




R
1


≈
⋅
2
 .
8 ⋅ t ⋅σ
2⋅ E ⋅t

+ 1 
2
2
 (1 − υ ) ⋅ σ ⋅ R

2
C m,k
(3.6)
Darin ist R der Radius der Membran, t die Dicke und σ die mechanische Spannung. Wieder
wurden numerische Simulationen durchgeführt und die relative Abweichung mit der
Näherungslösung (3.6) gebildet. Die Simulationsergebnisse von kreisförmigen Membranen
sind qualitativ mit denen der quadratischen Membranen vergleichbar: die geometrischen
Nichtlinearitäten der Spannungs- und Verformungsversteifung werden von der
Näherungslösung nicht erfasst und führen zu den beobachteten Abweichungen. Im nächsten
Abschnitt sollen numerische Simulationen zur Ableitung einer verbesserten Beziehung für die
mechanische Nachgiebigkeit von quadratischen und kreisförmigen Membranen genutzt
werden.
35
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
3.2.3 Ableitung einer erweiterten Beziehung zur nichtlinearen MembranNachgiebigkeit
In den numerischen Simulationen wurden zwei nichtlineare Effekte identifiziert, die zu einem
Fehler bei der Verwendung der analytischen Näherungslösungen führen:
•
•
die Verformungsversteifung bei großen Membrandurchbiegungen und
die Spannungsversteifung bei gemischten Platten- und Membranverhalten.
Die Verformungsversteifung kann vernachlässigt werden, wenn die Membrandicke
wesentlich größer als die Auslenkung ist, d.h. t>>∆x≈Cm⋅p gilt. Diese Bedingung sollte durch
das Membrandesign immer erfüllt werden, damit die Mikrofonempfindlichkeit mit höherem
Schalldruck nicht abnimmt.
Selbst unter diesen Umständen kann der Effekt der Spannungsversteifung zu nennenswerten
Fehlern in der Simulation führen, wenn die Näherungslösungen verwendet werden. Nach
Abbildung 3.2 beträgt der Simulationsfehler bei einer 1 µm dicken Membran mit einer
Kantenlänge von 500 µm bei 10 MPa etwa 20%. Ein Maß dafür, ob der Fehler relevant ist,
kann aus der Bedingung CPlatte=CMembran für die quadratische und kreisförmige Membran
bestimmt werden
σ c ,q =
σ c ,k
7.7 ⋅ E ⋅ t 2
,
(1 − υ 2 ) ⋅ a 2
2⋅ E ⋅t2
.
=
(1 − υ 2 ) ⋅ R 2
(quadratische Membran)
(3.7)
(Kreismembran)
(3.8)
Der Effekt der Spannungsversteifung hängt stark von dem Verhältnis der Membrandicke t zu
der lateralen Abmessung (R bzw. a) ab. Nimmt die Membranspannung σ Werte um die
charakteristische Spannung σc an, dann muss die Spannungsversteifung in die Betrachtungen
zur mechanischen Nachgiebigkeit einbezogen werden. Um eine verbesserte algebraische
Gleichung zu erhalten, die für die Netzwerkmodellierung des Mikrofons benötigt wird, wurde
mit einem weit gefassten Parameterbereich einer Polysilizium-Membran die mechanische
Nachgiebigkeit numerisch simuliert. Die Simulationsparameter sind der Membranradius bzw.
die Membrankantenlänge, die Membrandicke und die Membranspannung. Sie wurden in
folgenden Wertebereichen variiert:
•
•
•
•
Radius R:
Kantenlänge a:
Membrandicke t:
Membranspannung σ:
100-700 µm, t0=0.2 µm, σ0=32 MPa
400-1400 µm, t0=0.2 µm, σ0=32 MPa
0.05-1 µm, R0=500 µm (a0=1000 µm), σ0=32 MPa
1-256 MPa, R0=500 µm (a0=1000 µm), t0=0.2 µm
Der Parameterbereich deckt Membrannachgiebigkeiten von 0.2-125 nm/Pa ab, denen
typischerweise Leerlauf-Empfindlichkeiten von 0.2-125 mV/Pa entsprechen (U0=2V,
x0=2 µm).
Aus den Ergebnissen der FEM-Simulationen konnte ein Korrekturterm Km zur Einbeziehung
der nichtlinearen Spannungsversteifung abgeleitet werden, der für eine kreisförmige und
quadratische Membran gleichermaßen zu guten Ergebnissen führt
36
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
K m (σ , σ c ) =
1
σ 
1 + 1.1 ⋅  c 
σ 
0.6
.
(3.9)
Mit dem Korrekturterm und den herkömmlichen analytischen Näherungslösungen für die
mechanische Nachgiebigkeit Cm ergibt sich für die modifizierte Nachgiebigkeit Cm* eine sehr
kompakte Darstellung
Cm
*






1
≡ K m ⋅ Cm = 
⋅
0.6
σ


 1.1 ⋅  c  + 1 


4σ2444
144
3
Nichtlineare
Spannungsversteifung
 R2
( Kreis )

⋅  2 8 ⋅ t ⋅σ
.
a 30 ⋅ t ⋅ σ (quadr.)
1
σc
+1
σ23
1
(3.10)
Lineare
Spannungsversteifung
Km kann als eine nichtlineare Korrektur des Effektes der Spannungsversteifung interpretiert
werden. In Abbildung 3.3 ist die Abweichung zwischen der FEM-Simulation und der
Näherungslösung mit und ohne Korrektur gegen den Spannungsgrad σ/σc aufgetragen.
25
quadratische
Membran
Kreismembran
Dicke: 0.05-1 µm
10
verbesserte
Näherungslösung
C*m,q
5
Dicke: 0.05 -1 µm
20
Näherungslösung
Cm,q
15
Radius: 100-700 µm
Spannung: 1-250 MPa
Spannung: 1-250 MPa
Abweichung [%]
Abweichung [%]
20
25
Kantenlänge: 400-1400 µm
Näherungslösung
Cm,k
15
10
verbesserte
Näherungslösung
C*m,k
5
0
-5
0
10
100
1000
Spannungsgrad σ/σc
10000
10
100
1000
Spannungsgrad σ/σc
10000
Abbildung 3.3: Verringerung des Modellierungsfehlers durch die Einführung eines
nichtlinearen Korrekturterms.
Mit der Erweiterung der Gleichungen zur Membrannachgiebigkeit wird eine sehr gute
Übereinstimmung mit den numerischen FEM-Simulationen über einen weiten Wertebereich
der Designparameter erreicht. Der Restfehler der modifizierten Näherungsgleichung beträgt
weniger als 3% und ist damit kleiner als die technologisch bedingten Schwankungen in der
Membrandicke und der Schichtspannung, so dass die Simulationsgenauigkeit ausreichend ist.
37
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
3.3
Feder-Membranen
Mit Feder-Membranen sollen Membranen bezeichnet werden, deren kapazitiv wirksame
Fläche von einer bestimmten Anzahl von Biegebalken gehalten werden und daher nur an
wenigen Stützstellen befestigt sind. Im Vergleich zu einer am gesamten Umfang
eingespannten Kreismembran wirken kleinere Rückstellkräfte einer Durchbiegung der FederMembran entgegen. In Abbildung 3.4 ist eine Membran mit vier Federstrukturen dargestellt.
R0
b
R
t
Abbildung 3.4: Schematische Darstellung einer Feder-Membran.
Die spezifischen Designparameter sind der „Radius“ R, die Anzahl der Federn N, die
Stegbreite b und die kürzeste Entfernung zwischen der Membranmitte und dem Membranrand
R0. Zunächst wird an einer spannungsfreien Membran die erhöhte mechanische
Nachgiebigkeit einer Feder-Membran demonstriert (3.3.1). Anders als bei einer
Kreismembran, bei der die mechanische Spannung in der Schicht konstant ist, stellt sich in
einer Feder-Membran eine Spannungsverteilung ein. Die Nachgiebigkeit hängt daher nicht
allein von dem Betrag der intrinsischen Schichtspannung ab, sondern auch von der Verteilung
über die Membran (3.3.2). Der Einfluss des veränderten Spannungszustandes wird
exemplarisch an einer Feder-Membran untersucht, um schließlich auf eine allgemein gültige
Beschreibung der Nachgiebigkeit von Feder-Membranen einzugehen (3.3.3). Ergänzend wird
der Einfluss von vertikalen Spannungsgradienten in der Membran behandelt (3.3.4) um
abschließend die Simulationsergebnisse zu diskutieren (3.3.5).
3.3.1 Spannungsfreie Feder-Membran
Die aus der Geometrie einer Feder-Membran resultierende Erhöhung der Durchbiegung bei
einem statischen Druck (1 Pa) zeigt die Abbildung 3.5, in der die simulierten Biegelinien
einer Kreismembran und einer Feder-Membran mit gleichem Radius (500 µm) und gleicher
Membrandicke (1 µm) miteinander verglichen werden. Die Feder-Membran besitzt vier
100 µm breite Federstrukturen mit einem inneren Radius R0 von 250 µm. Insgesamt beträgt
bei diesem Design einer Feder-Membran die Membranfläche etwa 46% der Fläche einer
Kreismembran mit gleichem Radius. Durch das Setzen geeigneter Symmetriebedingungen
muss immer nur eine Feder der Membran berechnet werden. Nichtlineare Effekte können
vernachlässigt werden, da die Dicke der Membranen größer als deren Auslenkungen ist und
die Membranen als spannungsfrei angenommen werden.
38
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
180
160
120
100
80
60
40
20
Federmembran
0.9
normierte Auslenkung
140
Auslenkung [nm]
1
Federmembran (FEM)
Kreismembran (analytisch)
Kreismembran (FEM)
Kreismembran
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0
100
200
300
400
Entfernung von der Membranmitte [µm]
500
0
100
200
300
400
500
Entfernung von der Membranmitte [µm]
Abbildung 3.5: Biegelinien einer Kreis- und Feder-Membran ohne Schichtspannung.
Die Mittenauslenkung der Feder-Membran ist mit 156 nm mehr als doppelt so groß wie die
der Kreismembran (67 nm), obwohl die auf die Feder-Membran wirkende Kraft wegen der
geringeren Fläche deutlich kleiner ist. Die im rechten Graphen dargestellte und auf die
Mittenauslenkung normierte Membranauslenkung macht deutlich, dass sich eine FederMembran erwartungsgemäß im Bereich der Biegebalken stärker durchbiegt als eine
Kreismembran, deren Biegelinie durch
p
12 ⋅ (1 − υ 2 ) ⋅ p
w(r ) =
⋅ (r 2 − R 2 ) 2 ≡
⋅ (r 2 − R 2 ) 2
3
64 ⋅ D
64 ⋅ E ⋅ t
(3.11)
gegeben ist [Timo59]. w ist die vom Druck p abhängige Auslenkung bei der Entfernung r von
der Membranmitte. Der Vergleich mit der Biegelinie einer Kreismembran macht deutlich,
dass eine spannungsfreie Feder-Membran nicht einfach durch eine effektiv kleinere
Plattensteifigkeit D beschrieben werden kann.
3.3.2 Feder-Membran mit Schichtspannung
Nach der Betrachtung von rein biegesteifen Membranen soll nun das mechanische Verhalten
untersucht werden, wenn zusätzlich eine Zugspannung in der Membran wirkt. Bei einer
Kreismembran ist sie überall in der Membran gleich groß: σ(x,y)=σ0. In einer Feder-Membran
hingegen wird die Zugspannung eine Funktion des Ortes sein: σ(x,y)=f(x,y). In Abbildung 3.5
ist die simulierte Spannungsverteilung einer Feder-Membran dargestellt, in die eine
intrinsische Zugspannung von σ0=30 MPa eingebracht wurde.
39
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
45
Membranspannung [MPa]
40
35
Versteifung
intrinsische Schichtspannung
30
25
A
Entspannung
20
15
B
10
5
0
0
100
200
300
400
500
Entfernung von der Membranmitte [µm]
Abbildung 3.6: Spannungsverteilung in einer Feder-Membran.
Ausgehend von einer intrinsischen Schichtspannung von 30 MPa bildet sich im
Gleichgewicht eine Verteilung mit Spannungen von 10-42 MPa aus. Während es in den
mittleren Membranbereichen zu einer Entspannung über eine Ausdehnung der freistehenden
Membranränder kommt (Weg B), konzentriert sich die Spannung in den Bereichen der
Federstruktur (Weg A). Die über die Fläche der Feder-Membran gemittelte Spannung beträgt
<σ>=24.9 MPa, d.h. in Summe relaxiert ein Teil der Schichtspannung. Um den Einfluss der
Verteilung der Membranspannung auf das Auslenkungsverhalten zu untersuchen, wird in
einer Simulation eine konstante Spannung in der Feder-Membran erzwungen, indem die
Verschiebungsfreiheitsgrade in der Membranebene gesperrt werden. Abbildung 23 zeigt die
Durchbiegung einer Feder-Membran bei konstanter und verteilter mechanischer Spannung.
7
1
Auslenkung [nm]
0.9
Feder-Membran
σ(x,y)=f(x,y)
normierte Auslenkung
Entspannung
6
5
4
Feder-Membran
σ(x,y)=konst
3
2
Versteifung
1
Feder-Membran
σ(x,y)=konst
0.8
0.7
0.6
Feder-Membran
σ(x,y)=f(x,y)
0.5
0.4
Kreismembran
0.3
0.2
0.1
0
0
0
100
200
300
400
Entfernung von der Membranmitte [µm]
500
0
100
200
300
400
500
Entfernung von der Membranmitte [µm]
Abbildung 3.7: Auslenkungsfunktion einer Feder-Membran bei konstanter und verteilter
mechanischer Spannung.
Im Bereich der Membranmitte ist die Auslenkung bei einer Verteilung der Spannung größer,
da in diesem Membranbereich die mechanische Spannung nur etwa die Hälfte der
intrinsischen Spannung beträgt. Dagegen verursacht die Spannungskonzentration in den
Federbereichen eine geringere Auslenkung im Vergleich zu einer Simulation mit konstanter
Membranspannung. Insgesamt betrachtet verursacht der spezielle Spannungszustand einer
40
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
Feder-Membran eine Durchbiegung mit verstärkter Auslenkung der mittleren
Membranbereiche und ähnelt der einer Kreismembran unter Zugspannung (rechter Graph).
Dennoch ist der Einfluss auf das Auslenkungsverhalten verhältnismäßig gering, wenn man
bedenkt, dass sich die anfängliche intrinsische Spannung von 30 MPa um über 60% auf
10 MPa in der Membranmitte reduziert.
Für die Modellierung eines kapazitiven Mikrofons ist weniger die genaue
Auslenkungsfunktion, als die integrale Größe der mechanischen Nachgiebigkeit von Interesse.
In Tabelle 3.1 sind die aus den simulierten Biegelinien berechneten Nachgiebigkeiten einer
Kreis- und Feder-Membran mit verschwindender Zugspannung, konstanter Spannung und
verteilter Spannung zusammengetragen.
Nachgiebigkeit [nm/Pa]
Kreismembran
Feder-Membran
Verbesserung
Kreis ! Feder
spannungsfrei
σ0=0 MPa
22.5
99.7
konstante Spannung
σ(x,y)=σ0=30 MPa
0.9
3.6
verteilte Spannung
σ(x,y)=f(x,y)
0.9
3.5
×4.4
×4
×3.9
Tabelle 3.1: Nachgiebigkeit einer Kreis- und Feder-Membran bei verschiedenen
Spannungszuständen.
Die Simulationen machen deutlich, dass die Verteilung der mechanischen Spannung durch
Dehnungen in der Feder-Membran für die mechanische Nachgiebigkeit nur von
untergeordneter Bedeutung ist. Die durch die Einführung der Federstrukturen in der Membran
erlangte Verbesserung der Nachgiebigkeit beträgt jeweils etwa 400% und entspricht dem
Gewinn an Nachgiebigkeit des spannungsfreien Falls von 440%. Überraschenderweise geht
mit der Spannungsverteilung sogar eine geringfügig kleinere Nachgiebigkeit einher, obwohl
die mittlere Spannung statt 30 MPa nur 24.9 MPa beträgt. Die Spannungskonzentration in der
Feder kompensiert gerade den positiven Effekt der Membranentspannung.
3.3.3 Modellierung von Feder-Membranen
Die tatsächlichen Spannungen und Verschiebungen in einer Feder-Membran können aufgrund
ihrer geometrischen Struktur nicht analytisch berechnet werden. Das macht numerische
Simulationen notwendig, die allerdings immer nur einen speziellen Parametersatz untersuchen
können. Für die Modellierung des Mikrofons ist aber eine Beziehung für die mechanische
Nachgiebigkeit einer Feder-Membran wünschenswert, die für die variablen Parameter
allgemein gültig ist. Für quadratische und kreisförmige Membranen wurde mit Gleichung
(3.10) solch eine Darstellung gefunden. Da die ortsabhängige Spannungsverteilung einer
Feder-Membran trotz großer lokaler Unterschiede nur einen geringen Einfluss auf die
Durchbiegung und die mechanische Nachgiebigkeit hat und sich das Auslenkungsverhalten
einer Kreis- und Feder-Membran ähnelt, liegt es nahe, die Nachgiebigkeit einer FederMembran näherungsweise durch die einer Kreismembran darzustellen, wenn ein
Proportionalitätsfaktor der erhöhten Nachgiebigkeit einer Feder-Membran Rechnung trägt.
Dieser Federmembran-Faktor fFeder wurde für die in dieser Arbeit hergestellten Membranen
bei einer intrinsischen Schichtspannung von 32 MPa und einer Membrandicke von 0.4 µm
simuliert (Abbildung 3.8).
41
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
R=500 µm
t=0.4 µm
σ0=30 MPa
N=16
b=20 µm
R0=400 µm
N=16/32
b=20/10 µm
R0=400 µm
N=4
b=100 µm
R0=225 µm
6
N=4
b=50 µm
R0=221 µm
5.5
5
3.8
fFeder
4
3.0
3
2.1
2
1.0
1
0
Kreismembran
Netz A
Netz B
Feder A
Feder B
Abbildung 3.8: Federmembran-Faktoren fFeder (=Verbesserung der Nachgiebigkeit)
verschiedener Membrandesigns.
Die Membran mit 16 Federstrukturen, die zur besseren Unterscheidung mit Netz A bezeichnet
wird, ist etwa doppelt so empfindlich wie eine vergleichbare Kreismembran. Bei dem Design
Netz B werden zusätzlich Löcher in die Federbereiche eingebracht, wodurch eine zweite
ringförmige Anordnung von Federstrukturen entsteht. Die Breite dieser 32 Federn beträgt
jeweils etwa 10 µm. Diese Maßnahme erhöht die Nachgiebigkeit um weitere 50%. Besonders
hohe Nachgiebigkeiten erreicht man mit wenigen Federbalken (Feder A) und schmalen
Federn (Feder B).
Die Federmembran-Faktoren der Abbildung 3.8 wurden für eine feste Membranspannung und
–dicke bestimmt. Für eine universelle Modellierung der dargestellten Feder-Membranen
wurde der Federmembran-Faktor, d.h. das Verhältnis der mechanischen Nachgiebigkeiten
einer Feder- und Kreismembran, für Membranspannungen von 1-256 MPa (t0=0.4 µm) und
Membrandicken von 0.05-1.6 µm (σ0=32 MPa) simuliert und gegen den Spannungsgrad σ/σc
aufgetragen (Abbildung 3.9). Die numerischen Simulationen zeigen, dass die Nachgiebigkeit
einer Feder-Membran Cm,Feder näherungsweise durch eine von der Membranspannung und –
dicke unabhängige Konstante fFeder und der Nachgiebigkeit einer Kreismembran Cm,k* (3.10)
beschrieben werden kann
C m, Feder (t , σ ) ≡ f Feder ⋅ C m,k (t , σ ) .
*
(3.12)
Das bedeutet, dass der Skalierungsfaktor fFeder nur einmal für eine Feder-Membran numerisch
simuliert werden muss und dann mit variablen Membrandicken und -spannungen verwendet
werden kann. Ist die mechanische Nachgiebigkeit kleiner als 100 nm/Pa, beträgt der
Modellierungsfehler weniger als 5%. Nur bei Plattenverhalten und sehr hohen
Nachgiebigkeiten ist die Einführung eines konstanten Federmembran-Faktors nicht zulässig.
42
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
6
5.5
5
4.5
fFeder
4
3.5
3
2.5
2
x σ: 1-256 MPa, t0=0.4 mm
o t: 0.05-1.6 µm, σ0=32 MPa
1.5
1
1
10
100
1000
Spannungsgrad σ/σc
10000
100000
Abbildung 3.9: Federmembran-Faktoren bei verschiedenen Membranspannungen σ und
Dicken t gegen den Spannungsgrad.
3.3.4 Einfluss von Spannungsgradienten auf das mechanische Verhalten von
Feder-Membranen
Die mechanische Spannung ist im Allgemeinen nicht konstant über die Schichtdicke.
Insbesondere der intrinsische und Dotierstoff-induzierte Anteil besitzt häufig einen starken
Spannungsgradienten und hängt vom Schichtwachstumsprozess und Implantationsprofil ab.
Das in dieser Arbeit verwendete amorph abgeschiedene und nachträglich kristallisierte
Polysilizium hat anders als direkt polykristallin abgeschiedenes Silizium einen relativ
geringen intrinsischen Spannungsgradienten, da die Korngröße nur geringfügig von der
Schichtdicke abhängt [Elb98]. Von der Prozessführung abhängig kann der Spannungsgradient
dennoch bis zu 100 MPa/µm betragen [And01].
Die tatsächliche Verteilung der Membranspannung ist im allgemeinen nicht bekannt. Sie kann
aber in ihrer Wirkung durch die mittlere Spannung σ0 [MPa] und einem linearen Verlauf mit
dem Spannungsgradienten Σ [MPa/µm] dargestellt werden (Spannungslinearisierung). In den
Finite-Elemente-Simulationen wird mit einem geschichteten Schalenelement der lineare durch
einen stufenförmigen Spannungsverlauf in der Schichtdicke approximiert. (Abbildung 3.10).
Das Element besitzt 8 Knoten mit jeweils 6 Freiheitsgraden und unterstützt nichtlineare
Spannungs- und Verformungsversteifung.
43
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
σ(x)
σ0−Σ t/2+Σ x
Spannungslinearisierung
σ(Ν)
Diskretisierung
t
t
x
t
N
x
x
Abbildung 3.10: Modellierung inhomogener Spannungsverteilungen in der Membran mit
geschichteten Schalenelementen.
Im Folgenden soll die statische Membranverbiegung, d.h. ohne äußere Druckeinwirkung, und
die mechanische Nachgiebigkeit unter dem Einfluss eines vertikalen Spannungsgradienten in
der Membran untersucht werden.
Statische Membranverbiegung bei vertikalen Spannungsgradienten
Bei Kreismembranen ist aufgrund der festen Einspannung am gesamten Membranrand kaum
ein Einfluss von Spannungsgradienten zu erwarten. Anders verhält es sich bei FederMembranen, die auf die inneren Momente mit statischen Verbiegungen reagieren können. In
Abbildung 3.11 ist die Verbiegung einer Feder-Membran (Radius R=500 µm, innerer Radius
R0=225 µm, Federbreite b=100 µm, Anzahl Federn N=4, Membrandicke t=0.4 µm) entlang
der Federstruktur (A) und entlang der inneren Membrankapazität (B) aufgetragen. In der
FEM-Simulation wird von einer intrinsischen Schichtspannung von σ0=30 MPa und einem
linearen Gradienten von Σ=50 MPa/µm ausgegangen. Damit nimmt die Spannung von der
Membranoberseite ausgehend linear von 20 MPa zu 40 MPa mit der Schichtdicke zu.
0.2
A
Verbiegung [µm]
0.1
0
0
50
100
150
200
250
300
350
400
450
500
-0.1
-0.2
B
-0.3
-0.4
-0.5
Entfernung von der Membranmitte [µm]
Abbildung 3.11: Statische Verbiegung einer Feder-Membran aufgrund eines vertikalen
Spannungsgradienten.
Die in der Simulation mit dem Vorzeichen des Spannungsgradienten gewählte höhere
Zugspannung im unteren Schichtdickenbereich verursacht ein Biegemoment, das den freien
Membranrand in negative Richtung verbiegt und die mittige Membranfläche aufwölbt. Die
Membranverbiegung von –0.37 µm bis 0.13 µm kann bezogen auf die Membrandicke von
0.4 µm nicht vernachlässigt werden. Die Stärke der Verbiegung hängt von dem
Membrandesign, der Membrandicke, dem Spannungsgradienten und der mittleren Spannung
ab. Die grundlegenden Zusammenhänge sind in der Abbildung 3.12 am Beispiel der
44
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
550
σ0=30 MPa
t=0.4 µm
t=0.2 µm
500
maximale Membranverbiegung [nm]
maximale Membranverbiegung [nm]
maximalen Randverbiegung zweier Feder-Membranen dargestellt. Die durchgezogenen
Linien stehen für die 400 nm dicken Membranen; die gestrichelten Linien für die der
Membranen mit t=200 nm.
450
400
350
300
250
200
150
100
50
0
0
10
20
30
40
50
60
70
80
550
Σ=30 MPa
500
450
400
350
300
250
200
150
100
50
0
20
Spannungsgradient Σ [MPa/µm]
Abbildung 3.12: Maximale
Spannungsgradienten.
t=0.4 µm
t=0.2 µm
Membranverbiegung
30
40
50
60
70
80
90
100
mittlere Spannung σ0 [MPa]
von
Feder-Membranen
bei
Erwartungsgemäß nimmt die Randverbiegung bei einer konstanten mittleren
Membranspannung von 30 MPa mit dem Spannungsgradienten linear zu (linker Graph). Die
Membran mit vier Federn und daher sehr breitem Membranrand biegt sich etwa fünfmal
stärker durch als eine Membran mit 48 Federn. Darüber hinaus ist zu beobachten, dass die
Verbiegung von der Membrandicke abhängt und sich bei einer Verdopplung der Dicke
näherungsweise ebenfalls verdoppelt. Das Biegemoment nimmt also stärker als das
Flächenträgheitsmoment mit der Schichtdicke zu. Damit unterscheidet sich das Verhalten
einer Feder-Membran deutlich von dem eines einseitig eingespannten Biegebalkens, bei dem
sich die Dicken-Abhängigkeit des Biege- und Flächenträgheitsmomentes aufheben, so dass
die Durchbiegung lediglich vom Spannungsgradienten abhängt.
Bei einem konstanten Spannungsgradienten (Σ=30 MPa/µm) nimmt die Randverbiegung mit
der mittleren Spannung in der Membran ab, da die Membran mit zunehmender Spannung
mechanisch steifer wird (rechter Graph).
Mechanische Nachgiebigkeit bei Spannungsgradienten
In diesem Abschnitt soll untersucht werden, ob ein Spannungsgradient und die damit
einhergehende Verbiegung die mechanische Nachgiebigkeit der Membran beeinflusst. Die
simulierte mechanische Nachgiebigkeit in Abhängigkeit vom Spannungsgradienten ist in der
Abbildung 3.13 aufgetragen. Die mittlere Spannung in der 400 nm dicken Feder- und NetzMembran beträgt jeweils konstant 30 MPa. Im rechten Graph ist zur Verdeutlichung die
prozentuale Veränderung der Nachgiebigkeit mit dem Spannungsgradienten aufgetragen.
Trotz der zum Teil erheblichen Randverbiegungen in der Größenordnung der Membrandicke
wird die mechanische Nachgiebigkeit kaum beeinflusst. Bei Spannungsgradienten bis zu
70 MPa/µm, der bei einer 400 nm dicken Membran einem Spannungsverlauf von 16-44 MPa
bedeutet, ist nur eine geringfügige Verringerung der Nachgiebigkeit um max. 1.4% zu
beobachten. Die Nachgiebigkeit einer Membran ist also durch die mittlere Spannung und
nicht durch den tatsächlichen Spannungsverlauf über die Dicke gegeben.
45
10
Veränderung der Nachgiebigkeit [%]
mechanische Nachgiebigkeit [nm/Pa]
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
9
8
σ=30 MPa
t=0.4 µm
7
6
5
0
10
20
30
40
50
60
Spannungsgradient Σ [MPa/µm]
70
0
-0.2
-0.4
-0.6
σ=30 MPa
t=0.4 µm
-0.8
-1
-1.2
-1.4
-1.6
0
10
20
30
40
50
60
70
Spannungsgradient Σ [MPa/µm]
Abbildung 3.13: Mechanische Nachgiebigkeit einer Feder- und Netz-Membran unter dem
Einfluss eines vertikalen Spannungsgradienten in der Membran.
3.3.5 Diskussion der Simulationsergebnisse
Die durchgeführten Simulationen demonstrieren, wie wirkungsvoll Feder-Membranen zur
Erhöhung der mechanischen Nachgiebigkeit bei gleichem Platzbedarf auf dem Mikrofonchip
eingesetzt werden können. Die Modellierung der Feder-Membranen gelingt über die
analytische Näherungslösung einer Kreismembran und einem numerisch bestimmten
Skalierungsfaktor. Es konnte gezeigt werden, dass der spezielle Spannungszustand einer
Feder-Membran und ein vertikaler Spannungsgradient die Nachgiebigkeit kaum beeinflusst.
Die Simulationsergebnisse zur statischen Verbiegung bei Spannungsgradienten verdeutlichen,
dass bei dem Einsatz von Feder-Membranen ein Kompromiss zwischen einer hohen
Membrannachgiebigkeit und einer geringen Verbiegung gefunden werden muss. Bei
gegebenem Spannungsgradienten, der von der Fertigungstechnologie und dem Gesamtprozess
abhängt, muss das Membrandesign oder die Schichtspannung derart gewählt werden, dass
eine Berührung zwischen der Membran und der Gegenelektrode ausgeschlossen werden kann.
Als sichere Membranvariante bieten sich die als Netz-Membranen bezeichneten Membranen
mit vielen, schmalen und kurzen Federbalken an. Diese zeigen eine gute mechanische
Nachgiebigkeit und sind unempfindlich gegenüber Spannungsgradienten. Ein weiterer Vorteil
der Netz-Membranen ist der geringe Verlust an Membranfläche bzw. die höhere
Grundkapazität, die für geringe Umladeverluste bei parasitären Kapazitäten benötigt wird.
Prinzipiell sind dünne Membranen zu bevorzugen, da sie bei einer hohen mechanischen
Nachgiebigkeit eine geringere Verbiegung der freien Membranränder aufweisen.
3.4
Korrugierte Membranen
Ein weiterer Membrantyp mit einer Federstruktur soll nun untersucht werden. Dabei handelt
es sich um die Korrugationsmembran, bei der in einer geschlossenen Membran eine
bestimmte Anzahl von Stufen eingebracht werden (Abbildung 3.14). Neben dem Radius R,
der Dicke t und der Schichtspannung σ treten Korrugation-spezifische Parameter auf: die
46
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
Höhe hc und Weite wc einer Korrugation, die Anzahl Nc und der Abstand zwischen zwei
Korrugationen bc.
R
t
hc
bc/2
wc
Abbildung 3.14: Schematische Darstellung einer Korrugationsmembran.
Die vertikalen Korrugationen dienen wie die lateralen Biegebalken bei Feder-Membranen der
Erhöhung der mechanischen Nachgiebigkeit der Membran. Dennoch ist das Funktionsprinzip
einer Korrugationsmembran von der einer Feder-Membran zu unterscheiden. Bei einer FederMembran konnte gezeigt werden, dass die Erhöhung der Nachgiebigkeit auf die geringere
Biegesteifigkeit zurückzuführen ist und die Veränderung der Spannungsverteilung von
untergeordneter Bedeutung ist. Bei einer Korrugationsmembran ist es genau umgekehrt.
Vergleichbar mit der Wirkungsweise eines Wellblechdachs versteifen die Korrugationen die
Membran. Bei den in der Mikromechanik verwendeten Materialen muss aber von einer
mechanischen Spannung in der Membranschicht ausgegangen werden. Dann ist die
gewinkelte, stufenförmige Struktur der Korrugationen von Vorteil, da sie über eine Dehnung
oder Stauchung eine mechanische Spannung in der Membran verringern. Bei einer
Zugspannung ist dieses Verhalten gleichbedeutend mit einer höheren mechanischen
Nachgiebigkeit der Membran. Wirkt hingegen eine Druckspannung, etwa durch eine äußere
mechanische Beanspruchung der Einspannung, dann neigt die Korrugationsmembran weniger
dazu auszubeulen.
Eine Abschätzung für die Reduzierung der mechanischen Spannung in einer
Korrugationsmembran
erhält
man
durch
den
Vergleich
der
nichtlinearen
Verformungsversteifung einer planaren und einer korrugierten Membran [Schee94, Kres02].
In Abschnitt 3.4.1 wird die Spannungsreduktion mit Hilfe eines geometrischen Modells
analytisch berechnet. Dem folgt die numerische Simulation der Spannungsverteilung in einer
Korrugationsmembran (3.4.2), um dann auf das Auslenkungsverhalten bei Druckbelastung
einzugehen (3.4.3). Als Resultat der analytischen Rechnung und numerischen Simulationen
wird in 3.4.4 eine Beziehung für die mechanische Nachgiebigkeit angegeben. Ein wichtiger
Aspekt bei der Produktreife von Silizium-Mikrofonen ist die Reproduzierbarkeit der
Empfindlichkeit und somit der mechanischen Nachgiebigkeit. Die Schwankung der
Nachgiebigkeit von Korrugationsmembranen bei Fertigungstoleranzen wird in (3.4.5)
betrachtet. Abschließend werden die Simulationsergebnisse diskutiert (3.4.6).
3.4.1 Analytische Berechnung eines Korrugationsbalkens
Die elastische Federkonstante einer Korrugation wird mit dem Balkenmodell der Abbildung
3.15 untersucht. Das Modell besteht aus einem Freiträger der Länge l und einem daran
senkrecht befestigten Balken der Länge hc. An dessen Ende ziehe in der Ebene des Freiträgers
eine Kraft F. Ferner gelte hc<<l, so dass die Verbiegung des kurzen Endstückes vernachlässigt
47
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
werden kann. Die Balkendicke t, die Balkenbreite b und das Elastizitätsmodul E beider
Balken sei identisch.
α
l
hc
F
∆xc
Abbildung 3.15: Modell einer Korrugation mit zwei Balken.
Die gesuchte Verschiebung ∆xc wird über die Biegung des Freiträgers bei dem Moment
M=F⋅hc berechnet. Nach [Drey71] ist der Biegewinkel α am Ende des Freiträgers mit dem
Flächenträgheitsmoment I durch
α=
6 ⋅ F ⋅ l ⋅ hc
M ⋅l
=
2⋅ E ⋅ I
E ⋅b ⋅t3
(3.13)
gegeben. Die elastische Verschiebung für kleine Winkel α ist dann näherungsweise
6 ⋅ F ⋅ l ⋅ hc
∆xc = sin(α ) ⋅ hc ≈
.
E ⋅b ⋅t3
2
(3.14)
Die Erweiterung des Modells zeigt Abbildung 3.16. Eine Reihe von Nc=lc/(bc+wc)
Korrugationsvertiefungen wird über einen weiteren Balken der Länge lr beidseitig
eingespannt.
lc
lr
hc
t
bc wc
Abbildung 3.16: Beidseitig eingespanntes Korrugationsmodell.
Wird nun in dem Balken der Länge lr eine thermische Verschiebung ∆xT=α⋅∆T⋅lr eingeprägt,
dann muss die Summe aller elastischen und thermischen Verschiebungen verschwinden
∆xc + ∆x r + ∆xT = 0
6 ⋅ F ⋅ hc
F lr
⋅ (bc + wc ) ⋅ N c +
⋅ + α ⋅ ∆T ⋅ l r = 0
3
b ⋅t E
E ⋅b⋅t
2
⇔
∆xc ist die elastische Verschiebung im korrugierten Bereich und ∆xr die elastische
Verschiebung des Balkens der Lange lr. Nach der resultierenden Spannung im Gleichgewicht
48
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
σ=F/(b⋅t) aufgelöst, ergibt sich in Abhängigkeit von der intrinsischen thermischen
Spannung σ0
⇒σ =
σ0
6 ⋅ h (b + wc ) ⋅ N c
1+ 2c ⋅ c
lr
t
2
.
(3.15)
Den größten Einfluss hat das Verhältnis von Korrugationshöhe hc und Dicke t. Ist dieses
Verhältnis groß, genauer hc/t>> 1 / 6 ⋅ lr / lc , dann hängt die mechanische Spannung
quadratisch von t/hc ab, und die Anzahl der Korrugationen Nc geht annähernd linear ein.
3.4.2 Spannungszustand einer Korrugationsmembran
Zur Untersuchung der Wirkung von Korrugationen in einer kreisförmigen Membran wurde
der Spannungszustand simuliert. In der FEM-Simulation werden rotations-symmetrische 2DFlächenelemente mit zwei Verschiebungsfreiheitsgraden gewählt, die geometrische
Nichtlinearitäten unterstützen. Die Membrandicke von 200 nm beträgt ein Drittel der
Korrugationshöhe (600 nm), so dass nach der analytischen Lösung eine deutliche
Spannungsveränderung zu erwarten ist. Die weiteren Simulationsparameter sind Nc=8,
R=500 µm und bc=wc=5 µm. Die aus einer intrinsischen Schichtspannung von 30 MPa
resultierende Spannung in der Membran ist in der Abbildung 3.17 dargestellt.
Nc=8
Korrugationsmembran
50
Membranspannung [MPa]
45
40
35
intrinsische Schichtspannung
30
25
20
Entspannung
15
10
5
0
0
100
200
300
400
500
Entfernung von der Membranmitte [µm]
Abbildung 3.17: Spannungsverteilung in einer Membran mit acht Korrugationen.
Im überwiegenden Teil der Membranfläche beträgt die mechanische Spannung im
Gleichgewichtszustand nur noch etwa 4.4 MPa. Die Dehnung der Korrugationsrillen hat
folglich etwa 85% der intrinsischen Spannung aufgenommen. Es ist daher eine deutlich
stärkere Durchbiegung der Membran bei Belastung mit einem Druck zu erwarten.
49
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
3.4.3 Durchbiegung bei Druckbelastung
Die Wirkung der Spannungsrelaxation in einer Korrugationsmembran auf das
Auslenkungsverhalten zeigt anhand von Finiten-Elemente-Simulationen die Tabelle 3.2. Es
ist die Mittenauslenkung einer Kreis- und Korrugationsmembran (Nc=8, bc=wc=5 µm,
hc=600 nm) bei einem Schalldruck von einem Pascal und einer intrinsischen Spannung von
30 MPa aufgeführt. Außerdem ist der Spezialfall einer spannungsfreien Membran zur
Verdeutlichung der Erhöhung der reinen Biegesteifigkeit angegeben. Um sehr große
Auslenkungen und nicht-lineare Effekte zu verhindern, wird bei der Simulation ohne
Membranspannung ein Radius von 200 µm gewählt. Die Membrandicke beträgt jeweils
200 nm.
Mittenauslenkung [nm] @1 Pa
Kreismembran
korrugierte Membran
Änderung
Kreis ! Korrugation
σ0=30 MPa
(R=500 µm)
10
64
σ0=0 MPa
(R=200 µm)
158
72
× 6.4
× 0.46
Tabelle 3.2: Mittenauslenkung von Korrugations- und Kreismembran bei verschiedenen
Spannungszuständen.
Die Einführung von acht Korrugationen, deren Höhe das dreifache der Membrandicke
betragen, erhöht bei einer Simulation mit einer Zugspannung von 30 MPa die
Mittenauslenkung um mehr als das sechsfache im Vergleich zu einer Kreismembran. Das
Verhältnis von 6.4 gibt annähernd die Spannungsreduktion um den Faktor
30 MPa/4.4MPa=6.8 aus Abbildung 3.17 wider. Offensichtlich verhält sich eine
Korrugationsmembran unter Druckbelastung ähnlich wie eine Kreismembran mit reduzierter
mechanischer Spannung. Dieses Verhalten wird im nächsten Abschnitt näher untersucht und
zur Ableitung einer Beziehung für die Nachgiebigkeit von Korrugationsmembranen genutzt.
3.4.4 Modellierung der Nachgiebigkeit von Korrugationsmembranen
Überträgt man die Ergebnisse der analytischen Berechnung eines korrugierten Balkens
(Gleichung 3.15) auf eine Korrugationsmembran (lr!R-(bc+wc)⋅Nc), dann erhält man mit den
Notationen der Abbildung 3.14 einen Ausdruck für die effektive Spannung
σ corr =
σ0
h
(bc + wc ) ⋅ N c
1 + f c ⋅ c2 ⋅
R − (bc + wc ) ⋅ N c
t
2
.
(3.16)
Darin ist fc eine noch zu bestimmende Konstante. Der Haupteffekt, der eine korrugierte
Kreismembran von einer einfachen Kreismembran unterscheidet, ist die Verringerung der
intrinsischen Spannung σ0 auf die effektive Spannung σcorr. Die Nachgiebigkeit einer
Korrugationsmembran Cm,c kann daher durch der Nachgiebigkeit einer Kreismembran Cm,k
beschrieben werden, wenn die Spannung nach Gleichung (3.16) transformiert wird
R2
C m,c (σ 0 ) ≡ C m,k (σ corr ) ≈
8 ⋅ t ⋅ σ corr
50
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
⇒ C m ,c =
R2
8 ⋅ t ⋅σ 0
2

h
(bc + wc ) ⋅ N c
⋅ 1 + f c ⋅ c2 ⋅
R − (bc + wc ) ⋅ N c
t


 .


(3.17)
Anhand zahlreicher Finite-Elemente-Simulationen wurde die Korrugationskonstante zu
fc=2.55 bestimmt. Abbildung 3.18 zeigt die gute Übereinstimmung zwischen der Gleichung
(3.17) und Simulationen der mechanischen Nachgiebigkeit, wenn die Korrugationshöhe bzw.
Membrandicke variiert werden (R=500 µm, σ0=32 MPa, Nc=8, bc=wc=5 µm, hc=600 nm bzw.
t=200 nm).
250
45
FEM
halbanalytisch
FEM
halbanalytisch
Nachgiebigkeit [nm/Pa]
Nachgiebigkeit [nm/Pa]
40
35
30
25
20
15
10
200
150
100
50
5
0
0
0
100 200 300 400 500 600 700 800
Korrugationshöhe hc [nm]
0
100 200 300 400 500 600 700 800
Membrandicke t [nm]
Abbildung 3.18: Nachgiebigkeit korrugierter Membranen in Abhängigkeit von der
Korrugationshöhe und der Membrandicke.
In den Graphen kommt die starke Abhängigkeit der Nachgiebigkeit von der Höhe der
Korrugationen und der Membrandicke zum Ausdruck. Ist das Verhältnis hc/t klein, dann
verhält sich die Korrugationsmembran wie eine Kreismembran, deren Nachgiebigkeit
umgekehrt proportional mit der Membrandicke abnimmt. Ist hingegen das Verhältnis groß,
dann steigt die Nachgiebigkeit quadratisch mit der Korrugationshöhe an. Noch stärker geht
die Membrandicke ein, da zu der quadratischen Abhängigkeit der Spannungsrelaxation die
Dickenabhängigkeit einer Membran kommt.
In weiteren Simulationen wurde die Gültigkeit der Gleichung (3.17) überprüft, wenn der
Simulationsparameter die Anzahl der Korrugationen Nc oder die intrinsische Spannung σ0 ist
(Abbildung 3.19).
51
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
120
40
FEM
halbanalytisch
FEM
halbanalytisch
110
Nachgiebigkeit [nm/Pa]
Nachgiebigkeit [nm/Pa]
35
30
25
20
15
10
5
100
90
80
70
60
50
40
30
20
10
0
0
0
2
4
6
Korrugationsanzahl Nc
8
10
0
5
10 15 20 25 30 35 40 45 50 55
intrinsiche Spannung σ0 [nm]
Abbildung 3.19: Nachgiebigkeit korrugierter Membranen in Abhängigkeit von der
Korrugationsanzahl und der intrinsischen Spannung.
Erwartungsgemäß nimmt die Nachgiebigkeit annähernd linear mit der Anzahl der
Korrugationsrillen zu und umgekehrt proportional mit der intrinsischen Spannung ab. Wieder
ist die Übereinstimmung der FEM-Simulationen mit der halbanalytischen Lösung (3.17) sehr
gut. Sie eignet sich daher zur Berechnung der mechanischen Nachgiebigkeit von
Korrugationsmembranen. Weitere Simulationen zeigen, dass Gleichung (3.17) mit der
Konstante fc=2.55 auch für Membranradien von 400-600 µm und für Korrugationsabstände
bzw. Weiten von 1-10 µm eine gute Beschreibung darstellt. Der Modellierungsfehler bis zu
15% ist vor allem auf das vereinfachte Modell eines Korrugationbereiches mit rein elastischer
Verschiebung zurückzuführen.
3.4.5 Schwankung der Membrannachgiebigkeit bei Fertigungstoleranzen
Möchte man produkttaugliche Mikrofone fertigen, dann reicht eine hohe Empfindlichkeit
allein nicht aus. Vielmehr muss auch die Schwankungsbreite aufgrund von Unsicherheiten bei
der Herstellung die Spezifikationen der Anwendung erfüllen. Für konventionelle ElektretMikrofone wird typischerweise eine maximale Toleranz von 3 dB angegeben [Know01].
Abgeschiedene Schichten unterliegen fertigungsbedingt einer mit der Schichtdicke
zunehmenden Schwankung. Die Auswirkung auf die Nachgiebigkeit einer
Korrugationsmembran ist wegen der starken Dickenabhängigkeit höher als bei einer
einfachen Kreismembran. Hinzu kommt, dass auch die Tiefe der Trockenätzung zur
Erzeugung der Korrugation variiert. Nimmt man jeweils eine Abweichung um 5% von der
absoluten Membrandicke und Korrugationshöhe an, dann zeigt Abbildung 3.20 die
Schwankung der mechanischen Nachgiebigkeit von Korrugationsmembranen. In der
Berechnung wurde als Folge der nasschemischen Opferschicht-Ätzung zusätzlich eine
konstante Schichtdickenunsicherheit von 10 nm angenommen. Die Schwankung der
Nachgiebigkeit ist bei Korrugationsmembranen, vor allem mit abnehmender Schichtdicke,
deutlich höher als die einer Kreismembran und erreicht bereits allein die Größenordnung der
zulässigen Gesamtschwankung von 3 dB.
52
Numerische Simulationen zum mechanischen Verhalten von Mikrofonmembranen
Schwankung der Nachgiebigkeit
[dB]
3
hc=400 nm
hc=600 nm
hc=800 nm
Kreismembran (hc=0 nm)
2.5
2
Korrugationsmembranen
1.5
1
Kreismembran
0.5
0
100
150
200
250
300
350
400
Membrandicke t [nm]
Abbildung 3.20: Relative Schwankung der Nachgiebigkeit
Korrugationsmembran aufgrund von Fertigungstoleranzen.
von
Kreis-
und
3.4.6 Diskussion der Simulationsergebnisse
Mit korrugierten Membranen können sehr empfindliche und gleichzeitig kleine Mikrofone
realisiert werden, da die mechanische Spannung in der Membran reduziert wird. Mit Hilfe
einer analytischen Modellrechnung und Finiten-Elemente-Simulationen konnte ein Ausdruck
für die mechanische Nachgiebigkeit dieser Membranen abgeleitet werden.
Besonders aussichtsreich erscheint die Verwendung sehr dünner Membranen. Dem steht die
Reproduzierbarkeit entgegen, die bei dünnen Schichten geringer ist. Günstiger ist die
Einstellung der Membrannachgiebigkeit über die Anzahl oder die Höhe der Korrugationen, da
mit beiden Maßnahmen die Nachgiebigkeit aber nicht die Schwankung zunimmt.
53
Modellierung von kapazitiven Silizium-Mikrofonen
Kapitel 4
Modellierung von kapazitiven Silizium-Mikrofonen
Die Modellierung der Mikrofone hat allgemein zum Ziel, den Einfluss der technologischen
Parameter auf die Systemeigenschaften, Querabhängigkeiten und parasitäre Effekte zu
verstehen und verbesserte Entwürfe vorzubereiten. Diese konstruktive Vorgehensweise hat im
Gegensatz zu einer Versuch-und-Irrtum-Methode den Vorteil, die Zahl der
Entwicklungszyklen mit der zeit- und kostenintensiven Herstellung und Prüfung der Muster
zu verringern.
Das kapazitive Mikrofon als elektroakustischer Wandler beinhaltet elektrische, mechanische
und akustische Komponenten. Eine einheitliche FEM-Simulation des gesamten Systems ist
aufgrund dieser Komplexität sehr aufwändig. In dieser Arbeit wird das Gesamtsystem
zunächst geeignet partitioniert. Die Teilsysteme werden dann numerisch, wie in Kapitel 3
behandelt, oder analytisch berechnet und zu einem Gesamtmodell kombiniert. Der
grundsätzliche Aufbau der Mikrofon-Modellierung wird in Abschnitt 4.1 beschrieben.
Unter bestimmten Voraussetzungen und Näherungen können analytische Lösungen zu
mechanischen und akustischen Komponenten des Mikrofons gefunden werden. Sie werden in
Abschnitt 4.2 angegeben. Der aus den numerischen und analytischen Rechnungen gewonnene
Satz von analog-elektrischen Netzwerkelementen dient schließlich der Konstruktion des
gekoppelten mechanisch-akustischen Netzwerkmodells eines Silizium-Mikrofons. Es wird in
Abschnitt 4.3 beschrieben und zur Simulation von Nachgiebigkeiten, dem
Übertragungsverhalten und dem Eigenrauschen angewendet.
Zur Ableitung der elektrischen Mikrofonempfindlichkeit und des Gesamtrauschens wird
schließlich auf die kapazitive Wandlung (4.4) und die Beschaltung mit einem
Impedanzwandler eingegangen (4.5). Die Integration der Teilmodelle in einem numerischen
Netzwerklöser führt zu einem Systemmodell, das den vollständigen Signalweg ausgehend
vom Schalldruck bis zum elektrischen Nutzsignal beschreibt. In Abschnitt 4.6 wird als
Anwendung des Systemmodells die Optimierung des Signal/Rauschabstandes eines
kapazitiven Mikrofons untersucht.
4.1
Modellbildung
Die Modellierung des Systems aus Mikrofon, Gehäuse oder Messapparatur und elektrischer
Beschaltung verfolgt eine modulare Mixed-Level Strategie, bei der zur Reduktion der
Simulationskomplexität abhängig von der Problemstellung geeignete Teilsysteme analytisch
oder numerisch behandelt werden. Die Teilsysteme in Form von konzentrierten Elementen
werden dann zu einem analog-elektrischen Netzwerkmodell verknüpft und analytisch gelöst
oder mit einem Netzwerklöser numerisch simuliert. In der Abbildung 4.1 ist die Hierarchie
und Aufbau der Modellierung dargestellt.
54
Modellierung von kapazitiven Silizium-Mikrofonen
strukturgleiche
Transformation
duale
Transformation
Mittelwertbildung
+ Parametrisierung
räumliche
Diskretisierung
Abstraktion
räumliche
Konzentration
Abbildung 4.1: Hierarchischer Aufbau der Mikrofon-Modellierung mit konzentrierten
Elementen und Finite-Elemente-Simulationen.
Auf der untersten Abstraktionsebene der Modellierung steht ein Differential-Algebraisches
Gleichungssystem (DAE, Differential Algebraic Equations) des physikalischen Systems. Es
beinhaltet die partiellen Differentialgleichungen (pDGL), die Rand (RB)- und
Anfangsbedingungen (AB) der mechanischen, akustischen und elektrischen Feldgrößen.
Durch Integration über bestimmte Bereiche können die partiellen Differentialgleichungen der
kontinuierlichen Feldgrößen in ein einfaches Differentialgleichungssystem von
Zustandsvariablen überführt und Netzwerkmodelle mit räumlich konzentrierten Elementen
aufgebaut werden. Eine solche Unterteilung ist möglich, wenn die zeitliche Änderung der
Feldgröße in dem betrachteten Bereich bzw. Element näherungsweise unabhängig vom Ort
ist. Netzwerkmodelle können durch den Austausch einzelner Elemente einfach modifiziert
werden und liefern einen guten Zugang zum Verständnis des Systems, da sie das System
strukturell mit wenigen Element-Grundtypen nachbilden.
55
Modellierung von kapazitiven Silizium-Mikrofonen
Problemstellungen, die nicht analytisch behandelt werden können, wie z.B. der SpannungsVerformungszustand einer Feder-Membran, können durch numerische Verfahren wie der
Finite-Elemente-Methode näherungsweise gelöst werden. Wesentlicher Nachteil einer FEAnalyse ist die stark mit dem Umfang und der Komplexität des Modells ansteigende
Simulationszeit. Mikromechanische Systeme beinhalten typischerweise dreidimensionale
Strukturen mit großen Aspektunterschieden und nichtlinearen Effekten, die iterative
Berechnungen mit einer großen Anzahl an Elementen erfordern. Umfangreiche
Parameterstudien für das physikalische Verständnis und zur Entwurfsverbesserung sind daher
mit einem hohen Zeit- und Rechenaufwand verbunden. Wesentlich effizienter ist es, FEAnalysen nur an Systemkomponenten durchzuführen, die unabhängig vom Gesamtsystem
betrachtet werden können. Durch eine räumliche Mittelwertbildung und Parametrisierung der
diskreten Lösungen, wie sie in Kapitel 3 anhand der mechanischen Nachgiebigkeit
durchgeführt wurde, kann ein konzentriertes Element gewonnen und in das Netzwerkmodell
integriert werden.
Das Netzwerkmodell des Mikrofons besteht aus mechanischen und akustischen Subsystemen,
wie z.B. der Membran und dem Luftspalt. Eine einheitliche Darstellung wird durch eine
analog-elektrische Schaltung erreicht. Dieses Vorgehen gründet auf formalen Entsprechungen
zwischen der mathematischen Beschreibung mechanischer, akustischer und elektrischer
Systeme (Energieerhaltung, Kontinuitätsbeziehungen). Abhängig von der Zuordnung der
Zustandsgrößen kann entweder eine strukturtreue oder eine duale Beschreibung erreicht
werden, die formal gleichwertig sind. Allgemein resultiert aus der Umwandlung einer
Flussgröße in eine Flussgröße ein strukturgleiches Netzwerk, während die duale
Formulierung eine Flussgröße in eine Potentialgröße transformiert. Die gewählte Zuordnung
zwischen einem mechanischen bzw. akustischen Teilnetzwerk und dem analog-elektrischen
Netzwerk und die zugehörige Transformation kann der Abbildung 4.2 entnommen werden.
Abbildung 4.2: Zuordnung und Transformation zwischen mechanischen bzw. akustischen
Teilnetzwerken und dem analog-elektrischen Mikrofon-Gesamtnetzwerk.
Mechanische Subsysteme mit der Flussgröße Kraft F und der Potentialgröße Schnelle bzw.
Geschwindigkeit v werden mit einer dualen Formulierung transformiert. Durch die duale
Transformation werden mechanische Impedanzen einfach über das Flächenquadrat in
akustische Einheiten umgerechnet [Zoll93]. Die akustischen Elemente mit der Flussgröße
Fluss bzw. Volumenstrom q und der Potentialgröße Druck p dagegen werden strukturtreu
transformiert, da mit dieser Zuordnung eine anschauliche Darstellung des Netzwerkes erreicht
wird.
Das resultierende Netzwerkmodell des Mikrofons in Form einer äquivalenten Ersatzschaltung
wird schließlich über einen Wandler mit der realen elektrischen Schaltung zu einem
56
Modellierung von kapazitiven Silizium-Mikrofonen
Systemmodell kombiniert und mit den Methoden der Netzwerkanalyse, etwa durch einen
Schaltungssimulator, gelöst.
4.2
Konzentrierte Netzwerkelemente im kapazitiven Mikrofon
Die Grundelemente, aus denen sich ein Netzwerkmodell zusammensetzt sind mechanische
und akustische Feder-, Massen- und Widerstandselemente. Die für ein kapazitives Mikrofon
fundamentalen Elemente und deren analytische Lösung mit den zugrundeliegenden
Annahmen werden im Folgenden angegeben.
4.2.1 Akustische Federelemente
In einem Hohlraum eingeschlossene Luft als Speicher von potentieller Energie wirkt wie ein
Federelement und wird nach der strukturtreuen Transformation durch eine elektrische
Kapazität dargestellt (Abbildung 4.3). Unter der Annahme steifer Hohlraumwände, im
Vergleich zur Wellenlänge kleinen Abmessungen, kleinen Innendruckänderungen und der
Vernachlässigung der Luftmasse kann aus der Adiabatengleichung p/V=c2⋅/V (Wechselgrößen
mit Unterstrich) eine akustische Impedanz berechnet werden
1 ρ ⋅ c2
1
1
=
=
⋅
≡
⋅
.
Za =
q1 − q 2
j ⋅ ω ⋅V
j ⋅ω V
j ⋅ ω Ca
p
p
(4.1)
Darin ist q der akustische Fluss (Volumenstrom). Eine Hohlraumnachgiebigkeit [m4s2/kg]
CV =
V
ρ ⋅ c2
(4.2)
wird beim Mikrofon durch das eingeschlossene Luftvolumen des Gehäuses, dem freigeätzten
Chip-Rückvolumen und dem Kondensatorspalt verursacht und hängt abgesehen vom
jeweiligen Volumen nur von der Luftdichte ρ und der Schallgeschwindigkeit c ab.
V
q1
q2
strukturtreue
Transformation
q1
p1
q2
Ca
p2
p=p1=p2
Abbildung 4.3: Modellierung eines akustischen Hohlraumes durch eine Kapazität.
4.2.2 Akustische Widerstandselemente
Einem strömenden, viskosen Fluid wird infolge der Reibung an den Innenflächen starrer
Wände Energie in Form von Wärme entzogen. Der Druckabfall bei gegebenen Volumenstrom
wird durch ein Widerstandselement modelliert (Abbildung 4.4).
57
Modellierung von kapazitiven Silizium-Mikrofonen
p1
η
strukturtreue
Transformation
p2
Ra
p1
p2
q=q1=q2
Abbildung 4.4: Modellierung von viskosen Strömungsverlusten durch Widerstände.
Derartige Strömungsverluste beim Mikrofon treten am Gehäuseseingang, in den
Perforationslöchern der Gegenelektrode und im Kondensatorspalt auf.
Dämpfung in engen Kanälen
Den Strömungswiderstand eines Kanals bei einer laminaren Strömung erhält man mit dem
Gesetz von Hagen-Poisseuille, das einen Zusammenhang zwischen der Druckdifferenz der
beiden Öffnungen und dem Volumenstrom q herstellt. Ein Kriterium für eine laminare
Strömung liefert die Reynoldszahl, die das Verhältnis der Trägheitskraft zur Reibungskraft
angibt. Für die im Silizium-Mikrofon herrschenden Dimensionen ist die Bedingung einer
kleinen Reynoldszahl für Luft bei Frequenzen unter 100 kHz erfüllt. Für einen Kanal der
Länge lh gilt für einen runden bzw. quadratischen Querschnitt [Jog74]
 8 η ⋅ lh
 π ⋅ 4
p1 − p 2
rh

= Ra = 
Za =
q
 19 ⋅ η ⋅ l h
4

ah

Radius rh
.
(4.3)
Kantenlänge a h
Der akustische Strömungswiderstand Ra [kg/(m4s)] ist proportional zur Viskosität des Fluids
und hängt stark von der lateralen Abmessung des Kanals ab. Der Widerstandswert bei einem
quadratischen Querschnitt wird mit Hilfe einer Ersatzfläche aus dem runden Querschnitt
abgeschätzt.
Dämpfung im Kondensatorspalt
Die von der Membranbewegung verursachte Luftströmung im Kondensatorspalt erfährt
aufgrund der geringen Spalthöhe in Silizium-Mikrofonen eine nicht zu vernachlässigende
Reibung an der Membran- und Gegenelektrode. Berechnungen zum Strömungswiderstand
zwischen einem Membransegment und einem zugeordneten Loch in der Gegenelektrode
wurden von Z. Skvor [Skv68] durchgeführt. Bei einer Gesamtfläche A und einem
Spaltabstand x0 gilt
Ra =
12 ⋅ η ⋅ X 0
x0 ⋅ A
3
2
 1  X 0  3 1 rh 2 1 rh 4 
 − + ⋅ 2 − ⋅ 4  .
⋅  ⋅ ln
2
8 X 0 
r
 h  8 2 X0

(4.4)
Dabei ist 2⋅X0 ein von der Perforationsanordnung abhängiger effektiver Abstand zwischen den
Perforationslöchern. In einer Wabenanordnung mit dem gleichen Abstand dh zwischen
nächsten Nachbarn gilt 2⋅X0=1.05⋅dh. Geringfügig ungünstiger ist eine quadratische
Anordnung der Kantenlänge dh mit einem etwas längeren Strömungsweg: 2⋅X0=1.13⋅dh. Unter
Ausnutzung der Flächenäquivalenz werden näherungsweise Perforationslöcher mit
quadratischen Querschnitt beschrieben.
58
Modellierung von kapazitiven Silizium-Mikrofonen
4.2.3 Akustische Massenelemente
Ein beschleunigtes, inkompressibles Fluid der Dichte ρ speichert kinetische Energie und wird
durch eine Induktivität dargestellt (Abbildung 4.5). Für einen zylinderförmigen Kanal gilt
Z a = j ⋅ω ⋅ ρ ⋅
(l h + 2 ⋅ 0.8 ⋅ rh )
rh ⋅ π
2
.
(4.5)
Darin wurde eine Mündungskorrektur mit einer effektiven Länge ≈lh+2⋅0.8⋅rh durchgeführt,
welche die Belastung der Innen- und Außenseite der Öffnung mit einer Strahlungsimpedanz
berücksichtigt [Zoll93]. Sie beschreibt anschaulich die mitschwingende Luftmasse an den
Rohröffnungen. Daraus folgt die Induktivität einer akustischen Masse Ma
Ma = ρ ⋅
(l h + 2 ⋅ 0.8 ⋅ rh )
rh ⋅ π
2
.
(4.6)
Die Modellierung des Fluids im Kanal mit einem konzentrierten Massenelement setzt voraus,
dass der Rohrradius und die Rohrlänge klein gegenüber der Wellenlänge sind.
Akustische Massen werden in langen und schmalen Kanälen relevant. Im Mikrofon treten
diese als Perforation in der Gegenelektrode und als Schalleinlassloch im Gehäuses auf.
p1
ρ
p2
strukturtreue
Transformation
Ma
p1
p2
q=q1=q2
Abbildung 4.5: Modellierung eines inkompressiblen Fluids durch eine Induktivität.
4.2.4 Mechanische Elemente
Membran und Gegenelektrode sind mechanische Schwinger mit kontinuierlicher Steifigkeitsund Massenverteilung. Um eine Beschreibung mit konzentrierten Elementen zu ermöglichen
wird die tatsächliche Auslenkung und dynamisch wirksame Masse in eine entsprechende
kolbenförmige Bewegung umgerechnet, bei der jeder Punkt auf der Elektrode phasengleich
und mit der gleichen Amplitude schwingt. Dieses Vorgehen ist zulässig, wenn in der
Simulation nicht die tatsächliche ortsabhängige Auslenkungsfunktion benötigt wird, sondern
ein gemittelter Effektivwert ausreicht. Bei einem kapazitiven Wandler ist diese Voraussetzung
erfüllt sofern die Amplitude klein gegen den Kondensatorspalt ist.
Nach dem Kolbenmembran-Modell wird die Membran und Gegenelektrode jeweils durch
eine effektive Feder und Masse dargestellt und in analog-elektrischer Formulierung durch
eine Kapazität und eine Induktivität modelliert (Abbildung 4.6). Mechanische
Reibungsverluste können aufgrund der sehr guten elastischen Eigenschaften von Silizium
vernachlässigt werden. Die Transformation des Feder-Masse-Systems in ein analogelektrisches System erfolgt dual, da die Flussgröße Kraft in die Potentialgröße Spannung
überführt wird.
59
Modellierung von kapazitiven Silizium-Mikrofonen
F1
p
KolbenmembranModell
meff
duale
Transformation
keff
F1
M
C
F2
F2
Abbildung 4.6: Modellierung der Membran und Gegenelektrode nach dem KolbenmembranModell durch eine effektive Feder und Masse bzw. Kapazität und Induktivität.
Mechanische Federelemente
Aus der mittleren Auslenkung der Membran
x eff =
∫∫ w( x, y) ⋅ dx ⋅ dy .
(4.7)
A
wird bei einer über die Fläche konstanten Kraft F die effektive Federkonstante keff=F/xeff
berechnet. Darin beschreibt w(x,y) die tatsächliche Auslenkungsfunktion. Mit der effektiven
Nachgiebigkeit 1/keff kann dann mit der Membranfläche A eine Nachgiebigkeit Ca [m3/Pa] in
akustischen Einheiten definiert werden
Ca ≡
A2
=
k eff
∫∫ w( x, y) ⋅ dx ⋅ dy = C
p
m
⋅A .
(4.8)
Die akustischen Nachgiebigkeiten der verschiedenen Membrantypen für das Netzwerkmodell
sind durch die bereits in Kapitel 3 berechneten und simulierten mechanischen
Nachgiebigkeiten Cm und deren Membranfläche gegeben. Für geschlossene Membranen gilt
Gleichung (3.10), (3.12) für Feder-Membranen und (3.17) beschreibt die mechanische
Nachgiebigkeit von Korrugationsmembranen.
In gleicher Weise wird die akustische Nachgiebigkeit einer Gegenelektrode beschrieben, die
aufgrund ihrer Dicke ein dominierendes Plattenverhalten aufweist. Die Perforation in der
Gegenelektrode kann nach M. Pedersen [Ped96] durch ein effektives Elastizitätsmodul und
eine um den Flächenanteil der Perforation ρh reduzierte Materialdichte berücksichtigt werden
E eff ≡ E ⋅ (1 − ρ h ) ,
(4.9)
ρ eff ≡ ρ ⋅ (1 − ρ h ) .
(4.10)
Der Vergleich der Durchbiegung bei Druckbelastung einer perforierten Platte und einer
soliden Platte mit dem effektiven Elastizitätsmodul zeigt nach FEM-Simulationen eine gute
Übereinstimmung.
Mechanische Massenelemente
Zur Berechnung der dynamisch wirksamen Membranmasse wird die kinetische Energie der
tatsächlichen Membranschwingung mit der einer Kolbenmembran gleichgesetzt
! 1
1
2
⋅ meff ⋅ ω 2 ⋅ x eff = ⋅ ω 2 ⋅ ∫ w( x, y ) 2 ⋅ dm .
2
2
60
(4.11)
Modellierung von kapazitiven Silizium-Mikrofonen
Mit der mittleren Auslenkung von Gleichung 4.7, einer konstanten Schichtdicke t und
dm=dx⋅dy⋅t erhält man die dynamische Masse der Membran in akustischen Einheiten
⇒ Ma =
meff
A
2
∫∫ w( x, y) ⋅ dx ⋅ dy
=t⋅ρ ⋅
(∫∫ w( x, y) ⋅ dx ⋅ dy )
2
2
≡
t⋅ρ
⋅ f mass .
A
(4.12)
Der durch die Gleichung definierte Massenfaktor fmass gibt das Verhältnis von dynamisch
wirksamer Masse und der „physikalischen“ Membranmasse an und hängt von dem speziellen
Durchbiegungsverhalten einer Membran ab. Für eine geschlossene Membran unter einer
mechanischen Spannung beträgt er nach [Hoh86] etwa 1.5. In guter Übereinstimmung wurde
aus der nach der FE-Methode simulierten Durchbiegung von Kreismembranen ein
Massenfaktor von 1.37 bis 1.44 berechnet, der geringfügig von der Membrandicke und
Spannung abhängt. Für die in Kapitel 3 simulierten Feder-Membranen wurde ein
Massenfaktor von 1.12 (Feder B) und 1.18 (Netz) bestimmt. Trotz der sehr unterschiedlichen
Formen der Feder-Membranen unterscheidet sich der Massenfaktor nur wenig. Der im
Vergleich zu einer Kreismembran kleinere Massenfaktor einer Feder-Membran ist auf die
verstärkte Konzentration der Membranmasse in Bezug auf die Membranmitte
zurückzuführen. Mit dem mechanischen Feder- und Massenelement kann nun die
Eigenfrequenz einer Membran formuliert werden
f0 =
1
1
1
1
.
⋅
=
⋅
2 ⋅π
Ca ⋅ M a 2 ⋅ π
C m ⋅ t ⋅ ρ ⋅ f mass
(4.13)
Bei einer geschlossenen Membran hebt sich die Dickenabhängigkeit der mechanischen
Nachgiebigkeit Cm~1/t und der dynamischen Masse ~t gegenseitig auf, so dass die
Eigenfrequenz von der Membrandicke unabhängig ist.
4.2.5 Strahlungsimpedanz
Die Strahlungsimpedanz beschreibt die Interaktion eines Senders mit der umgebenen
Fluidmasse. Sie setzt sich aus den Abstrahlverlusten einer sich bewegenden Membran an das
umgebene Schallmedium und der an der Oberfläche der Membran mitbeschleunigten Masse
des Schallmediums zusammen [Hsu89]
 2 ⋅π ⋅ ρ ⋅ f 2 
ρ 
8
 + j ⋅ ω ⋅  ⋅
Z rad = R rad + j ⋅ ω ⋅ M rad = 
 .
2

c
 3 R ⋅π 


(4.14)
Bei der Berechnung wird von einer einseitigen Schallabstrahlung mit einer kolbenförmigen
Bewegung ohne Störungen der Umgebung ausgegangen.
4.3
Netzwerkmodellierung und Simulation von Mikrofonen
Mit den zuvor beschriebenen akustischen und mechanischen konzentrierten Elementen wird
das Netzwerkmodell eines Silizium-Mikrofons konstruiert. Es beschreibt die dynamische
Nachgiebigkeit des Mikrofon, d.h. die Differenz der Auslenkung von Membran und
61
Modellierung von kapazitiven Silizium-Mikrofonen
Gegenelektrode bei Druckbelastung bei verschiedenen Frequenzen. Außerdem kann das
akustische Eigenrauschen des Mikrofons berechnet werden.
4.3.1 Mechanisch-akustisches Netzwerkmodell
Da sich der grundlegende Aufbau und das Funktionsprinzip der hergestellten Mikrofone
gleicht, wird das Netzwerkmodell exemplarisch für einen Mikrofontyp gebildet. Abbildung
4.7 zeigt das äquivalente Ersatzschaltbild eines Mikrofons mit Gehäuse.
Cv
pbp
Cgap
pm
Mbp
Mp
Mvent
Cbp
Rp
Rvent
Ca Rgap
Mm
Mrad
Rrad
Rin
Cin
Min
p~
Gehäusewand
Abbildung 4.7: Schematischer Querschnitt eines Mikrofons mit Gehäuse und zugehörigem
Netzwerkmodell.
Von der Schallquelle p~ ausgehend, setzt sich das Netzwerkmodell aus den folgenden
Bereichen zusammen:
•
•
•
•
62
Eingangsbereich: Der Schalldruck tritt durch die Gehäuseöffnung mit einer akustischen
Masse (Induktivität Min) und dem Strömungswiderstand Rin in das freigeätzte
Chiprückvolumen mit einer Hohlraum-Nachgiebigkeit (Kapazität Cin) ein.
Membranbereich: Der Schalldruck an der Membran beschleunigt die Gesamtmasse, die
sich aus der dynamischen Membranmasse (Mm) und dem Massenanteil der
Strahlungsimpedanz (Mrad) zusammensetzt und lenkt die Membran aus (Ca). Der Realteil
der Strahlungsimpedanz Rrad beschreibt die Abstrahlverluste. Durch eine Öffnung in der
Membran, z.B. dem Druckausgleichloch oder dem offenen Bereich einer Feder-Membran
kann Luft einströmen. Da die Membran i.a. sehr dünn ist, kann ein akustischer Widerstand
und eine akustische Masse der Öffnung vernachlässigt werden.
Kondensatorspalt: Im flachen Kondensatorspalt konkurriert die Kompression des
Luftpolsters (Cgap) mit der seitlichen Strömung zu den Perforationslöchern (Rgap).
Perforierte Gegenelektrode: Die bewegliche Rückseitenplatte (Schwinger mit Cbp, Mbp)
wird in zwei Bereiche unterteilt. Die von der Membran überdeckten
Perforationsöffnungen in der Gegenelektrode werden durch eine akustische Masse Mp und
Modellierung von kapazitiven Silizium-Mikrofonen
•
einem Strömungswiderstand Rp dargestellt. Dementsprechend bezeichnen Mvent und Rvent
Masse und Strömungswiderstand der Perforationsöffnungen im freiliegenden
Membranbereich, d.h. über dem Druckausgleichsloch oder der Öffnung einer FederMembran. Eine Querströmung zwischen beiden Perforationsgebieten wird vernachlässigt.
Gehäuse: Das abgeschlossene Rückvolumen des Gehäuses wird durch die HohlraumNachgiebigkeit CV beschrieben.
Die Berechnung der konzentrierten Elemente erfolgt mit den Gleichungen aus Abschnitt 4.2
und den Technologie- und Geometrieparametern von Mikrofon und Gehäuse.
4.3.2 Analytische Berechnung der Mikrofon-Nachgiebigkeit
Prinzipiell eignet sich die vorgestellte Netzwerkmodellierung für alle Wandlerprinzipien, bei
denen der Schall über eine mechanische Auslenkung sensiert wird. Auch ist sie mit
verschiedenen Auswerteschaltungen kombinierbar. Für den kapazitiven Wandler ist die
Änderung des Spaltabstandes, d.h. die relative Auslenkung von Membran xm und
Gegenelektrode xbp, bei einem Schalldruck p~ von Interesse. Nach der gewählten
Transformation ist die Flussgröße im Netzwerkmodell der Volumenstrom q bzw. die Schnelle
v mal Flächenelement. Mit dem Zusammenhang zwischen der Auslenkung und der Schnelle
v=j⋅ω⋅x und der akustischen Nachgiebigkeit p/q=(j⋅ω⋅C)-1 kann die Mikrofon-Nachgiebigkeit
durch den Druckabfall an der Membran pm und der Gegenelektrode pbp dargestellt werden
C Mikrofon ≡
x m − xbp
p~
=
q m qbp
−
Am Abp
j ⋅ ω ⋅ p~
C ⋅ p
C bp ⋅ pbp
= a m −
 Am
Abp

 1
⋅
.
 p~

(4.15)
Diese Größe wird als Mikrofon-Nachgiebigkeit bezeichnet, obwohl sie nicht nur vom
eigentlichen Mikrofon, sondern auch vom Gehäusedesign abhängt. Die Aufgabe besteht in der
analytischen Berechnung oder numerischen Simulation der Druckübertragungsfunktionen
pm/p~ und pbp/p~ des Netzwerkmodells. Zur Vereinfachung der analytischen Berechnung der
Mikrofon-Nachgiebigkeit wird angenommen, die Gegenelektrode sei derart steif und
perforiert, dass sie keinen Beitrag zur Nachgiebigkeit liefert. Außerdem sollen die akustischen
Massen der Perforation, der akustische Widerstand des Schalleintrittslochs, der
Strahlungswiderstand und die akustischen Nachgiebigkeiten des Eingangsbereiches und des
Kondensatorspaltes wegen ihrer sehr kleinen Volumina vernachlässigt werden. Unter diesen
Voraussetzungen liefert die Auflösung des Netzwerkes die Druckübertragungsfunktion
p
VMikrofon ≡
p
m
Ca
=
~
1
CV


 1
2
+
+ j ⋅ ω ⋅ (R
+ R ) − ω ⋅ ( M rad
gap
p
C
a 44
1
42444
3

Hochpass

−1
.
 

 

1
 
 −ω2 ⋅M
+ M m ) ⋅ 1 +
in
 j ⋅ ω ⋅ CV ⋅ Rvent 
  1442443 
 
Tiefpass


(4.16)
63
Modellierung von kapazitiven Silizium-Mikrofonen
Die frequenzabhängige Funktion VMikrofon gibt die Übertragung des Eingangsdruckes an die
Membran wieder. Im Wesentlichen beschreibt sie ein Bandpass-Filter und einen LCSerienschwingkreis. Die Mikrofon-Nachgiebigkeit ist wegen Ca=Cm⋅Am
C
Mikrofon
≈C
m
⋅V
Mikrofon
.
(4.17)
Mit Ausnahme von Resonanzüberhöhungen kann die Mikrofon-Nachgiebigkeit maximal den
Wert der mechanischen Membran-Nachgiebigkeit Cm erreichen.
4.3.3 Simulationen zur Mikrofon-Nachgiebigkeit
Zur Erläuterung der Frequenzabhängigkeit der Mikrofon-Nachgiebigkeit werden Mikrofone
mit drei verschiedenen Silizium-Membranen simuliert. Die Simulationsparameter sind in der
Tabelle 4.1 aufgelistet:
Materialparameter
• E-Modul Silizium
166 GPa
• Poissonzahl Silizium
0.27
• Dichte Silizium
2330 kg/m3
• Dichte Luft
1.29 kg/m3
• Schallgeschwindigkeit
344 m/s
• Viskosität Luft
1.86⋅10-5 kg/ms
Gehäusedesign
• Volumen
5⋅5⋅5 mm3
• Wandstärke
1 mm
• Öffnung
1 mm
Rückseitenplatte
LuftMembran
spalt
• Radius 500 µm
• Höhe 2 µm • Radius
500 µm
• Dicke 5 µm
• Dicke
• Radius Perforation
200 nm
2.5 µm
• Spannung
• Perforationsabstand
30 MPa
10 µm
Tabelle 4.1: Parameter zur Simulation der Mikrofon-Nachgiebigkeit.
Die Materialdaten von Silizium wurden [Bea85] entnommen. Neben diesen allgemeinen
Simulationsparametern werden abhängig vom Membrandesign die folgenden Parameter
verwendet:
•
•
•
Kreismembran: Die offene Fläche in der Membran ist durch vier 5⋅5 µm2 große
Druckausgleichslöcher gegeben.
Feder-Membran: Bei 16 Federn mit einer Breite von jeweils 20 µm sollen 10% der
Rückseitenplatte nicht bedeckt sein. Nach den FEM-Simulationen in Kapitel 3.3 mit dem
Design Netz A ist diese Membran etwa doppelt so nachgiebig wie eine vergleichbare
Kreismembran (Federmembran-Faktor fFEder=2.1).
Korrugationsmembran: Die Korrugationshöhe sei 600 nm, die Weite und der Abstand 5
µm und die Korrugationsanzahl 8.
Abbildung 4.8 gibt die simulierte Mikrofon-Nachgiebigkeit der Mikrofone mit den
verschiedenen Membranen wider. Die durch Symbole gekennzeichneten Kurven wurden mit
Hilfe der Schaltungssoftware „PSPICE“ von Cadence Design Systems und dem vollständigen
Netzwerkmodell nach der Abbildung 4.7 numerisch simuliert. Der Vergleich mit der
64
Modellierung von kapazitiven Silizium-Mikrofonen
analytischen Näherung der Gleichung 4.16 (durchgezogene Linien) zeigt die Gültigkeit der
durchgeführten
Vereinfachungen
bei
der
Berechnung
für
die
gewählten
Simulationsparameter.
Mikrofon-Nachgiebigkeit [nm/Pa]
30
25
Korrugationsmembran (numerisch)
Feder-Membran (numerisch)
20
Kreismembran (numerisch)
analytische Näherung
15
10
5
0
10
100
1000
10000
100000
Frequenz [Hz]
Abbildung 4.8: Analytisch und numerisch simulierte Mikrofon-Nachgiebigkeit mit einer
Kreis, Feder- bzw. Korrugationsmembran.
Die Mikrofon-Nachgiebigkeit resultiert überwiegend aus der mechanischen Nachgiebigkeit
der Membranen (5.2-28 nm/Pa), da die Gegenelektrode statisch verhältnismäßig starr (ca. 0.2
nm/Pa) und dynamisch über die Perforierung kurzgeschlossen ist. Das Rückvolumen vom
Gehäuse hat ebenfalls kaum einen Einfluss. Die entsprechende Hohlraum-Nachgiebigkeit ist
mit umgerechnet 1 µm/Pa im Vergleich zu den Membran-Nachgiebigkeiten sehr weich.
Erwartungsgemäß ist die Nachgiebigkeit der Kreismembran am niedrigsten. Sie zeigt bis zur
ersten Resonanzfrequenz einen flachen Frequenzgang. Die Eigenfrequenz der Membran von
ca. 80 kHz wird durch die Massenbelastung der Strahlungsimpedanz auf 60 kHz und durch
die akustische Masse der Gehäuseöffnung auf die System-Resonanz von 30 kHz gesenkt. Bei
dem Mikrofon mit Feder-Membran ist die Resonanzfrequenz aufgrund der höheren
Nachgiebigkeit bereits derart gedämpft, dass keine Resonanzüberhöhung zu beobachten ist.
Oberhalb der durch die Membran-Nachgiebigkeit und dem Strömungswiderstand im
Kondensatorspalt und der Perforation definierten Grenzfrequenz fällt die SystemNachgiebigkeit auf die sehr niedrige Hohlraum-Nachgiebigkeit des Kondensatorspaltes von
0.01 nm/Pa ab. Die akustische Dämpfung führt besonders bei empfindlichen Mikrofonen, wie
die Simulation des Mikrofons mit Korrugationsmembran zeigt, zu einem ausgeprägten
Tiefpass-Verhalten, das bis in das Audioband reichen kann. Mikrofone mit Feder-Membranen
zeigen zusätzlich eine untere Grenzfrequenz, die auf einen akustischen Kurzschluss bei tiefen
Frequenzen über die nicht von der Membran bedeckten Perforationsöffnungen und dem
Gehäusevolumen zurückzuführen ist.
Mit dem vorgestellten Netzwerkmodell ist eine effektive Simulation der verschiedenen
Mikrofone möglich, die nur bekannte Eingangsgrößen (Design-, Technologie und
Materialdaten) benötigt. Durch die Integration von Simulationsergebnissen der numerischen
FE-Analysen können auch erstmals Feder- und Korrugationsmembranen simuliert werden. Da
65
Modellierung von kapazitiven Silizium-Mikrofonen
aus der Literatur Netzwerkmodelle mit ähnlichem Aufbau bekannt sind, soll an dieser Stelle
nicht im Detail die Abhängigkeit der System-Nachgiebigkeit von den einzelnen Parametern
diskutiert werden. Vielmehr soll auf die bisher nicht untersuchten Zusammenhänge zwischen
der dynamischen Bandbreite und dem Perforationsdesign in der Gegenelektrode eingegangen
werden.
4.3.4 Dynamische Bandbreite und Perforationsdesign
Die untere und obere Grenzfrequenz der Mikrofon-Nachgiebigkeit wird aus der
Druckübertragungsfunktion VMikrofon berechnet. Bei Vernachlässigung der ersten
Resonanzfrequenz sind sie durch
fu =
fo =
1
2 ⋅ π ⋅ Rvent ⋅ CV
und
(4.18)
1
2 ⋅ π ⋅ ( R gap + R p ) ⋅ C m
(4.19)
gegeben. Die nicht von der Membran bedeckten Perforationslöcher in der Rückseitenplatte
bilden zusammengenommen den Strömungswiderstand Rvent, der mit der HohlraumNachgiebigkeit des Rückvolumens Cv die untere Grenzfrequenz definiert. Der für die obere
Grenzfrequenz maßgebliche Strömungswiderstand setzt sich dagegen aus dem Anteil der
Strömung im Kondensatorspalt (Rgap) und durch die Perforationslöcher unter der Membran
(Rp) zusammen. Zum besseren Verständnis ist die Aufteilung der Rückseitenplatte in zwei
Strömungsbereiche anhand einer Feder-Membran in Abbildung 4.9 dargestellt.
Membran
rh
Membran
dh
Rvent
Rgap+Rp
Rvent
Perforation
Abbildung 4.9: Strömungswiderstände im Kondensatorspalt und der Rückseitenplatte.
Da sich das Bandpass-Verhalten von geschlossenen Membranen und Feder-Membranen
unterscheidet, werden beide Membrantypen getrennt voneinander untersucht.
Mikrofone mit geschlossenen Membranen
Befinden sich in der Membran nur wenige, schmale Öffnungen zum Ausgleich von
Schwankungen des atmosphärischen Druckes, dann ist die untere Grenzfrequenz aufgrund des
kleinen Widerstandswertes von Rvent selbst bei sehr kleinen Gehäusen deutlich unter 10 Hz.
Die für das Tiefpass-Verhalten verantwortlichen Strömungswiderstände Rgap und Rp hängen
von dem Abstand zwischen den Perforationenöffnungen dh und deren Radius rh und Länge ab.
Die Länge einer Perforation ist durch die Dicke der Rückseitenplatte festgelegt. Wird als
Randbedingung eine konstante Perforationsflächendichte
66
Modellierung von kapazitiven Silizium-Mikrofonen
ρh =
π ⋅ rh 2
dh
(4.20)
2
vorgegeben, dann ist bei variierendem Radius rh einer Perforationsöffnung der Abstand
zwischen den Perforationen dh über die obige Beziehung festgelegt. Mit den
Simulationsparametern von Tabelle 4.1, die einer Perforationsflächendichte von ρh=20%
entsprechen, und der Korrugationsmembran erhält man den in Abbildung 4.10 dargestellten
Frequenzgang bei verschiedenen Perforationsradien.
Mikrofon-Nachgiebigkeit [nm/Pa]
100
rh=5 µm
(dh=20 µm)
rh=3 µm
(dh=12 µm)
10
rh=1 µm
(dh=4 µm)
1
10
100
1000
10000
100000
Frequenz [Hz]
Abbildung 4.10: Tiefpass-Verhalten
Perforationsflächendichte.
der
Mikrofon-Nachgiebigkeit
bei
konstanter
Bei sehr schmalen Perforationenöffnungen mit einem Radius von 1 µm reicht die
Entdämpfung des Luftpolsters im Kondensatorspalts nicht aus und die MikrofonNachgiebigkeit fällt bereits bei 1 kHz ab. Die Ursache ist die starke Abhängigkeit vierter
Ordnung der viskosen Kanalströmung vom Perforationsradius. Da bei einer konstanten
Perforationsflächendichte mit zunehmenden Radius die Anzahl der Perforationen abnimmt,
führt eine Verdreifachung auf rh=3 µm lediglich zu einer etwa zehnfach höheren
Grenzfrequenz von etwa 10 kHz. Wird der Radius weiter erhöht (rh=5 µm), ist eine
Umkehrung mit zunehmender Dämpfung zu beobachten. In diesem Fall dominiert der
Strömungswiderstand im Kondensatorspalt Rgap gegenüber dem Strömungswiderstand durch
die Perforationen Rp. Dieser nimmt mit dem Abstand zwischen zwei Perforationen dh und
daher bei konstanter Perforationsdichte mit dem Perforationsradius zu.
Bei gegebener Perforationsflächendichte existiert also ein optimaler Perforationsradius, bei
dem der gesamte Strömungswiderstand Rgap+Rp minimiert wird. Dieser wird aus der ersten
Ableitung des gesamten Strömungswiderstandes nach dem Perforationsradius berechnet
67
Modellierung von kapazitiven Silizium-Mikrofonen
d ( R p + R gap )
drh
16
⋅
⇒ rh =
4 3 ⋅π
=0 ,
t bp ⋅ x0
*
X0
2
3


ρh
ρh2
3
π


⋅ ln X 0 ⋅
− +
−
2
2
2
4 
4
8
⋅
ρ
(
2
)
8
(
/
2
)
⋅
π
⋅
X
⋅
π
⋅
X
h
0
0


. (4.21)
Der optimale Perforationsradius hängt nur von der Perforationsflächendichte ρh, dem Abstand
der Perforationen, dem Spaltabstand x0 und der Länge einer Perforationsöffnung, im Mikrofon
die Dicke der Rückseitenplatte tbp, ab. Danach ist bei dem Perforationsradius rh* mit
Ausnahme von Resonanzeffekten die obere Grenzfrequenz maximal. In Abbildung 4.11 ist
die simulierte obere Grenzfrequenz der Mikrofon-Nachgiebigkeit bei einer
Perforationsflächendichte von 10%, 20% und 30% dargestellt. Darin ist die obere
Grenzfrequenz durch diejenige Frequenz definiert, bei der die Nachgiebigkeit um ±3 dB vom
Nominalwert abweicht.
obere Grenzfrequenz fo [kHz]
25
20
ρh=0.3
15
ρh=0.2
10
5
ρh=0.1
0
1
2
3
4
5
6
7
8
9
10
Perforationsradius rh [µm]
Abbildung 4.11: Obere Grenzfrequenz der Mikrofon-Nachgiebigkeit in Abhängigkeit vom
Perforationsdesign.
Deutlich ist die zunächst mit dem Perforationsradius ansteigende obere Grenzfrequenz zu
erkennen. Bei einer Perforationsflächendichte von 10% beträgt in Einklang mit dem
berechneten Wert der simulierte optimale Perforationsradius, der eine minimale Dämpfung
und maximale obere Grenzfrequenz liefert, etwa 3.2 µm. Dennoch ist die obere
Grenzfrequenz mit 4.3 kHz zu niedrig. Erst mit der Erhöhung der Perforationsflächendichte
auf 20% kann die Forderung einer Grenzfrequenz >10 kHz erfüllt werden. Dazu kommen
Radien von 2.5 µm bis 6 µm in Frage. Bei weiterer Erhöhung der Perforationsflächendichte
wird das System so stark entdämpft, dass die Resonanzüberhöhung die 3 dB-Toleranz verletzt
und die obere Grenzfrequenz bei rh=3.5 µm schlagartig sinkt. Höhere
Perforationsflächendichten führen zu einer weiteren Verschlechterung des Frequenzganges.
68
Modellierung von kapazitiven Silizium-Mikrofonen
Mit Hilfe des Netzwerkmodells kann in der vorgestellten Weise für jedes Mikrofon mit einer
geschlossenen Membran ein optimales Design der Perforation in der Gegenelektrode
angegeben werden, so dass die Anforderung an den Frequenzgang erfüllt wird. Die bisherigen
Betrachtungen zur dynamischen Bandbreite sollen im nächsten Abschnitt auf Mikrofone mit
Feder-Membranen erweitert werden.
Mikrofone mit Feder-Membranen
Betrachtet man nur die Perforation unterhalb der Membran, sind die Überlegungen zur oberen
Grenzfrequenz bei geschlossenen Membranen in der gleichen Weise für Feder-Membranen
gültig. Das heißt, dass es wiederum einen optimalen Perforationsradius gibt. Neu bei FederMembranen ist, dass ein beträchtlicher Teil der Luft durch die nicht von der Membran
bedeckten Perforationslöcher mit dem Widerstand Rvent strömen kann. Da der
Widerstandswert verhältnismäßig klein ist, existiert abhängig vom Gehäusevolumen, d.h. von
der Hohlraum-Nachgiebigkeit CV, eine nicht zu vernachlässigende untere Grenzfrequenz.
Diese Dämpfung der Mikrofonempfindlichkeit bei niedrigen Frequenzen ist häufig zur
Filterung von Störgeräuschen erwünscht. Insbesondere bei empfindlichen Membranen und
miniaturisierten Gehäusen mit geringem Luftvolumen kann der Fall eintreten, dass die
Anforderungen an die dynamische Bandbreite nicht erfüllt werden. Den Zusammenhang
zwischen der unteren Grenzfrequenz und der Gehäusegröße zeigt die Abbildung 4.12, bei der
die Nachgiebigkeit eines Mikrofons mit Feder-Membran für Volumen von 0.3⋅10-9, 27⋅10-9,
125⋅10-6 m3 und einem unendlichen Volumen simuliert wurde (rh=2.5 µm, ρh=0.2). Ersteres
entspricht dem Fall, dass der Mikrofonchip direkt auf eine Platine montiert und von der
Vorderseite beschallt wird, so dass nur die Substrat-Ätzgrube das Rückvolumen bildet. Bei
der Feder-Membran sollen 10% aller Perforationsöffnungen nicht von der Membran bedeckt
sein und zum akustischen Kurzschluss beitragen.
Mikrofon-Nachgiebigkeit [nm/Pa]
12
10
8
offen
V=125 mm 3
V=27 mm 3
Chipvolumen (0.3 mm3 )
6
4
2
0
10
100
1000
10000
100000
Frequenz [Hz]
Abbildung 4.12: Frequenzgang eines Mikrofons mit Feder-Membran in Abhängigkeit vom
Gehäusevolumen.
69
Modellierung von kapazitiven Silizium-Mikrofonen
Bereits bei einem Gehäusevolumen von 125⋅10-6 m3 ist der Einfluss der Hohlraum-Feder am
akustischen Kurzschluss zu beobachten. Die Mikrofon-Nachgiebigkeit im mittleren
Frequenzbereich hingegen wird kaum beeinflusst. Sowohl der akustische Kurzschluss als
auch die vom Luftvolumen auf die Membran ausgeübte Rückstellkraft nimmt mit den
erwünschten kleinen Gehäusedimensionen zu. Wird im Extremfall das Rückvolumen
lediglich durch den Mikrofonchip realisiert, dann setzt sich die Mikrofon-Nachgiebigkeit
größtenteils aus der kleinen Hohlraum-Nachgiebigkeit von 2.5 nm/Pa zusammen.
4.3.5 Analytische Berechnung des akustischen Eigenrauschens
Bisher wurde auf die Simulation und Optimierung der Nachgiebigkeit der Mikrofone, d.h. im
Wesentlichen auf die Empfindlichkeit eingegangen. Für einen hohen Signal/Rauschabstand
muss ferner das Rauschen des Mikrofons möglichst gering sein. In diesem Abschnitt soll
zunächst das Eigenrauschen des Mikrofons im Gehäuse ohne elektrische Beschaltung
untersucht werden.
Leistungsverbrauch und Schwankung sind durch die Nyquist-Beziehung miteinander
verknüpft. Demnach ist das thermische Rauschen nur von seinem Widerstandswert und nicht
von speziellen Mechanismen abhängig. Das Eigenrauschen des Mikrofons ergibt sich daher
aus den Widerständen seiner analog-elektrischen Schaltung [Ols57]. In dem vorgestellten
Netzwerkmodell sind das die Widerstände
•
•
•
•
•
der Schalleintrittsöffnung im Gehäuse Rin,
der Strömung im Kondensatorspalt Rgap,
der Kanalströmung durch die perforierte Gegenelektrode Rp,
der Strömung durch die Perforationslöcher im offenen Membranbereich Rvent und
der Strahlungsimpedanz Rrad.
Man kann sich anschaulich vorstellen, dass durch die thermisch aktivierte Luftbewegung ein
„Rauschdruck“ über die akustischen Widerstände abfällt, der wiederum zu einer Vibration der
Membran führt. Der Rauschanteil des Strahlungswiderstandes kann als die Störung der auf
die Oberfläche der Membran aufprallenden Moleküle interpretiert werden.
Das gesamte Eigenrauschen kann aus dem Realteil der Ausgangsimpedanz der äquivalenten
Schaltung des Mikrofons bestimmt werden. Zur Berechnung der einzelnen Beiträge zur
Rauschdichte wird jedem Widerstand ein idealer rauschfreier Widerstand und seine
Rauschquelle zugeordnet und die Übertragung an die Membran berechnet. Je nach
Zweckmäßigkeit kann eine parallele Rauschstromquelle oder eine Rauschspannungsquelle in
Serie verwendet werden. Da die konzentrierten Elemente im mechanisch-akustischen
Netzwerkmodell in akustischen Einheiten formuliert sind, erhält man die Rauschdruckdichte
[Pa2/Hz]
Np =V
p ,q 2
⋅ W q, p .
(4.22)
Darin ist Vp,q die jeweilige Übertragungsfunktion der Rauschquelle (Wq,p⋅∆f)1/2 mit der
Rauschstromdichte Wq=4⋅k⋅T/R [(m3/s)2/Hz] bzw. Rauschdruckdichte Wp=4⋅k⋅T⋅R [Pa2/Hz].
Der Index p bzw. q kennzeichnet Größen, die sich auf den Druck bzw. den Volumenstrom
beziehen. Die Berechnungen gehen davon aus, dass die Gegenelektrode steif ist und nur die
thermische Vibration der Membran betrachtet werden muss. Außerdem soll die akustische
70
Modellierung von kapazitiven Silizium-Mikrofonen
Masse der Perforation und die akustische Nachgiebigkeit des Eingangsbereiches und des
Kondensatorspaltes vernachlässigbar klein sein. Das Rauschersatzschaltbild unter diesen
Annahmen gibt die folgende Abbildung an.
Min
Rrad Mrad Mm Cm Rgap Rp
Rin
W p ( Rrad + Rgap + R p ) ⋅ ∆f
Cv
W p Rin ⋅ ∆f
Rvent
W p Rvent ⋅ ∆f
Abbildung 4.13: Vereinfachtes Rauschersatzschaltbild zur Berechnung des Eigenrauschens.
Thermisches Widerstandsrauschen vom Schalleintritt Rin
Bei Verwendung einer Rauschdruckquelle ist sofort ersichtlich, dass die
Übertragungsfunktion in der selben Weise wie die Druckübertragungsfunktion VMikrofon zu
berechnen ist (Abschnitt 4.3.2). Die Rauschdruckdichte der Gehäuseöffnung ist daher durch
N Rin = V Mikrofon
p
2
⋅ 4 ⋅ k ⋅ T ⋅ Rin
(4.23)
gegeben. Sie zeigt das von der Mikrofon-Nachgiebigkeit bekannte spektrale Tief- und
Hochpass-Verhalten und ist proportional zum Widerstandswert.
Thermisches Widerstandsrauschen von Rgap, Rp und Rrad
Die Strömungswiderstände Rgap (Kondensatorspaltströmung) und Rp (Perforationsströmung)
und der Strahlungswiderstand Rrad befinden sich im selben Pfad im Rauschersatzschaltbild
und haben daher dieselbe Übertragungsfunktion, die mit Hilfe der Druckübertragungsfunktion
VMikrofon durch

1
V Rgap = V R p = V Rrad = V Mikrofon ⋅ 1 +
j ⋅ ω ⋅ CV ⋅ Rvent




(4.24)
ausgedrückt werden kann. Für den Fall CV<<Ca, d.h. einem ausreichend großen
Gehäusevolumen, weist die Übertragungsfunktion die Form eines Tiefpasses mit der von der
Mikrofon-Nachgiebigkeit bekannten oberen Grenzfrequenz auf. Insgesamt erhält man die
Rauschdruckdichte
N Rgap + R p + Rrad
p
= V Mikrofon

1
⋅ 1 +
j ⋅ ω ⋅ CV ⋅ Rvent

2

 ⋅ 4 ⋅ k ⋅ T ⋅ ( R gap + R p + R rad ) .

(4.25)
Thermisches Rauschen des „Ventilationswiderstandes“ Rvent
Der Strömungswiderstand der freistehenden Perforationslöcher liefert eine Rauschdichte an
der Membran, die ebenfalls ein Tiefpass-Verhalten zeigt
71
Modellierung von kapazitiven Silizium-Mikrofonen
N Rvent = V Mikrofon
p

j ⋅ ω ⋅ M in
1
⋅ 
+
Rvent
 j ⋅ ω ⋅ CV ⋅ Rvent
2

 ⋅ 4 ⋅ k ⋅ T ⋅ Rvent .

(4.26)
Die obere Grenzfrequenz der Rauschdichte ist bei Vernachlässigung der akustischen Masse
der Gehäuseöffnung durch f=1/(2⋅π⋅Rvent⋅CV) gegeben. Ein großer Widerstandswert muss nicht
zwangsläufig ein hohes Rauschen erzeugen, da gleichzeitig die obere Grenzfrequenz der
Rauschdichte sinkt und aus dem Nutzband geschoben wird.
Akustisches Gesamtrauschen
Die gesamte akustische Rauschdruckdichte des Mikrofon-Eigenrauschens wird durch die
Addition der einzelnen Rauschdichten gebildet
N p akustisch = N Rin + N Rgap + R p + N Rvent + N Rrad .
p
p
p
p
(4.27)
Für den Fall, dass das Gesamtrauschen eines Mikrofons vom akustischen Eigenrauschen
dominiert wird, wird das Signal/Rausch-Verhältnis eines Mikrofons durch eine höhere
Membran-Nachgiebigkeit nicht unmittelbar verbessert. Sowohl das Nutzsignal, d.h. die
Auslenkung der Membran, als auch die Übersetzung des „Rauschdruckes“ in eine thermische
Vibration steigt mit der Membran-Nachgiebigkeit.
4.3.6 Simulationen zum akustischen Eigenrauschen
Mit den Simulationsparametern der Tabelle 4.1 sind in Abbildung 4.14 die spektralen
akustischen Rauschdichten der einzelnen Rauschwiderstände eines Mikrofons mit Federbzw. Korrugationsmembran dargestellt. Die Beiträge zum thermischen Widerstandsrauschen
wurden sowohl mit dem vollständigen Netzwerkmodell numerisch mit der
Schaltungssoftware PSPICE simuliert (Symbole) als auch mit den abgeleiteten Gleichungen
analytisch berechnet (Linien).
0.5
akustische Rauschdichte [dB(P/Hz )]
akustische Rauschdichte [dB(P/Hz0.5)]
-90
-100
-110
-120
-130
-140
-150
-160
Rp
Rgap
Rin
Rvent
Rrad
analytisch
-170
-180
-190
100
-100
-110
-120
-130
-140
-150
-160
Rp
Rgap
Rin
Rvent
Rrad
analytisch
-170
-180
-190
-200
-200
10
-90
1000
10000
Frequenz [Hz]
100000
10
100
1000
10000
100000
Frequenz [Hz]
Abbildung 4.14: Akustische Rauschdruckdichte von Mikrofonen mit einer geschlossenen
Korrugationsmembran (links) und einer Feder-Membran (rechts).
72
Modellierung von kapazitiven Silizium-Mikrofonen
Sämtliche Rauschkurven zeigen einen Abfall bei hohen Frequenzen, der mit der Dämpfung
der Membranauslenkung zu erklären ist. Der Widerstandswert Rin vom einzelnen
Schalleintrittsloch im Gehäuse ist verhältnismäßig klein, so dass seine Rauschdruckdichte
vernachlässigbar ist. Der Strömungswiderstand Rvent ist bei der Korrugationsmembran sehr
groß und wird deshalb fast vollständig aus dem akustischen Frequenzbereich gefiltert. Bei der
Feder-Membran mit kleinerem Rvent dagegen resultiert aus der Grenzfrequenz bei 10 Hz eine
dominierende Rauschdichte bei tiefen Frequenzen. Über den akustischen Bereich integriert ist
der Rauschbeitrag dennoch sehr gering. Die Filterwirkung bei 3 kHz ist auf die MassenInduktivität des Schalleintrittlochs zurückzuführen. Der von der Frequenz abhängige
Strahlungswiderstand Rrad und die zugehörige Rauschdichte ist im akustisch relevanten
Frequenzbereich ebenfalls zu vernachlässigen. Den weitaus größten Beitrag zum akustischen
Eigenrauschen liefert das Rauschen der Strömungswiderstande im Kondensatorspalt Rgap und
durch die Perforationslöcher Rp.
Die in der Akustik gebräuchliche Größe zur Beschreibung des Signal/Rausch-Verhältnisses
ist ein äquivalenter Schallpegel, der ein dem Rauschen entsprechendes Signal erzeugen
würde. Da ein Schalldruck von 2⋅10-5 Pa im Mittel den niedrigsten vom Menschen
wahrnehmbaren Pegel entspricht, wird der Eigengeräuschpegel LE auf diese Hörschwelle
bezogen


L E ≡ 20 ⋅ log


⋅ df 
.
2 ⋅ 10 −5 

∫N
p
(4.28)
Der Eigengeräuschpegel wird durch Integration der Rauschdichte über einen definierten
Frequenzbereich berechnet. In Tabelle 4.2 sind die A-bewerteten Eigengeräuschpegel der
Rauschquellen zusammengestellt (Frequenzband 10 Hz – 20 kHz).
Rauschwiderstand
Rvent
Rrad
Rin
Rgap
Rp
Mikrofon total
LE [dB(A)]
korrugierte Membran
-31
-4.6
-5.6
17
24.3
25.1
LE [dB(A)]
Feder-Membran
1.8
-1.1
-4.1
18.9
26.3
27.1
Tabelle 4.2: Eigengeräuschpegel in einem Mikrofon mit Korrugations- bzw. Feder-Membran.
Der Eigengeräuschpegel des Mikrofons mit der Feder-Membran ist um etwa 2 dB(A) größer
als der des Mikrofons mit Korrugationsmembran. Dieser Unterschied hängt mit der höheren
mechanischen Membran-Nachgiebigkeit der korrugierten Membran zusammen, die zu einer
stärkeren spektralen Begrenzung der Rauschdichte führt. Für ein möglichst geringes
Eigenrauschen sollte die Summe der beiden dominierenden Strömungswiderstände Rgap und
Rp möglichst klein sein. Diese Zielsetzung steht in Einklang mit der Anforderung an eine
hohe obere Grenzfrequenz der Mikrofon-Nachgiebigkeit. In Abschnitt 4.3.4 wurde bereits die
Minimierung des gesamten Strömungswiderstandes Rp+Rgap behandelt. Das optimale
Perforationsdesign für eine maximale obere Grenzfrequenz ist demzufolge identisch mit dem
für ein minimales Eigenrauschen. Den Zusammenhang zwischen akustischen Rauschen und
Perforationsdesign verdeutlicht die Abbildung 4.15, in der bei einer konstanten
73
Modellierung von kapazitiven Silizium-Mikrofonen
Perforationsflächendichte von 20% bzw. 30% der Eigengeräuschpegel des Mikrofons mit
Korrugationsmembran in Abhängigkeit vom Perforationsradius aufgetragen ist.
Eigengeräuschpegel [dB(A)]
26.5
Perforationsflächendichte 20%
26
25.5
25
24.5
24
23.5
Perforationsflächendichte 30%
23
1
2
3
4
5
6
7
8
9
10
Perforationsradius rh [µm]
Abbildung 4.15: Reduzierung des Eigengeräuschpegels durch Optimierung der Perforation in
der Gegenelektrode.
Der Perforationsradius mit minimalem Eigenrauschen stimmt mit dem einer maximalen
Grenzfrequenz überein. Der Vergleich mit der Abbildung 4.11 liefert bei einer
Perforationsflächendichte von 20% jeweils einen optimalen Perforationsradius von 3.8 µm.
Der Eigengeräuschpegel ist bei einer Dichte von 30% selbst im Minimum mit 23.3 dB(A)
relativ hoch. Hinzu kommt, dass häufig der niedrigste Eigengeräuschpegel nicht erreicht
werden kann, da die dazu notwendigen weiten Perforationsöffnungen nicht oder nur unter
hohem technologischen Aufwand realisiert werden können. Die durch das Eigenrauschen
gesetzte untere Grenze des Signal/Rausch-Verhältnisses kann durch eine höhere
Empfindlichkeit nicht herabgesetzt werden.
4.4
Kapazitive Wandlung in einer Niederfrequenz-Schaltung
Im vorherigen Abschnitt wurde die durch einen Schalldruck verursachte Membranauslenkung
mit Hilfe eines Netzwerkmodells abgeleitet. Die Membranauslenkung kann prinzipiell
optisch, piezoresistiv, piezoelektrisch oder kapazitiv sensiert werden. In dieser Arbeit wird
das kapazitive Wandlerprinzip in einer Niederfrequenz-Schaltung verwendet. Dazu wird die
Mikrofonkapazität über einen hochohmigen Widerstand aufgeladen, so dass die
Kapazitätsänderung in eine Wechselspannung transformiert wird. Betrachtet man die
Spannung UC über die Wechselkapazität C~ des Mikrofons
UC =
x
Q Q ⋅ ( x0 + x ~ ) Q
=
=
+UC0 ⋅ ~
ε0 ⋅ A
C~
C0
x0
,
(4.29)
so ist ersichtlich, dass die Wechselkapazität spannungsmäßig durch die Ruhekapazität C0 und
eine geeignete Spannungsquelle u~=UC0⋅x~/x0 in Serie dazu dargestellt werden kann. Nach
74
Modellierung von kapazitiven Silizium-Mikrofonen
dem Modell kolbenartiger Auslenkungen ist x~ die frequenzabhängige, mittlere Änderung der
Kondensatorspalthöhe,
d.h.
die
Differenz
zwischen
der
Membranund
Gegenelektrodenauslenkung. Analog dazu ist eine Darstellung mit der Ruhekapazität und
einer parallelen Stromquelle möglich. Das Modell eines Mikrofons in einer
Gleichspannungsschaltung ist in Abbildung 4.16 dargestellt. Dabei wurde bereits eine kleine
Auslenkungsamplitude x~<<x0 und ein unbelasteter Ausgang angenommen, so dass UC0≈U0
gilt. Parasitäre Kapazitäten, die nicht an der kapazitiven Signalwandlung beteiligt sind und zu
Umladeverlusten führen, werden durch die Kapazität Cp berücksichtigt. Zu ihr trägt
beispielsweise der Bereich der Membraneinspannung bei, dessen Wirkung durch die
Dielektrizitätskonstante des Stützstellenmaterials (εr=3.9 für Siliziumdioxid) verstärkt wird.
Rg ist ein hochohmiger Widerstand, über den die Mikrofonkapazität aufgeladen wird.
C0
C~
U0 ⋅
x~
x0
~
Cp
Rg
Uout
U0
Abbildung 4.16: Modellierung der kapazitiven Wandlung in einer DC-Schaltung.
Bevor die Übertragungsfunktion der Membranauslenkung zur Signalspannung angegeben
werden kann, muss auf die speziellen Eigenschaften einer Mikrofonkapazität mit einer
perforierten Gegenelektrode und einer hochempfindlichen Membran eingegangen werden, die
zu Korrekturen an der Ruhekapazität und dem Spaltabstand führen.
4.4.1 Ruhekapazität und Perforationsdesign
Bei einem mikromechanischen Mikrofon muss aufgrund der kleinen Dimensionen und der
damit verbundenen akustischen Dämpfung die Gegenelektrode hochgradig perforiert sein. Im
Vergleich zu einer Kapazität mit zwei soliden Elektroden wird die Ruhekapazität durch die
Perforationslöcher reduziert. Eine sehr einfache Modellvorstellung geht davon aus, dass die
Kapazität um den Anteil der Perforationsfläche kleiner ist. Abbildung 4.17 zeigt ein
verbessertes Modell mit einem Perforationsloch (Radius rh, Abstand dh), bei dem ein von der
Spalthöhe x0 abhängiger Anteil an elektrischen Randfeldern bei der Berechnung der Kapazität
berücksichtigt wird.
dh
x0
x0
x0
2rh
Abbildung 4.17: Modell zur Berechnung der Mikrofonkapazität mit perforierter Elektrode.
75
Modellierung von kapazitiven Silizium-Mikrofonen
Die anteilig zu einer Perforationsöffnung gehörende Kapazität Ch ist nach diesem Modell
durch
Ch =
[d
2
h
]
− (rh − x 0 ) ⋅ π
⋅ε0
x0
2
(4.30)
gegeben. Drückt man den Perforationsabstand durch die Perforationsflächendichte ρh aus und
führt eine Nullpunktverschiebung bezüglich des Perforationsradius durch (rh→rh+x0), dann
erhält man die vom Perforationsdesign abhängige Ruhekapazität C0 in Relation zu einem
unperforierten Segment eines Plattenkondensators Csolid=ε0⋅dh2/x0
C0
r ⋅ ρh
.
=1− h
C solid
(rh + x0 )2
2
(4.31)
Zur Beurteilung dieser analytischen Näherungslösung wurden FEM-Simulationen
durchgeführt. Bei einer vorgegebenen Potentialdifferenz ∆U auf den Elektroden wird die
Kapazität aus der elektrostatischen Energie W berechnet: C=2⋅W/∆U2. In Abbildung 4.18 sind
die numerischen und analytischen Rechnungen für verschiedene Perforationsradien
aufgetragen.
1
0.95
Dichte ρh=0.2
C0/Csolid
0.9
0.85
0.8
Dichte ρh=0.3
0.75
analytisches Modell
numerische Simulation
0.7
0
1
2
3
4
5
6
7
8
9
10
11
Perforationsradius [µm]
Abbildung 4.18: Relative Kapazitätsänderung bei einer perforierten Elektrode nach dem
analytischen Modell und numerischen FEM-Analysen.
Bei jeweils konstanter Perforationsflächendichte nimmt die Ruhekapazität mit dem
Perforationsradius ab, da der Kapazitätsbeitrag der räumlich begrenzten Randfelder abnimmt.
Im Grenzfall sehr weiter Perforationsöffnungen reduziert sich die Kapazität nach dem
einfachen Modell um den Anteil der Perforationsflächendichte, d.h. C0/Csolid=(1-ρh). Ist die
76
Modellierung von kapazitiven Silizium-Mikrofonen
gesamte Mikrofonkapazität näherungsweise durch ein Vielfaches eines perforierten
Segmentes darzustellen, dann kann aufgrund der guten Übereinstimmung mit den FEMSimulationen die analytische Näherung zur Beschreibung der Ruhekapazität eines Mikrofons
mit perforierter Gegenelektrode im Netzwerkmodell verwendet werden.
4.4.2 Elektrostatische Membrananziehung
Die Beschaltung des Mikrofons mit einer Gleichspannung U0 verursacht eine Rückwirkung
auf das Mikrofon, indem die über die Mikrofonkapazität abfallende Spannung eine Änderung
der statischen Kondensatorspalthöhe x0 verursacht. Der anziehenden elektrostatischen
Kraft Fe steht die mechanische Rückstellkraft der Membran Fm entgegen, die sich im
Gleichgewicht gegenseitig aufheben. Mit dem Modell einer kolbenartigen
Membranauslenkung x0‘ und der Vernachlässigung einer Durchbiegung der steifen
Gegenelektrode muss
F = Fe + Fm =
1
⋅
2




 ⋅U 02
!
(rh + x0 − x0 ') 
−
⋅
'
=
0
k
x
eff
0
( x0 − x0 ' ) 2
ε 0 ⋅ R 2 ⋅ π ⋅ 1 −
rh ⋅ ρ h
2
2
(4.32)
erfüllt werden. Vernachlässigt man die zusätzliche Kopplung zwischen der
Membranauslenkung und dem Korrekturterm der Perforationslöcher, dann erhält man für die
elektrostatische Auslenkung x0‘ eine algebraische Gleichung dritten Grades, die nach der
Cardanischen Formel gelöst wird [Bron91]
2




rh ⋅ ρ h
2




27
U
C
1
ε
⋅
⋅
⋅
⋅
−
m 
0
0

1

(rh + x0 )2
2



x 0 ' = ⋅ x 0 ⋅ 1 − cos ⋅ arccos1 −
3

3
3

4 ⋅ x0








   

 
 

  

  
(4.33)
Die Kollapsspannung erhält man aus der Diskriminante (=0) der kubischen Gleichung
Up =
8 ⋅ x0
3
2

r ⋅ ρh
27 ⋅ ε 0 ⋅ C m ⋅ 1 − h
 (r + x )2
0
h





(4.34)
Trägt man die relative Änderung des Spaltabstandes x0‘/x0 gegen das Verhältnis der
Vorspannung und der Kollapsspannung U0/Up auf, dann erhält man den allgemein gültigen
funktionalen Zusammenhang der Abbildung 4.19. Die Beziehung hängt nicht vom
Spaltabstand, der Membran-Nachgiebigkeit oder dem Perforationsdesign ab.
77
Modellierung von kapazitiven Silizium-Mikrofonen
normierte elektrostatische
Membranauslenkung %
35
30
25
20
15
10
5
0
0
0.2
0.4
0.6
0.8
1
U0/Up [V]
Abbildung 4.19: Elektrostatische Membranauslenkung nach der kubischen Gleichung.
Insbesondere bei Vorspannungen in der Nähe der Kollapsspannung muss der reduzierte
Spaltabstand im Modell berücksichtigt werden, da dieser das elektrische Feld im
Kondensatorspalt und die Kapazität und damit die Empfindlichkeit beeinflusst. Nach diesem
Kolbenmembran-Modell liegt die maximale statische Membranauslenkung bei 1/3 des
Ruheabstandes. Dies gilt in dem Sinne, dass bei einer größeren Auslenkung der
elektrostatische Kollaps eintritt.
Die Näherung einer kolbenförmigen Bewegung mildert den Einfluss der Vorspannung auf den
Spaltabstand. Tatsächlich trägt der mittlere Membranbereich stärker zur elektrostatischen
Anziehungskraft bei. Eine Abschätzung für den Gültigkeitsbereich der Vereinfachung einer
kolbenförmigen Membranverbiegung erhält man mit der elektrostatischen Kraft Fe0 beim
Ruheabstand x0. Die anfängliche Auslenkung sollte wesentlich kleiner als der Ruheabstand
sein: Fe0/keff<<x0. Eine weitere Einschränkung der Lösung 4.33 besteht durch die bereits im
Abschnitt 3.2.3 diskutierte mechanische Nichtlinearität der Verformungsversteifung, die für
Auslenkungen in der Größenordnung der Membrandicke auftreten, d.h. bei t≈x0‘≈0.3⋅x0.
4.4.3 Kapazitives Wandlerverhalten
Die Transformationsfunktion ADC [V/m] der Kondensatorspaltänderung zur Spannung Uout
über den Ladewiderstand Rg ist nach der Schaltung von Abbildung 4.16 durch
ADC ≡
U out
x~
=
2 ⋅ π ⋅ f ⋅ (C 0 + C p ) ⋅ R g
U0
C0
⋅
⋅
x0 − x0 ' C 0 + C p
1 + 2 ⋅ π ⋅ f ⋅ (C 0 + C p ) ⋅ R g
(
)
2
(4.35)
gegeben. Sie ist proportional zum elektrischen Feld im Kondensatorspalt, einem kapazitiven
Spannungsteiler und einem Hochpass-Filter, der den Ladungsverlust auf der
Mikrofonkapazität über den endlichen Ladewiderstand bei niedrigen Frequenzen beschreibt.
78
Modellierung von kapazitiven Silizium-Mikrofonen
Für eine optimale kapazitive Wandlung ist daher auf geringe parasitäre Kapazität und einen
möglichst großen Ladewiderstand zu achten. Eine schaltungstechnische Möglichkeit bei
Ansteuerung mit einer Impedanzwandlerschaltung ist die Bootstrap-Mitkopplung, bei der die
parasitäre Kapazität nicht auf Massepotential, sondern auf den Ausgang geführt wird. Man
erreicht damit eine beidseitige Aufladung, die entsprechend der Spannungsverstärkung der
Impedanzwandlerschaltung die parasitäre Kapazität reduziert.
In der Ruhekapazität C0 des Mikrofons sind die Korrekturen der elektrostatischen
Membranauslenkung und der Perforation enthalten. So gilt für eine Kreismembran
C 0=
4.5
ε 0 ⋅ R 2 ⋅ π 
r ⋅ ρh
⋅ 1− h

x 0 − x 0 '  (rh + x 0 )2
2

.


(4.36)
Impedanzwandlerschaltung
Die Leerlaufempfindlichkeit gibt die Empfindlichkeit im unbelasteten Fall an, d.h. bei einer
unendlichen Eingangsimpedanz der Ausleseschaltung. In der Praxis wird man die hohe
Ausgangsimpedanz des Mikrofons in der Gleichspannungsschaltung mit einem
Impedanzwandler in eine kleine Ausgangsimpedanz transformieren müssen, bevor die
Wechselspannung als Signal genutzt werden kann. Traditionell werden für rauscharme
Schaltungen Sperrschicht-Feldeffekttransistoren gegenüber MOSFETs bevorzugt, da sie
keinen 1/f-Rauschanteil durch Streuung an Oberflächenladungszuständen der Oxid-Halbleiter
Grenzschicht aufweisen [Mue90]. In dieser Arbeit wurde ein Sperrschicht-Feldeffekttransistor
(JFET, Junction Field-Effect Transistor) in der Impedanzwandlerschaltung der Abbildung
4.20 eingesetzt.
JFET
G
Uin ~
D
Udd
G
Cgs
S
Rs
Cgd
D
gmVgs
gds-1
Uout
S
Abbildung 4.20: Impedanzwandlerschaltung und vereinfachtes Kleinsignal-Ersatzschaltbild
des JFETs im Normalbetrieb.
Der n-Kanal JFET wird als eine gesperrte pn-Diode betrieben, deren Raumladungszone den
leitenden Kanal zwischen Drain (D) und Source (S) abschnürt. Der von der
Eingangsspannung Uin modulierte Kanalstrom wird als Ausgangsspannung Uout über den
Lastwiderstand Rs abgegriffen. Im linearisierten Kleinsignal-Ersatzschaltbild wird der Kanal
durch den vom Arbeitspunkt abhängigen Leitwert gds und einer geregelten Stromquelle
beschrieben. Dieser Strom ist proportional zur Steuerspannung Vgs zwischen Gate und Source
und zur Steilheit des Transistors gm. Die Kapazitäten Cgd und Cgs beschreiben die
Sperrschichtkapazitäten der pn-Übergänge im Arbeitspunkt.
79
Modellierung von kapazitiven Silizium-Mikrofonen
4.5.1 Analytische Berechnung der Spannungsverstärkung und
Ausgangsimpedanz
Die Spannungsverstärkung der Impedanzwandlerschaltung lässt sich leicht mit Hilfe des
Kleinsignal-Ersatzschaltbildes der Abbildung 4.20 berechnen
A jfet
Rs ⋅ g m + j ⋅ ω ⋅ Rs ⋅ C gs
U
= out =
U in
1 + Rs ⋅ g m + j ⋅ ω ⋅ Rs ⋅ C gs
f <<
1
2⋅π ⋅ Rs ⋅C gs
=
Rs ⋅ g m
.
1 + Rs ⋅ g m
(4.37)
Für Frequenzen unterhalb der Grenzfrequenz f=1/(2πRsCgs), die typischerweise im MHzBereich liegt, ist die Übertragungsfunktion konstant und nur von der Transistorsteilheit und
dem Lastwiderstand abhängig. Die Rückkopplung in der Impedanzwandlerschaltung bewirkt,
dass die Spannungsverstärkung stets kleiner als 1 ist. Die Wirkungsweise der Schaltung als
Wandler der Impedanz ist an der Ausgangsimpedanz
Z jfet =
U out
Rs
=
1 + ⋅ g m ⋅ Rs
I out
(4.38)
ersichtlich. Sie ist für Rs>>gm-1 durch das Inverse der Transistorsteilheit gegeben und beträgt
daher nur wenige kΩ im Vergleich zur Eingangsimpedanz von einigen GΩ.
4.5.2 Simulationen zur Spannungsverstärkung und Ausgangsimpedanz
Zur Simulation der Impedanzwandlerschaltung ist es zweckmäßig, auf eine
Simulationssoftware zurückzugreifen, die den Arbeitspunkt und die Kleinsignal-Parameter
berechnet. In dieser Arbeit wurde der Schaltungssimulator PSPICE verwendet. Das JFETModell in PSPICE verwendet eine quadratische Näherungsformel für das Großsignalverhalten
des Drainstromes IDS
I ds = β ⋅ (Vgs − Vt ) 2 ⋅ (1 + λ ⋅ Vds ) .
(4.39)
Diese Gleichung gilt im reversen Betriebsmodus, d.h. die Drain-Source Spannung Vds ist im
Sättigungsbereich und die pn-Übergänge sind in Sperrrichtung gepolt. Der
Simulationsparameter λ beschreibt die Verkürzung der Kanallänge durch die Ausweitung der
Raumladungsladungszone mit steigendem Vds. Der Simulationsparameter β entspricht im
Wesentlichen der Transistorsteilheit gm=δIds/δVgs und die Spannung Vt ist die zur
Kanalabschnürung notwendige Gate/Source-Spannung. Die Stromquelle bildet zusammen mit
zwei Dioden und Kapazitäten ein Großsignal-Modell zur Simulation des Arbeitspunktes. Das
Kleinsignal-Modell ist ähnlich dem in der Abbildung 4.20 dargestellten. Einzelheiten zur
Modellierung von Sperrschicht-Feldeffekttransistoren unter PSPICE können der Literatur
entnommen werden [Ant93]. Ein Vorteil der Verwendung der Schaltungssoftware ist, dass
nach der einmaligen Vermessung der Modellparameter eines JFETs das Verhalten einer
beliebigen Schaltung analysiert werden kann.
Die folgenden Berechnungen und Simulationen orientieren sich an den Kenndaten des
kommerziell erhältlichen Sperrschicht-Feldeffekttransistors „J201“ von Vishay Siliconix. Die
Klein- und Großsignalparameter werden dem Datenblatt für den abgeschnürten Betrieb
80
Modellierung von kapazitiven Silizium-Mikrofonen
entnommen: gm=0.45 mS, Cgs≈Cgd=1.6 pF, Kf=3⋅10-17 A, Ig=3.4 pA. Die eingangsseitige
Gesamtkapazität C soll sich aus einer Mikrofonkapazität von 3.5 pF und einer parasitären
Kapazität von 1 pF zusammen. Sie wird über einem Ladewiderstand Rg von 1 GΩ mit einer 1
V Spannungsquelle aufgeladen werden. Die Betriebsspannung des JFET Udd sei 5 V und der
Lastwiderstand 20 kΩ. In Abbildung 4.21 wird die vom Lastwiderstand Rs abhängige
Spannungsverstärkung nach PSPICE-Simulationen mit der analytischen Lösung verglichen.
Außerdem wird der Ausgangswiderstand angegeben.
1
6
PSPICE-Simulation
Ausgangswiderstand [kΩ]
Spannungsverstärkung
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
PSPICE-Simulation
0.1
analytisch
0
analytisch
5
4
3
2
1
0
1
10
Lastwiderstand Rs [kΩ]
100
1
10
100
Lastwiderstand Rs [kΩ]
Abbildung 4.21: Spannungsverstärkung und Ausgangswiderstand der Impedanzwandlerschaltung.
Die Spannungsverstärkung der Impedanzwandlerschaltung ist über einen weiten
Frequenzbereich konstant und durch die Transistorsteilheit und dem Lastwiderstand gegeben.
Mit einem hohen Lastwiderstand nähert sie sich dem Wert 1 an. Selbst bei einem
Lastwiderstand von 100 kΩ bleibt der Ausgangswiderstand deutlich unter 10 kΩ. Die
Diskrepanz zwischen der analytischen Rechnung und der Simulation mit PSPICE hängt mit
der Abhängigkeit der Transistorsteilheit gm vom Arbeitspunkt, d.h. vom Lastwiderstand Rs
zusammen. Mit dem Lastwiderstand nimmt die Transistorsteilheit monoton ab. Die
analytische Rechnung mit einer konstanten Transistorsteilheit kann daher zwangsläufig nur
für einen Arbeitspunkt und einem Lastwiderstand gelten (im Beispiel für Rs=16 kΩ). Bei
kleineren Lastwiderständen führt die Annahme einer konstanten Transistorsteilheit bei der
analytischen Berechnung zu einer zu geringen Spannungsverstärkung und bei hohen
Lastwiderständen entsprechend zu überhöhten Spannungsverstärkungen. Der Unterschied in
der Transistorsteilheit ist besonders gut an der Ausgangsimpedanz zu beobachten, da diese bei
einem hohem Lastwiderstand näherungsweise durch gm-1 gegeben ist.
4.5.3 Analytische Berechnung der Rauschspannungsdichte
Das elektrische Rauschen der Impedanzwandlerschaltung bei Beschaltung mit einem
Mikrofon setzt sich aus verschiedenen Rauschquellen und Mechanismen zusammen, die nun
kurz erläutert werden:
•
Thermisches Widerstandsrauschen: Die thermische Bewegung von Ladungsträgern
erzeugt weißes Rauschen an ohmschen Widerständen. In der Impedanzwandlerschaltung
81
Modellierung von kapazitiven Silizium-Mikrofonen
•
•
•
ist das der Lastwiderstand Rs und der Ladewiderstand Rg (Rauschstromdichte WIRs und
WIRg). Widerstandsrauschen parasitärer Bahnwiderstände im JFET können wegen der
kleinen Widerstandswerte im Bereich weniger Ohm vernachlässigt werden.
Thermisches Kanalrauschen: Die thermische Ladungsträgerbewegung verursacht in
jedem infinitesimalen Widerstandselement im Kanal eine Rauschspannung, die zu einer
Schwankung des Drainstromes führt. Die über die gesamte Kanallänge integrierte
Rauschstromdichte WIgm hat die Form eines thermischen Widerstandsrauschens mit der
Transistorsteilheit gm.
Generations-Rekombinations-Rauschen (Funkel-Rauschen): Aufgrund von Kristallfehlern
oder Verunreinigungen in Halbleitern können Ladungsträger ständig entstehen und
rekombinieren. In der Raumladungszone des JFETs führt diese statistische Schwankung
des Ladungszustandes zu einem Rauschen des Drainstromes im Kanal
(Rauschstromdichte WIIds). Weitere Quellen für Funkel-Rauschen können die
Korngrenzenzustände in Widerständen aus Polysilizium sein. Charakteristisch für FunkelRauschen ist die 1/f-Frequenzabhängigkeit, die auf ein breites Spektrum der Generationsbzw. Lebensdauer der Ladungsträger zurückzuführen ist („Hooge“-Modell).
Schrotrauschen: Schrotrauschen entsteht durch die Quantisierung der elektrischen
Ladungen in Portionen der Elementarladung. An Potentialbarrieren, etwa einem pnÜbergang, führt die Zufallsverteilung der Elektronen zu einer Abweichung eines
Gleichstromes von seinem Mittelwert. Im JFET tritt Schrotrauschen an der gesperrten
Gate/Kanal-Diode auf (Rauschstromdichte WIIgs und WIIgd). Weitere Beiträge zum
Schrotrauschen können nicht-ohmsche pn-Kontakte liefern.
Mit der Impedanzwandlerschaltung, der Kleinsignalschaltung des Feldeffekttransistors und
dem Abschluss des Einganges mit der Mikrofonkapazität samt Ladewiderstand ergibt sich das
in Abbildung 4.22 dargestellte Rauschersatzschaltbild.
W i I ds ⋅ ∆f
Cgd
W i I gs ⋅ ∆f
C
Rg
Cgs
gmVgs
W i g m ⋅ ∆f
gds-1
W i R g ⋅ ∆f
idealer, rauschfreier JFET
Rs
W i Rs ⋅ ∆f
Abbildung 4.22: Rauschersatzschaltbild der Impedanzwandlerschaltung mit eingangsseitiger
Gleichspannungsschaltung.
Die einzelnen Rauschspannungsdichten Nu [V2/Hz] am Ausgang können mit der
Übertragungsfunktion jeder Quelle, im Fall einer Rauschstromdichte eine Impedanz Z, und
der jeweiligen Rauschstromdichte WI [A2/Hz] berechnet werden, wenn der DC-Arbeitspunkt
und die Kleinsignalparameter bekannt sind. Die Rauschspannungsdichte am Ausgang Nu, d.h.
über den Lastwiderstand Rs, ist dann durch
82
Modellierung von kapazitiven Silizium-Mikrofonen
2
N u = Z ⋅W I
(4.40)
gegeben.
Thermisches Rauschen vom Lastwiderstand Rs
Für die Übertragungsimpedanz der Rauschstromquelle an den Ausgang gilt unter der
Vernachlässigung des kleinen Kanalleitwertes im Sperrbetrieb
Z Rs ≈
1
1


) 
 C gd + C ⋅ (1 +
2
π
⋅
⋅
⋅
⋅
⋅
j
f
C
R
1


g
+ gm ⋅ 

1
Rs
)
 C gd + C gs + C ⋅ (1 +

j ⋅ 2 ⋅ π ⋅ f ⋅ C ⋅ R g 

.
(4.41)
Bei der Berechnung wurde davon Gebrauch gemacht, dass für Mikrofonanwendungen immer
f<<gm/2πCgs>>100 kHz gilt. Für Frequenzen f>>1/Rg⋅C und der Rauschstromdichte des
Lastwiderstandes WIRs=4⋅k⋅T/Rs beträgt die Rauschspannungsdichte am Lastwiderstand
N u Rs ≈
1

1 + R ⋅ g
s
m


 C gd + C  

⋅
 C gd + C gs + C  


2
⋅ 4 ⋅ k ⋅ T ⋅ Rs .
(4.42)
Der Rauschbeitrag vom Lastwiderstand ist immer kleiner als das reine
Widerstandsspannungsrauschen 4⋅k⋅T⋅Rs. Die Rauschspannungsdichte würde sogar mit dem
Widerstandswert abfallen, wenn nicht gleichzeitig durch die Verschiebung des Arbeitspunktes
die Transistorsteilheit abnehmen würde.
Thermisches Rauschen vom Ladewiderstand Rg
Zur Berechnung des Rauschbeitrages des Ladewiderstandes ist es zweckmäßig, von der
Rauschspannungsdichte auszugehen. Diese Quelle sieht einen Tiefpass, bestehend aus dem
Widerstandwert Rg und den Kapazitäten des Mikrofons und des JFETs, und wird mit der
Spannungsverstärkung der Impedanzwandlerschaltung Ajfet an den Ausgang transformiert.
Infolge der Mitkopplung zwischen dem Ausgang und dem Eingang wird die Gate/SourceSperrkapazität Cgs mit der Spannungsverstärkung bewertet (Miller-Effekt [Leh74]). Mit dem
Rauschersatzschaltbild berechnet die Rauschspannungsdichte am Lastwiderstand zu
N u Rg


1
=
 1 + 2 ⋅ π ⋅ f ⋅ R g ⋅ (C + C gs ⋅ (1 − A jfet ) + C gd )

(
2
)
2


2
 ⋅ A jfet ⋅ 4 ⋅ k ⋅ T ⋅ R g .


(4.43)
Der Rauschbeitrag des Ladewiderstandes hängt in zweierlei Hinsicht von seinem
Widerstandwert ab. Er beeinflusst sowohl den maximalen Betrag als auch die spektrale
Verteilung. Ein großer Widerstandswert des Ladewiderstandes ist vorteilhaft, wenn das
Rauschspektrum z.B. durch eine A-Bewertung begrenzt ist. Dann erreicht man mit einem
hohen Ladewiderstand eine niedrige Grenzfrequenz und eine Verschiebung der Rauschdichte
aus dem Nutzband.
83
Modellierung von kapazitiven Silizium-Mikrofonen
Thermisches Kanalrauschen und Generations-Rekombinations-Rauschen
Das thermische und Funkel-Rauschen des JFET-Kanals kann zu einer Rauschstromdichte
zusammengefasst werden
W I g m + W I I ds =
K f ⋅ I ds
2
⋅ 4 ⋅ k ⋅ T ⋅g m+
.
3
f
(4.44)
Der erste Term beschreibt das thermische Kanalrauschen [Mue90] und der zweite das FunkelRauschen. Da die Dichte und energetische Lage der Rekombinationsstellen stark von dem
Herstellungsprozess und der Technologie abhängt, muss der Funkel-Rauschfaktor Kf
empirisch bestimmt werden.
Die Berechnung der Übertragungsfunktion dieser Rauschquellen erfolgt analog zu der des
Lastwiderstandes. Für Frequenzen f>>1/Rg⋅C ist die gesamte Rauschspannungsdichte am
Ausgang durch
N u g m + I ds ≈
K f ⋅ I ds 
2

⋅  ⋅ 4 ⋅ k ⋅ T ⋅ g m +
f
 1

 C gd + C    3
 + g ⋅

m 

 Rs
 C gd + C gs + C  

1
2
(4.45)
gegeben. Die Rauschdichte setzt sich aus einem weißen und einem frequenzabhängigen
Rauschanteil zusammen, die sich bei der charakteristischen Frequenz ff=3⋅Kf⋅Ids/(8⋅k⋅T⋅gm)
schneiden. Der DC-Drainstrom kann im Sperrbetrieb durch Ids≈0.6/Rs angenähert werden, so
dass das Funkel-Rauschen indirekt vom Lastwiderstand abhängt.
Schrotrauschen des Gate Sperrstromes
Die Rauschstromdichte von Schrotrauschen setzt sich aus der Elementarladung e=1.6⋅10-19 C
und dem DC-Sperrstrom zusammen
W I I gs = 2 ⋅ e ⋅I gs
(4.46)
W I I gd = 2 ⋅ e ⋅I gd
(4.47)
Beschränkt man sich bei der Berechnung auf Frequenzen unterhalb von einigen MHz
(f<<1/2πRsCgs, f<<1/2πRsCgd) und geht von etwa gleich großen Sperrschicht-Kapazitäten aus,
dann sind die Übertragungsimpedanzen für beide Rauschquellen gleich und das
Schrotrauschen kann durch den gesamten Sperrstrom Ig=Igs+Igd ausgedrückt werden
N u Ig

Rg

≈
 1 + 2 ⋅ π ⋅ f ⋅ R g ⋅ (C + C gs ⋅ (1 − A jfet ) + C gd )

(
2
)
2


2
 ⋅ A jfet ⋅ (2 ⋅ e ⋅ I g ) .


(4.48)
Der Rauschbeitrag des Schrotrauschen verhält sich in Bezug auf die Frequenzabhängigkeit
äquivalent
zum
Rauschen
des
Ladewiderstandes.
Der
Vergleich
beider
Rauschspannungsdichten liefert einen Widerstand
Rg ≡ 2 ⋅
*
84
k ⋅T
,
e⋅ Ig
(4.49)
Modellierung von kapazitiven Silizium-Mikrofonen
der angibt, welcher Rauschterm überwiegt. Für Rg<Rg* dominiert das thermische
Widerstandsrauschen vom Ladewiderstand und entsprechend für Rg>Rg* das Schrotrauschen
des Sperrstromes. Für Sperrströme im pA-Bereich beträgt der Wert Rg* mehrere GΩ, so dass
in den meisten Fällen das Schrotrauschen unter dem thermischen Rauschen des
Ladewiderstandes liegt.
Gesamtrauschen
Die gesamte elektrische Rauschspannungsdichte am Impedanzwandlerausgang ist durch die
Addition der einzelnen Rauschdichten gegeben
N u elektrisch = N u Rs + N u Rg + N u g m + I ds + N u I g .
(4.50)
4.5.4 Simulationen zur Rauschspannungsdichte
Die Rauschspannungsdichten der einzelnen Rauschquellen am Ausgang der
Impedanzwandlerschaltung nach den abgeleiteten Gleichungen und einem PSPICE-Modell ist
in der Abbildung 4.23 dargestellt. Die Symbole kennzeichnen die numerisch simulierten
Rauschdichten und die durchgezogene Linien die zugehörige analytische Lösung.
-100
Summe
Widerstandsrauschen Rg
Schrotrauschen Ig
Funkelrauschen JFET
Kanalrauschen JFET
Widerstandsrauschen Rs
analytische Rechnung
0.5
Rauschdichte [dB(V/Hz )]
-110
-120
-130
-140
-150
-160
-170
-180
10
100
1000
10000
100000
Frequenz [Hz]
Abbildung 4.23: Rauschspannungsdichte der Impedanzwandlerschaltung.
Den weitaus größten Beitrag zum Gesamtrauschen liefert das Widerstandsrauschen vom
Ladewiderstand. Die A-bewertete Rauschspannung von dem 1 GΩ Ladewiderstand beträgt 4
µV(A). Bei einer Rauschspannung von 4.2 µV(A) der gesamten Schaltung ist dies ein
prozentualer Anteil von ca. 94%. Das Schrotrauschen des Sperrstromes ist im gesamten
Spektrum um 12 dB niedriger, da der charakteristische Widerstand Rg*=15 GΩ im Vergleich
zu dem 1 GΩ Ladewiderstand groß ist. Bei hohen Frequenzen beherrscht das nahezu weiße
85
Modellierung von kapazitiven Silizium-Mikrofonen
Kanalrauschen die Rauschspannungsdichte. Die Rauschspannung ist mit 0.7 µV(A) dennoch
verhältnismäßig klein. Das thermische Rauschen des Lastwiderstandes liegt um 7 dB unter
dem Kanalrauschen und ist zu vernachlässigen, wenn Rs>>3/2⋅gm-1 ist. Auch das
Funkelrauschen spielt bei dem in der Simulation angenommen Funkel-Rauschfaktor keine
Rolle. Die folgende Tabelle fasst die Rauschspannungen der verschiedenen Rauschquellen in
der Impedanzwandlerschaltung zusammen:
Rauschwiderstand
Rauschspannung [µV (A)]
Ladewiderstand Rg
Schrotrauschen
Funkelrauschen
Kanalrauschen
Lastwidertand Rs
Total
3.95
1
0.1
0.7
0.3
4.2
Tabelle 4.3: Rauschspannungen des Impedanzwandlers mit DC-Schaltung.
Der Vergleich der elektrischen Rauschquellen zeigt, dass für ein geringes Rauschen in erster
Linie der Beitrag des Ladewiderstandes optimiert werden muss. Dies gelingt durch einen
hohen Widerstandswert oder eine hohe Mikrofonkapazität, da diese die obere Grenzfrequenz
der Rauschdichte verschieben. Im Gegensatz zur Mikrofonkapazität, die durch das
Membrandesign und dem Spaltabstand festgelegt wird, ist der Ladewiderstand, soweit
technologisch möglich, frei wählbar. In der Abbildung 4.24 ist die Abhängigkeit der
Rauschspannungen vom Widerstandswert des Ladewiderstandes angeben (Frequenzband
10 Hz-20 kHz).
Rauschspannung [µV(A)]
100
Widerstandsrauschen Rg
Schrotrauschen
Widerstandsrauschen Rs
Kanalrauschen
Funkelrauschen
Summe
10
1
0.1
0.1
1
10
100
Ladewiderstand Rg [GΩ]
Abbildung 4.24: A-bewertete Rauschspannungen der Impedanzwandlerschaltung in
Abhängigkeit vom Ladewiderstand.
86
Modellierung von kapazitiven Silizium-Mikrofonen
Mit der Erhöhung des Widerstandwertes erreicht man eine Verschiebung der spektralen
Rauschdichte des Ladewiderstandes in der Weise, dass die integrale Größe der
Rauschspannung bei einer A-Bewertung abnimmt. Geht man beispielsweise von einer
Mikrofon-Empfindlichkeit von 10 mV/Pa aus, dann setzt ein äquivalenten Rauschschallpegel
unter 30 dB(A) eine Rauschspannung <6.5 µV, d.h. einen Ladewiderstand >400 MΩ voraus.
Erreicht der Widerstandswert den charakteristischen Wert Rg*=16 GΩ, dann dominiert das
Schrotrauschen, das aufgrund seiner quadratischen Abhängigkeit vom Ladewiderstand zu
einer nahezu konstanten Rauschspannung führt. Eine Erhöhung des Ladewiderstandes über
diesen charakteristischen Wert bringt daher kaum eine weitere Reduzierung der
Rauschspannung. Fasst man die Simulationsergebnisse zusammen, dann kann festgestellt
werden, dass das elektrische Rauschen der Impedanzwandlerschaltung hauptsächlich über den
Ladewiderstand und dem Sperrstrom des Feldeffekt-Transistors optimiert wird. Dazu sollte
der Sperrstrom möglichst gering (entspricht großem Rg*) und der Ladewiderstand groß sein
(≈Rg*).
4.6
Simulationen zum Gesamtsystem aus Mikrofon mit Beschaltung
Nach der Betrachtung der einzelnen Komponenten soll nun das System aus Mikrofon und
elektrischer Beschaltung untersucht werden. Dazu wird das mechanisch-akustische
Netzwerkmodell aus Kapitel 4.3 über die gesteuerte Spannungsquelle der NiederfrequenzSchaltung (Kapitel 4.4) mit der Impedanzwandlerschaltung (Kapitel 4.5) verknüpft. Das
Netzwerkmodell des Gesamtsystems (Abbildung 4.25) kann analytisch gelöst oder vorteilhaft
in einem Schaltungssimulator implementiert werden. Mit dem Modell wird der vollständige
Signalweg vom Schalldruck bis zur Ausgangsspannung und das Gesamtrauschen simuliert.
Die bisher gewonnenen Erkenntnisse zu den Einzelkomponenten können zum Teil auf das
Gesamtsystem angewendet werden. Es werden daher vor allem Querabhängigkeiten, die
durch die Verschaltung der einzelnen Modelle entstehen untersucht. Zunächst wird die
Mikrofonempfindlichkeit und das Gesamtrauschen exemplarisch dargestellt. Abschließend
wird der Einfluss wichtiger Technologie-Parameter auf den Signal/Rauschabstand betrachtet.
Systemmodell
Mikrofonmodell
p(f)
Wandler
DC-Schaltung
Impedanz
-wandler
gesteuerte
Quelle
U(f)
Abbildung 4.25: Schematischer Aufbau des Gesamtmodells aus den Submodellen.
87
Modellierung von kapazitiven Silizium-Mikrofonen
4.6.1 Empfindlichkeit und Rauschen
Die Empfindlichkeit des Systems aus Mikrofon, Gehäuse und Schaltung SSystem wird
multiplikativ aus den bisherigen Berechnungen gebildet
(2 ⋅ π ⋅ f ⋅ R g ⋅ C )
U C
S System ( f ) = −C Mikrofon ⋅ 0 ⋅ 0 ⋅
⋅ A jfet .
2
{
1
424
3 x0 {
C
(
)
+
⋅
⋅
⋅
⋅
f
R
C
1
2
π
{ ( 3)
( 5)
g
(1)
1444
424444
3
( 2)
(4.51)
( 4)
Der erste Term (1) ist die Mikrofon-Nachgiebigkeit, d.h. die Empfindlichkeit der akustischmechanischen Wandlung des Mikrofons. Der zweite Term (2), das elektrische Feld in der
Mikrofonkapazität, beschreibt eine elektrostatische „Verstärkung“ des Mikrofons. Zusammen
bilden die beiden ersten Terme die maximal erreichbare Leerlaufempfindlichkeit. Der dritte
Term (3) beinhaltet den Verlust an Ausgangsspannung durch das verschlechterte relative
Kapazitätsänderung bei parasitären und sonstigen Kapazitäten. Die Kapazität C0 steht dabei
für die elektrisch aktive Mikrofonkapazität und C für die Summe aller Kapazitäten, d.h. der
Mikrofonkapazität, den Randkapazitäten der Membranaufhängung, den SperrschichtKapazitäten im Feldeffekt-Transistor etc. Eine weitere Empfindlichkeitseinbuße entsteht
durch den endlichen Ladewiderstand, der zu einem frequenzabhängigen Verlust an
Kondensatorladung führt. Das resultierende Tiefpass-Verhalten der kapazitiven Wandlung in
der Gleichspannungsschaltung beschreibt der Term (4). Schließlich wird die
Mikrofonempfindlichkeit durch die Spannungsverstärkung der Impedanzwandlerschaltung
(<1) reduziert (5).
Die gesamte Rauschdichte des Systems am Lastwiderstand setzt sich aus dem akustischen
Rauschen des Mikrofons und dem elektrischen Rauschen zusammen
N System = N
p
Mikrofon
 S System
⋅
 V Mikrofon

2

 + N u elektrisch .


(4.52)
Die akustische Rauschdruckdichte wird mit der Membran-Nachgiebigkeit und der
Übertragungsfunktion der Niederfrequenz- und Impedanzwandlerschaltung an den Ausgang
transformiert. Die Darstellung der Gleichung verdeutlicht, dass der akustische Rauschanteil
mit der Empfindlichkeit steigt. Das bedeutet, wenn das akustische Rauschen gegenüber dem
elektrischen Rauschen dominiert, dann verbessert sich der Signal/Rauschabstand nicht mit
einer höheren Empfindlichkeit. Das akustische Eigenrauschen des Mikrofons stellt eine untere
Grenze für das Gesamtrauschen dar. Im Umkehrschluss verbessert eine höhere
Empfindlichkeit den Signal/Rauschabstand, wenn das elektrische Rauschen das
Gesamtrauschen beherrscht.
Als Beispiel für die Anwendung des Gesamtmodells ist in der Abbildung 4.26 die simulierte
Empfindlichkeit und Rauschdichte eines Mikrofons mit einer 8-fach korrugierten
Kreismembran für einen Ladewiderstand von 1GΩ und 10 GΩ dargestellt. Die
Simulationsparameter richten sich nach Tabelle 4.1 und den Ausführungen unter Abschnitt
4.5.2. Gesondert ausgezeichnet durch eine gestrichelte Linie ist die Leerlaufempfindlichkeit
und das akustische Eigenrauschen. Der Vergleich mit der System-Empfindlichkeit und dem
Gesamtrauschen verdeutlicht, wie stark das Systemverhalten von der elektrischen
Beschaltung beeinflusst wird. So wird die Empfindlichkeit durch die Spannungsverstärkung
der Impedanzwandlerschaltung mehr als halbiert und das Gesamtrauschen setzt sich
überwiegend aus elektrischen Rauschquellen zusammen.
88
Modellierung von kapazitiven Silizium-Mikrofonen
100
-100
Eigenrauschen
Rauschdichte [dB(V/Hz0.5)]
Empfindlichkeit [mV/Pa]
-110
10
Rg=1 GΩ
Rg=10 GΩ
1
Leerlaufempfindlichkeit
Gesamtrauschen
-120
Rg=1 GΩ
-130
Rg=10 GΩ
-140
-150
-160
-170
System-Empfindlichkeit
0.1
-180
10
100
1000
10000
100000
10
Frequenz [Hz]
100
1000
10000
100000
Frequenz [Hz]
Abbildung 4.26: Simulierte Mikrofonempfindlichkeit und Rauschdichte nach dem
Systemmodell.
4.6.2 Signal/Rauschabstand
Die wichtigste Kenngröße des Mikrofon-Systems ist der Signal/Rauschabstand. Mit dem
äquivalenten Rauschschallpegel
LSystem


N System ⋅ df


= 20 ⋅ log
.
−5
 S System ( f 0 ) ⋅ 2 ⋅ 10 Pa 


∫
(4.53)
kann bei einem bestimmten Nutzschallpegel direkt der Rauschspannungsabstand angegeben
werden. Er bezieht sich auf die Empfindlichkeit bei f0=1 kHz und die Rauschspannung über
ein bestimmtes Frequenzband. Die Optimierung des äquivalenten Rauschschallpegels und der
dynamischen Bandbreite kann mit Hilfe des aufgestellten Systemmodells durchgeführt
werden. Viele der bisher abgeleiteten Ergebnisse zur Optimierung der einzelnen
Systemkomponenten können direkt übernommen werden. So sollte der Einfluss von
parasitären Kapazitäten durch Design- oder Schaltungsmaßnahmen minimiert, eine hohe
Spannungsverstärkung der Impedanzwandlerschaltung erreicht und ein großer
Ladewiderstand verwendet werden. Im Folgenden soll auf die Parameter eingegangen
werden, bei denen Querabhängigkeiten und Randbedingungen berücksichtigt werden müssen
und daher nur im Gesamtmodell behandelt werden können. Dabei wird der Einfluss der
mechanischen Membranparameter und des Perforationsdesigns betrachtet.
Mechanische Nachgiebigkeit und äquivalenter Rauschschallpegel
Die Nachgiebigkeit einer Membran kann auf unterschiedliche Art gesteuert werden. Sie hängt
beispielsweise von der intrinsischen Schichtspannung, der Membrandicke oder der Anzahl der
Korrugationen ab. Aus Sicht der Simulation ist es dabei irrelevant, welche dieser Größen
verändert wird, da sie keine Querabhängigkeiten aufweisen und nur die mechanische
Membran-Nachgiebigkeit Sm beeinflussen. Eine Ausnahme stellt der Radius der Membran
89
Modellierung von kapazitiven Silizium-Mikrofonen
dar, da von ihm auch die Mikrofonkapazität abhängt. Der Membranradius wird daher
gesondert behandelt. Zunächst soll der Einfluss der unabhängigen Parameter untersucht
werden, so dass als übergeordneter Parameter die mechanische Membran-Nachgiebigkeit
verwendet wird. Ob es sich in der praktischen Umsetzung um die Veränderung der
Membrandicke oder der Membranspannung handelt, hängt in erster Linie von den
technologischen Möglichkeiten bei der Herstellung der Mikrofone ab.
Die elektrostatische Anziehung zwischen den Elektroden einer kapazitiven Anordnung führt
zu einer Randbedingung bei der Wahl der Membran-Nachgiebigkeit, die daher immer
zusammen mit der elektrischen Vorspannung und dem Spaltabstand betrachtet werden muss.
Nach der in Abschnitt 4.4.2 angegebenen Beziehung für die Kollapsspannung ist die
Spalthöhe durch
x0,min =
3
U 
27 ⋅ ε 0 ⋅ C m ⋅  0 
α 
8
2
(4.54)
beschränkt, wenn in erster Näherung die Perforation in der Gegenelektrode die
elektrostatische Anziehung zwischen den Platten nur geringfügig beeinflusst. Der Parameter
α ist ein Sicherheitsfaktor, der kleiner eins sein muss. In den folgenden Simulationen soll der
Spaltabstand nach der obigen Gleichung gegeben sein. Dabei wird vorausgesetzt, dass die
Vorspannung in jedem Fall 60% der Kollapsspannung beträgt, d.h. α=0.6. Natürlich kann der
Spaltabstand etwa aus Gründen der Robustheit gegenüber Umwelteinflüssen größer gewählt
werden. In diesem Fall wird allerdings Empfindlichkeit „geopfert“.
Bei unterschiedlicher Membran-Nachgiebigkeit führt die notwendige Anpassung der
Spalthöhe zu einer Querabhängigkeit über die Mikrofonkapazität, die das Rauschen und den
kapazitiven Spannungsteiler beeinflusst. Die Abhängigkeit des Rauschschallpegels von der
Membran-Nachgiebigkeit bei Beachtung aller Querabhängigkeiten ist in Abbildung 4.27 für
das Frequenzband von 10 Hz bis 20 kHz dargestellt. Die sekundäre Ordinate gibt den
korrespondierenden Spaltabstand an. Die Membran sei geschlossen und habe einen Radius
von 500 µm. Der Ladewiderstand betrage 10 GΩ, die parasitäre Kapazität 1 pF und das
Gehäusevolumen 125 mm3. Bei einer Perforationsflächendichte von 20% sei der Lochradius
2.5 µm und der Lochabstand 10 µm. Nach den Simulationen der Abbildung 4.18 ist die
elektrische Wirkung der Perforation verhältnismäßig gering und die oben angegebene
Gleichung für den Spaltabstand ist eine gute Näherung. Die Gegenelektrode wird mit einer
Dicke von 5 µm angenommen. Da der äquivalente Rauschschallpegel keine Aussage über die
Bandbreite macht, wird jeweils die obere Grenzfrequenz angegeben, bei der die
Empfindlichkeit um 3 dB von der Empfindlichkeit bei 1 kHz abweicht.
90
Modellierung von kapazitiven Silizium-Mikrofonen
3.5
50
3
40
2.5
35
2
1.5
30
1
25
0.5
20
1
10
0
100
Membran-Nachgiebigkeit [nm/Pa]
U0=1 V
U0=2 V
45
obere Grenzfrequenz [kHz]
U0=1 V
U0=2 V
Spaltabstand [µm]
Rauschschallpegel [dB(A)]
45
40
35
30
25
20
15
10
5
0
1
10
100
Membran-Nachgiebigkeit [nm/Pa]
Abbildung 4.27: Äquivalenter Rauschschallpegel und obere Grenzfrequenz in Abhängigkeit
von der Membran-Nachgiebigkeit und der Vorspannung.
Die Simulationen verdeutlichen, dass über eine Erhöhung der mechanischen Nachgiebigkeit
der Membran der äquivalente Rauschschallpegel des Mikrofons, d.h. der
Signal/Rauschabstand, wirkungsvoll reduziert werden kann. Bei hohen Nachgiebigkeiten wird
die Erniedrigung des Rauschschallpegels allerdings durch einen eingeschränkten
Frequenzbereich erkauft, da die obere Grenzfrequenz mit der Nachgiebigkeit abnimmt. Die
Verschiebung der oberen Grenzfrequenz, die für die akustische Rauschdichte gleichermaßen
gilt, ist auch die Ursache dafür, dass der akustische Rauschanteil kontinuierlich mit der
Nachgiebigkeit abfällt und sich daher kein unterer Grenzwert beim äquivalenten
Rauschschallpegel einstellt. Bemerkenswerterweise erreicht man mit einer Verdopplung der
Vorspannung nur eine geringe Verbesserung des Signal/Rauschabstandes. Das liegt daran,
dass bei gleicher Membran-Nachgiebigkeit ein größerer Spaltabstand gewählt werden muss
und dieser aufgrund der niedrigeren Kapazität zur einem schlechteren kapazitiven Verhältnis
und einem höheren elektrischen Rauschen führt. Ein Teil des Vorteils einer höheren
elektrischen Vorspannung wird damit kompensiert. Dafür wird die obere Grenzfrequenz
durch die geringeren Strömungsverluste im Kondensatorspalt zu größeren Frequenzen
verschoben, so dass sich die Bandbreite und damit der Parameterbereich sinnvoller
Nachgiebigkeiten deutlich verbessert. Mit den angesetzten Simulationsparametern ist bei
einer Vorspannung von 1 V und einer Grenzfrequenz von 10 kHz maximal ein äquivalenter
Rauschschallpegel von 31 dB(A) möglich. Dies gilt, wenn die mechanische MembranNachgiebigkeit auf 7.5 nm/Pa und der Kondensatorspalt auf den kleinstmöglichen Abstand
von 0.85 µm eingestellt wird. Zum Vergleich ermöglicht eine Vorspannung von 2V unter der
Bedingung einer oberen Grenzfrequenz von maximal 10 kHz eine Membran-Nachgiebigkeit
von etwa 30 nm/Pa (Spaltabstand x0=2.15 µm) und einen äquivalenten Rauschschallpegel von
26 dB(A).
Membranradius und äquivalenter Rauschschallpegel
Eine zusätzliche Querabhängigkeit besteht, wenn die mechanische Nachgiebigkeit über den
Membranradius verändert wird, da dieser direkt die Mikrofonkapazität beeinflusst. Abbildung
4.28 zeigt die Simulation des äquivalenten Rauschschallpegels und der oberen Grenzfrequenz
bei verschiedenen Membranradien unter der Randbedingung einer konstanten mechanischen
Membran-Nachgiebigkeit von 7.5 nm/Pa (x0=0.85 µm) bzw. 30 nm/Pa (x0=2.15 µm). In der
91
Modellierung von kapazitiven Silizium-Mikrofonen
Simulation wird eine Verdopplung des Membrandurchmessers durch eine Vervierfachung der
intrinsischen Schichtspannung kompensiert, so dass zusammen genommen die MembranNachgiebigkeit und daher auch die Spalthöhe nicht verändert wird.
20
U0=1 V
U0=2 V
35
30
25
20
250
350
450
550
650
750
850
Membranradius R [µm]
950
obere Grenzfrequenz [kHz]
Rauschschallpegel [dB(A)]
40
U0=1 V
U0=2 V
15
10
5
0
250
350
450
550
650
750
850
950
Membranradius R [µm]
Abbildung 4.28: Rauschschallpegel und obere Grenzfrequenz in Abhängigkeit vom
Membranradius bei konstanter Membran-Nachgiebigkeit.
Obwohl die Membran-Nachgiebigkeit für die verschiedenen Membranradien durch die
gleichzeitige Veränderung der Membranspannung in der Simulation konstant ist, zeigt sich
ein mit dem Membranradius abnehmender äquivalenter Rauschschallpegel. Abgesehen von
technologischen oder wirtschaftlichen Gesichtspunkten ist ein großer Membrandurchmesser
für die Mikrofon-Eigenschaften günstiger. Der Grund ist die größere Mikrofonkapazität, die
ein günstigeres Verhältnis von aktiver zu parasitärer Kapazität und eine Reduzierung des
Rauschens über eine spektrale Verschiebung der Rauschdichte des Ladewiderstandes und des
Sperrstromes bewirkt. Die obere Grenzfrequenz der Mikrofone ist abgesehen von einer
leichten Verschiebung aufgrund der veränderten Membranmasse und somit der Eigenresonanz
der Membran konstant, da die Membran-Nachgiebigkeit dieselbe ist.
Mit der Miniaturisierung der Mikrofone wird der Signal/Rauschabstand zunehmend
schlechter. So erreicht man unter den Annahmen der Simulation bei einem Membranradius
von 300 µm und einer Vorspannung von 1 V maximal einen äquivalenten Rauschpegel von
etwa 36 dB(A). Über eine Erhöhung der mechanischen Membran-Nachgiebigkeit kann der
Rauschschallpegel nicht verbessert werden, da sich die obere Grenzfrequenz bereits im
Bereich der unteren Schranke von 10 kHz bewegt.
Perforationsdesign und äquivalenter Rauschschallpegel
Die obere Grenzfrequenz stellt eine Randbedingung auf, die eine Verbesserung des
äquivalenten Rauschschallpegels über die Erhöhung der mechanischen MembranNachgiebigkeit Grenzen setzt. Einen Ausweg liefert die Minimierung der akustischen
Dämpfung, die bereits in Abschnitt 4.3.4 behandelt wurde. Dort wurde ein Perforationsradius
angegeben, der sowohl die obere Grenzfrequenz als auch das akustische Rauschen optimiert.
In den folgenden Simulationen soll von diesem optimalen Perforationsradius nach Gleichung
4.20 ausgegangen werden. Freier Design- bzw. Simulationsparameter ist damit die
Perforationsflächendichte. Da die Perforation der Gegenelektrode auch die Mikrofonkapazität
beeinflusst, muss das Gesamtmodell untersucht werden. Die Abbildung 4.29 zeigt den
92
Modellierung von kapazitiven Silizium-Mikrofonen
simulierten äquivalenten Rauschschallpegel und die obere Grenzfrequenz eines Mikrofons bei
einer Variation der Perforationsflächendichte. In Anlehnung an die vorherigen Simulationen
soll bei einem Membranradius von 500 µm und einer Vorspannung von 1 V die MembranNachgiebigkeit 7.5 nm/Pa betragen. Für den Kondensatorspalt ergibt sich wegen der
Randbedingung der elektrostatischen Anziehung wiederum eine Höhe von 0.85 µm.
45
33
40
Rg=1 GΩ
obere Grenzfrequenz [kHz]
Rauschschallpegel [dB(A)]
34
32
31
30
Rg=10 GΩ
29
28
27
35
30
25
20
15
10
5
26
0
0
0.2
0.4
0.6
0.8
Perforationsflächendichte ρ h %
1
0
0.2
0.4
0.6
0.8
Perforationsflächendichte ρh %
Abbildung
4.29:
Rauschschallpegel
und
Grenzfrequenz
Perforationsflächendichte in der Gegenelektrode (Rg Ladewiderstand).
bei
1
variierender
Mit steigender Perforationsflächendichte durchläuft der äquivalente Rauschschallpegel
aufgrund der gegenläufigen Effekte der Abnahme des Eigenrauschens und dem
Empfindlichkeitsverlust durch den Wegfall von aktiver Mikrofonkapazität ein Minimum. Das
Minimum ist besonders ausgeprägt und liegt bei hohen Perforationsdichten, wenn der Anteil
vom Eigenrauschen am Gesamtrauschen groß ist (Ladewiderstand Rg=10 GΩ). Überwiegt
dagegen das elektrische Rauschen (Rg=1 GΩ), dann ist eine Optimierung über das Design der
Perforation nur begrenzt möglich.
Gleichzeitig erreicht man mit hohen Perforationsdichten Grenzfrequenzen über 10 kHz, die
höhere mechanische Membran-Nachgiebigkeiten und bessere Rauschschallpegel erlauben.
Unstetigkeiten bei der Simulation der oberen Grenzfrequenz entstehen durch den Übergang
von akustischer Dämpfung (-3 dB) zu Entdämpfung mit Resonanzüberhöhung (+ 3dB).
4.7
Zusammenfassung
Die Netzwerkmodellierung von kapazitiven Silizium-Mikrofonen bietet eine Reihe von
Vorteilen. Sie liefert eine anschauliche Darstellung, ist durch den modularen Aufbau einfach
zu modifizieren, führt zu kurzen Simulationszeiten und lässt sich durch den Einsatz eines
Netzwerklösers komfortabel mit der Schaltungssimulation kombinieren.
Das aufgestellte Gesamtmodell von Mikrofon, Gehäuse und Schaltung eignet sich zur
Simulation der frequenzabhängigen Empfindlichkeit und der Rauschdichte und kann durch
die Integration von Ergebnissen der FEM-Analysen auch bei Mikrofonen mit Feder- oder
Korrugationsmembran angewendet werden. Es wurde gezeigt, dass die MembranNachgiebigkeit, das Perforationsdesign und die elektrische Beschaltung das Verhalten der
Mikrofone maßgeblich bestimmt. Zu diesen wichtigen Einflussfaktoren konnten Maßnahmen
zur Optimierung der Mikrofon-Eigenschaften abgeleitet werden.
93
Angewandte experimentelle Untersuchungsmethoden
Kapitel 5
Angewandte experimentelle Untersuchungsmethoden
Bei der Herstellung von mikromechanischen Mikrofonen können zahlreiche Prozessfehler zu
Abweichungen vom idealen entworfenen Mikrofonaufbau bzw. zum totalen Ausfall führen.
Eine unvollständige Freiätzung des Opferoxides, Verkleben der Elektroden beim Trocknen,
Verunreinigungen und mechanische Defekte durch äußere Einwirkung haben
unterschiedlichste Auswirkungen auf das Verhalten eines Mikrofons. Hinzu kommen
Verbiegungen der dünnen, empfindlichen Strukturen durch innere und äußere mechanische
Spannungen. Um diese unerwünschten Einflüsse vor der elektrischen und akustischen
Untersuchung der Mikrofon-Eigenschaften zu identifizieren, ist vorab eine optische Kontrolle
und gegebenenfalls eine Selektion sinnvoll. Grobe Herstellungsfehler werden mit Hilfe eines
hochauflösenden Lichtmikroskops beobachtet. Detailliertere Messungen zur statischen
Verbiegung der Membran und Rückseitenplatte werden mit einem Interferometer
durchgeführt, das in Abschnitt 5.1 erläutert wird.
Aussagen über das elektromechanische und akustische Mikrofonverhalten werden mit
verschiedenen Messmethoden erzielt. Die Eigenfrequenz einer Membran stellt eine wichtige
Messgröße dar, die eine unabhängige experimentelle Bestimmung der mechanischen
Nachgiebigkeit ermöglicht. Der Messaufbau zur Eigenfrequenzanalyse wird in Abschnitt 5.2
erläutert. Ergänzende Untersuchungen erfolgen mit der Messung der spannungsabhängigen
Mikrofonkapazität (Abschnitt 5.3). Die wichtigsten Größen sind die dynamische
Mikrofonempfindlichkeit bei Schallanregung und das Mikrofonrauschen. Der Aufbau zu
deren Messung wird in Abschnitt 5.4 beschrieben.
5.1
Interferometrische Messung
Das in dieser Arbeit verwendete Interferometer mit der Typenbezeichnung „Wyko NT2000“
stammt von der Firma Veeko Metrology Group. Der Geräteaufbau entspricht einem
Standardinterferometer, bei dem mit Hilfe eines Strahlteilers ein Referenzstrahl und ein von
der Messprobe reflektierter Strahl zur Interferenz gebracht wird [Wyk98]. Eine Besonderheit
des Interferometers sind zwei wählbare Betriebsmodi. Die Betriebsmode PSI (phase-shifting
interferometry) ist die bekannte Messung des Weglängenunterschiedes über die durch die
Phasenverschiebung verursachte Änderung der Intensität von kohärentem Licht (λ=632 nm).
Diese Messmethode ermöglicht eine äußerst genaue Bestimmung von Höhenprofilen mit
hoher vertikaler Auflösung (< 1 nm), versagt allerdings bei steilen Stufen, deren Höhe im
Bereich von λ/4 liegen. In diesem Fall steht die Betriebsmode VSI (vertical-scanning
interferometry) zur Verfügung, die mit einer inkohärenten Lichtquelle arbeitet. Aufgrund der
geringen Kohärenzlänge von weißem Licht ist der Grad der Interferenzmodulation im Fokus
maximal und erlaubt bei Verschiebung des Fokuses durch einen Piezotranslator einen
Rückschluss auf das Höhenprofil. Der vertikale Messbereich ist daher nicht durch eine
Wellenlänge, sondern durch die maximale Verschiebungsvariation des Piezotranslators
begrenzt (ca. 500 µm). Die Auflösungsgrenze liegt bei 3 nm. Unabhängig vom Betriebsmodus
ist die Auflösung in horizontaler Richtung durch das verwendete Objektiv gegeben. Für die in
94
Angewandte experimentelle Untersuchungsmethoden
dieser Arbeit angestrebte Untersuchung des Oberflächenprofils der Membranen ist die zur
Verfügung stehende Auflösung ausreichend.
5.2
Eigenfrequenzanalyse
Die Eigenfrequenzanalyse einer Membran bzw. Rückseitenplatte ist eine vom Spaltabstand
unabhängige Messmethode zur Bestimmung des Verhältnisses von dynamischer Masse und
mechanischer Nachgiebigkeit. Sie eignet sich daher insbesondere zur Messung der
mechanischen Spannung in der Membran. Der Vorteil der Eigenfrequenzanalyse im Vergleich
zur Messung der Schichtspannung über die Wafer-Bow Methode liegt in der Messung der
effektiv wirksamen Membranspannung unter den tatsächlichen Randbedingungen. So können
auch lokale Schwankungen über den Siliziumwafer, der Einfluss des thermischen Budget des
Gesamtprozesses und äußere Beiträge zur Membranspannung erfasst werden. Der Aufbau zur
Messung der Eigenfrequenzen ist schematisch in der Abbildung 5.1 dargestellt.
Netzwerk Analysator
HP 4195A
Ventil
Vakuum-Kammer
VakuumPumpe
DC
AC
Ref IN
Splitter
KoppelKondensator
Abbildung 5.1: Aufbau zur Messung von Eigenfrequenzen.
Zur Unterdrückung von Resonanzfrequenzverschiebungen durch die Luftdämpfung im
Kondensatorspalt und der Massenbelastung der Strahlungsimpedanz wird die Messung bei
einem Unterdruck von 10-5 bar durchgeführt. Die elektrische Kontaktierung erfolgt mit
Probennadeln direkt auf den Bondpads des Mikrofonchips. Die Mikrofonkapazität kann über
eine Elektrode mit einer Gleichspannungsquelle aufgeladen werden. Mit einer möglichst
geringen Vorspannung minimiert man den Einfluss der (negativen) elektrischen Federkraft
auf die Messung der Eigenfrequenz. Auf dieselbe Elektrode wird über einen Kondensator (1
nF) eine Wechselspannung eingekoppelt. Mit dem Mess-Signal der zweiten Elektrode und
dem über einen Leistungsteiler bereitgestellten Referenzsignal berechnet der Netzwerk/Spektralanalysator „HP4195A“ von Hewlett Packard die Admittanz, die im Resonanzfall
maximal wird.
95
Angewandte experimentelle Untersuchungsmethoden
5.3
Kapazitätsmessung
Für die Messungen zur Mikrofonkapazität in Abhängigkeit von der Vorspannung steht das
LCR-Meter „HP4274A“ von Hewlett-Packard zur Verfügung. Die elektrische Kontaktierung
erfolgt über feine Messnadeln auf Chip-Ebene. Zur Eliminierung von Streukapazitäten,
Induktivitäten und Leitungswiderständen des Messaufbaus wird ein Nullabgleich
durchgeführt. Die Kapazitätsmessung benötigt keine evakuierte Messkammer und ist daher
schnell und einfach durchzuführen. Zugleich erlaubt die Messung der Kollapsspannung
Rückschlüsse auf die Spalthöhe bzw. auf die Membran-Nachgiebigkeit.
5.4
Messung der Mikrofonempfindlichkeit und Rauschspannung
Für gewöhnlich wird das zu testende Mikrofon in ein Gehäuse geklebt, durch Bonden mit den
Gehäusekontakten verbunden und in einem schalltoten Raum oder einer reflexionsarmen
Kammer gemessen. Zur Kalibrierung der gemessenen Empfindlichkeit wird zuvor am selben
Ort eine Messung mit einem Freifeld-Mikrofon mit bekanntem Frequenzverhalten
durchgeführt.
Der Nachteil dieser Messmethode besteht in der Notwendigkeit, jeden einzelnen
Mikrofonchip zu sägen, zu montieren und zu bonden. Um Entwicklungszeit und -kosten zu
reduzieren ist die Schallankopplung und Messung auf Ebene des Wafers oder eines Chips von
Vorteil. Ein entsprechender „On-Wafer-Scale“-Aufbau wurde von M. Pedersen [Ped98]
publiziert. Der in dieser Arbeit zur Verfügung stehende abgewandelte Messplatz eignet sich
für einzelne Chips oder Chipverbände und ist in der Abbildung 5.2 schematisch dargestellt.
Die Ansteuerung der Messgeräte und die Datenaufnahme an einem PC erfolgt mit Hilfe der
Software LABVIEW von National Instruments [Brau03].
metallische Abschirmung
Verstärker IN
SR560
OUT
Spektrum-Analysator
HP 35670A
AC
UBat
U0
Referenz-Mikrofon
Ref IN
Lautsprecher
Abbildung 5.2: Aufbau zur On-Chip Messung.
96
Angewandte experimentelle Untersuchungsmethoden
Der Schalldruck eines Lautsprechers wird rückseitig durch ein kleines Loch in der
Probenhalterung eingekoppelt. In dieser Konfiguration ist das Rückvolumen des Mikrofons
quasi unendlich. Mit dem Signal des Referenz-Mikrofons, welches sich in der
Probenhalterung befindet, wird über eine Regelschleife ein konstanter Schallpegel eingeprägt.
Als Referenzmikrofon dient das ¼ Zoll große Druckmikrofon „40BP“ von G.R.A.S
Sound & Vibration mit einer Empfindlichkeit von 1.68 mV und einem flachen Frequenzgang
(± 1 dB) von 10 Hz – 30 kHz. Der verwendete Lautsprecher kann bei Regelung zwischen 20
Hz und 10 kHz einen Schallpegel von 94 dB liefern. Bei Mikrofonen mit Feder-Membran, die
relativ große Membranöffnungen besitzen, führt der Druckabfall bei tiefen Frequenzen am
Referenzmikrofon über die Regelung zu einem überhöhten Schalldruck. Diese Mikrofone
werden daher ungeregelt gemessen, wobei das Referenzsignal nachträglich zur Kalibrierung
der Messsignale herangezogen wird. Da der Lautsprecher außerhalb seiner Bandbreite nur
geringe Schallpegel leistet, liefert die ungeregelte Messung relativ verrauschte Signale.
Um eine nennenswerte Phasenverschiebung zwischen dem Druck am Referenz- und
Testmikrofon zu vermeiden, sind diese möglichst nahe beieinander montiert, was allerdings
zu Beugungserscheinen führt. Die geometrische Auslegung des Aufbaus erlaubt Messungen
bis zu ca. 9 kHz. Der offene Aufbau macht eine besonders sorgfältige Abschirmung gegen die
Einkopplung von elektromagnetischen Störsignalen notwendig. Dazu wird der
Impedanzwandler mit den Messnadeln möglichst nah am Mikrofon angebracht. Außerdem
wird die metallische Messbox mit dem Massenpotential der Impedanzwandlerschaltung
verbunden, so dass sich äußere Störungen durch die differentielle Messkonfiguration
auslöschen. Der Impedanzwandler wird als diskrete Schaltung mit dem rauscharmen
Feldeffekt-Transistor „J201“ von Vishay Siliconix aufgebaut. Da die untere Rauschdichte des
Spektrum-Analysator „HP 35670A“ von Hewlett-Packard bei –140 dB(V/√Hz) liegt, wird zur
Messung der Rauschspannung zusätzlich der Verstärker „SR560“ von Stanford Research
Systems mit einer Rauschgrenze von –168 dB(V/√Hz) eingesetzt.
Die Messmethode direkt am Chip erlaubt eine Charakterisierung des reinen
Mikrofonverhaltens ohne die Überlagerung mit externen Effekten, wie z.B. der
Schallbeugung am Gehäuse oder der äußeren Einprägung von mechanischen Spannungen,
etwa durch das Klebemittel. Erfolgt die Schallankopplung durch ein rückwärtiges Loch im
Gehäuse, dann kann die Reduzierung der Empfindlichkeit aufgrund der HohlraumNachgiebigkeit des Gehäusevolumens oder der akustische Kurzschluss bei Feder-Membranen
ebenfalls untersucht werden.
97
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
Kapitel 6
Messergebnisse zu Mikrofonen mit epitaktischer SiliziumGegenelektrode
In diesen Kapitel werden die Ergebnisse zu den Mikrofonen mit einer epitaktisch
gewachsenen Gegenelektrode präsentiert. Die Herstellung und der Aufbau der Mikrofone mit
geschlossenen SOI-Membranen wurde in Abschnitt 2.2 bzw. mit unterschiedlichen
Membranen aus Polysilizium in Abschnitt 2.3 beschrieben. Zur besseren Übersicht sind in
Abbildung 6.1 der schematische Querschnitt der Mikrofone und die prozessierten
Membranvarianten dargestellt. Die geschlitzten Membranen mit je vier Federstrukturen
werden zur Unterscheidung mit Feder I bzw. II gekennzeichnet.
Abschnitt 6.1 beschäftigt sich mit der Analyse der Oberflächenprofile von Membran und
Gegenelektrode. Dazu wird die statische Auslenkung mit einem Interferometer vermessen.
Das dynamische Verhalten der Membran und Gegenelektrode wird zunächst anhand der
Eigenfrequenz untersucht (Abschnitt 6.2). Sie erlaubt erste Rückschlüsse auf die
Empfindlichkeit der Mikrofone. Die Anordnung der Elektroden und der Spaltabstand wird
durch die Messung der spannungsabhängigen Kapazität in die Betrachtungen einbezogen
(Abschnitt 6.3). Bevor die elektroakustische Empfindlichkeit der Mikrofone beurteilt werden
kann, muss zunächst die Messumgebung charakterisiert werden. Dies geschieht in Abschnitt
6.4 durch die Messung der Spannungsverstärkung und Rauschdichte von der
Impedanzwandlerschaltung und dem gesamten Aufbau. Schließlich wird auf die
Empfindlichkeit (6.5) und das Rauschen (6.6) der Silizium-Mikrofone eingegangen. In
Abschnitt 6.7 werden die gewonnenen Ergebnisse zusammengefasst.
Gegenelektrode
Membran
Membran-Designs
Mono-Si und
Poly-Si
Poly-Si
(Feder I)
Poly-Si
(Feder II)
Abbildung 6.1: Kapazitive Mikrofone mit epitaktischer Silizium-Gegenelektrode und
Membranen aus mono- und polykristallinem Silizium.
98
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
6.1
Oberflächenanalyse von Membran und Gegenelektrode
3.9 µm
1 mm
0 µm
Membranauslenkung [µm]
Bei der ersten optischen Begutachtung der Mikrofon-Membranen mit einem Lichtmikroskop
beobachtet man schwache Interferenzstreifen, die auf eine statische Verbiegung der
Membranen hinweisen. Daher wurde zunächst das Oberflächenprofil einer Membran mit
einem Weißlicht-Interferometer untersucht. Die Abbildung 6.2 zeigt die gemessene
Auslenkung einer SOI-Membran mit einer Kantenlänge von 1 mm. Die Messung erfolgt bei
umgedrehtem Mikrofonchip von der Rückseite her, so dass die Membran über die KOHÄtzgrube eingesehen werden kann.
4
3
2
1
0
0
0.2
0.4
0.6
0.8
1
Ort auf der Membran [mm]
Abbildung 6.2: Interferometrische Messung der Oberfläche einer unbelasteten SOI-Membran
(Kantenlänge 1 mm, Dicke 1µm).
Die Messung des Oberflächenprofils zeigt eine Auslenkung der Membran um bis zu 3.9 µm
im Vergleich zum eingespannten Membranrand, ohne dass eine elektrische Vorspannung
anliegt oder ein Druck auf der Membran lastet. Die Orientierung der Auslenkung ist derart,
dass sie von der Gegenelektrode weg weist. Die Stärke der Auslenkung deutet auf das
Phänomen der Plattenbeulung. Die Plattenbeulung ist ein nichtlineares Stabilitätsproblem, das
bei einer kritischen Querbelastung auftritt. Bei vollständiger Symmetrie und geringer
Belastung ist die Platte zunächst flach. Erst mit der sogenannten Eulerschen Knicklast kommt
es zur schlagartigen Ausbeulung der Platte. Bis zur Beulung 2. Ordnung führt eine weitere
Erhöhung der Last oder eine größere Kantenlänge der Platte zu einer annähernd linearen
Zunahme der Auslenkung [Zie99]. Dieses Verhalten zeigt die gemessene Mittenauslenkung
von SOI-Membranen verschiedener Kantenlänge (Abbildung 6.3). Offenbar erreicht die
Querbelastung nicht die Knickspannung der 5 µm dicken Rückseitenplatte, da deren
Mittenauslenkung relativ konstant nur etwa 200 nm beträgt. Die verbleibende Auslenkung
unterhalb der kritischen Last ist mit der nicht vollständig symmetrischen Befestigung der
Rückseitenplatte zu erklären.
99
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
5
Mittenauslenkung [µm]
4.5
4
3.5
3
2.5
SOI-Membran
2
Rückseitenplatte
1.5
1
0.5
0
0.75
0.8
0.85
0.9
0.95
1
1.05
1.1
1.15
1.2
1.25
Kantenlänge [mm]
Abbildung 6.3: Mittenauslenkung bei Beulung von SOI-Membranen (Dicke 1 µm) und
Rückseitenplatten (Dicke 5 µm).
Vergleichbare Messergebnisse erzielt man mit Membranen aus polykristallinem Silizium. Die
geschlossenen bzw. an vier kurzen Federbalken befestigten Polysilizium-Membranen (Feder
I) zeigen ebenfalls Mittenauslenkungen im Bereich von 3-5 µm. Die mechanisch sehr
empfindlichen Membranen mit vier langen Federstrukturen (Design Feder II) buckeln mit
5-7 µm noch deutlich stärker aus der Ruhelage. Abbildung 6.4 gibt die Beulung einer solchen
Federmembran mit einer Kantenlänge von 0.8 mm wieder. Die Länge einer Federstruktur
(Position A nach B, Abbildung 6.4) beträgt etwa 0.6 mm.
8
B
A
C
0.8 mm
Membranauslenkung [µm]
B
7
C
6
5
4
3
2
A
1
0
0
0.2
0.4
0.6
0.8
1
Ort auf der M embran [mm]
Abbildung 6.4: Beulung einer Polysilizium-Membran mit vier Federbalken.
Die niedrig dotierten Membranen aus Polysilizium mit einer Dotierstoffkonzentration von ca.
3⋅1018 cm-3 stehen nach den Erkenntnissen aus Kapitel 2 (Abbildung 2.12) unter einer
100
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
mechanischen Zugspannung. Die Druckspannung, die zu dem Buckeln der Membranen führt,
muss daher von außen auf die Membran eingeprägt werden. Vermutlich ist das als
Einspannmaterial verwendete Siliziumdioxid an den Membranrändern in Kombination mit
dem Hochtemperaturprozess der Silizium-Epitaxie der Rückseitenplatte für die
Druckspannung verantwortlich. Beim Abkühlen von der hohen Prozesstemperatur von
1100° C auf Raumtemperatur erzeugt der im Vergleich zu Silizium geringere thermische
Ausdehnungskoeffizient von Siliziumdioxid eine hohe thermische Druckspannung. Im
freigeätzten Zustand resultiert daraus eine partielle Expansion und eine Druckspannung in der
Membran, die schließlich zum Ausbeulen der Membran führt. Dieses Modell der Beulung bei
den hergestellten Mikrofonen wird durch FEM-Simulationen gestützt [Fue01].
Trotz der Beulung der Membranen im Bereich mehrerer Mikrometer sind diese über die
gesamte Membranfläche (~mm2) betrachtet relativ eben. Dennoch ist mit einer erheblichen
Beeinflussung des mechanischen und kapazitiven Verhaltens zu rechnen, wenn die Dicke der
Membran von 0.4-1 µm und die Kondensatorspalthöhe von 1.15 µm in Betracht gezogen
wird. Die nächsten beiden Abschnitte beschäftigen sich daher mit den Eigenfrequenzen und
den Mikrofonkapazitäten.
6.2
Eigenfrequenz und mechanische Nachgiebigkeit von Membran und
Rückseitenplatte
Die Eigenfrequenz der Rückseitenplatte wurde an Mikrofonen und an Teststrukturen
gemessen. Die Teststruktur ist ein Mikrofonchip ohne Prozessierung der Rückseite, d.h. vor
dem Ätzen von Substrat und Substratoxid. Bei ihr wird lediglich das Opferoxid im
Kondensatorspalt entfernt, so dass nur die Rückseitenplatte beweglich ist. Eine Skizze der
Teststruktur und die gemessenen Eigenfrequenzen in Abhängigkeit von der Kantenlänge ist in
der Abbildung 6.5 dargestellt. Ferner ist die theoretische Eigenfrequenz einer 5 µm dicken,
spannungsfreien Platte mit Perforationslöchern (Breite 1.5 µm, Abstand 4 µm) angegeben.
Teststruktur
240
Eigenfrequenz [kHz]
220
200
180
160
140
120
100
80
Messung an Mikrofon
Messung an Teststruktur
Theorie spannungsfreie Platte
60
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
1.05
Kantenlänge [mm]
Abbildung 6.5: Eigenfrequenz der Rückseitenplatte vor und nach der Substratätzung.
101
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
Vor der Substrat- und Substratoxid-Ätzung ist das unter einer Druckspannung stehende
Randoxid zu einem großen Teil durch die Unterlage eingespannt. Es relaxiert und drückt
daher nur wenig auf den Rand der Rückseitenplatte. Dementsprechend misst man eine
Eigenfrequenz an der Teststruktur, die der theoretisch zu erwartenden Eigenfrequenz einer
spannungsfreien Platte sehr nahe kommt. Die Abweichung zwischen Messung und Theorie ist
zum Teil mit der Schichtdickenschwankung der Rückseitenplatte von 4.7-5.7 µm zu erklären,
die mit einem Rasterelektronenmikroskop gemessen wurde und mit dem von der Polierfläche
abhängigen Abtrag des chemisch-mechanischen Polierens der Epitaxie-Schicht
zusammenhängt. Am vollständig freigeätzten Mikrofon misst man im Vergleich zur
Teststruktur eine erhöhte Eigenfrequenz der Rückseitenplatte. Dieser Versteifungseffekt
deutet wieder darauf hin, dass die Expansion des Randoxides eine Druckspannung in die
Rückseitenplatte (und Membran) einbringt.
In stärkerer Form ist die äußere Druckspannung des Randoxides bei den dünnen Membranen
zu beobachten. In Abbildung 6.6 ist die gemessene Eigenfrequenz von SOI-Membranen und
die mechanische Nachgiebigkeit aufgetragen, die bei bekannter dynamischer Masse aus der
Eigenfrequenz abgeleitet werden kann (Abschnitt 4.2.4). Außerdem wird die theoretische
Nachgiebigkeit einer rein biegesteifen Platte, d.h. einer idealen SOI-Membran, angegeben.
100
70
Messung Eigenfrequenz
90
Nachgiebigkeit [nm/Pa]
80
Eigenfrequenz [kHz]
Nachgiebigkeit nach Messung
60
theoret. Eigenfrequenz Platte
70
60
50
40
30
20
theoret. Nachgiebigkeit Platte
50
40
30
20
10
10
0
0
0.6
0.7
0.8
0.9
1
Kantenlänge [mm]
1.1
1.2
0.6
0.7
0.8
0.9
1
1.1
1.2
Kantenlänge [mm]
Abbildung 6.6: Gemessene Eigenfrequenz und abgeleitete Nachgiebigkeit von SOIMembranen (Dicke 1 µm) im Vergleich zum Erwartungswert einer spannungsfreien Platte.
Bei geeigneter Auftragung ist das mechanische Verhalten einer biegesteifen Platte mit der
quadratischen Abhängigkeit der Eigenfrequenz von der Kantenlänge zu beobachten. Dennoch
ist die gemessene Eigenfrequenz deutlich größer bzw. die abgeleitete mechanische
Nachgiebigkeit deutlich niedriger als eine spannungsfreie Platte aus Silizium erwarten lässt.
Theoretisch sollte bei einer Kantenlänge von 1 mm die Nachgiebigkeit etwa 25 nm/Pa
betragen. Stattdessen wird indirekt eine Nachgiebigkeit von 5.3 nm/Pa gemessen. Die
beachtliche Diskrepanz zwischen Messung und Entwurf beruht auf der nichtlinearen
Verformungsversteifung, die aufgrund der Beulung in der Größenordnung der Membrandicke
auftritt (vgl. Abschnitt 3.2).
102
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
6.3
Mikrofon-Kapazität und Kollapsspannung
Die Beulung der Membran beeinträchtigt nicht nur die mechanische Nachgiebigkeit, sondern
sie führt zusätzlich zu einem effektiv größeren Spaltabstand. So wird bei einer 1 mm2
Teststruktur mit flacher Membran eine Ruhekapazität von 11.5 pF gemessen. Im Vergleich
dazu beträgt die Mikrofonkapazität bei vollständiger Prozessierung mit einer gebeulten
Membran 10.5 pF. Die Auswirkung des größeren Spaltabstandes ist besonders deutlich an der
Kapazitätsänderung mit einer Vorspannung zu beobachten. Die gemessene und theoretische
relative Kapazitätsänderung einer Teststruktur und eines Mikrofons mit SOI-Membran ist in
Abbildung 6.7 angegeben. In die theoretischen Kurven geht die über die Eigenfrequenz
bestimmte Nachgiebigkeit der Membran und Rückseitenplatte und eine parasitäre
Randkapazität von 3.8 pF der Siliziumdioxid-Einspannung ein.
1.1
Mikrofon
Teststruktur
Theorie
normierte Kapazität C(U)/C(0)
1.09
1.08
1.07
1.06
elektrostatischer Kollaps
1.05
1.04
1.03
1.02
1.01
1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Vorspannung [V]
Abbildung 6.7: Spannungsabhängige Kapazitätsänderung bei der Teststruktur und einem
Mikrofon mit SOI-Membran (Kantenlänge 1 mm).
Messung und Theorie stimmen für die Teststruktur, die sich aus der flachen, beweglichen
Rückseitenplatte und einer unbeweglichen Membran zusammensetzt, sehr gut überein. Die
Kollapsspannung eines Mikrofons mit einer ausgebeulten Membran ist erwartungsgemäß
größer und die Kapazitätsänderung weicht von der Theorie einer flachen Membran mit einem
konstanten Spaltabstand ab.
6.4
Impedanzwandlerschaltung und Messaufbau
Zur Analyse von Empfindlichkeit und Rauschen der Mikrofone ist es erforderlich, die
Spannungsverstärkung und das elektrische Rauschen der Impedanzwandlerschaltung und des
Messaufbaus zu kennen. Die Messungen wurden an dem On-Chip Messplatz mit einem
103
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
Ladewiderstand von 1 GΩ , einem Lastwiderstand von 10 kΩ und dem Feldeffekt-Transistor
„J201“ durchgeführt.
Spannungsverstärkung
Die Spannungsverstärkung bei einer direkten Signaleinkopplung am Gate-Knoten des JFET
(Messkonfiguration A, Abbildung 6.8) ist im Frequenzbereich von 10 Hz – 50 kHz nahezu
konstant und beträgt 0.82. In einer Niederfrequenz-Schaltung mit einer Kapazität von 10 pF,
die als passives Element das Mikrofon nachbilden soll, fällt die Verstärkung aufgrund des
Spannungsteilers mit den Sperrschicht-Kapazitäten des Transistors auf 0.63 ab
(Messkonfiguration B, Abbildung 6.8). Darüber hinaus verursacht die Gesamtkapazität im
Zusammenspiel mit dem Ladewiderstand einen Hochpass mit einer unteren Grenzfrequenz
von 13 Hz. Die Messungen zur Spannungsverstärkung stimmen sehr gut mit den
Erwartungswerten der PSPICE-Simulationen überein. Die geringe Abweichung kann auf die
Exemplarstreuung des Feldeffekt-Transistors zurückgeführt werden.
1
0.9
Spannungsverstärkung
A
A: Signaleinkopplung am Gate-Knoten
5 V
J201
0.8
Uin ~
0.7
10 kΩ
Uout
0.6
B: Signaleinkopplung über C=10 pF
0.5
B
0.4
5 V
J201
0.3
10 pF
0.2
Messung
0.1
1 GΩ
Uin ~
Simulation (PSPICE)
10 kΩ
Uout
0
10
100
1000
10000
100000
Frequenz [Hz]
Abbildung 6.8: Messungen
Impedanzwandlerschaltung.
und
Simulationen
zur
Spannungsverstärkung
der
Rauschdichte
Die untere Messgrenze der Rauschdichte ist durch den Vorverstärker bestimmt und wird bei
kurzgeschlossenem Eingang gemessen (Messung A, Abbildung 6.9). Gemäß der Spezifikation
des Herstellers liegt die Rauschgrenze bei etwa –168 dB(V/√Hz). Die Rauschdichte des
gesamten On-Chip Messaufbaus und der Impedanzwandlerschaltung mit dem Gate-Knoten
auf Massepotential liegt nur etwa 5 dB darüber (Messung B). Das Funkel- und Kanalrauschen
des verwendeten Feldeffekt-Transistors ist damit sehr niedrig. Erwartungsgemäß wird in der
Niederfrequenzschaltung das Rauschen durch das thermische Widerstandrauschen des
Ladewiderstandes mit einem Tiefpass-Verhalten dominiert (Messung C). Die A-bewertete
Rauschspannung im Frequenzband von 10 Hz – 20 kHz beträgt etwa 5 µV. Unter
Berücksichtigung des Grundrauschens vom Vorverstärker entsprechen die Messungen den
theoretischen Werten der Simulationen.
104
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
-80
A
-90
Rauschdichte [dB(V/sqrt(Hz)]
Verstärker
SR560
IN OUT
Messung
Simulation (PSPICE)
Uout
-100
B
-110
5 V
J201
C: JFET+DC-Schaltung
-120
-130
10kΩ
Verstärker
SR560
IN OUT
Uout
-140
B: JFET
-150
C
5 V
J201
-160
10pF
-170
1GΩ
A: Vorverstärker
10kΩ
-180
10
100
1000
10000
Verstärker
SR560
IN OUT
Uout
100000
Frequenz [Hz]
Abbildung 6.9: Messungen und Simulationen zur elektrischen Rauschspannungsdichte der
Impedanzwandlerschaltung.
6.5
Mikrofon-Empfindlichkeiten
Die Messung der elektroakustischen Empfindlichkeit der Mikrofone erfolgt auf Chip-Level
bei einem Schallpegel von 94 dB mit dem zuvor charakterisierten Impedanzwandler. Den
charakteristischen Frequenzgang eines Mikrofons mit einer 1 mm2 SOI-Membran (Dicke 1
µm) für Vorspannungen von 1-3 V zeigt die Abbildung 6.10. Aufgrund des beschriebenen
Buckelphänomens der SOI-Membranen ist ein Abgleich mit dem Netzwerkmodell, das von
einer spannungsfreien und planaren Membran ausgeht, nicht möglich. Eine Abschätzung der
Empfindlichkeit kann mit Hilfe einer FEM-Simulation der buckelnden Membran angegeben
werden, die bei einem Druck von 1 Pa eine relative Kapazitätsänderung der aktiven
Mikrofonkapazität von ∆C/C0=0.2% liefert [Fue01]. Mit der parasitären Kapazität Cp und der
Spannungsverstärkung der Impedanzwandlerschaltung Ajfet erhält man bei einer Vorspannung
von 1 V als Abschätzung für die Empfindlichkeit
S ≈U0 ⋅
C0
mV
∆C
⋅
⋅ A jfet = 1.05
.
C0 C0 + C p
Pa
Im Vergleich dazu wird bei 100 Hz eine Empfindlichkeit von 0.65 mV/Pa gemessen.
105
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
Empfindlichkeit [mV/Pa]
10
U0=3 V
U0=2 V
1
U0=1 V
0.1
10
100
1000
10000
Frequenz [Hz]
Abbildung 6.10: Empfindlichkeit eines Mikrofons mit einer 1mm2 großen SOI-Membran bei
einer Vorspannung U0 von 1 V, 2 V und 3 V.
Wie bereits die Messungen zur Eigenfrequenz und der spannungsabhängigen
Kapazitätsänderung andeuteten, liegt die Mikrofon-Empfindlichkeit unter den Erwartungen.
Außerdem ist zu beobachten, dass die Herstellung der Perforationsöffnungen in der
Rückseitenplatte durch das einfache Ätzen und Füllen der Öffnungen, das eine beschränkte
Perforationsweite bedingt (vergleiche dazu Kapitel 2.4.2), nicht ausreichend stark die
akustische Hohlraum-Nachgiebigkeit des Kondensatorspaltes entdämpfen kann. Die 1.5 µm
weiten Perforationsöffnungen führen bei der Perforationsflächendichte von 14% zu einer
oberen Grenzfrequenz von ca. 0.8 kHz.
Die Empfindlichkeit von Mikrofonen mit 0.8, 1 und 1.2 mm großen SOI-Membranen zeigt
die Abbildung 6.11. Die Vorspannung beträgt jeweils 1 V. Der starke Anstieg der
Empfindlichkeit von 0.13 mV/Pa (Kantenlänge a=0.8 mm) auf 0.65 mV/Pa (a=1 mm) und
1.3 mV/Pa (a=1.2 mm) deutet wieder auf das mechanische Verhalten einer biegesteifen Platte
mit einer Abhängigkeit vierten Ordnung von der Kantenlänge hin. Bei den 1 mm und 1.2 mm
Membranen spiegelt sich das Verhältnis der Nachgiebigkeiten von Abbildung 6.6 mit
11.6/5.3=2.2 in der Steigerung der Empfindlichkeit der Abbildung 6.11 um den Faktor
1.3/0.65=2 wider. Dagegen bleibt die Empfindlichkeit der 0.8 mm Membran hinter den
(reduzierten) Erwartungen zurück, was mit dem schlechteren kapazitiven Teilerverhältnis
zusammenhängen könnte.
106
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
10
Empfindlichkeit [mV/Pa]
SOI-Mikrofone
a=1.2 mm
1
a=1 mm
a=0.8 mm
0.1
10
100
1000
10000
Frequenz [Hz]
Abbildung 6.11: Empfindlichkeit von Mikrofonen mit SOI-Membranen unterschiedlicher
Kantenlänge a (Vorspannung 1 V, Membrandicke 1 µm).
Trotz der Schwierigkeiten mit äußerer Spannungseinprägung und akustischer Dämpfung
werden relativ gute Empfindlichkeiten von 1.3 mV/Pa/V der Mikrofone mit einer SOIMembran erreicht. Die Empfindlichkeit der mit derselben Technologie hergestellten
Mikrofone mit einer 0.4 µm dicken Membran aus Polysilizium zeigt Abbildung 6.12.
Dargestellt ist ein charakteristischer Frequenzgang eines Mikrofons mit einer geschlossenen
Membran und einer Federmembran (Feder I). Die Kantenlänge ist bei beiden Mikrofonen
1 mm und die Vorspannung 1 V.
10
Empfindlichkeit [mV/Pa]
Feder- Membran aus Polysilizium (Design Feder I)
1
geschlossene Polysilizium-Membran
0.1
10
100
1000
10000
Frequenz [Hz]
Abbildung 6.12: Mikrofon-Empfindlichkeit mit einer geschlossenen Membran und einer
Feder-Membran (Material Polysilizium, Vorspannung 1 V, Dicke 0.4 µm).
107
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
Der Einsatz einer dünneren Membran erhöht dem Dickenverhältnis von 1 µm/0.4 µm=2.5
entsprechend die gemessene Empfindlichkeit bei Frequenzen <100 Hz von 0.65 nm/Pa auf
1.67 nm/Pa. Das Membranmaterial selbst hat hingegen keinen Einfluss auf die
Empfindlichkeit. Dieses Ergebnis stimmt mit den bisherigen Messungen dahingehend
überein, dass offenbar nicht die intrinsische Schichtspannung, sondern eine externe
mechanische Spannung der Aufhängung das mechanische Verhalten der Membranen
bestimmt. Mit dem Design einer Federmembran kann eine zusätzliche Erhöhung der
Empfindlichkeit von ca. 40% erreicht werden. Akustische Messungen am Federdesign II
führten aufgrund der sehr starken Membranbeulung dieser Variante zu keinem Ergebnis.
Die akustische Dämpfung bei hohen Frequenzen fällt bei den untersuchten Mikrofonen
unterschiedlich aus und ist durchgängig etwas stärker, als das Perforationsdesign erwarten
lässt. Die Ursache für die zufällige Schwankung der akustischen Dämpfung liegt
wahrscheinlich an einer sehr knappen Tiefenätzung der Perforationslöcher, so dass abhängig
von der Dicke der Gegenelektroden-Epitaxie und dem chemisch-mechanischen Polieren
teilweise Perforationslöcher nicht vollständig ausgeführt werden. Diese Annahme wird durch
Querschnittaufnahmen der Gegenelektrode mit einem Rasterelektronenmikroskop unterstützt.
6.6
Rauschen der Mikrofone
Die elektrische Rauschdichte wurde ebenfalls auf Chip-Level gemessen. Zahlreiche
Messungen an verschieden empfindlichen Mikrofonen bei unterschiedlichen Vorspannungen
lassen keine signifikanten Unterschiede im Rauschen erkennen. Dieses Ergebnis stimmt mit
den Vorhersagen des Netzwerkmodells überein, das selbst bei einem hohen Ladewiderstand
von 1 GΩ ein über das Eigenrauschen dominierendes elektrisches Rauschen der
Impedanzwandlerschaltung vorhersagt. Daher geht von Seiten des Mikrofons lediglich die
Mikrofonkapazität ein. Die Abbildung 6.13 zeigt eine typische spektrale Rauschdichte. Bei
der Messung handelt es sich um ein Mikrofon mit einer gefederten Polysilizium-Membran.
Die Kantenlänge der Membran beträgt 1 mm (C=11 pF).
Rauschdichte [dB(V/sqrt(Hz)]
-80
Messung
Simulation Ladewiderstand
Simulation Kanalrauschen
Simulation Eigenrauschen
-100
-120
-140
-160
-180
-200
10
100
1000
10000
100000
Frequenz [Hz]
Abbildung 6.13: Spektrale Rauschdichte eines Silizium-Mikrofons in einer Niederfrequenzund Impedanzwandlerschaltung.
108
Messergebnisse zu Mikrofonen mit epitaktischer Silizium-Gegenelektrode
Deutlich ist das tiefpassgefilterte thermische Rauschen des Ladewiderstandes mit der
Gesamtkapazität, bestehend aus der Mikrofonkapazität, der Siliziumdioxid-Randkapazität und
den Sperrschichtkapazitäten, zu erkennen. Oberhalb von 10 kHz geht das Gesamtrauschen in
das weiße Kanalrauschen des Feldeffekt-Transistors über. Dem Rauschspektrum überlagert ist
ein 50 Hz-Netzbrummen. Zur Simulation des Mikrofon-Eigenrauschens wurde eine effektive
Membranspannung und Spalthöhe angenommen, welche die gemessene Empfindlichkeit
korrekt wiedergeben. Im Frequenzband von 10 Hz - 20 kHz beträgt die A-bewertete
Rauschspannung 6.8 µV bzw. 5 µV, wenn die Störspitzen im Rauschspektrum
herausgerechnet werden.
6.7 Zusammenfassung der Messergebnisse
Mit der Technologie einer epitaktisch gewachsenen Gegenelektrode konnten
funktionstüchtige Silizium-Mikrofone hergestellt und getestet werden. Aufgrund einer
äußeren Einwirkung von mechanischen Spannungen kommt es sowohl bei Membranen aus
monokristallinem als auch polykristallinem Silizium zu einer Beulung, die eine Reduzierung
der Empfindlichkeit zur Folge hat. Weiterhin führt die eingeschränkte Weite der
Perforationsöffnungen in der Gegenelektrode zu einer niedrigen oberen Grenzfrequenz. Das
Gesamtrauschen hat seine Ursache in Rauschquellen der elektrischen Beschaltung. Basierend
auf der Mikrofon-Empfindlichkeit bei 100 Hz wird bei einer Vorspannung von 1 V ein
äquivalenter Rauschschallpegel von 40 dB(A) erreicht.
109
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
Kapitel 7
Messergebnisse zu Mikrofonen mit polykristalliner
Siliziummembran und Gegenelektrode
Dieses Kapitel stellt die Ergebnisse zu den Mikrofonen mit einer Membran und
Gegenelektrode aus polykristallinem Silizium vor. Der Aufbau der Mikrofone und die
Schwerpunkte der Technologieentwicklung mit der Realisierung empfindlicher Membranen
und einer perforierten Gegenelektrode wurden in Abschnitt 2.4 beschrieben. Zum besseren
Verständnis ist in Abbildung 7.1 ein schematischer Querschnitt der in diesem Kapitel
untersuchten Mikrofone dargestellt.
Die Untersuchung der mechanischen Nachgiebigkeit der verschiedenen Membrantypen
erfolgt über die Messung der Eigenfrequenzen (Abschnitt 7.1). Es werden die verschiedenen
Typen von Kreis-, Feder- und Korrugationsmembranen und die mechanische
Schichtspannung von dotiertem Polysilizium betrachtet. Eine besondere Eigenschaft von
Feder-Membranen ist die statische Membranverbiegung unter dem Einfluss von
Spannungsgradienten, auf die in Abschnitt 7.2 anhand von Messungen mit einem
Interferometer eingegangen wird. In Abschnitt 7.3 und 7.4 werden schließlich Messungen zur
elektroakustischen Empfindlichkeit und zum Rauschen der Silizium-Mikrofone vorgestellt,
die zur experimentellen Überprüfung verschiedener Aspekte des entwickelten
Netzwerkmodells herangezogen werden.
Polysilizium-Membran
Polysilizium-Gegenelektrode
EpitaxieRückseitenplatte
Abbildung 7.1: Schematischer Querschnitt des Mikrofons mit einer polykristallinen
Siliziummembran und Gegenelektrode.
110
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
7.1
Eigenfrequenzanalyse
Nachgiebigkeit
zur
Untersuchung
der
mechanischen
Die Empfindlichkeit der Silizium-Mikrofone in dieser Arbeit wird über die geometrische
Abmessung und dem Design der Membran und der gezielten Implantation von Dotierstoff in
das Polysilizium zur Auslösung von Rekristallisationsprozessen gesteuert. In den folgenden
Abschnitten werden die voneinander unabhängigen Maßnahmen zur Erhöhung der MembranNachgiebigkeit anhand der Eigenfrequenzen demonstriert und zur Verifizierung der Modelle
verwendet. Die Messung der Eigenfrequenz über die Kapazitätsänderung des Mikrofons bei
elektrischer Aktuation der Membran wurde in Abschnitt 5.2 geschildert.
7.1.1 Eigenfrequenz und Nachgiebigkeit von Feder-Membranen
Die Feder-Membranen bestehen aus einer 0.4 µm dicken Polysiliziumschicht, die amorph
abgeschieden, kristallisiert, mit Phosphor-Ionen implantiert (Dosis 1015 cm-2) und bei 900° C
für 60 min getempert wurde. Abbildung 7.2 gibt die Eigenfrequenzen der unterschiedlichen
Membranen wieder. Von jeder Variante wurden jeweils mehrere, von einem
Fertigungsdurchlauf und demselben Wafer stammende Membranen gemessen.
160
Eigenfrequenz [kHz]
140
120
100
80
60
40
20
0
Netz A
Netz B
Feder A
Feder B
Abbildung 7.2: Gemessene Eigenfrequenz von Feder-Membranen.
Erwartungsgemäß ist das Design Netz A aufgrund der 16 relativ kurzen Federstrukturen am
unempfindlichsten und weist die höchste Eigenfrequenz auf. Das Design Netz B mit einer
zweiten ringförmigen Anordnung von Federstrukturen, die durch zusätzliche Löcher in der
Membran realisiert wird, besitzt dementsprechend eine kleinere Eigenfrequenz. Der Trend
einer niedrigeren Eigenfrequenz bei einer höheren Nachgiebigkeit setzt sich bei den
Membranen mit nur vier Federstrukturen (Feder A und Feder B) fort. Aus der gemessenen
111
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
Eigenfrequenz f0 kann nach Gleichung (4.13) die mechanische Nachgiebigkeit Cm der FederMembranen bestimmt werden. Die Umformung der Gleichung liefert
Cm =
(2 ⋅ π ⋅ f 0 )
1
2
⋅ t ⋅ ρ ⋅ f mass
.
(7.1)
Die Membrandicke t=400 nm, die Dichte von Polysilizium ρ=2330 kg/m3 und der
dynamische Massenfaktor fmass≈1.15 (Abschnitt 4.2.4) sind bekannt und ergeben die in der
Tabelle 7.1 aufgeführten Membran-Nachgiebigkeiten. Zum Vergleich sind die theoretischen
Nachgiebigkeiten nach Gleichung 3.12 angegeben. Mit Ausnahme der mechanischen
Schichtspannung gehen in die theoretische Berechnung nur Technologie- und
Geometrieparameter ein. Die Schichtspannung wird aus der unabhängigen Messung der
Eigenfrequenz einer kreisförmigen Testmembran (Radius 110 µm) ermittelt. Aus der
gemessenen Eigenfrequenz von 800 kHz wird eine Schichtspannung von 110 MPa der 0.4 µm
dicken Polysiliziumschicht abgeleitet.
Nachgiebigkeit [nm/Pa]
Netz A
Netz B
Feder A
Feder B
Messung
Theorie
Abweichung vom Mittelwert
1.20 ±0.16
1.46
18%
1.80 ±0.21
2.11
15%
2.67 ±0.15
2.68
<1%
3.85 ±0.15
3.88
1%
Tabelle 7.1: Über die Eigenfrequenz gemessene und theoretische Nachgiebigkeit von FederMembranen.
Die Übereinstimmung zwischen den Messungen und der theoretischen Nachgiebigkeit von
Feder-Membranen ist sehr gut. Das heißt, die FEM-unterstützte Modellierung der
Nachgiebigkeit von Feder-Membranen über die Nachgiebigkeit einer Kreismembran ist
zulässig.
Im Vergleich zur theoretischen Nachgiebigkeit einer Kreismembran mit gleichem Radius,
gleicher Dicke und Schichtspannung wird mit der Membranaufhängung an Federstrukturen
eine Empfindlichkeitssteigerung von 70-440% erreicht. Die nach dem Gaußschen
Fehlerfortpflanzungsgesetz berechnete Schwankung zwischen gleichen Membranen ist mit
<15% relativ gut. Allerdings gehen Schichtdickenschwankungen der Membran durch die
Messung über die Eigenfrequenz nicht ein. Hauptursache für die Schwankung ist vermutlich
die von der Freiätzung des Opferoxides abhängige Länge eines Federelementes.
7.1.2 Eigenfrequenz und Nachgiebigkeit von Membranen mit Korrugationen
Die Untersuchungen zur Wirkung von Korrugationen auf die Nachgiebigkeit wurden an
0.2 µm dicken Polysilizium-Membranen mit einer Implantationsdosis von 6⋅1014 cm-2
durchgeführt. Die gemessenen Eigenfrequenzen von kreisförmigen Membranen mit Nc=4, 6
und 8 umlaufenden Korrugationsrillen sind im Vergleich mit einer einfachen Kreismembran
ohne Korrugation in Abbildung 7.3 zusammengestellt.
112
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
100
90
Eigenfrequenz [kHz]
80
70
60
50
40
30
20
10
0
Kreismembran
(Nc=0)
N c =4
N c=6
N c =8
Abbildung 7.3: Gemessene Eigenfrequenz von einfachen und mit Nc Korrugationen
ausgestatteten Kreismembranen.
Aus der Eigenfrequenz von 98 kHz der Kreismembran ohne Korrugation berechnet man die
Schichtspannung der 0.2 µm dicken Polysiliziumschicht zu 37.5 MPa. Trotz vergleichbarer
Dotierstoffkonzentration ist die Schichtspannung bei einer Dicke von 0.2 µm deutlich
niedriger als bei einer Dicke von 0.4 µm mit 110 MPa. Aufgrund der komplizierten
Kristallisations- und Rekristallisationsvorgänge muss bei Veränderungen der Membrandicke
oder des thermischen Budgets des Gesamtprozesses die mechanische Spannung von neuem
optimiert werden.
Nach dem zuvor beschrieben Vorgehen erhält man aus den gemessenen Eigenfrequenzen die
Membran-Nachgiebigkeiten der Tabelle 7.2. Die theoretische Nachgiebigkeit wird mit Hilfe
der Gleichung 3.17 aus Abschnitt 3.4.4 berechnet. Da die intrinsische Schichtspannung aus
der Eigenfrequenz der Kreismembran bestimmt wird, ist ein Abgleich mit dem theoretischen
Wert dieser Membran nicht möglich.
Nachgiebigkeit
[nm/Pa]
Kreismembran
4-fach korrugierte
Kreismembran
Messung
Theorie
Abweichung
4.03 ±0.11
-
12.60 ±0.96
12.48
1%
6-fach korrugierte 8-fach korrugierte
Kreismembran
Kreismembran
15.59 ±0.37
17.21
9%
21.10 ±1.57
22.38
6%
Tabelle 7.2: Indirekt gemessene und theoretische Nachgiebigkeit von korrugierten
Kreismembranen.
Die hergeleitete Beziehung zur Schichtentspannung und Nachgiebigkeit von korrugierten
Membranen beschreibt sehr gut die gewonnenen Messergebnisse. Der direkte Vergleich mit
einer Kreismembran verdeutlicht den Vorteil einer Korrugationsmembran. Bei gleichem
Platzbedarf auf dem Siliziumwafer erreicht man eine mehr als fünffache Empfindlichkeit. Die
113
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
Reproduzierbarkeit auf einem Wafer ist etwas schlechter als bei Kreismembranen ohne
Korrugation. Die relative Schwankung liegt unabhängig von der Anzahl der Korrugationen
unterhalb von 10%.
7.1.3 Dotierstoff-abhängige Schichtspannung von Membranen
Die Membrandotierung ist ein wichtiger Technologieparameter, der zur Einstellung der
Schichtspannung im Membranmaterial verwendet wird. Die Abhängigkeit der Eigenfrequenz
von der Dosis einer Phosphor-Implantation (1015, 4⋅1015 und 6⋅1015 cm-2 Feder A, 8⋅1015 cm-2
Netz A) und die daraus mit Hilfe von FEM-Simulationen berechnete Schichtspannung zeigt
Abbildung 7.4. Die Polysilizium-Membranen mit einer Dicke von 0.4 µm wurden nach der
Implantation bei 900° C für 60 min rekristallisiert.
In Übereinstimmung mit Waferbow-Messungen an ganzflächig abgeschiedenen
Polysiliziumschichten auf Siliziumsubstrat (Abbildung 2.12) ist zur deutlichen
Spannungsreduzierung eine Dotierstoffdosis >1015 cm-2 bzw. eine Dotierstoffkonzentration
>1015 cm-2/0.4 µm=2.5⋅1019 cm-3 notwendig. Darüber nimmt die mechanische Spannung
annähernd linear mit der Implantationsdosis ab. Mit einer Dosis von 8⋅1015 cm-2 wird sogar
eine Schichtspannung unter 10 MPa realisiert. Die relative Schwankung der Spannung
zwischen Membranen eines Wafers nimmt geringfügig mit der Dosis von 5% bei 1015 cm-2
auf 11% bei 8⋅1015 cm-2 zu.
120
110
Eigenfrequenz [kHz]
100
Messung Eigenfrequenz
110
Spannung nach Messung
100
90
90
80
70
80
60
70
50
60
40
30
50
20
40
mechanische Spannung [MPa]
120
10
30
0
0
1
2
3
4
5
6
15
7
8
9
-2
Implantationsdosis [10 cm ]
Abbildung 7.4: Eigenfrequenz in Abhängigkeit der Dosis von implantierten Phosphor-Ionen
und abgeleitete Schichtspannung.
114
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
7.2
Statische Randverbiegung
Spannungsgradienten
bei
Feder-Membranen
aufgrund
von
Ein Nachteil von Feder-Designs liegt in der Anfälligkeit gegenüber vertikalen
Spannungsgradienten in der Membranschicht aus Polysilizium, die zu einem Verbiegen der
freien Membranränder und einem Aufwölben des mittleren Membranbereichs führen. Dieser
Effekt tritt besonders ausgeprägt bei mechanisch empfindlichen Membranen mit wenigen
Federstrukturen und geringer Schichtspannung auf. Die Abhängigkeit vom Membrandesign
und der Schichtspannung wurde an den Membranen vom Typ Feder A und Netz A untersucht.
In Abbildung 7.5 ist die mit einem Interferometer gemessene maximale Randverbiegung in
der Mitte eines Bogens zwischen zwei Federstrukturen gegen Implantationsdosen von 1015,
4⋅1015, 6⋅1015 und 8⋅1015 cm-2 aufgetragen. Nach den Ergebnissen des letzten Abschnittes
stehen die Implantationsdosen für mechanische Schichtspannungen von 110 MPa bis 8 MPa.
Die Membran Netz A verbiegt sich bei der niedrigsten Schichtspannung aufgrund der engen
Bögen maximal um -0.5 µm aus der Ebene. Dagegen kommt es bei dem Design Feder A mit
einer gemessenen Auslenkung von -1.4 µm bereits zum Kontakt zwischen den Bumps im
Randbereich und der Rückseitenplatte. Die Schichtspannung kann daher bei der Verwendung
von Feder-Membranen nicht beliebig reduziert werden, wenn nicht gleichzeitig der
Spannungsgradient kontrolliert wird.
Die Auslenkung in positiver Richtung bei der niedrigsten Implantationsdosis deutet darauf
hin, dass sich der Spannungsgradient in der Polysiliziumschicht aus einem intrinsischen,
positiven Beitrag und einen Dotierstoff-abhängigen, negativen Beitrag zusammensetzt.
maximale Randverbiegung [µm]
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
-1.2
Messung Netz A
-1.4
Messung Feder A
-1.6
0
1
2
3
4
5
6
7
8
9
Implantationsdosis [1015 cm-2]
Abbildung 7.5: Randverbiegung von Feder-Membranen bei Spannungsgradienten in
Abhängigkeit der Phosphor-Implantationsdosis.
115
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
7.3
Elektroakustische Empfindlichkeit von Silizium-Mikrofonen
Nachdem bisher auf das mechanische Verhalten der Membranen eingegangen wurde, wird in
diesem Abschnitt das Mikrofon als kapazitiver Wandler anhand seiner elektroakustischen
Empfindlichkeit untersucht. Besonderer Bedeutung kommt dabei der Verifizierung des
Systemmodells in Form des analog-elektrischen Netzwerks zu.
7.3.1 Empfindlichkeit
von
Mikrofonen
mit
Kreis-,
Netzund
Korrugationsmembran
In Abbildung 7.6 ist die Empfindlichkeit von Mikrofonen mit Kreis-, Netz- und
Korrugationsmembran bei einer Vorspannung von 1 V angeben. Die Messung erfolgte bei
einer Frequenz von 100 Hz. Die Spannungsverstärkung der Messschaltung beträgt etwa 0.6,
d.h. ca. 40% Empfindlichkeitsverlust entfällt auf den Impedanzwandler und parasitären
Kapazitäten. Die Dicke der Membranen ist 0.2 µm, der Membranradius 500 µm, die
intrinsische Schichtspannung ca. 35 MPa und der Spaltabstand ca. 2 µm.
Die Empfindlichkeit wird durch die FEM-unterstützte Netzwerkmodellierung in Anbetracht
der Vielzahl und zum Teil mit Schwankungen behafteten Parameter sehr gut beschrieben. Mit
den neuartigen Membranen können bei einer sehr niedrigen Vorspannung von 1 V
Empfindlichkeiten bis 8 mV/Pa erreicht werden. Auf den Frequenzgang wird in den
folgenden beiden Abschnitten eingegangen.
Empfindlichkeit [mV/Pa] _
10
9
Messung (1 V)
8
Simulation
8.2
7.9
7
6
5
4.0
4.3
4
2.8
3
2
2.5
1.2
1
0
Kreismembran
Netz A
4 Korrugationen
8 Korrugationen
Abbildung 7.6: Gemessene Empfindlichkeit von Silizium-Mikrofonen verschiedener
Membranen und Simulationsergebnisse.
116
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
7.3.2 Einfluss der Strömungsdämpfung auf das Tiefpass-Verhalten der
Empfindlichkeit
Der Durchmesser einer Perforation in der Rückseitenplatte ist ein kritischer Designparameter,
der bei empfindlichen Mikrofonen die obere Grenzfrequenz bestimmt. In Abschnitt 2.4.2
wurde ein Verfahren für die integrierte Herstellung von weiten Perforationsöffnungen
vorgestellt. Abbildung 7.7 zeigt dazu die Frequenzabhängigkeit der Empfindlichkeit bei
unterschiedlichem Radius und Abstand der Perforationsöffnung. Die untersuchten Mikrofone
besitzen bei einer Vorspannung von 1 V etwa dieselbe Empfindlichkeit von 6-8 mV/Pa, so
dass die Unterschiede im Frequenzgang auf den veränderten akustischen Widerstand der
Strömung im Kondensatorspalt und in den Perforationen zurückzuführen ist.
5
Empfindlichkeit [dB ref. 100 Hz]
3
rh=2.5 µm
dh=9.2 µm
0
2
-5
rh=2.1 µm
dh=9.2 µm
1
-10
rh=2.1 µm
dh=13.4 µm
-15
Messung
rh=0.85 µm
dh=4.3 µm
Simulation
-20
100
1000
10000
Frequenz [Hz]
Abbildung 7.7: Messung und Simulation der akustischen Dämpfung in Abhängigkeit vom
Radius rh und Abstand dh der Perforationsöffnungen in der Rückseitenplatte.
Die starke Dämpfung der Empfindlichkeit bei einem Perforationsradius von etwa 0.9 µm und
einem Abstand von 4.3 µm mit einer oberen Grenzfrequenz von 1 kHz stimmt mit den
Messungen aus Kapitel 6.5 überein. Die Messung zeigt nochmals, dass die mit der
konventionellen Technologie einer Trockenätzung und einer Abscheidung mögliche
Perforationsweite nicht ausreicht (typischerweise rh<1 µm). Dagegen ist mit der neuen
Perforationstechnologie, d.h. mit Perforationsradien rh>2 µm, eine Empfindlichkeit innerhalb
der Schwankungsbreite von ±3 dB bis 10 kHz erreichbar.
Die Übereinstimmung zwischen den Messungen und den Simulationen mit dem
Netzwerkmodell des Mikrofons ist sehr gut. Dies gilt sowohl für verschiedene
Perforationsabstände als auch für verschiedene Perforationsweiten. Der Vergleich zwischen
der Messung 1 und 2 demonstriert die Änderung der oberen Grenzfrequenz bei einer
Verringerung der Perforationsabstände von 13.4 µm auf 9.2 µm, die in etwa einer
Verdopplung der Anzahl der Perforationen von 4400 auf 9300 gleichkommt
(Perforationsflächendichte ρh=8% bzw. 16%). Der linearen Abhängigkeit des
Strömungswiderstandes von der Anzahl der Perforationen entsprechend, erhöht sich die obere
Grenzfrequenz von 2.1 kHz auf 4.4 kHz. Wie die Frequenzgänge 2 und 3 zeigen, geht der
117
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
Perforationsradius besonders stark in den Strömungswiderstand ein. Bereits die relativ
geringe Aufweitung der Öffnungen von einem Radius von 2.1 µm auf 2.5 µm führt bei
gleicher Perforationsanzahl zu einer oberen Grenzfrequenz über 10 kHz. In dieser
Konfiguration werden 23% der Gesamtfläche der Rückseitenplatte von den
Perforationsöffnungen eingenommen.
7.3.3 Einfluss des Gehäusevolumens auf das Hochpass-Verhalten der
Empfindlichkeit
Das vom Gehäuse eingeschlossene Luftvolumen wirkt wie ein Federelement, dessen
Federkonstante mit der Verringerung des Volumens ansteigt. Bei sehr kleinem Volumen kann
daher die Empfindlichkeit des Mikrofons durch das Gehäuse beeinträchtigt werden. Bei
Mikrofonen mit luftdurchlässigen Bereichen in der Membran und Rückseitenplatte, z.B. den
Druckausgleichslöchern oder den offenen Flächen einer Feder-Membran, kommt es zusätzlich
zu einen Hochpass-Verhalten, da es über diese Bereiche zu einen frequenzabhängigen
akustischen Kurzschluss kommt. Nach den theoretischen Überlegungen von Abschnitt 4.3.4
hängt die Grenzfrequenz vom Strömungswiderstand und dem Gehäusevolumen ab (vergleiche
auch Abbildung 4.7, Strömungswiderstand Rvent und Hohlraum-Nachgiebigkeit des Gehäuses
Cv).
Bei der vierfach korrugierten Membran mit 48 Federstrukturen (Abbildung 2.15) entfallen
etwa 500 Perforationsöffnungen auf den Ventilationspfad und tragen zum akustischen
Kurzschluss bei. Die Empfindlichkeit eines Mikrofons mit dieser Membran bei einem
Gehäusevolumen von 27 mm3 ist in Abbildung 7.8 dargestellt. Die Vergleichsmessung mit
geöffnetem Gehäusedeckel stellt bei dem On-Chip-Messaufbau den Fall eines unendlich
großen Volumens dar. Die Messungen wurden bei einer Vorspannung von 3 V durchgeführt.
100
Messung
Empfindlichkeit [mV/Pa]
Simulation
"unendliches" Gehäusevolumen
10
Gehäusevolumen 27 mm3
1
10
100
Frequenz [Hz]
1000
10000
Abbildung 7.8: Einfluss des Gehäusevolumens auf den Frequenzgang und die
Empfindlichkeit eines Mikrofons.
118
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
Das Hochpass-Verhalten des Mikrofons stammt bei der Messung mit „unendlichen“
Gehäusevolumen allein von der Filterwirkung der Niederfrequenzschaltung, d.h. von dem
Ladungsverlust durch den endlichen Ladewiderstand. Dem ist beim Mikrofon mit endlichem
Gehäusevolumen der oben besprochene akustische Hochpass überlagert, so dass sich die
untere Grenzfrequenz nach 70 Hz verschiebt. Im mittleren Frequenzbereich ist ein
Empfindlichkeitsverlust von 17 mV/Pa auf 15 mV/Pa aufgrund der Hohlraum-Nachgiebigkeit
des Gehäuses von ca. 200 nm/Pa zu beobachten. Beide Effekte, sowohl der akustische
Kurzschluss als auch die Empfindlichkeitsreduzierung, werden von dem Netzwerkmodell
richtig widergegeben. Die Abweichung zwischen der Messung und der Simulation bei hohen
Frequenzen wird vermutlich durch eine zu starke Rückseitenätzung verursacht, die eine
dünnere Rückseitenplatte bedingt.
7.4
Elektrisches und akustisches Rauschen
Das Rauschen der Mikrofone wurde mit dem in Abschnitt 5.4 beschriebenen On-Chip
Messplatz mit einem Impedanzwandler in Niederfrequenz-Schaltung gemessen
(Abschnitt 6.4). Abbildung 7.9 zeigt eine typische spektrale Rauschdichte eines Mikrofons bei
einer Vorspannung von 3 V. Zur Unterscheidung zwischen dem elektrischen Rauschen der
Beschaltung und dem akustischen Mikrofon-Eigenrauschen wurde die Rauschdichte
zusätzlich bei einer Vorspannung von 0 V gemessen, bei der das akustische Eigenrauschen
verschwindet.
Unterhalb einer Frequenz von 1 kHz überwiegt das thermische Rauschen des
Ladewiderstandes. Für Frequenzen von ca. 1 kHz bis 30 kHz ist in Einklang mit der
Simulation ein Beitrag vom Mikrofon-Eigenrauschen zu beobachten. Die A-bewertete
Rauschspannung beträgt bei 3 V ca. 7 µV(A). Mit dem elektrischen Grundrauschen von ca.
5 µV(A) bei 0 V berechnet sich ein Eigenrauschbeitrag von ebenfalls 5 µV(A).
-80
Messung
Simulation
0.5
Rauschdichte [dB(V/Hz )]
-90
-100
-110
-120
-130
3V
-140
-150
0V
-160
-170
-180
10
100
1000
10000
100000
Frequenz [kHz]
Abbildung 7.9: Rauschspannungsdichte eines Mikrofons in Niederfrequenz-Schaltung.
119
Messergebnisse zu Mikrofonen mit polykristalliner Siliziummembran und Gegenelektrode
Der Signal/Rauschabstand wird durch die Messung der zugehörigen Empfindlichkeit
bestimmt. In Abbildung 7.10 ist der äquivalente Rauschschallpegel bei verschiedenen
Vorspannungen gegen die Empfindlichkeit aufgetragen. Mit steigender Vorspannung
verbessert sich der äquivalente Rauschschallpegel aufgrund der höheren Empfindlichkeit und
nähert sich für sehr hohe Empfindlichkeiten dem Eigenrauschen der Mikrofone, das bei
24 dB(A) liegt.
äquivalenter Rauschschallpegel [dB(A)]
50
Messung
Simulation
45
40
1V
35
1.5 V
30
2V
3V
25
20
0
2
4
6
8
10
12
14
16
18
Empfindlichkeit [mV/Pa]
Abbildung 7.10:
Empfindlichkeit.
7.5
Abhängigkeit
des
äquivalenten
Rauschschallpegels
von
der
Zusammenfassung der Messergebnisse
Mit den neuartigen Membranen konnten bei kleinen lateralen Abmessungen hohe
Nachgiebigkeiten erzielt werden, die sich in den elektroakustischen Empfindlichkeiten der
Silizium-Mikrofone widerspiegeln. Die besten Ergebnisse lassen sich mit korrugierten
Membranen erzielen, die mit Hilfe von gezielter Dotierung mit Phosphor-Ionen und
anschließenden Temperaturschritten bezüglich ihrer Schichtspannung optimiert werden.
Feder-Membranen sind aufgrund ihrer Anfälligkeit gegenüber Spannungsgradienten und dem
Hochpass-Verhalten bei kleinen Gehäusegeometrien nur begrenzt einsetzbar. Designs mit
ausreichend vielen Federstrukturen können aber erfolgreich mit dem Konzept einer
korrugierten Membran kombiniert werden. Abhängig von der Empfindlichkeit überwiegt das
elektrische Grundrauschen der Beschaltung oder das elektroakustische MikrofonEigenrauschen. Das durch Finite-Elemente-Simulationen unterstützte Netzwerkmodell der
Silizium-Mikrofone wurde erfolgreich experimentell bestätigt.
120
Zusammenfassung und Ausblick
Kapitel 8
Zusammenfassung und Ausblick
Zusammenfassung
In dieser Arbeit wurden verschiedene Silizium-Mikrofone entworfen, in BiCMOSTechnologie hergestellt und bezüglich ihrer mechanischen und elektroakustischen
Eigenschaften theoretisch und experimentell untersucht.
Die einheitliche Simulation der kapazitiven Silizium-Mikrofone, bestehend aus Mikrofonchip,
Gehäuse und elektrischer Beschaltung, gelingt mit einem speziell entwickelten
Netzwerkmodell. Dieses beinhaltet erstmals die Nichtlinearität der Verformungsversteifung
und das mechanische Verhalten von Membranen mit Federstrukturen und Korrugationen, die
mit der Methode der Finiten-Elemente untersucht wurden. Damit steht der Entwicklung ein
universelles und schnelles Simulationswerkzeug zur Verfügung, das eine Optimierung der
Mikrofone ermöglicht.
Unter Berücksichtigung der elektrostatischen Anziehung im kapazitiven Mikrofon konnte
gezeigt werden, dass die Erhöhung der Empfindlichkeit über die Membran-Nachgiebigkeit
eine Anpassung der Kondensatorspalthöhe erfordert und durch ein verschlechtertes
Übertragungsverhalten beschränkt wird. Als Lösung dieser Problemstellung wurde ein Design
der Perforation in der Rückseitenplatte abgeleitet, das die obere Grenzfrequenz maximiert und
gleichzeitig den Eigengeräuschpegel minimiert. Das Rauschen des Mikrofons in
Niederfrequenzschaltung setzt sich nahezu vollständig aus dem thermischen
Widerstandsrauschen des Ladewiderstandes zusammen und wird mit einem hohen
Widerstandswert durch die Verschiebung der spektralen Rauschdichte reduziert.
Die monolithische Prozessierung auf einem Chip schafft die Voraussetzung für eine
kostengünstige Massenfertigung, stellt aber gleichzeitig hohe Anforderungen an die
Entwicklung. Zur Realisierung von Silizium-Mikrofonen mit guten elektroakustischen
Eigenschaften wurden verschiedene Herstellungskonzepte verfolgt.
Ein neu entwickelter Mikrofonprozess verwendet erstmals die monokristalline
Siliziumschicht eines SOI-Wafers als spannungsfreie Membran zusammen mit einer
epitaktisch gewachsenen Silizium-Gegenelektrode. Die Mikrofone dieser Technologie
erreichen bei einer niedrigen Vorspannung von 1 V und einer geringen Membranfläche von
1 mm2 Empfindlichkeiten zwischen 0.6 mV/Pa und 2.4 mV/Pa. Mit der verwendeten
Messschaltung wurde eine A-bewertete Rauschspannung von 5 µV bzw. ein äquivalenter
Rauschschallpegel von 40 dB(A) erreicht. Ein stark eingeschränkter Übertragungsbereich der
Mikrofone verdeutlicht, dass die konventionelle Herstellung von Perforationsöffnungen in der
Rückseitenplatte nicht zur Kondensatorspaltentdämpfung ausreicht. Die experimentellen
Untersuchungen zeigen ferner, dass die Hochtemperatur-Epitaxie thermische Spannungen
einprägt und eine Reduzierung der Empfindlichkeit zur Folge hat.
121
Zusammenfassung und Ausblick
Weitergehende Arbeiten zur Verbesserung der Empfindlichkeit und dem
Übertragungsverhalten wurden an Mikrofonen mit einer Membran aus polykristallinem
Silizium durchgeführt. Mit neuartigen Membranen konnte bei gleicher Membranfläche eine
Steigerung der mechanischen Nachgiebigkeit um den Faktor 5 erzielt werden. Dabei sind aus
rein mechanischen Gesichtspunkten grundsätzlich korrugierte Membranen gegenüber den
Feder-Membranen zu bevorzugen, da Spannungsgradienten im Polysilizium statische
Verbiegungen verursachen. Kombinierte Membrandesigns mit Korrugationen und mehreren
kurzen Federstrukturen führen die Vorteile beider Ansätze mit der Reduzierung der
mechanischen Spannung in der Membran und einer reduzierten Randkapazität der
Membraneinspannung zusammen.
Die Versuche zur mechanischen Schichtspannung von Polysilizium zeigen, dass mit der
gezielten Implantation von Phosphor-Ionen und einem anschließenden Temperaturprozess die
Spannung um den Faktor 10 reduziert werden kann.
Das Übertragungsverhalten der Silizium-Mikrofone wurde mit einer neu entwickelten
Technologie zur integrierten Herstellung von weiten Perforationsöffnungen in der statischen
Elektrode soweit verbessert, dass eine konstante Empfindlichkeit bis zu 10 kHz realisiert
werden konnte.
Das optimierte Membran- und Perforationsdesign spiegelt sich in den erreichten MikrofonEmpfindlichkeiten wider, die mit über 10 mV/Pa bei einer Versorgungsspannung von 3 V und
einem Nutzband von 20 Hz – 10 kHz zu den bisher besten veröffentlichten Ergebnissen
zählen. Mit dem vom thermischen Rauschen des Ladewiderstandes und dem akustischen
Rauschen der Strömungsdämpfung in den Perforationslöchern dominierten Gesamtrauschen
ergibt sich ein äquivalenter Rauschschallpegel von ca. 27 dB(A).
Anhand der experimentellen Ergebnisse konnte eine umfassende Verifizierung der
aufgestellten Modelle durchgeführt werden. Die Übereinstimmung zwischen den Messungen
und den Simulationen zu den Membran-Nachgiebigkeiten, den Empfindlichkeiten, dem
Rauschen, der perforationsabhängigen Strömungsdämpfung und dem akustischen Kurzschluss
ist in Anbetracht der technologisch bedingten Ungenauigkeiten in den Simulationsparametern
als sehr gut anzusehen.
Ausblick
Für Anwendungen mit Richtcharakteristik, wie sie mit der Firma „Peiker acustic“ für
Freisprecheinrichtungen im Automobil und mit „Siemens Audiologische Technik“ für
Hörgeräte im Rahmen des BMBF-Verbundprojektes „Integrierte mikromechanische SiliziumMikrofone für Array-Anwendungen“ (Förderkennzeichen 16SV1273) angestrebt werden, ist
eine Erweiterung der Modelle zur Simulation von unidirektionalen Mikrofonen notwendig.
Dazu erscheint die bereits erfolgreich angewandte Netzwerkmodellierung in Kombination mit
Finite-Elemente-Simulationen als erfolgsversprechend. Ein entsprechendes Makromodell
könnte sich aus dem Elementarmodell des Mikrofons, den parametrisierten Ergebnissen aus
numerischen Simulationen des Schallfeldes im Umfeld des Gehäuses und der elektrischen
Auswerteelektronik zusammensetzen.
Eine weitere Verbesserung des äquivalenten Rauschschallpegels auf 24 dB(A) könnte durch
die Reduzierung des Rauschens der Niederfrequenzschaltung mit der Integration von sehr
hochohmigen Ladewiderständen >10 GΩ auf dem Mikrofonchip gelingen. Die
122
Zusammenfassung und Ausblick
technologische Herausforderung besteht in der Herstellung von Polysiliziumbahnen mit
extrem kleinem Schichtwiderstand.
Ein Großteil der experimentellen Untersuchungen wurde an Mikrofonen auf Chip-Ebene
durchgeführt.
Thermische
und
mechanische
Einflüsse
der
Gehäuseund
Verbindungstechnologie können die Mikrofon-Eigenschaften beeinflussen und sollten auch
hinsichtlich ihrer Langzeitstabilität untersucht werden.
Die Reproduzierbarkeit stellt eine wichtige Voraussetzung für die Massenfertigung dar und
muss bei der Prozess- und Designentwicklung stärker als bisher miteinbezogen werden.
Insbesondere in Arrayanordnungen werden sehr hohe Anforderungen an die Amplituden- und
Phasentreue zwischen den Mikrofonen gestellt. Eine in dieser Arbeit bereits aufgegriffene
Fragestellung betrifft die Schwankung der Membran-Nachgiebigkeit und sollte auf das
Gesamtsystem ausgeweitet werden. Auf der Grundlage von Experimenten zu den einzelnen
Technologieschwankungen könnte mit dem vorgestellten Netzwerkmodell eine statistische
Fehleranalyse durchgeführt werden.
Abschließend kann festgestellt werden, dass die durchgeführten theoretischen und
technologischen Weiterentwicklungen eine wichtige Grundlage für den kommerziellen
Einsatz von mikromechanischen Silizium-Mikrofonen bilden. Mit den erreichten MikrofonEigenschaften bezüglich der Empfindlichkeit, dem Frequenzgang und dem Rauschen eignen
sich die vorgestellten Silizium-Mikrofone für Telekommunikationsanwendungen. Eine
Anwendung in Hörgeräten erscheint in naher Zukunft als nicht realistisch, da bei einer sehr
niedrigen Versorgungsspannung von ca. 1 V eine weitere Erhöhung der Empfindlichkeit
notwendig wäre.
123
Zusammenfassung und Ausblick
124
Literaturverzeichnis
Literaturverzeichnis
[And01] C. Andriot, Untersuchung und Optimierung des Einfluss von Schichtstress auf die
Eigenschaften von Polysilizium-Membranen, Diplomarbeit, Universität Stuttgart,
2001
[Ant93] P. Antognetti, Semiconductor Device Modeling with SPICE, 1993, McGraw-Hill,
NY
[Bath90] K. - J. Bathe, Finite-Elemente-Methoden, 1990, Springer Verlag Berlin
[Bay97] J. Bay, Silicon Microphone for Hearing Aid Applications, Dissertation,
Mikroelektronik Center, Lyngby, Dänemark, 1997
[Bea85] W.E. Beadle, J.C.C. Tsai, R.D. Plummer, Quick Reference Manual for Silicon
Integrated Circuit technology, 1985, Wiley
[Berg94] J. Bergqvist, F. Rudolf, A silicon condenser microphone using bond and etch-back
technology, Sensors and Actuators A, 45:115-124, 1994
[Berg94] J. Bergqvist, J. Gobet, Capacitive Microphone with a Surface Micromachined
Backplate Using Electroplating Technology, J. of Microelectromech. Systems, Vol.
3, No. 2,:69:75, 1994
[Bern96] J. J. Bernstein, J. T. Borenstein, A Micromachined Silicon Condenser Microphone
With On-Chip Amplifier, Hilton Head Tech. Dig., 1996, pp. 239-243
[Bev99] T. Bever, R. Aigner, C. Burrer, A. Dehé, D. Draxelmayr, M. Füldner, E. Pettenpaul,
S. Schmitt, H. J. Timme, BiCMOS Compatible Silicon Microphone Packaged as
Surface Mount Device, Sensor EXPO, Conference Paper, 1999
[Bib95]
M. Biebl, G. T. Mulhern, R. T. Howe, In Situ Phosphorus-doped Polysilicon For
Integrated MEMS, TRANSDUCERS '95. International Conference on Solid-State
Sensors and Actuators. Digest of Technical Papers, Stockholm, Sweden, 25-29
June 1995. p. 198-201
[Bour92] T. Bourouina, S. Spirkovitch, F. Baillieu, C. Vauge, A new condenser microphone
with a p+ silicon membrane, Sensors and Actuators A, 31:149-152, 1992
[Brau03] M. Brauer, Arbeiten im Rahmen der Dissertation an der Universität Bremen,
voraussichtlich 2003
[Bron91] I. N. Bronstein, K. A. Semendjajew, Taschenbuch der Mathematik, 1991, Teubner
Verlagsgesellschaft, Stuttgart
[Col91]
J. P. Colinge, Silicon-on-Insulator Technology: Materials to VLSI, Kluwer
Academic Publishers, 1991, Boston
125
Literaturverzeichnis
[Drey71] G. Dreyer, E. Münder, Festigkeitslehre und Elastizitätslehre, 1971, VEB Verlag
Leipzig
[Elb97]
L. Elbrecht, R. Catanescu, J. Zacheja, Highly phosphorus-doped polysilicon films
with low tensile stress for surface micromachining using POCl3 diffusion doping,
Sensors and Actuators A 61 (1997), pp. 374-378
[Elb98]
L. Elbrecht, Möglichkeiten und Grenzen der Silizium-Planartechnologie zur
Herstellung mikromechanischer Sensoren und deren Verkapselung, Dissertation,
Universität Bremen, Shaker Verlag, 1998, Aachen
[Fue01] M. Füldner, A. Dehé, R. Aigner, T. Bever, R. Lerch, Silicon Microphones with low
Stress Membranes, Proceedings of Transducers 2001, Volume 1, pp. 126-129, Juni
2001. München, 10.-14.06.01.
[Graf93] E. Graf, W. Kronast, S. Dühring, B. Müller, A. Stoffel, Silicon membrane condenser
microphone with integrated field-effect transistor, Sensors and Actuators A, 3738:708-711, 1993
[Hall01] N. A. Hall, F. L. Degertekin, Self-Calibrating Micomachined Microphones with
Integrated Optical Displacement Detection, Proc. Transducers‘01/ Eurosensors
XV, 1:118-121, München, 2001
[Heu89] A. Heuberger, Mikromechanik, Springer-Verlag, 1989, Berlin
[Hoh83] D. Hohm, G. M. Sessler, An Integrated Silicon-Electret-Condenser Microphone,
Proc. 11e ICA, Paris, 1983, pp. 29-32
[Hoh86] D. Hohm, Kapazitive Silizium-Sensoren für Hörschallanwendungen, Reihe 10,
Informatik/Kommunikationstechnik, Nr. 60, Fortschrittsberichte, VDI, VDI-Verlag,
Dissertation, 1986
[Hoh89] D. Hohm, G. Hess, A subminiature condenser microphone with silicon nitride
membrane and silicon back plate, J. Acoust. Soc. Am., 85(1), 1989, pp. 476-480
[Hsi99]
W. H. Hsieh, T. J. Yao, Y. C. Tai, A high performance mems thin-film teflon
electret microphone, Transducers 99
[Hsu98] P. C. Hsu, C. H. Mastrangelo, K. D. Wise, High sensitivity polysilicon diaphragm
condenser microphone, IEEE MEMS’98 Conference, 1998
[Hu91]
S. M. Hu, Stress Related Problems in Silicon Technology, J. Appl. Physics., 70,
1991, R53-R80
[Jog74]
A. Jogwich, Strömungslehre, 1974, Verlag W. Girardet, Essen
[Kap00] H. Kapels, Stabilität der elastischen Eigenschaften mikromechanischer
Schichtmaterialen der VLSI-Technologie, Dissertation, Universität Bremen, 2000
126
Literaturverzeichnis
[Kres02] R. Kressmann, M. Klaiber, G. Hess, Silicon condenser microphones with
corrugated silicon oxide/nitride electret membranes, Sensors and Actuators A,
100:301-309, 2002
[Kueh91] W. Kühnel, Silicon Condenser Microphone with Integrated Field-effect Transistor,
Sensors and Actuators A, 25-27:521-525, 1991
[Kueh92] W. Kühnel, G. Hess, Micromachined subminiature condenser microphone in
silicon, Sensors and Actuators A, 32:560-564, 1992
[Know01]www.knowlesinc.com, Technische Spezifikationen von Hörgeräten
[Kron01] W. Kronast, B. Müller, W. Siedel, A. Stoffel, Single-chip condenser microphone
using porous silicon as sacrifical layer for the air gap, Sensors and Actuators A,
87:188-193, 2001
[Lee98] S. S. Lee, R. M. White, Piezoelectric cantilever acoustic transducer, J. Micromech.
Microeng., 8:230-238, 1998
[Leh74] J. Lehmann, Feldeffekttransistoren kurz und bündig, 1974, Vogel, Weinsberg
[Ler93]
R. Lerch, Sensors, A Comprehensive Survey, Volume 7 Mechanical Sensors,
Chapter 16, Sensors for Measuring Sound, VCH, 1993
[Mai95] D. Maier-Schneider, J. Maibach, E. Obermeier, A New Analytical Solution for the
Load-Deflection of Square Membranes, Journal of Microelectromechanical
Systems, Vol. 4, No. 4, 1995, pp. 238-241
[Mee71] R. Meek, Electrochemically Thinned N/N+ Epitaxial Silicon-Method and
Applications, J. Electrochem. Soc.: Electrochemical Technology, Vol. 118, No. 7,
1971, pp. 1240-1246
[Mue90] R. Müller, Rauschen, 1990, Springer Verlag, Berlin
[Muel00] M. Müllenborn, P. Rombach, U. Klein, K. Rasmussen, J. F. Kuhmann, M. Heschel,
S. Bouwstra, M. Amskov, J. Janting, A. Hoogerwerf, Stacked Silicon Microphone,
Proc. Eurosensors XIV, pp. 209-212, Kopenhagen, 2000
[Mul93] G. T. Mulhern, D. S. Soane, R. T. Howe, Supercritical carbon dioxide drying of
microstructures",Proc. 7th Inth. Conf. Solid-State Sensors and Actuators
(Transducers `93), Yokohama, Japan, June 7-10 1993, pp. 296-299.
[Mur89] P. Murphy, K. Hübschi, N. Rooij, C. Racine, Subminiature silicon integrated
electret capacitor microphone, IEEE Trans. Electr. Insul., 24:495-498, 1989
[Ning95] Y. B. Ning, A. W. Mitchell, Fabrication of a silicon micromachined capacitive
microphone using a dry-etch process, Proc. Transducers‘95/Eurosensors IX, pp.
704-707, Stockholm, 1995
[Niu01] M. N. Niu, E. S. Kim, Bimorph piezoelectric acoustic transducer, Proc.
Transducers‘01/ Eurosensors XV, 1:110-113, München, 2001
127
Literaturverzeichnis
[Ols57]
H. F. Olson, Acoustical Engineering, 1957, D. Van Nostrand Company, New York
[Orp91] M. Orpana, A. O. Korhonen, Control of residual stress of polysilicon thin films by
heavy doping in surface micromachining, TRANSDUCERS '91. International
Conference on Solid-State Sensors and Actuators. Digest of Technical Papers (Cat.
No.91CH2817-5), San Francisco, CA, USA, 24-27 June 1991. p. 957-60
[Pan90] J. Y. Pan, P. Lin, F. Masehh,S. D. Senturia, Verification of FEM analysis of loaddeflection methods for measuring mechanical properties of thin films, Tech. Dig.
IEEE Solid-State Sensors and Actuators Workshop, Hilton Head, 1990, pp. 70-73
[Ped96] M. Pedersen, W. Olthuis, P. Bergveld, On the mechanical behaviour of thin
perforated plates and their application in silicon condenser microphones, Sensors
and Actuators A, 54: 499-504, 1996
[Plis94] P. Pliska, W. Lukosz, Integrated-optical acoustical sensors, Sensors and Actuators
A, 41-42:93-97, 1994
[Prim02] www.primomic.de, Technische Spezifikationen von Elektret-Mikrofone
[Rie93]
R. P. Ried, E. S. Kim, D. M. Hong, R. S. Muller, Piezoelectric Microphone with
On-Chip CMOS Circuits, J. Micromechan. Sys., 2:111-120, 1993
[Rom00] P. Rombach, ,Müllenborn, U. Klein, K. Rasmussen, The first low voltage, low noise
differential condenser silicon microphone, Proc. Eurosensors XIV, pp. 213-216,
Kopenhagen, 2000
[Ros88] M. Rossi, Acoustics and Electroacoustics, Artech House, 1988
[SAT01] Siemens Audiologische Technik, interne Diskussion, siehe auch www.siemenshearing.com
[Schaf98] D. Schafer, S. Shoaf, P. Loeppert, Micromachined condenser microphone for
hearing aid use, Solid-State Sensor and Actuator Workshop, Hilton Head Island,
June 8-11, pp. 27-30, 1998
[Schee92] P. R. Scheeper, W. Olthuis, P. Βergveld, A silicon condenser microphone with a
silicon nitride diaphragm and backplate, J. Micromech. Microeng., 2:187-189,
1992
[Schee94] P. R. Scheeper, W. Olthuis, P. Bergveld, The Design, Fabrication and Testing of
Corrugated Silicon Nitride Diaphragms, Journal of Microelectromechanical
Systems, Vol. 3, No.1, pp. 86-90, 1994
[Schee94] P. R. Scheeper, A. G. H. van der Donk, W. Olthuis, P. Bergveld, A review of
silicon microphones, Sensors and Actuators A, 44:1-11, 1994
[Schee94] P. R. Scheeper, W. Olthuis, P. Bergveld, Improvement of the performance of
microphones with a silicon nitride diaphragm and backplate, Sensors and
Actuators A, 40:179-186, 1994
128
Literaturverzeichnis
[Schei95] T. Scheiter, M. Biebl, C. Hierhold, H. Klose, Rapid Thermal Annealing of Doped
Silicon Films to Relax Intrinsic Stress, Sensors and Materials (1996) vol.8, no.7,
p.445-54
[Schel98] R. Schellin, Integrierte piezosensitive und kapazitive Ein-Chip-Silizium-Mikrofone,
Shaker Verlag, 1998, Dissertation
[Schn94] U. Schneider, R. Schellin, A phase-modulating microphone utilizing integrated
optics and micromachining in silicon, Sensors and Actuators A, 41-42:695-698,
1994
[Schu91] G. Schumicki, P. Seegebrecht, Prozeßtechnologie, Springer-Verlag, 1991, Berlin
[See99]
J. I. Seeger, B. E. Boser, Dynamics and Control of Parallel-Plate ctuators Beyond
The Electrostatic Instability, Transducers ’99, pp. 474-477, Sendai, June 1999
[Seif89] M. Seifert, Analoge Schaltungen, 1989, VEB Verlag Berlin
[Ses87]
G. M. Sessler, Electrets, Springer-Verlag, 1987, Berlin
[Ses91]
G. M. Sessler, Acoustic Sensors, Sensors and Actuators A, 25-27:323-330, 1991
[Ses96]
G. M. Sessler, Silicon Microphones, J. Audio Eng. Soc., Vol. 44, No 1/2, pp. 16-21,
1996
[Shep99]
M. Sheplak, J. M. Seiner, A MEMS Microphone for Aeroacoustics
Measurements, 37th AIAA Aerospace, Reno, NV, 1999
[Spre89] A. J. Sprenkels, R. A. Groothengel, A. J. Verloop, P. Bergveld, Development of an
electret microphone in silicon, Sensors and Actuators A, 17:509-512, 1989
[Stad92] M. Stadtmueller, Mechanical Stress of CVD-Dielectrics, J. Electrochem. Soc., Vol.
139, No. 12, 1992, pp. 3669-3674
[Thie99] C. Thielemann, G. Hess, A Micro-machined capacitive electret microphone, Proc.
of the Microfabrication of MEMS/MOEMS, pp. 748-756, Paris, 1999
[Timo59] S. Timoshenko, Theory of Plates and Shells, McGraw-Hill, New York, 1959
[Tor99]
A. Torkkeli, H. Sipola, H. Seppä, J. Saarilahti, O. Rusanen, J. Hietanen, Capacitive
microphone with low-stress polysilicon membrane and high-stress polysilicon
backplate, Proc. Eurosensors XIII, pp. 57-60, den Haag, 1999
[Wad78] Y. Wada, S. Nishimatsu, Grain Growth Mechanisms of Heavily PhosphorusImplanted Polycrystalline Silicon, J. Electrochem. Soc.: Solid-State Science and
Technology, 1978, pp. 1499-1504
[Wid96] D. Widmann, H. Mader, H. Friedrich, Technologie hochintegrierter Schaltungen,
Springer-Verlag, 1996, Berlin
129
Literaturverzeichnis
[Wyk98] WYKO Surface Profilers, Technical Reference Manual, 1998, Veeco Process
Metrology, Tucson
[Yas94] Y. Yasuno, Y. Riko, A Chronological Review of Production and Apllications of
Electret Condenser Microphone for Consumer Use, 7-9. Sept. 1994, 8th
International Symposium on Electrets, pp.943-948, Paris, France
[Zie99]
V. Ziebart, O. Paul and H. Baltes, Strongly buckled square micromachined
membranes, Sensors and Actuators A, 78:139-142, 1999
[Zoll93] M. Zollner, E. Zwicker, Elektroakustik, 1987, Springer Verlag Berlin
[Zou97] Q. Zou, Z. Li, L. Liu, Theoretical and experimental studies of single-chip-processed
miniature silicon condenser microphone with corrugated diaphragm, Sensors and
Actuators A, 63:209-215, 1997
130
Veröffentlichungen
Veröffentlichungen
1.
M. Füldner, A. Dehé, R. Aigner, T. Bever, R. Lerch und M. Kaltenbacher,
Empfindlichkeits- und Rauschanalyse eines kapazitiven Mikrofons in BICMOSTechnologie, 4. Chemnitzer Fachtagung Mikromechanik & Mikroelektronik, 1999
2.
T. Bever, R. Aigner, C. Burrer, A. Dehé, M. Füldner, E. Pettenpaul, S. Schmitt and
H.-J. Timme, BICMOS compatible Silicon microphone packaged as surface mount
device, Proceedings of the Senor Expo, Cleveland, Ohio, Sept. 14-16, 1999
3.
M. Füldner, A. Dehé, R. Aigner, T. Bever, H. R. Kretschmer and R. Lerch, Silicon
microphone with high sensitivity diaphragm using SOI substrate, Proceedings of
Eurosensors XIV, Copenhagen, Denmark, 27-30 August 2000
4.
M. Brauer, A. Dehé, T. Bever, S. Barzen, S. Schmitt, M. Füldner and R. Aigner,
Silicon microphone based on surface and bulk micromachining, Uppsala, Sweden,
MME 2000
5.
M. Brauer, A. Dehé, T. Bever, S. Barzen, S. Schmitt, M. Füldner and R. Aigner,
Silicon microphone based on surface and bulk micromachining, J. Micromech.
Microeng., Vol. 11, 2001
6.
M. Füldner, A. Dehé, R. Aigner, T. Bever and R. Lerch, Silicon Microphones with
low Stress Membranes, Proceedings of Transducers 2001, volume 1, Munich, June
2001
7.
M. Füldner, A. Dehé, R. Aigner, R. Lerch, FEM-unterstützte Netzwerksimulation
kapazitiver Silizium-Mikrofone, 29. Deutsche Fachtagung für Akustik DAGA’03,
Aachen, März 2003
8.
M. Füldner, A. Dehé, S. Barzen, M. Brauer und R. Aigner, Modellierung von
kapazitiven Silizium-Mikrofonen zur Optimierung von Design und Technologie,
Tagungsband: 9. GMM-Workshop Methoden und Werkzeuge zum Entwurf von
Mikrosystemen, Bielefeld, 31.03.-01.04.2003
9.
M. Brauer, S. Barzen, A. Dehé, M. Füldner, B. Lustig, R. Schledz und R. Laur,
Funktionalitätserweiterung
von
Silizium-Mikrofone
durch
hybride
Schaltungsintegration, Tagungsband: 9. GMM-Workshop Methoden und
Werkzeuge zum Entwurf von Mikrosystemen, Bielefeld, 31.03.-01.04.2003
10.
S. Barzen, A. Dehé, M. Brauer, M. Füldner und R. Aigner, Herstellung von
Silizium Mikrofonen, Tagungsband: 9. GMM-Workshop Methoden und Werkzeuge
zum Entwurf von Mikrosystemen, Bielefeld, 31.03.-01.04.2003
11.
M. Hofer, M. Kaltenbacher, R. Peipp, H. Landes, M. Füldner and R. Lerch, CAE
Environment for the Design of Capacitive Micromachined Sound and Ultrasound
Transducers, IEEE International Ultrasonics Symposium, Honolulu, Hawaii, Oct.
2003
131
Lebenslauf des Verfassers
Persönliche Daten
.
Name:
Marc Füldner
Anschrift:
Mainstr. 17, 85579 Neubiberg
Tel.: 089/69998331
E-mail: [email protected]
Geburtsdatum/-ort:
Nationalität:
Familienstand:
12. August 1972 in Kassel
deutsch
verheiratet, eine Tochter
Schulbildung
Aug. 79 - Juli 85
Aug. 85 - Juli 89
Aug. 89 - Mai 92
Grundschule, Orientierungsstufe
Werra-Realschule
Grotefend-Gymnasium
18. Mai 1992
Allgemeine Hochschulreife
Hann. Münden
Hann. Münden
Hann. Münden
Studium der Physik
Okt. 92 - März 95
14. Okt. 1994
April 95 - Feb. 99
Jan. 98 – Dez. 98
Georg-August-Universität
Diplomvorprüfung
Universität Hamburg
Siemens AG, ZT ME1
Diplomarbeit: CMOS-Technologie
5. Februar 1999
Diplomhauptprüfung
Göttingen
Hamburg
München
Promotion
April 99 – Feb. 04
132
Universität Erlangen-Nürnberg,
Infineon Technologies AG
Doktorvater: Prof. Dr.-Ing. R. Lerch
Erlangen
München