Brüche subtrahieren – Einführung (2)

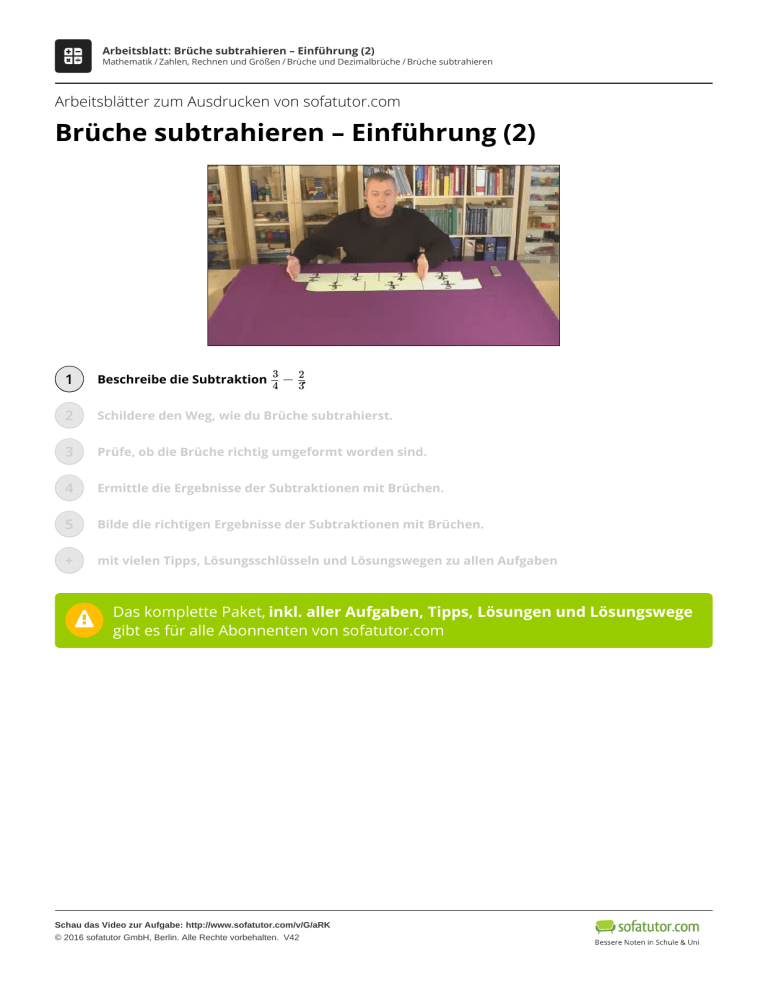
Arbeitsblatt: Brüche subtrahieren – Einführung (2)
Mathematik / Zahlen, Rechnen und Größen / Brüche und Dezimalbrüche / Brüche subtrahieren
Arbeitsblätter zum Ausdrucken von sofatutor.com
Brüche subtrahieren – Einführung (2)
3
4
− 23.
1
Beschreibe die Subtraktion
2
Schildere den Weg, wie du Brüche subtrahierst.
3
Prüfe, ob die Brüche richtig umgeformt worden sind.
4
Ermittle die Ergebnisse der Subtraktionen mit Brüchen.
5
Bilde die richtigen Ergebnisse der Subtraktionen mit Brüchen.
+
mit vielen Tipps, Lösungsschlüsseln und Lösungswegen zu allen Aufgaben
Das komplette Paket, inkl. aller Aufgaben, Tipps, Lösungen und Lösungswege
gibt es für alle Abonnenten von sofatutor.com
Schau das Video zur Aufgabe: http://www.sofatutor.com/v/G/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V42
Arbeitsblatt: Brüche subtrahieren – Einführung (2)
Mathematik / Zahlen, Rechnen und Größen / Brüche und Dezimalbrüche / Brüche subtrahieren
Beschreibe die Subtraktion 34
−
1
von 5
2
.
3
Wähle die richtigen Aussagen aus.
Auf diesem Bild sehen wir zwei unterschiedliche Papierstreifen.
Der eine ist in Viertel unterteilt und der andere in Drittel.
Sie sind so angeordnet, dass wir sehen wie viel übrig bleibt, wenn wir von drei
Viertel zwei Drittel abziehen.
A
Die grünen Striche unterteilen den Zeitstrahl in Drittel.
B
Die blaue Striche unterteilen den Zeitstrahl in Drittel.
C
Brüche müssen vor der Subtraktion auf einen gemeinsamen Nenner gebracht werden.
D
1
1
Der kleinste gemeinsame Nenner von und ist 24
3
4
E
Wir bringen die Brüche auf einen Hauptnenner, indem wir die einzelnen Brüche erweitern.
So erhalten wir
3
4
−
2
3
=
9
12
−
8
.
12
F
Um Zeit zu sparen, können wir auch einfach rechnen 3
4
−
2
3
=
1
.
4
Dabei werden einfach nur die Zähler subtrahiert, was das Ergebnis aber nicht verändert.
Schau das Video zur Aufgabe: http://www.sofatutor.com/v/G/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V42 | E23182
Arbeitsblatt: Brüche subtrahieren – Einführung (2)
Mathematik / Zahlen, Rechnen und Größen / Brüche und Dezimalbrüche / Brüche subtrahieren
Unsere Tipps für die Aufgaben
1
von 5
Beschreibe die Subtraktion 34
−
2
.
3
1. Tipp
Der Nenner eines Bruches gibt immer an, in wie viele Teile etwas unterteilt worden ist.
2. Tipp
Um den kleinsten gemeinsamen Nenner von zwei oder mehreren Brüchen zu bestimmen, kann man die
Nenner zusammen multiplizieren.
Nur bekommt man so nicht zwanghaft den kleinsten gemeinsamen Nenner.
3. Tipp
Wenn wir Brüche erweitern, verändert sich nicht nur der Nenner.
Auch der Zähler wird mit verändert.
Schau das Video zur Aufgabe: http://www.sofatutor.com/v/G/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V42
Arbeitsblatt: Brüche subtrahieren – Einführung (2)
Mathematik / Zahlen, Rechnen und Größen / Brüche und Dezimalbrüche / Brüche subtrahieren
Lösungen und Lösungswege für die Aufgaben
1
von 5
Beschreibe die Subtraktion 34
−
2
.
3
Lösungsschlüssel: B, C, E
Wir schauen uns zunächst noch mal die beiden Zahlensträhle an.
Der obere wurde mit den grünen Strichen in 4 Teile zerteilt. Er
wurde also in Viertel geteilt. Der untere Strahl wurde in Drittel geteilt.
Wir wollen nun zwei Brüche subtrahieren. In diesen Fall
3
4
− 23 .
Um dies zu tun, müssen die Brüche zunächst auf den kleinsten
gemeinsamen Nenner gebracht werden.
Dabei suchen wir das kleinste gemeinsame Vielfache der Nenner. Bei 1 und 2 ist dies die
4
Denn
3
12.
3 ⋅ 4 = 12 und ebenso 4 ⋅ 3 = 12.
Wir erweitern nun beide Brüche, sodass sie den selben Nenner haben. Dabei muss der Zähler ebenfalls
verändert werden, denn nur so bleibt das Verhältnis zwischen Zähler und Nenner gleich. Wir erweitern
zunächst
3
, indem wir Zähler und Nenner mit
4
Wir rechnen also
3
4
=
3⋅3
4⋅3
=
3 multiplizieren.
9
.
12
Nun erweitern wir 2 , indem wir Zähler und Nenner mit
3
4 multiplizieren. Wir bekommen so
Nun haben beide Brüche den selben Nenner und wir können rechnen
Wenn wir noch mal einen Blick auf das Bild werfen, dann ist
Schau das Video zur Aufgabe: http://www.sofatutor.com/v/G/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V42
3
4
− 23 =
9
12
2
3
− 128 =
=
2⋅4
3⋅4
=
8
.
12
1
.
12
1
der Teil des Papierstreifens, der übersteht.
12