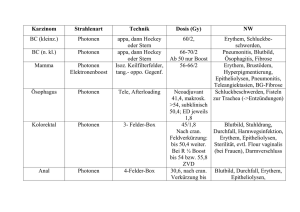
Präsentation als pps-Datei
Werbung

Slide 1
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 2
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 3
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 4
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 5
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 6
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 7
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 8
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 9
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 10
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 11
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 12
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 13
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 14
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 15
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 16
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 17
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 18
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 19
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 20
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 21
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 22
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 23
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 24
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 25
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 26
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 27
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 28
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 29
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 2
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 3
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 4
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 5
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 6
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 7
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 8
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 9
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 10
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 11
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 12
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 13
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 14
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 15
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 16
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 17
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 18
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 19
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 20
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 21
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 22
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 23
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 24
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 25
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 26
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 27
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 28
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35
Slide 29
Fachbereich Physik
Seminar Kernphysik – Sommersemester 2004
Experimente mit reellen Photonen
Johannes Gutenberg-Universität Mainz, 14. Juni 2004
Sebastian Will
Inhaltsübersicht
•
Kurze Einführung
•
Erinnerung an grundlegende Konzepte
•
Zwei Prozesse zur Herstellung hochenergetischer Photonen
•
Verwendung der energiemarkierten Photonen im Experiment:
Messung der Polarisierbarkeit des Protons (MAMI)
2
Einführung
•
reelle Photonen sind ganz „normale“ Photonen
•
Nukleonen haben innere Struktur
•
Photonen sind nützliche Sonden, um die innere Struktur von Kernen
zu untersuchen:
•
E h h
•
für E ~ 100 MeV ist Wellenlänge ~ 10 fm
•
Wechselwirkung mit Kernmaterie ist relativ schwach
c
Compton-Streuung von Photonen an Nukleonen
z.B. zur Bestimmung der elektrischen und magnetischen
Polarisierbarkeit des Protons
3
Zentrale experimentelle Herausforderung
•
Wie kann man hochenergetische Photonen herstellen?
Lösung: Bremsstrahlung oder LASER-Rückstreuung
•
Man benötigt Information über Energie der Photonen vor der Streuung!
Wie kann man die Energie der Photonen bestimmen,
ohne sie zu zerstören?
Lösung: Indirekte Bestimmung durch sog.
Photonenmarkierung (engl.: tagging)
4
Erinnerung an grundlegende Konzepte
•
•
Energie- und Impulserhaltung (ES und IS)
Wirkungsquerschnitt – wichtigste Größe bei Streuprozessen:
Geometrische Deutung:
Reaktionsrate:
N j n s
verdeckte Fläche!
j = Teilchenstrom der einf. Teilchen/Fläche
n = Anzahl der Targetteilchen
s = Fläche der Targetteilchen
Einheit: 1 barn= 1b = 10-24 cm2
s
Zahl der Reakt. eines gegebenen Typs pro Streuzentr um/s
Stromdichte der einfallenden Teilchen
5
Bremsstrahlung
•
freies Elektron kann kein
Photon emittieren (Verstoß
gegen ES und IS)
Aber:
•
Im Feld eines schweren Kerns
ist Emission eines Photons
möglich
Impulssatz:
Energiesatz:
p0 p k q
E0 E k T
vernachlässigbar klein: ~ keV
6
Energiespektrum der Bremsstrahlung
Energieverteilung folgt grob der Beziehung:
ds const . s
ˆ
dk k
k
k
sehr viele niederenergetische und sehr wenige hochenergetische Photonen!
7
Winkelverteilung der Bremsstrahlung (1)
Wichtigster Winkel:
mec 2
c
E0
charakteristischer Winkel
Bsp.:
c
0,5 MeV
855 MeV
~ 0,6 mrad
Für relativistische Elektronen und kleine Winkel gilt näherungsweise:
ds
2
d ( c2 )2
unabhängig von k !
Anteil der Photonen, die in einen Öffnungswinkel abgestrahlt werden:
( )
•
•
•
1
1 c
2
Näherung!
In Winkel c wird die Hälfte der Photonen abgestrahlt!
wachsendes E0: Öffnungswinkel wird kleiner!
In jedem Winkelbereich komplettes Energiespektrum zu sehen!
8
Winkelverteilung der Bremsstrahlung (2)
Näherung:
ds
2
d ( c2 )2
9
Tagging mit Bremsstrahlung – praktische Umsetzung
Magnet
•
Elektronen auf Radiator:
Bremsstrahlung
•
Ablenkung der Stoßelektronen
und Impuls-/Energieanalyse
Falls zeitliche Koinzidenz zwischen Experimentdetektor und Leitersignal:
k E0 E
Photonenenergie bekannt!
10
Compton-Effekt – Laser-Rückstreuung
•
•
•
Elastische Streuung von Photonen an Elektronen
Für ruhende Elektronen:
m0c 2
k ( )
m0c 2 k0 (1 cos )
Bei Laser-Rückstreuung: relativistische Elektronen!
Formel „einfach“ Lorentz-transformieren:
4 2 k 0
k ( )
1
4 k 0
me c
2
2 2
Streuwinkel der Photonen
1
1 v e c
2
11
Energie der Photonen
4 2 k 0
k ( )
1
4 k 0
me c
•
•
•
2
2 2
Streuwinkel der Photonen
1
1 v e c
Höchste Energie für 0
In feste Winkelbereiche wird eine definierte Energie abgestrahlt!
Maximalenergie der Photonen wesentlich kleiner als Elektronenenergie:
Bsp.: Eph= 2.4eV und Ebeam= 6.0 GeV
•
2
Photonenstrahl stark polarisiert:
k ~ 1000MeV
P Plaser
12
Winkel- & Energieverteilung bei Laser-Rückstreuung
Winkelverteilung
Energieverteilung
Energien der Compton-Photonen quasi gleichverteilt!
13
Tagging mit Compton-Photonen
•
resonante optischer Kavität: Steigerung des Photonenflusses!
14
Gegenüberstellung
Bremsstrahlung
+
•
•
konstruktiv leicht zu realisieren
•
hoher Photonenfluss
•
hoher Anteil
niederenergetischer Photonen
•
•
schwieriger Polarisation
Gleichverteilung der PhotonenEnergien
nur ~ 1GeV Elektronenstrahl
notwendig
-
Laser-Rückstreuung
•
•
•
•
hoch polarisierter Photonenstrahl
konstruktive Komplikationen
niedriger Photonenfluss
hohe Elektronenenergie
hervorzurufen
15
Anwendung: Messung der Polarisierbarkeiten des Protons
Fragen:
•
Was bedeutet „Polarisierbarkeiten des Protons“?
•
Was muss eigentlich gemessen werden?
•
Wie wird gemessen?
•
Wozu braucht man einen Tagger?
16
Polarisierbarkeit - klassisch
Dielektrisches Objekt in E-Feld
Ladungen ordnen sich
Für ein Atom in E-Feld gilt:
p Elok
Dipolmoment
Für ein Atom in B-Feld gilt:
Polarisation!
elektrische Polarisierbarkeit
m Blok
magnet. Moment
magnetische Suszeptibilität
17
Einfaches Modell der elektronischen Polarisierbarkeit
Elektronen mit Federn an Kern gebunden:
e Elok kx m02 x
Federkonstante k
resultierende „Polarisierbarkeit“:
e2
k
p
ex
e2
Elok Elok m02
k groß:
starres Objekt - kleine Polarisierbarkeit
k klein:
elastisches Objekt - große Polarisierbarkeit
18
Polarisierbarkeiten des Protons
•
Durch Streuprozesse stellte man fest:
Proton hat innere Struktur – positive und negative Ladungen!
•
Definition von elektrischer Polarisierbarkeit und magnetischer
Suszeptibilität bei Proton analog zu klassischer E‘dynamik!
Beispiele:
System
Polarisierbarkeit (fm3)
H-Atom
~ 1015
Deuteron
~ 1.5
Proton
~ 10-3
Neutron
~ 10-4 ?
Polarisierbarkeiten ( und ) sind fundamentale Struktureigenschaften!
19
Bestimmung der Polarisierbarkeiten: Compton-Streuung
•
•
Streuung von Photonen an Protonen
Messung des differentiellen Wirkungsquerschnitts der ComptonStreuung!
•
Die QFT liefert (Entwicklung für kleine Energien):
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
abhängig von:
•
•
•
Energien von
Ladung
ein- und aus-
Masse
laufendem
magn. Moment
Photon
Vorwärtsrichtung
Rückwärtsrichtung
20
TAPS-Tagger-Aufbau
Target: flüssiger Wasserstoff
•
Markierungseffizienz:
T
Anzahlder Photonen im Experiment target N
Anzahlder Elektronen im Tagger
Ne
21
Der TAPS-Detektor
Photonen aus Tagger
•
•
Nachweis der Photonen
Winkel-, Energie- und
Zeitmessung!
•
•
384 BaF2-Kristalle
Vor Kristall:
Veto-Detektor für geladene Teilchen
22
Bestimmung des Wirkungsquerschnitts
•
Anzahl der Compton-Photonen nach einer gewissen Messdauer:
NComp N
mit NT
•
ds
d
NT
N A H2 LTarget
AH2
Targetteilchen pro Fläche
für Markierungseffizienz gilt:
ds
d
T Ne N
NComp
T Ne NT
23
„Tricks“ zur Bestimmung des Wirkungsquerschnitts
ds
d
•
T Ne NT
größte Schwierigkeit: Bestimmung von
NComp
Koinzidenz-Analyse
•
•
NComp
Photon in TAPS und Elektron in Tagger gleichzeitig?
Missing-Energy-Analyse: Energiemessung ist überbestimmt!
•
Aus TAPS: Photonenenergie E , Streuwinkel des Photons
Compton-Theorie:
Eberechnet
•
Aus Tagger:
E
E
1
(1 cos )
MProton
Egemessen
!
Compton-Ereignisse, wenn
Emiss Egemessen Eberechnet 0
24
Zeitspektrum und Missing-Energy-Spektrum
Compton-Photonen!
•
starker Untergrund durch:
Pionenzerfall, Höhenstrahlung, Elektronenpaarproduktion
25
Ergebnisse der Messung - Wirkungsquerschnitte
ds
d
NComp
T Ne NT
e 2
ds
ds
2
2
1
cos
(
1
cos
)
2
2
d LET d Point M c 2
26
gemessen! rote Kurven!
Ergebnisse der Messung - Polarisierbarkeiten
12.1 0.3stat 0.4syst 104 fm3
1.6 0.4stat 0.4syst 104 fm3
e 2
ds
ds
2
1
cos
(1 cos )2
2
2
d LET d Point M c 2
gemessen!
27
Zusammenfassung
•
Herstellung von hochenergetischen Photonen
•
•
•
•
•
Bremsstrahlung
Laser-Rückstreuung
zerstörungsfreie Energiebestimmung der Photonen
Polarisierbarkeit des Protons
Experimentelle Umsetzung der Messung der Polarisierbarkeit des Protons
FRAGEN?
28
Formel für Wirkungsquerschnitt
µ
¶
µ ¶
µ ¶µ
¶½
¾
d¾
d¾
e2 ! 0
!!0
®+ ¯
®¡
¯
2
2
=
¡
(1
+
cos#)
+
(1
¡
cos#)
d LET
d P oi n t M !
~2 c2
2
2
35