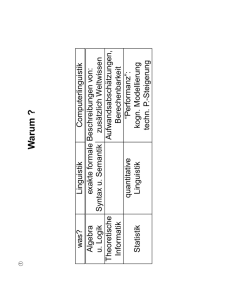
Modellierung - IMN/HTWK

Modellierung
Prof. Dr. Sibylle Schwarz
HTWK Leipzig, Fakultät IMN
Gustav-Freytag-Str. 42a, 04277 Leipzig
Zimmer Z 411 (Zuse-Bau)
http://www.imn.htwk-leipzig.de/~schwarz
[email protected]
Wintersemester 2016/17
1
Informatik
Informatik Lehre von der Darstellung und Verarbeitung von
Information durch Algorithmen
Teilgebiete der Informatik:
theoretisch
technisch
Sprachen zur Formulierung von Information und
Algorithmen,
I Möglichkeiten und Grenzen
der Berechenbarkeit durch Algorithmen,
I Grundlagen für technische und praktische
(und angewandte) Informatik
I
maschinelle Darstellung von Information
Mittel zur Ausführung von Algorithmen
(Rechnerarchitektur, Hardware-Entwurf, Netzwerk, . . . )
I
I
praktisch Entwurf und Implementierung von Algorithmen
(Betriebssysteme, Compilerbau, SE, . . . )
angewandt Anwendung von Algorithmen
(Text- und Bildverarbeitung, Datenbanken, KI, Medizin-,
Bio-, Wirtschafts-, Medieninformatik, . . . )
2
Syntax und Semantik
algorithmische Verarbeitung von Information erfordert
geeignete Darstellung der Information
I
Formalismus (Kalkül):
Maschinen-( und Menschen-)lesbare Sprache
I
eindeutige Zuordnung einer Bedeutung zu den Elementen des
Formalismus
Semantik (Bedeutung)
Was wird dargestellt?
Syntax (Darstellungsform)
Wie wird es dargestellt?
(meist viele verschiedene Möglichkeiten)
3
Beispiel Münzenspiel
Spielfeld:
(beidseitig unendliche) Folge von Stapeln von Münzen
...
...
1. Zu Beginn liegen 5 Münzen auf einem Stapel, alle anderen
Stapel sind leer.
2. In jedem Zug werden zwei Münzen von einem Stapel
(auf dem wenigstens zwei Münzen liegen) genommen und eine
davon auf den rechten, die andere auf den linken
Nachbarstapel gelegt.
3. Das Spiel ist zuende, wenn kein Zug mehr möglich ist.
4
Münzenspiel: Fragen
I
In welchen Spielzuständen sind keine Züge möglich?
I
Welche Zustände sind aus dem Startzustand erreichbar?
I
Wieviele Züge können (mindestens / höchstens) gespielt
werden, bis kein Zug mehr möglich ist?
Münzenspiel für zwei Personen:
4. Beide Spieler ziehen abwechselnd.
5. Wer am Zug ist, wenn kein Zug mehr möglich ist, verliert.
(Der andere gewinnt.)
I
Kann der Spieler, der den ersten Zug macht, gewinnen?
I
Wie kann der Spieler, der den zweiten Zug macht, gewinnen?
I
Wie kann der Spieler, der den ersten Zug macht, gewinnen?
I
Gewinnt immer der Spieler, der den ersten Zug macht?
I
(Wie) Hängt das von der Anzahl der Münzen zu Beginn ab?
5
Modellierung des Münzenspiels: Zustände
...
...
Zustand (Konfiguration): Momentaufnahme des Spielfeldes
vor oder nach einem (vollständigen) Spielzug
maschinenlesbare Modellierung eines Spielzustandes, z.B. durch
I
Folge von Stapeln von Münzen verschiedener Werte, z.B.
...
20
2
10
2
5
...
oder
...
2
10
2
5
20
I
Folge natürlicher Zahlen (Anzahlen der Münzen je Stapel),
z.B. [. . . , 0, 5, 0, . . .] oder [. . . , 0, 1, 3, 1, 0, . . .]
I
endliche Folge natürlicher Zahlen (nur relevanter Bereich),
z.B. [5] oder [1, 3, 1] oder [0, 5, 0] oder [0, 1, 3, 1, 0]
...
Abstraktion von Art und Anzahl der Objekte
ermöglicht einfache Übertragung auf ähnliche Aufgaben
6
Modellierung des Münzenspiels: Ablauf
Modellierung aller möglichen Übergänge zwischen Zuständen
z.B. als
I
formale Darstellung der Spielregeln
Startzustand : [. . . , 0, 5, 0 . . .]
Spielzug: Ersetzung einer Teilfolge des Zustandes der
Form [x, y + 2, z] durch [x + 1, y , z + 1]
Regel: [x, y + 2, z] → [x + 1, y , z + 1]
Spielende , wenn jedes Element der Folge < 2
(kein Zug mehr möglich)
I
formale (graphische) Darstellung aller möglichen Spielzüge
(Tafel)
Modellierung des Verlaufes eines Spieles z.B. als
I
Weg im Spielgraphen
I
(gültige) Folge von Positionen, an der die Regel angewendet
wurde
7
Modelle
Modelle sind Abstraktionen
realer Dinge, Eigenschaften, Beziehungen, Vorgänge
I Auswahl der (für den Anwendungsbereich, zur Problemlösung)
wichtigen Informationen
I Vernachlässigung unwichtiger Details
Beispiele:
I Liniennetzplan
wichtig: Stationen, Verbindungen zwischen Stationen,
Art der Verbindung (z.B. Liniennummer)
unwichtig: genaue Linienführung, aktuelle Verspätungen,
Baustellen,. . .
I Grundriss
I Stundenplan
I Ablaufplan
spezielle Form der Modelle abhängig von
I Problembereich
I geplante Verwendung
8
Prozess beim Lösen von Aufgaben (Problemen)
Analyse der (informalen) Aufgabe, Identifikation von
I Aufgabenbereich (Kontext)
I Eingabedaten (Typ, mögliche Werte)
I Frage, gewünschte Lösung
(Typ, Eigenschaften, Zusammenhang mit Eingabe)
Modellierung (Abstraktion, formale Darstellung) von
I Aufgabenbereich (Kontext)
I Anforderungen an Eingaben
I Anforderungen an Lösungen
Modellierung von Daten
und deren Eigenschaften und Beziehungen zueinander
Entwurf einer Lösungsstrategie für die modellierte Aufgabe
(mit vorhandenen oder neuen Methoden)
Modellierung von Abläufen und deren Eigenschaften
Realisierung der Lösungsstrategie im Modellbereich
Ausführung der Lösungsstrategie im Modellbereich
Übertragung der Lösung vom Modellbereich in die Realität
9
Logisches Schließen
Beispiel:
1. Tom besucht heute das Kino oder das Konzert.
Tom ist nicht im Kino.
Also besucht Tom das Konzert.
√
2. √2 ist eine rationale oder eine irrationale Zahl.
2 6∈ .√
Also ist 2 irrational.
Abstraktion: gemeinsames Schema
Q
Aus (P oder Q) und (nicht P) lässt sich Q schließen.
formal: {P ∨ Q, ¬P} |= Q
oder allgemeiner (Abstraktion von spezieller Person / Zahl) :
∀x (((P(x) ∨ Q(x)) ∧ ¬P(x)) → Q(x))
maschinelle Verarbeitung logischer Formeln möglich
z.B. durch SAT-Solver, Inferenzsysteme, Prolog-Interpreter
10
Vorteile der formalen Darstellung
Abstraktion von unwichtigen Details
(Entwicklung und Verwendung von Modellen)
Präzisierung der relevanten Aussagen
(eindeutige Semantik)
Systematisches Lösen (auch maschinell) von formal dargestellten
Problemen möglich
Struktureigenschaften formaler Beschreibungen
Schlussweisen unabhängig von Bedeutung der
Aussagen
11
Aus der Modulbeschreibung
Modul 1010 Modellierung
Arbeitsaufwand: Präsenzzeit 90 h (= 4 h V + 2 h Ü je Woche)
Vor- und Nachbereitungszeit 120 h (≈ 8 h je Woche)
Lernziele: Die Studierenden können mathematische und
logische Grundkonzepte zur Modellierung praktischer
Aufgabenstellungen anwenden.
Sie können Anforderungen an Software und Systeme
formal beschreiben und wissen, dass deren
Korrektheit mit formalen Methoden nachweisbar ist.
12
Inhalt der Lehrveranstaltung Modellierung
Einführung in formale Beschreibungsverfahren in der Informatik
Modellierung von
Aussagen durch aussagenlogische Formeln
Daten durch
I Mengen
I Wörter (Folgen) und Sprachen
I Terme
I Abstrakte Datentypen
Zusammenhängen (Beziehungen) durch
I Relationen
I Graphen
I Strukturen
Abläufen durch Zustandübergangssysteme
Eigenschaften, Anforderungen (für Daten und Systeme) durch
Formeln der Prädikatenlogik (der ersten Stufe)
(Ausblick in nichtklassische Logiken)
13
Lernziele (und Nebenwirkungen)
I
Fähigkeit zur Abstraktion
I
Verständnis der grundlegenden Modellierungs-Formalismen der
Informatik:
Logik, Mengen, Relationen, Graphen, Terme, Strukturen,
Datentypen
I
anwendungsbereite Kenntnisse zur Modellbildung
I
Zusammenhänge zu anderen Gebieten der Informatik und zur
Mathematik
14
Literatur
Folien zur Vorlesung, jeweils nach der Vorlesung veröffentlicht
www.imn.htwk-leipzig.de/~schwarz/lehre/ws16/modellierung
empfohlene Bücher:
I zur Modellierung:
I
I
Uwe Kastens, Hans Kleine Büning:
Modellierung - Grundlagen und formale Methoden,
Hanser 2008
zur Logik
I
I
I
Michael Huth, Mark Ryan: Logic in Computer Schience,
Cambridge University Press 2010
Uwe Schöning: Logik für Informatiker, Spektrum, 1995
Martin Kreuzer, Stefan Kühling: Logik für Informatiker,
Pearson Studium, 2006
15
Organisation der Lehrveranstaltung
Folien, Übungsserien, Termine, Änderungen, . . . unter
www.imn.htwk-leipzig.de/~schwarz/lehre/ws16/modellierung
Präsenzstudium
Lehrveranstaltungen für jeden Studenten:
(90 h ≈ 6 h / Woche)
Vorlesung jeden Mittwoch und Freitag
(4 h / Woche)
Übung (5 Gruppen) Montag/Dienstag
(2 h / Woche)
Wiederholer vor JG 15: mit AMB, (MIB1, MIB2)
I Besprechung der Übungsserien (Vorrechnen)
I Fragen zum aktuellen Vorlesungsinhalt
Selbststudium:
(120 h ≈ 8 h / Woche)
Übungsaufgaben
schriftliche Übungsserien wöchentlich
Autotool -Aufgaben etwa wöchentlich
Vor- und Nachbereitung der Vorlesungen
Literaturstudium ergänzend, Beitrag zur Lösung der Aufgaben
16
Selbstudium
Vor- und Nachbereitung jeder Lehrveranstaltung
(Vorlesung, Seminar, Praktikum, ...)
Unterlagen zu den Lehrveranstaltungen (Folien, eigene Notizen)
durcharbeiten
(enthalten auch zum Lösen der Übungsaufgaben
notwendige Definitionen, Herleitungen, Beispiele, . . . )
Übungsaufgaben regelmäßig und rechtzeitig lösen,
(Aufgaben vom Typ der) Übungsaufgaben gehören
zum Stoff der LV und werden geprüft
Bücher benutzen (Bibliothek, E-Books),
enthalten Erklärungen, zusätzliche Übungsaufgaben
(Internet-Quellen sind oft unzuverlässig)
Lerngruppen bilden und gemeinsam lernen und Aufgaben lösen
Nachfragen bei Dozenten (E-Mail, Sprechzeit, nach der
Lehrveranstaltung,. . . ), Mitstudenten, älteren
Studenten, Fachschaft, . . .
17
Schriftliche Übungsaufgaben (Übungsserien)
I
gestellt jeweils am Mittwoch
(Aufgaben zu den Vorlesungen am Mittwoch und Freitag)
I
Lösungen bis zum folgenden Dienstag ausschließlich online über
OPAL einzusenden (wie in der Einführungswoche erklärt)
genau eine Datei je Aufgabe mit Dateiname serieX-aufY-Z.pdf
für Lösung zu Aufgabe Y von Übungsserie X vom Studierenden mit
Familienname Z
I
Lösung in Gruppen aus ≤ 3 Studierenden zulässig (und empfohlen),
Namen aller Mitglieder der Gruppe oben auf der Lösung vermerken,
jedes Gruppenmitglied sendet die (gemeinsame) Lösung zu Opal
Dateiname serieX-aufY-Z1-Z2-Z3.pdf
I
Bewertung bis zum folgenden Sonntag
(0: falsch, 1: überwiegend richtig, 2: korrekt)
I
Besprechung in der darauffolgenden Übung
Vorträge (Vorrechnen) zu den Aufgabenlösungen
Übungsserien auch unter
www.imn.htwk-leipzig.de/~schwarz/lehre/ws16/modellierung
Nicht im Opal-Kurs eingesendete Lösungen werden nicht gewertet.
18
Seminar (Übungen)
Lernziele bei der Bearbeitung der Übungsaufgaben:
I
Nachbereitung der letzten Vorlesung anhand
der Vorlesungsfolien und Literatur (z.B. der angegebenen)
I
Vorbereitung der nächsten Vorlesung
I
Vorbereitung der Seminarvorträge zu jeder Aufgabe
Seminar (Übungen):
I
Besprechung der Lösungen der schriftlichen Übungsaufgaben,
Vorrechnen zur Prüfungszulassung
I
Fragen zum aktuellen Vorlesungsstoff und zu den neuen
schriftlichen und praktischen Übungsaufgaben
I
in jede Übung mitbringen: (alles auf Papier)
alle bisherigen Vorlesungsfolien und eigene Notizen dazu,
Übungsblätter und eigene Lösungen (der ganzen Gruppe)
19
Prüfung
Zulassungsvoraussetzungen (Prüfungsvorleistungen):
I
regelmäßige erfolgreiche Lösung der Übungsaufgaben, d.h.:
I
I
I
Lösung wenigstens 70% aller gestellten schriftlichen
Übungsaufgaben mit wenigstens 1 Punkt,
mindestens drei Vorträge in den Übungen
(richtiges Vorrechnen“ der Lösungen)
”
50% aller Punkte für praktische Pflichtaufgaben (Autotool)
Prüfung: Klausur 120 min
Aufgabentypen aus den Übungsserien
einziges zugelassenes Hilfsmittel:
ein beidseiting handbeschriebenes A4-Blatt
20
Aussagen
Aussage = Behauptung
Beispiele:
I
Es regnet.
I
Die Straße ist naß.
I
I
9 ist eine Primzahl.
√
2∈
I
3<5
I
x < 5 (hängt von x ab, keine Aussage)
I
Ist x < 5? (keine Aussage)
I
Sei x < 5. (keine Aussage)
I
Morgen regnet es.
I
Es ist nicht alles Gold, was glänzt.
Q
21
Wahrheitswerte
Prinzipien der klassischen Logik:
Zweiwertigkeit Jede Aussage ist wahr oder falsch.
ausgeschlossener Widerspruch
Keine Aussage ist sowohl wahr als auch falsch.
Wahrheitswerte 1 (wahr) oder 0 (falsch)
Jede Aussage p hat genau einen Wahrheitswert W(p) ∈ {0, 1}.
Beispiele:
I
W(Es regnet.) = ?
I
W(Die Straße ist naß.) = ?
I
I
W(9 ist eine Primzahl.) = 0
√
W( 2 ∈ ) = 0
I
W(3 < 5) = 1
I
W(Morgen regnet es.) = ?
I
W(Es ist nicht alles Gold, was glänzt.)=1
Q
22
Zusammengesetzte Aussagen – Junktoren
Junktor (mit zugeordneter Stelligkeit):
Symbol (Syntax) für Verknüpfung von Aussagen
z.B. und“ (zweistellig), nicht“ (einstellig)
”
”
Gottlob Frege (1848–1925):
Die Bedeutung des Ganzen ist eine Funktion der
Bedeutung seiner Teile.
Wahrheitswert einer zusammengesetzten Aussage lässt sich aus
den Wahrheitswerten ihrer Teilaussagen berechnen.
Semantik (Bedeutung) eines n-stelligen Junktors ∗:
[∗] : {0, 1}n −→ {0, 1}
(n-stellige Funktion auf der Menge {0, 1})
Wahrheitswertkonstanten (nullstellige Junktoren):
t mit [t] = 1
f mit [f] = 0
23
Konjunktion ∧
Es regnet und 9 ist eine Primzahl.
I W(9 ist eine Primzahl.)= 0
I W(Es regnet.)=?
I W(Es regnet und 9 ist eine Primzahl.)=0
p ∧ q ist genau dann wahr,
wenn beide Aussagen p und q wahr sind.
W(p) W(q) W(p ∧ q)
0
0
0
0
1
0
1
0
0
1
1
1
W(p ∧ q) = min(W(p), W(q))
[∧] = min ist kommutativ, assoziativ
n
^
pi = p1 ∧ p2 ∧ · · · ∧ pn
i=1
24
Disjunktion ∨ (inklusiv)
Es regnet oder 3 < 5.
I W(3 < 5) = 1
I W(Es regnet)=?
I W(Es regnet oder 3 < 5.)=1
p ∨ q ist genau dann wahr,
wenn wenigstens eine der Aussagen p und q wahr ist.
W(p) W(q) W(p ∨ q)
0
0
0
0
1
1
1
0
1
1
1
1
W(p ∨ q) = max(W(p), W(q))
[∨] = max ist kommutativ, assoziativ
n
_
pi = p1 ∨ p2 ∨ · · · ∨ pn
i=1
25
Negation ¬
√
¬( 2 ∈
I
I
Q)
√
Q
(meist
√
2 6∈
Q)
W( 2 ∈ ) = 0
√
W(¬( 2 ∈ )) = 1
Q
¬p ist genau dann wahr, wenn p falsch ist.
W(p) W(¬p)
0
1
1
0
W(¬p) = 1 − W(p)
26
Implikation →
Wenn es regnet, dann ist die Straße naß.
I
W(Es regnet.)=?
I
W(Die Straße ist naß.)=?
I
W(Wenn es regnet, dann ist die Straße naß.)=1
p → q ist genau dann wahr,
wenn die Aussage p falsch oder die Aussage q wahr ist.
W(p) W(q) W(p → q)
0
0
1
0
1
1
1
0
0
1
1
1
W(p → q) =
1 falls W(p) ≤ W(q)
0 sonst
27
Äquivalenz ↔
3 < 5 gilt genau dann, wenn 0 < 5 − 3 gilt.
I
W(3 < 5) = 1
I
W(0 < 5 − 3) = 1
I
W(3 < 5 gilt genau dann, wenn 0 < 5 − 3 gilt.)=1
p ↔ q ist genau dann wahr, wenn
entweder beide Aussagen p und q gelten
oder beide nicht gelten.
W(p) W(q) W(p ↔ q)
0
0
1
0
1
0
1
0
0
1
1
1
W(p ↔ q) =
1 falls W(p) = W(q)
0 sonst
28
Was bisher geschah
(Klassische) Aussagenlogik:
I
Aussage = Behauptung
I
klassische Logik: Wahrheitswerte 0 (falsch) und 1 (wahr)
Jede Aussage hat genau einen Wahrheitswert.
I
Verbindung von Aussagen durch Junktoren
I
Wahrheitswert eines zusammengesetzten Ausdruckes lässt sich
aus den Wahrheitswerten seiner Teilausdrücke berechnen.
Syntax
Semantik
Stelligkeit Symbol Wahrheitswertfunktion
wahr
falsch
Konjunktion
Disjunktion
Negation
Implikation
Äquivalenz
0
0
2
2
1
2
2
t
f
∧
∨
¬
→
↔
1
0
min
max
x 7→ 1 − x
≤
=
Modellierungsbeispiel Party
umgangssprachliche Beschreibung der Situation (Kontext):
Anna geht zur Party, wenn Max oder Paul hingehen.
Max geht zur Party, wenn Paul nicht hingeht.
Anna geht nirgends ohne ihren Hund hin.
(1)
(2)
(3)
formale Beschreibung der Situation:
I elementare Aussagen (Atom):
a Anna geht zur Party.
m Max geht zur Party.
p Paul geht zur Party.
h Annas Hund geht zur Party.
P = {a, h, m, p} (Menge von Aussagenvariablen)
I zusammengesetzte Aussage (aussagenlogische Formel):
(((m ∨ p) → a) ∧ (¬p → m)) ∧ ¬(a ∧ ¬h)
| {z }
|
{z
}
| {z }
(1)
(2)
(3)
29
Aussagenlogische Formeln (Syntax)
Junktoren z.B. t, f (nullstellig), ¬ (einstellig),
∧, ∨, →, ↔ (zweistellig)
Aussagenvariablen (Atome), z.B. p, q, r , s, . . . oder p1 , p2 , . . .
Definition (induktiv)
Die Menge AL(P) aller aussagenlogischen Formeln mit
Aussagenvariablen aus der Menge P ist definiert durch:
IA: Alle Aussagenvariablen p ∈ P sind Formeln. (P ⊆ AL(P)).
I t und f sind Formeln.
IS:
I
I
Ist ϕ eine Formel, dann ist auch ¬ϕ eine Formel.
Sind ϕ und ψ Formeln, dann sind auch
ϕ ∨ ψ, ϕ ∧ ψ, ϕ → ψ und ϕ ↔ ψ Formeln.
IS’: (Verallgemeinerung aller Unterpunkte zu IS)
Sind j ein n-stelliger Junktor und ϕ1 , . . . , ϕn Formeln,
dann ist auch j(ϕ1 , . . . , ϕn ) eine Formel.
(Aus {ϕ1 , . . . , ϕn } ⊆ AL(P) folgt j(ϕ1 , . . . , ϕn ) ∈ AL(P).)
30
Aussagenlogische Formeln (Beispiele)
Junktoren der klassischen Aussagenlogik: {t, f, ¬, ∨, ∧, →, ↔}
kürzere Notation:
ohne äußere Klammern und Klammern um ¬ϕ
Beispiele:
t ∧ (¬t)
Formel ohne Aussagenvariablen
(∈ AL(∅))
¬¬¬p
Formel mit Aussagenvariable p
(∈ AL({p}))
∧(p ∨ q)
¬(p → q)
→q
keine Formel (syntaktisch unkorrekt)
Formel mit Aussagenvariablen p, q
keine Formel (syntaktisch unkorrekt)
(6∈ AL(P))
(∈ AL({p, q}))
(6∈ AL(P))
Baumstruktur (analog arithmetischen Termen)
Beispiel (Tafel):
ϕ = ((p ∧ ¬q) → (¬r ∨ (p ↔ q)))
∈ AL({p, q, r })
31
Menge aller Aussagenvariablen einer Formel
Definition (induktiv):
Für jede aussagenlogische Formel ϕ ∈ AL(P) ist die Menge var(ϕ)
aller in ϕ vorkommenden Aussagenvariablen definiert durch:
IA: falls ϕ = p (Atom), dann var(ϕ) = {p}
I nullstellige Junktoren (t, f):
IS:
I
I
für ϕ = t oder ϕ = f gilt var(ϕ) = ∅
einstellige Junktoren (¬):
für ϕ = ¬ϕ1 gilt var(ϕ) = var(ϕ1 )
zweistellige Junktoren (∗ ∈ {∨, ∧, →, ↔}):
für ϕ = ϕ1 ∗ ϕ2 gilt var(ϕ) = var(ϕ1 ) ∪ var(ϕ2 )
Beispiel (Tafel):
Für ϕ = p → ((q ↔ t) ∨ (r → q)) gilt var(ϕ) = {p, q, r }
32
Anzahl der Variablenvorkommen in einer Formel
Definition (induktiv):
Für jede aussagenlogische Formel ϕ ∈ AL(P) ist die ANzahl von
Varablenvorkommen varcount(ϕ) definiert durch:
IA: falls ϕ = p (Atom), dann varcount(ϕ) = 1
I nullstellige Junktoren (t, f):
IS:
I
I
varcount(t) = varcount(f) = 0
einstellige Junktoren (¬):
varcount(¬ϕ) = varcount(ϕ)
zweistellige Junktoren (∗ ∈ {∨, ∧, →, ↔}):
varcount(ϕ ∗ ψ) = varcount(ϕ) + varcount(ψ)
Beispiel (Tafel):
ϕ = p → ((q ↔ t) ∨ (r → q)) gilt varcount(ϕ) = 4
varcount(ϕ) ist die Anzahl aller mit Variablen markierten Blätter
im Formelbaum von ϕ
Allgemein gilt varcount(ϕ) ≥ |var(ϕ)|
33
Menge aller Teilformeln einer Formel
Definition (induktiv):
Für jede aussagenlogische Formel ϕ ∈ AL(P) ist die Menge TF(ϕ)
aller in ϕ vorkommenden Teilformeln definiert durch:
IA: falls ϕ = p (Atom), dann TF(ϕ) = {p}
I nullstellige Junktoren (t, f):
IS:
I
I
für ϕ = t oder ϕ = f gilt TF(ϕ) = {ϕ}
einstellige Junktoren (¬):
für ϕ = ¬ϕ1 gilt TF(ϕ) = {ϕ} ∪ TF(ϕ1 )
zweistellige Junktoren (∗ ∈ {∨, ∧, →, ↔}):
für ϕ = ϕ1 ∗ ϕ2 gilt ∗ ∈ {∨, ∧, →, ↔}
TF(ϕ) = {ϕ} ∪ TF(ϕ1 ) ∪ TF(ϕ2 )
34
Prinzip der strukturellen Induktion
Beobachtung:
Bestimmung von Variablenmenge, Größe, Menge der Teilformeln
einer aussagenlogischen Formel geschah nach demselben Schema:
Definition einer Funktion f : AL(P) → X durch
Induktion über die Struktur der Formel
Für jede aussagenlogische Formel ϕ ∈ AL(P) ist der Funktionswert
f (ϕ) definiert durch:
IA: Definition des Funktionswertes f (ϕ) für Atome ϕ = p
(Blätter im Formelbaum)
IS: Definition des Funktionswertes f (ϕ) für zusammengesetzte
Formeln ϕ durch die Funktionswerte der Teilformeln von ϕ
35
Aussagenlogische Interpretationen (Semantik)
(Belegungen der Aussagenvariablen mit Wahrheitswerten)
Interpretation (Belegung) für Formeln ϕ ∈ AL(P)
ordnet jeder Aussagenvariable einen Wahrheitswert zu
Funktion W : P −→ {0, 1}
(eine Zeile in der WW-Tabelle für ϕ)
Beispiel: P = {p, q} und W mit W (p) = 1 und W (q) = 0
36
Wahrheitswerte für Formeln
Erweiterung der Belegung W : P −→ {0, 1} zu einer Funktion
W : AL(P) −→ {0, 1}
Der Wert W (ϕ) der Formel ϕ in der Interpretation W wird induktiv mit
den Wahrheitswertfunktionen der Junktoren
aus den Werten der Teilformeln von ϕ bestimmt:
IA: falls ϕ = p (Atom), dann W (ϕ) = W (p)
IS:
I
I
I
nullstellige Junktoren t, f: W (t) = 1 , W (f) = 0
einstelliger Junktor ¬:
für ϕ = ¬ψ gilt W (¬ψ) = [¬]W (ψ) = 1 − W (ψ)
zweistellige Junktoren ∗ ∈ {∨, ∧, →, ↔}:
W (ψ1 ∧ ψ2 ) =
W (ψ1 ∨ ψ2 ) =
W (ψ1 → ψ2 ) =
W (ψ1 ↔ ψ2 ) =
W (ψ1 )[∧]W (ψ2 ) = min (W (ψ1 ), W (ψ2 ))
W (ψ1 )[∨]W (ψ2 ) = max (W (ψ1 ), W (ψ2 ))
W (ψ1 )[→]W (ψ2 ) = 1 gdw. W (ψ1 ) ≤ W (ψ2 )
W (ψ1 )[↔]W (ψ2 ) = 1 gdw. W (ψ1 ) = W (ψ2 )
Beispiel (Tafel): ϕ = ((p ∧ ¬q) → (¬r ∨ (p ↔ q)))
W (p) = 0, W (q) = 1, W (r ) = 0, W (ϕ) = . . .
37
Wahrheitswerttabellen
Darstellung der Werte einer Formel ϕ ∈ AL(P) in
allen möglichen Interpretationen W ∈ (P) in einer Tabelle
W
Jede Zeile repräsentiert eine Interpretationen W : var(ϕ) :→ {0, 1}
W (p1 ) W (p2 ) · · ·
0
0
···
0
0
···
..
.
1
1
···
W (pn−1 ) W (pn ) W (ϕ)
0
0
0
1
1
1
Beispiel (Tafel): ((p ∧ ¬q) → (¬r ∨ (p ↔ q)))
Wahrheitswerttabellen von Formeln mit n Aussagenvariablen sind
Wertetabellen n-stelliger Boolescher Funktionen
fϕ : {0, 1}n −→ {0, 1}.
Die Semantik jeder aussagenlogischen Formel mit n
Aussagenvariablen ist eine n-stellige Boolesche Funktion.
38
Erfüllbarkeit und Allgemeingültigkeit
Eine Formel ϕ ∈ AL(P) heißt
erfüllbar , wenn (wenigstens) eine Belegung W : P → {0, 1}
mit W (ϕ) = 1 existiert.
Beispiel: ¬p → p
unerfüllbar (Widerspruch), wenn keine Belegung W : P → {0, 1}
mit W (ϕ) = 1 existiert.
(wenn also für jede Belegung W gilt W (ϕ) = 0),
Beispiel: p ∧ ¬p
allgemeingültig (Tautologie), wenn für jede Belegung
W : P → {0, 1} gilt W (ϕ) = 1
(wenn also keine Belegung W mit W (ϕ) = 0
existiert).
Beispiel: p ∨ ¬p
Fakt
Eine Formel ϕ ∈ AL(P) ist genau dann allgemeingültig, wenn die
Formel ¬ϕ unerfüllbar ist.
39
Semantische Äquivalenz aussagenlogischer Formeln
Definition
Zwei Formeln ϕ, ψ ∈ AL(P) heißen
genau dann (semantisch) äquivalent (ϕ ≡ ψ), wenn
für jede Belegung W : P → {0, 1} gilt W (ϕ) = W (ψ).
Äquivalente Formeln haben dieselbe Semantik (Wahrheitswertfunktion).
Nachweis der Äquivalenz von Formeln z.B. durch Wahrheitswerttabellen
Beispiele:
p→q
≡
¬p ∨ q
p∨q
≡
¬p → q
p∧q
≡
¬(p → ¬q)
p↔q
≡ (p → q) ∧ (q → p)
Achtung: Das Symbol ≡ ist kein Junktor (Syntax), sondern ein
Symbol für eine Beziehung zwischen Formeln (Semantik).
40
Wichtige Äquivalenzen
Für alle aussagenlogischen Formeln ϕ, ψ, η gilt:
I
ϕ ∨ ϕ ≡ ϕ,
ϕ ∧ ϕ ≡ ϕ,
ϕ ∨ f ≡ ϕ,
ϕ∧t≡ϕ
I
ϕ ∨ ψ ≡ ψ ∨ ϕ, ϕ ∧ ψ ≡ ψ ∧ ϕ
(Kommutativität von ∧ und ∨)
I
ϕ ∨ (ψ ∨ η) ≡ (ϕ ∨ ψ) ∨ η
ϕ ∧ (ψ ∧ η) ≡ (ϕ ∧ ψ) ∧ η
(Assoziativität von ∧ und ∨)
I
ϕ ∧ (ψ ∨ η) ≡ (ϕ ∧ ψ) ∨ (ϕ ∧ η)
ϕ ∨ (ψ ∧ η) ≡ (ϕ ∨ ψ) ∧ (ϕ ∨ η)
(Distributivgesetze)
I
¬¬ϕ ≡ ϕ (Doppelnegation)
I
¬(ϕ ∨ ψ) ≡ ¬ϕ ∧ ¬ψ, ¬(ϕ ∧ ψ) ≡ ¬ϕ ∨ ¬ψ
(DeMorgansche Regeln)
I
ϕ ∨ ψ ≡ ¬(¬ϕ ∧ ¬ψ), ϕ ∧ ψ ≡ ¬(¬ϕ ∨ ¬ψ)
(Dualität von ∧ und ∨)
I
ϕ → ψ ≡ ¬ψ → ¬ϕ (Kontraposition)
I
(ϕ ∧ ψ) ∨ (¬ϕ ∧ ψ) ≡ ψ (Fallunterscheidung)
41
Was bisher geschah: klassische Aussagenlogik
Syntax Symbole und Struktur
I
I
Junktoren: t, f , ¬ , ∨, ∧, →, ↔
aussagenlogische Formeln AL(P)
induktive Definition:
IA Atome (Aussagenvariablen) p, q, r , . . . ∈ P
IS zusammengesetzte Formeln (ϕ, ψ, η, . . .):
Verknüpfung von Formeln durch Junktoren
Prinzip der strukturellen Induktion über Baumstruktur von Formeln
Semantik (Bedeutung der Syntaxelemente)
eines Junktors: Wahrheitswertfunktion
einer Aussagenvariablen: Wahrheitswert
aller Aussagenvariablen einer Menge P:
durch Belegung (Interpretation) W : P → {0, 1}
I einer Formel aus AL(P): Funktion
W : AL(P) → {0, 1} Boolesche Funktion
I Erfüllbarkeit, Allgemeingültigkeit von Formeln
I Äquivalenz von Formeln, z.B. p → q ≡ ¬p ∨ q
I
I
I
Modelle aussagenlogischer Formeln
Die Aussagenvariablen-Belegung W : P → {0, 1}
erfüllt die Formel ϕ ∈ AL(P) (ist ein Modell für ϕ)
genau dann, wenn W (ϕ) = 1.
Beispiel: Modelle (erfüllende Belegungen) für
p ∨ (q ∧ ¬p) ∈ AL({p, q}):
W10 mit W10 (p) = 1 und W10 (q) = 0,
W01 mit W01 (p) = 0 und W01 (q) = 1,
W11 mit W11 (p) = 1 und W11 (q) = 1
42
Modellmengen aussagenlogischer Formeln
Menge aller Modelle von ϕ ∈ AL(P):
Mod(ϕ) = {W : P → {0, 1} | W (ϕ) = 1}
(kürzere Darstellung als WW-Tabellen)
Beispiele:
Mod(p ∨ (q ∧ ¬p)) = {W10 , W01 , W11 },
Mod(p → p) = {W0 , W1 } = {W : {p} → {0, 1}},
Mod(p ∧ ¬p) = ∅
Formel ϕ ∈ AL(P) ist
unerfüllbar gdw. Mod(ϕ) = ∅
erfüllbar gdw. Mod(ϕ) 6= ∅
allgemeingültig gdw. Mod(ϕ) = {W : P → {0, 1}}
äquivalent zu ψ ∈ AL(P) gdw. Mod(ϕ) = Mod(ψ)
43
Wiederholung: wichtige Äquivalenzen
Für alle aussagenlogischen Formeln ϕ, ψ, η gilt:
I
ϕ ∨ ϕ ≡ ϕ,
ϕ ∧ ϕ ≡ ϕ,
ϕ ∨ f ≡ ϕ,
ϕ∧t≡ϕ
I
ϕ ∨ ψ ≡ ψ ∨ ϕ, ϕ ∧ ψ ≡ ψ ∧ ϕ
(Kommutativität von ∧ und ∨)
I
ϕ ∨ (ψ ∨ η) ≡ (ϕ ∨ ψ) ∨ η
ϕ ∧ (ψ ∧ η) ≡ (ϕ ∧ ψ) ∧ η
(Assoziativität von ∧ und ∨)
I
ϕ ∧ (ψ ∨ η) ≡ (ϕ ∧ ψ) ∨ (ϕ ∧ η)
ϕ ∨ (ψ ∧ η) ≡ (ϕ ∨ ψ) ∧ (ϕ ∨ η)
(Distributivgesetze)
I
¬¬ϕ ≡ ϕ (Doppelnegation)
I
¬(ϕ ∨ ψ) ≡ ¬ϕ ∧ ¬ψ, ¬(ϕ ∧ ψ) ≡ ¬ϕ ∨ ¬ψ
(DeMorgansche Regeln)
I
ϕ ∨ ψ ≡ ¬(¬ϕ ∧ ¬ψ), ϕ ∧ ψ ≡ ¬(¬ϕ ∨ ¬ψ)
(Dualität von ∧ und ∨)
I
ϕ → ψ ≡ ¬ψ → ¬ϕ (Kontraposition)
I
(ϕ ∧ ψ) ∨ (¬ϕ ∧ ψ) ≡ ψ (Fallunterscheidung)
44
Umformen von Formeln
Satz (Ersetzbarkeitstheorem)
Für drei Formeln ϕ, ψ, η ∈ AL(P), wobei ψ ≡ η und ψ eine
Teilformel von ϕ ist, gilt ϕ ≡ ϕ0 ,
wobei ϕ0 entsteht, indem in ϕ ein Vorkommen von ψ durch η
ersetzt wird.
(Nachweis durch strukturelle Induktion)
Formeln können also durch Ersetzung äquivalenter Teilformeln in
semantisch äquivalente Formeln umgeformt werden.
(Änderung der Syntax bei unveränderter Semantik)
45
Junktorbasen (vollständige Operatorensysteme)
Eine Menge J von Junktoren heißt genau dann Junktorbasis
(vollständiges Operatorensystem), wenn zu jeder aussagenlogische
Formel ϕ eine äquivalente aussagenlogische Formel ψ (d.h. ϕ ≡ ψ)
existiert, wobei ψ nur Junktoren aus der Menge J enthält.
Beispiele: Die Mengen
I
{¬, ∨, ∧}
I
{¬, ∨}
I
{¬, ∧}
I
{¬, →}
(ÜA)
I
{f, →}
(ÜA)
sind Junktorbasen.
Die Mengen {∨, ∧} und {∨, ∧, →} sind keine Junktorbasen.
46
Normalformen
spezielle Formeln:
Literal Atom oder negiertes Atom
NNF Formeln, in denen das Negationssymbol ¬ höchstens
auf Atome angewendet wird, heißen in
Negations-Normalform.
Beispiel: ¬p ∨ ((¬q ∨ p) ∧ q), ¬p, p
W
V
mi
CNF Formeln der Form ni=1
l
j=1 i,j
mit Literalen li,j
heißen in konjunktiver Normalform.
Beispiel: (¬p ∨ ¬q) ∧ (p ∨ q) ∧ ¬q, p ∨ q, p ∧ ¬q, ¬p
V
W
mi
DNF Formeln der Form ni=1
j=1 li,j
mit Literalen li,j
heißen in disjunktiver Normalform.
Beispiel: ¬p ∨ (¬q ∧ p) ∨ (p ∧ q), p ∨ q, p ∧ ¬q, ¬p
47
Satz über Normalformen
Satz
Zu jeder Formel ϕ ∈ AL(P) existieren
I
eine äquivalente Formel ϕ1 ∈ AL(P) in NNF,
I
eine äquivalente Formel ϕ2 ∈ AL(P) in CNF und
I
eine äquivalente Formel ϕ3 ∈ AL(P) in DNF.
Beweis (konstruktiv) durch Angabe einer Transformationsvorschrift
beliebiger Formeln in Normalformen:
1. Formeln mit Junktoren →, ↔, t, f schrittweise durch Formeln
mit ausschließlich ∨, ∧, ¬ ersetzen
2. Konstruktion einer NNF durch (mehrmalige) Anwendung der
deMorganschen Regeln
3. Konstruktion der CNF und DNF durch (mehrmalige)
Anwendung der Distributivgesetze auf die NNF
Beispiele (Tafel): p ↔ q , (a → b) → c
48
Was bisher geschah
Modellierung von Aussagen in (klassischer) Aussagenlogik
Syntax:
I Atome sind Aussagenvariablen
I Junktoren ¬, ∨, ∧, →, ↔
I induktive Definition: Baumstruktur der Formeln
I strukturelle Induktion
I äquivalente Unformungen
I Junktorbasen
I Normalformen: NNF, CNF, DNF
Semantik:
I Belegungen der Aussagenvariablen
I Wahrheitswerte von Formeln unter Belegungen
I WW-Tabelle einer Formel
I Modellmenge einer Formel
I erfüllbare, allgemeingültige Formeln
I semantische Äquivalenz von Formeln
Formelmengen
Formelmenge Φ ⊆ AL(P)
(Menge von Bedingungen)
Beispiele:
I
{p, p → q} ⊆ AL(P)
I
{p, p → q, ¬q} ⊆ AL(P)
I
{p → q} ⊆ AL(P)
I
∅ ⊆ AL(P)
49
Semantik von Formelmengen
Eine Belegung W : P → {0, 1} erfüllt eine Menge Φ ⊆ AL(P) von
Formeln genau dann, wenn W jede Formel ϕ ∈ Φ erfüllt.
Bestimmung der Modelle (erfüllenden Belegungen) z.B. durch
Wahrheitswerttabellen
Beispiele:
I
einziges Modell für {p, p → q}: W11 = [p 7→ 1, q 7→ 1],
I
{p, p → q, ¬q} hat kein Modell,
I
Modelle für {p → q}: W00 , W01 , W11
I
Jede Belegung ist ein Modell für die Formelmenge ∅.
50
Modellmengen von Formelmengen
Menge aller Modelle einer Menge Φ ⊆ AL(P) von Formeln:
\
Mod(Φ) =
Mod(ψ)
ψ∈Φ
(Eine Interpretation W : P −→ {0, 1} ist ein Modell für eine Menge
Φ ⊆ AL(P) von Formeln, wenn W Modell für jede Formel ϕ ∈ Φ ist.)
Beispiele:
I
Mod({p, p → q}) = {W11 },
I
Mod({p, p → q, ¬q}) = ∅,
I
Mod({p → q}) = {W00 , W01 , W11 }
I
Mod(∅) = {W : P → {0, 1}} (Menge aller Belegungen)
Fakt
Eine Belegung W : P → {0, 1} erfüllt eine endliche Formelmenge
Φ = {ϕ1 , . . . , ϕn } genau dann, wenn sie die Formel ϕ1 ∧ · · · ∧ ϕn erfüllt.

dasselbe kurz:
Mod(Φ) = Mod 

^
ψ
ψ∈Φ
51
Modellierung durch aussagenlogische Formelmengen
Aussagen:
1. Es wird nicht mehr viel Eis gekauft, wenn es kalt ist.
2. Der Eisverkäufer ist traurig, wenn nicht viel Eis gekauft wird.
3. Es ist kalt.
Darstellung als Formelmenge Φ ⊆ AL({k, t, v }):
Φ = {k → ¬v , ¬v → t, k}
Mod(Φ) ={W110 }
neue zusätzliche Aussage:
4. Der Eisverkäufer ist nicht traurig.
Erweiterung der Formelmenge Φ zu
Φ0 = Φ ∩ {¬t} = {k → ¬v , ¬v → t, k, ¬t}
Mod(Φ0 ) = ∅
(Formelmenge Φ unerfüllbar)
52
Modellierungsbeispiel Zuordnungen
In einem Eisenbahnabteil sitzen die Herren Lehmann und Müller. Einer ist
Sachse und einer Thüringer.
Jeder der beiden Personen kommt aus genau einem Land, also
1. Jede Person kommt aus wenigstens einem Land.
LS ∨ LT , MS ∨ MT
2. Aus jedem Land kommt wenigstens eine Person.
LS ∨ MS, LT ∨ MT
3. Jede Person kommt aus höchstens einem Land.
LS → ¬LT , LT → ¬LS, MS → ¬MT , MT → ¬MS
oder (äquivalent) ¬LS ∨ ¬LT , ¬MS ∨ ¬MT
4. Aus jedem Land kommt höchstens eine Person. (ÜA)
Zuordnungen kommen (mit viel mehr beteiligten Individuen) in vielen
praktischen Anwendungen vor, z.B. Ressourcen-Planung
I
Stundenplan
I
Aufgabenverteilung
I
Job-Scheduling (Betriebssystem)
53
DNF-SAT
Aufgabe DNF-SAT:
W Vki
gegeben: DNF ϕ = m
i=1 j=1 li,j
Frage: Ist ϕ erfüllbar?
Instanz, z.B. (p ∧ ¬q ∧ ¬p) ∨ (q ∧ p ∧ ¬q) ∨ (¬p ∧ ¬q)
Lösungsidee:
I ϕ ist genau dann erfüllbar, wenn (wenigstens) eine der m
Vi
Konjunktionen kj=1
li,j erfüllbar ist.
Vk i
I Konjunktion
j=1 li,j ist genau dann unerfüllbar, wenn für
eine Aussagenvariable x ∈ var(ϕ) gilt:
{x, ¬x} ⊆ {li,j | j ∈ {1, . . . , ki }} (Widerspruch).
W Vk i
Lösungsverfahren: ϕ = m
i=1 j=1 li,j ist genau dann
Vi
li,j
erfüllbar , wenn eine der m Konjunktionen kj=1
widerspruchsfrei ist,
unerfüllbar , wenn alle m Konjunktionen einen Widerspruch
enthalten.
DNF-SAT ist einfach (schnell) zu lösen.
54
CNF-SAT
Aufgabe CNF-SAT:
V Wki
gegeben: CNF ϕ = m
i=1 j=1 li,j
Frage: Ist ϕ erfüllbar?
Instanz z.B. (p ∨ ¬q) ∧ (q ∨ p) ∧ (¬p ∨ ¬q)
Lösungsansätze:
I
Test aller möglichen Belegungen, aufwendig
für große Anzahl an Aussagenvariablen unpraktikabel
I
Umformung in eine zu ϕ äquivalente DNF ψ
Test von ψ auf Erfüllbarkeit
für große Anzahl an Aussagenvariablen unpraktikabel
Konstruktion einer Formel ψ mit
I
1. ψ erfüllbar gdw. ϕ erfüllbar und
2. Erfüllbarkeit für ψ einfach zu testen
CNF-SAT ist schwierig zu lösen. (zeitaufwendig)
55
SAT-Solver
SAT-Solver: Werkzeug zum Lösen von CNF-SAT-Instanzen
SAT-Solver
I
benutzen heuristische Verfahren,
I
finden für praktische Probleme oft schnell eine Lösung,
I
meist Ausgabe einer erfüllenden Belegung (wenn eine existiert)
aktive Forschung auf diesem Gebiet:
jährlich Wettbewerbe (www.satcompetition.org/)
typische Anwendung von SAT-Solvern:
1. Modellierung des ursprünglichen Problems P als
CNF-SAT-Instanz P 0 (Darstellung als CNF ϕ)
2. Lösung von P 0 mit SAT-Solver
3. Übersetzung erfüllender Belegung für ϕ in Lösung für P
56
Beispiel Bahnfahrer (Übungsaufgabe 1.3)
In einem Eisenbahnabteil sitzen
...

LB → MT



(¬MB) → RT
Φ=
LS ∨ LT ∨ LB



LS → ¬LT
die Herren Lehmann, Müller und Richter

,
LT → MS
,



,
RS → LT
,
, MS ∨ MT ∨ MB , . . . 


,
LS → ¬LB
, ...
Darstellung als CNF
ϕ=
∧
∧
∧
(¬LB ∨ MT )
(MB ∨ RT )
(LS ∨ LT ∨ LB)
(¬LS ∨ ¬LT )
∧
∧
∧
∧
(¬LT ∨ MS)
(¬RS ∨ LT )
(MS ∨ MT ∨ MB) ∧
(¬LS ∨ ¬LB)
∧
···
···
Was für ein Landsmann ist jeder?
gesucht ist also ein Modell (erfüllende Belegung) für ϕ
(repräsentiert Zuordnung: {L, M, R} → {S, T , B})
57
Lösung mit SAT-Solver
Eingabe im DIMACS-Format für CNF (ASCII):
erste Zeile enthält Typ (cnf), Anzahl der Aussagenvariablen und
Disjunktionen (z.B. p cnf 9 25)
I Aussagenvariablen {1, . . . , n}
I jede Disjunktion (Klausel) eine Zeile,
- statt ¬, Literale durch Leerzeichen getrennt,
0 markiert Ende der Klausel
I
Darstellung der Bahnfahrer-Aufgabe als CNF in DIMACS-Format
p cnf 9 25
c 1:LS, 2:LT, 3:LB, 4:MS, 5:MT, 6:MB, 7:RS, 8:RT, 9:RB
-3 5 0
-2 4 0
...
Lösung mit SAT-Solver, z.B. MiniSat, Lingeling
SATISFIABLE
1 -2 -3 -4 -5 6 -7 8 -9 0
Ausgabe: erfüllende Belegung {1 7→ 1, 6 7→ 1, 8 7→ 1} (sonst 0)
wahr sind also 1 : LS, 6 : MB und 8 : RT
58
Modellierungsbeispiel: n-Damen-Aufgabe
Frage: Lassen sich n Damen so auf einem n × n-Schachbrett
anordnen, dass keine Dame eine andere bedroht?
Lösung: zulässige Anordnung, falls möglich
Bedingungen für zulässige Anordnungen:
I
n Damen auf dem Feld, also in jeder Zeile (wenigstens) eine
I
keine Zeilenbedrohung
I
keine Spaltenbedrohung
I
keine diagonale Bedrohung
59
Repräsentation der 3-Damen-Aufgabe
9 Felder – Aussagenvariablen {x1 , . . . , x9 }
Bedingungen:
I
I
I
I
in jeder Zeile (wenigstens) eine Dame
x1 ∨ x2 ∨ x3 ,
x4 ∨ x5 ∨ x6 ,
x7 ∨ x8 ∨ x9
keine Zeilenbedrohung
x1 → ¬x2 (≡ ¬x1 ∨ ¬x2 ),
x4 → ¬x5 ,
x7 → ¬x8 ,
x1 → ¬x3 ,
x4 → ¬x6 ,
x7 → ¬x9 ,
x2 → ¬x3
x5 → ¬x6
x8 → ¬x9
keine Spaltenbedrohung
x1 → ¬x4 ,
x2 → ¬x5 ,
x3 → ¬x6 ,
x1 → ¬x7 ,
x2 → ¬x8 ,
x3 → ¬x9 ,
x4 → ¬x7
x5 → ¬x8
x6 → ¬x9
x1 → ¬x9 ,
x5
x4
x5
x6
keine diagonale Bedrohung
x1 → ¬x5 ,
x2 → ¬x6 ,
x3 → ¬x5 ,
x2 → ¬x4 ,
x3 → ¬x7 ,
→ ¬x9
→ ¬x8
→ ¬x7
→ ¬x8
Man vergleiche mit den Kontext-Bedingungen aus ÜA 1.3
60
4 Damen
16 Felder – Aussagenvariablen {x1 , . . . , x16 }
eine mögliche Lösung (Modell, erfüllende Belegung):
¬1 ∧ ¬2 ∧ 3 ∧ ¬4 ∧ 5 ∧ ¬6 ∧ ¬7 ∧ ¬8 ∧ ¬9 ∧ ¬10 ∧ ¬11 ∧ 12 ∧
¬13 ∧ 14 ∧ ¬15 ∧ ¬16
×
×
×
×
61
Einsatz von SAT-Solvern
typische Anwendungen für SAT-Solver z.B.
I
Schaltkreisentwurf und -verifikation
I
Konfiguration
I
Model-Checking
I
Planen
I
Constraint-Lösen
I
kombinatorische Suchprobleme, z.B.
Graph-Färbungen (Register-Zuordnung, Sudoku)
62
Was bisher geschah
Klassische Aussagenlogik zur Modellierung von Aussagen
Syntax: induktive Definition der Menge AL(P)
IA: Alle Aussagevariablen (Atome) aus P sind Formeln
IS: Aus Formeln lassen sich durch die Junktoren
¬, ∨, ∧, →, ↔ weitere Formeln zusammensetzen.
Alle Zeichenketten, die sich nicht so konstruieren lassen, sind keine
aussagenlogischen Formeln.
Semantik:
I
Belegungen von Aussagenvariablen
I
Modellmengen von Formeln und Formelmengen
I
erfüllbare, allgemeingültige Formeln
I
semantische Äquivalenz von Formeln
Erfüllbarkeits-Aufgaben:
I
Modellierungsbeispiele, Anwendungen
I
Lösung durch SAT-Solver
Beschränkte Ausdrucksstärke der Aussagenlogik
I
Aussagen immer zweiwertig
(nur wahr oder falsch, keine Zwischenwerte),
z.B.: Die Rose ist rot. Das Bier ist kalt. Der Student ist fleißig.
(Erweiterung zu mehrwertigen Logiken, fuzzy logic)
I
Aussagen immer absolut
(keine Abhängigkeit vom Kontext, z.B. Ort, Zeitpunkt),
z.B.: Es regnet. x > 3
(Erweiterung zur Modal- und Temporallogiken)
I
Aussagen über alle Elemente großer“ Mengen aufwendig
”
(Erstellung, Platzbedarf), z.B. Zuordnungen
I
keine Aussagen über Elemente einer unendlichen Mengen oder
Mengen unbestimmter Mächtigkeit möglich, z.B.
I Jede durch 4 teilbare Zahl ist gerade.
I In jedem zusammenhängenden Graphen mit ≥ 2 Knoten hat
jeder Knoten einen Nachbarn.
I Es ist nicht alles Gold was glänzt.
(Erweiterung zur Prädikatenlogik)
63
Modellierungsbeispiel
1. Max ist ein Fisch.
2. Alle Fische schwimmen.
3. Also schwimmt Max.
Individuenbereich (Objekte): Lebewesen
Individuen (Konstanten) Max
Eigenschaften: istFisch, schwimmt
prädikatenlogische Formeln:
1. istFisch(Max)
2. ∀x(istFisch(x) → schwimmt(x))
3. schwimmt(Max)
64
Modellierung in Prädikatenlogik
Grundannahme:
Die zu modellierende Welt besteht aus Individuen, die
Eigenschaften haben und zueinander in Beziehungen (Relationen,
Funktionen) stehen.
Aussagen beschreiben Eigenschaften von und und Beziehungen
zwischen Individuen.
Formalisierung solcher Aussagen durch prädikatenlogische Formeln.
65
Prädikatenlogische Aussagen – Beispiele
Personen sind genau dann Geschwister, wenn sie dieselbe
Mutter oder denselben Vater haben.
I A ist genau dann Nachfahre von B, wenn B A’s Vater oder A’s
Mutter ist oder ein Elternteil von A Nachfahre von B ist.
I Nachfahren derselben Person sind verwandt.
Individuenbereich: Menge von Personen
Beziehungen: Nachfahre, verwandt, Geschwister, =
Funktionen: Mutter, Vater
I
Primzahlen sind genau diejenigen natürlichen Zahlen, die
genau zwei verschiedene Teiler haben.
I Gerade Zahlen sind genau diejenigen natürlichen Zahlen, die
durch 2 teilbar sind.
I Es existieren gerade Primzahlen.
I Nachfolger ungerader Primzahlen sind nicht prim.
I Das Quadrat jeder geraden Zahl ist gerade.
Individuenbereich: Menge
aller natürlichen Zahlen
Eigenschaft: prim, gerade
Beziehung: teilt, =
Funktion: Nachfolger, Quadrat
I
N
66
Atome (elementare Aussagen)
Aussagenlogik : Aussagenvariable,
bekommt festen Wahrheitswert durch Belegung
Prädikatenlogik : (parametrisierte) Aussage über Eigenschaften
von oder Beziehungen zwischen Individuen
Wahrheitswert abhängig von beteiligten Individuen
z.B. nebeneinander(x, y ),gerade(n) , x < 3, x < y ,
geschwister(x, mutter(y ))
67
Prädikatenlogik (der ersten Stufe) – Syntax
bekannt: aussagenlogische Junktoren t, f, ¬, ∨, ∧, →, ↔
neu: prädikatenlogische Atome, Quantoren ∀, ∃
Definition (induktiv)
Die Menge aller Formeln der Prädikatenlogik ist definiert durch:
IA: Alle Atome sind Formeln.
IS:
I
I
I
t und f sind Formeln.
Ist ϕ eine Formel und x eine Individuenvariable,
dann sind auch ¬ϕ, ∀xϕ, ∃xϕ Formeln.
Sind ϕ und ψ Formeln, dann sind auch
ϕ ∨ ψ, ϕ ∧ ψ, ϕ → ψ und ϕ ↔ ψ Formeln.
Baumstruktur der Formeln
68
Modellierung in Prädikatenlogik – Beispiel Topfdeckel
Auf jeden Topf passt ein Deckel.
I
Individuenbereich: Kochgeschirr
I
Eigenschaften: ist-Topf T ( ), ist-Deckel D( )
I
Beziehung: passt-auf P( , )
Schrittweise Entwicklung einer Formel:
1. Atome: P(x, y ) (x passt auf y ),
D(x) (x ist ein Deckel), T (y ) (y ist ein Topf)
2. Formel D(x) ∧ T (y ) ∧ P(x, y )
Der Deckel x passt auf den Topf y .
3. Formel ∃x (D(x) ∧ T (y ) ∧ P(x, y ))
Es gibt einen Deckel, welcher auf den Topf y passt.
4. Formel ∀y ∃x (D(x) ∧ T (y ) ∧ P(x, y ))
Zu jedem Topf gibt es einen Deckel, der auf diesen Topf passt.
bedeutet dasselbe wie: Auf jeden Topf passt ein Deckel.
69
Modellierung in Prädikatenlogik – Beispiel Geschwister
Personen sind genau dann Geschwister, wenn sie dieselbe Mutter oder
denselben Vater haben.
I
I
Individuenbereich: Personen
Beziehungen: sind-Geschwister G ( , ), =
ist-Mutter-von M( , ) , ist-Vater-von V ( , )
Zwischenschritte:
Atome: G (x, y ), M(z, x), M(z, y ), V (u, x), V (u, y )
M(z, x) ∧ M(z, y )
z ist Mutter von x und y .
I ∃z (M(z, x) ∧ M(z, y ))
x und y haben dieselbe Mutter (z).
I ∃z (M(z, x) ∧ M(z, y )) ∨ ∃u (V (u, x) ∧ V (u, y ))
x und y haben dieselbe Mutter (z) oder denselben Vater (u).
I G (x, y ) ↔ (∃z (M(z, x) ∧ M(z, y )) ∨ ∃u (V (u, x) ∧ V (u, y )))
x und y sind genau dann Geschwister, wenn Sie dieselbe Mutter
oder denselben Vater haben.
I
I
(Zwei beliebige) Personen sind genau dann Geschwister, wenn Sie
dieselbe Mutter oder denselben Vater haben.
∀x∀y (G (x, y ) ↔ (¬(x = y ) ∧ ∃z (M(z, x) ∧ M(z, y )) ∨ ∃u (V (u, x) ∧ V (u, y ))))
70
Naiver Mengenbegriff
Georg Cantor (1845-1918):
Eine Menge ist eine Zusammenfassung bestimmter,
wohlunterschiedener Dinge unserer Anschauung oder unseres
Denkens, welche Elemente der Menge genannt werden, zu einem
Ganzen.
Mengen werden dargestellt:
extensional durch Angabe aller Elemente
(nur für endliche Mengen möglich)
Beispiel: {0, 1, 2, 3}, {{a}, 5, {a, b}}
intensional durch Angabe der gemeinsamen Eigenschaft aller
Elemente (oft durch prädikatenlogische Formeln)
Beispiele:
{x | x ∈ ∧ ∃y ((y ∈ ) ∧ (x = 2y ))}
= {2y | y ∈ } = 2
{x | (x ∈ ) ∧ (x < 4)} = {x ∈ | x < 4}
N
N
N
N
N
N
71
Modellierungsbeispiel Skat
Modellierung:
(wichtig)
I
Jede Karte hat Farbe und Wert
I
deutsches oder französisches Blatt?
I
Ordnung zwischen Karten derselben Farbe
(wichtig)
z.B. 7 < 8 < 9 < 10 < B < D < K < A bei Null-Spiel
I
Bedienregeln
I
Trumpfregeln
(egal)
Formale Darstellung der Karten:
Jede Karte ist eindeutig repräsentiert durch Paar von
Farbe aus der Menge {♦, ♥, ♠, ♣} und
Wert
I
I
Zahl aus der Menge {7, 8, 9, 10} oder
Bild aus der Menge {B, D, K , A}
72
Modellierungsbeispiel gerade Zahlen
Gerade Zahlen sind genau die durch 2 teilbaren ganzen Zahlen.
Individuen:
Z (Menge aller ganzen Zahlen)
Eigenschaften: gerade
Beziehungen: Teilbarkeit ganzer Zahlen
präziser mit Definition der Teilbarkeit:
x ∈ ist genau dann gerade, wenn ein y ∈
Bedingung für x ist ist eine gerade Zahl“
”
als prädikatenlogische Formel:
Z
Z
Z mit 2y = x existiert.
Z
(x ∈ ) ∧ ∃y ((y ∈ ) ∧ (2y = x))
Menge aller geraden Zahlen:
Z
{2y | y ∈ Z}
2Z
Z
{x | (x ∈ ) ∧ ∃y ((y ∈ ) ∧ (2y = x))}
=
=
73
Endliche Mengen
N
Menge A heißt endlich gdw. eine Zahl n ∈ existiert,
so dass A genau n Elemente enthält.
Die leere Menge ∅ ist die (eindeutig bestimmte) Menge,
die kein Element enthält.
Beispiele:
I
I
I
I
N) ∧ (x ≤ 10)}
{x | (x ∈ N) ∧ (x ist gerade ) ∧ (x < 100)}
{x | (x ∈ Z) ∧ (x ist gerade ) ∧ (x < 100)}
{x | (x ∈
{x | x ist Primzahl }
endlich
endlich
nicht endlich
nicht endlich (Widerspruchsbeweis)
|A| heißt Mächtigkeit (Kardinalität) von A.
Beispiele:
I
|{rot, grün, blau, gelb}| = 4
I
|{x | x ∈
I
|{a, b, {a, b}, {a, a, b}, b}| = 3
I
|∅| = 0
N ∧ x ≤ 10}| = 11
74
Beziehungen zwischen Mengen
∈ Element-Relation
Notation x ∈ M für: x ist Element der Menge M
Negation kurz 6∈: a 6∈ M gdw. ¬(a ∈ M)
Beispiele: a ∈ {a, b, 2}, {a} 6∈ {a, b, 2}
⊆ Teilmengen-Relation
A ⊆ B gdw. ∀x (x ∈ A → x ∈ B)
Beispiele: {a, b} ⊆ {2, a, b, {2}}, {a} ⊆ {a},
{a} 6⊆ {{a}}, aber {a} ∈ {{a}}
= Mengengleichheit
A = B gdw. ∀x (x ∈ A ↔ x ∈ B)
6 {a, {b}, 2}
Beispiele: {a, b, 2} = {2, a, b, 2}, {a, b, 2} =
⊂ echte Teilmenge
A ⊂ B gdw. (A ⊆ B) ∧ ¬(A = B)
Beispiele: {2, a} ⊂ {a, b, 2},
{2, a} 6⊂ {2, a} , {2, a, b} 6⊂ {2, a}
75
Was bisher geschah
Modellierung von Aussagen
in klassischer Aussagen- und Prädikaten-Logik
Modellierung von Daten durch Mengen
I
Darstellung:
extensional durch Angabe aller Elemente
(nur für endliche Mengen möglich)
intensional durch Angabe der charakterisierenden
Eigenschaft aller Elemente der Menge
(als prädikatenlogische Formel)
I
leere Menge ∅
I
Mengenbeziehungen ∈, ⊆, =, ⊂
Aussonderungsprinzip
Zu jeder Menge A und jeder Eigenschaft P existiert eine Menge
B = {x | (x ∈ A)∧ (x hat die Eigenschaft P)} = {x | x ∈ A∧P(x)}
Beispiele:
I
A = Menge aller Frauen und P(x), falls x blond
B = Menge aller blonden Frauen
I
A = Menge aller Skatkarten und P(x), falls x bedient (♠, A)
B = {(♠, W ) | W ∈ {7, 8, 9, 10, B, D, K }}
I
A = {x | (x ∈ ) ∧ (x ≤ 100)} = {0, . . . , 100} und
P(x), falls x gerade
B = {x | (x ∈ ) ∧ (x ≤ 100) ∧ (2|x)}
N
N
I
I
N und P(x), falls x ≤ 100
A = N und P(x), falls 2|x und x ≤ 100
A=2
76
Russells Paradox
(Problem der naiven Mengenlehre)
I
Menge A, die alle Mengen (als Elemente) enthält
I
Mengeneigenschaft P: P(x), falls ¬(x ∈ x)
Wenn die Menge A existiert, dann existiert nach
Aussonderungsprinzip auch die Menge
B = {x | (x ∈ A) ∧ P(x)} = {x | (x ∈ A) ∧ ¬(x ∈ x)}
Gilt B ∈ A ? Nein
(Tafel)
Also kann keine solche Menge A existieren, die jede Menge
(und damit insbesondere auch B) als Element enthält.
alternative Formulierungen: Barbier, Kreter
77
Operationen auf Mengen
Vereinigung A ∪ B = {x | (x ∈ A) ∨ (x ∈ B)}
(x ∈ (A ∪ B)) ↔ ((x ∈ A) ∨ (x ∈ B))
Beispiel: {a, c, d} ∪ {b, c} = {a, b, c, d}
Schnitt A ∩ B = {x | (x ∈ A) ∧ (x ∈ B)}
(x ∈ (A ∩ B)) ↔ ((x ∈ A) ∧ (x ∈ B))
Beispiel: {a, c, d} ∩ {b, c} = {c}
Differenz A \ B = {x | (x ∈ A) ∧ ¬(x ∈ B)}
(x ∈ (A \ B)) ↔ ((x ∈ A) ∧ ¬(x ∈ B))
Beispiel: {a, c, d} \ {b, c} = {a, d}
symmetrische Differenz A∆B = (A \ B) ∪ (B \ A)= (A ∪ B) \ (A ∩ B)
Beispiel: {a, c, d}∆{b, c} = {a, b, d}
bei gegebenem Universum U mit A ⊆ U:
Komplement A = U \ A = {x ∈ U | ¬(x ∈ A)}
(x ∈ A) ↔ ¬(x ∈ A)
Beispiel: Für U = {a, b, c, d} gilt {a, c} = {b, d}
78
Wichtige Mengenbeziehungen
(analog Regeln für ¬, ∨, ∧ in der Aussagenlogik)
Für alle Mengen A, B, C gilt
I A ∪ A = A, A ∩ A = A
I A ∪ B = B ∪ A und A ∩ B = B ∩ A
(Kommutativität von ∩ und ∪)
I A ∪ (B ∪ C ) = (A ∪ B) ∪ C
A ∩ (B ∩ C ) = (A ∩ B) ∩ C
(Assoziativität von ∩ und ∪)
I A ∩ (B ∪ C ) = (A ∩ B) ∪ (A ∩ C )
A ∪ (B ∩ C ) = (A ∪ B) ∩ (A ∪ C )
(Distributivgesetze)
I
I
I
(ÜA)
A=A
A ∪ B = A ∩ B und A ∩ B = A ∪ B
(DeMorgansche Regeln)
A ∩ B = A ∪ B und A ∪ B = A ∩ B
(Dualität von ∩ und ∪)
79
Potenzmengen
Die Potenzmenge 2A einer Menge A ist die Menge aller Teilmengen
von A
2A = {B | B ⊆ A}
Beispiele:
I Für A = {0} gilt 2A = 2{0} = {∅, {0}},
I Für A = {♥} gilt 2A = 2{♥} = {∅, {♥}},
I 2{a,b,c} = {∅, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}},
A
{0}
I Für A = {0} gilt 2(2 ) = 2(2 ) = {∅, {∅}, {{0}}, {∅, {0}}},
Amtssprachen in der Schweiz:
S = {Deutsch, Französisch, Italienisch, Rätoromanisch}
mögliche Amtssprachkenntnisse der Bewohner: 2S
Mächtigkeit der Potenzmengen endlicher Mengen:
Für jede endliche Menge A gilt
A
2 = 2|A|
I
80
Modellierungsbeispiele
I
aus ÜA 2.6:
Menge aller Möglichkeiten, die Bauteile A, B, C , D
einzusetzen (nicht notwendig alle, jedes höchstens einmal)
= Menge aller Teilmengen der Menge {A, B, C , D}
= 2{A,B,C ,D}
Anzahl aller Möglichkeiten:
|2{A,B,C ,D} | = 2|{A,B,C ,D}| = 24 = 16
I
Menge aller in einem Skatblatt aus 7 Karten möglichen
Farbkombinationen
= Menge aller nichtleeren Teilmengen von {♦, ♥, ♠, ♣}
= 2{♦,♥,♠,♣} \ {∅}
(24 − 1 = 15 Möglichkeiten)
81
(Kartesisches) Produkt von Mengen
A × B = {(x, y ) | (x ∈ A) ∧ (y ∈ B)}
Beispiele:
I
{a, b} × {1, 2, 3} = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3)}
I
{1, . . . , m} × {1, . . . , n}
= {(i, j) | i ∈ {1, . . . , m} ∧ j ∈ {1, . . . , n}}
häufig als Indexmenge in Matrizen, digitalen Bildern,. . .
I
Namen = Vornamen × Familiennamen
I
Telefonbuch = ( Namen × Vornamen )× Nummer
I
Zeit = ( Stunde × Minute )× Sekunde
= {0, . . . , 23} × {0, . . . , 59} × {0, . . . , 59}
Für alle endlichen Mengen A und B gilt |A × B| = |A| · |B|
82
Beispiele
I
(1, 2) ∈ ({0, 1} × {1, 2}), aber (1, 2) 6∈ ({1, 2} × {0, 1})
({0, 1} × {1, 2}) ∩ ({1, 2} × {0, 1}) = {(1, 1)}
I
Cafeteria-Essen aus
{Bratwurst,Wiener,Knacker} × {Kartoffelsalat, Nudelsalat}
3 · 2 = 6 Möglichkeiten
I
12 · 15 mögliche (gemischte) Tanzpaare aus
je einem von 12 Männern und je einer von 15 Frauen
I
{a} ×
N = {(a, 0), (a, 1), (a, 2), . . .} = {a0, a1, a2, . . .}
83
Eigenschaften des Produktes von Mengen
I
× ist nicht kommutativ
{a, b} × {1, 2} = {(a, 1), (a, 2), (b, 1), (b, 2)}
6= {1, 2} × {a, b} = {(1, a), (2, a), (1, b), (2, b)}
I
× ist fast“ assoziativ
”
(A × B) × C kann mit A × B × C identifiziert werden.
z.B. ({a} × {1, 2}) × {α, β} = {(a, 1), (a, 2)} × {α, β}
= {((a, 1), α), ((a, 2), α), ((a, 1), β), ((a, 2), β)}
und {a} × ({1, 2} × {α, β}) = {a} × {(1, α), (1, β), (2, α), (2, β)}
= {(a, (1, α)), (a, (2, α)), (a, (1, β)), (a, (2, β))}
lassen sich beide eineindeutig zuordnen zu
{(a, 1, α), (a, 2, α), (a, 1, β), (a, 2, β)}
I
Distributivgesetze: Für alle Mengen A, B, C gilt
(A ∪ B) × C = (A × C ) ∪ (B × C ) und
(A ∩ B) × C = (A × C ) ∩ (B × C )
I
Für jede Menge A gilt A × ∅ = ∅.
I
Für alle Mengen A, B gilt:
Aus A ⊆ B folgt A × C ⊆ B × C
(ÜA)
84
Modellierungsbeispiel Skatkarten
Formale Darstellung der Karten:
Jede Karte ist eindeutig repräsentiert durch
Farbe aus der Menge F = {♦, ♥, ♠, ♣} und
Wert I Zahl aus der Menge Z = {7, 8, 9, 10} oder
I Bild aus der Menge B = {B, D, K , A}
Menge aller Werte W = Z ∪ B
Menge aller Karten:
K = {(x, y ) | x ∈ F ∧ y ∈ W } = F × (Z ∪ B)
Verteilung der Karten nach dem Geben:
I Skat: S = {ks,1 , ks,2 } ⊆ K mit |S| = 2
I für jedes i ∈ {1, 2, 3} Blatt des Spielers i:
Bi = {ki,1 , . . . , ki,10 } ⊆ K mit |Bi | = 10
wobei
1. B1 ∩ B2 = ∅, B1 ∩ B3 = ∅, B2 ∩ B3 = ∅,
S ∩ B1 = ∅, S ∩ B2 = ∅, S ∩ B3 = ∅ und
2. K = S ∪ B1 ∪ B2 ∪ B3
85
Zerlegungen
Mengen A und B mit A ∩ B = ∅ heißen disjunkt.
Beispiele:
I
I
Z und 2Z + 1 sind disjunkt
2Z und 3Z sind nicht disjunkt,
denn 0 ∈ 2Z ∩ 3Z, also 2Z ∩ 3Z 6= ∅
2
Eine Familie von Mengen {Ai }i∈I heißt genau dann
disjunkte Zerlegung einer Menge B, wenn
1. ∀i∀j ((i =
6 j) → ((Ai ∩ Aj ) = ∅))
(alle Ai paarweise disjunkt) und
S
(die Mengen Ai überdecken B vollständig)
2. i∈I Ai = B
Beispiele:
Z Z
Z
I
{2 , 2 + 1} ist eine (endliche) disjunkte Zerlegung von
I
für Ai = Menge aller Personen, die höchstens i cm groß sind,
ist {Ai | i ∈ } keine disjunkte Zerlegung der Menge P aller
Personen
I
für Bi = Menge aller Personen, die zwischen i und i + 1 cm groß
sind, ist {Bi | i ∈ } eine disjunkte Zerlegung von P
I
{[n, n + 1) ⊆
N
N
R|n ∈ Z} ist eine (unendliche) Zerlegung von R
86
Was bisher geschah
Modellierung von Aussagen in Logiken:
I
klassische Aussagenlogik
I
klassische Prädikatenlogik
Modellierung von Daten durch
Mengen
I
I
I
I
I
I
extensionale und intensionale Darstellung
Mächtigkeiten von (endlichen) Mengen |M|
Beziehungen zwischen Mengen ⊆, =, ⊂
leere Menge ∅
Potenzmenge 2M
Mengen-Operationen ∪, ∩, , \, ∆,
(kartesisches) Produkt ×,
Vereinigung disjunkter Mengen
˙ = {x | (x ∈ A) ∨ (x ∈ B)}
Vereinigung A∪B
Beispiel: Kunden K = {a, b, d}, Lieferanten L = {b, c, d},
Vereinigung G = K ∪ L = {a, b, c, d} (Geschäftspartner)
enthält keine Information darüber, ob b Kunde oder Lieferant ist
Idee: Mengen vor Vereinigung durch Hinzufügen einer
Kennzeichen-Komponente disjunkt machen“
”
(Verwaltung von Paaren aus Kennzeichen und Element)
Disjunkte Vereinigung der Mengen {Ai }i∈I mit Indexmenge I :
[
˙
i∈I
Ai =
[
A0i
mit
A0i = {i} × Ai = {(i, x) | x ∈ Ai }
i∈I
Mächtigkeit der disjunkten Vereinigung der Mengen {Ai }i∈I :
[
X
˙
A
|Ai |
i
i∈I =
i∈I
87
Beispiel Geschäftspartner
I
Menge aller Kunden: AK = {a, b, d}
I
Menge aller Lieferanten: AL = {b, c, d},
I
Kennzeichnung (Indexmenge) I = {K , L}
I
gekennzeichnete Geschäftspartner:
Kunden: A0K = {K } × AK = {(K , a), (K , b), (K , d)},
Lieferanten: A0L = {L} × AL = {(L, b), (L, c), (L, d)}
I
Menge aller (gekennzeichneten) Geschäftspartner:
˙ L = A0K ∪ A0L =
AK ∪A
{(K , a), (K , b), (L, b), (L, c), (K , d), (L, d)}
Anzahl der (gekennzeichneten) Geschäftspartner
˙ L | = |Ak | + |AL | = 6
|AK ∪A
88
Kartesisches Produkt mehrerer Mengen
n
×A = A
i
1
× · · · × An = {(x1 , . . . , xn ) | ∀i ∈ {1, . . . , n} : xi ∈ Ai }
i=1
Für endlich viele endliche Mengen Ai gilt
n
n
Y
Ai =
|Ai |
i=1 ×
i=1
Beispiele:
I
5-Gänge-Menü: Auswahl aus
3 Vorspeisen, 2 Suppen, 5 Hauptgerichten, 3 Desserts, 2 Käse
3 · 2 · 5 · 3 · 2 = 180 mögliche Kombinationen
I
|{0, 1}| = 2n Binärwörter mit n Stellen
I
103 höchstens dreistellige Dezimalzahlen
I
65 verschiedene Ergebnisse beim fünfmal aufeinanderfolgenden
Würfeln mit einem Würfel
I
65 verschiedene Ergebnisse beim Würfeln mit fünf
verschiedenfarbigen Würfeln
n
89
Iterierte Produkte einer Menge
n
An =
×A
i=1
A0 = {ε}
[
A∗ =
An
n∈
+
A
=
N[
N
mit leerem Wort ε
An = A∗ \ {ε}
n∈ \{0}
(Notation: statt ε mitunter auch (), [])
Elemente aus An , A+ , A∗ heißen
I
Folgen (Vektoren) (a1 , a2 , . . . , an ),
I
Listen [a1 , a2 , . . . , an ], [a1 , a2 , . . .] oder
I
Wörter (Strings) a1 a2 . . . an (endlich)
90
Iteriertes Produkt – Beispiele
I
{0, 1}∗ Menge aller Binärwörter (beliebiger Länge)
z.B. 10, 10010, 010, ε
I
Menge aller Binärwörter der Länge 3
{0, 1}3 = {000, 001, 010, 011, 100, 101, 110, 111}
I
{0, 1, 2}∗ Menge aller Ternärwörter (beliebiger Länge)
z.B. 20, 1202010, ε
I
Menge aller Ternärwörter der Länge 2
{0, 1, 2}2 = {00, 01, 02, 10, 11, 12, 20, 21, 22}
I
{0} ∪ {1, 2, 3, 4, 5, 6, 7, 8, 9} × {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}∗
Menge aller natürlichen Zahlen in Dezimaldarstellung (ohne
führende Nullen)
I
{a, b}∗ alle Wörter (beliebiger Länge), die nur die Buchstaben
a und b enthalten (z.B. aba, ababa, aaaa, bbbaaa, ε)
I
{{a, b}∗ }∗ alle Folgen solcher Wörter
(z.B. (a, aa, aaa), (ba), ε, (ε, ε, ε))
91
Folgen
Folgen (Listen, Wörter) werden definiert:
extensional durch Angabe der Elemente und ihrer Reihenfolge
Beispiele: 3210, [1, 4, 9, 16, 25], abababababa
intensional durch Angabe einer Eigenschaft, die für jeden Index i
das i-te Element eindeutig bestimmt.
Beispiele: (4 − i)1≤i≤4 , (i 2 )i∈{1,...,5} ,
(wi )0≤i≤10 mit wi =
(vi )i∈N mit vi =
a falls i ∈ 2
b sonst
a falls i ∈ 2
b sonst
Z
Z
(i 2 )i∈N = [0, 1, 4, 9, . . .], (3)k∈N = [3, 3, 3, 3, . . .]
Länge der Folge (an )n∈I :
Anzahl der Elemente (= Mächtigkeit der Indexmenge I ⊆
N)
92
Modellierung durch Folgen
Beispiel Würfelfolgen:
I
Menge der möglichen Werte (Augenzahlen): {1, 2, . . . , 6},
z.B. 3 ∈ {1, 2, . . . , 6}
I
Menge aller Folgen von Werten bei viermaligem Würfeln
(nacheinander): {1, 2, . . . , 6}4 ,
z.B. [3, 6, 5, 3] ∈ {1, 2, . . . , 6}4
I
Menge aller Folgen von Werten beim Würfeln beliebig oft
nacheinander: {1, 2, . . . , 6}∗ ,
z.B. [3, 2, 2, 5, 1] ∈ {1, 2, . . . , 6}∗ , ε ∈ {1, 2, . . . , 6}∗
93
Modellierung durch Mengen und Folgen
I
Menge aller Skatkarten:
S = {♦, ♥, ♠, ♣} × ({7, 8, 9, 10} ∪ {B, D, K , A})
I
Folge aller Unter (B) nach Wert aufsteigend geordnet
[(♣, B), (♠, B), (♥, B), (♦, B)] ∈ S 4
I
Folge aller Karten der Farbe ♠ nach Wert (Nullspiel) aufsteigend
geordnet
[(♠, 7), (♠, 8), (♠, 9), (♠, 10), (♠, B), (♠, D), (♠, K ), (♠, A)] ∈ S 8
I
Menge aller Möglichkeiten der (zwei) Karten im Skat:
{{h, k} | h ∈ K ∧ k ∈ K ∧ h 6= k} ⊆ 2S (Warum nicht ⊆ S 2 ? )
I
Blatt = Menge aller Karten auf der Hand (zu Beginn des Spieles)
B ∈ 2S mit |B| = 10 (10 verschiedene Karten)
I
Kartenfächer (zu Beginn des Spieles): Folge (k1 , . . . , k10 ) ∈ S 10 mit
|{k1 , . . . , k10 }| = 10 (alle Karten verschieden), z.B.
[(♠, B), (♥, B), (♦, A), (♦, 9), (♣, A), (♣, K ), (♣, 9), (♥, 10), (♥, 8), (♥, 7)]
I
Stich: Folge von drei nacheinander gelegten Karten
(geordnetes Tripel) (k1 , k2 , k3 ) ∈ S 3 mit |{k1 , . . . , k3 }| = 3
I
Spiel: Folge der (während des Spiels gefallenen) Stiche ∈ S 3
10
94
Zusammenhänge Folgen – Mengen
zu gegebener Folge (an )n∈I :
I Menge {an | n ∈ I } der Elemente der Folge (an )n∈I
(eindeutig)
I
I
Folge [1, 4, 9, 16], Menge der Elemente {1, 4, 9, 16}
Folge [a, a, a, . . .], Menge der Elemente {a}
(Gegebene Folge nicht eindeutig rekonstruierbar)
I Menge aller Anfangsstücke der Folge (eindeutig)
Beispiel: (2n )n∈N , Menge {[1], [1, 2], [1, 2, 4], . . .}
(Folge lässt sich eindeutig rekonstruieren.)
zu gegebener Menge A:
I Folgen (an )n∈I sind durch Mengen definiert (A∗ , Aω )
I beliebige Anordnung der Elemente einer Menge zu Folgen
(i.A. nicht eindeutig, mehrere Möglichkeiten), z.B.
I
I
I
M = {a, b, c, d}, Folgen [a, b, c, d], [b, d, b, c, d, a]
M = , Folgen [0, 1, 2, . . .] , [0, 2, 4, 6, 8, 1, 3, 5, 7, 9, 10, 12 . . .]
M = , Folgen [0, 1, −1, 2, −2, 3, −3, . . .]
[0, 1, 2, 3, −3, −2, −1, 4, 5, . . .]
N
Z
95
Alphabet, Wort, (formale) Sprache
Alphabet (endliche) Menge A von Symbolen
Wort endliche Folge von Symbolen w = w1 · · · wn mit
∀i ∈ {1, . . . , n} : wi ∈ A
Länge eines Wortes |w | = Anzahl der Symbole in w
Anzahl der Vorkommen eines Symboles in einem Wort
|w |a = Anzahl der a in w (für a ∈ A)
Sprache Menge von Wörtern L ⊆ A∗
96
Wörter – Beispiele
banane
ist ein Wort (Zeichenkette) mit Symbolen aus der Menge {a, b, e, n},
neben und abbbeeeab auch,
ananas und ab + bea nicht
2009
ist ein Wort mit Symbolen aus der Menge {0, 2, 9},
90 und 09020090 auch,
−2090 nicht
(x + y ) · (z − x)
ist ein Wort mit Symbolen aus der Menge {x, y , z, (, ), +, −, ·},
()xz(xy + − auch,
x + 3 · z nicht
(¬p ∧ p) → q
ist ein Wort mit Symbolen aus der Menge {p, q, ∧, ¬, →, (, )},
q → (p → q) und ∧)(¬p∧ auch,
p ↔ q nicht
otto holt obst .
ist ein Wort mit Symbolen aus der Menge {otto, obst, holt, .},
. otto . . otto auch,
los otto nicht
97
Verkettung von Wörtern (Folgen)
Verkettung ◦ von Wörtern:
Für alle Wörter u = u1 · · · um ∈ A∗ , v = v1 · · · vn ∈ A∗ gilt
u ◦ v = u1 · · · um v1 · · · vn
Beispiel: anne ◦ marie = annemarie
Eigenschaften der Operation ◦:
I ◦ ist assoziativ, d.h.
∀u ∈ A∗ ∀v ∈ A∗ ∀w ∈ A∗ ((u ◦ v ) ◦ w = u ◦ (v ◦ w ))
I
Das leere Wort ε ist neutrales Element für ◦, d.h.
∀w ∈ A∗ (ε ◦ w = w ◦ ε = w )
I
◦ ist nicht kommutativ.
Gegenbeispiel: u = marie, v = anne
u ◦ v = marieanne 6= annemarie = v ◦ u
98
Umkehrung (gespiegeltes Wort)
Umkehrung von w = w1 · · · wn : w R = wn · · · w1
Beispiele: marie R = eiram, 2013R = 3102, 101R = 101
to ◦
m ◦ (ate)R
Für jedes Wort w ∈ A∗ gilt w R
R
R
R !R
◦n
= ...
= w.
99
Palindrome
Palindrom: Wort w mit w = w R
B: anna, neben, ε, jedes Wort der Länge 1
Die Menge aller Palindrome über dem Alphabet A ist
Lpal = {w ∈ A∗ | w = w R }
= {w ◦ w R | w ∈ A∗ } ∪ {w ◦ a ◦ w R | w ∈ A∗ ∧ a ∈ A}
|
{z
} |
{z
}
Lpal0
Lpal1
Beispiele für Wörter aus Lpal :
I
otto = ot ◦ to = ot ◦ (ot)R für w = ot ∈ A∗ = {a, . . . , z}∗
I
reliefpfeiler = relief ◦ p ◦ feiler = relief ◦ p ◦ (relief )R
für w = relief ∈ A∗ = {a, . . . , z}∗
I
1 = ε ◦ 1 ◦ ε = ε ◦ 1 ◦ εR
I
ε=ε◦ε=ε◦
für A = {0, 1}
εR
100
Präfix-Beziehung zwischen Wörtern (Folgen)
Präfix (Anfangswort) v
∀u ∈ A∗ ∀v ∈ A∗ ((u v v )
↔
(∃w ∈ A∗ (u ◦ w = v )))
(Für zwei beliebige Wörter u ∈ A∗ , v ∈ A∗ gilt u v v genau dann,
wenn ein Wort w ∈ A∗ existiert, so dass u ◦ w = v gilt.)
Beispiele:
I
an v anna (mit w = na)
I
n 6v anna
I
tom v tomate (mit w = ate)
I
oma 6v tomate
I
für jedes Wort u ∈ A∗ gilt ε v u (mit w = u)
I
für jedes Wort u ∈ A∗ gilt u v u (mit w = ε)
(analog zur Teiler-Beziehung zwischen natürlichen Zahlen)
101
Was bisher geschah
Modellierung von Aussagen durch Logiken
Modellierung von Daten durch
Mengen
extensionale und intensionale Darstellung
Mächtigkeiten endlicher Mengen, ∅
Beziehungen zwischen Mengen ⊆, =, ⊂
I Mengen-Operationen ∪, ∩, , \, ∆, ×, n , ∗ , 2M
I
I
I
Folgen über einer Menge A
extensionale und intensionale Darstellung
Länge von Folgen, leeres Wort ε (leere Folge)
unendliche Folgen,
endliche Folgen fester Länge (Tupel, Vektoren),
endliche Folgen variabler Länge (Wörter, Listen)
I Operationen auf Wörtern: (iterierte) Verkett. ◦, ∗
I Beziehung zwischen Wörtern: Präfix
I
I
I
Sprachen Mengen von Wörtern (endlichen Folgen)
Beispiele
Wiederholung: Präfix-Beziehung zwischen Wörtern
Präfix (Anfangswort) v
∀u ∈ A∗ ∀v ∈ A∗ ((u v v )
↔
(∃w ∈ A∗ (u ◦ w = v )))
(Für zwei beliebige Wörter u ∈ A∗ , v ∈ A∗ gilt u v v genau dann,
wenn ein Wort w ∈ A∗ existiert, so dass u ◦ w = v gilt.)
Beispiele:
I
an v anna (mit w = na)
I
n 6v anna
I
tom v tomate (mit w = ate)
I
oma 6v tomate
I
für jedes Wort u ∈ A∗ gilt ε v u (mit w = u)
I
für jedes Wort u ∈ A∗ gilt u v u (mit w = ε)
(analog zur Teiler-Beziehung zwischen natürlichen Zahlen)
Postfix-Beziehung auf Wörtern (Folgen)
∀u ∈ A∗ ∀v ∈ A∗ (Postfix(u, v ) ↔ (∃w ∈ A∗ (w ◦ u = v )))
Für zwei Wörter u = u1 · · · um ∈ A∗ , v = v1 · · · vn ∈ A∗ heißt
u genau dann Postfix (Suffix) von v , wenn ein Wort w ∈ A∗
existiert, so dass w ◦ u = v gilt.
Beispiel: enten ist Postfix von studenten (mit w = stud)
102
Infix-Beziehung auf Wörtern (Folgen)
Infix-Beziehung (Teilwort, Faktor):
∀u ∈ A∗ ∀v ∈ A∗ Infix(u, v ) ↔ ∃w ∈ A∗ ∃w 0 ∈ A∗ (w ◦ u ◦ w 0 = v )
Für zwei Wörter u = u1 · · · um ∈ A∗ , v = v1 · · · vn ∈ A∗ heißt
u genau dann Infix von v , wenn zwei Wörter w , w 0 ∈ A∗ existieren,
so dass w ◦ u ◦ w 0 = v gilt.
Beispiel: uwe ist Infix von sauwetter (mit w = sa, w 0 = tter )
satt ist kein Infix von sauwetter
103
Beispiele für (formale) Sprachen
I
Menge aller englischen Wörter L1 ⊂ {a, . . . , z}∗
I
Menge aller deutschen Wörter L2 ⊂ {a, . . . , z, ß,ä,ö,ü}∗
I
Menge aller möglichen DNA L3 ⊆ {A, T , G , C }∗
I
Menge aller natürlichen Zahlen in Dezimaldarstellung
L4 = {0, . . . , 9}∗ (evtl. mit führenden Nullen)
I
Menge aller natürlichen Zahlen in Binärdarstellung (Bitfolgen
beliebiger Länge) L5 = {0, 1}∗
I
Menge aller aussagenlogischen Formeln in AL({p, q, r })
L6 ⊂ {p, q, r , t, f, ¬, ∨, ∧, →, ↔, (, )},
I
Menge aller arithmetischen Ausdrücke über
L7 ⊂ {0, . . . , 9, +, ·, −, /, (, )},
I
Menge aller deutschen Sätze L8 ⊂ (L2 ∪ {., , , !, ?, (, ), −})
Z (ohne Variablen)
∗
Wie lassen sich unendliche Sprachen endlich darstellen?
(Voraussetzung für maschinelle Verarbeitung)
verschiedene Darstellungen in den LV zur theoretischen Informatik
z.B. Automaten und formale Sprachen im 3. Semester (INB)
104
Sprachen als Mengen
Sprachen L ⊆ A∗ sind Mengen von Wörtern (endlichen Folgen)
Mengenbeziehungen auf Sprachen:
L ⊆ L0 gdw.
∀w ∈ A∗ ((w ∈ L) → (w ∈ L0 ))
L = L0 gdw.
∀w ∈ A∗ ((w ∈ L) ↔ (w ∈ L0 ))
Mengenoperationen auf Sprachen:
L ∪ L0 = {w | w ∈ L ∨ w ∈ L0 }
L ∩ L0 = {w | w ∈ L ∧ w ∈ L0 }
L \ L0 = {w | w ∈ L ∧ w 6∈ L0 }
Komplement einer Sprache L ⊆ A∗ : L = A∗ \ L
Beispiel:
N(|w | = 2n)}
∧ ∃n ∈ N(|w | = 2n + 1)}
L = {w | w ∈ {0, 1}∗ ∧ ∃n ∈
L = {w | w ∈ {0, 1}
∗
105
Verkettung von Sprachen
Verkettung ◦ von Sprachen:
L1 ◦ L2 = {u ◦ v | (u ∈ L1 ) ∧ (v ∈ L2 )}
Beispiel:
L1 = {111, 1, 10} L2 = {00, 0}
L1 ◦ L2 = {111, 1, 10} ◦ {00, 0}
= {1110, 11100, 10, 100, 1000}
106
Iterierte Verkettung
I
für Sprachen L ⊆ A∗
L0 = {ε}
∀n ∈
N:
Ln+1 = Ln ◦ L = L
· · ◦ L}
| ◦ ·{z
n+1−mal
∗
L =
[
n∈
I
N
L
n
+
L =
[
N
n
L
n∈ \{0}
für Wörter (endliche Folgen) u ∈ A∗ :
un
u
+
∈ A∗ ,
= u
· · u}
| ·{z
u ∗ = {u}∗ = {u n | n ∈
n−mal
∗
= u \ {ε} = {u}+ = {u n | n ∈
N \ {0}}
N}
⊆ A∗
⊆ A∗
Beispiele:
(101)3
a∗
∗
(ab)
=
101101101
und
1013 = 10111
N} = {ε, a, aa, aaa, . . .}
| i ∈ N} = {ε, ab, abab, ababab, . . .}
= {ai | i ∈
i
= {(ab)
107
Mehr Beispiele für Sprachen
I
{aa, b}∗
= {u1 ◦ · · · ◦ un | n ∈
N ∧ ∀i ∈ {1, . . . , n}
(ui ∈ {aa, b})}
= {ε, b, aa, bb, aab, baa, bbb, aaaa, aabb, baab, bbaa, bbbb, . . .}
ab 6∈ {aa, b}∗ , ba 6∈ {aa, b}∗ , aba 6∈ {aa, b}∗
I
∅ ◦ {aba, bb} = ∅
I
{ε} ◦ {aba, bb} = {aba, bb}
I
{bb}∗ = {w ∈ {b}∗ | |w | ∈ 2 } = {ε, bb, bbbb, . . .}
I
({1} ◦
{0}∗ )∗
= {w ∈
{0, 1}∗
N
| w1 = 1} ∪ {ε}
108
Reguläre Ausdrücke – Syntax
Die Menge RegExp(A) aller regulären Ausdrücke über einem
Alphabet A ist (induktiv) definiert durch:
IA: ∅ ∈ RegExp(A),
ε ∈ RegExp(A) und
für jedes Symbol a ∈ A gilt a ∈ RegExp(A)
IS: für alle E ∈ RegExp(A) und F ∈ RegExp(A) gilt
(E + F ), EF , (E )∗ ∈ RegExp(A).
(Baumdarstellung)
Beispiele:
I (∅ + 1) ∈ RegExp({0, 1}),
I (ε + ((ab)∗ a)∗ ) ∈ RegExp({a, b}),
I (♠∅♦)∗ ∈ RegExp({♦, ♥, ♠, ♣}),
I für beliebiges Alphabet A gilt ε ∈ RegExp(A),
(ε + ∅) ∈ RegExp(A),
I 0+(1+2+3+4+5+6+7+8+9)(0+1+2+3+4+5+6+7+8+9)∗
∈ RegExp({0, 1, 2, 3, 4, 5, 6, 7, 8, 9})
109
Reguläre Ausdrücke – Semantik
Jeder reguläre Ausdruck E ∈ RegExp(A) repräsentiert
eine Sprache L(E ) ⊆ A∗ .
L(∅)
L(ε)
∀a ∈ A :
L(a)
∀E , F ∈ RegExp(A) : L(E + F )
∀E , F ∈ RegExp(A) :
L(EF )
∀E , F ∈ RegExp(A) :
L(E ∗ )
= ∅
= {ε}
= {a}
= L(E ) ∪ L(F )
= L(E ) ◦ L(F )
∗
= (L(E ))
Eine Sprache L ⊆ A∗ heißt genau dann regulär, wenn ein regulärer
Ausdruck E ∈ RegExp(A) existiert, so dass L = L(E ).
Beispiele: Für A = {a, b} gilt
L(ab ∗ )
N}
N}
=
{a, ab, abb, abbb, abbbb, . . .} = {ab i | i ∈
L((ab) )
=
{ε, ab, abab, ababab, . . .} = {(ab)i | i ∈
L((a + b)∗ )
=
{a, b}∗
L(a∗ b ∗ )
=
{u ◦ v | u ∈ a∗ ∧ v ∈ b ∗ }
∗ ∗ ∗
L((a b ) )
=
{a, b}∗
L(A∗ aba)
=
{u ◦ aba | u ∈ A∗ }∗
∗
110
Beispiele
I
L (0 + (1 + 2 + · · · + 9)(0 + 1 + · · · + 9)∗ ) =
Menge aller Dezimaldarstellungen natürlicher Zahlen
I
für A = {A, B, . . . , Z , a, b, . . . , z} ist L(A∗ (oma + otto)A∗ ) =
Menge aller Wörter mit Infix oma oder otto
z.B. tomate ∈ L(A∗ (oma + otto)A∗ ), lotto ∈ L(A∗ (oma + otto)A∗ ),
ottomat ∈ L(A∗ (oma + otto)A∗ ),
hottentottenpotentatentantenattentat 6∈ L(A∗ (oma + otto)A∗ )
I
für A = {A, B, . . . , Z , a, b, . . . , z, 0, 1, . . . , 9, ., −} ist
L(A∗ @htwk-leipzig.de) ≈
Menge aller möglichen HTWK-Email-Adressen
Reguläre Ausdrücke ermöglichen eine endliche Darstellung unendlicher
Sprachen.
Aber: Nicht jede (unendliche) Sprache ist regulär.
( mehr dazu in den LV zur theoretischen Informatik,
z.B. Automaten und Formale Sprachen im 3. Semester )
111
Beispiele regulärer Sprachen
I
I
I
I
I
I
I
L1 = ∅,
wegen ∅ ∈ RegExp(A) und L(∅) = ∅ = L1
L2 = {a, bab},
wegen a + bab ∈ RegExp(A) und L(a + bab) = L2
L3 = {w ∈ {a, b, c}∗ | abba v w },
wegen abba(a + b + c)∗ ∈ RegExp({a, b, c}) und
L(abba(a + b + c)∗ ) = L3
L4 = {w ∈ {a, b, c}∗ | aa oder bbb sind Infix von w }, wegen
(a + b + c)∗ (aa + bbb)(a + b + c)∗ ∈ RegExp({a, b, c}) und
L((a + b + c)∗ (aa + bbb)(a + b + c)∗ ) = L4
{w ∈ {a, b}∗ | |w | ∈ 2 } = L((aa + ab + ba + bb)∗ )
{w ∈ {a, b}∗ | |w |a ∈ 2 } = L((b ∗ ab ∗ ab∗)∗ )
alle möglichen HTWK-Email-Adressen
⊆ L(A∗ @htwk-leipzig.de) mit
A = {A, B, . . . , Z , a, b, . . . , z, 0, 1, . . . , 9, ., −}
(ASCII-Symbole)
N
N
112
Was bisher geschah
Modellierung von
I Aussagen durch Logiken
I
I
klassische Aussagenlogik
klassische Prädikatenlogik:
Aussagen über
I
I
Eigenschaften von und
Zusammenhängen zwischen
Individuen (Elementen von Mengen)
I
Daten durch
I
I
I
Mengen
Folgen
Sprachen
Relationen
Relationen repräsentieren Zusammenhänge zwischen Individuen
Definition
Jede Menge R ⊆ A × B heißt Relation zwischen den Mengen A und B.
Beispiele:
I
I
I
I
I
I
I
H ⊆ Studenten × Dozenten mit (s, d) ∈ H gdw.
s hört (wenigstens) eine Vorlesung bei d.
S ⊆ Skatkarten × Skatkarten mit (h, k) ∈ S gdw.
Karte h hat höheren Wert als Karte k
B ⊆ Spieler × Skatkarten mit (s, k) ∈ B gdw.
Spieler hat s die Karte k auf der Hand.
R ⊆ {a, b, c} × {1, 2, 3, 4} mit R = {(a, 2), (a, 3), (c, 2), (c, 4)}
R ⊆ 2 mit R = {(m, n) ∈ 2 | m = n + 5}
R ⊆ 2 mit R = {(x, y ) ∈ 2 | x 2 + y 2 = 1}
≤ ⊆ 2 mit ≤ = {(m, n) ∈ 2 | m ≤ n}
N
R
R
N
R
R
Zur Definition einer Relation R ⊆ A × B gehören (sind anzugeben):
die Mengen A, B (Typ der Relation) und
I die Menge R (extensional oder intensional)
I
113
Beispiel EU-Arbeitskreise
nach Uwe Kastens, Hans Kleine Büning:
Modellierung - Grundlagen und formale Methoden
I
3 Arbeitskreise
I
4 Nationen : D, F, A, P
I
aus jeder Nation 3 Delegierte
Bedingungen:
I
I
I
Jede Nation ist in jedem AK vertreten.
In jedem AK gibt es eine Sprache, die alle Mitglieder des AK
sprechen.
114
Modellierung EU-Arbeitskreise
Modellierung der (relevanten)
Daten: Mengen aller beteiligten
I Nationen L = {D, F , A, P}
I Sprachen S = {d, f , p},
I AK-Index A = {1, 2, 3},
I Delegierten-Index I = {1, 2, 3}
daraus konstruierte Mengen, z.B.
Menge aller Delegierten P = L × I
deutsche Delegation {D} × I = {D1, D2, D3}
Menge aller möglichen Sprachkompetenzen 2S
Menge aller möglichen Delegiertengruppen 2P
Zusammenhänge z.B.
Amtssprache ⊆ S × L (z.B. (d, A) ∈ Amtssprache)
spricht ⊆ P × S (z.B. (D1, p) ∈ spricht)
lernt ⊆ P × S
Notation: meist (spricht(D1, p)) statt ((D1, p) ∈ spricht)
115
Relationen verschiedener Stelligkeit
∅ Die leere Relation ∅ ist Relation zwischen beliebigen
Mengen A und B.
Relation R ⊆ A × B für spezielle A
B = A , also A × B = A2
R ⊆ A2 heißt binäre Relation auf A.
Beispiele: ≤ ∈ 2 mit ≤ = {(x, y ) ∈ 2 | x ≤ y },
Identität auf A: IA ⊆ A2 mit IA = {(x, x) | x ∈ A}
R
R
B = An−1 , also A × B = A × An−1 = An
R ⊆ An heißt n-stellige Relation auf A.
Beispiel: R = {(x, y , z) ∈ 3 | x 2 + y 2 = z 2 } ⊆
N
N3
B = A0 = {ε}, also A × B = A × {ε} = {(a, ε) | a ∈ A}
Relation entspricht einer Teilmenge R ⊆ A.
R ⊆ A heißt dann auch einstellige Relation auf A.
(Eigenschaft von Elementen aus A)
Beispiel: G ⊆ mit G = {n ∈ | 2 > n}
N
N
116
Anzahl von Relationen auf endlichen Mengen
Wiederholung: Für endliche Mengen A und B gilt
|A × B| = |A| · |B|
Menge aller Relationen {R | R ⊆ A × B} = 2A×B
Wieviele Relationen (Teilmengen) R ⊆ A × B? Es existieren
2|A×B| = 2|A|·|B| verschiedene Relationen zwischen A und B.
Spezialfälle:
|B| = 1 : 2|A|·|B| = 2|A| einstellige Relationen auf A.
2
A = B : 2|A×A| = 2(|A| ) binäre Relationen auf A.
n−1
n
B = An−1 : 2(|A|·|A| ) = 2(|A| ) n-stellige Relationen auf A.
117
Häufige Anwendungen
I
Datenbanken: jede Tabelle repräsentiert eine Relation T , z.B.
Id
Vorname Name Studieng. Jg. Gruppe
34567 Lisa
Klein
AMB
15 1
12345 Erwin
Meier
MIB
15 2
56789 Paula
Müller INB
14 1
..
..
..
..
..
..
.
.
.
.
.
.
mit T ⊆ {0, 1, . . . , 9}5 × Vornamen × Namen
×{AMB, INB, MIB} × {0, 1, . . . , 9}2 × {1, 2}
und z.B. ( 12345, Erwin, Meier, MIB, 15, 2 ) ∈ T
I
Ontologien, z.B. Komponenten eines Systems:
istTeilVon (Hand, Arm), istTeilVon (Finger, Hand),
istEin (Daumen, Finger)
I
Abläufe, z.B. durch Übergangsrelation T zwischen Zuständen
Münzspiel: (0230, 1040) ∈ T , (0230, 0311) ∈ T , (0311, 1121) ∈ T ,
(1040, 1121) ∈ T , (1121, 1202) ∈ T
118
Abgeleitete Relationen
Inverse der binären Relation R ⊆ A × B:
R −1 = {(b, a) | (a, b) ∈ R} ⊆ B × A
Beispiele: {(1, a), (1, b), (2, b)}−1 = {(a, 1), (b, 1), (b, 2)},
istKindVon−1 = istElternteilVon, istTeilVon−1 = hatTeil, ≤−1 = ≥
Einschränkung von R ⊆ A × B auf M ⊆ A:
R|M = {(a, b) ∈ R | a ∈ M}
Beispiele: {(1, a), (1, b), (2, b), (3, a)}|{2,3} = {(2, b), (3, a)},
istElternteilVon|Frauen = istMutterVon,
Projektionen von R ⊆ A × B:
π1 (R)
= {a ∈ A | (a, b) ∈ R} ⊆ A
π2 (R)
= {b ∈ B | (a, b) ∈ R} ⊆ B
Beispiele: π1 ({(1, a), (1, b), (2, b), (3, a)}) = {1, 2, 3},
π2 (istKindVon) = Menge aller Eltern
119
Verkettung von Relationen
Verkettung R ◦ S ⊆ A × C
der Relationen R ⊆ A × B und S ⊆ B × C :
R ◦ S = {(x, y ) ∈ A × C | ∃z ∈ B((x, z) ∈ R ∧ (z, y ) ∈ S)}
Beispiele:
I
für A = {1, 2, 3}, B = {a, b, c}, C = {♦, ♥} und
R = {(1, a), (1, c), (2, b), (3, c)}, S = {(a, ♥), (a, ♦), (b, ♦)}
R ◦ S= {(1, a), (1, c), (2, b), (3, c)} ◦ {(a, ♥), (a, ♦), (b, ♦)}
= {(1, ♥), (1, ♦), (2, ♦)}
I
istKindVon ◦ istKindVon = istEnkelVon
I
≤ ◦ ≤=≤
120
Eigenschaften der Verkettung von Relationen
Für alle Relationen R ⊆ A × B, S ⊆ B × C , T ⊆ C × D gilt:
I
(R ◦ S) ◦ T = R ◦ (S ◦ T )
I
i.A. R ◦ S 6= S ◦ R
(nicht kommutativ)
Gegenbeispiel: für R = {(a, b)}, S = {(b, c)} gilt
R ◦ S = {(a, c)}, aber S ◦ R = ∅
I
R ◦ IB = R = IA ◦ R
I
(R ◦
S)−1
=
S −1
◦
(assoziativ)
(IA , IB sind neutrale Elemente)
R −1
121
Modellierungsbeispiel
Mengen:
B
P
O
L
={
={
={
={
Blumen, Pferde, Schiffe }
Tom, Max, Ilse }
Leipzig, Hamburg, Genf }
D, S }
(Buchtitel)
(Personen)
(Orte)
(Länder)
Relationen:
hatAutor ⊆ B × P mit
hatAutor = { (Blumen, Max), (Schiffe, Tom),
(Schiffe, Ilse), (Pferde, Max), (Pferde, Ilse) }
wohntIn ⊆ P × O mit
wohntIn = {(Tom,Hamburg),(Ilse,Leipzig),(Max,Genf)}
liegtIn ⊆ O × L mit
liegtIn = {(Leipzig, D), (Hamburg, D), (Genf, S)}
Verkettungen der Relationen:
wohntIn ◦ liegtIn ⊆ P × L mit
wohntIn ◦ liegtIn ={(Tom,D), (Ilse,D), (Max, S)}
I hatAutor ◦ wohntIn ⊆ B × O mit hatAutor ◦ wohntIn = . . .
I
122
Modellierungsbeispiel
I
Worüber wird in welchen Ländern geschrieben?
R = (hatAutor ◦ wohntIn ◦ liegtIn) ⊆ B × L
mit R ={(Blumen, S), (Schiffe, D), (Pferde, S), (Pferde, D)}
I
In welchen Orten wohnen Autoren von Büchern über Pferde?
M = π2 (hatAutor ◦ wohntIn) |{Pferde} ⊆ O
mit M = {Genf, Leipzig}
I
Bücher zu welchen Themen schreiben deutsche Autoren?
M 0 = π2 (hatAutor ◦ wohntIn ◦ liegtIn)−1 |{D} ⊆ B
mit M 0 = {Schiffe, Pferde}
123
Darstellung binärer Relationen
Darstellungsformen für binäre Relation R ⊆ A × B auf
endlichen Mengen A und B:
I
Menge geordneter Paare (intensional oder extensional)
I
für A = {a1 , . . . , am } und B = {b1 , . . . , bn }
|A| × |B|-Matrix mit Einträgen aus {0, 1}
(
1 falls (ai , bj ) ∈ R
mij =
0 sonst
Verkettung von Relationen durch Matrixmultiplikation
(mit max statt + und min statt ·)
I
(gerichteter) Graph G = (A ∪ B, R) mit
Eckenmenge A ∪ B und Kantenmenge R
falls (wenigstens) eine der Mengen A und B unendlich ist,
i.A. intensionale Darstellung von Relationen R ⊆ A × B nötig
124
Was bisher geschah
Modellierung von
I
I
Aussagen durch Logiken
Daten durch
I
I
I
I
Mengen
Folgen
Sprachen
Zusammenhängen und Eigenschaften durch Relationen
I
I
I
I
Definition, Beispiele
Operationen auf Relationen:
inverse Relation, Verkettung, Projektionen, Einschränkung
Modellierungsbeispiele
Darstellungsformen binärer Relationen
Eigenschaften binärer Relationen
Eine binäre Relation R ⊆ M 2 heißt
reflexiv gdw. ∀x ∈ M : ((x, x) ∈ R)
z.B. R = {(a, a), (a, b), (b, b)} ⊆ {a, b}2 , =, ≤, v, ⊆
irreflexiv gdw. ∀x ∈ M : ((x, x) 6∈ R)
z.B. R = {(a, b), (b, a)} ⊆ {a, b}2 ,
<, ⊂, istGeschwisterVon, istKindVon
symmetrisch gdw. ∀x, y ∈ M : ((x, y ) ∈ R → (y , x) ∈ R)
z.B. R = {(a, b), (b, a), (b, b)} ⊆ {a, b}2 ,
=, istGeschwisterVon
asymmetrisch gdw. ∀x, y ∈ M : ((x, y ) ∈ R → (y , x) 6∈ R)
z.B. R = {(a, b)} ⊆ {a, b}2 , <, istKindVon,
antisymmetrisch gdw. ∀x, y ∈ M : (((x, y ) ∈ R ∧ (y , x) ∈ R) → x = y )
z.B. R = {(b, b)} ⊆ {a, b}2 , ≤, v, ⊆,
transitiv gdw. ∀x, y , z ∈ M :
(((x, y ) ∈ R ∧ (y , z) ∈ R) → (x, z) ∈ R)
z.B. R = {(c, b), (a, b), (a, c)} ⊆ {a, b, c}2 ,
=, ≤, <, v, ⊆, istVorfahreVon
mehr Beispiele und Gegenbeispiele in Kastens: Modellierung
125
Hüllen binärer Relationen
Die reflexive (symmetrische, transitive, reflexiv-transitive) Hülle einer
Relation R ⊆ M 2 ist die kleinste (bzgl. ⊆) Relation S ⊆ M 2 mit
1. R ⊆ S und
2. S reflexiv (symmetrisch, transitiv, reflexiv und transitiv).
reflexive Hülle von R: R ∪ IM
symmetrische Hülle von R: R ∪ R −1
Wiederholung: Verkettung ◦ der Relationen R ⊆ M 2 und S ⊆ M 2
R ◦ S = {(x, z) ∈ M 2 | ∃y ∈ M : (x, y ) ∈ R ∧ (y , z) ∈ S}
Iterierte Verkettung von R ⊆ M 2 mit sich selbst:
R0
R
n+1
R
+
= IM
= Rn ◦ R
[
=
Rn ⊆ M2
N
transitive Hülle
n∈ \{0}
R∗
=
[
N
Rn ⊆ M2
reflexiv-transitive Hülle
n∈
126
Beispiel
R ⊆ ({a, b, c})2
mit
R = {(a, b), (b, c)}
R −1 = {(b, a), (c, b)}
R ∪ R −1 = {(a, b), (b, c), (b, a), (c, b)}
(symmetrische Hülle)
R 0 = {(a, a), (b, b), (c, c)}
R ∪ R 0 = {(a, b), (b, c), (a, a), (b, b), (c, c)}
(reflexive Hülle)
R 2 = {(a, c)}
R3 = ∅
R
+
(= R n
2
für beliebige n ≥ 3)
3
= R ∪ R ∪ R ∪ · · · = {(a, b), (b, c), (a, c)}
(transitive Hülle)
R
∗
0
= R ∪R
+
= {(a, a), (b, b), (c, c), (a, b), (b, c), (a, c)}
(reflexiv-transitive Hülle)
127
Modellierungsbeispiel: Lineares Solitaire
Spielbeginn: n Spielsteine, je einer auf n benachbarten Spielfeldern
in einer Reihe.
Spielzug: Springe mit einem Stein über einen benachbarten
Stein auf das dahinterliegende freie Feld und entferne
den übersprungenen Stein.
Spielende: Das Spiel endet, wenn kein Spielzug möglich ist.
Modellierung für n = 4:
I
Spielfeld ∈ {0, 1} (frei, belegt)
I
Spielzustand: Folge von Spielfeldern,
z.B. 011110 (Spielbeginn), 100110, 010010
Menge aller Spielzustände ⊆ {0, 1}6 (4 + 2 Randfelder)
128
Modellierung: Lineares Solitaire
I
I
I
Menge der Spielzustände Q = {0, 1}6 ,
Startzustand 011110 ∈ Q,
Übergangsrelation T ⊆ Q 2 mit


 (011110, 100110) , (011110, 011001) 
(100110, 100001) , (011001, 100001)
T =


(100110, 101000) , (011001, 000101)
Hüllen der Übergangsrelation enthalten
zusätzliche Möglichkeiten für Spielzüge:
I reflexive Hülle T ∪ IQ
Aussetzen
I symmetrische Hülle T ∪ T −1
umgekehrte Züge
I transitive Hülle T +
mehrere Züge auf einmal (aber wenigstens einer)
I reflexiv-transitive Hülle T ∗
beliebig viele Züge auf einmal (Aussetzen erlaubt)
129
Quasiordnungen
Relation R ⊆ M 2 heißt Quasiordnung gdw. R reflexiv und transitiv
Beispiele:
I
R ⊆ {a, b, c}2 mit
R = {(a, a), (a, b), (b, b), (b, c), (a, c), (c, c)}
I
T ⊆ (Menge aller Personen)2 mit
(p, q) ∈ T gdw. p höchstens so alt ist wie q
I
S⊆
Z2 mit S = {(a, b) ∈ Z2 | |a| ≥ |b|}
130
Äquivalenzrelationen
Relation R ⊆ M 2 heißt Äquivalenzrelation
gdw. R reflexiv, transitiv und symmetrisch
(symmetrische Quasiordnung)
Beispiele:
I
R ⊆ {a, b, c}2 mit R = {(a, a), (a, b), (b, a), (b, b), (c, c)}
I
Relation haben dieselbe Farbe“ für Paare von Skatkarten
”
R ⊆ (F × W )2 für F = {♦, ♥, ♠, ♣} und
W = ({7, 8, 9, 10} ∪ {B, D, K , A}) mit
R = {((f , w1 ), (f , w2 )) | (f ∈ F ) ∧ (w1 ∈ W ) ∧ (w2 ∈ W )}
I
I
Relation sind im selben Studiengang“ für Studenten
”
R ⊆ (A∗ )2 mit R = {(u, v ) ∈ (A∗ )2 | |u| = |v |} (gleiche
Länge)
I
Gleichmächtigkeit von Mengen: (A, B) ∈ R gdw. |A| = |B|
I
Ähnlichkeit von Dreiecken
I
für jede Menge M: IM ⊆ M 2 mit IM = {(x, x) | x ∈ M}
131
Äquivalenzklassen
Zu jeder Äquivalenzrelation R ⊆ M 2 heißen
I
zwei Elemente a ∈ M und b ∈ M genau dann
äquivalent bzgl. R, wenn (a, b) ∈ R
I
die Menge aller zu a ∈ M äquivalenten Elemente aus M
[a]R = {x ∈ M | (a, x) ∈ R}
Äquivalenzklasse von a bzgl. R
Beispiele:
I
Äquivalenzklassen bzgl. der Äquivalenzrelation R ⊆ {a, b, c}2
mit R = {(a, a), (a, b), (b, a), (b, b), (c, c)}:
[a]R = {a, b} = [b]R und [c]R = {c}
I
Äquivalenzklassen bzgl. der Äquivalenzrelation
haben dieselbe Farbe“ für Skatkarten:
”
K♦ , K♥ , K♠ , K♣ (siehe Übungsaufgabe 5.1.a)
[(♦, B)]R = K♦ = {(♦, w ) | w ∈ {7, 8, 9, 10, B, D, K , A}}
132
Äquivalenzrelationen und disjunkte Zerlegungen
1. Jede Äquivalenzrelation R ⊆ M 2 definiert eine disjunkte Zerlegung
von M in die Menge aller Äquivalenzklassen
{[a]R | a ∈ M}
2. Jede (disjunkte) Zerlegung P = {Mi | i ∈ I } einer Menge M
definiert eine Äquivalenzrelation
RP ⊆ M 2
mit
RP = {(a, b) | ∃i ∈ I : {a, b} ⊆ Mi }
Beispiele:
I
Relation R ⊆ {a, b, c}2 mit R = {(a, a), (a, b), (b, a), (b, b), (c, c)}
definiert Zerlegung {[a]R , [b]R , [c]R } = {{a, b}, {c}}
der Menge {a, b, c}
I
Zerlegung F = {K♦ , K♥ , K♠ , K♣ } der Menge aller Skatkarten
definiert die Relation RF (haben dieselbe Farbe)
I
Zerlegung P = {3 , 3 + 1, 3 + 2}
definiert die Relation RP = {(m, n) ∈
N N
N
N2 | 3|(m − n)}
133
Was bisher geschah
Modellierung von
I
Aussagen durch Logiken
I
Daten durch Mengen, Folgen, Sprachen
I
Zusammenhängen und Eigenschaften durch Relationen
I
I
I
I
I
Definition, Beispiele
Operationen auf Relationen:
inverse Relation, Verkettung, Einschränkung, Projektionen
Eigenschaften binärer Relationen R ⊆ M 2
reflexive, symmetrische, transitive Hüllen
spezielle binäre Relationen auf einer Menge:
Quasiordungen, Äquivalenzrelationen
Halbordnungen (partielle Ordnungen)
Relation R ⊆ M 2 heißt Halbordnung
gdw. R reflexiv, transitiv und antisymmetrisch
(antisymmetrische Quasiordnung)
a ∈ M und b ∈ M heißen genau dann vergleichbar bzgl. R,
wenn (a, b) ∈ R oder (b, a) ∈ R
Beispiele:
I
R ⊆ {a, b, c, d}2 mit
R = {(a, a), (a, b), (a, c), (a, d), (b, b), (b, d), (c, c), (d, d)}
I
≤⊆
I
R ⊆ ( Menge aller AMB-Studenten )2 mit
(p, q) ∈ R gdw. (Matrikelnr. von p) ≤ (Matrikelnr. von q)
I
v ⊆ ({a, b}∗ )2
I
Teilerrelation | ⊆ 2 mit a|b gdw. ∃n ∈
(Warum ist | ⊆ 2 keine Halbordnung?)
I
Teilmengenrelation ⊆ auf 2{a,b,c}
N2 (≤ ⊆ Z2, ≤ ⊆ R2)
N
Z
Z | an = b
134
Hasse-Diagramme von Halbordnungen
(für Halbordnungen auf endlichen Mengen)
graphische Darstellung der Relation mit folgenden Konventionen:
I
Pfeilspitzen weglassen,
stattdessen optische Ausrichtung (nach oben)
I
reflexive Kanten (Schlingen) weglassen
I
transitive Kanten weglassen
Beispiele (Tafel):
I
Teiler-Halbordnung | auf {0, . . . , 6}
I
≤ auf {0, . . . , 6},
I
Halbordnung ⊆ auf 2{a,b,c} ,
135
Totale Ordnungen
Jede Halbordnung R ⊆ M 2 mit
∀(a, b) ∈ M 2 ((a, b) ∈ R ∨ (b, a) ∈ R)
(alternativ)
heißt totale (lineare) Halbordnung.
(alle Elemente miteinander vergleichbar)
Beispiele:
I
R ⊆ ({a, b, c})2 mit
R = {(a, a), (a, b), (a, c), (c, b), (b, b), (c, c)}
I
≤⊆
I
R ⊆ ( Menge aller AMB-Studenten )2 mit
(p, q) ∈ R gdw. (Matrikelnr. von p) ≤ (Matrikelnr. von q)
I
alphabetische Ordnung der Wörter im Wörterbuch
N2 (≤ ⊆ Z2, ≤ ⊆ R2)
136
Totale Ordnungen
häufige Aufgabe: Sortieren von Elementen
z.B. Menge von Wörtern aus A∗ : {ab, ε, a, ac, abc, c}
Präfix-Relation v A∗ × A∗ mit
∀(u, v ) ∈ A∗ × A∗ ((u v v ) ↔ ∃v 0 ∈ A∗ (u ◦ v 0 = v ))
ist reflexiv,transitiv, antisymmetrisch, also eine Halbordnung
Gilt ∀(u, v ) ∈ (A∗ × A∗ ) : ((u v v ) ∨ (v v u)) ?
nein, z.B. für A = {a, b, c}, u = ab, v = ac gilt ab 6v ac und
ac 6v ab
v ist also keine totale Ordnung auf A∗
Sortieren lassen sich nur Elemente aus totalen Ordnungen
totale Ordnungen auf A∗ ?
137
Ordnungen auf A∗
Relationen auf A∗ ohne Beachtung der Ordnung auf Alphabet A:
Präfix-, Postfix-, Infix-Relation auf A∗ sind
Halbordnungen, nicht total (linear)
bei gegebener totaler Ordnung < auf dem Alphabet A:
lexikographische Ordnung auf A∗ :
∀u, v ∈ A∗ : u ≤lex v gdw.
1. u v v oder
2. ∃w ∈ A∗ ∃a, b ∈ A : a < b ∧ wa v u ∧ wb v v
quasi-lexikographische Ordnung auf A∗ :
∀u, v ∈ A∗ : u ≤qlex v gdw.
1. |u| < |v | oder
2. |u| = |v | ∧ u ≤lex v
Beispiele: für A = {a, b} mit a < b
I ab v aba, ab ≤lex aba, ab ≤qlex aba
I abab 6v abba, aber abab ≤lex abba und abab ≤qlex abba,
I aaa ≤lex ab, aber aaa 6≤qlex ab
I ab 6≤lex aaba, aber ab ≤qlex aaba
138
Funktionen (Wiederholung)
Funktion: spezielle Relation mit Richtung
Relation f ⊆ A× B heißtgenau dann partielle Funktion,
wenn ∀a ∈ A : π2 f |{a} ≤ 1
Relation f ⊆ A× B heißtgenau dann (totale) Funktion,
wenn ∀a ∈ A : π2 f |{a} = 1
Beispiele:
I
Relation zwischen Personen und ihrem Geburtstag
ist eine totale Funktion
I
Relation zwischen Tagen und Personen, die an diesem Tag
Geburtstag haben, ist keine Funktion
I
R⊆
I
I
I
Z2 mit R = {(x, x 2 ) | x ∈ Z} ist (totale) Funktion
R −1 ⊆ Z2 mit R −1 = {(x 2 , x) | x ∈ Z} ist keine Funktion
S ⊆ N2 mit S = {(x 2 , x) | x ∈ N} ist partielle Funktion
T ⊆ R2 mit T = {(sin x, x) | x ∈ R} ist keine Funktion
139
Definition von Funktionen
Funktion f : A → B wird definiert durch Angabe von:
Typ (Signatur):
Definitionsbereich : Menge A
Wertebereich : Menge B
Werte Zuordnung f
extensional z.B. f = {a 7→ 1, b 7→ 0}
(statt f = {(a, 1), (b, 0)})
intensional z.B. ∀x ∈ : f (x) = x 2
Syntax
Semantik
N
Graph von f : Relation f ⊆ A × B = {(x, f (x)) | x ∈ A}
140
Mehrstellige Funktionen auf einer Menge
Funktion f : A → B mit
A = B n : Funktion f : B n → B heißt auch
n-stellige Funktion auf B
Achtung: n-stellige Funktionen auf B sind
(n + 1)-stellige Relationen auf B.
Beispiel: f : × → mit
∀(x, y ) ∈ 2 : f (x, y ) = 2x + y
N
A=
B0
N N N
= {ε}:
Nullstellige Funktionen f : B 0 → B heißen auch
Konstanten f ∈ B.
Beispiel: c : 0 → mit c = 3
N
N
141
Abgeleitete Funktionen
Für Funktion f : A → B heißt
f (A) = π2 (f ) ⊆ B Bild von f ,
f (M) = π2 (f |M ) ⊆ B für M ⊆ A Bild von M unter f ,
f (a) = π2 f |{a} ∈ B für a ∈ A Bild von a unter f ,
f −1 (N) = π2 f −1 |N ⊆ A für N ⊆ B Urbild von N unter f ,
f −1 (b) = π2 f −1 |{b} ⊆ A für b ∈ B Urbild von b unter f
Für jede (totale) Funktion f : A → B gilt f −1 (B) = A
142
Eigenschaften von Funktionen (Wiederholung)
Funktion f : A → B heißt
injektiv , falls für alle b ∈ B gilt f −1 (b) ≤ 1,
surjektiv , falls für alle b ∈ B gilt f −1 (b) ≥ 1,
bijektiv , falls für alle b ∈ B gilt f −1 (b) = 1,
Eine Funktion ist genau dann bijektiv,
wenn sie injektiv und surjektiv ist.
Beispiele:
N → N mit ∀x ∈ N : f (x) = x 2 ist injektiv, nicht surjektiv
: Z → Z mit ∀x ∈ Z : f (x) = x 2 ist weder injektiv noch
I
f :
I
f
surjektiv
I
f : ≥0 →
surjektiv
R
R≥0 mit ∀x ∈ R≥0 : f (x) = x 2 ist injektiv und
143
Mengen von Funktionen
Menge aller (totalen) Funktionen von A nach B:
B A = {f : A → B} = {f ⊆ A × B | ∀a ∈ A : π2 f |{a} = 1}
Beispiel: {0, 1}{p,q,r } = {W : {p, q, r } → {0, 1}}
Für alle endlichen Mengen A, B gilt B A = |B||A| .
( Es existieren |B||A| verschiedene Funktionen von A nach B.)
Beispiele:
I
|{0, 1}||{p,q,r }| = 23 = 8 Funktionen W : {p, q, r } → {0, 1}
I
3|A| Funktionen f : A → {rot, grün, blau}
I
4|A| Funktionen f : A → {1, 2, 3, 4}
I
4|A| Funktionen f : A → {0, 1}2
144
Was bisher geschah
Modellierung von
I
Aussagen durch Logiken
I
Daten durch Mengen, Folgen, Sprachen
Darstellungsformen, Anwendungen, Beziehungen, Operationen
I
Zusammenhängen und Eigenschaften durch Relationen
Darstellungsformen, Anwendungen, Beziehungen, Operationen
I
I
I
I
Eigenschaften binärer Relationen R ⊆ M 2
reflexive, symmetrische, transitive Hüllen
Äquivalenzrelationen, Halbordungen, totale Ordnungen
Zuordnungen durch Funktionen (spezielle Relationen)
Darstellungsformen, Anwendungen, Beziehungen, Operationen
I
I
Menge B A aller (totalen) Funktionen f : A → B
injektive, surjektive, bijektive Funktionen (Wiederholung)
Funktionen auf Anfangsstücken von
Funktion f : I → B mit I = {0, . . . , n} ⊂
N
N
Beispiel:
f : {0, . . . , 4} → B, wobei ∀n ∈ {0, 1, . . . , 4} : f (n) = 7n + 2
f (0) = 2, f (1) = 9, f (2) = 16, f (3) = 23, f (4) = 30
alternative Darstellung:
f0 = 2, f1 = 9, f2 = 16, f3 = 23, f4 = 30
Folge f = [2, 9, 6, 23, 30] =(7n + 2)i∈{0,...,4}
Jede Funktion f : I → B mit I = {0, . . . , n} repräsentiert
eine eindeutig definierte Folge (f (i))i∈I ∈ B ∗
Jede Folge (ai )i∈I ∈ B ∗ repräsentiert
eine eindeutig definierte Funktion a : I → B mit a(i) = ai
145
Funktionen nach {0, 1}
Für endliche Mengen A und B
I
I
(Anzahl)
A0
nullstellige Funktionen f :
→ {0, 1}
f0 = 0, f1 = 1 (Konstanten)
0
2|A | = 21 = 2
2|A|
einstellige Funktionen f : A → {0, 1}
Beispiel: für A = {a, b}
f00 = {a 7→ 0, b 7→ 0}
f01 = {a 7→ 0, b 7→ 1}
f10 = {a 7→ 1, b 7→ 0}
f11 = {a 7→ 1, b 7→ 1}
mögliche Urbilder der 1:
−1
−1
−1
−1
f00
(1) = ∅, f01
(1) = {b}, f10
(1) = {a}, f11
(1) = {a, b}
für
beliebige
Menge
A:
−1
f (1) ∈ A | f ∈ 2A = 2A (Potenzmenge von A)
I
zweistellige Funktionen f : A × B → {0, 1}
2(|A||B|)
146
Charakteristische Funktion einer Menge
Menge A definiert für jede Teilmenge B ⊆ A die
charakteristische Funktion χB : A → {0, 1} mit
(
1 falls x ∈ B
∀x ∈ A : χB (x) =
0 sonst
Beispiel: für A = {a, b, c, d} und B = {a, d} ⊆ A gilt
χB : A → {0, 1} mit χB = {a 7→ 1, b 7→ 0, c 7→ 0, d 7→ 1}
(χB ordnet jedem x ∈ A den Wahrheitswert der Aussage x ∈ B zu.)
Umgekehrt definiert jede Funktion f : A → {0, 1} eine Teilmenge
f −1 (1) ⊆ A
Für endliche Mengen A = {a1 , . . . , an } und
beliebige feste Anordnung [a1 , . . . , an ]
lässt sich jede Teilmenge B ⊆ A durch das eindeutige
Binärwort (charakteristischer Vektor) b1 . . . bn ∈ {0, 1}n mit bi = χB (ai )
repräsentieren.
147
Multimengen (Vielfachmengen, Bags)
zur Beschreibung von Elementen mit Vielfachheit
Beispiele:
I Bibliothek mit mehreren Exemplaren von Büchern
I Vorrat an Münzen
I Rommé-Blatt
Teilmenge A einer Menge U (Universum)
als charakteristische Funktion von A bzgl. U:
χA : U → {0, 1} mit
∀x ∈ U : χA (x) = |A ∩ {x}|
N
Multimenge A über Menge U: Funktion A : U →
alternative Darstellungen von Multimengen:
z.B. für U = {a, b, c, d} und A : U → mit
A(a) = 3, A(b) = 3, A(c) = 0, A(d) = 1 durch
I {a 7→ 3, b 7→ 3, c 7→ 0, d 7→ 1} (Reihenfolge egal)
I {a, b, a, b, d, b, a} (Reihenfolge egal)
I als Relation A ⊆ U × ( \ 0) mit {(a, 3), (b, 3), (d, 1)}
N
N
148
Beziehungen zwischen Multimengen
Multimenge A : U →
Multimenge B : U →
N ist genau dann Teil(multi)menge der
N, wenn
∀x ∈ U : A(x) ≤ B(x)
(A punktweise ≤ B)
N
Zwei Multimengen A : U → und B : U →
gleich, wenn
∀x ∈ U : A(x) = B(x)
N sind genau dann
(Charakteristische Funktionen von) Mengen A ⊆ U sind spezielle
Multimengen mit der Eigenschaft ∀x ∈ U : A(x) ≤ 1
149
Operationen auf Multimengen
Für Multimengen A : U →
N und B : U → N
Vereinigung ∀x ∈ U : (A ∪ B)(x) = max(A(x), B(x))
˙
disjunkte Vereinigung ∀x ∈ U : (A∪B)(x)
= A(x) + B(x)
Schnitt ∀x ∈ U : (A ∩ B)(x) = min(A(x), B(x))
Differenz ∀x ∈ U : (A \ B)(x) = max(0, A(x) − B(x))
(mehr dazu und weitere Operationen in den
LV zu Datenbanken)
Für den Spezialfall Mengen (Funktionen nach {0, 1}) ergibt das
genau die Mengenoperationen
Mächtigkeit der Multimenge A : U →
N:
|A| =
P
x∈U
A(x)
150
Was bisher geschah
Modellierung von
I
I
Aussagen durch Logiken
Daten durch
I
I
I
I
I
Mengen (endliche und unendliche Mächtigkeiten)
Folgen als Funktionen f : {0, . . . , n} → B
Multimengen, Folgen, Sprachen
charakteristische Funktionen
χA : U → {0, 1} von (Teil-)Mengen A ⊆ U
Multimengen A : U →
N
I
Zusammenhängen und Eigenschaften durch Relationen
Spezielle binäre Relationen:
Äquivalenzrelationen, Halbordnungen, totale Ordnungen
I
Zuordnungen durch Funktionen (spezielle Relationen)
Anzahl injektiver Funktionen
Satz
Die Anzahl aller injektiven Funktionen von einer endlichen Menge
A in eine endliche Menge B ist
|A|−1
|{f : A → B | f injektiv}| =
Y
(|B| − i)
i=0
Folgerung
Für endliche Mengen A und B mit |A| > |B| existiert keine
injektive Funktion f : A → B.
151
Endlicher Schubfachschluss
(pigeonhole principle)
Satz (endlicher Schubfachschluss)
Sind O und S zwei endliche Mengen mit |O|
> |S|, dann existiert
für jede Funktion f : O → S ein s ∈ S mit f −1 (s) > 1.
umgangssprachliche Formulierung:
O – Menge von Objekten
S – Menge von Schubfächern
Für jede Aufteilung von n Objekten auf k < n Schubfächer
existiert ein Schubfach, welches mehr als ein Objekt enthält.
152
Beispiele
I
Von 13 Personen haben wenigstens zwei im gleichen Monat
Geburtstag.
O: 13 Personen, S: 12 Monate
I
Bei 5mal Rast auf einer Wanderung in einem Gebiet mit 3
Einkehrmöglicheiten (wenigstens) eine mehrfach besucht.
O: 5 Zeitpunkte, S: 3 Einkehrmöglichkeiten
I
10 verschiedenfarbige Paare Socken
Wieviele blind nehmen für einfarbiges Paar?
O: x < 20 Socken, S: 10 Farben
gesucht: kleinstes x mit x > |S| (x = 11)
I
je 10 schwarze und weiße Socken
Wieviele blind nehmen für einfarbiges Paar?
O: x < 20 Socken, S: 2 Farben (x = 3)
I
Partygespräche: n ≥ 2 Personen
Anzahl Gesprächspartner ist für zwei Personen gleich.
O: n Gäste, S: Anzahl der Gesprächspartner ∈ {0, . . . , n − 1}
Problem: |O| = |S|
Fallunterscheidung: {p1 , . . . , pn } enthält 0 oder nicht
153
Erweiterter Schubfachschluss
Satz
Sind O und S zwei endliche Mengen, dann existiert für jede
Funktion f : O → S ein s ∈ S mit
−1 f (s) ≥ |O|
|S|
umgangssprachliche Formulierung:
Für jede Aufteilung von n Objekten auf k Schubfächer existiert ein
Schubfach, welches mindestens d kn e Objekte enthält.
154
Beispiele
I
Unter 30 Personen sind mindestens 5 am gleichen Wochentag
geboren.
O: 30 Personen, S: 7 Wochentage
also existiert Wochentag s ∈ S mit f −1 (s) ≥ 30
7 =5
I
Von 5 Aussagen haben wenigstens 3 denselben Wahrheitswert.
O: 5 Aussagen, S: {0, 1}
also existiert Wahrheitswert s ∈ {0, 1} mit f −1 (s) ≥ 25 = 3
I
Wieviele Karten höchstens nötig für komplette Farbe aus
Skatblatt?
−1
O: x ≤ 32 Karten, S: 4 Farben,
x für jede f (s) = 8
gesucht: kleinstes x mit 7 < 4 , also x = 29
I
Unter je 6 Personen existieren immer entweder 3, die einander
kennen oder 3, die einander nicht kennen.
155
Unendlicher Schubfachschluss
endlicher (erweiterter) Schubfachschluss:
Sind O und S zwei endliche Mengen, dann existiert für jede
Funktion f : O → S ein s ∈ S mit
−1 |O|
f (s) ≥
|S|
mit |O| wächst (bei festem S) auch
|O|
|S|
Satz (unendlicher Schubfachschluß)
Sind O eine unendliche und S eine endliche Menge, dann existiert
für jede Funktion f : O → S ein s ∈ S mit unendlichem Urbild
f −1 (s).
umgangssprachliche Formulierung:
Für jede Aufteilung unendlich vieler Objekte auf endliche viele
Schubfächer existiert ein Schubfach, welches unendlich viele
Objekte enthält.
156
Beispiele
N
I
In jeder unendlichen Menge A ⊆ enden unendlich viele
Zahlen auf dieselbe Ziffer.
O: A, S: 10 mögliche letzte Stellen
I
In jeder unendlichen Folge von Ziffern kommt (wenigstens)
eine Ziffer unendlich oft vor.
O: Folgen-Indices , S: 10 mögliche Ziffern
N
I
In jeder unendlichen Folge von Symbolen aus einem endlichen
Alphabet A kommt (wenigstens) ein Symbol aus A unendlich
oft vor.
O: Folgen-Indices , S: |A| Symbole
N
157
Modellierungsbeispiel EU-Arbeitskreise
(nach Kastens, Kleine Büning: Modellierung )
Ziel: Modellierung der Situation
I
drei Arbeitskreise
I
Nationen D,F,A,S senden je 3 Delegierte
I
Jedem Arbeitskreis soll aus jeder Nation (wenigstens) ein
Delegierter angehören.
I
In jedem Arbeitskreis gibt es (wenigstens) einen gemeinsame
Sprache.
Wertebereiche:
Arbeitskreise
Länder
Sprachen
Delegierten-Nr.
Delegierte
:
:
:
:
:
A = {A} × {1, 2, 3} = {A1, A2, A3}
N = {D, F , A, P}
S = {d, f , p}
D = {1, 2, 3}
D0 = N × D
Was repräsentieren π1 (D 0 ), D 0 |{A,F } ?
158
Modellierungsbeispiel EU-Arbeitskreise
I
Zuordnung der (momentanen) Sprachkenntnisse zu Delegierten
0
I als Relation s
D ⊆ D × S, z.B.
sD = {(D1, d), (D1, f ), (D2, d), (D2, p), (D3, d), (F 1, f ),
(F 2, f ), (F 3, f ), (F 3, p), (A1, d), (A2, d), (A2, f ), (A3, p), . . .}
I als Funktion s 0 : D 0 → 2S , z.B. mit
D
sD0 (D1) = {d, f }, sD0 (D2) = {d, p}, sD0 (D3) = {d},
sD0 (F 1) = {f } = sD0 (F 2), sD0 (F 3) = {f , p},. . .
I
Sprachkenntnisse in der Delegation einer Nation
I als Relation s
N ⊆ N × S,
z.B. sN = {(D, d), (D, f ), (D, p), (F , f ), (F , p), . . .}
I als Funktion s 0 : N → 2S (Mengen von Sprachen),
N
z.B. sN0 (D) = {d, f , p}, sN0 (F ) = {f , p}, . . .
s
I als Funktion s 00 : N →
(Multimengen von Sprachen), z.B.
N
00
sN (D) = {d 7→ 3, f 7→ 1, p 7→ 1}, sN00 (F ) = {f 7→ 3, p 7→ 1},
sN00 (A) = {d 7→ 2, p 7→ 1},. . .
N
Was repräsentieren
sD |{D1,A2,F 1} , sD0 (D 0 |{A,D} ), sN0 (D) ∩ sN0 (F ), sN00 (D) ∩ sN00 (F ),
(sN0 )−1 ({f , p}) ?
159
Was bisher geschah
Modellierung von
I
Aussagen durch Logiken
I
Daten durch
Mengen (endliche und unendliche Mächtigkeiten)
Multimengen, Folgen, Sprachen
I
Zusammenhängen und Eigenschaften durch Relationen
Spezielle binäre Relationen:
Äquivalenzrelationen, Halbordnungen, totale Ordnungen
I
Zuordnungen durch Funktionen (spezielle Relationen)
jeweils mit Anwendungsbeispielen
Wiederholung: Darstellung binärer Relationen
Darstellungsformen für binäre Relation R ⊆ M 2 auf
endlicher Menge M:
I
Menge geordneter Paare (intensional oder extensional)
I
n × n-Matrix (für M = {a1 , . . . , an }) mit Einträgen aus {0, 1}
(
1 falls (ai , aj ) ∈ R
mij =
0 sonst
I
(Charakteristische Funktion der Relation)
(gerichteter) Graph G = (M, R) mit
I
I
Menge M von Ecken und
Menge R von Kanten
(Diagramm)
wichtige Eigenschaften binärer Relationen:
(ir)reflexiv, transitiv, (a)symmetrisch, antisymmetrisch
160
Gerichtete Graphen
gerichteter Graph G = (V , E ) (Digraph)
I Menge V von Ecken oder Knoten (vertex)
I Menge E ⊆ V 2 von Kanten (edge)
häufige Notation: ab statt (a, b)
Start- und Endpunkt von (a, b) ∈ E sind a, b ∈ V
Schlinge Kante (a, a) ∈ E mit a ∈ V
Beispiele:
I G = (V , E ) mit
V
= {0, 1, . . . , 4}
E
= {(i, j) ∈ V 2 | j = i + 1 ∨ j = i + 3}
Abläufe (z.B. lineares Solitaire)
gerichteter Graph:
(endliche) Menge V mit einer zweistelligen Relation E ⊆ V 2
I
161
Repräsentationen endlicher Graphen
Graph G = (V , E )
2
Relation E ⊆ V 2 (also E ∈ 2(V ) )
(extensionale oder intensionale) Angabe aller
Elemente in V und E
Diagramm des Graphen
Adjazenzmatrix von G = (V , E ) mit V = {v1 , . . . , vn }:
2
|V |2 -Matrix MG ∈ {0, 1}(|V | ) mit
1 wenn (vi , vj ) ∈ E
2
∀(i, j) ∈ |V | : MG (i, j) =
0 sonst
(charakteristische Funktion der Relation E ⊆ V 2 )
Adjazenzliste von G = (V , E ):
V
LG ⊆ V
× 2 mit LG = v , π2 E |{v } | v ∈ V
= {(v , U) | v ∈ V ∧ U = {u ∈ V | (v , u) ∈ E }}
162
Ungerichtete Graphen
ungerichteter schlingenfreier Graph (V , E ):
Menge V von Ecken
I Menge E ⊆ V von Kanten
2
häufige Notation: ab statt {a, b}
V
= {M ⊆ V | |M| = k} = {M ⊆ V | M enthält genau k Elemente}
k
I
ungerichteter Graph mit Schlingen: (V , E ) mit
V
V
E⊆
∪
= {M ⊆ V | |M| = 2 ∨ |M| = 1}
2
1
Beispiele:
I
G =n
(V , E ) mit V = {0, 1, . . . , 4} undo
E = {i, j} ∈ V2 | i − j ≡ 0 (mod 2)
I
Liniennetz Nahverkehr
Graph (ohne Zusatz) bedeutet im Folgenden immer
endlich, ungerichtet und schlingenfrei
(Darstellung einer symmetrischen irreflexiven Relation)
163
Spezielle Graphen
(ungerichtet, schlingenfrei)
Ordnung des Graphen (V , E ): Anzahl |V | der Ecken
leerer Graph (V , E ) mit V = ∅ und E = ∅
Der Graph (V , E ) mit V = {v1 , . . . , vn } heißt
isoliert: In = ({v1 , . . . , vn }, ∅) (n isolierte Ecken)
vollständig: Kn = ({v1 , .. . , vn }, E )
mit E = V2 ) (n paarweise verbundene Ecken)
Pfad: Pn = ({v1 , . . . , vn }, E )
mit E = {{vi , vi+1 } | i ∈ {1, . . . n − 1}}
Kreis: Cn = ({v1 , . . . , vn }, E )
mit E = {{vi , vi+1 } | i ∈ {1, . . . n − 1}} ∪ {{vn , v1 }}
164
Nachbarschaft
Ecken u, v ∈ V heißen im Graphen (V , E )
benachbart (adjazent) gdw. uv ∈ E
unabhängig gdw. uv 6∈ E
Nachbarschaft (Menge aller Nachbarn) einer Ecke v in G :
NG (v ) = {u ∈ V | uv ∈ E }
Ecke v ∈ V mit NG (v ) = ∅ heißt isoliert.
Graph G = (V , E ) definiert Funktion gradG : V →
N mit
∀a ∈ V : gradG (a) = |NG (a)|
gradG (a) heißt Grad der Ecke a.
(V , E ) heißt n-regulär (regulär) gdw. ∀a ∈ V : gradG (a) = n
165
Eckengrad in gerichteten Graphen
Nachbarn in gerichteten Graphen G = (V , E ):
I
∀v ∈ V : Ni,G (v ) = {u ∈ V | uv ∈ E }
(in v eingehende Kanten)
I
∀v ∈ V : No,G (v ) = {u ∈ V | vu ∈ E }
(von v ausgehende Kanten)
gerichteter Graph G = (V , E ) definiert Funktionen
I
gradi,G : V →
N mit
∀a ∈ V : gradi,G (a) = |Ni,G (a)|
gradi,G (a) heißt Eingangs-Grad der Ecke a.
I
grado,G : V →
N mit
∀a ∈ V : grado,G (a) = |No,G (a)|
grado,G (a) heißt Ausgangs-Grad der Ecke a.
166
Graph-Isomorphie
Für Graphen G = (VG , EG ) und H = (VH , EH ) heißt eine Bijektion
f : VG → VH Isomorphismus gdw.
∀a, b ∈ VG ((f (a), f (b)) ∈ EH ↔ (a, b) ∈ EG )
Graphen G und H, zwischen denen ein Isomorphismus existiert,
heißen isomorph (G ' H).
Isomorphie ist Äquivalenzrelation auf Menge aller Graphen.
Kn , In , . . . bezeichnen Äquivalenzklassen von Graphen bzgl. '
167
Teilgraph-Relationen
Für Graphen G = (VG , EG ) und H = (VH , EH ) heißt H
Teilgraph von G , gdw. VH ⊆ VG und EH ⊆ EG
echter Teilgraph von G , gdw. H Teilgraph von G und H 6= G
induzierter Teilgraph von G , gdw.
VH ⊆ VG und EH = {{a, b} ∈ EG | {a, b} ⊆ VH }
(Autotool: Beschränkung von G auf VH )
aufspannender Teilgraph von G , gdw.
H Teilgraph von G und VH = VG
Alle dieser Teilgraph-Relationen sind Halbordnungen.
168
Operationen auf Graphen
Für zwei Graphen G = (VG , EG ) und H = (VH , EH ):
G ∪ H = (VG ∪ VH , EG ∪ EH )
G ∩ H = (VG ∩ VH , EG ∩ EH )
G ∗ H = (VG ∪ VH , EG ∪ EH ∪ (VG × VH ))
für VG und VH disjunkt (ggf. Knoten umbenennen)
spezielle Graphen:
Km,n = Im ∗ In (vollständige bipartite Graphen)
K1,n = I1 ∗ In (Sterne)
Kn1 ,...,nm = In1 ∗ · · · ∗ Inm für m > 1
169
Was bisher geschah
I
gerichtete / ungerichtete Graphen G = (V , E )
I
Darstellungen von Graphen
I
Spezielle Graphen: In , Kn , Pn , Cn , Km,n , K1,n , Kn1 ,...,nm
I
Beziehungen zwischen Graphen:
Isomorphie, Teilgraph-Relationen
I
Operationen auf Graphen: ∪, ∩, ∗
I
Nachbarschaften und Eckengrade in Graphen,
n-reguläre Graphen
Komplementärgraph
für G = (V , E ) und Eckenmenge U ⊆ V
G − U = (V \ U, E \ {{u, v } | {u, v } ∩ U 6= ∅})
Für G = (V , E ) und Kantenmenge F ⊆
V
2
G − F = (V , E \ F )
Komplementärgraph zu G = (V , E ):
V
G = V,
\ E = K|V | − E
2
G heißt selbstkomplementär gdw. G ' G
Beispiele: P4 , C5
170
Pfade in Graphen
Pfad im Graphen G :
Teilgraph P von G , der für ein n ∈
N isomorph zu Pn ist.
Pfad P = (V 0 , E 0 ) in G = (V , E ) ist eindeutig bestimmt durch
I
Menge E 0 ⊆ E der Kanten oder
I
Folge [v1 , . . . , vn ] der Ecken in V 0 ⊆ V
Länge des Pfades = Anzahl der Kanten im Pfad
z.B. Länge von P5 ist 4
Pfad von a nach b im Graphen G :
Pfad p = [v1 , . . . , vn ] in G mit v1 = a und vn = b
Maximaler Pfad in G bzgl. Teilgraph-Relation:
Pfad P = (V 0 , E 0 ) ist maximaler Pfad in G = (V , E ) gdw.
für alle Kanten ab ∈ E gilt:
(V 0 ∪ {a, b}, E 0 ∪ {ab}) ist kein Pfad in G
171
Kreise in Graphen
Kreis im Graphen G :
Teilgraph C von G , der für ein n ∈
N isomorph zu Cn ist.
echte Kreise: Cn mit n ≥ 3
Kreis C = (V 0 , E 0 ) in G = (V , E ) ist eindeutig bestimmt durch
I
Menge E 0 ⊆ E der Kanten oder
I
Folge [v1 , . . . , vn ] der Ecken in V 0 ⊆ V
Länge des Kreises = Anzahl der Kanten im Kreis
z.B. Länge von C5 ist 5
172
Wege in Graphen
Weg w im Graphen G = (V , E ):
Folge von Kanten w = [v1 v2 , . . . , vn vn+1 ] ∈ E ∗
(Kanten können mehrfach vorkommen)
durch Folge der Ecken [v1 , . . . , vn+1 ] eindeutig bestimmt
Weg von a nach b in G :
Weg [v1 , . . . , vn ] in G mit v1 = a und vn = b
Für jede Ecke v ∈ V ist [v ] ein Weg von v nach v
Wege [v1 , . . . , vn ] mit v1 = vn heißen geschlossen
173
Zusammenhang in ungerichteten Graphen
Reflexiv-transitive Hülle E ∗ ⊆ V 2 der Kanten-Relation E ⊆ V 2
heißt Zusammenhangsrelation im Graphen G = (V , E )
also: (u, v ) ∈ E ∗ (u und v sind in G zusammenhängend) gdw. ein
Weg von u nach v in G existiert
Für jeden ungerichteten Graphen G = (V , E ) ist E ∗ eine
Äquivalenzrelation auf V .
(Äquivalenzklassen [u]E ∗ sind Mengen von Knoten)
Von den Äquivalenzklassen [u]E ∗ induzierte Teilgraphen von G
heißen Zusammenhangskomponenten von G
Graph G = (V , E ) heißt zusammenhängend gdw.
G aus genau einer Zusammenhangskomponente besteht.
174
Zusammenhang in gerichteten Graphen
Transitive Hülle E ∗ ⊆ V 2 der Kanten-Relation E ⊆ V 2 heißt
Zusammenhangsrelation im Graphen G = (V , E )
also:
(u, v ) ∈ E ∗ (u und v sind in G zusammenhängend)
gdw. ein (gerichteter) Weg von u nach v in G existiert
gerichteter Graph G = (V , E ) heißt
stark zusammenhängend gdw. ∀(u, v ) ∈ V 2 : (u, v ) ∈ E ∗
schwach zusammenhängend gdw. der ungerichtete Graph
G 0 = (V , E ∪ E −1 ) zusammenhängend ist
starke Zusammenhangskomponenten von G : maximale stark
zusammenhängende induzierte Teilgraphen von G
schwache Zusammenhangskomponenten von G :
Zusammenhangskomponenten von
G 0 = (V , E ∪ E −1 )
175
Was bisher geschah
I
gerichtete / ungerichtete Graphen G = (V , E )
I
Darstellungen von Graphen
I
Spezielle Graphen: In , Kn , Pn , Cn , Km,n , K1,n , Kn1 ,...,nm
I
Beziehungen zwischen Graphen:
Isomorphie, Teilgraph, induzierter Teilgraph, aufspannender
Teilgraph
I
Operationen auf Graphen: ∪, ∩, ∗,
I
Nachbarschaften und Eckengrade in Graphen,
n-reguläre Graphen
I
Zusammenhangs-Relation E ∗ auf G = (V , E )
(Erreichbarkeit)
Zusammenhangskomponenten: Äquivalenzklassen bzgl. E ∗
I
Pfade, Kreise, Wege in Graphen
Eulerwege und -kreise
Eulerweg in G = (V , E ):
Weg w = [v1 v2 , . . . , vn vn+1 ] ∈ E ∗ in G , der jede Kante in E genau
einmal enthält, d.h.
I E = {e1 , . . . , en },
S
I V =
i∈{1,...,n} ei und
I ∀i 6= j ∈ {1, . . . , n} : ei 6= ej
Eulerkreis (geschlossener Eulerweg) in G = (V , E ):
Eulerweg w = [e1 , . . . , en , e1 ] in G
Satz
1. Ein Graph G = (V , E ) enthält genau dann einen
geschlossenen Eulerweg, wenn er zusammenhängend ist und
grad(v ) für jeden Knoten v ∈ V gerade ist.
2. Ein zusammenhängender Graph G = (V , E ) enthält genau
dann einen Eulerweg, wenn er genau zwei oder keine Ecke
ungeraden Grades enthält.
176
Multigraphen
Wiederholung: ungerichteter Graph G = (V , E ) mit E ⊆ V2
z.B. G = ({a, b, c, d}, E ) mit der charakteristischen Funktion
V
1 falls xy ∈ {ab, ac, bd, dc}
χE :
→ {0, 1} mit χE (xy ) =
0
sonst
2
Multigraph G = (V , E ) mit Multimenge E : V2 →
(statt Teilmenge χE : V2 → {0, 1} )
z.B. G 0 = ({a, b, c, d}, E 0 ) mit

1 falls xy = ab



2 falls xy ∈ {bd, dc}
0
E (xy ) =
4 falls xy = ac



0 sonst
N
(analog für gerichtete Graphen mit E : V 2 →
Modellierungsbeispiele:
N statt E : V 2 → {0, 1})
I
Königsberger-Brücken-Problem (Eulerweg im Multigraphen)
I
Ketten oder Kreise aus Domino-Steinen, z.B. für
Stein(multi-)menge [1, 3], [2, 2], [1, 2], [2, 4], [1, 3], [1, 4]
I
Prozessketten
177
Hamiltonpfade und -kreise
Hamiltonpfad in G = (V , E ):
Pfad w = (v1 , . . . , vn ) in G mit V = {v1 , . . . , vn }
Hamiltonkreis in G = (V , E ):
Kreis w = (v1 , . . . , vn ) in G mit V = {v1 , . . . , vn }
Beispiele: Cn , Kn für alle n ≥ 3
Anwendungen
I
Problem des Handlungsreisenden
(TSP: Travelling Salesman Problem)
I
Logistik
I
Robotik
I
Hardware-Entwurf
178
Bipartite Graphen
Ein Graph G = (V , E ) heißt bipartit gdw. eine Zerlegung {V0 , V1 }
von V (d.h. V0 ∩V1 = ∅ und V0 ∪ V1 = V )
mit V20 ∪ V21 ∩ E = ∅ existiert.
Beispiele:
N
I
Pn für alle n ∈
I
Km,n für alle m, n ∈
I
kein Kn für n > 2
I
Cn für alle n ≥ 1 mit n ≡ 0 (mod 2)
N
Ein Graph G = (V , E ) ist genau dann bipartit, wenn ein
Km,n = (V , E 0 ) existiert, so dass E ⊆ E 0 ist.
179
Anwendung bipartiter Graphen
Modellierung von Zuordnungen, z.B.
I
Sprachkenntnisse zu Personen
I
Personen zu Arbeitskreisen
I
Getränke-Angebot zu Restaurants
I
Aufgaben zu Mitarbeitern mit unterschiedlichen
Qualifikationen
I
Flugzeuge zu Piloten mit Ausbildung auf verschiedenen
Flugzeugtypen
180
Gefärbte (markierte) Graphen
Graph G = (V , E )
Menge CV von Eckenmarkierungen,
Menge CE von Kantenmarkierungen
Eckenfärbung von G : Zuordnung f : V → CV
Kantenfärbung von G : Zuordnung f : E → CE
zur Modellierung z.B.:
I Linennetzplan mit CE = Fahrzeiten zwischen Stationen
I Straßennetz mit CE = Entfernung (Kosten)
(TSP: Hamilton-Kreis mit geringsten Kosten gesucht)
I Straßennetz mit CE = Höchstgeschwindigkeit
I Spielplan mit CV = Ereignisfeld-Beschreibung
I Spielplan mit CE = Straßen-Bebauungszustand
I Ablauf-Graphen mit CE = Options-Auswahl (z.B. Spielzug)
I Formelbaum mit CV = Junktoren und Aussagevariablen
I Multigraphen mit CE =
\ {0}
N
181
Eckenfärbung
Graph G = (V , E ), Farben {1, . . . , n}
f : V → {1, . . . , k} heißt (konfliktfreie) k-Färbung für G gdw.
∀u ∈ V ∀v ∈ V ((uv ∈ E ) → ¬(f (u) = f (v )))
(für keine Kante {u, v } ∈ E gilt f (u) = f (v ))
Jede Eckenfärbung f : V → {1, . . . , n} definiert
eine Zerlegung der Eckenmenge V
{f −1 (i) | i ∈ {1, . . . , n}}
G = (V , E ) heißt k-färbbar gdw. k-Färbung für G existiert.
Beispiele:
I C5 ist 5- ,4- und 3-färbbar, aber nicht 2-färbbar
I K3,3 ist 2-färbbar,
I I2 ∗ I2 ∗ I1 ist 3-färbbar, aber nicht 2-färbbar
Anwendungen z.B. bei
I Register-Zuteilung (Übersetzerbau)
I kombinatorische Aufgaben, z.B. Sudoku
182
Was bisher geschah
I
gerichtete / ungerichtete Graphen G = (V , E )
I
Darstellungen von Graphen
I
Spezielle Graphen: In , Kn , Pn , Cn , Km,n , K1,n , Kn1 ,...,nm
I
Beziehungen zwischen Graphen:
Isomorphie, Teilgraph, induzierter Teilgraph, aufspannender
Teilgraph
I
Operationen auf Graphen: ∪, ∩, ∗,
I
Nachbarschaften und Eckengrade in Graphen,
n-reguläre Graphen
I
Zusammenhangs-Relation E ∗ auf G = (V , E )
(Erreichbarkeit)
Zusammenhangskomponenten: Äquivalenzklassen bzgl. E ∗
I
Pfade, Kreise, Wege in Graphen
I
Eulerwege, Eulerkreise (geschlossene Euler-Wege)
I
Hamiltonpfade, Hamiltonkreise
I
Graphen mit Knoten- und Kantenfärbungen
Modellierungsbeispiel Sudoku
Aufgabe informal:
I
9 × 9 Felder
I
einzutragen sind die Ziffern 1 bis 9 in alle leeren Felder
I
Startkonfiguration: einige Felder schon mit Ziffern belegt
Bedingungen: keine Zahl mehrfach in
I
I
I
I
I
einer Zeile
einer Spalte
einem der neun 3 × 3-Blöcke
Aufgabe: korrektes Eintragen von Ziffern in jedes freie Feld
Idee: Repräsentation korrekter Lösungen als gefärbte Graphen mit
Felder als Ecken des Graphen
Zahlen {1, . . . , 9} als Farben für Knoten
Bedingungen (Konflikte) als Kanten des Graphen
Aufgabe: Finden einer konfliktfreien Färbung des Graphen
183
Modellierungsbeispiel Sudoku
formal (Verallgemeinerung auf n2 × n2 -Feld):
Graph G = (V , E ) mit
V = {1, . . . , n2 }2
CV = {1, . . . , n2 }
n
E = {(z, s), (z 0 , s 0 )} ∈
(n2 × n2 Felder)
(n2 Zahlen als Farben)
V
2
| (s = s 0 ) ∨ (z = z 0 )
o
0
0
∨ d ns e = d sn e ∧ d nz e = d zn e
Beispiel für n = 2 (also 4 × 4-Feld und 4 Farben):
3
2
4
1
184
Chromatische Zahl
chromatische Zahl des Graphen G :
χ(G ) = min{k | G ist k-färbbar }
Beispiele:
I
χ(C5 ) = 3
I
für alle n ∈
I
N gilt χ(Kn ) = n
für alle n ∈ N gilt χ(In ) = 1
I
für alle n > 1 gilt χ(Pn ) = 2
I
für alle n > 2 gilt
χ(Cn ) =
I
2 falls n ≡ 0
3 falls n ≡ 1
mod 2
mod 2
für min(m, n) ≥ 1 gilt χ(Km,n ) = 2
185
Baum-Strukturen
I
Hierarchien
I
Komponenten-Strukturen
I
Familien-Stammbäume
I
Enscheidungsbäume
I
Formeln, arithmetische Ausdrücke
sind spezielle Graphen
I
zusammenhängend
I
enthalten keine Kreise
186
Ungerichtete Bäume
G = (V , E ) heißt Baum, wenn
I
G zusammenhängend ist und
I
kein Teilgraph von G ein echter Kreis ist.
G = (V , E ) heißt Wald, wenn kein Teilgraph von G ein echter
Kreis ist.
v ∈ V mit grad(v ) ≤ 1 heißt Blatt
Jeder Baum mit mindestens 2 Ecken hat mindestens 2 Blätter.
In jedem Baum G = (V , E ) gilt |V | = |E | + 1
187
Charakterisierung der Bäume
Für jeden Graphen G = (V , E ) sind folgenden Aussagen
äquivalent:
1. G ist ein Baum.
2. Zwischen je zwei Ecken u, v ∈ V existiert genau ein Pfad in G .
3. G ist minimal zusammenhängend.
(G ist zusammenhängend und für jede Kante uv ∈ E ist
(V , E \ {uv }) nicht zusammenhängend)
4. G ist maximal kreisfrei.
(G enthält
keinen echten Kreis und für jede Kante
uv ∈ V2 \ E enthält (V , E ∪ {uv }) einen echten Kreis)
188
Gerichtete Bäume
Gerichteter Baum:
gerichteter Graph G = (V , E ) mit
1. G enthält keinen Kreis als Teilgraphen
2. Es existiert genau ein v ∈ V mit gradi,G (v ) = 0
3. ∀u ∈ V u 6= v → gradi,G (u) = 1
(Wurzel)
Modellierung durch gerichtete Bäume, z.B.
I
Hierarchien, Klassifikationen
I
Verzeichnis-Strukturen
I
Abstammung
I
Entscheidungsbäume
I
Wege in Graphen
I
Ableitungsbäume für Sprachen
189
Gerüste
Teilgraph H von G heißt Gerüst (Spannbaum) von G , falls
I
H ein Baum und
I
H ein aufspannender Teilgraph von G ist.
Beispiele:
I
P5 in K5
I
K1,4 in K5
I
G für jeden Baum G
I
I3 hat kein Gerüst
I
P2 ∪ K4 hat kein Gerüst
Ein Graph G ist genau dann zusammenhängend, wenn G ein
Gerüst besitzt.
(mehr dazu in LV Algorithmen und Datenstrukturen im
2. Semester)
190
Gerichtete kreisfreie Graphen (DAG)
Graph G = (V , E ) heißt gerichteter kreisfreier Graph
gdw. G keinen gerichteten Kreis als Teilgraphen enthält
Quelle u ∈ V mit gradi,G = 0
Senke u ∈ V mit grado,G = 0
Jeder DAG hat wenigstens eine Quelle und eine Senke.
I
Arithmetische Terme mit gleichen Teiltermen
I
Hasse-Diagramme
I
Abhängigkeiten
I
Binäre Entscheidungsdiagramme (BDDs)
I
Graphen zu Spielverläufen (z.B. Münzenspiel)
I
Abläufe mit unabhängigen Teilaufgaben
I
Programmablaufstrukturen
I
Geschäftsprozesse
191
Was bisher geschah
Modellierung von
Aussagen durch logische Formeln
Daten durch Mengen, Multimengen, Folgen, Sprachen
Zusammenhängen und Eigenschaften von Elementen von Mengen
durch Relationen
(Eigenschaften von Relationen)
Spezielle binäre Relationen (QO, ÄR, HO, LO)
Darstellung binärer Relationen durch Graphen
Zuordnungen zwischen Elementen von Mengen durch Funktionen
(Eigenschaften von Funktionen)
Wiederholung: Modellierung in Prädikatenlogik
Grundannahme:
Die zu modellierende Welt besteht aus Individuen, die
Eigenschaften haben und zueinander in Beziehungen
(Relationen, Funktionen) stehen.
Prädikatenlogik zur Formalisierung von Aussagen über
Eigenschaften oder Beziehungen von Individuen aus
(algebraischen) Strukturen
192
Wiederholung: Prädikatenlogische Aussagen
I
Personen sind Geschwister, wenn sie dieselbe Mutter oder
denselben Vater haben.
I
A ist genau dann Nachfahre von B, wenn B A’s Vater oder
A’s Mutter ist oder ein Elternteil von A Nachfahre von B ist.
I
Nachfahren derselben Person sind verwandt.
Individuenbereich: Menge von Personen
Beziehungen: ist-Nachfahre-von, sind-verwandt, sind-Geschwister
Funktionen: Mutter-von, Vater-von
193
Wiederholung: Prädikatenlogische Aussagen
I
Primzahlen sind genau diejenigen natürlichen Zahlen, die
genau zwei verschiedene Teiler haben.
I
Gerade Zahlen sind genau diejenigen natürlichen Zahlen, die
durch zwei teilbar sind.
I
Es existieren gerade Primzahlen.
I
Nachfolger ungerader Primzahlen sind nicht prim.
I
Das Quadrat jeder geraden Zahl ist gerade.
N
Individuenbereich: Menge
aller natürlichen Zahlen
Eigenschaften: prim, gerade
Beziehung: teilt |
Funktionen: Nachfolger, Quadrat
194
(Algebraische) Strukturen – Beispiele
(Träger-)Mengen (Individuenbereiche) mit
Relationen (Eigenschaften, Beziehungen) und
Funktionen (Operationen) auf den Elementen, z.B.
I
Menge aller Personen
Relationen: ist-älter-als, sind-Geschwister (zweistellig)
einstellige Relationen (Eigenschaften): blond
Funktion (einstellig): Mutter-von
I
Menge
aller natürlichen Zahlen
Relationen: ≥ (zweistellig), | (teilt, zweistellig)
einstellige Relationen (Eigenschaften): prim, gerade
Funktionen: Nachfolger (einstellig), + (zweistellig)
I
Menge 2 aller Punkte der Ebene
Relationen: hat-kleineren-Abstand-von-0 (zweistellig),
bilden-gleichseitiges-Dreieck (dreistellig)
Funktionen: verschieben (einstellig), Mittelpunkt (zweistellig)
I
Menge A∗ aller endlichen Wörter über Alphabet A
Relation: Anfangswort, lexikographische Ordnung (zweistellig)
Funktion: Verkettung (zweistellig)
N
R
195
Relationale Strukturen
Eine relationale Struktur A = (A, {Ri | i ∈ I }) besteht aus
I
einer nichtleeren Menge A und
I
einer Menge von Relationen Ri ⊆ Ani (je mit Stelligkeit ni )
Beispiele:
N
I
( , |, ≤)
I
({0, 1}, ≤, =)
I
(2A , ⊆)
I
(A∗ , v)
I
Graph mit Knoten- und Kantenfärbungen
I
Menge aller endlichen Graphen mit ' und
Teilgraph-Relationen
196
Algebraische Strukturen – noch mehr Beispiele
(funktionale) algebraische Strukturen (Algebren) aus den
Mathematik-LV:
∗
Halbgruppe , z.B. ( , +), (2 , ·), (2X , ∪) , (A∗ , ◦), (2(A ) , ◦)
Monoid , z.B. ( , ·, 1), ( , +, 0), (2X , ∪, ∅) , (A∗ , ◦, ε),
∗
(2(A ) , ◦, {ε})
Gruppe , z.B. ( , +, 0), ( n , +, 0), ( n , ·, 1) für Primzahl n
∗
Halbring , z.B. (2 , +, ·), ({0, 1}, XOR, ·), (2(A ) , ∪, ◦)
Ring , z.B. ( , +, ·, 0, 1), ( n , +, ·, 0, 1) für Primzahl n
Körper , z.B. ( , +, ·, 0, 1), ( n , +, ·, 0, 1) für Primzahl n
Vektorraum n
zwei Trägermengen (Individuen verschiedener Typen):
Skalare , Vektoren n
Funktionen, z.B. skalare Addition, Multiplikation
+, · : × →
Vektoraddition + : n × n → n , Skalarprodukt
(·, ·) : n × n →
Kombinationen (Strukturen mit Funktionen und Relationen)
z.B. halbgeordnete Gruppe ( , +, 0, ≤)
R
N
N
Z
N
Z
Z
Z
Q
Z
Z
Z
R
R
R R R
R
Z
R
Z
R
R
R
R
197
Algebraische Strukturen desselben Types
A Menge {0, 1} mit
I Konstanten 0, 1
I Funktionen min, max (zweistellig)
I Eigenschaft gerade
I Relation ≤ (zweistellig)
B Menge aller Studenten im Raum mit
I Konstanten Anton, Berta
I Funktionen Älterer,
kleinere-Matrikelnummer(zweistellig)
I Eigenschaft blond
I Relation befreundet (zweistellig)
C Menge 2N mit
I Konstanten ∅,
I Funktionen ∩, ∪ (zweistellig)
I Eigenschaft endlich
I Relation ⊆ (zweistellig)
N
198
Signaturen – Motivation
(syntaktische) Gemeinsamkeiten der Strukturen A, B, C:
I
I
I
I
I
eine Trägermenge
zwei Konstanten (nullstellige Funktionen)
zwei zweistellige Funktionen
eine Eigenschaft (einstellige Relation)
eine zweistellige Relation
Symbole (mit zugeordneter Stelligkeit)
zur Bezeichnung von Relationen und Funktionen
199
Signaturen
Signatur Σ = (ΣF , ΣR ) mit Mengen
ΣF = {(f , n) | n ∈ } von Funktionssymbolen (mit Stelligkeit)
ΣR = {(R, n) | n ∈ } von Relationssymbolen (mit Stelligkeit)
(nullstellige Funktionssymbole heißen Konstantensymbole)
N
N
Signatur definiert einen Typ von Strukturen (Syntax)
Strukturen mit derselben Signatur unterscheiden sich in der
Semantik (Bedeutung) der Symbole:
I Trägermengen
I Bedeutung der Funktions- und Relationssymbole
200
Beispiele für Signaturen
I
Signatur für arithmetische Ausdrücke über natürlichen,
rationalen, reellen, . . . Zahlen
ΣF = {(+, 2), (−, 2), (·, 2), (/, 2)} ∪ {(x, 0) | x ∈ }
(je ein nullstelliges Symbol (Konstante) für jede Zahl aus der
Trägermenge, hier z.B. )
ΣR = ∅
N
N
I
Signatur für Mengen mit einer zweistelligen Relation
(Äquivalenzrelation, Halbordnung, Graph)
ΣF = ∅, ΣR = {(R, 2)}
I
Signatur für aussagenlogische Formeln
ΣF = {(∨, 2), (∧, 2), (¬, 1), (f, 0), (t, 0)},
ΣR = {(=, 2), (≡, 2), (erfüllbar, 1)}
I
Signatur für alle drei Strukturen A, B, C auf einer füheren Folie
ΣF = {(apfel, 0), (banane, 0), (kirsche, 2), (pflaume, 2)}
ΣR = {(rettich, 1), (tomate, 2)}
201
Σ-Strukturen
Für eine Signatur Σ = (ΣF , ΣR ) heißt eine algebraische Struktur
A = (A, J·KA ) Σ-Struktur gdw.
I
A 6= ∅ Trägermenge (Individuenbereich, Universum)
I
∀(f , n) ∈ ΣF : Jf KA : An → A
I
∀(R, n) ∈ ΣR : JRKA ⊆ An (bzw. JRKA : An → {0, 1} )
J·KA ordnet jedem Funktions- und Relationssymbol seine Bedeutung in A
(Funktion / Relation passender Stelligkeit) zu.
Beispiel: Σ-Strukturen für die Signatur Σ = (ΣF , ΣR )
mit ΣR = {(R, 2)} und ΣF = {(f , 2), (c, 0)} sind z.B.
I
I
N
A = ( , J·KA ) mit
JcKA = 0, ∀(x, y ) ∈ 2 : Jf KA (x, y ) = x + y ,
JRKA = {(x, y ) ∈ 2 | x|y }
Z
N
N
B = ( , J·KB ) mit
JcKB = −3, ∀(x, y ) ∈ 2 : Jf KB (x, y ) = x · y ,
JRKB = {(x, y ) ∈ 2 | x ≤ y }
Z
Z
202
Wiederholung Strukturen – Beispiel Halbring
klassische Definition (Menschen-lesbar):
Eine algebraische Struktur (A, ☼, $) heißt genau dann Halbring, wenn sie
die folgenden Bedingungen erfüllt:
I
I
(A, ☼) und (A, $) sind Halbgruppen und
$ ist distributiv über ☼
formale Definition (maschinell zu verarbeiten):
Signatur Σ = (ΣF , ΣR ) mit
Axiome (Anforderungen)

(
 ∧ (
∀x∀y ∀z 
 ∧ (
∧ (
prominente Halbringe:
A = ( , J·KA )
B = (2 , J·KB )
C = ({0, 1}, J·KC )
D = (2M , J·KD )
∗
E = (2{a,b} , J·KE )
F = ( ∪ {+∞}, J·KF )
N
Z
R
mit
mit
mit
mit
mit
mit
ΣF = {(☼, 2), ($, 2)}, ΣR = {(=, 2)}

x☼(y ☼z) = (x☼y )☼z
)
x$(y $z) = (x$y )$z
) 

x$(y ☼z) = (x$y )☼(x$z) ) 
(x☼y )$z = (x$z)☼(y $z) )
J☼KA = +
J☼KB = +
J☼KC = max
J☼KD = ∪
J☼KE = ∪
J☼KF = min
und
und
und
und
und
und
J$KA = ·
J$KB = ·
J$KC = min
J$KD = ∩
J$KE = ◦
J$KF = +
203
Terme
Beispiele: für Signatur Σ = (ΣF , ΣR ) mit
ΣF = {(3, 0), (5, 0), (+, 2), (·, 2)} und ΣR = {(>, 2)} und Menge
= {x, y , z} von Variablen
X
I
Ausdrücke 3 + x, 5, y , ((y + 5) · (3 · x)) + x sind korrekt aus
Symbolen aus ΣF und
zusammengesetzt
I
Ausdrücke 3x+, +5, 3(x + y ), (3x5) + z sind nicht korrekt aus
Symbolen aus ΣF und
zusammengesetzt
X
X
Definition (induktiv)
X
Die Menge Term(ΣF , ) aller Terme über der (funktionalen) Signatur
ΣF mit Variablen aus der Menge
ist definiert durch:
IA: Jede Variable x ∈
X
X ist ein Term.
(
X ⊆ Term(ΣF , X))
IS: Sind (f , n) ∈ ΣF (f ist n-stelliges Funktionssymbol) und t1 , . . . , tn
Terme aus Term(ΣF , ),
dann ist f (t1 , . . . , tn ) ein Term aus Term(ΣF , ).
X
X
verschiedene Darstellungen von Termen möglich,
z.B. Baum, Infix-, Präfix-, Postfixform
204
Grundterme
Terme ohne Variablen heißen Grundterme.
Term (ΣF , ∅) ist Menge aller Grundterme über Signatur ΣF
Beispiele:
für ΣF = {(f , 1), (g , 2), (h, 2), (c, 0)} und = {x, y , z} gilt
c ∈ Term(ΣF , ∅) ⊆ Term(ΣF , )
(Grundterm)
(kein Grundterm)
z ∈ Term(ΣF , ), aber z 6∈ Term(ΣF , ∅)
f (c) ∈ Term(ΣF , ∅) ⊆ Term(ΣF , )
h(f (x), c) ∈ Term(ΣF , ), aber h(f (x), c) 6∈ Term(ΣF , ∅)
f 6∈ Term(ΣF , ), h(c) 6∈ Term(ΣF , ), x(c) 6∈ Term(ΣF , )
X
X
X
X
X
X
X
X
Warum gilt für alle Signaturen ΣF ohne Konstantensymbole
Term (ΣF , ∅) = ∅?
(ÜA)
205
Spezialfall: aussagenlogische Formeln
Terme über der funktionalen Signatur
ΣF = {(t, 0), (f, 0), (¬, 1), (∨, 2), (∧, 2), (→, 2), (↔, 2)}
mit Aussagenvariablen aus P
sind genau alle aussagenlogischen Formeln ϕ ∈ AL(P)
Für diese Signatur ΣF gilt also AL(P) = Term(ΣF , P)
Beispiele: für P = {a, b, c, d}
I
a ∨ (c → b) ∈ AL(P) = Term(ΣF , P)
I
(b → t) ∧ (b → f) ∈ AL(P) = Term(ΣF , P)
I
(a¬b) ∧ (b → f) 6∈ AL(P) = Term(ΣF , P)
I
(f → t) ∈ AL(P) = Term(ΣF , P),
sogar (f → t) ∈ AL(∅) = Term(ΣF , ∅)
206
Mehr Beispiele
I
I
Q
für ΣF = {(+, 2), (−, 2), (·, 2), (/ 2)} ∪ {(q, 0) | q ∈ } ist
Term(ΣF , ∅) die Menge aller arithmetischen Ausdrücke
(Terme) mit rationalen Zahlen (z.B. 3/5+1/4),
Term(ΣF , {a, b, c}) die Menge aller arithmetischen Ausdrücke
(Terme) mit rationalen Zahlen und Variablen aus der Menge
{a, b, c} (z.B. (3 · a) + ((2 · b)/c)),
ΣF = {(apfel, 0), (banane, 0), (kirsche, 2), (pflaume, 2)}
I
I
I
I
apfel ∈ Term(ΣF , ∅), Grundterm
kirsche (x, pflaume(y , banane)) ∈ Term(ΣF , {x, y , z})
kein Grundterm
banane(apfel(pflaume, kirsche(pflaume))) 6∈ Term(ΣF ,
pflaume(apfel, kirsche(banane, apfel)) ∈ Term(ΣF , ∅)
X)
207
Größe von Termen
Für jeden Term t ∈ Term(ΣF ,
definiert durch:
IA: falls t = x ∈
X) ist seine Größe size(t) (induktiv)
X, dann size(t) = 1
IS: falls t = f (t1 , . . . , tn ), dann
size(t) = 1 +
n
X
size(ti )
i=1
Beispiele für ΣF = {(f , 1), (g , 2), (h, 2), (c, 0)} und
I
size(c) = 1
I
size(z) = 1
I
size(f (c)) = 2
I
size(h(f (x), c)) = 4
X = {x, y , z}:
208
Menge aller Variablen in einem Term
X
Für jeden Term t ∈ Term(ΣF , ) ist die Menge var(t) aller in t
vorkommenden Variablen (induktiv) definiert durch:
IA: falls t = x ∈
X (Variable), dann var(t) = {x}
IS: falls t = f (t1 , . . . , tn ) mit (f , n) ∈ ΣF , dann
var(t) = var(t1 ) ∪ · · · ∪ var(tn )
Beispiel: Für t = f (g (x, a), g (f (a, y ), x)) gilt var(t) = {x, y }
209
Wert von Grundtermen in Strukturen
gegeben: funktionale Signatur ΣF = {(f , n) | n ∈
Σ-Struktur A = (A, J·KA )
N}
Definition (induktiv)
Der Wert des ΣF -Grundtermes t = f (t1 , . . . , tn ) ∈ Term(ΣF , ∅)
in der ΣF -Struktur A = (A, J·KA ) ist
JtKA = Jf KA (Jt1 KA , . . . , Jtn KA )
Fehlt hier der Induktionsanfang?
nein, ist als Spezialfall enthalten:
Für Terme t = c mit (c, 0) ∈ ΣF (Konstante) gilt JtKA = JcKA
(Bedeutung der Konstante c in A, gegeben in Definition von A)
210
Wert von Grundtermen in Strukturen
gegeben: funktionale Signatur ΣF = {(f , n) | n ∈
Σ-Struktur A = (A, J·KA )
N}
Definition (induktiv)
Der Wert des ΣF -Grundtermes t = f (t1 , . . . , tn ) ∈ Term(ΣF , ∅)
in der ΣF -Struktur A = (A, J·KA ) ist
JtKA = Jf KA (Jt1 KA , . . . , Jtn KA )
Fehlt hier der Induktionsanfang?
nein, ist als Spezialfall enthalten:
Für Terme t = c mit (c, 0) ∈ ΣF (Konstante) gilt JtKA = JcKA
(Bedeutung der Konstante c in A, gegeben in Definition von A)
211
Beispiel
Signatur Σ = (ΣF , ΣR ) mit
ΣF = {(apfel, 0), (banane, 0), (kirsche, 2), (pflaume, 2)}
ΣR = {(rettich, 1), (tomate, 2)}
s = apfel t = pflaume(apfel, kirsche(banane, apfel))
Σ-Struktur A = (A, J·KA ) mit
A =
N
JapfelKA = 5
für alle (x, y ) ∈
für alle (x, y ) ∈
A2 :
A2 :
JbananeKA = 3
JkirscheKA (x, y ) = x + y
JpflaumeKA (x, y ) = x · y
JrettichKA = {0, . . . , 10}
JtomateKA = {(2n, n) | n ∈
JsKA = JapfelKA = 5 JtKA = . . .
N}
212
Weiteres Beispiel
s = apfel t = pflaume(apfel, kirsche(banane, apfel))
Σ-Struktur B = (B, J·KB ) mit
B = {0, 1}
JapfelKB = 0
für alle (x, y ) ∈
B 2:
JbananeKB = 1
JkirscheKB (x, y ) = min(x, y )
für alle (x, y ) ∈ B 2 : JpflaumeKB (x, y ) = max(x, y )
JrettichKB = {0}
JtomateKB = {(0, 0), (0, 1), (1, 1)}
JsKB = JapfelKB = 0,
JtKB = . . .
213
Weiteres Beispiel
s = apfel t = pflaume(apfel, kirsche(banane, apfel))
Σ-Struktur C = (C , J·KC ) mit
C
= Menge aller Studenten hier
JapfelKC = Student hinten rechts
für alle (x, y ) ∈
C 2:
JbananeKC = Student daneben
JkirscheKC (x, y ) = x
für alle (x, y ) ∈ C 2 : JpflaumeKC (x, y ) = y
JrettichKC = {x ∈ C | x ist blond}
JtomateKC = {(x, y ) ∈ C 2 | x hilft y }
JsKC = JapfelKC = Student hinten rechts
JtKC = . . .
214
Noch ein Beispiel
s = apfel t = pflaume(apfel, kirsche(banane, apfel))
Σ-Struktur D = (D, J·KD ) mit
D = 2N
JapfelKD = ∅
JbananeKD =
N
für alle M, N ∈ D: JkirscheKD (M, N) = M ∩ N
für alle M, N ∈ D: JpflaumeKD (M, N) = M ∪ N
JrettichKD = {M ⊆
N | |M| ∈ N}
JtomateKD = {(M, N) ∈ D 2 | M ⊆ N}
JsKD = JapfelKD = ∅,
JtKD = . . .
215
Äquivalenz von Grundtermen in einer Struktur
ΣF -Grundterme s, t ∈ Term(ΣF , ∅) mit JsKA = JtKA heißen
äquivalent in A (s ≡A t).
In den Beispielen oben gilt
s 6≡A t
s
≡B
t
s
6≡C
t
s ≡D t
schon bekannter Spezialfall:
semantische Äquivalenz aussagenlogischer Formeln
(ohne Aussagenvariablen)
216
Was bisher geschah
(algebraischen) Strukturen zur zusammenhängenden Modellierung von
Mengen von Individuen (evtl. verschiedener Typen)
Funktionen auf Individuen dieser Mengen
Relationen zwischen Individuen dieser Mengen
klare Unterscheidung zwischen
Syntax: Symbole zur formalen (maschinell zu verarbeitenden)
Darstellung von Sorten (Typen, Mengen),
Individuen, Funktionen und Relationen
Signatur Σ = (ΣF , ΣR )
Terme über der Signatur ΣF : Term(ΣF , )
Spezialfall Grundterme (ohne Variablen)
strukturelle Induktion über Terme
(Definition von Funktionen,
Nachweis von Eigenschaften)
X
Semantik: Σ-Strukturen definieren Bedeutung der Symbole aus Σ
Wert von Grundtermen in Σ-Strukturen
Äquivalenz von Grundtermen in Σ-Strukturen
(induktiv)
Interpretation von Termen mit Variablen
gegeben:
I
Signatur Σ = (ΣF , ΣR ),
I
Variablenmenge
I
Σ-Struktur A = (A, J·KA )
I
t ∈ Term(ΣF ,
X
X)
Welchen Wert (Individuum) in A haben Variablen x ∈
X
X?
Belegung β : → A der Individuenvariablen
(ordnet jeder Variablen einen Wert aus dem Träger von A zu)
Eine Interpretation für einen Term t ∈ Term(ΣF ,
(A, β) aus
I
I
X) ist ein Paar
einer Σ-Struktur A = (A, J·KA ) und
einer Belegung β :
X → A.
217
Beispiele
Term s = f (g (x, a), g (f (a, y ), x)) über der Signatur Σ = . . .
I
N
Interpretation (A, α) mit Σ-Struktur A = ( , J·KA ), wobei
JaKA = 1
Jf KA (x, y ) = x + y
Jg KA (x, y ) = x · y
N
I
und Variablenbelegung α : {x, y } → , wobei
α(x) = 2 und α(y ) = 1
Interpretation (B, β) mit Σ-Struktur B = (2{a,b,c} , J·KB ):
JaKB = {b, c}
Jf KB (x, y ) = x \ y
Jg KB (x, y ) = x ∪ y
und Variablenbelegung β : {x, y } → 2{a,b,c} , wobei
β(x) = ∅ und β(y ) = {b}
218
Werte von Termen mit Variablen
X
Der Wert des Termes t ∈ Term(ΣF , ) in der
ΣF -Interpretation (A, β), bestehend aus
I
I
der ΣF -Struktur A = (A, J·KA ) und
der Belegung β :
X→A
ist (induktiv) definiert durch
IA für t = x ∈
X gilt JtK(A,β) = β(x)
IS für t = f (t1 , . . . , tn ) gilt
JtK(A,β) = Jf KA Jt1 K(A,β) , . . . , Jtn K(A,β)
Der Wert eines Termes in einer Interpretation ((A, J·KA ), α) ist ein
Element aus A.
(Man bemerke die Analogie zur Berechnung des Wahrheitswertes
einer aussagenlogischen Formel mit Aussagenvariablen.)
Der Wert von Grundtermen aus Term(ΣF , ∅) in einer Interpretation
(A, α) hängt nicht von der Belegung α ab.
219
Beispiele
Signatur Σ = (ΣF , ΣR ) mit
ΣF = {(a, 0), (b, 0), (f , 1), (g , 2), (h, 2)} und ΣR = ∅
Variablenmenge = {x, y }
Σ-Struktur S = (S, J·KS ) mit
X
S
JaKS
JbKS
=
N
= 5
= 3
Jf KS (a) = 1 + a
Jg KS (a, b) = a + b
JhKS (a, b) = a · b
N
N
β : {x, y } → mit β(x) = 0, β(y ) = 1
γ : {x, y } → mit γ(x) = 2, γ(y ) = 0
Terme s = g (h(f (a), x), h(x, y )) und t = h(f (x), g (y , a))
JsK(S,β) = . . . , JtK(S,β) = . . . , JsK(S,γ) = . . . , JtK(S,γ) = . . . (Tafel)
Variablenbelegungen
220
Atome (elementare Aussagen)
Atome in
Aussagenlogik : Aussagenvariable,
bekommt festen Wahrheitswert durch
Belegung (der Aussagenvariablen)
Prädikatenlogik : (parametrisierte) Aussage über Eigenschaften
von oder Beziehungen zwischen Individuen
Wahrheitswert abhängig von beteiligten Individuen
z.B. nebeneinander(x, y ), gerade(n), x < 3, x < y ,
sindGeschwister(x, Mutter(y ))
221
Atome – Syntax
Atom elementare Formel,
repräsentiert Eigenschaft von oder Beziehung
zwischen Individuen
Signatur Σ = (ΣF , ΣR ) mit
I
Menge ΣF von Funktionssymbolen mit Stelligkeit (f , n)
I
Menge ΣR von Relationssymbolen mit Stelligkeit (R, n)
Definition
Menge aller Σ-Atome mit Variablen aus der Menge
Atom(Σ,
X:
X) = {R(t1 , . . . , tn ) | (R, n) ∈ ΣR und t1 , . . . , tn ∈ Term(ΣF , X)}
Atome ohne Individuenvariablen heißen Grundatome.
Menge aller Grundatome: Atom(Σ, ∅)
222
Atome – Beispiele
I
Signatur Σ = (ΣF , ΣR√) mit
ΣF = {(1, 0), (2, 0), ( , 1), (+, 2)}
ΣR = {(=, 2), (≤, 2)}
Variablenmenge = {x, y , z}
X
I
I
I
I
X
X
√
√
√x = 2 ∈ Atom(Σ, )
) (aber x + 2 ∈ Term(ΣF ,
px + 2√ 6∈ Atom(Σ,
p√
1+ 2≤
2 ∈ Atom(Σ, ∅)
X))
Signatur Σ = (ΣF , ΣR ) mit
ΣF = {(a, 0), (b, 0), (k, 2), (d, 2)}
ΣR = {(P, 1), (Q, 2)}
Variablenmenge = {x, y }
X
I
I
I
I
I
X
y 6∈ Atom(Σ, )
P(x) ∈ Atom(Σ, )
P(a) ∈ Atom(Σ, ∅)
P(Q(P(a), k(x, y ))) 6∈ Atom(Σ, )
Q(k(a, d(y , a)), x) ∈ Atom(Σ, )
X
X
X
223
Atome – Semantik
Signatur Σ = (ΣF , ΣR ), Variablenmenge
Σ-Interpretation (A, α) mit
I
X
Σ-Struktur A = (A, J·KA )
X→A
Wert des Atomes a = P(t1 , . . . , tn ) ∈ Atom(Σ, X)
I
Belegung der Individuenvariablen α :
in der Interpretation (A, α):
JaK(A,α)
= JP(t1 , . . . , tn )K(A,α)
= JPKA Jt1 K(A,α) , . . . , Jtn K(A,α)
1 falls Jt1 K(A,α) , . . . , Jtn K(A,α) ∈ JPKA
=
0 sonst
(Spezialfall Atom a mit (a, 0) ∈ ΣR : JaK(A,α) = JaKA )
Der Wert eines Atomes in einer Interpretation (A, α) ist ein
Wahrheitswert.
Der Wert von Grundatomen aus Atom(Σ, ∅) in einer Interpretation
(A, α) hängt nicht von der Belegung α ab.
224
Semantik von Atomen – Beispiele
Signatur Σ = (ΣF , ΣR ) mit
ΣF = {(a, 0), (f , 1)} und ΣR = {(P, 1), (R, 2)},
Variablenmenge = {x, y }
Σ-Struktur S = (S, J·KS ) mit
X
S
= {0, 1, 2}
JaKS
= 1
JPKS
= {0, 2}
∀d ∈ S : Jf KS (d) = 2 − d
JRKS
= {(1, 0), (1, 2), (2, 2)}
Belegung β : {x, y } → {0, 1, 2}: β(x) = 0, β(y ) = 1
Wert der folgenden Atome aus Atom(Σ, )
in der Interpretation (S, β) (Tafel):
JP(x)K(S,β) = . . . , JP(a)K(S,β) = . . .,
JP(f (a))K(S,β) = . . . , JP(f (f (x)))K(S,β) = . . .,
JR(x, a)K(S,β) = . . ., JR(f (y ), x)K(S,β) = . . .
X
225
Prädikatenlogik (der ersten Stufe) – Syntax
I
aussagenlogische Junktoren t, f, ¬, ∨, ∧, →, ↔
I
Σ-Atome
I
Quantoren ∀, ∃
X
Die Menge FOL(Σ, ) aller Formeln der Prädikatenlogik (der
ersten Stufe, first order logic) über der Signatur Σ mit
(Individuen-)Variablen aus der Menge
ist (induktiv) definiert
durch:
X
X
X
IA: Atom(Σ, ) ⊆ FOL(Σ, )
(alle Atome sind Formeln)
IS:
I
I
X
Aus {ϕ1 , . . . , ϕn } ⊆ FOL(Σ, ) folgt für jeden
n-stelligen Junktor ∗:
∗(ϕ1 , . . . , ϕn ) ∈ FOL(Σ, )
Aus ϕ ∈ FOL(Σ, ) und x ∈ folgt
{∀xϕ, ∃xϕ} ⊆ FOL(Σ, )
X
X
X
X
(Baumstruktur, analog zur Definition von Termen)
226
Beispiele
I
Signatur Σ = (ΣF , ΣR ) mit
ΣF = {(a, 0), (f , 1)} und ΣR = {(P, 1), (R, 2)}
Variablenmenge = {x, y }
Formeln aus FOL(Σ, ):
X
I
X
ϕ1
= P(f (x))
ϕ2
ϕ3
= (P(x) ↔ (¬P(f (x)) ∧ (∀x∃y ((P(x) ↔ P(y )) ∧ R(x, y )))))
= ∀x∀y ϕ2
Σ = (∅, ΣR ) mit ΣR = {(p, 0), (q, 0)},
X=∅
Formeln aus FOL(Σ, ∅):
ψ1
= p∨q
ψ2
= ¬p ∨ ¬(q ∨ p)
(Syntax der Aussagenlogik ist Spezialfall der FOL-Syntax)
227
Was bisher geschah
Klassische Prädikatenlogik der ersten Stufe FOL(Σ,
X):
Syntax : Signatur Σ = (ΣF , ΣR ), Individuenvariablen
X
X
X
X
Terme Term(Σ, ) (aus Σ nur ΣF relevant),
Grundterme Term(Σ, ∅)
Atome Atom(Σ, ), Grundatome Atom(Σ, ∅)
Formeln FOL(Σ, )
Semantik in Σ-Strukturen A = (A, J·KA ): Wert von
Grundtermen t ∈ Term(Σ, ∅): JtKA ∈ A
Äquivalenz ≡A in Struktur A
Grundatomen a ∈ Atom(Σ, ∅): JaKA ∈ {0, 1}
in Σ-Interpretationen (A, α) mit Struktur A und
Belegung der Individuenvariablen α : → A:
Wert von
X
X
X
Termen t ∈ Term(Σ, ): JtK(A,α) ∈ A
Atomen A ∈ Atom(Σ, ): JaK(A,α) ∈ {0, 1}
WH: Prädikatenlogik (der ersten Stufe) – Syntax
I
aussagenlogische Junktoren t, f, ¬, ∨, ∧, →, ↔
I
Σ-Atome
I
Quantoren ∀, ∃
X
Die Menge FOL(Σ, ) aller Formeln der Prädikatenlogik (der
ersten Stufe, first order logic) über der Signatur Σ mit
(Individuen-)Variablen aus der Menge
ist (induktiv) definiert
durch:
X
X
X
IA: Atom(Σ, ) ⊆ FOL(Σ, )
(alle Atome sind Formeln)
IS:
I
I
X
Aus {ϕ1 , . . . , ϕn } ⊆ FOL(Σ, ) folgt für jeden
n-stelligen Junktor ∗:
∗(ϕ1 , . . . , ϕn ) ∈ FOL(Σ, )
Aus ϕ ∈ FOL(Σ, ) und x ∈ folgt
{∀xϕ, ∃xϕ} ⊆ FOL(Σ, )
X
X
X
X
(Baumstruktur, analog zur Definition von Termen)
WH: Beispiele
I
Signatur Σ = (ΣF , ΣR ) mit
ΣF = {(a, 0), (f , 1)} und ΣR = {(P, 1), (R, 2)}
Variablenmenge = {x, y }
Formeln aus FOL(Σ, ):
X
ϕ1
I
X
= P(f (x))
(P(x) ↔ (¬P(f (x)) ∧ (∀x∃y ((P(x) ↔ P(y )) ∧ R(x, y )))))
ϕ2
=
ϕ3
= ∀x∀y ϕ2
Σ = (∅, ΣR ) mit ΣR = {(p, 0), (q, 0)},
X=∅
Formeln aus FOL(Σ, ∅):
ψ1
= p∨q
ψ2
= ¬p ∨ ¬(q ∨ p)
(Syntax der Aussagenlogik ist Spezialfall der FOL-Syntax)
Variablen in Formeln
Eine Individuenvariable x ∈
X kommt vor in
Term t, falls t = x oder
t = f (t1 , . . . , tn ) und x in einem ti vorkommt,
Atom a = p(t1 , . . . , tn ), falls x in einem ti vorkommt,
Formel ϕ, falls x in einem Atom in ϕ
(Teilformel von ϕ, die ein Atom ist) vorkommt.
var(ϕ): Menge aller in ϕ vorkommenden Indiviuenvariablen
Beispiele (Tafel: Formelbäume):
I
für ϕ1 = R(x, a) gilt var(ϕ1 ) = {x}
I
für ϕ2 = ∃xR(x, f (y , x)) gilt var(ϕ2 ) = {x, y }
I
für ϕ3 =
(P(x) ↔ (¬P(f (x)) ∧ (∀x∃y ((P(x) ↔ P(y )) ∧ R(x, y )))))
gilt var(ϕ3 ) = {x, y }
228
Freie und gebundene Vorkommen von Variablen
Ein Vorkommen der Indiviuenvariablen x in ϕ heißt
gebunden , falls x in einer Teilformel von ϕ der Form ∃xψ oder
∀xψ vorkommt,
bvar(ϕ): Menge aller in ϕ gebunden vorkommenden
Variablen
frei , sonst
fvar(ϕ): Menge aller in ϕ frei vorkommenden
Variablen
var(ϕ) = fvar(ϕ) ∪ bvar(ϕ) gilt immer.
fvar(ϕ) ∩ bvar(ϕ) 6= ∅ ist möglich, aber nicht notwendig.
229
Beispiele
ϕ1 = R(x, a)
ϕ2 = ∃xR(x, f (y , x))
bvar(ϕ1 ) = ∅, fvar(ϕ1 ) = {x}
bvar(ϕ2 ) = {x}, fvar(ϕ2 ) = {y }
ϕ3 = (P(x) ↔ (¬P(f (x)) ∧ (∀x∃y ((P(x) ↔ P(y )) ∧ R(x, y )))))
bvar(ϕ3 ) = {x, y }, fvar(ϕ3 ) = {x}
ϕ4 = ∀x∀y ϕ3
bvar(ϕ4 ) = {x, y }, fvar(ϕ4 ) = ∅
230
Sätze
Jede Formel ϕ ∈ FOL(Σ,
X) mit fvar(ϕ) = ∅ heißt Satz.
Beispiele: Für Σ = (ΣF , ΣR ) mit ΣF = {(c, 0)}, ΣR = {(R, 2)}
und = {x, y } sind
X
X),
I
∀x∀y (R(x, y ) → R(y , x)) ein Satz in FOL(Σ,
I
R(c, c) ein Satz in FOL(Σ,
I
∃y (R(c, y ) → R(y , c)) ein Satz in FOL(Σ,
I
R(x, y ) → R(y , x),
∀x(R(x, y ) → R(y , x)),
∃y (R(x, y ) → R(y , x)),
∀x(R(x, y ) → ∃yR(y , x)) keine Sätze in FOL(Σ,
für ϕ ∈ FOL(Σ,
X),
X) mit fvar(ϕ) = {x1, . . . , xn }:
X),
X).
universeller Abschluss ∀ϕ := ∀x1 · · · ∀xn ϕ
existentieller Abschluss ∃ϕ := ∃x1 · · · ∃xn ϕ
Für jede Formel ϕ ∈ FOL(Σ,
X) sind ∀ϕ und ∃ϕ Sätze.
231
Modifizierte Interpretationen
gegeben:
I
Signatur Σ,
I
Variablenmenge
I
Σ-Struktur A = (A, J·KA ),
X,
X → A der Variablen aus X in A
modifizierte Belegung β[x 7→ d] : X → A mit
I
Belegung β :
β[x 7→ d](y ) =
d
für y = x
β(y ) sonst
Σ-Interpretation (A, β) mit
I
I
Σ-Struktur A = (A, J·KA )
Variablenbelegung β :
X→A
modifizierte Interpretation (A, β[x 7→ d])
232
Wert in Interpretationen
Wert in Σ-Interpretation (S, β) mit S = (S, J·KS )
I
I
I
I
X: JxK(S,β) = β(x)
eines Termes t = f (t1 , . . . , tn ) ∈ Term(Σ
F , X):
einer Individuenvariable x ∈
∈S
JtK(S,β) = Jf KS Jt1 K(S,β) , . . . , Jtn K(S,β)
∈S
eines Atomes a = p(t1 , . . . , tn ) ∈ Atom(Σ,
JaK(S,β) = JpKS (Jt1 K(S,β) , . . . , Jtn K(S,β) )
einer Formel ϕ ∈ FOL(Σ,
X):
X): JϕK(S,β)
∈ {0, 1}
∈ {0, 1}
J¬ϕK(S,β) = 1 − JϕK(S,β)
Jϕ ∨ ψK(S,β) = max(JϕK(S,β) , JψK(S,β) )
Jϕ ∧ ψK(S,β) = min(JϕK(S,β) , JψK(S,β) )
J∃xϕK(S,β) = max{JϕK(S,β[x7→a]) | a ∈ S}
J∀xϕK(S,β) = min{JϕK(S,β[x7→a]) | a ∈ S}
(zur Semantik des Allquantors siehe auch
http://spikedmath.com/445.html)
233
Beispiele
Σ = (ΣR , ΣF ) mit ΣF = {(f , 1)},ΣR = {(R, 2)},
ϕ = ¬R(x, y ) ∧ ∃zR(z, z)
I
I
X = {x, y , z}
ψ = ∀x∃yR(x, f (y ))
Σ-Struktur A = (A, J·KA ) mit A = {a, b, c}
Jf KA (a) = Jf KA (b) = c, Jf KA (c) = a
JRKA = {(a, a), (b, a), (a, c)}
Belegung α(x) = b, α(y ) = a , α(z) = b
JϕK(A,α) = . . .
JψK(A,α) = . . .
Z
Σ-Struktur B = (B, J·KB ) mit B =
Jf KB (d) = −d, JRKB =≤
Belegung β(x) = 5, β(y ) = 3, β(z) = −1,
JϕK(B,β) = . . .
JψK(B,β) = . . .
234
Modelle für Formeln
Σ-Interpretation (S, β) erfüllt (ist Modell für) die Formel ϕ ∈ FOL(Σ,
genau dann, wenn JϕK(S,β) = 1.
X)
X
Menge aller Modelle der Formel ϕ ∈ FOL(Σ, )
S = (S, J·KS ) ist Σ-Struktur und β :
Mod(ϕ) = (S, β) und JϕK(S,β) = 1
Formel ϕ ∈ FOL(Σ,
X→S
X) heißt
erfüllbar gdw. Mod(ϕ) 6= ∅
(z.B. ∀x (P(x) ∨ Q(x)))
unerfüllbar gdw. Mod(ϕ) = ∅
(z.B. ∀xP(x) ∧ ∃x¬P(x) )
allgemeingültig gdw.
Mod(ϕ) = {(S, β) | S = (S, J·KS ) ist Σ-Struktur und β :
X → S}
(Menge aller Σ-Interpretationen)
235
Beispiele
ϕ = R(x) ∧ ∃y ((¬R(y )) ∧ E (y , x))
I
Struktur G = ({1, . . . , 4}, J·KG ) mit
JRKG = {1, 2, 4},
JE KG = {(1, 2), (3, 2)} und
Belegung α : {x, y } → {1, . . . , 4} mit α(x) = 2, α(y ) = 2
(G, α) ∈ Mod(ϕ)
I
Struktur H = ({a, b}, J·KH ) mit
JRKH = {a},
JE KH = {(a, a), (b, b)},
Belegung β : {x, y } → {a, b} mit β(x) = a, β(y ) = a
(H, β) 6∈ Mod(ϕ)
I
Struktur J = ( , J·KJ ) mit
JRKJ = 2 (Menge aller geraden Zahlen),
JE KJ = {(i, i + 1) | i ∈ } und
Belegung γ : {x, y } → mit γ(x) = γ(y ) = 0
(J , γ) ∈ Mod(ϕ)
Z
Z
Z
Z
236
Semantische Äquivalenz von Formeln
(analog Aussagenlogik)
Für ϕ, ψ ∈ FOL(Σ, ) gilt
X
ϕ≡ψ
gdw.
Mod(ϕ) = Mod(ψ)
Beispiele:
I
¬∀xP(x) ≡ ∃x¬P(x)
(d.h.: für alle Σ-Interpretationen (S, β) gilt
J¬∀xP(x)K(S,β) = J∃x¬P(x)K(S,β) )
X) gilt
I
Für alle Formeln ϕ, ψ ∈ FOL(Σ,
∃xϕ ∨ ∃xψ ≡ ∃x(ϕ ∨ ψ)
I
∀x∃yR(x, y ) 6≡ ∀x∃yR(y , x),
(d.h.: es gibt Interpretationen (S, β), mit
J∀x∃yR(x, y )K(S,β) 6= J∀x∃yR(y , x)K(S,β) )
I
∀x∃yR(x, y ) 6≡ ∃x∀yR(x, y )
237
Wichtige Äquivalenzen mit Quantoren
Für alle Formeln ϕ, ψ ∈ FOL(Σ,
X) gilt
¬∀xϕ ≡ ∃x¬ϕ
¬∃xϕ ≡ ∀x¬ϕ
∀xϕ ∧ ∀xψ ≡ ∀x(ϕ ∧ ψ)
∃xϕ ∨ ∃xψ ≡ ∃x(ϕ ∨ ψ)
∀x∀y ϕ = ∀y ∀xϕ
∃x∃y ϕ = ∃y ∃xϕ
falls x 6∈ fvar(ψ) und ∗ ∈ {∨, ∧}, gilt außerdem
∀xϕ ∗ ψ ≡ ∀x(ϕ ∗ ψ)
∃xϕ ∗ ψ ≡ ∃x(ϕ ∗ ψ)
∃y ϕ ≡ ∃xϕ[x7→y ]
∀y ϕ ≡ ∀xϕ[x7→y ]
Notation ϕ[x7→y ] :
Umbenennung aller gebundenen Vorkommen von y in ϕ durch x
238
Was bisher geschah
Klassische Prädikatenlogik der ersten Stufe FOL(Σ,
X):
Syntax :
I
I
I
I
I
Signatur Σ = (ΣF , ΣR ),
(Individuen-)Variablen
Terme Term(Σ, ), Grundterme
Atome Atom(Σ, ), Grundatome
Formeln FOL(Σ, ), Sätze
I
I
I
Σ-Strukturen A = (A, J·KA )
Belegung der Individuenvariablen α :
Σ-Interpretationen (A, α)
X
X
X
X
Semantik :
X→A
Werte von (Individuen-)Variablen, Termen, Atomen
und Formeln in Σ-Interpretationen
I Modellmengen von Formeln
I erfüllbare, unerfüllbare, allgemeingültige Formeln
I (semantische) Äquivalenz von Formeln
I
Modelle von Formelmengen
Menge aller Modelle der Formelmenge Φ ⊆ FOL(Σ,
\
Mod(Φ) =
Mod(ϕ)
X):
ϕ∈Φ
Beispiel: Signatur Σ = (∅, ΣR ) mit ΣR = {(P, 1), (E , 2)}
∀x (P(x) ∨ P(y )) ,
Φ=
∀x∀y ((P(x) ∧ E (x, y )) → ¬P(y ))
I
Für (A, α) mit A = ({0, . . . , 5}, J·KA ), wobei JPKA = {0, 2} und
JE KA = {(i, i + 1) | i ∈ {0, . . . , 4}} und α(x) = 1, α(y ) = 2
gilt (A, α) ∈ Mod(Φ)
I
Für (B, β) mit B = ( , J·KB ), wobei JPKB = 2
JE KB = {(i, 2i) | i ∈ } und α(x) = α(y ) = 0
gilt (B, β) 6∈ Mod(Φ)
Z
Z
Z und
Für jede endliche Formelmenge Φ = {ϕ1 , . . . , ϕn } ⊆ FOL(Σ,
X) gilt
Mod(Φ) = Mod (ϕ1 ∧ · · · ∧ ϕn )
239
Modelle von Sätzen
X
Auf den Wert eines Satzes ϕ ∈ FOL(Σ, ) (Formel ohne freie
Variablen) in einer Interpretation I = (S, β) hat die Belegung β
keinen Einfluss, d.h. für beliebige Belegungen α, β : → S gilt
X
JϕK(S,α) = JϕK(S,β)
Beispiel: ϕ = ∀x∃y (P(x) ∧ E (x, y ) → ¬P(y ))
X
Für Sätze ϕ ∈ FOL(Σ, ) genügt es also, den Wert in Strukturen
(statt in Interpretationen) zu betrachten:
JϕKS = JϕK(S,β)
für jede beliebige Belegung β :
Menge aller Modelle des Satzes ϕ ∈ FOL(Σ,
X→S
X):
Mod(ϕ) = {S | S = (S, J·KS ) ist Σ-Struktur und JϕKS = 1}
240
Modelle prädikatenlogischer Sätze – Beispiel
ϕ = ∀x(¬G (x) → G (f (x))
I
A = (A, J·KA ) mit A = Menge aller Menschen,
Jf KA (x) = Vater von x, JG KA (x) gdw. x männlich
A ∈ Mod(ϕ)
I
B = (B, J·KB ) mit B = Menge aller Orte 51◦ nördlicher Breite
Jf KB (x) = Ort 50 km westlich von x, JG KB (x) gdw. x in Sachsen
B 6∈ Mod(ϕ)
I
C = ( , J·KC ) mit
Jf KC (x) = x + 1, JG KC (x) gdw. x Primzahl
I
I
N
Z
D = ( , J·KD ) mit Jf KD (x) = x + 1,
JG KD = 2
Z
C 6∈ Mod(ϕ)
D ∈ Mod(ϕ)
R
2
E = (E , J·KE ) mit E =
(Menge aller Punkte der Ebene),
E 6∈ Mod(ϕ)
Jf KE (x, y ) = (−x, −y ), JG KE (x, y ) gdw. x < y
241
Was bisher geschah
Modellierung in Logiken:
X)
I
klassische Prädikatenlogik FOL(Σ,
I
Spezialfall (Fragment) klassische Aussagenlogik AL(P)
Syntax
I
I
I
I
Signatur, Variablen
Terme (induktive Definition, Baumform)
Atome (in AL(P): Aussagevariablen)
Formeln (Junktoren, Quantoren)
Semantik
I
Σ-Interpretation (S, β) mit
I Σ-Struktur S = (S, J·KS )
I Belegung β :
→S
Wert von Termen, Atomen, Formeln in
Σ-Interpretationen
Modellmengen von Formeln und Formelmengen
semantische Äquivalenz von Formeln
erfüllbare, unerfüllbare, allgemeingültige Formeln
Modellmengen von Sätzen und Mengen von Sätzen
X
I
I
I
I
I
Modelle von Satzmengen – Beispiel
Signatur Σ = (∅, ΣR ) mit ΣR = {(R, 2), (P, 1)}

∃x P(x),




 ∃x ¬P(x),
∀x R(x, x),
Φ=


∀x∀y (R(x, y ) → R(y , x)) ,



∀x∀y ∀z ((R(x, y ) ∧ R(y , z)) → R(x, z))
I
I











Für Σ-Struktur A = ({a, b, c}, J·KA ) mit JPKA = {b, c} und
JRKA = {(a, a), (a, c), (b, b), (c, a), (c, c)} gilt A ∈ Mod(Φ)
N
Für Σ-Struktur B = ( , J·KB ) mit
JPKB = 7 und JRKB = ≤ gilt B 6∈ Mod(Φ)
N
Mod(Φ) = Menge aller Σ-Strukturen S = (S, J·KS ), für die
JPKS 6= ∅, S \ JPKS 6= ∅ (und damit |S| ≥ 2)
und JRKS eine Äquivalenzrelation ist
242
Modelle von Satzmengen – Beispiel
Signatur Σ0 = (Σ0F , Σ0R ) mit Σ0F = {(f , 2), (e, 0)}, Σ0R {(=, 2)}
∀x∀y (f (f (x, y ), z) = f (x, f (y , z))),
0
Φ =
∀x (f (x, e) = x)
N
N
I
Für Σ0 -Struktur A = ( , J·KA ) mit
J=KA = IN , ∀(m, n) ∈ 2 : Jf KA (m, n) = m · n, JeKA = 1 gilt
A ∈ Mod(Φ0 )
I
Für Σ0 -Struktur B = ({0, 1}, J·KB ) mit
J=KB = I{0,1} , Jf KB = max, JeKB = 1 gilt B 6∈ Mod(Φ0 )
Mod(Φ0 ) = Menge aller Σ0 -Strukturen S = (S, J·KS ), für die
J=KS = IS und
S mit Jf KS ein Monoid mit neutralem Element JeKS bildet
Spezialfall Gleichheit: (=, 2) ∈ ΣR wird in jeder Σ-Struktur
S = (S, J·KS ) interpretiert durch die Identität auf S, d.h. J=KS = IS
243
Charakterisierung von Strukturen durch Satzmengen
Beispiel: Graphen mit Eckenfärbung mit Farben aus {R, G , B}
Signatur Σ = (∅, ΣR ) mit ΣR = {(R, 1), (G , 1), (B, 1), (E , 2)}


∀x¬E
(x,
x),




 ∀x∀y (E (x, y ) → E (y , x)),









∀x(R(x) ∨ G (x) ∨ B(x)),
Φ=
∀x(R(x) → ¬(G (x) ∨ B(x)), 








∀x(G
(x) → ¬(R(x) ∨ B(x)), 




∀x(B(x) → ¬(G (x) ∨ R(x))
(jede Ecke mit genau einer Farbe aus {R, G , B} gefärbt)
Konfliktfreiheit der Eckenfärbung:
ψ = ∀x∀y (((R(x)∧R(y ))∨(G (x)∧G (y ))∨(B(x)∧B(y ))) → ¬E (x, y ))
Mod(Φ) = Menge aller ungerichteten schlingenfreien Graphen mit
Eckenfärbung mit Farben aus {R, G , B}
Mod(Φ ∪ {ψ}) = Menge aller ungerichteten schlingenfreien
Graphen mit konfliktfreier Eckenfärbung mit Farben aus {R, G , B}
244
Aussagenlogik als FOL-Spezialfall
Wiederholung:
Syntax : für Signatur ΣP = (ΣF , ΣR ) mit ΣF = ∅ und
ΣR = {(p, 0) | p ∈ P}. gilt AL(P) = FOL(ΣP , ∅)
(Alle Formeln in FOL(ΣP , ∅) sind Sätze, enthalten
keine Individuenvariablen, Terme und Quantoren)
Semantik : Jede ΣP -Struktur S = (S, J·KS ) definiert für jedes
p ∈ P einen Wahrheitswert JpKS ∈ {0, 1},
also Funktion WS : P → {0, 1} (Belegung aller
Aussagenvariablen p ∈ P mit Wahrheitswerten)
mit ∀p ∈ P : WS (p) = JpKS
Damit gilt auch für alle Formeln ϕ ∈ FOL(ΣP , ∅):
WS (ϕ) = JϕKS
245
Beispiel
P = {p, q, r } definiert die Signatur Σ{p,q,r } = (ΣF , ΣR )
mit ΣF = ∅ und ΣR = {(p, 0), (q, 0), (r , 0)}
ϕ = p ∧ (¬r ∨ q)
∈
FOL(Σ{p,q,r } , ∅) = AL({p, q, r })
Σ{p,q,r } -Struktur S = (S, J·KS ) mit
JpKS = Jr KS = 1
und JqKS = 0
entspricht der Belegung (der Aussagenvariablen)
WS : {p, q, r } → {0, 1}:
WS = {p 7→ 1, q 7→ 0, r 7→ 1}
Wert von ϕ in S: JϕKS = 0 = WS (ϕ)
Modellmenge von ϕ:
I in AL({p, q, r }): Mod(ϕ) = . . .
I in FOL(Σ{p,q,r } , ∅): Mod(ϕ) = . . .
246
WH: Modellierungsbeispiel Party
umgangssprachliche Beschreibung der Situation:
Anna geht zur Party, wenn Max oder Paul hingehen.
Max geht zur Party, wenn Paul nicht hingeht.
Anna geht nirgends ohne ihren Hund hin.
Frage: Wird Annas Hund auf der Party sein?
formale Beschreibung:
I
elementare Aussagen (Atome): P = {a, h, m, p}
I
Beschreibung der Situation (Kontext) als Formelmenge:
ΦP = {(m ∨ p) → a, ¬p → m, ¬(a ∧ ¬h)} ⊆ AL(P)
I
Formulierung der Frage als Behauptung : h
(positive Antwort auf die Frage)
Alle Situationen, in denen alle Angaben erfüllt sind:


 {a 7→ 1, h 7→ 1, m 7→ 1, p 7→ 0}, 
{a 7→ 1, h 7→ 1, m 7→ 0, p 7→ 1},
Mod(ΦP ) =


{a 7→ 1, h 7→ 1, m 7→ 1, p 7→ 1}
Antwort auf die Frage: ja (weil in jedem W ∈ Mod(ΦP ) gilt W (h) = 1)
247
Semantisches Folgern
Für Φ ⊆ FOL(Σ,
X) (Kontext) und ψ ∈ FOL(Σ, X) (Aussage) gilt
Φ |= ψ
gdw.
Mod(Φ) ⊆ Mod(ψ)
(Behauptung ψ ist semantische Folgerung aus dem Kontext Φ.)
Folgerungsrelation
|= ⊆ 2FOL(Σ,X) × FOL(Σ,
X)
Beispiele:
I
{p, p → q} |= q
I
{p, ¬(q ∧ p)} |= ¬q
I
{p} |= q → p
I
∅ |= p ∨ ¬p
I
{∀x(P(x) ∨ Q(x)), ¬P(y )} |= Q(y )
I
{∀x(P(x) ∨ Q(x)), ¬P(x)} |= Q(x)
Notation für Spezialfälle
für Φ = {ϕ} : ϕ |=
für Φ = ∅
:
|=
ψ
ψ
(statt
(statt
{ϕ}
∅
|=
|=
ψ)
ψ)
248
Was bisher geschah
Modellierung von
Daten durch Mengen (Individuenbereiche),
häufig zusammengesetzt durch Mengenoperationen,
Zusammenhängen zwischen Individuen durch
Relationen (auch Eigenschaften)
Funktionen (Operationen)
gemeinsam in algebraischen Strukturen
Modellierung von
Bedingungen (Eigenschaften, Anforderungen) an Individuen und
Beziehungen durch Formel(menge)n in (klassischen)
Logiken:
FOL(Σ, ) Prädikatenlogik mit
AL(P) Aussagenlogik als Spezialfall
(Fragment)
X
Charakterisierung algebraischer Strukturen durch Satzmengen
Sematisches Folgern |=
Semantisches Folgern – Beispiele
I
für Φ = {∀x(P(x) ∨ Q(x)), ¬P(x)} und ψ = Q(y ) gilt
Φ 6|= ψ, weil
für (S, β) mit S = ({a, b}, J·KS ) mit
JPKS = {b}, JQKS = {a} und β = {x 7→ a, y 7→ b} gilt:
(S, β) ∈ Mod(Φ), aber (S, β) 6∈ Mod(ψ)
I
{∀x (P(x) ∨ Q(x)), ∀x ¬P(x)} |= ∀x Q(x)
I
für Φ = {∀x (P(x) ∨ Q(x)), ∃x ¬P(x)} und ψ = (∀x Q(x))
gilt Φ 6|= ψ, weil
für S = ({a, b}, J·KS ) mit JPKS = {b} und JQKS = {a}
gilt S ∈ Mod(Φ), aber S 6∈ Mod(ψ)
Für alle Formeln ϕ, ψ ∈ FOL(Σ,
X) gilt
I
{ϕ → ψ, ϕ} |= ψ
(Modus ponens)
I
{ϕ → ψ, ¬ψ} |= ¬ϕ
(Modus tollens)
I
∀xϕ |= ϕ
249
Eigenschaften der Folgerungsrelation
Für jede endliche Formelmenge Φ = {ϕ1 , . . . , ϕn } gilt
Φ |= ψ
genau dann, wenn
n
^
ϕi |= ψ
i=1
Für jede Formelmenge Φ ⊆ FOL(Σ,
gilt
(ψ ∈ Φ)
→
Φ |= ψ
gdw.
X) und jede Formel ψ ∈ FOL(Σ, X)
(Φ |= ψ)
Mod(Φ) = Mod(Φ ∪ {ψ})
gdw.
Mod(Φ ∪ {¬ψ}) = ∅
gdw.
Φ ∪ {¬ψ} unerfüllbar
gdw.
Φ ∪ {¬ψ} |= f
Für alle Formeln ϕ, ψ ∈ FOL(Σ,
X) gilt
|= ψ
gdw.
ψ allgemeingültig
ϕ≡ψ
gdw.
(ϕ |= ψ) ∧ (ψ |= ϕ)
ϕ |= ψ
gdw.
|= (ϕ → ψ)
ϕ≡ψ
gdw.
|= (ϕ ↔ ψ)
250
Modellierungsbeispiel: Taxi
Sachverhalt (Kontext) informal:
I
Bei Zugverspätung ist Tom nicht pünktlich, falls kein Taxi am
Bahnhof steht.
I
Der Zug hat Verspätung.
I
Tom ist pünktlich.
Modellierung als (aussagenlogische) Formelmenge:
ΦT = {v → (¬t → ¬p), v , p}
Frage:
informal: Stand ein Taxi am Bahnhof ?
formal Gilt ΦT |= t ?
251
Weitere Modellierungsbeispiele mit Folgerungsfragen
I
Lieblingsgetränke: Kontext siehe ÜA 6.7
Fragen:
I
I
I
I
Haben Anna und Paul (wenigstens) ein gemeinsames
Lieblingsgetränk?
Welche?
Welche Restaurants bieten diese an?
Familienbeziehungen: Kontext
I
I
allgemein:
Zwei Personen sind Geschwister gdw. . . .
(Großeltern, verwandt,. . . )
Aufgaben-spezifisch:
Paul ist Vater von Anna und Tom. . . .
Fragen:
I
I
I
Sind Paul und Tina verwandt?
Wer sind Annas Großeltern, Nichten, . . . ?
Erreichbarkeit:
Kontext: Menge von Orten A, B, C , . . ., existierende Straßen,
Verbindungen
Fragen: (Wie) Ist B von A erreichbar?
252
Anwendungen von Folgerungsaufgaben: Verifikation
Verifikation: Nachweis der Korrektheit von Software und Systemen
bzgl. einer gegebenen Spezifikation
Beispiel Schaltkreis-Verifikation:
gegeben: Schaltung: Ausgabe-Verhalten (boolesche Funktion)
als Formel ϕ ∈ AL(P)
Spezifikation: Zielfunktion als logische Formel ψ ∈ AL(P)
Frage: Erfüllt die Schaltung die Spezifikation?
(Folgt ψ aus {ϕ} ? Gilt {ϕ} |= ψ ?)
Lösung: ja / nein, evtl. mit Gegenbeispiel (unkorrekter Zustand)
Beispiel Korrektheit von Software:
gegeben: Programm : tatsächlicher Zusammenhang
zwischen Ein- und Ausgaben als Formelmenge Φ ⊆ FOL(Σ, )
Spezifikation: gewünschter Zusammenhang
zwischen Ein- und Ausgaben als logische Formel ψ ∈ FOL(Σ, )
Frage: Erfüllt das Programm die Spezifikation?
(Folgt ψ aus Φ ? Gilt Φ |= ψ ?)
Lösung: ja / nein, evtl. mit Gegenbeispiel (Eingabe mit falscher Ausgabe)
X
X
253
Syntaktisches Ableiten – Ziel
gegeben: Formelmenge Φ
Formel ψ
Frage : Gilt Φ |= ψ ?
Ziel:
Verfahren zur Beantwortung dieser Frage durch syntaktische
Operationen (ohne Verwendung der Semantik, Modellmengen)
Syntaktische Ableitungsrelation ` ⊆ 2FOL(Σ,X) × FOL(Σ, )
passend zur
semantischen Folgerungsrelation |= ⊆ 2FOL(Σ,X) × FOL(Σ, )
X
X
` passt zu |= gdw.
für jede Formelmenge Φ ∈ FOL(Σ,
ψ ∈ FOL(Σ, ) gilt
X
Φ`ψ
X) und jede Formel
gdw.
Φ |= ψ
254
Kalküle – Motivation
Formale Methode zur schrittweisen syntaktischen Ableitung von
sematischen Folgerungen (Formeln) aus einer Menge von Formeln
(Hypothesen)
Definition von
Schlussregeln zur syntaktischen Ableitung von Folgerungen aus
Formelmengen (Hypothesen, Annahmen)
(analog Spielregeln),
oft mehrere Voraussetzungen und eine Folgerung
Ableitungen (und Beweisen) durch geeignete Kombinationen von
Schlussregeln (Baumstruktur)
255
Kalküle - Definition
Kalkül K = (A, R) mit Mengen von
Axiome A, d.h. (Schema für) Formeln, deren
Gültigkeit vorausgesetzt wird,
Regeln R zur syntaktischen Ableitung von
Folgerungen (weitere gültige Formeln)
aus Formelmengen (Axiomen und
Hypothesen)
häufige Darstellung von Regeln:
ϕ1
···
ψ
I
I
ϕn
Voraussetzungen (oben): ϕ1 , . . . , ϕn
Folgerung (unten): ψ
Beispiel: Regel (∧-Einführung)
ϕ
ψ
(∧I)
ϕ∧ψ
256
Beispiel: Kalkül des natürlichen Schließens
(Gerhard Gentzen, 1935)
Idee: formale Beschreibung des menschlichen Vorgehens beim
logischen Schließen und Beweisen
Für jeden Junktor ∗ ∈ {∧, ∨, →, ¬} und jeden Quantor
I
eine Einführungsregel (∗I)
Junktor in der Folgerung (unten), aber in keiner
Voraussetzung (oben) der Regel
I
eine Eliminierungsregel (∗E)
Junktor in einer Voraussetzung (oben), aber nicht in der
Folgerung (unten) der Regel
Beispiel: Modus Ponens eliminiert die Implikation →
ϕ
ϕ→ψ
(MP)
ψ
257
Einige Regeln im Kalkül des natürlichen Schließens
ϕ
ψ
(∧I)
ϕ∧ψ
ϕ
(∨I)
ϕ∨ψ
ϕ∧ψ
(∧E)
ψ
ϕ∧ψ
(∧E)
ϕ
ψ
(∨I)
ϕ∨ψ
[ϕ]
..
.
ψ
(→I)
ϕ→ψ
ϕ
¬¬ϕ (¬¬I)
∀xϕ
(∀E)
ϕ[x 7→ t]
ϕ∨ψ
ϕ
¬¬ϕ
ϕ (¬¬E)
[ϕ]
..
.
η
η
(∨E)
ϕ→ψ
(→E)
ψ
ϕ→ψ
¬ϕ
ϕ[x 7→ t]
(∃I)
∃xϕ
[ψ]
..
.
η
¬ψ
t=t
(MT)
(=I)
258
Ableitungen in Kalkülen
gegeben: Kalkül K = (A, R),
Formelmenge Φ (Hypothesen, Annahmen)
Definition (induktiv): Ableitung der Formel ψ aus Φ in K
IA: Ist ψ eine Hypothese (also ψ ∈ Φ) oder ein Axiom, dann
ist
ψ
eine Ableitung für ψ aus Φ in K .
IS: Sind
ϕ1
···
ψ
ϕn
eine Schlussregel in K und B1 , . . . , Bn Ableitungen für
ϕ1 , . . . , ϕn aus Φ in K , dann ist
B1
···
ψ
Bn
eine Ableitung für ψ aus Φ in K .
259
Beispiel Taxi
Ableitungsbaum für {v → (¬t → ¬p), v , p} ` t:
v
v → (¬t → ¬p)
p
(→E)
¬¬p (¬¬I)
¬t → ¬p
(MT)
¬¬t (¬¬E)
t
sequentielle Darstellung der Ableitung (des Beweises):
1. v
(Annahme)
2. v → (¬t → ¬p)
(Annahme)
3. ¬t → ¬p
(→E) mit 1 und 2
4. p
(Annahme)
5. ¬¬p
(¬¬I) mit 4
6. ¬¬t
(MT) mit 3 und 5
7. t
(¬¬E) mit 6
260
Was bisher geschah
Modellierung von
Daten durch Mengen (Individuenbereiche),
häufig zusammengesetzt durch Mengenoperationen,
Zusammenhängen zwischen Individuen durch
Relationen (auch Eigenschaften)
Funktionen (Operationen)
gemeinsam in algebraischen Strukturen
Modellierung von
Bedingungen (Eigenschaften, Anforderungen) an Individuen und
Beziehungen durch Formel(menge)n in (klassischen)
Logiken:
FOL(Σ, ) Prädikatenlogik mit
AL(P) Aussagenlogik als Spezialfall
(Fragment)
X
Charakterisierung algebraischer Strukturen durch Satzmengen
Sematisches Folgern |=
Syntaktisches Schließen ` (Kalkül des natürlichen Schließens)
Modellierung in Logiken
Häufige Fragen für gegebene Strukturen, Interpretationen, Formeln
und Formelmengen:
I
Erfüllt eine gegebene Struktur / Interpretation eine gegebene
Formel / Formelmenge?
I
In welchen Interpretationen gilt eine Formel?
I
Ist eine gegebene Formel / Formelmenge erfüllbar?
I
Ist eine gegebene Formel allgemeingültig?
I
Folgt eine gegebene Formel aus einer gegebenen
Formelmenge?
Gibt es automatische Verfahren (Algorithmen), die diese Aufgaben
löst (entscheidet),
also zu jeder Eingabe die Frage in endlicher Zeit korrekt mit ja
oder nein beantwortet.
261
Gültigkeitsproblem
(Allgemein)-Gültigkeitsproblem in einer Logik:
gegeben: Formel ϕ in dieser Logik
Frage:
Ist ϕ allgemeingültig?
Logiken, für die diese Aufgabe algorithmisch lösbar ist, heißen
entscheidbar.
Erfüllbarkeits- und Folgerungs-Probleme lassen sich auch als
Gültigkeits-Probleme darstellen.
Die klassische Aussagenlogik ist entscheidbar.
(Überprüfung endlich vieler endlicher Strukturen genügt)
Beispiele für Verfahren zur Lösung dieser Aufgaben in der
Aussagenlogik:
I
semantisch: Modellmengen, Wahrheitswerttabellen
I
syntaktisch: Beweis in Kalkülen (z.B. natürliches Schließen)
I
Werkzeug: SAT-Solver
262
Unentscheidbarkeit
der Prädikatenlogik der ersten Stufe FOL(Σ,
X)
Satz
Es existiert kein Algorithmus, der für jede beliebige Formel
ϕ ∈ FOL(Σ, X ) entscheidet, ob ϕ allgemeingültig ist.
X
Damit ist FOL(Σ, ) unentscheidbar.
(mehr dazu in der LV Theoretische Informatik)
263
Eignung von Logiken zur Modellierung verschiedener
Aufgabenbereiche
verschiedene Logiken unterschieden sich in
I Ausdrucksstärke:
I
I
I
Aussagen über welche Bereiche lassen sich überhaupt
formulieren?
kompakte Darstellung typischer Aussagen
Verständlichkeit der Formalisierung
Repräsentation von Informationen
I
algorithmische Entscheidbarkeit wichtiger Fragen
(maschinelle) Verarbeitung von Informationen
264
Vergleich verschiedener Logiken
klassische Logiken:
I klassische Prädikatenlogik der ersten Stufe FOL:
I
I
I
I
hohe Ausdrucksstärke,
kompakte, verständliche Formulierungen,
unentscheidbar
klassische Aussagenlogik AL
(Spezialfall, Fragment von FOL):
I
I
I
geringe Ausdrucksstärke
umfangreiche Darstellung
entscheidbar
Speziallogiken für verschiedene Anwendungsbereiche, z.B.
I Temporallogiken (Spezifikation, Verifikation von Systemen)
I Hoare-Logik (Spezifikation, Verifikation imperativer Software)
I Beschreibungslogiken (Wissensextraktion aus Ontologien,
Semantic Web)
oft entscheidbare Fragmente von FOL mit modifizierter Syntax
mehr dazu in Lehrveranstaltungen später im Studium
265
Mehrsortige Strukturen
Modellierung von Strukturen mit verschiedenen Sorten
(Trägermengen, Typen) = {Si | i ∈ I } von Elementen
S
Beispiele mehrsortiger Strukturen:
I
Vektorraum mit
Sorten: Skalar, Vektor
Operationen, z.B. smult: Skalar × Vektor → Vektor
Relationen, z.B. gleichlang ⊆ Vektor × Vektor
I
Sorten: Personen, Bücher
Relation: A ⊆ Personen × Bücher
wobei (m, b) ∈ A gdw. m ist Autor von b
I
Sorten: Personen, , Orte
Relation: B ⊆ Personen ×
× Orte
wobei (m, j, o) ∈ B gdw. m wurde im Jahr j in o geboren
N
N
266
Mehrsortige Signaturen
S
mehrsortige Signatur Σ = ( , ΣF , ΣR ) besteht aus
S
ΣF
ΣR
= {Si | i ∈ I }: Menge der Symbole für Sorten
: Menge der Funktionssymbole
mit Argument- und Ergebnistypen (f : ∗ → )
: Menge der Relationssymbole
mit Argumenttypen (s ⊆ ∗ )
S
S
S
Beispiel: Bücher mit Autoren und Erscheinungsjahr
Z
Sorten B (Bücher), P (Personen), (Jahreszahlen),
2B (Mengen von Büchern), also = {B, P, , 2B }
Funktionssymbole (mit Argument- und Ergebnistypen):


:B →
 Erscheinungsjahr

erstes-Buch-von
:P
→B
ΣF =


gemeinsame-Buecher-von : P 2 → 2B
S
Z
Z
Relationen (mit Argumenttypen):
ist-Autor-von
ΣR =
sind-Coautoren
⊆P ×B
⊆ P2
267
Terme über mehrsortigen Signaturen
S
gegeben: mehrsortige Signatur Σ mit Menge von Sorten
Variablenmenge 0 = ×
(jede Variable mit einer zugeordneter Sorte aus )
X X S
S
Definition (induktiv)
S
X
Für jede Sorte S ∈ ist die Menge TermS (Σ, 0 ) aller
Terme der Sorte S mit Variablen aus der Menge 0 definiert durch:
IA:
IS:
X
{x | (x : S) ∈ X0 } ⊆ TermS (ΣF , X0 )
Für alle f mit (f : S∗ → S) ∈ Σ und alle Tupel
(t1 , . . . , tn ), wobei für alle k ∈ {1, . . . , n} gilt
tk ∈ TermS (Σ, X0 ),
ist f (t1 , . . . , tn ) ∈ TermS (Σ, X0 )
k
Spezialfall: Jede Konstante f : S ∈ Σ ist Σ-Term der Sorte S.
Beispiele: t = Erscheinungsjahr(erstes-Buch-von(x))
mit (x : P) ∈ 0 ist ein Term in TermJ (Σ, 0 )
erstes-Buch-von(Erscheinungsjahr(x)) ist kein Σ-Term
X
X
268
Mehrsortige Σ-Strukturen
S
gegeben: mehrsortige Signatur Σ = ( , ΣF , ΣR )
S
mehrsortige Σ-Struktur A = ({AS | S ∈ }, J·KA ) mit
S
I
für jede Sorte S ∈ eine nichtleere Menge AS
(Trägermenge, Universum der Sorte)
I
für jedes Funktionssymbol f : S1 . . . Sn → S
eine Funktion Jf KA : AS1 × . . . × ASn → AS
I
für jedes Relationssymbol R ⊆ S1 × . . . × Sn
eine Relation JRKA ⊆ AS1 × . . . × ASn
269
Beispiel Vektorraum
mehrsortige algebraische Struktur mit
I Sorten (Symbole für Trägermengen):
I
I
I
Operationen, z.B.
I
I
I
I
I
I
I
I
Menge V von Vektoren
Menge S von Skalaren
Addition von Skalaren +s : S × S → S
Multiplikation von Skalaren ·s : S × S → S
Addition von Vektoren +v : V × V → V
Multiplikation von Skalaren mit Vektoren : S × V → V
Skalarprodukt h·, ·i : V × V → S
Skalare nS ∈ S, eS ∈ S
Nullvektor nV ∈ V
Relationen, z.B.
I
I
Gleichheit von Skalaren =s ⊆ S 2
Gleichheit von Vektoren =v ⊆ V 2
270
Beispiel Vektorraum – Signatur
S
mehrsortige Signatur ΣV = ( , ΣF , ΣR ) mit
S
ΣF
ΣR
= {S, V }

+s




·s




 +v
=


 nS




e

 S
nV
:
:
:
:
:
:
:
S2
S2
V2
S ×V
→
→
→
→
S
S
V
V
S
S
V



















= {=s ⊆ S 2 , =v ⊆ V 2 }
Vektorraum =
(mehrsortige) ΣV -Struktur A = ({AS | S ∈ }, J·KA ), welche alle
für Vektorräume charakteristischen Bedingungen (Axiome) erfüllt.
S
271
Beispiel Vektorraum – Axiome
S bildet mit +s , ·s , ns , es einen Körper, d.h. erfüllt die Axiome
∀x ∀y ∀z
((x +s y ) +s z =s x +s (y +s z))
∀x ∀y
(x +s y =s y +s x)
∀x ∀y ∀z
((x ·s y ) ·s z =s x ·s (y ·s z))
..
.
∀x ∀y ∀z
(x ·s (y +s z) =s (x ·s y ) +s (x ·s z))
und (Axiome für )
∀x∀y ∀v
((x ·s y ) v =v x (y v ))
∀x∀y ∀v
((x +s y ) v =v x v +v y v )
∀x∀u ∀v
(x (u +v v ) =v x u +v a v )
∀v
(es v =v v )
∀v
(ns v =v nV )
Axiome: Menge ΦV ∈ FOL(ΣV , X) (mehrsortiger) Formeln (Sätze) mit
X = {(x : S), (y : S), (z : S), (u : V ), (v : V )}
272
Vektorraum – Beispiel
Vektorraum:
ΣV -Struktur, die alle Axiome (Formeln aus ΦV ) erfüllt
Beispiel: ΣV -Struktur A = (A, J·KA ) mit
AS
AV
= {0, 1} (Skalare)
= {~0} (Vektor)
Jns KA = 0, JeS KA = 1 (∈ AS )
Jnv KA = ~0 (∈ AV )
(
0 falls x = y
J+s KA (x, y ) =
(∈ AS )
1 sonst
J·s KA (x, y ) = x · y (∈ AS )
JKA (0, ~0) = ~0 (∈ AV )
J=s KA = I(AS ) = {(0, 0), (1, 1)}
J=v KA = I(A ) = {(~0, ~0)}
V
erfüllt alle Sätze in ΦV (Axiome)
Menge aller Vektorräume : Modellmenge Mod(ΦV )
273
Mehrsortige Strukturen in der Informatik
Programmierung:
Datentypen (Sorten) int, float, bool, string
mit Operationen (Signatur), z.B.:
floor
duplicate
length
>
:
:
:
:
float
string × int
string
float × float
→
→
→
→
int
string
int
bool
Datenbanken:
Tabellen sind extensionale Darstellungen (meist) mehrsortiger
Relationen
274
Relationen als mehrsortige Funktionen
Beispiel:
I
(einsortige) Signatur Σ = (ΣF , ΣR ) mit
ΣF = ∅ und ΣR = {(r , 2)}
I
Interpretation von r in (einsortigen) Σ-Strukturen
A = (A, Jr KA ) mit Jr KA ⊆ A × A
Einführung der Sorten
S (für Trägermenge) und
I
I
B = {t, f } (für Wahrheitswerte)
{S, B}-sortige Signatur Σ = (ΣF , ΣR ) mit
ΣF = {fr : S × S → B} und ΣR = ∅
Interpretation in {S, B}-sortigen Σ-Strukturen
A0 = (({A, {0, 1}}, J·KA0 ) mit Jfr KA0 : A × A → {0, 1} mit
∀(x, y ) ∈ A2 : Jfr KA0 (x, y ) = 1 gdw. (x, y ) ∈ Jr KA
275
Relationen als mehrsortige Funktionen
für beliebige Stelligkeit n:
Übersetzung jedes Relationssymbols (r , n) ∈ ΣR in ein
Funktionssymbol fr : S n → , so dass
in jeder {S, }-sortigen Σ-Struktur A0 = ({A, {0, 1}}, J·KA0 ) gilt:
Jfr KA0 : An → {0, 1}, wobei
B
B
∀(x1 , . . . , xn ) ∈ An : Jfr KA0 (x1 , . . . , xn ) = 1 gdw. (x1 , . . . , xn ) ∈ Jr KA
Jeder (einsortigen) Signatur Σ = (ΣF , ΣR ) lässt sich so eine
{S, }-sortige rein funktionale Signatur Σ0 = (Σ0F ∪ Σ0R , ∅)
zuordnen:
B
Σ0F
= {f : S n → S | (f , n) ∈ ΣF }
Σ0R
= {fr : S n →
B | (r , n) ∈ ΣR }
Analog lassen sich mehrsortige Relationen durch mehrsortige
Funktionen ersetzen.
Es genügt also, mehrsortige Strukturen ohne Relationen (Algebren)
zu betrachten.
276
Charakterisierung algebraischer Strukturen
Algebraische Strukturen sind eindeutig definiert durch
Syntax:
Trägermengen (Typen, Sorten), z.B. {0, 1}, , {a, b}∗ , 2M
Funktionen (Operationen), z.B. len : {a, b}∗ → , + : 2 → ,
◦ : ({a, b}∗ )2 → {a, b}∗ , 0 ∈ , ε ∈ {a, b}∗ , ∅ ∈ 2M
Relationen , z.B. ≤ ⊆ 2 , prim ⊆ , v ⊆ ({a, b}∗ )2 ,
Semantik:
Zusammenhänge zwischen Funktionen und Relationen, z.B.
N
N
N3
∀x ∈ N
∀(x, y ) ∈ N2
∀(x, y , z) ∈
N
N
N
N
N
: (x + y ) + z = x + (y + z)
: x +0=x
: x +y =y +x
∀u ∈ {a, b}∗ : (len(u) = 0) ↔ (u = ε)
∀(u, v ) ∈ ({a, b}∗ )2 : len(u ◦ v ) = len(u) + len(v )
∀(u, v ) ∈ ({a, b}∗ )2 : (u v v ) → (len(u) ≤ len(v ))
277
Formale Darstellung algebraischer Strukturen
(abstrakte Algebra, abstrakter Datentyp, ADT)
I
I
I
I
I
S
Signatur Σ = ( , ΣF , ΣR ) mit
S
Menge von Sortensymbolen,
Menge ΣF von Funktionssymbolen
mit Stelligkeit / Typdeklaration
Menge ΣR von Relationssymbolen
mit Stelligkeit / Typdeklaration
Menge von Axiomen beschreibt Zusammenhänge zwischen
den Symbolen
(meist prädikatenlogische Formeln, Gleichungen)
ADT zur Definition von Software-Schnittstellen:
Festlegung der
Syntax in Sorten und Signatur (z.B. Java-Interfaces)
Semantik (Anforderungen an Implementierung) in Axiomen
Abstraktion von konkreten Repräsentationen der Daten
(Trägermengen) und konkrete Implementierung der Operationen
278
Konkrete Datentypen
(konkreter) Datentyp:
I
Trägermenge (nichtleer, Menge aller Werte)
I
Eigenschaften von und Relationen zwischen den Elementen
der Trägermenge
I
Operationen auf der Trägermenge
(= algebraische Struktur)
Beispiele:
I
integer mit +,-,*,/
I
string mit ++, reverse
I
boolean mit And, Or, Not
I
string ∪ integer mit length
Jeder ADT repräsentiert eine Menge konkreter Datentypen:
genau alle Σ-Strukturen (konkreten Datentypen,
Implementierungen), die alle Axiome des ADT erfüllen
(= Mod(Φ))
279
Kombination von Strukturen
einfache (einsortige) Datentypen, z.B. int, bool, float, ...
zusammengesetzte Datentypen
Konstruktion durch Operationen auf den Trägermengen:
Vereinigung ∪ von Datentypen
Beispiel Skat: W = Z ∪ B
Produkt (kartesisches) × von Datentypen:
Beispiel Skat: K = F × W
mehrfaches Produkt desselben Typs,
z.B. Tupel
Beispiel Skat:
Blatt in der Hand nach dem Geben ∈ K 10
Rekursion : rekursive Datentypen, z.B. Listen, Bäume
Funktion : zwischen Datentypen (Abbildung)
z.B. Multimengen, Maps
Zusammengesetzte Datentypen = mehrsortige Strukturen
280
Modellierungsbeispiel ID-Nummern
Aufgabe:
Verwaltung einer (endlichen) Menge ganzer Zahlen (z.B. ID-Nummern),
so dass festgestellt werden kann, ob eine Zahl darin enthalten ist und
Zahlen zur Menge hinzugefügt und daraus entfernt werden können.
Sorten (Wertebereiche): , 2N , = {t, f } (Wahrheitswerte)
Signatur: Funktionen zum Finden, Hinzufügen, Entfernen, . . .


contains :
2N × →






add, remove : 2N × → 2N
ΣF =
isempty :
2N →






∅:
2N
N
B
N
N
B
B
Axiome (definieren die Semantik der Operationen):








∀n ∈
∀s ∈ 2N ∀n ∈
Φ=
∀s ∈ 2N ∀n ∈




∀s ∈ 2N ∀m, n ∈



∀s ∈ 2N ∀n ∈
N
N
N
N
N
:
:
:
:
:
isempty(∅) = t,
contains(∅, n) = f ,
contains(add(s, n), n) = t,
contains(remove(s, n), n) = f ,
add(add(s, n), m) = add(add(s, m), n),
add(add(s, n), n) = add(s, n), . . .















281
Konkrete Datentypen (Implementierung) – Beispiele
verschiedene Möglichkeiten zur Repräsentation der Sorten:
I
Wahrheitswerte z.B. als {0, 1} oder {−1, 1}
I
Zahlen in verschiedenen Zahlendarstellungen, z.B.
dezimal, binär, zu anderer Basis,
Maschinenzahlen (eingeschränkter Bereich)
I
Mengen als (sortierte) Folgen von Zahlen
(mit / ohne Wiederholungen)
I
Mengen als Zuordnung Zahl → {0, 1} mit
1, falls Zahl in der Menge, 0 sonst
(charakteristische Funktion der Menge)
I
Mengen als {0, 1}-Folgen variabler Länge
(z.B. nur relevanter Teil der charakteristischen Funktion,
charakteristischer Vektor)
abstrakter Datentyp: Signatur Σ und Axiome Φ,
exakte Formulierung der Aufgabe, Spezifikation
konkreter Datentyp: Σ-Struktur, welche Φ erfüllt (Modell für Φ)
Umsetzung, Implementierung
282
Was bisher geschah
Modellierung von
Daten durch Mengen
Beziehungen (Zusammenhänge und Eigenschaften) durch
Relationen, Graphen und Funktionen
Anforderungen durch Logiken
Modellierung zusammenhängender Datenbereiche durch
algebraische Strukturen (konkrete Datentypen)
Trägermengen, Funktionen (, Relationen)
283
Algebraische Spezifikation
abstrakte Datentypen (ADT) werden definiert durch
Syntax : (mehrsortige) Signatur
Σ = ( , ΣF , ΣR ),
Semantik : Menge von Axiomen (Sätzen)
Φ ⊆ FOL(Σ, )
zur Modellierung zusammenhängender Datenbereiche
und derer Eigenschaften
S
X
konkrete Datentypen : Σ-Strukturen (Syntax)
in Mod(Φ) (Semantik)
Abstrakter Datentyp (Spezifikation, Schnittstellen-Beschreibung)
(Σ, Φ)
repräsentiert eine
Menge konkreter Datentypen (Strukturen, Implementierungen)
Mod(Φ)
284
Modellierungsbeispiel Navigation
ADT für (Blickrichtung in) Himmelsrichtungen Norden, Osten,
Süden, Westen
mit Operationen für Rechts- und Linksabbiegen und Umlenken
ADT Himmelsrichtungen (Spezifikation):
Sorten: eine Sorte (Himmelsrichtung) HR = {N, O, S, W}
Signatur:
N, O, S, W :
HR
rechts, links, um : HR → HR
Axiome:

rechts(N) = O, links(N) = W, . . .




um(N)
= S, um(O) = W, . . .

∀h ∈ HR : rechts(links(h)) = h,


∀h ∈ HR : links(rechts(h)) = h,



∀h ∈ HR : rechts(rechts(h)) = um(h), . . .











285
Konkrete Datentypen (Beispiele)
Implementierung des ADT Himmelsrichtungen, z.B.:
cos ϕ − sin ϕ
I als Punkte im 2 mit Drehmatrizen
sin ϕ cos ϕ
0 1
0 −1
ϕ = −π/2 : R =
ϕ = π/2 : L =
−1 0
1 0
R
A = ({(0, 1), (1, 0), (0, −1), (−1, 0)}, J·KA ) mit
JNKA = (0, 1), JOKA = (1, 0), JSKA = (0, −1), JWKA = (−1, 0),
x
x
∀(x, y ) : JrechtsKA (x, y ) = R
∧ JlinksKA (x, y ) = L
y
y
∀(x, y ) : JumKA (x, y ) = (−x, −y )
Ist diese Implementierung korrekt (d.h. Modell aller Axiome)?
I
B = ({0, 1, 2, 3}, J·KB ) mit
JNKB = 0, JOKB = 1, JSKB = 2, JWKB = 3,
∀x : JrechtsKB (x) = (x + 1) mod 4
∀x : JlinksKB (x) = (x − 1) mod 4,
∀x : JumKB (x) = (x + 2) mod 4
Ist diese Implementierung korrekt?
286
Modellierungsbeispiel Papierstapel
I
Individuenmengen:
I
I
I
I
Blätter (oben einseitig bedruckt)
Stapel (von Blättern)
Eigenschaft: (Stapel) ist leer“
”
Funktionen:
top : Stapel → Blatt
(oberes Blatt auf dem Stapel)
pop : Stapel → Stapel
(oberes Blatt vom Stapel entfernen)
push : Blatt × Stapel → Stapel
(Blatt oben auf den Stapel legen)
new : Stapel
(neuer leerer Stapel)
287
Eigenschaften der Stapel-Operationen
Operationen:
top : Stapel → Blatt
pop : Stapel → Stapel
push : Blatt × Stapel → Stapel
einige Zusammenhänge zwischen den Stapel-Operationen:
für alle Blätter (Stapelelemente) e und alle Stapel s gilt:
I Wird zuerst ein Blatt e auf einen Stapel s gelegt und dann
von diesem Stapel das obere Blatt weggenommen, enthält
man den ursprünglichen Stapel s
pop(push(e, s)) = s
I top(push(e, s)) = e
I push(top(s), pop(s)) = s
Beobachtung:
Dieselben Eigenschaften gelten auch für Bücher-, Teller- und
andere Stapel,
sind also unabhängig vom Typ der Stapelelemente
288
ADT Stack (Stapel, Keller)
Abstraktion von der Realisierung
(Trägermengen, Implementierung der Operationen)
Sorten E : Elementtyp,
S: Stapel von Elementen vom Typ E ,
= {t, f } (Wahrheitswerte)
Signatur Σ: top
:S
→E
pop
:S
→S
push
: E ×S →S
new
:
S
isEmpty : S
→
Axiome , z.B.
isEmpty(new)
∀s ∈ S ∀e ∈ E : isEmpty(push(e, s))
∀s ∈ S ∀e ∈ E :
top(push(e, s))
∀s ∈ S ∀e ∈ E :
pop(push(e, s))
∀s ∈ S ∀e ∈ E : push(top(s), pop(s))
B
B
konkrete Datentypen (Implementierungen) dazu in
LV Algorithmen und Datenstrukturen
=
=
=
=
=
t
f
e
s
s
289
ADT Stack (Stapel, Keller)
Aus den Axiomen
isEmpty(new)
∀s ∈ S ∀e ∈ E :
∀s ∈ S ∀e ∈ E :
∀s ∈ S ∀e ∈ E :
isEmpty(push(e, s))
top(push(e, s))
pop(push(e, s))
∀s ∈ S ∀e ∈ E : push(top(s), pop(s))
(1)
=
(2)
=
(3)
=
(4)
=
(5)
=
t
f
e
s
s
lassen sich durch syntaktische Umformungen
(ohne Wissen über Realisierung, konkreten Datentyp)
weitere Eigenschaften ableiten, welche in jeder Realisierung gelten,
z.B. gilt top(pop(push(a, push(b, s)))) = top(push(b, new)) wegen
top(pop(push(a, push(b, s))))
(4)
=
(3)
=
(3)
top(push(b, s)) = b
top(push(b, new))
290
Spezifikation und Verifikation
Jeder ADT spezifiziert eine Menge konkreter Datentypen:
genau alle Implementierungen (Σ-Strukturen), die alle Axiome des
ADT erfüllen
Menge aller korrekten Implementierungen des ADT
= Modellmenge der Menge Φ der Axiome des ADT
Verifikation:
formaler Nachweis der Korrektheit von Implementierungen bzgl.
der Spezifikation (ADT)
oft durch Ableitungen in geeigneten Kalkülen
maschinelle Unterstützung durch Werkzeuge wie
z.B. Coq, pvs, Isabelle, KIV, KeY
(mehr dazu in LV im Master-Studium)
291
WH: Prozess beim Lösen von Aufgaben (Problemen)
Analyse der (informalen) Aufgabe, Identifikation von
I Aufgabenbereich (Kontext)
I Eingabedaten (Typen, mögliche Werte)
I gewünschte Lösung
(Typ, Eigenschaften, Zusammenhang mit Eingabe)
Modellierung (Abstraktion, formale Darstellung) von
I Aufgabenbereich (Kontext)
I Anforderungen an Eingaben
I Anforderungen an Lösungen
Modellierung von Daten
und deren Eigenschaften und Beziehungen zueinander
Entwurf einer Lösungsstrategie für die modellierte Aufgabe
(mit vorhandenen oder neuen Methoden)
Modellierung von Abläufen und deren Eigenschaften
Umsetzung der Lösungsstrategie im Modellbereich
Ausführung der Lösungsstrategie im Modellbereich
Übertragung der Lösung vom Modellbereich in die Realität
292
Maschinelle Lösung von Aufgaben
Modellierung Übertragung aller relevanten Informationen von der
Realität in einen Modellbereich (geeignet gewählt) durch
Analyse und Formalisierung der Eigenschaften von
Aufgabenbereich (Kontext): (strukturierte) Daten,
Eigenschaften, Zusammenhänge
Eingabedaten: Typ, mögliche Werte, Einschränkungen
Ausgabedaten (Lösung): Typ und Anforderungen:
Einschränkungen
Zusammenhänge mit den Eingabedaten
Formalisierung in abstrakten Datentypen (ADT)
Lösung der Aufgabe im Modellbereich mit
vorhandenen Methoden, z.B.
SAT-Solver, SW-Bibliotheken
speziellen (eigens entwickelten) Algorithmen
(Realisierung in konkreten Datentypen, Implementierung)
Übertragung der Lösung aus Modellbereich in Realität
293
Modellierungsbeispiel: Winterbekleidung
Kontext (informal):
I
Wenn es kalt ist, trägt Paul immer eine Mütze, einen Schal
oder Handschuhe.
I
Ohne Handschuhe oder Schal trägt er keine Mütze.
I
Mütze und Handschuhe trägt er nie zusammen.
I
Handschuhe und Schal trägt er immer zugleich.
Aufgabe: Beantwortung der folgenden Fragen (mit ja/nein)
Welche der folgenden Aussagen sind semantische Folgerungen
daraus:
I
Bei Kälte trägt er immer seinen Schal.
I
Bei Kälte trägt er immer Handschuhe oder Mütze.
I
Er trägt nie Handschuhe.
294
Modellierungsbeispiel: Winterbekleidung
Idee (Lösungsstrategie): Lösung mit SAT-Solver
Lösungsprozess:
1. Formale Darstellung des Kontext als (aussagenlogische)
Formelmenge
Φ = {m ∨ s ∨ h, ¬(h ∨ s) → ¬m, ¬(m ∧ h), h ↔ s}
2. Formale Darstellung der Aufgabestellungen (Fragen)
ψ1 = s, ψ2 = h ∨ m, ψ3 = ¬h
3. Übersetzung der Folgerungsprobleme Φ |= ψi in
Erfüllbarkeitsprobleme
(Φ |= ψi gdw. Φ ∪ {¬ψi } unerfüllbar)
4. Darstellung von Φ ∪ {¬ψi } als CNF, z.B. für ψ1 = s:
ϕ = (m ∨ h ∨ s) ∧ (¬m ∨ h ∨ s) ∧ (¬m ∨ ¬h) ∧ (¬h ∨ s) ∧ (¬s ∨ h) ∧ (¬s)
5. Übertragung der CNF in Dateien im DIMACS-Format
6. Lösung der Erfüllbarkeitsprobleme mit einem SAT-Solver
7. Übersetzung der Ergebnisse in Antworten auf die Fragen:
unerfüllbar 7→ ja, erfüllbar 7→ nein
295
Algorithmen
(Wiederholung aus LV zu Programmierung)
Algorithmus: in Schritte geordnete Arbeitsvorschrift
I
in einer formalen Beschreibungssprache
I
endlich beschriebene
I
schrittweise ausgeführte
Arbeitsvorschrift
zur Lösung einer (Berechnungs-)Aufgabe,
d.h. zur Transformation einer Eingabe in eine Ausgabe
zur Ausführung eines Algorithmus ist nötig:
Akteur (z.B. Maschine), welche die Beschreibungssprache
interpretieren kann
296
Beispiel: Summe der ersten n natürlichen Zahlen
informale Aufgabenstellung:
Addiere alle natürlichen Zahlen von 1 bis n.
Spezifikation (formale Aufgabenbeschreibung, Anforderungen):
N
P
Ausgabe s ∈ N mit s = ni=1 i
Vorbedingung: Eingabe n ∈
Nachbedingung:
verschiedene Algorithmen, welche diese Spezifikation erfüllen:
Algorithmus : Summe1
Eingabe : n ∈
Ausgabe : s ∈
N
N
s←0
für jedes i ← 1, . . . , n :
s ←s +i
Algorithmus : Summe2
Eingabe : n ∈
Ausgabe : s ∈
s←
N
N
n(n+1)
2
297
Was bisher geschah
Modellierung von
Daten durch Mengen (einfach, zusammengesetzt)
Beziehungen (Zusammenhänge und Eigenschaften)
durch Relationen, Graphen und Funktionen
Abläufen durch Zustandsübergangssysteme
sequentiell (ein Akteur):
endliche Automaten mit Erweiterungen
Anleitungen durch Algorithmen
(strukturierte Anweisungsfolgen, Programme)
Anforderungen (Spezifikation) an Daten, Eigenschaften,
Zusammenhänge, Abläufe, Algorithmen, . . .
durch Logiken
298
Beispiel: größter gemeinsamer Teiler
Aufgabe: Zu zwei natürlichen Zahlen soll ihr größter gemeinsamer Teiler
(ggT) berechnet werden.
Kontextwissen (Definitionen):
I
t ist Teiler von x:
N : (t · k = x))
Menge aller gemeinsamen Teiler von x ∈ N und y ∈ N:
∀(t, x) ∈ N2 : T (x, y ) = {t ∈ N | (t|x) ∧ (t|y )}
größter gemeinsamer Teiler von x ∈ N und y ∈ N
∀(t, x, y ) ∈ N3 : ((ggT(x, y ) = t) ↔ ((t ∈ T (x, y ))∧(∀s ∈ T (x, y )(s|t))))
∀(t, x) ∈
I
I
N2 : (t | x
↔ ∃k ∈
Spezifikation (Anforderungen):
N, y ∈ N
(an Ausgaben): z ∈ N mit z = ggT(x, y )
Vorbedingungen (an Eingaben): x ∈
Nachbedingungen
299
Beispiel: Algorithmus für ggT
Kontextwissen: (bekannte) Eigenschaften des ggT:
N:
N2 :
N2 :
∀x ∈
∀(x, y ) ∈
∀(x, y ) ∈
((x > y ) →
ggT(x, x) = x
ggT(x, y ) = ggT(y , x)
(ggT(x − y , y ) = ggT(y , x)))
führen zur Idee des ( einfachen ) Euklidischen Algorithmus:
Algorithmus : Größter gemeinsamer Teiler
N
Eingabe : x ∈ , y ∈
Ausgabe : ggT(x, y )
N
solange x 6= y :
wenn x > y dann
x ←x −y
sonst
y ←y −x
Rückgabe x
300
Struktur von Algorithmen
Konstruktion komplexer Berechnungsvorschriften aus
Grundbausteinen: elementare Algorithmen (Schritte), z.B.
I Zuweisung,
I Aufruf eines Unterprogrammes,
I Ein- oder Ausgabe (Interaktion)
Verknüpfungen von Algorithmen durch
sequentielle Ausführung (nacheinander)
parallelle Ausführung (gleichzeitig, benötigt
mehrere Ausführende, z.B. Prozessoren)
bedingte Ausführung, Alternative (Verzweigung)
wiederholte Ausführung (Schleifen)
rekursive Ausführung
Blöcke , Unterprogramme
(Notation in Struktogramm, Pseudocode, . . . )
301
Algorithmen-Entwicklung
1. Analyse der informalen Aufgabenstellung
2. (formale) Spezifikation:
Was (welche Berechnungsaufgabe) soll gelöst werden?
exakte (formale) Beschreibung der Aufgabe:
I Anforderungen an Eingaben des Algorithmus
I Anforderungen an Ausgaben des Algorithmus
I Zusammenhang zwischen Ein- und Ausgabe
3. Entwurf des Algorithmus:
Wie soll es gelöst werden?
I formale Darstellung der Arbeitsschritte
I zu jedem Schritt:
I
I
I
Was wird getan? (Aktionen, Anweisungen)
Womit wird es getan? (Daten)
Wie geht es weiter? (nächster Schritt)
4. Verifikation:
Nachweis der Korrektheit des Algorithmenentwurfes bzgl. der
Spezifikation
5. Realisierung (Implementierung)
302
Algorithmen – Analyse der Aufgabe
Was soll gelöst werden?
I
ist zu Beginn des Software-Entwicklungsprozesses oft noch
nicht klar,
I
zunächst grober Ansatz,
I
wird schrittweise verfeinert,
formale Darstellung fördert
I
I
I
I
I
Problemverständnis,
Abstraktion (Auswahl relevanter Eigenschaften),
Dokumentation während des Entwicklungsprozesses,
Ideen für Lösungsansätze
303
Algorithmen – Spezifikation
Ausgangspunkt:
Ergebnis:
umgangssprachlich formulierte und oft
ungenaue Aufgabenbeschreibung
exakte und vollständige Definition des
Problemes
Spezifikation einer Berechnungaufgabe:
korrekte formale Beschreibung des Zusammenhanges zwischen
Eingaben und Ausgaben
Spezifikation einer Berechnungsaufgabe enthält
Vorbedingung: Anforderungen an die Eingaben
Nachbedingung: Anforderungen an die Ausgaben
304
Beispiel: Minimum-Suche
informale Aufgabenstellung:
Entwurf eines Verfahrens, welches in jeder Folge natürlicher Zahlen das
Minimum findet
formale Spezifikation:
Vorbedingung: Eingabe (x1 , x2 , . . . , xn ) ∈
Nachbedingung: Ausgabe m ∈
I
I
N mit
N∗
∀i ∈ {1, . . . , n} : m ≤ xi und
∃i ∈ {1, . . . , n} : m = xi
aus Spezifikation lässt sich folgender Algorithmus ablesen“:
”
Algorithmus : Minimum
Eingabe : x = (x1 , . . . , xn ) ∈
Ausgabe : m ∈
N
N∗
m ← x1
für jedes i ← 2, . . . , n :
wenn xi < m dann
m ← xi
305
Himmelsrichtungen (Wiederholung)
(Blickrichtung in) Himmelsrichtungen
Norden, Osten, Süden, Westen
mit Operationen für Rechts- und Linksabbiegen und Umlenken
Himmelsrichtungen (Zustände) {N, O, S, W }
Norden, Osten, Süden, Westen
Operationen (Aktionen) {R, L, U}
rechts drehen, links drehen, umdrehen
Ausführung einer Aktion bewirkt
Übergang (Relation) zwischen zwei Zuständen
d.h. jede Aktion a ∈ A definiert eine zweistellige Relation δ(a) auf
der Menge der Zustände,
im Beispiel:
δ(R) ⊆ {N, O, S, W }2
δ(R) = {(N, O), (O, S), (S, W ), (W , N)}
δ(L) ⊆ {N, O, S, W }
2
δ(L) = {(N, W ), (O, N), (S, O), (W , S)}
δ(U) ⊆ {N, O, S, W }
2
δ(U) = {(N, S), (O, W ), (S, N), (W , O)}
306
Übergänge zwischen Himmelsrichtungen
gemeinsame Darstellung dieser Relationen als Graph (V , E ) mit
Kantenfärbung
V = {N, O, S, W } Menge der Zustände
E = δ(R) ∪ δ(L) ∪ δ(U) Kantenrelation
A = {R, L, U} Menge der Aktionen als Kantenfarben
N
R
R
L
L
U
W
O
U
U
U
L
L
R
R
S
307
Zustandsübergangssysteme
Zustandsübergangssystem (Q, X , δ)
Q (endliche) Menge von Zuständen
X endliche Menge von Aktionen
δ : X → (Q × Q) Übergangsrelationen
δ ordnet jeder Aktion a ∈ X eine Relation
δ(a) ⊆ Q × Q zu
(Graph mit Kantenfärbung, Farben: Aktionen)
Spezifikation (formale Beschreibung von Anforderungen) von
Zustandsübergangssystemen
Darstellung der Eigenschaften von
I
Zuständen
I
(zulässigen) Aktionen
I
Wirkung der Aktionen (Zustandsübergänge)
als (prädikatenlogische) Formelmengen.
308
Modellierung mit Zustandsübergangssystemen
Anwendungsbeispiele:
I
reale Automaten,
z.B. Getränke-, Fahrschein, Bankautomaten
I
Verkehrssysteme,
z.B. Stellwerk, Ampelschaltungen
I
Steuerung von Industrieanlagen
I
Bedien-Oberflächen,
z.B. Folgen von Bedienoperationen
I
Digitaltechnik, Schaltwerke
I
Zeit- und Ablaufplanung
I
Geschäftsprozesse
I
Spiel-Abläufe
309
Beispiel: Münzschließfach
Aktionen: A aufschließen
Eigenschaften: g bezahlt
Z zuschließen
o offen
O Tür öffnen
b belegt
S Tür schließen
G Geld einwerfen
Anforderungen (Spezifikation), z.B.
Am Münzschließfach sollen nur Abläufe (Wort w ∈ {A, Z , O, S, G }∗ )
möglich sein, die folgende Anforderungen (Eigenschaften) erfüllen:
I
Offene Fächer können nicht zugeschlossen werden.
∀x(o(x) → ¬∃yZ (x, y ))
I
In belegte Fächer kann kein Geld eingeworfen werden.
∀x(b(x) → ¬∃yG (x, y ))
I
Kein nicht bezahltes Fach kann zugeschlossen werden.
¬∃x(¬g (x) ∧ ∃yZ (x, y ))
Dazu werden auch häufig nichtklassische Logiken verwendet,
z.B. Temporallogiken: (entscheidbare) FOL-Fragmente
(mehr dazu in späteren LV zu Verifikation)
310
Beispiel Münzschließfach
Entwurf des Systems:
{b}
∅
S
A
O
{o}
G
S
{g , o}
Z
{g }
O
Beispiele für mögliche Abläufe (während eines Tages)
w ∈ {A, Z , O, S, G }∗ :
OGSZAGSZA: zwei vollständige Belegungszyklen
OSOSOS: Tür wiederholt öffnen und schließen
I ε
I OSOGSOSZASOSOGSZASO
I
I
Jeder mögliche Ablauf erfüllt die Spezifikation (Anforderungen):
∀x(o(x) → ¬∃yZ (x, y )), ∀x(b(x) → ¬∃yG (x, y )),
Φ=
¬∃x(¬g (x) ∧ ∃yZ (x, y ))
Menge aller möglichen Abläufe ist reguläre Sprache
(Alphabet: Aktionen)
mehr dazu in den LV zur Theoretischen Informatik
311
Endliche Automaten – Definition
NFA (nondeterministic finite automaton) A = (X , Q, δ, I , F ) mit
X endliches Alphabet,
Q endliche Menge von Zuständen,
δ Übergangsrelationen δ : X → (Q × Q),
I ⊆ Q Startzustände,
F ⊆ Q akzeptierende Zustände.
Beispiel:
A = (X , Q, δ, {0, 3}, {2, 3, 4}) mit
X
=
{a, b, c}
Q
=
{0, 1, 2, 3, 4}
δ(a) =
{(0, 0), (0, 1), (1, 3)}
δ(b)
=
{(0, 0), (1, 2)}
δ(c)
=
{(0, 3), (3, 3), (4, 1)}
a,b
a
0
c
3
b
1
a
2
c
c
4
312
Anwendung endlicher Automaten
Endliche Automaten können z.B.
I
reguläre Sprachen akzeptieren,
d.h. bei Eingabe mit ja / nein antworten
Anwendungen z.B.
I
Zulässigkeit von Email-Adressen
I
Suchen von (auch mehreren) Zeichenketten in Texten
I
Programmtransformation (z.B. im Compiler):
Syntax-Überprüfungen: Bezeichner, Zahl-Darstellungen,
korrekte Schlüsselwörter
Endliche Automaten können z.B. nicht
I
Werte ausgeben
I
Zeichenvorkommen zählen
I
beliebig lange Zeichenketten speichern
I
korrekte Klammerung erkennen
I
rechnen, z.B. addieren
313
Beispiel Kaffee-Automat
(einfacher) Kaffee-Automat:
I
liefert nach Einwurf von 2 e und Bedienung der Kaffee-Taste einen
Becher Kaffee
I
erlaubt Einwurf von Münzen zu 1 e und 2 e
I
Rückgabe der gezahlten Münzen nach Bedienung der Rückgabetaste
formale Beschreibung als Mealy-Automat (Ausgabe bei Übergängen):
Zustände Q = {0, 1, 2} (Anzahl der bisher gezahlten e)
Aktionen A = {1E, 2E, KT, RT}
Ausgaben O = {K , 1 e, 2 e}
2E
1E
0
1
1E
2
RT / 1 e
KT / K , RT / 2 e
314
Berechnungen als Zustandsübergangssysteme
imperative Programmierung (von-Neumann-Modell):
Programm (imperativ): Folge von Anweisungen
Ausführungsmodell: abstrakte Maschine
Zustand der abstrakten Maschine besteht aus
I Belegung der Variablen im Speicher und
I nächste Anweisung (Programmzähler)
Startzustand für Programm p und Eingabe i:
I Variablen im Speicher mit Werten aus i belegt,
I erste Anweisung von p (Programmzähler)
Berechnung (Ausführung) des Programmes p:
sequentielle Ausführung der Anweisungen in p
Modellierung durch (endliche oder unendliche) Folge von
Zustandsübergängen (Rechenschritten)
Ausgabe: Speicherbelegung nach Ende der Berechnung
Semantik (Wirkung) eines imperativen Programmes p:
Abbildung (partielle Funktion) von Eingaben auf Ausgaben
und Nebenwirkungen (z.B. Änderung der Speicherbelegung)
315
Beispiel: Vertauschen mit Hilfsvariable
Aufgabe (informal): Vertauschen der Werte zweier Variablen
Spezifikation: Vorbedingung: Eingabe a = A ∈ , b = B ∈
Nachbedingung: Ausgabe a = B ∈ , b = A ∈
Zustände (A, B, C ) ∈ 3 (unendlich viele), wobei
A Wert der Variable (Speicherplatz) a (B, C analog)
Übergänge definiert durch Anweisungen des Programmes
N
N
N
N
N
Beispiel: Zustandsübergangssystem
der Berechnung für Eingabe a = 3, b = 5:
Programm z.B.
c
← a
a
← b
b
← c
(3, 5, ?)
(c ← a)
(3, 5, 3)
(a ← b)
(5, 5, 3)
(b ← c)
(5, 3, 3)
Verifikation des Programmes (Nachweis der Korrektheit bzgl.
Spezifikation) durch Ausführung mit symbolischen Werten (A, B, C )
manuell oder maschinell möglich
(mehr dazu in Master-LV zu Software-Verifikation)
316
Visuelle Darstellungen für Abläufe und Algorithmen
Beispiele:
I
UML statecharts (in späteren LV)
I
BPMN zur Modellierung von Geschäftsprozessen
I
Lego Mindstorms Software
317