Drehbewegungen

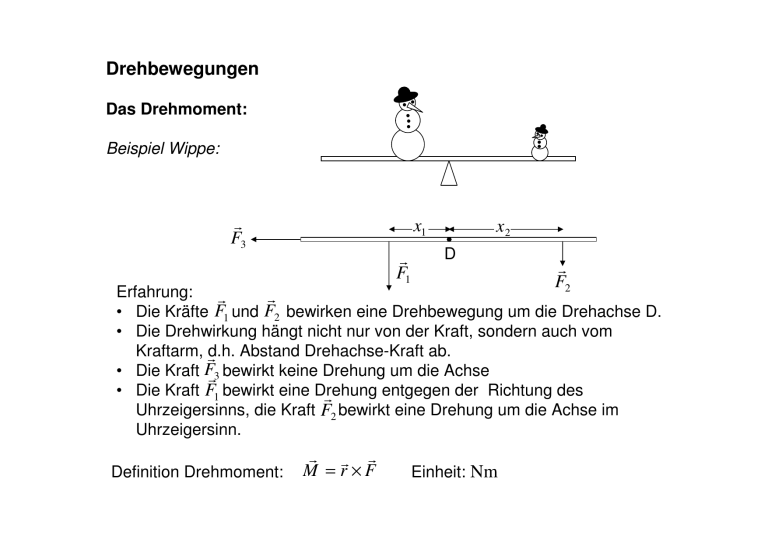
Drehbewegungen
Das Drehmoment:
Beispiel Wippe:
r
F3
x1
r
F1
x2
D
r
F2
Erfahrung:
r
r
• Die Kräfte F1 und F2 bewirken eine Drehbewegung um die Drehachse D.
• Die Drehwirkung hängt nicht nur von der Kraft, sondern auch vom
Kraftarm, rd.h. Abstand Drehachse-Kraft ab.
• Die Kraft Fr3 bewirkt keine Drehung um die Achse
• Die Kraft F1 bewirkt eine Drehung
entgegen der Richtung des
r
Uhrzeigersinns, die Kraft F2 bewirkt eine Drehung um die Achse im
Uhrzeigersinn.
Definition Drehmoment:
r r r
M = r ×F
Einheit: Nm
r
F3
x3
x1
r
F1
x2
D
r
F2
r
r r
r r
M 1 = x1 × F1 ⇒ M 1 = x1 F1 sin( x1 , F1 ) = x1 F1 sin 90° = x1 F1
r
M 1 zeigt aus der Folie heraus (nach oben/vorne)
r
r r
r r
M 2 = x2 × F2 ⇒ M 2 = x2 F2 sin( x2 , F2 ) = x2 F2 sin 90° = x2 F2
r
M 2 zeigt in die Folie hinein (nach unten/hinten)
r
r r
r r
M 3 = x3 × F3 ⇒ M 3 = x3 F3 sin( x3 , F3 ) = x3 F3 sin 0° = 0
Wenn
, findet keine Drehung statt.
r
r
r
∑ M = M1 + M 2 = 0
r r r
M = r ×F
α
r
F
r
r0
r
r
M = rF sin α = r sin αF = r0 F
Beispiel Garnrolle:
D
D
D
D
D
Das Kräftepaar
Zusammensetzung von zwei an einem starren Körper angreifenden
gleichgerichteten Kräften:
r
− FHilfs
r
FHilfs
S : Kräftemittelpunkt
r
F1
r
r r
FR = F1 + F2
r
F2
Eine resultierende Kraft, die im Kräftemittelpunkt angreift.
Zusammensetzung von zwei an einem starren Körper angreifenden
entgegengesetzt gerichteten Kräften:
r
− FHilfs
r
F2
r
F1
r
FHilfs
r
r r
FR = F1 + F2
S
Eine resultierende Kraft, die im Kräftemittelpunkt angreift.
Aber: Wenn F 1 = F2 ist diese Konstruktion nicht anwendbar.
Kräftepaar : Zwei antiparallele Kräfte mit dem gleichen Betrag, die nicht auf
derselben Geraden liegen.
Es ist nicht möglich, ein Kräftepaar durch eine resultierende Einzelkraft zu
ersetzen oder durch eine Einzelkraft zu kompensieren.
Wirkung eines Kräftepaares auf einen starren Körper, der um eine durch den
Punkt A gehende, auf der Folie senkrecht stehende Achse drehbar ist:
r
r
s
r
F1
s1
A
s2
s
r
F2
r
r r
M 1 = r1 × F1
r
r r
M 2 = r2 × F2
M 1 = F1 s1
M 2 = F2 s2 = F1 s2
r
Resultierendes Drehmoment M
M = M 1 − M 2 = s1 F1 − s 2 F1 = ( s 1 − s 2 ) F1 = sF1
s: Arm des Kräftepaares, d.h. Abstand der
Wirkungslinien der beiden Kräfte
An einem frei beweglichen
starren Körper mit dem Schwerpunkt S greift im
r
Punkt P die Kraft F an.
r
FH 2
S
P
S
r
F
r
rS
r
FH 1
P
r
F
r
r
Hilfskräfte: FH 1 = − FH 2
r
r
Kräftepaar: F und FH 2
r
r r
Drehmoment um den Schwerpunkt: M S = rS × F
r
Kraft: FH 1
Beschleunigung des Schwerpunktes.
Der Körper befindet sich im Gleichgewicht, wenn sowohl die Summe aller
Drehmomente als auch die Summe aller Einzelkräfte Null ist.
Gleichgewichte
Stabiles Gleichgewicht: Das Drehmoment oder die Kräfte, die nach einer
Verschiebung auf den Körper wirken, bringen ihn wieder in die ursprüngliche
Lage zurück.
Instabiles Gleichgewicht
Indifferentes Gleichgewicht
Das Trägheitsmoment
Ein Massenpunkt der Masse m
r
m
rotiert mit konstanter Winkelgeschwindigkeit ω
auf einer Kreisbahn mit dem Radius r.
Kinetische Energie der Rotation des Massenpunktes: E rot =
Mit v = rω ergibt sich: E rot =
1 2 2 1 2
mr ω = Jω
2
2
Trägheitsmoment des Massenpunktes: J = mr 2
1 2
mv
2
Einheit: kgm2
Um eine feste Achse mit konstanter Winkelgeschwindigkeit rotierender starrer
Körper:
Zerlegung in einzelne Massenelemente ∆mi
Rotationsenergie des Massenelements ∆mi :
1
1
1
∆E rot = ∆mi vi2 = ∆mi ri 2ω 2 = (∆mi ri 2 )ω 2
2
2
2
N
Rotationsenergie des starren Körpers:
Erot = ∑ ∆Erot
i =1
Für ∆mi → 0: E rot =
1 2N
= ω ∑ ∆mi ri 2
2 i =1
1 2 2
1
ω ∫ r dm = Jω 2
2
2
2
Mit dem Trägheitsmoment: J = ∫ r dm
Analogie:
1
1
E kin = mv 2 ↔ E rot = Jω 2
2
2
Aber: Die Masse stellt eine unveränderliche Körpereigenschaft dar, das
Trägheitsmoment hängt von der Wahl der Drehachse ab. Ein Körper kann
bei gleich bleibender Masse unterschiedliche Trägheitsmomente haben.
Beispiele: Homogener dünner Stab
y
z
x
x
x=l
dx
dm = m ges
dx m ges
=
dx
l
l
l
J = ∫ x dm = ∫ x
2
0
2
m ges 1 3  l
dx =
∫ x dx = l  3 x 
l
l 0
0

m ges
m ges
l
2
m ges 1 3 m ges l 2
1
⇒J=
⇒ J = m ges l 2
l =
l 3
3
3
y
x
x = −l / 2
J = ∫ x dm =
2
x =l/2
dx
l/2
∫ x
−l / 2
2
m ges 1 3  l / 2
dx =
∫ x dx = l  3 x 
l
l −l / 2

 −l / 2
m ges
m ges
l/2
2
m ges  l 3 − l 3  m ges  l 3 
1

 =
 2 ⋅  ⇒ J = m ges l 2
⇒J=
−
l  3 ⋅ 8 24 
l  24 
12
Satz von Steiner
N
JA = ?
JS
2
N
r r
J A = ∑ r ∆mi = ∑ a + rSi ∆mi ⇒
2
Ai
i =1
i =1
N
rr
J A = ∑ (a 2 + rSi2 + 2arSi )∆mi ⇒
r
a
S
r
rSi
rA
rAi
∆mi
i =1
N
rr
J A = ∑ (a 2 ∆mi + rSi2 ∆mi + 2arSi ∆mi ) ⇒
i =1
N
N
i =1
⇒ J A = a 2 m ges + J S
N
rr
J A = ∑ a ∆mi + ∑ r ∆mi + ∑ 2arSi ∆mi
2
i =1
2
Si
i =1
Definition des
Schwerpunktes!
Satz von Steiner
Beispiel homogener Stab:
2
1
1
l
1
1
1
J S = ml 2 Satz von Steiner J Ende= ml 2 −   m = ml 2 + ml 2 = ml 2
12
12
12
4
3
 2
Der Drehimpuls
r r r
Drehimpuls: L = r × p
z
Drehimpuls bezüglich des Kreismittelpunktes:
r r r r
r
L = r × p = r × mv =
r
(rmv sin 90°)e z =
r
r
rmve z = r 2 mωe z ⇒
r
r
L = Jω
r
L
r
ω r
r
r r r
v =ω×r
y
x
Drehimpuls für einen ausgedehnten starren Körper, der um eine
Symmetrieachse rotiert:
Zerlegung in Massenelemente: ∆mi
r
r
Li = ri 2 ∆miω
N
r N r
r
r
L = ∑ Li = ∑ ri 2 ∆miω = Jω
i =1
i =1
Änderung des Drehimpulses
r
Auf ein Teilchen/Massenelement am Ort r wirken j = 1,..., k Kräfte.
Drehmoment:
r
k
r
r r
r k r r r r dp
M = ∑ (r × F j ) = r × ∑ F j = r × F = r ×
dt
j =1
j =1
r
r
r
r
dL d r r
dr r r dp r
r r dp
Änderung des Drehimpulses:
= (r × p) = × p + r ×
= v × mv + r ×
dt dt
dt
dt
dt
⇒
r
r
dL
=M
dt
r
Starrer Körper aus
N r
N dL
r
d
i = 1,..., N Masselelementen: M ges = ∑ M i = ∑ i =
i =1
i =1
dt
r
∑ Li =
N
dt i =1
r
dLges
dt
Für einen ausgedehnten starren Körper, der um eine Symmetrieachse rotiert gilt:
r
r
dL d
dω
r
r r
⇒
= ( Jω ) = J
= Jα = M
dt dt
dt
r
r
r
r
Analogie: F = ma ↔ M = Jα
r
r
L = Jω
r
Winkelbeschleunigung: α
Einheit: rad/s2
Analogien:
Translation
Rotation
r
r
Strecke s
Winkel ϕ
r
r ds
Bahngeschwindigkeit v = dt
r
d
v
r
Bahnbeschleunigung a =
dt
Masse m
r
r
Impuls p = mv
r dpr
Kraft F =
dt
r
dϕ
Winkelgeschwindigkeit ω = dt
r
d
ω
r
Winkelbeschleunigung α =
dt
Trägheitsmoment J
r
r
Drehimpuls L = Jω
r
r dL
Drehmoment M =
dt
kinetische Energie
1
der Translation
E kin = mv 2
kinetische Energie
1 2
E
=
Jω
der Rotation
rot
2
r
2
Übungen
Auf einer mit konstanter Winkelgeschwindigkeit rotierenden Scheibe sind
zwei Punkte markiert, einer auf dem Rand A und einer in der Mitte
zwischen dem Rand und der Drehachse B.
•
•
•
•
•
•
Welcher der Punkte bewegt sich in einer bestimmten Zeit über die
größere Entfernung?
Welcher dreht sich um den größeren Winkel?
Welcher hat die höhere tangentiale Geschwindigkeit?
Welcher hat die größere Winkelgeschwindigkeit?
Die größere Winkelbeschleunigung?
Die größere Zentripetalbeschleunigung?
Richtig oder Falsch?
• Wenn die Winkelgeschwindigkeit eines Körpers zu einem bestimmten
Zeitpunkt Null ist, muss auch das resultierende Drehmoment auf den
Körper Null sein.
• Das Trägheitsmoment eines Körpers hängt davon ab wo sich die
Drehachse befindet.
• Das Trägheitsmoment hängt auch von seiner Winkelgeschwindigkeit ab.
Eine Scheibe rotiert frei um eine Achse. Eine Kraft, die im Abstand d von der
Achse tangential angreift, verursacht eine Winkelbeschleunigung α . Welche
Winkelbeschleunigung wird verursacht, wenn die Kraft im Abstand 2d von der
Achse angreift?
•
•
•
•
α
2α
α /2
4α
Füllen Sie die Lücke im Satz aus:
Das Trägheitsmoment eines Körpers bezüglich einer Achse, die nicht durch
seinen Massenmittelpunkt verläuft ist ………….. Trägheitsmoment bezüglich
einer dazu parallelen Achse durch den Massenmittelpunkt.
•
•
•
•
immer geringer als das
manchmal geringer als das
manchmal gleich dem
immer größer als das
Ein Ring mit der Masse m und dem Radius r rollt auf einer horizontalen
Ebene. Welche Aussage stimmt? (Bezogen auf eine Drehachse, die durch
die Mitte des Rings geht und senkrecht zur Ringebene steht)
•
•
•
•
•
Die kinetische Energie der Translation ist größer als die der Rotation.
Die kinetische Energie der Rotation ist größer als die der Translation.
Beide Energien sind gleich groß.
Welche der beiden Energien größer ist, hängt vom Radius ab.
Welche der beiden Energien größer ist, hängt von der Masse ab.
Ein Teilchen bewegt sich mit konstanter Geschwindigkeit auf einer geraden
Bahn. Sind die folgenden Aussagen richtig oder falsch?
•
•
•
•
•
Der Impuls ist konstant.
Der Drehimpuls nimmt zu.
Der Drehimpuls nimmt ab.
Der Drehimpuls ist Null.
Der Drehimpuls ist konstant.
Zweites Keplersches Gesetz und die Drehimpulserhaltung:
r1
r2
∆A1 ∆ϕ1
r1
∆ϕ 2
∆A2
r2
In dem kleinen Zeitintervall ∆t überstreicht der Fahrstrahl mit der
Winkelgeschwindigkeit ω1 den Winkel ∆ϕ1 und zu einem späteren Zeitpunkt
r
überstreicht der Fahrstrahl im Zeitintervall ∆t mit der Winkelgeschwindigkeit ω 2
den Winkel ∆ϕ 2.
Drehimpulserhaltung:
J 1ω1 = J 2ω 2 ⇒ J 1
Trägheitsmomente:
J 1 = mr12
Einsetzen: ⇒ mr12
2
und J 2 = mr2
∆ϕ1
∆ϕ 2
= mr22
∆t
∆t
Vom Fahrstrahl r
1
überstrichene Fläche: ∆A = r 2 ∆ϕ
2
∆ϕ1
∆ϕ 2
= J2
∆t
∆t
⇒ r12 ∆ϕ1 = r22 ∆ϕ 2
⇒ ∆A1 = ∆A2
„Der Fahrstrahl
überstreicht in
gleichen Zeiten
gleiche Flächen.“
Übung
Ein Planet läuft auf einer elliptischen Bahn um die Sonne, die in einem
Brennpunkt der Ellipse steht.
r2
r1
r
v2
r
v1
Wie groß ist das Drehmoment bezüglich des Mittelpunktes der Sonne, das die
Gravitationsanziehung der Sonne auf den Planeten ausübt?
mS mP
mS mP
a) M = γ
b) Null
c) M = γ
2
2
1 (r + r )
r
+
r
2
1
2
1
2
Wie groß ist das Verhältnis
v
r
a) 1 = 2
v2 r1
v1
?
v2
v1 r1
=
b)
v2 r2
v1 r2 + r1
=
c)
v2 r2 − r1