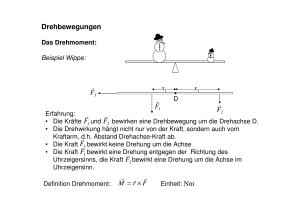
Trägheitsmoment, Rotationsenergie

Physik – Klasse 10
Seite:1
Trägheitsmoment
Trägheitsmoment und Rotationsenergie
Bisher wurden alle Bewegungen bei gleicher Winkelgeschwindigkeit ausgeführt.
Betrachten wir einen Körper, der ständig seine
Winkelgeschwindigkeit ändert. Dann ist:
=

t
Die Winkelbeschleunigung ß ist die Veränderung der
Winkelgeschwindigkeit ω in der Zeit t.
Das Drehmoment: Für einen Schwerpunkt mit dem
Abstand r können wir einen dazugehörigen Weg s = αr
bestimmen, wobei α = ßr ist.
Für die tangentielle Beschleunigung benötigen wir die Kraft F.
Sie hängt von der Winkelbeschleunigung ab. Dieses ist
v
wie gesagt für einen Schwerpunkt. Betrachten wir
F = m  a, wobei a =
t
mehrere Massenschwerpunkt mit verschiedenen Bahnen,
so sollen sie gleiche Winkelbeschleunigungen ß besitzen
mit v = r dann ist
(z.B. ein starrer Körper).
v
 r
F = m
= m
= mr
t
t
Dynamisches Grundgesetz der Rotation (vgl. Newtonsche
Gesetze)
An einem drehbaren Körper erzeugt ein Drehmoment eine Winkelbeschleunigung.
Das Verhältnis des wirkenden Drehmomentes zur erzielten Winkelbeschleunigung
nennt man das Massenträgheitsmoment des Körpers.
Massenträgheitsmoment =
Drehmoment
Winkelbeschleunigung
Das Drehmoment M ist:
F  r = m  a  r = m    r  r = m    r2
F  r = m    r2
Für jeden Massenschwerpunkt haben wir bei
gleicher Winkelbeschleunigung verschiedene
Abstände r.
Die Summe alle Drehmomente sei M (M1 + M2 + ....), dann gilt:
M = M 1 + M 2 + ....+ M n
M = m1 r 12  + m2 r 22  + ...+ mn r 2n 
M =  mi r i2  , mit i = 1, 2, .... , n
Die Winkelbeschleunigung ß ist uns bekannt, damit können wir das Massenträgheitsmoment
formulieren, wie es oben aufgeschrieben wurde. Dazu wird in jedem Summanden des
Drehmomentes die Winkelbeschleunigung ausgeklammert und kann damit aus dem Ausdruck
gekürzt werden:
75901872.doc
angefertigt:1996 I. 07 , Norbert Burmeister
konvertiert: 2004.XII.27
Physik – Klasse 10
Seite:2
Trägheitsmoment
 = m1 r 12 + m2 r 22 + ...+ mn r 2n
Unter dem Massenträgheitsmoment Θ eines Körpers
 =  mi r i2 , mit i = 1, 2, .... , n
versteht man die Summe der Produkte aus den Massenelementen und den Quadraten ihrer
Abstände von der Drehachse. Maßeinheit [kg  m2]
Die Rotationsenergie
Die kinetische Energie eines Körpers ist allgemein:
m
E = v2
Da es sich um eine Rotationsbewegung handelt, ist v = ω  r .
2
Handelt es sich dabei um mehrere (z.B. n) Massenschwerpunkte schreiben wir:
m1 2 m2 2
mn 2
v1 + v 2 + ... + v n
2
2
2
2 2
2 2
2 2
m1  r 1 m2  r 2
m
+
+ ... + n r n
E rot =
2
2
2
E rot =
E rot =
2 (
2
2
2
2
m1 r 1 + m2 r 2 + ... + mn r n )
Der Ausdruck in der Klammer ist aber genau das Massenträgheitsmoment Θ. Damit ist die
Rotationsenergie
E rot = 
2
2
Die Massenträgheitsmomente einiger ausgewählter Körper:
Körper
Lage der Drehachse
Massenträgheitsmoment
Kreisring, dünn (Reifen)
Senkrecht zur Ringebene
m r2
Vollzylinder
Längsachse
m 2
r
2
Hohlzylinder, dickwandig
Längsachse
m 2 2
( r1 + r 2 )
2
Kreisscheibe
senkrecht zur Scheibenebene
m 2
r
2
Kreisscheibe
Durchmesser
m 2
r
4
Kugel
durch Mittelpunkt
2m 2
r
5
Hohlkugel, dünnwandig
durch Mittelpunkt
2m 2
r
3
75901872.doc
angefertigt:1996 I. 07 , Norbert Burmeister
konvertiert: 2004.XII.27
Physik – Klasse 10
Seite:3
Trägheitsmoment
Körper
Lage der Drehachse
Massenträgheitsmoment
Stab, dünn mit Länge l
senkrecht zur Stabmitte
m 2
l
12
Stab, dünn mit Länge l
senkrecht zum Stabende
m 2
l
3
Der Drehimpuls (Drall)
Unter dem Drehimpuls D (Drall) eines rotierenden Körpers versteht man das Produkt aus
seinem Massenträgheitsmoment und seiner Winkelgeschwindigkeit.
Wenn
D
Drehimpuls des rotierenden Körpers,
Θ, J
Massenträgheitsmoment des Körpers,
ω
Winkelgeschwindigkeit des rotierenden Körpers,
dann gilt
D =  , gemessen in
kg m2
s
Die Größe des Drehimpulses, den ein Körper erhält, hängt von Dauer und Größe des
beschleunigten Drehmomentes ab.
ΔD
Änderung des Drehimpulses,
M
beschleunigtes Drehmoment,
t
Dauer der Beschleunigung,
Θ, J
Massenträgheitsmoment des Körpers (auf die Drehachse),
Δω
Änderung der Winkelgeschwindigkeit des Körpers,
dann gilt entsprechend aus dem Grundgesetz der Rotation
Wenn
M =  = 

t
, aus  =
M

Wir erhalten:
D = Mt = 
Das Produkt Mt heißt Antriebsmoment. Es ist gleich der erzielten Drehimpulsänderung.
Für den Fall, dass kein Drehmoment vorhanden ist. (z.B. zwei Körper rotieren um ihren
gemeinsamen Schwerpunkt. Da ihre Kräfte zum Mittelpunkt gerichtet sind und gleich sind
(isoliertes, geschlossenes System) verrichten sie kein Drehmoment).
0 = 
Ist die Winkelbeschleunigung gleich null, bedeutet es, dass der Drehimpuls konstant ist.
75901872.doc
angefertigt:1996 I. 07 , Norbert Burmeister
konvertiert: 2004.XII.27
Physik – Klasse 10
Seite:4
Trägheitsmoment
v
D =  = konstant,mit  = ,
r
2
und  = m r erhalten wir
v
vr
m r 2 = mvr = 2m 
r
2
Hierbei bezeichnen wir vr/2 als die Flächengeschwindigkeit. Es ist die Fläche, die bei einer
Geschwindigkeit v, vom Radius r überstrichen wird.
Der Drehimpuls ist ebenfalls eine vektorielle Größe in Richtung der Drehachse des Körpers.
Es lässt sich folgendes formulieren:
(1)
Ein Drehmoment bewirkt an einem starren Körper eine Änderung des Drehimpulses.
(2)
Wenn auf einen starren Körper kein Drehmoment wirkt, so ist sein Drehimpuls
konstant.
Analog zur Translation wird ein Erhaltungssatz formuliert:
Satz von der Erhaltung des Drehimpulses:
In einem abgeschlossenen System ist die Summe der Drehimpulse konstant.
D =  = konstant
(  1 + 2 + ...+ n ) =  1  1 + 2  2 + ... m  m
(Es wirken keine äußeren Drehmomente.)
75901872.doc
angefertigt:1996 I. 07 , Norbert Burmeister
konvertiert: 2004.XII.27