Dynamische Systeme 1

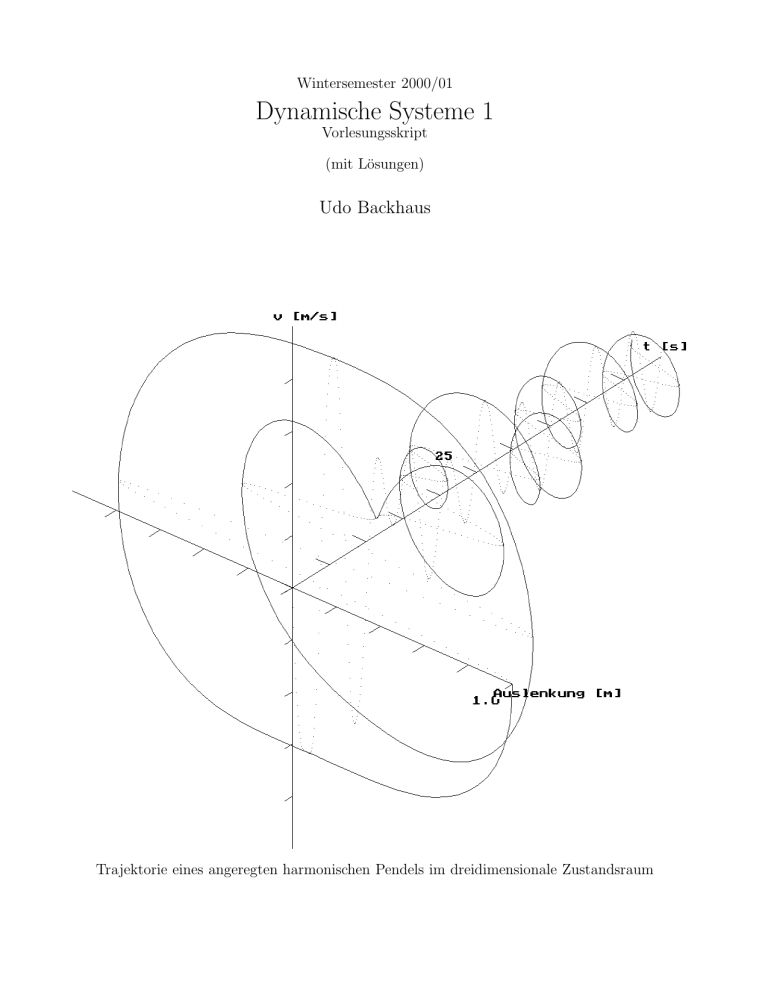
Wintersemester 2000/01
Dynamische Systeme 1
Vorlesungsskript
(mit Lösungen)
Udo Backhaus
Trajektorie eines angeregten harmonischen Pendels im dreidimensionale Zustandsraum
i
INHALTSVERZEICHNIS
Inhaltsverzeichnis
Anlagen
ii
Lernziele
iv
1 26.
1.1
1.2
1.3
Oktober 2000: Einführung
Organisatorisches . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Überblick . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
konkreter Einstieg: Das Federpendel . . . . . . . . . . . . . . . . . . . . . .
1
1
1
3
2 2. November 2000: Das Schraubenfederpendel
2.1 Wiederholung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Experimente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Messwertaufnahme mit einem Computer . . . . . . . . . . . . . . . . . . .
4
4
4
7
3 16.
3.1
3.2
3.3
3.4
3.5
3.6
November 2000: Theorie des Federpendels
Ergänzungen zu den Freihandmessungen . .
Beispielmessungen mit dem Computer . . .
Ableitung der Bewegungsgleichung . . . . .
Qualitatives Verhalten der Lösung . . . . . .
Analytische Lösung der Bewegungsgleichung
Übung . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
10
10
11
12
13
14
15
4 23. November 2000: Numerische Integration 1
18
4.1 Wiederholung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
4.2 Das Euler-Verfahren (Ganzschritt-Verfahren) . . . . . . . . . . . . . . . . . 18
5 30.
5.1
5.2
5.3
5.4
November 2000: Numerische Integration 2
Wiederholung . . . . . . . . . . . . . . . . .
Numerische Fehler . . . . . . . . . . . . . .
Simulation mit Modellbildungssystem . . . .
Übung: Die Berücksichtigung der Reibung .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
22
22
22
23
26
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
29
29
30
33
34
Dezember 2000: Erzwungene Schwingungen
Wiederholung . . . . . . . . . . . . . . . . .
Das Runge-Kutta-Verfahren 4. Ordnung . .
Angeregte Schwingungen . . . . . . . . . . .
Übung: Analytische Lösung . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
36
36
36
38
40
6 7. Dezember 2000: Gedämpfte Schwingungen
6.1 Wiederholung und Nachtrag . . . . . . . .
6.2 Gedämpfte Schwingungen . . . . . . . . .
6.3 Das Halbschritt-Verfahren . . . . . . . . .
6.4 Übung . . . . . . . . . . . . . . . . . . . .
7 14.
7.1
7.2
7.3
7.4
ii
INHALTSVERZEICHNIS
8 4. Januar 2001: Das periodisch angeregte Pendel
42
8.1 Wiederholung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
8.2 Eigenschaften der stationären Schwingung . . . . . . . . . . . . . . . . . . 43
8.3 Übung: Phasendiagramme . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
9 11.
9.1
9.2
9.3
Januar 2001: Einschwingvorgang und Phasendiagramme
48
Experimente mit dem Pohl’schen Drehpendel . . . . . . . . . . . . . . . . . 48
Der Einschwingvorgang . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
Übung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
10 18. Januar 2001: Simulation und Experiment
10.1 Angeregte Schwingungen im grafischen Modellbildungssystem
10.2 Phasenraum und Zustandsraum, Attraktoren . . . . . . . . . .
10.3 Die Bewegungsgleichung des Drehpendels . . . . . . . . . . . .
10.4 Übung: Experimentelle Bestimmung der Systemparameter . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
54
54
57
59
60
11 25. Januar 2001: Nichtlinearität
11.1 Wiederholung und Ergänzung . . . . . . .
11.2 Einführung in die Nichtlinearität . . . . .
11.3 Experimente mit dem Fadenpendel . . . .
11.4 Die Bewegungsgleichung des Fadenpendels
11.5 Übung: Die Dämpfung des Drehpendels . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
62
62
64
66
68
69
12 1. Februar 2001: Drehpendel mit Unwucht
12.1 Wiederholung . . . . . . . . . . . . . . . .
12.2 Diskussion der Bewegungsgleichung . . . .
12.3 Simulation des Fadenpendels . . . . . . . .
12.4 Das Drehpendel mit Unwucht . . . . . . .
12.5 Übung . . . . . . . . . . . . . . . . . . . .
12.5.1 Federquerschwingungen . . . . . . .
12.5.2 Exakte Simulation des Drehpendels
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
72
72
72
74
75
76
76
77
13 8. Februar 2001: Klausur
80
13.1 Fragestunde . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
13.2 Klausur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
14 15. Februar 2001: Das Drehpendel mit Unwucht
14.1 noch einmal: Nichtlineare Querschwingungen . . . . .
14.2 Phänomene am Drehpendel mit Unwucht . . . . . . .
14.3 Ergänzung der Bewegungsgleichung des Drehpendels
14.4 Simulation . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
87
87
89
89
90
INHALTSVERZEICHNIS
iii
Anlagen
1. Folien
• numerische Integration
• Das Euler-Verfahren
• Resonanzkurve ϕ0 (Ω)
• Resonanzkurven A(Ω), B(Ω)
• Phasenverschiebung ϕ(Ω)
• Trajektorie im dreidimensionalen Raum
• Nichtlinearität von Federschwingungen
2. Pascal-Programme
• Kern.pas, Modul.pas, Kern2.pas, Math.pas: Units zum Übersetzen der zur
Verfügung gestellten Quelltexte
• numinteg: Numerische Integration der harmonischen Schwingungsgleichung;
Vergleich der numerischen Fehler von Ganzschritt-, Halbschritt- und RungeKutta-Verfahren
• Resonanz: Resonanzkurven
• Pendel4: Abhängigkeit der Frequenz von der Dämpfung mit verschiedenen
Integrationsverfahren
• HarmSch9: Untersuchung gedämpfter harmonischer Schwingungen
• Zustandsr: Zeichnung von Trajektorien im dreidimensionalen Zustandsraum
• PHASEND: Zeichnung zweidimensionaler Phasendiagramme
• Pendel51: Nichtlineare Federschwingungen
• PENDEL2: Messung“ der Schwingungsdauer bei nichtlinearen Schwingungen
”
• POHLRAD1: Simulation des Drehpendels mit Unwucht
3. Dynasys-Modelle
• Pendel1: Harmonisches Pendel
• Pendel2: Harmonisches Pendel, Vergleich der numerischen Lösung mit der
Theorie
• Pendel3: Linear gedämpftes Pendel, Vergleich der numerischen Lösung mit der
Theorie (Schwingfall)
• Pendel4: Linear gedämpftes Pendel. Vergleich der numerischen Lösung mit der
analytischen Lösung der harmonischen Schwingung; Untersuchung der Abhängigkeit der Schwingungsdauer von der Dämpfung; Kriechfall
• Pendel50, Pendel51: Erweiterung des gedämpften harmonischen Pendels zum
angeregten Pendel
INHALTSVERZEICHNIS
• Fadenp: Fadenpendel
• Pohlrad1: realistische Simulation des Drehpendels
• Pohlrad2: Erweiterung der Drehpendelsimulation um eine Unwucht
• Querschw: Federquerschwingungen
• KlWS00: Lösung der Klausur-Aufgabe
iv
INHALTSVERZEICHNIS
v
Lernziele
Die Teilnehmer sollen am Ende der Veranstaltung folgendes können:
1. aus der Numerik:
(a) . . . die Idee der numerischen Integration anhand eines Graphen und eines Flussdiagrammes für das Ganzschritt-Verfahren beschreiben,
(b) . . . das Halbschritt-Verfahren am konkreten Beispiel erläutern,
(c) . . . analytische und numerische Lösungen miteinander vergleichen,
(d) . . . beschreiben können, woran man Integrationsfehler bemerken und wie man
sie verringern kann,
(e) . . . die Bewegungsgleichungen einfacher Systeme in ein Differentialgleichungssystem 1. Ordnung umwandeln,
(f) . . . die Struktur eines Simulationsmodelles für einfache Systeme grafisch darstellen und die zugehörigen Gleichungen formulieren,
2. aus der Theorie dynamischer Systeme:
(a) . . . aus der Newton’schen Grundgleichung der Mechanik die Bewegungsgleichung konkreter Systeme ableiten,
(b) . . . Ort, Geschwindigkeit und Beschleunigung einer harmonischen Schwingung
als Funktion der Zeit angeben,
(c) . . . die Bewegungsgleichung der (evtl. gedämpften und angeregten) harmonischen Schwingung kennen und aufstellen,
(d) . . . am Beispiel der ungedämpften harmonischen Schwingung das qualitative
Verhalten der Lösung aus der Bewegungsgleichung ablesen,
(e) . . . die Bewegungsgleichung der (gedämpften) harmonischen Schwingung mit
einem naheliegenden Ansatz durch Einsetzen analytisch lösen,
(f) . . . zwei Darstellungsarten der allgemeinen Lösung der harmonischen Bewegungsgleichung (ohne Dämpfung) kennen und ineinander umrechnen,
(g) . . . die Lösung der gedämpften harmonischen Bewegungsgleichung für gegebene
Anfangswerte von Auslenkung und Geschwindigkeit angeben,
(h) . . . den Ansatz zum Auffinden einer stationären analytischen Lösung der Bewegungsgleichung einer angeregten Schwingung nennen,
(i) . . . zeigen, daß die Summe aus spezieller Lösung der inhomogenen und allgemeiner Lösung der homogenen Bewegungsgleichung wieder eine Lösung der
inhomogenen Gleichung ist,
(j) . . . Definition und Bedeutung von Phasendiagrammen an Beispielen erläutern,
(k) . . . Phasendiagramme einfacher Systeme zeichnen und umgekehrt mit Hilfe des
Phasendiagramms das Verhalten des Systems beschreiben,
(l) . . . den Zustandsraum eines Systems angeben und allgemeine Eigenschaften
von Trajektorien nennen und begründen,
INHALTSVERZEICHNIS
vi
(m) . . . den Begriff des Attraktors erläutern und Beispiele nennen,
3. aus der Experimentalphysik:
(a) . . . das Grundprinzip der automatischen Messwerterfassung mit einem Computer erklären,
(b) . . . 2. Newton’sches Gesetz (Grundgleichung der Mechanik) und Hooke’sches
Gesetz kennen und anwenden,
(c) . . . Thomson’sche Schwingungsformel (Abhängigkeit der Frequenz bzw. Schwingungsdauer von den Systemparametern bei Schraubenfeder- und Fadenpendel)
kennen und anwenden,
(d) . . . halbquantitative und quantitative Experimente zur Demonstration und
Überprüfung dieser Gesetzmäßigkeiten beschreiben,
(e) . . . die Bewegungsgleichungen für folgende Systeme ableiten:
i. Schraubenfederpendel (mit und ohne Reibung, mit und ohne Anregung),
ii. Fadenpendel (mit und ohne Reibung),
iii. senkrechter Wurf.
und aus ihr die Abhängigkeit der Schwingungsdauer von den relavanten Parametern gewinnen,
(f) . . . die wesentlichen Eigenschaften harmonisch angeregter harmonischer Schwingungen nennen und Amplitude und Phasenverschiebung als Funktion der Zeit
darstellen,
(g) . . . das Fadenpendel als Beipiel einer nichtharmonischen Schwingung diskutieren,
(h) . . . die experimentelle Untersuchung gedämpfter Schwingungen beschreiben,
insbesondere
i. die Untersuchung auf exponentielles Abklingverhalten und
ii. die Messung der Dämpfungskonstanten,
(i) . . . am konkreten Beispiel die experimentelle Bestimmung der Systemparameter und die Untersuchung der Simulation, in die die Messwerte eingehen,
beschreiben.
1 26. OKTOBER 2000: EINFÜHRUNG
1
1
26. Oktober 2000: Einführung
1.1
Organisatorisches
• Termin für Vorlesung: 12.00-13.30 Uhr, für Übung: 14.00-14.45 Uhr
• Die zweisemestrige Vorlesung gilt als Fortgeschrittene Experimentalphysik“ im Sin”
ne der Prüfungsordnung. Der entsprechende Schein wird am Ende des Sommersemesters vergeben. Voraussetzung ist die Teilnahme an den Klausuren beider Semester, das Bestehen mindestens einer dieser Klausuren und eine Gesamtpunktzahl von
mindestens 50% der zu erreichenden Gesamtpunktzahl.
• Es wird Skript zur Vorlesung erstellt, das in der Regel jeweils in der folgenden
Sitzung ausgeteilt wird.
• Teilnehmerliste: Mit Computern umgehen können alle Teilnehmer, programmieren
die wenigsten (2-4 von 13). Alle Teilnehmer haben Mathematik als 2. Fach.
1.2
Überblick
• Dynamische Systeme
– Alle physikalischen Systeme sind dynamische Systeme, aber nicht alle dynamischen Systeme sind physikalische Systeme. Ihr Verhalten als Ganzes beruht auf
dem Zusammenwirken ihrer Teile. Dieses Zusammenwirken wird durch Bewegungsgleichungen beschrieben. Bei mechanischen Systemen z.B. gewinnt man
die Bewegungsgleichungen aus den Newton’schen Gleichungen für die Einzelteile.
– Das zukünftige Verhalten eines dynamischen Systems ist durch den momentanen Zustand festgelegt.
– In der Veranstaltung wird das Schwergewicht auf folgenden Beispielen liegen:
∗ Punktmechanik,
∗ Mehrteilchensysteme (Himmelsmechanik?),
∗ lineare und nichtlineare (mechanische und elektromagnetische) Schwingungen und
∗ Bewegungen ausgedehnter Körper (Sport).
– Bewegungsgleichungen
∗ Das Verhalten dynamischer Systeme wird durch (kontinuierliche) Differentialgleichungen oder durch (diskrete) Differenzengleichungen beschrieben.
∗ Diese haben (unter gewissen Voraussetzungen) eindeutige Lösungen, die
vom momentanen Zustand abhängen. D.h.: Die gesamte Vergangenheit
und Zukunft ist im momentanen Zustand des Systems und in seinen Bewegungsgleichungen enthalten.
∗ Die Lösungen der dynamischen Gleichungen sind manchmal analytisch,
meist aber nur numerisch zu finden.
1 26. OKTOBER 2000: EINFÜHRUNG
2
∗ Die Teilnehmer sollen analytische und numerische Lösungsverfahren für
Differential- und Differenzengleichungen und ihre Vor- und Nachteile kennenlernen.
– Reguläres und chaotisches Verhalten einfacher Systeme wird demonstriert an
folgenden Beispielen:
∗ einem Dreifachpendel,
∗ einem Fadenpendel, dessen Stahlkugel über drei Magneten schwingt, und
∗ mehreren Spielzeugen.
An ihnen wird veranschaulicht, dass das zukünftige Verhalten auch einfacher
Systeme trotz bekannter Bewegungsgleichungen unvorhersagbar wird, wenn im
Laufe der Bewegung Entscheidungspunkte“ (z.B. die Überschlagspunkte bei
”
einem Pendel) durchlaufen werden, bei denen winzige Unterschiede zu völlig
verschiedenem Folgeverhalten führen. Aufgrund nicht zu vermeidender Ungenauigkeiten (in der Bestimmung der Anfangsbedingungen, bei der Messung der
Systemparameter, bei der Berücksichtigung äußerer Einflüsse) kann das Verhalten der Systeme an solchen Punkten bereits nach kurzer Zeit nicht mehr
vorhergesagt werden.
• In der Theorie werden folgende Punkte behandelt und geübt werden:
– das Aufstellen von Bewegungsgleichungen,
– die analytische Lösung einfacher Differentialgleichungen,
– numerische Integrationsverfahren und
– die mathematische und grafische Darstellung von Systemverhalten (Zeitkurven,
Phasendiagramme, Attraktoren, Poincaré-Schnitte, Einzugsgebiete).
• Das Verhalten linearer und nichtlinearer Systeme soll durch Simulation untersucht
werden, und zwar
– mit öffentlich zugänglichen Programmen (Internet),
– mit kommerziellen Programmen,
– durch selbst erstellte Pascalprogramme und
– mit Hilfe grafischer Modellbildung.
• Bei den Experimenten werden die folgenden Gesichtspunkte im Vordergrund stehen:
– die Messung von Systemparametern und die Bestimmung von Systemzuständen,
– die Erfassung und Auswertung von Messwerten mit Computern und
– insbesondere der Vergleich zwischen Theorie und Experiment.
1 26. OKTOBER 2000: EINFÜHRUNG
1.3
3
konkreter Einstieg: Das Federpendel
In Freihandexperimenten werden Schraubenfederpendel mit unterschiedlichen Federn und
verschieden schweren Pendelkörpern vorgeführt.
• Qualitative Beschreibung des Systemverhaltens
– Das Pendel kommt immer zur Ruhe, wenn es nicht angetrieben (keine Energie
hineingesteckt) wird.
– Die Bewegung ist nahezu periodisch. Mit geringfügiger Idealisierung kann sie
als periodisch angesehen werden.
• Qualitative Aussagen über den Zusammenhang der Schwingungsdauer T mit
anderen Systemparametern:
– T ist bei verschiedenen Federn unterschiedlich.
– T hängt ab von der Härte der Feder und von ihrer Länge.
– T ändert sich mit der Masse des Pendelkörpers.
– T hängt nicht ab von der Amplitude der Schwingung.
– T ist unabhängig vom Ort auf der Erde (von der Fallbeschleunigung g). (Diese
Aussage ist tatsächlich nur schwierig zu realisieren!)
• Halbquantitative Aussagen:
– Je härter die Feder, desto kleiner die Schwingungsdauer.
– Je länger die Feder, desto größer die Schwingungsdauer.
– Je größer die Masse des Pendelkörpers, desto größer die Schwingungsdauer.
• Hausaufgaben:
– Formulieren Sie quantitative Aussagen über die Abhängigkeit der Schwingungsdauer des Pendels von den Systemparametern!
– Wie lautet der formelmäßige Zusammenhang (Thomson’sche Schwingungsgleichung)?
– Bereiten Sie sich auf die Ableitung dieser Formel vor!
2 2. NOVEMBER 2000: DAS SCHRAUBENFEDERPENDEL
2
4
2. November 2000: Das Schraubenfederpendel
Der jeweils aktuellste Stand des Vorlesungsskriptes (inklusive der Planung für die kommende Vorlesung) kann im Internet eingesehen werden unter
http://www.uni-koblenz.de/∼backhaus/lectures/dynsws00.pdf
In demselben Verzeichnis befinden sich auch die Skripte der letzten Vorlesung über dynamische Systeme (../lectures/dynsws97.exe und ../lectures/dynsss98.exe).
2.1
Wiederholung
• Das Schraubenfederpendel soll als Einführungsbeispiel dienen für
– die experimentelle Untersuchung einfacher Systeme,
– die Aufstellung der Bewegungsgleichung,
– die analytische und numerische Lösung der Bewegungsgleichung,
– einfache Pascal-Programmierung und
– einfache grafische Modellbildung.
• Qualitative und halbquantitative Aussagen, die das Verhalten solcher Pendel beschreiben, sind bereits gefunden worden.
2.2
Experimente
• Freihandexperimente führen zu den folgenden quantitativen Aussagen:
– Zusamenhang zwischen Schwingungsdauer und Pendelmasse:
m in kg
5T in s
0.5
1.0
2.0
4.1
5.5
7.9
√T
m
in √s
kg
1.16
1.10
1.12
Folgerungen:
∗ Die Schwingungsdauer wächst mit der Masse des Pendelkörpers.
∗ Schwingungsdauer und Masse hängen nicht proportional zusammen.
∗ Die Schwingungsdauer des Federpendels ist proportional zur Wurzel aus
der Masse des Pendelkörpers:
T ∼
√
m
(1)
Verallgemeinerungen:
∗ Dieser Satz ist gültig bei beliebig schweren Pendelkörpern (in dieser Allgemeinheit sicher falsch!).
∗ Der Satz gilt für alle Schraubenfedern – natürlich mit anderen Werten der
Proportionalitätskonstanten.
2 2. NOVEMBER 2000: DAS SCHRAUBENFEDERPENDEL
5
– Zusammenhang zwischen Schwingungsdauer und Länge der Feder (dabei wird
die Federlänge durch Halbieren der Feder und durch Aneinanderhängen zweier
gleichartiger Federn variiert):
l in rel. Einh.
2
1
0.5
5T in s
5.9
4.1
3.0
T
√
l
0.83
0.82
0.85
Folgerungen:
∗ Die Schwingungsdauer wächst mit der Länge der Feder.
∗ Schwingungsdauer und Länge hängen nicht proportional zusammen.
∗ Bei gleichartigen Federn ist die Schwingungsdauer des Federpendels proportional zur Wurzel aus der Länge der Feder:
T ∼
√
l
(2)
Verallgemeinerungen:
∗ Dieser Satz ist gültig bei beliebig langen Federn.
∗ Der Satz gilt für alle Arten von Schraubenfedern – natürlich mit anderen
Werten der Proportionalitätskonstanten.
• Die Härte von Federn wird durch die so genannte Federkonstante D beschrieben:
1. Es zeigt sich: Die Verlängerung ∆l einer Schraubenfeder ist – in gewissen Grenzen – proportional zur Kraft F , mit der sie auseinandergezogen wird. Z.B.
ergibt sich bei einer einzelnen Feder:
m in kg
0.5
1.0
2.0
∆l ∼ F
F in N
4.9
9.8
19.6
∆l in m
0.162
0.307
0.607
F
∆l
in N
m
30.2
31.9
32.3
(Hooke’sches Gesetz).
(3)
2. Die Federkonstante wird definiert gemäß:
D :=
F
∆l
(4)
Man erkennt: Je größer die Federkonstante, desto weniger dehnt sich die Feder bei einer bestimmten Kraft (oder: desto größer ist die Kraft, die für eine
bestimmte Verlängerung erforderlich ist), desto härter ist sie also.
3. Mit der Federkonstanten lässt sich das Hooke’sche Gesetz für Schraubenfedern
auch folgendermaßen formulieren:
D = const
(Hooke’sches Gesetz)
2 2. NOVEMBER 2000: DAS SCHRAUBENFEDERPENDEL
6
• Wenn zwei gleichartige Federn aneinander gehängt werden, dann wird die zusammengesetzte Feder (doppelter Länge) offensichtlich doppelt so stark gedehnt, wenn
sie durch dieselbe Kraft auseinander gezogen wird. Denn jede der beiden Kräfte wird
durch dieselbe Kraft gedehnt! Die Federkonstante der zusammengesetzten Feder ist
also nach Definition (4) halb so groß wie die einer einzelnen Feder. Mit anderen
Worten:
Die Federkonstante gleichartiger Federn ist umgekehrt proportional zu ihrer Länge.
Damit ergibt sich aber:
T ∼
√
l
1
T ∼√
D
=⇒
(5)
Aufgabe: Überlegen Sie sich auf ähnliche Weise, wie groß die Federkonstante zweier
parallelgeschalteter“ gleichartiger Federn ist!
”
Die Federkonstante von aus gleichartigen Federn zusammengesetzten Federn ist proportional zur Anzahl der parallelgeschalteten Federn.
• Die beiden gefundenen Proportionalitäten (1) und (5) lassen sich zu einer zusammenfassen:
√ )
T ∼ m
T ∼ √1D
=⇒
T ∼
r
m
D
=⇒
T =k
r
m
D
(6)
Diese Zusammenfassung zweier Proportionalitäten zu einer kann folgendermaßen
begründet werden:
√
1. Bei konstanter Federkonstante ist der Quotient aus T und m konstant. Diese
Konstante ist jedoch für verschiedene Federn unterschiedlich groß:
T
√ = const = c(D)
m
2. Um die Abhängigkeit der Konstanten von D zu untersuchen, wird der Wert der
Konstanten c(D) für verschiedene Federn bestimmt. Dafür muss der Quotient
√T streng genommen jeweils nur einmal gemessen werden (denn für andere
m
Massen ergibt sich nach 1. derselbe Wert!).
Bei diesen Messungen zeigt sich:
1
c(D) ∼ √
D
oder
T
1
√ ∼√
m
D
=⇒
T ∼
r
m
D
2 2. NOVEMBER 2000: DAS SCHRAUBENFEDERPENDEL
7
• Dimensionsanalyse von (6) ergibt:
{k} = 1
Die Konstante k hat also keine Einheit.
Der Zahlenwert von k kann aus jedem zusammenhängenden Tripel von Messwerten gewonnen werden. Z.B. wird die einfache Feder durch einen Körper der Masse
m = 1kg um ∆l = 0.307m gedehnt (s.o.). Das entsprechende Pendel hat die Schwingungsdauer T = 1.1s. Damit ergibt sich:
k=T
s
D
=T
m
s
s
1kg · 9.8 sm2
F
= 1.1s
= 6.2
∆lm
0.307m · 1kg
Einen genaueren Wert kann man durch Mittelwertbildung über alle Messwerte erhalten.
• Zusammengenommen ergibt sich also:
T = 6.2
2.3
r
m
D
(7)
Messwertaufnahme mit einem Computer
• Prinzip einer Messung: Analog-Digital-Wandlung von Spannungswerten, gleichzeitiges Auslesen der internen Uhr
• Zu messende Größen müssen also in proportionale Spannungen umgewandelt werden
(z.B. mit Dehnungsmessstreifen, veränderlichen Widerständen usw.).
Bei der vorliegenden Wegmessung wird durch die Speichen eines sich mit der Bewegung drehenden Rades eine Lichtschranke unterbrochen. Jede Unterbrechung entspricht einem bestimmten Wegintervall ∆s. Den Versuchsaufbau zeigt Abb. 1
• Die Messwerte werden simultan zur Messung auf dem Bildschirm grafisch dargestellt (Abb. 2) und intern so gespeichert, dass sie anschließend weiter verarbeitet
werden können. Die Abspeicherung der Messwerte in Tabellenform ermöglicht die
nachfolgende Auswertung auch mit anderen Programmen (z.B. Tabellenkalkulation,
eigene Programme).
• Der Computer kann die gemessene Kurve, z.B. zur Bestimmung von Geschwindigkeit
und Beschleunigung, ein- oder zweimal numerisch differenzieren gemäß
x(ti+1 ) − x(ti−1 )
ti+1 − ti−1
ẋ(ti+1 ) − ẋ(ti−1 )
ẍ(ti ) ≈
ti+1 − ti−1
ẋ(ti ) ≈
(8)
(9)
2 2. NOVEMBER 2000: DAS SCHRAUBENFEDERPENDEL
Abbildung 1: Versuchsaufbau zur automatischen Erfassung der Bewegungen eines
Schraubenfederpendels
Abbildung 2: Mit dem Computer erfasste Weg-Zeit-Kurve des Schraubenfederpendels
8
2 2. NOVEMBER 2000: DAS SCHRAUBENFEDERPENDEL
9
Abbildung 3: Mit dem Computer erfasste Weg-Zeit-Kurve des Schraubenfederpendels, zusammen mit nachträglich berechneten Geschwindigkeitsund Beschleunigungs-Zeitkurven
Abbildung 4: Mit dem Computer erfasste Weg-Zeit-Kurve des Schraubenfederpendels, zusammen mit simultan berechneten Geschwindigkeitsund Beschleunigungs-Zeitkurven
Bei der numerischen Differentiation werden Messfehler verstärkt. Das macht sich
besonders bei der 2. Ableitung stark bemerkbar. Deshalb wird meist über mehrere
Werte gemittelt (Abb. 3).
Lässt man die Ableitungen simultan mit der Messung anzeigen, schafft der Computer diese Mittelung nicht. Die Kurven werden nicht geglättet und zeigen alle
Messungenauigkeiten ungeschönt (Abb. 4):
3 16. NOVEMBER 2000: THEORIE DES FEDERPENDELS
3
10
16. November 2000: Theorie des Federpendels
3.1
Ergänzungen zu den Freihandmessungen
• Experimentell lässt sich zeigen, dass die Schwingung des Federpendels harmonisch
ist. Dazu kann man die Auslenkung als Funktion der Zeit messen (z.B. durch automatische Messwerterfassung mit einem Computer). Qualitativ kann man es dadurch
zeigen, dass man die Projektion einer gleichförmigen Kreisbewegung mit der Pendelschwingung synchronisiert (Demonstration).
• Damit aber lässt sich die Bewegung des Pendels als Funktion der Zeit beschreiben.
Dazu muss zunächst das Koordinatensystem festgelegt werden:
– Die Stoppuhr wird gestartet (d.h. die Zeit wird auf 0 gesetzt), wenn sich das
Pendel im oberen Umkehrpunkt befindet.
– Die x-Achse wird parallel zur Bewegungsrichtung orientiert. Die Richtung wird
so gewählt, dass die Anfangsauslenkung positiv ist (d.h. nach oben).
– Der Nullpunkt der x-Achse wird in den Gleichgewichtspunkt des Pendels gelegt.
Dann gilt nach den experimentellen Ergebnissen für die Auslenkung:
2π
x = x0 cos t ≈ x0 cos
T
s
D
t
m
(10)
Wegen
2π
2π
2π
(t + T ) = x0 cos
t + 2π = x0 cos t = x(t)
T
T
T
ist T die Schwingungsdauer des Pendels.
x(t + T ) = x0 cos
Mit (7) haben wir deshalb gefunden:
x(t) ≈ x0 cos
s
D
t
m
(11)
Die Konstante in dieser Gleichung heißt die Kreisfrequenz ω0 des Pendels:
2π
ω0 =
≈
T
s
D
m
(12)
Hier lässt sich vermuten, dass der Zahlenwert der Konstanten k in (7) theoretisch
gleich 2π sein sollte!
3 16. NOVEMBER 2000: THEORIE DES FEDERPENDELS
2
4
6
8
10
12
11
14
16t [s]
Abbildung 5: Anpassung
einer Kosinuskurve
an vom Computer aufgenommene Messwerte:
2π
x(t) = xmax cos 1.105s t − 0.25s
• Geschwindigkeit und Beschleunigung des Pendelkörpers werden deshalb beschrieben
durch:
dx
= ẋ(t) = −ω0 sin ω0 t
dt
dv
d2 x
a(t) =
= 2 = ẍ(t) = −ω02 cos ω0 t
dt
dt
v(t) =
3.2
Beispielmessungen mit dem Computer
• Beispielmessung (nicht durchgeführt): Messung der Schwingungsdauer für zwei Pendelkörper unterschiedlicher Masse:
1. durch grafische Messung der Abstände aufeinander folgender Extrema,
2. anhand der Messwerttabelle.
Die so zu erzielenden Ergebnisse haben wir aber bereits einfacher mit einer Freihandmessung erhalten!
• Die Frage, ob es sich bei der Bewegung des Federpendels um eine harmonische
Schwingung handelt, lässt sich allerdings mittels Computer durch Anpassung einer Kosinuskurve viel leichter als im Einzelexperiment prüfen: Amplitude, Periode und Zeitnullpunkt werden durch Versuch und Irrtum so lange verändert, bis
möglichst gute Übereinstimmung zwischen gemessener und berechneter Kurve besteht (s. Abb. 5).
3 16. NOVEMBER 2000: THEORIE DES FEDERPENDELS
3.3
12
Ableitung der Bewegungsgleichung
l0
@
@
l0
@
@
x
@
@
lG
@
@
@
@
?
6
y
~
Ausgangspunkt bilden die Newton’sche Bewegungsgleichung
F~ = m~a
(13)
und das Hook’sche Gesetz (3).
Für die Wahl des Koordinatensystems gibt es verschiedene (geschickte und ungeschickte) Möglichkeiten. Zwei davon sollen zum Vergleich durchgespielt werden:
1. linke Seite: Koordinate x, Ursprung an der Decke, Richtung nach unten
F = −D(x − l0 ) + mg
=⇒ mẍ = −D(x − l0 ) + mg
D
mg
=⇒ ẍ = − (x − l0 −
)
m
D
D
mg
=⇒ ẍ′ = − x′
mit
x′ = x − l0 −
m
D
Wegen
x′ = 0
⇐⇒
D(x − l0 ) = mg
stellt die Koordinatentransformation x −→ x′ die Verschiebung des Nullpunktes
in die Gleichgewichtslage dar.
2. rechte Seite: Koordinate y, Ursprung in der Gleichgewichtslage, Richtung nach oben
=⇒
mÿ = D(lG − y − l0 ) − mg
mÿ = −Dy
(wegen
D(lG − l0 ) = mg)
In beiden Fällen ist also die folgende Differentialgleichung zu lösen:
ẍ(t) + kx(t) = 0
(14)
3 16. NOVEMBER 2000: THEORIE DES FEDERPENDELS
3.4
13
Qualitatives Verhalten der Lösung
• Benutzt wird:
– ẋ = Steigung der Kurve (Geschwindigkeit),
– ẍ = Krümmung der Kurve (Beschleunigung):
∗ ẍ < 0 (Beschleunigung entgegen der x-Richtung): Rechtskrümmung, bzw.
Krümmung nach unten,
∗ ẍ > 0 (Beschleunigung in x-Richtung): Linkskrümmung, bzw. Krümmung
nach oben.
• Die Anfangsbedingungen x0 = x(t = 0) und v0 = ẋ(t = 0) müssen bekannt sein.
• Wenn x0 = 0 und v0 = 0, dann ist nach (14) auch a0 = 0. Geschwindigkeit und
damit auch Auslenkung bleiben Null.
• Wenn x0 = 0, aber v0 > 0 ist, dann wird im nächsten Moment die Auslenkung positiv
sein. Damit wird aber die Beschleunigung negativ und damit die Geschwindigkeit
kleiner.
• Leicht zu sehende Eigenschaften:
– x>0
=⇒
Rechtskrümmung,
– x<0
=⇒
Linkskrümmung,
– die Kurve ist also immer zur Zeitachse hingekrümmt.
– Der Betrag der Krümmung ist proportional zu |x|.
– Es gibt also immer wieder Nulldurchgänge.
x
t
• Nicht so leicht zu erkennen sind die folgenden Eigenschaften der Lösung:
– Der Abstand der Nulldurchgänge ist immer gleich.
– Die Höhe der Extremstellen ist immer gleich.
• Diese Aussagen gewinnt man folgendermaßen:
– Man lasse die Zeit in der umgekehrten Richtung laufen, spule“ also den Film
”
”
zurück“, d.h. dt −→ −dt
3 16. NOVEMBER 2000: THEORIE DES FEDERPENDELS
14
– Dann folgen
∗ v −→ −v und
∗ a −→ a.
– Die Differentialgleichung bleibt also dieselbe. Das heißt aber: Die Kurve muss
symmetrisch in der Zeit, d.h. symmetrisch zur x-Achse sein.
– Da aber der Zeitnullpunkt völlig beliebig gewählt wurde, müssen deshalb alle
Extrema gleich hoch sein und die Nulldurchgänge denselben Abstand haben.
• Bei diesen Überlegungen muss die Kurve schrittweise konstruiert werden: Aus jedem
Zustand ergibt sich der Folgezustand“. Wir werden sehen, dass dies gerade die Idee
”
der numerischen Integration ist.
3.5
Analytische Lösung der Bewegungsgleichung
• Das Verhalten des Federpendels wird durch die Differentialgleichung (14) beschrieben. Darin beschreibt die Funktion x(t) das zeitliche Verhalten des Ortes des Pendelkörpers.
• In (14) ist die Funktion x(t) nicht direkt gegeben, sondern stattdessen ein Zusammenhang zwischen der Funktion und ihren Ableitungen nach der Zeit: Die Funktion
x(t) geht durch zweimalige Ableitung bis auf das Vorzeichen und einen (positiven)
Faktor in sich selbst über.
• Sinus und Kosinus sind solche Funktionen; tatsächlich sind es (im Wesentlichen) die
einzigen.
• Die Differentialgleichung hat folgende Eigenschaften:
– Sie ist von 2. Ordnung, d.h. sie enthält die zweite Ableitung, aber keine
höheren Ableitungen.
– Die Differentialgleichung ist linear, d.h. die Funktion selbst und ihre Ableitungen kommen nur in der 1. Potenz vor.
– Sie ist homogen, d.h. die Gleichung enthält keinen konstanten Summanden.
Diese Eigenschaften haben eine wichtige Konsequenz: Wenn zwei Funktionen f1 und
f2 die Gleichung erfüllen, dann tun es auch ihre Linearkombinationen:
=⇒
f¨1 + kf1 = 0
und
f¨2 + kf2 = 0
af¨1 + akf1 + bf¨2 + bkf2 = af¨1 + bf¨2 + k(af1 + bf2 ) = 0
• Da Sinus und Kosinus die Bewegungsgleichung erfüllen können, macht man den
folgenden Ansatz zu ihrer Lösung:
3 16. NOVEMBER 2000: THEORIE DES FEDERPENDELS
Ansatz:
=⇒
=⇒
=⇒
x(t)
ẋ(t)
ẍ(t)
ẍ(t)
=
=
=
=
A sin ω0 t + B cos ω0 t
ω0 A cos ω0 t − ω0 B sin ω0 t
−ω02 A sin ω0 t − ω02B cos ω0 t
−ω02 x(t)
15
(15)
(16)
(17)
• Der Ansatz (15) ist also eine Lösung der Differentialgleichung (14), wenn gilt:
ω02 = k =
D
m
(18)
• Damit muss gelten:
2π
T =
ω0
T = 2π
=⇒
r
m
D
(19)
• Der Ansatz (15) stellt in Wirklichkeit die allgemeine Lösung der Differentialgleichung (14) dar!
• Die Lösung eines konkreten Problems, bei dem die Anfangsbedingungen bekannt
sind, erhält man folgendermaßen:
x(t = 0) = x0
v(t = 0) = v0
=⇒
)
x(t) =
=⇒
(
B = x0
A = ωv00
v0
sin ω0 t + x0 cos ω0 t
ω0
(20)
• Diese analytische Lösung ermöglicht es, im Gegensatz zum numerischen Verfahren,
zu jedem Wert von t sofort, d.h. ohne Berechnung aller Zwischenzustände, Auslenkung, Geschwindigkeit und Beschleunigung zu berechnen.
3.6
Übung
Aufgaben:
1. Stellen Sie zwei unterschiedliche Lösungen der Bewegungsgleichung (14) in einem
qualitativen Diagramm dar:
(a) Anfangsauslenkung x0 positiv, Anfangsgeschwindigkeit v0 = 0 (d.h. der Pendelkörper wird aus der Ruhe losgelassen),
3 16. NOVEMBER 2000: THEORIE DES FEDERPENDELS
16
(b) dieselbe Anfangsauslenkung x0 , aber v0 > 0 (d.h. der Pendelkörper erhält einen
Schubs“ nach oben).
”
Wie groß ist in diesem Falle die Amplitude der Schwingung?
x
t
T
Wegen (18) hat die Schwingung in beiden Fällen dieselbe Frequenz. Im 2. Fall
hat sie aber wegen der positiven Anfangsgeschwindigkeit eine größere Amplitude
und erreicht den Maximalausschlag erst später. Es tritt also eine Phasenverschiebung auf.
Die allgemeine Lösung (20) lässt sich mit Hilfe des Additionstheorems für die
Kosinusfunktion
cos(α + β) = cos α cos β − sin α sin β
folgendermaßen umschreiben:
x(t) = x0 cos ω0 t +
=
s
v0
ω0
2
v0
sin ω0 t
ω0


x0
+ x20 
 r 2
v0
ω0
+ x20
= x1 cos(ωt + ϕ)
cos ω0 t + r
v0
ω0
v0
ω0
2

+ x20

sin ω0 t

Dabei sind die Amplitude x1 und die Phasenverschiebung ϕ der neuen Schwingung gegeben durch
x1 =
s
v0
ω0
2
+
x20 ,
cos ϕ =
x0
r
v0
ω0
2
, sin ϕ =
+ x20
r
v0
ω0
v0
ω0
2
+ x20
2. Lösen Sie die Bewegungsgleichung des Pendels mit Hilfe des Ansatzes
Ansatz:
x(t) = xA (cos ω0 t + ϕ)
Der Ansatz lässt sich wie eben mit dem Additionstheorem umschreiben:
(21)
3 16. NOVEMBER 2000: THEORIE DES FEDERPENDELS
17
x(t) = −xA sin ϕ sin ω0 t + xA cos ϕ cos ω0 t
= A sin ω0 t + B cos ω0 t
Der Ansatz ist also äquivalent zu dem in der Vorlesung behandelten. Das dort erhaltene Ergebnis kann also direkt übernommen werden:
−xA sin ϕ= ωv00
xA cos ϕ=x0
)
=⇒









xA =
v0
ω0
sin ϕ= xA
x0
cos ϕ= xA
r
v0
ω0
2
=⇒
Die Frequenz ω0 muss wieder die Bedingung (18) erfüllen.
+ x20
tan ϕ =
v0
x 0 ω0
4 23. NOVEMBER 2000: NUMERISCHE INTEGRATION 1
4
18
23. November 2000: Numerische Integration 1
4.1
Wiederholung
• Die Schwingung des Federpendels ist harmonisch. Das lässt sich experimentell zeigen
durch
– Simultane Projektion mit einer gleichförmigen Kreisbewegung oder
– durch Anpassung einer harmonischen Kurve an mit einem Computer aufgenommene Daten.
• Die Bewegungsgleichung des Pendels ist gegeben durch:
ẍ = −
D
x
m
• Die allgemeine Lösung dieser Differentialgleichung ist
x(t) = A sin ω0 t + B cos ω0 t
q
D
Dabei ist ω0 = m
unabhängig von der Amplitude der Schwingung und von der
Erdbeschleunigung g!
Alle diese Lösungen stellen harmonische Schwingungen mit derselben Frequenz, aber
unterschiedlichen Amplituden und Phasenlagen dar.
• Bei gegebenen Anfangsbedingungen x0 , v0 gibt es eine eindeutige Lösung. Sie ist
charakterisiert durch
A=
4.2
v0
, B = x0
ω0
Das Euler-Verfahren (Ganzschritt-Verfahren)
• Die Idee wurde bereits bei der qualitativen Lösung der Differentialgleichung beschrieben.
• Grafisch kann das Verfahren folgendermaßen veranschaulicht werden:
4 23. NOVEMBER 2000: NUMERISCHE INTEGRATION 1
19
x
r
x0
r
r
x′1 = x0 + v0 ∆t
x1
r
r
x′2 = x′1 + v1′ ∆t
t1
t1 + ∆t
v0
a0 = a(x0 )
v1′ = v0 + a0 ∆t
a′1 = a(x′1 )
v2′ = v1′ + a′1 ∆t
a′2 = a(x′1 )
t1 + 2∆t
t
• Algorithmisch kann es folgendermaßen formuliert werden:
1. Zum Zeitpunkt t = 0.0 sind Auslenkung x und Geschwindigkeit v gegeben
(Anfangsbedingungen).
2. Die zugehörige Beschleunigung a lässt sich mit Hilfe der Bewegungsgleichung
berechnen.
3. Erhöhe t um ∆t, und berechne die zugehörigen Werte von x und v gemäß
x = x + v∆t
v = v + a∆t
4. Gehe zurück nach 2.
• Und schließlich als Flussdiagramm:
Anfangsbedingungen:
x = x0
v = v0
?
-
Bewegungsgleichung:
a = a(x, v, t)
-
x = x + v∆t
v = v + a∆t
t = t + ∆t
-
4 23. NOVEMBER 2000: NUMERISCHE INTEGRATION 1
20
• Aufgabe: Für den Fall D = 1 N
, m = 1kg, v0 = 0, x0 = 1.0 teile die erste Viertelm
periode in 6 Integrationsschritte und berechne die numerische Lösung von Hand !
Lösung:
t[s] x[m] xNum[m]
0.00 1.00
1.00
0.26 0.97
1.00
0.52 0.87
0.93
0.79 0.71
0.79
1.05 0.50
0.59
1.31 0.26
0.34
1.57 -0.00
0.04
1.0
r
x
x0
r
v[m/s]
0.00
-0.26
-0.50
-0.71
-0.87
-0.97
-1.00
vNum[m/s]
0.00
-0.26
-0.52
-0.77
-0.98
-1.13
-1.22
a[m/s2 ] aNum[m/s2 ]
-1.00
-1.00
-0.97
-1.00
-0.87
-0.93
-0.71
-0.79
-0.50
-0.59
-0.26
-0.34
0.00
-0.04
r
r
0.8
r
0.6
0.4
r
0.2
r
2
4
6
t
dt
• Zur Konkretisierung ein leicht abgeändertes Flussdiagramm:
Bewegungsgleichung:
a = −ω02 x
Anfangsbedingungen:
x = x0
v = v0
t = 0.0
-
ja
6
H
HH
?
HtH≤ tmax
H
nein
?
Ende
x = x + v∆t
v = v + a∆t
t = t + ∆t
Ausgabe
4 23. NOVEMBER 2000: NUMERISCHE INTEGRATION 1
• direkte Pascal-Übersetzung
x:=x0;
v:=v0;
t:=0.0;
while t<=tMax do
begin
a:=-Omega02*x;
WriteLn(...);
x:=x+v*dt;
v:=v+a*dt;
t:=t+dt;
end;
(* Anfangsbedingungen: *)
(* Schleife *)
(* Ausgabe *)
21
5 30. NOVEMBER 2000: NUMERISCHE INTEGRATION 2
5
22
30. November 2000: Numerische Integration 2
5.1
Wiederholung
• Die Demonstrationsprogramme und ihre Quelltexte befinden sich im Netz unter
http://www.uni-koblenz.de/∼backhaus/lectures/dynsyst
Ebenfalls dort zu finden sind die zur Übersetzung erforderlichen Dateien Kern.pas
und Modul.pas und der zur Laufzeit der Programme erforderliche Grafiktreiber
egavga.bgi.
• Beim Ganzschritt-Verfahren der numerischen Integration wird während eines
Zeitschrittes angenommen, Geschwindigkeit und Beschleunigung seien konstant:
x(t + ∆t) = x(t) + v∆t
v(t + ∆t) = v(t) + a∆t
• Dieses Verfahren entspricht einer Zerlegung einer Differentialgleichung 2. Ordnung in
einer Variablen in eine System zweier Differentialgleichungen 1. Ordnung mit zwei
Variablen. Die Gleichungen dieses Systems sind gekoppelt, da beide Gleichungen
beide Variablen enthalten:
ẍ = f (x, ẋ)
v=ẋ
−→
(
ẋ = v
v̇ = f (x, v) = a
(22)
Auf ganz entsprechende Weise kann eine Differentialgleichung n-ter Ordnung in ein
System aus n gekoppelten Differentialgleichungen 1. Ordnung umgewandelt werden.
Genau eine dieser Gleichungen enthält den Kern des physikalischen Problems.
5.2
Numerische Fehler
• Beim numerischen Integrieren entstehen numerische Fehler, die sich in kurzer Zeit
so aufschaukeln können, dass das Verhalten der numerischen Lösung nichts mehr zu
tun hat mit dem Verhalten des realen Systems (s. Abb. 6).
• Diese Fehler können verringert werden, indem die Integrationsschrittweite verkleinert wird. Dadurch steigt allerdings die Rechenzeit umgekehrt proportional zur
Schrittweite an, ohne dass das Problem grundsätzlich beseitigt wäre.
• In der nächsten Sitzung werden wir verbesserte Integrationsverfahren kennen lernen.
Aber auch dann wird es immer erforderlich bleiben, sich über die Genauigkeit von
Simulationen Rechenschaft abzulegen!
r
5 30. NOVEMBER 2000: NUMERISCHE INTEGRATION 2
r
x
x0
r
1.5
1.0
0.5
rrr
r
r
r
-1.0
-1.5
23
r
r
r
r
r
r
r
r
r
-0.5
rrr
r
r
10
r
r
20
r
r
30
r
40
t
dt
r
r
r
rrr
r
r
r
r
r
r
r
r
r
r
rr
r
Abbildung 6: Trotz nur kleiner Fehler zu Beginn schaukeln sich die Abweichungen hoch
und spiegeln eine Schwingung mit wachsender Amplitude vor.
5.3
Simulation mit Modellbildungssystem
Modellbildungssysteme ermöglichen es, das Verhalten dynamischer Systeme zu simulieren,
ohne eine Programmiersprache wie Pascal erlernen zu müssen. Die Größen des Systems
und ihre gegenseitigen Abhängigkeiten werden dabei grafisch konstruiert. Die numerische
Integration der so definierten Differentialgleichungen und die grafische Darstellung ihrer
Lösung erledigt dann das Programm.
Die ursprüngliche Funktion von Modellbildungssystemen war die Simulation von wirtschaftlichen Zusammenhängen und Entwicklungen. Eine zentrale Rolle spielen deshalb
Vorratsbehälter und Zu- bzw. Abflüsse. In der Physik werden daraus Zustandsgrößen und
ihre zeitlichen Ableitungen. Vorratsbehälter werden durch Rechtecke, die Flüsse durch
Rohre (Doppelpfeile) mit Ventilen dargestellt.
Die Funktion eines Modellbildungssystems soll am Beispiel der schrittweisen Konstruktion eines dynamischen Systems erlernt werden, durch das das Verhalten des Federpendels
simuliert werden kann:
• Die Änderung einer Geschwindigkeit bei konstanter Beschleunigung wird durch das
in Abb. 7 gezeigte System simuliert. Rechts ist ein typisches Diagramm gezeigt,
das auf Knopfdruck erzeugt werden kann, nachdem die Beschleunigung einen Wert
und die Geschwindigkeit einen Anfangswert erhalten hat. Im Hintergrund wird das
System dabei gemäß
Geschwindigkeit(t + ∆t) = Geschwindigkeit(t) + ay ∆t
integriert. Die dazu gehörenden, vom Programm automatisch erzeugten, Gleichungen lauten:
5 30. NOVEMBER 2000: NUMERISCHE INTEGRATION 2
24
Abbildung 7: Änderung der Geschwindigkeit durch eine konstante Beschleunigung
Abbildung 8: Steuerung der Änderung der Höhe durch die Geschwindigkeit
Zustandsgleichungen
Geschwindigkeit.neu <-- Geschwindigkeit.alt + dt*(ay)
Startwert Geschwindigkeit = 0
Zustandsänderungen
ay = 1
• Die dazu gehörende Höhe erhält man, indem man das System entsprechend Abb. 8
erweitert: vy spielt nun die Rolle des Ventils für den Zufluss des Behälters Höhe.
Entscheidend ist, dass die Einstellung dieses Ventils von Geschwindigkeit gesteuert
wird (genauer: mit ihm übereinstimmt). Diese Abhängigkeit wird durch einen Pfeil
symbolisiert. Im Hintergrund wird nun zusätzlich
Hoehe(t + ∆t) = Hoehe(t) + vy ∆t
integriert. Die automatisch erzeugten Zeilen lauten:
Zustandsgleichungen
Geschwindigkeit.neu <-- Geschwindigkeit.alt + dt*(ay)
Startwert Geschwindigkeit = 0
Höhe.neu <-- Höhe.alt + dt*(vy)
Startwert Höhe = 1
5 30. NOVEMBER 2000: NUMERISCHE INTEGRATION 2
25
Abbildung 9: Steuerung der Beschleunigung durch die Höhe: Rückkopplung
Zustandsänderungen
vy = Geschwindigkeit
ay = 1
Offensichtlich ist hier gerade die Differentialgleichung 2. Ordnung (ẍ = ay ) in zwei
Gleichungen 1. Ordnung zerlegt worden, und diese Zerlegung wird durch die zwei
Flussdiagramme dargestellt. Ihre Kopplung spiegelt sich dabei in dem Pfeil.
Die Veränderung von Höhe und Geschwindigkeit mit der Zeit kann durch zwei verschiedene Diagramme, aber auch in einem gemeinsamen Diagramm (Abb. 8, rechts)
dargestellt werden.
• Die Änderung zu einem Schraubenfederpendel geschieht nun einfach durch Einfügung
einer neuen Abhängigkeit (Abb. 9)): Das Ventil ay wird durch den Inhalt von Höhe
gesteuert. Diese Art der Rückkopplung ist typisch für dynamische Systeme.
Die zugehörigen Gleichungen lauten:
Zustandsgleichungen
Geschwindigkeit.neu <-- Geschwindigkeit.alt + dt*(ay)
Startwert Geschwindigkeit = 0
Höhe.neu <-- Höhe.alt + dt*(vy)
Startwert Höhe = 1
Zustandsänderungen
ay = -Höhe
vy = Geschwindigkeit
Das Diagramm rechts zeigt das bekannte Verhalten von Ausschlag und Geschwindigkeit.
• Um deutlich zu machen, dass die Beschleunigung von zwei Parametern abhängt,
können zwei Kreise für Konstanten eingefügt werden (Abb. 10). Den Vergleich mit
der analytischen Lösung ermöglicht die Definition einer Funktion der Zeit (theorHöhe),
die nur von den beiden Konstanten Masse und Federkonstante abhängt.
Die entsprechenden Gleichungen lauten:
5 30. NOVEMBER 2000: NUMERISCHE INTEGRATION 2
26
Abbildung 10: Veränderung des Systems anhand der Parameter Masse und
Federkonstante und Vergleich mit der analytischen Lösung
Zustandsgleichungen
Geschwindigkeit.neu <-- Geschwindigkeit.alt + dt*(ay)
Startwert Geschwindigkeit = 0
Höhe.neu <-- Höhe.alt + dt*(vy)
Startwert Höhe = 1
Zustandsänderungen
ay = -Federkonstante/Masse*Höhe
vy = Geschwindigkeit
Konstanten
Masse = 1
Federkonstante = 1
Zwischenwerte
theorHöhe = cos(Wurzel(Federkonstante/Masse)*Zeit)
Natürlich zeigt sich auch hier das oben besprochene Aufschaukeln numerischer Fehler!
Das Modellbildungssystem ermöglicht also eine einfache Erzeugung der Struktur eines
dynamischen Systems und automatische Darstellung des zeitlichen Verhaltens in Form
von Diagrammen. Die entscheidende Analyse der Struktur und die quantitative Formulierung der Zusammenhänge bleibt aber weiterhin Aufgabe des Benutzers. Es ist deshalb
weitgehend eine Frage des persönlichen Geschmacks und der Vorkenntnisse, ob man sich
für die eigene Erstellung eines Pascal-Programmes und die Benutzung eines Modellbildungssystems entscheidet.
In dieser Vorlesung werden beide Arten der Programmierung parallel verwendet.
5.4
Übung: Die Berücksichtigung der Reibung
• Tatsächlich ist die Schwingung des Schraubenfederpendels gedämpft: Durch eine
zusätzliche Kraft FR , die Reibungskraft, wird dem System ständig Energie entzogen.
5 30. NOVEMBER 2000: NUMERISCHE INTEGRATION 2
27
Die Reibungskraft führt zu einer ständigen Verringerung der Geschwindigkeit, ihre
Richtung ist also der der Geschwindigkeit entgegengesetzt.
• Diese Kraft ist umso größer, je schneller die Bewegung ist. Nimmt man Proportionalität zwischen Geschwindigkeit und Reibungsbeschleunigung an,
aR ∼ v
=⇒
FR ∼ mv,
(viskose oder Stokessche Reibung)
(23)
ändert sich die Bewegungsgleichung (14) in
Fges = ma
Fg + FR = mẍ
mẍ = −Dx − mρvx
=⇒
ẍ(t) + ρẋ(t) + ω02 x(t) = 0
(24)
• Das exponentielle Abklingen der Amplitude der Schwingung wird zunächst als bekannt vorausgesetzt. Es wird evtl. später noch experimentell demonstriert. Diese
Kenntnis führt zu dem folgenden
Ansatz für die Lösung der Differentialgleichung (24):
x(t) = e−ct (A sin ωt + B cos ωt)
(25)
(26)
Aufgabe: Leiten Sie ab, unter welchen Bedingungen dieser Ansatz eine Lösung der
Differentialgleichung (24) darstellt!
Anleitung:
1. Leisten Sie den Ansatz zweimal nach der Zeit ab.
⇒
⇒
ẋ(t) = −ce−ct (A sin ωt + B cos ωt) + ωe−ct (A cos ωt − B sin ωt)
ẍ(t) = c2 e−ct (A sin ωt + B cos ωt) − cωe−ct (A cos ωt − B sin ωt)
−cωe−ct (A cos ωt − B sin ωt) − ω 2 e−ct (A sin ωt + B cos ωt)
2. Setzen Sie die Ergebnisse in die Differentialgleichung ein. Dabei ergibt sich eine
Gleichung vom Typ
a sin ωt + b cos ωt = 0 für alle t.
Das kann nur richtig sein, wenn beide Koeffizienten Null sind. Aus dieser Bedingung ergeben sich zwei Gleichungen mit den beiden Unbekannten A und
B.
5 30. NOVEMBER 2000: NUMERISCHE INTEGRATION 2
28
Ac2 + 2cωB − Aω 2 − cρA − ωρB + ω02 A = 0
Bc2 − 2cωA − Bω 2 − cρB + ωρA + ω02 B = 0
Umordnen ergibt:
A(c2 − ω 2 − cρ + ω02) + B(2cω − ωρ) = 0
A(−2cω + ωρ) + B(c2 − ω 2 − cρ + ω02 ) = 0
3. Ein bekannter Satz aus der linearen Algebra sagt, dass das lineare homogene
Gleichungssystem für A und B
aA + bB = 0
cA + dB = 0
nur lösbar ist, wenn die Koeffizientendeterminante Null ist:
ad − bc = 0
Aus dieser Bedingung ergeben sich die gesuchten Bedingungen für die Konstanten ω und c.
(c2 − ω 2 − cρ + ω02)2 + (2cω − ωρ)2 = 0
Also müssen beide Summanden einzeln Null sein. Daraus folgt aber:
c=
ρ
2
und
ω 2 = ω02 −
ρ2
4
4. Wie lautet also die Lösung der Differentialgleichung (24)?
Die Bewegungsgleichung (24) kann also mit dem Ansatz (25) tatsächlich
erfüllt werden, wenn
ρ
c=
2
und
ρ2
ω02 −
>0
4
und
ω=
s
ω02 −
ρ2
4
Die allgemeine Lösung der Differentialgleichung (24) lautet also:
− ρ2 t
x(t) = e
(A sin ωt + B cos ωt) mit ω =
s
ω02 −
ρ2
4
6 7. DEZEMBER 2000: GEDÄMPFTE SCHWINGUNGEN
6
29
7. Dezember 2000: Gedämpfte Schwingungen
6.1
Wiederholung und Nachtrag
• Die Modelle für das Modellbildungssystem DYNASYS befinden sich im Netz im
Unterordner dynasys. Eine Diskette mit dem dazu dazu gehörenden Programm
kann bei mir ausgeliehen werden.
• Um eine Differentialgleichung 2. Ordnung
ẍ = ax (x, ẋ)
numerisch zu integrieren, wird sie in ein System gekoppelter Differentialgleichungen
1. Ordnung umgewndelt:
ẋ = vx
v̇x = ax (x, vx )
Dieses Gleichungssystem wird numerisch folgendermaßen gelöst:
ax (t) = f (x(t), vx (t))
x(t + ∆t) = x(t) + vx (t)∆t
v(t + ∆t) = v(t) + ax (t)∆t
(Bewegungsgleichung)
Als Pascal-Quelltext sieht die Lösung folgendermaßen aus:
ax:=f(x,vx)
x:=x+vx*dt
vx:=vx+ax*dt
(* Bewegungsgleichung *)
Bei der Behandlung mit einem Modellbildungssystem wird grafisch das folgende
dynamische System erzeugt,
für das das Programm die folgenden Zeilen generiert:
6 7. DEZEMBER 2000: GEDÄMPFTE SCHWINGUNGEN
30
Zustandsgleichungen
xGeschwindigkeit.neu <-- xGeschwindigkeit.alt + dt*(ax)
Startwert xGeschwindigkeit = 0
x.neu <-- x.alt + dt*(vx)
Startwert x = 1
Zustandsänderungen
ax = -10
vx = xGeschwindigkeit
Hier zeigen sich die beiden Differentialgleichungen 1. Ordnung in den beiden miteinander verkoppelten Flussdiagrammen bzw. in den durch vy = Geschwindigkeit
gekoppelten Gleichungen für die Berechnung der neuen Werte von Höhe und Geschwindigkeit.
6.2
Gedämpfte Schwingungen
• Die allgemeine Lösung der Differentialgleichung (24) lautet, wenn ρ2 < 4ω02:
− ρ2 t
x(t) = e
(A sin ωt + B cos ωt) mit ω =
s
ω02 −
ρ2
4
(27)
• Aufgabe: Zeigen Sie, dass mit den Anfangsbedingungen x(t = 0) := x0 und ẋ(t =
0) := v0 aus der allgemeinen Lösung (27) die folgende spezielle Lösung wird:
ρ
x(t) = e− 2 t
2v0 + ρx0
sin ωt + x0 cos ωt
2ω
(28)
Einsetzen von t = 0 in die Lösung ergibt:
x(0) = 1(0 + B) = x0
=⇒
B = x0
Einsetzen von t = 0 in die 1. Ableitung ergibt:
ẋ(0) = −
ρ
1(0+B)+1(ωA−0) = v0
2
=⇒
A=
v0 + ρ2 B
2v0 + ρx0
=
ω
2ω
• Bei einer linear gedämpften Schwingung ändert sich also die Amplitude exponentiell
mit der Zeit. Das kann man auch umgekehrt ausdrücken: Wenn sich experimentell
ein exponentielles Abklingen einer Schwingung zeigt, ist damit nachgewiesen, dass
die Reibung proportional zur Geschwindigkeit ist!
6 7. DEZEMBER 2000: GEDÄMPFTE SCHWINGUNGEN
31
• Experiment: Um die Abhängigkeit der Reibungskraft von der Geschwindigkeit
zu finden, wird die Dämpfung experimentell untersucht. Um zu prüfen, ob es sich
um ein exponentielles Abklingen der Schwingung handelt, wird an zwei Systemen
gemessen, wie lange es jeweils dauert, bis die Amplitude der Schwingung auf die
Hälfte und auf ein Viertel abgenommen hat (s. Übung):
– Schraubenfederpendel, bei dem die Luftreibung durch eine große kreisrunde
horizontale Pappscheibe vergrößert wurde,
– Pohl’sches Drehpendel, bei dem die Dämpfung über eine Wirbelstrombremse
eingestellt werden kann1 .
Ergebnis: Beim Federpendel klingt die Schwingung schwächer als exponentiell, beim
Drehpendel schneller ab. In beiden Fällen kann es sich also nicht um ein linear
gedämpftes Pendel handeln.
• Diskussion der Lösung der linear gedämpften Schwingung:
– Wenn die Dämpfungskonstante ρ von Null verschieden ist, ist die Frequenz der
Schwingung kleiner, die Schwingungsdauer also größer als bei der ungedämpften Schwingung:
ρ>0
=⇒
ω=
s
ω02 −
ρ2
< ω0
4
⇐⇒
T > T0
(29)
– Diese Abhängigkeit der Frequenz von der Dämpfung ist allerdings sehr schwach:
Eine Vergrößerung der Schwingungsdauer macht sich erst bemerkbar, wenn das
System so stark gedämpft ist, dass es kaum noch schwingt! (s. Übung!)
– Simulation mit Pendel4: Abhängigkeit der Frequenz von der Dämpfung: Vergleich der numerischen Lösung mit der theoretischen Kurve ohne Dämpfung
mit ∆t = 0.1, tmax = 30. (Bei ω0 = 1 ist bis ρ = 1 kaum etwas zu bemerken.)
– Wie sieht die Lösung aus, wenn die Dämpfung so groß ist, dass ρ2 > 4ω02 gilt?
(s. Abb. 11)
• Puh! Es war nicht leicht, diese analytische Lösung zu finden!
Numerisch dagegen ist die Reibung sehr viel einfacher zu berücksichtigen:
ax = −ω02 x
−→
ax = −ω02 x − ρvx
Hier wird zum ersten Mal der Vorteil numerischer Integration deutlich: Analytisch
macht die Berücksichtigung der Reibung eine völlig neue Lösung erforderlich, numerisch muss lediglich ein additiver Zusatzterm eingeführt werden!
• Noch deutlicher wird das bei einer Reibungskraft, die quadratisch mit der Geschwindigkeit wächst: Die zugehörige Differentialgleichung lässt sich analytisch kaum noch
lösen (obwohl das Pendelverhalten sehr ähnlich aussieht, s. Abb. 12!), während die
numerische Lösung ebenso einfach ist wie beim linearen Ansatz.
1
Dieses System werden wir später noch sehr genau untersuchen.
6 7. DEZEMBER 2000: GEDÄMPFTE SCHWINGUNGEN
32
x
t
Abbildung 11: Vergleich linear gedämpfter Schwingungen mit verschiedener Dämpfungskonstante: ρ = 0.0, ρ = 0.5ω0 (Schwingfall), ρ = 2ω0 (aperiodischer Grenzfall), ρ = 4ω0
(Kriechfall)
x
t
Abbildung 12: Vergleich einer linear gedämpften Schwingung mit einer quadratisch
gedämpften (dick): Letzter klingt wesentlich langsamer ab.
6 7. DEZEMBER 2000: GEDÄMPFTE SCHWINGUNGEN
33
Abbildung 13: Die Behandlung des linear gedämpften Pendels mit einem Modellbildungssystem
• Abbildung 13 zeigt die Lösung der Bewegungsgleichung des gedämpften Pendels
mit dem Modellbildungssystem und den Vergleich mit der analytischen Lösung.
Entscheidend ist hier die durch einen Pfeil gekennzeichnete zusätzliche Abhängigkeit
der Beschleunigung ay von der Geschwindigkeit.
Hier zeigt sich, dass die numerischen Fehler so groß sind, dass eine ungedämpfte
Schwingung vorgetäuscht wird. Es wird also höchste Zeit, sich mit der Verbesserung
der numerischen Integration zu befassen!
6.3
Das Halbschritt-Verfahren
• Die zu integrierenden Differentialgleichungen lauten:
ẋ = vx
v̇x = ax (x, vx )
• Ganzschritt-Verfahren (Wiederholung)
a
x(t + ∆t)
vx (t + ∆t)
t
=
=
=
=
a(x(t), vx (t))
x(t) + vx (t)∆t
vx (t) + a∆t
t + ∆t
• Halbschritt-Verfahren
– Grundidee: Statt die Geschwindigkeit des Intervallanfanges zu nehmen, um
den Ort am Intervallende zu approximieren, ist es in der Regel besser, die
Geschwindigkeit in der Intervallmitte zu verwenden:
6 7. DEZEMBER 2000: GEDÄMPFTE SCHWINGUNGEN
r
x
34
r
r
r
∆t
2
∆t
t
Entsprechendes gilt für die Approximation der Geschwindigkeit am Intervallende.
– Die zugehörigen Gleichungen lauten:
a = a(x(t), vx (t))
(Beschleunigung zu Beginn)
hx = x(t) + vx (t) ∆t
2
(Halbschritt)
hvx = vx (t) + a ∆t
2
ha = a(hx , hvx )
(Beschleunigung zur Halbzeit)
x(t + ∆t) = x(t) + hvx ∆t
(30)
Ganzschritt)
vx (t + ∆t) = vx (t) + ha (hx , hvx )∆t
t = t + ∆t
– Ist mit diesem Verfahren überhaupt etwas gewonnen? Schließlich ist nun bei
jedem Integrationsschritt der Rechenaufwand doppelt so groß! Es zeigt sich
jedoch, dass mit dem Halbschritt-Verfahren meist sehr viel bessere Ergebnisse
erzielt werden als mit dem Ganzschritt-Verfahren bei halbierter Schrittweite
(s. Abb. 14).
6.4
Übung
Aufgabe: Beweisen Sie für exponentiell gedämpfte Schwingungen die beioden folgenden
Aussagen:
1. Die Zeitspanne, in der die Amplitude der Schwingung um einen bestimmten Faktor
abnimmt, ist näherungsweise konstant.
e−c(t+tk ) = ke−ct
=⇒
e−ctk = k
=⇒
tk = −
ln k
c
2. Der Quotient aufeinanderfolgender Amplituden ist näherungsweise konstant.
e−c(t+∆t)
= e−c∆t = const
e−ct
6 7. DEZEMBER 2000: GEDÄMPFTE SCHWINGUNGEN
35
x
x0
1.5
1.0
0.5
sr r sr r
rs
r
rs
r
rs
r
8
-0.5
sr
r
sr
16
r
-1.0
sr
24
s
r s
r
s
r
s
s s
r
r
r r
r
r r r
r
r
s r
r
s
r
r
sr
r
r s
r
r
r
s
r
r r
s
32
s
40
t
dt
-1.5
Abbildung 14: Vergleich zwischen Ganzschritt- und Halbschritt-Verfahren: Die mit
dem Halbschritt-Verfahren berechnete Lösung (dicke Punkte) approximiert die korrekte Lösung (dünne Linie ohne Punkte) trotz doppelter Schrittweite wesentlich besser als
die mit dem Ganzschritt-Verfahren berechnete.
Diese beiden Aussagen sind Charakteristika von Exponentialfunktionen, die ohne explizite Kenntnis von Exponentialfunktion und Logarithmus behandelt und untersucht
werden können.
Aufgabe: Bei welcher Dämpfung ist die Schwingungsdauer um 10% größer als die der
ungedämpften Schwingung? Wie sieht dann die Schwingung aus?
• Die Dämpfung ergibt sich Einsetzen:
T = 1.1T0
⇐⇒
ω0 = 1.1ω
=⇒
ω02
= 1.21
ω02
ρ2
−
4
!
ρ2
=⇒
= 0.21ω02
4
=⇒ ρ = 0.92ω0
• Für das Verhältnis aufeinander folgender Amplituden ergibt sich damit:
0.92ω0
πρ
An+1 An − ρ T
−π
e 2 = e− ω = e 1.1ω0 ≈ 0.04
=
Die Schwingung ist also sehr stark gedämpft!
7 14. DEZEMBER 2000: ERZWUNGENE SCHWINGUNGEN
7
36
14. Dezember 2000: Erzwungene Schwingungen
7.1
Wiederholung
• exponentielles Verhalten
• Vergleich analytische – numerische Lösung
• Halbschritt-Verfahren
• Beispiel: Halbschritt-Verfahren beim gedämpften Federpendel
a = −ω02 x(t) − ρv(t)
∆t
hx = x(t) + vx (t)
2
∆t
hvx = vx (t) + a
2
ha = −ω02 hx − ρhvx
x(t + ∆t) = x(t) + hvx ∆t
vx (t + ∆t) = vx (t) + ha ∆t
t = t + ∆t
7.2
Das Runge-Kutta-Verfahren 4. Ordnung
Es gibt weiter verbesserte Verfahren zur numerischen Integration von Differentialgleichungen. Das bekannteste ist das so genannte Runge-Kutta-Verfahren 4. Ordnung2 :
2
Die exakten Gleichungen lauten:
v1
=
v(t)
a1
=
hx
=
hv
=
v2
a2
=
=
hx
=
hv
=
v3
=
a(x(t), vx (t))
∆t
x(t) + v1
2
∆t
v(t) + a1
2
hv
a(hx , hv )
∆t
x(t) + v2
2
∆t
v(t) + a2
2
hv
a3
hx
=
=
a(hx , hv )
x + v3 ∆t
hv
v4
=
=
v + a3 ∆t
hv
a4
=
a(hx , hv )
7 14. DEZEMBER 2000: ERZWUNGENE SCHWINGUNGEN
37
x
x0
1.5
1.0
0.5
sr r
r
sr
r
r
r
r
sr
r
-0.5
-1.0
r
10
r
sr
r
r sr r
r
r rs r
r
r
r s
sr
r
20
r r sr
r
r
rs
r
rs
r
s
r
30 r
40
r
sr
r
s
r
r
r sr r
r
r
s
r
r
s
t
dt
-1.5
Abbildung 15: Vergleich zwischen Halbschritt- und Runge-Kutta-Verfahren: Die mit dem
Runge-Kutta-Verfahren berechnete Lösung (dicke Punkte) approximiert die korrekte
Lösung (dünne Linie ohne Punkte) trotz dreifacher Schrittweite deutlich besser als die
mit dem Halbschritt-Verfahren berechnete.
• Die Grundidee ist dieselbe wie beim Halbschritt-Verfahren: Jeder Zeitschritt wird
in zwei Teilintervall zerlegt.
• Dann werden vier Steigungen berechnet: am Intervallanfang, zwei verschiedene in
der Intervallmitte und am Intervallende.
• Aus diesen Zwischenwerten wird ein Mittel gebildet, in das die Zwischenwerte mit
unterschiedlichen Gewichten eingehen.
• Mit dieser gemittelten Steigung wird schließlich das ganze Intervall überbrückt.
Es zeigt sich, dass trotz des vergrößerten Rechenaufwandes pro Integrationsschritt in
gleicher Rechenzeit deutlich verbesserte Ergebnisse erzielt werden, weil die Schrittweite
start vergrößert werden kann (Abb. 15).
Modellbildungssysteme bieten meist die Option, zwischen Ganzschritt- und RungeKutta-Verfahren zu wählen.
Simulationen:
x =
v
=
∆t
6
∆t
v + (a1 + 2a2 + 2a3 + a4 )
6
x + (v1 + 2v2 + 2v3 + v4 )
7 14. DEZEMBER 2000: ERZWUNGENE SCHWINGUNGEN
38
• mit Pendel4
– Ganzschritt-Verfahren bei ∆t = 0.01
– Runge-Kutta-Verfahren bis ∆t = 0.8
• mit numInteg
7.3
Angeregte Schwingungen
• Alle Schwingungen kommen aufgrund verschiedener Dämpfungsmechanismen zur
Ruhe, wenn ihnen nicht ständig Energie zugeführt wird. Diese Energiezufuhr kann
kontinuierlich geschehen, z.B.
– bei Uhren durch Federn oder Gewichte,
– bei Streichinstrumenten durch den Bogen oder
– beim Quietschen von Kreide, die gleichmäßig über die Tafel gezogen wird,
oder periodisch, z.B.
– beim Ballprellen,
– beim Jojo,
– bei einer schwingenden Lautsprechermembran.
• Eine gedämpfte Federschwingung kann man entdämpfen, z.B. indem man den Aufhängepunkt (Koordinate yA ) periodisch auf- und abbewegt. Die entstehende Schwingung kann man mit folgendem Aufbau untersuchen:
p
r
p
7 14. DEZEMBER 2000: ERZWUNGENE SCHWINGUNGEN
39
Dabei zeigen sich folgende Eigenschaften der erzwungenen Schwingung:
– Nach einer Einschwingzeit, in der das Pendel unregelmäßige Schwingungen
vollführt, schwingt das Pendel stationär (näherungsweise) harmonisch mit der
Frequenz der Anregung. In diesem Zustand wird dem Pendel im zeitlichen
Mittel ebenso viel Energie zugeführt, wie durch Reibung dissipiert wird.
– Die Schwingungsamplitude des stationären Verhaltens ist von der Anregungsfrequenz abhängig: Bei kleinen und großen Anregungsfrequenzen ist die Amplitude klein, in der Nähe der Eigenfrequenz des Pendels groß: Resonanz.
Das Aufschaukeln der Schwingung in der Resonanz kann zur Zerstörung des
Systems führen: Resonanzkatastrophe.
– Die stationäre erzwungene Schwingung weist eine Phasenverschiebung zur Anregung auf: Bei kleinen Anregungsfrequenzen ist sie etwa gleichphasig, bei
großen etwa gegenphasig. Der Übergang geschieht in der Nähe der Resonanzfrequenz – umso schneller, je geringer die Dämpfung ist.
• Die Bewegungsgleichung des angeregten Pendels ist einfach aufzustellen: Aus der
bisherigen Bewegungsgleichung
mÿ = −Dy − mρvy
wird, weil die Länge der Feder sich nun nicht nur durch die Schwingung des Pendelkörpers, sondern auch durch die Bewegung des Aufhängepunktes bei yA ändert:
mÿ = −D(y − yA ) − mρvy
Wird nun der Aufhängepunkt mit der Anregungsfrequenz Ω harmonisch hin- und
herbewegt,
yA = yA0 cos Ωt
dann wird aus der bisherigen Bewegungsgleichung:
ÿ = −ω02 y − ρvy + f cos Ωt mit ω02 =
D
m
und f = ω02 yA0
(31)
• Diese Bewegungsgleichung ist explizit von der Zeit abhängig. Unsere Integrationsverfahren sind aber nur anwendbar bei Differentialgleichungen, deren Koeffizienten nicht von der Zeit abhängen. Dieses Problem läßt sich formal einfach durch
Einführung einer 3. Variablen bzw. eines 3. Freiheitsgrades beseitigen, der Phase
der Anregung p = Ωt. Damit läßt sich die Bewegungsgleichung schreiben als:
ẏ = vy
v̇y = −ω02 y − ρvy + f cos p
ṗ = Ω
(32)
7 14. DEZEMBER 2000: ERZWUNGENE SCHWINGUNGEN
40
Damit läßt sich die angeregte Schwingung ebenso wie die gedämpfte Schwingung
untersuchen. Allerdings wird der Phasenraum dreidimensional (y, ẏ, p) – mit
weitreichenden Konsequenzen, wie wir noch sehen werden.
• Die Bewegungsgleichung (31) läßt sich ganz entsprechend wie die des gedämpften Pendels analytisch lösen. Allerdings ist die Anforderung an das Durchhalte”
vermögen“ etwas größer.
Die Beobachtung des Experimentes legt folgenden Ansatz für den stationären Fall
nahe:
Ansatz:
y(t) = A(Ω) sin Ωt + B(Ω) cos Ωt
In diesem Ansatz wird die experimentelle Erfahrung berücksichtigt, dass die Frequenz der stationären Schwingung mit der Anregungsfrequenz Ω übereinstimmt und
sich Amplitude und Phasenlage der Schwingung mit der Anregungsfrequenz ändern:
Wie wir bei der Behandlung gedämpfter Schwingungen gesehen haben, sind sowohl
die Schwingungsamplitude, als auch die Phasenlage in den beiden Faktoren A und
B enthalten.
7.4
Übung: Analytische Lösung
• Die Abhängigkeit der Amplituden A und B von der Anregungsfrequenz kann man
bestimmen, indem man (wie früher) den Ansatz in die Bewegungsgleichung einsetzt
und die Koeffizienten von Sinus und von Kosinus Null setzt.
• Zweimaliges Differenzieren des Ansatzes ergibt:
y = A sin Ωt + B cos Ωt
ẏ = ΩA cos Ωt − ΩB sin Ωt
ÿ = −Ω2 A sin Ωt − Ω2 B cos Ωt
• Einsetzen in die Differentialgleichung ergibt:
=⇒
sin Ωt(−Ω2 A − ρΩB + ω02 A) + cos Ωt(−Ω2 B + ρΩA + ω02B − f ) = 0
(
(ω02 − Ω2 )A − ρΩB=0 =⇒ A = ω2ρΩ
2B
0 −Ω
=⇒
2
2
ρΩA + (ω0 − Ω )B=f
ρ2 Ω2
=⇒
B + (ω02 − Ω2 )B = f =⇒
ω02 − Ω2
(ω02 − Ω2 )f
B
=
(antisymmetrisch in ω02 − Ω2 ) (33)
(ρΩ)2 + (ω02 − Ω2 )2
ρΩf
A
=
(symmetrisch in ω02 − Ω2 )
(34)
2
(ρΩ) + (ω02 − Ω2 )2
Beide Faktoren – und damit auch die Amplitude der stationären Schwingung! – sind
also proportional zur Amplitude f der Anregung.
7 14. DEZEMBER 2000: ERZWUNGENE SCHWINGUNGEN
41
• Aufgaben für zu Hause:
1. Berechnen Sie mit Hilfe dieses Ergebnisses, wie die Amplitude der stationären
Schwingung und ihre Phasenlage von der Anregungsfrequenz Ω abhängen.
2. Stellen Sie die beiden Funktionen grafisch dar.
3. evtl.: Stellen Sie auch die Funktionen A(Ω) und B(Ω) grafisch dar.
8 4. JANUAR 2001: DAS PERIODISCH ANGEREGTE PENDEL
42
A,B
f
5
0.5
1.0
1.5
2.0
2.5
Ω
ω0
Abbildung 16: Elastische Amplitude A (dick) und absorbierende Amplitude B
8
4. Januar 2001: Das periodisch angeregte Pendel
8.1
Wiederholung
• Schwingungen können durch periodische Anregung entdämpft werden. Nach einer
unregelmäßigen Einschwingphase schwingen sie dann stationär mit der Frequenz Ω
der Anregung.
• Die Bewegungsgleichung für ein harmonisch angeregtes Federpendel lautet:
ÿ = −ω02 y − ρvy + f cos Ωt mit ω02 =
D
und f = ω02 yA0
m
(35)
• Um die stationäre Lösung dieser Differentialgleichung zu finden macht man den
Ansatz:
y(t) = A(Ω) sin Ωt + B(Ω) cos Ωt
Einsetzen in die Bewegungsgleichung ergibt die folgenden Abhängigkeiten der elastischen Amplitude A und der absorbierenden Amplitude B von Amplitude f
und Frequenz Ω der Anregung:
ρΩf
+ (ω02 − Ω2 )2
(ω02 − Ω2 )f
B =
(ρΩ)2 + (ω02 − Ω2 )2
A =
(ρΩ)2
(symmetrisch in ω02 − Ω2 )
(36)
(antisymmetrisch in ω02 − Ω2 )
(37)
8 4. JANUAR 2001: DAS PERIODISCH ANGEREGTE PENDEL
43
y0
f
5
0.5
1.0
1.5
2.0
2.5
Ω
ω0
Abbildung 17: Die Schwingungsamplitude y0 des harmonisch angeregten Pendels als
Funktion der Anregungsfrequenz bei unterschiedlicher Dämpfung (ρ = 0.1ω0 (dick) und
ρ = 0.3ω0)
8.2
Eigenschaften der stationären Schwingung
• Den Ausdrücken (36) und (37) sieht man folgende Eigenschaften der stationären
Schwingung an:
– Für ω0 ≈ Ω werden beide Amplituden – und damit die Schwingungsamplitude!
– groß (weil dann der Nenner klein wird): Resonanz.
– Für das ungedämpfte Pendel (ρ = 0) ist A = 0, die stationäre Schwingung
ist also in Phase mit der Anregung. Bei Resonanz (ω0 = omega) würde die
Schwingungsamplitude unendlich groß werden: Resonanzkatastrophe.
– Bei ω0 = Ω ist B = 0, die stationäre Schwingung hinkt also um
Viertelperiode hinter der Anregung her.
π
2
oder eine
• Schwingungsamplitude y0 und Phasenverschiebung ϕ erhält man durch Koeffizientenvergleich:
y = y0 cos(Ωt + ϕ) = −y0 sin ϕ sin Ωt + y0 cos ϕ cos Ωt
= A sin Ωt + B cos Ωt
=⇒
(
−y0 sin ϕ=A
y0 cos ϕ=B
)
=⇒
(38)
8 4. JANUAR 2001: DAS PERIODISCH ANGEREGTE PENDEL
44
ϕ[◦ ]
0.5
1.0
1.5
2.0
2.5
Ω
ω0
-90
Abbildung 18: Die Phasenverschiebung ϕ des harmonisch angeregten Pendels als Funktion
der Anregungsfrequenz bei unterschiedlicher Dämpfung (ρ = 0.1ω0 (dick) und ρ = 0.3ω0 )
y0 =
√
tan ϕ = −
A2 + B 2
f
(36),(37)
=
q
(ρΩ)2 + (ω02 − Ω2 )2
A
ρΩ
= 2
B
Ω − ω02
(39)
(40)
oder besser (weil auch eine Phasenverschiebung von mehr als 90◦ richtig wiedergegeben wird):
tan
1 − cos ϕ (38) B − y0
ϕ
=
=
2
sin ϕ
A
=
q
(ω02 − Ω2 ) −
(ρΩ)2 + (ω02 − Ω2 )
ρΩ
(41)
(42)
• Diskussion:
– Je größer die Dämpfung ist, desto kleiner ist – bei jeder Anregungsfrequenz! –
die Amplitude der stationären Schwingung (Abb. 17).
– Ω=0
=⇒
y0 =
f
ω0
– Die stationäre Schwingung hat in der Nähe der Eigenfrequenz ω0 des ungedämpften Pendels die größte Amplitude.
Aufgabe: Zeigen Sie, dass das Maximum erreicht wird bei:
Ω=
s
ω02 −
ρ2
2
8 4. JANUAR 2001: DAS PERIODISCH ANGEREGTE PENDEL
45
f2
(ρΩ)2 + (ω02 − Ω2 )2
2ρ2 Ω − 4Ω(ω02 − Ω2 )
= −f 2
((ρΩ)2 + (ω02 − Ω2 )2 )2
y02 =
=⇒
=⇒
dy02
=0
dΩ
dy02
dΩ
2ρ2 − 4(ω02 − Ω2 ) = 0
⇐⇒
ω02 − Ω2 =
=⇒
ρ2
2
Die Resonanzfrequenz stimmt damit weder mitqder Eigenfrequenz ω0 des un2
gedämpften, noch mit der Eigenfrequenz ω = ω02 − ρ4 des gedämpften Pendels exakt überein. Allerdings sind die Unterschiede bei nicht zu großen Dämpfungen gering.
– Exakt bei Ω = ω0 beträgt die Phasenverschiebung ϕ = − π2 (s.o.). Der Übergang zwischen ϕ = 0 bei kleinen zu ϕ ≈ −π bei großen Anregungsfrequenzen
geschieht umso schneller, je kleiner die Dämpfung ist (Abb. 18).
8.3
Übung: Phasendiagramme
Aufgabe: Konstruieren Sie ein so genanntes Phasendiagramm (v = v(x)) eines ungedämpften Federpendels! Dabei wird die Geschwindigkeit des Pendelkörpers über seiner
Auslenkung aufgetragen.
Die y-Achse zeige senkrecht nach oben, ihr Ursprung befinde sich in der Gleichgewichtsposition des Pendels. Die Uhr startet, wenn sich das Pendel im oberen Umkehrpunkt
befindet.
1. qualitative Vorhersage: Welche ungefähre Gestalt hat die Kurve, und wie wird sie
durchlaufen?
Lösung durch punktweises Konstruieren für v0 = 0:
vx 4
r
r
3
p (Start mit Anfangsgeschwindigkeit)
r
5
r
r
1
x
2
(a) Zu Beginn ist die Auslenkung maximal und die Geschwindigkeit Null.
(b) Beim 1. Nulldurchgang ist die Auslenkung Null und die Geschwindigkeit negativ extremal.
(c) Im unteren Umkehrpunkt ist die Auslenkung minimal und die Geschwindigkeit
wieder Null.
8 4. JANUAR 2001: DAS PERIODISCH ANGEREGTE PENDEL
46
Abbildung 19: Phasendiagramm einer ungedämpften harmonischen Schwingung,
erzeugt mit Programm HarmSch9
(d) Beim 2. Nulldurchgang ist die Auslenkung wieder Null und die Geschwindigkeit
positiv extremal.
(e) Ist beim Start die Geschwindigkeit positiv, dann beginnt das Diagramm an
anderer Stelle, und es ergibt sich eine größere Trajektorie.
Es ergibt sich eine geschlossene Kurve, die symmetrisch zur x- und zur y-Achse ist.
2. Berechnen Sie die Kurve!
Vermutung: Die Trajektorie formt eine Ellipse. Beweis:
=⇒
oder
x = x0 cos ωt ∧ vx = −ωx0 sin ωt
ω 2 x2 + vx2 = ω02 x20
x2
vx2
+
= 1
x20 (ωx0 )2
(43)
Hausaufgaben:
1. Was für Kurven ergeben sich für dasselbe Pendel bei verschiedenen Anfangsbedingungen?
Die Frage ist vollständig beantwortet, wenn
(a) drei unterschiedliche Trajektorien in ein Diagramm eingezeichnet und
(b) durch ein oder zwei Sätze die wesentlichen Charakteristika der Kurven beschrieben sind.
8 4. JANUAR 2001: DAS PERIODISCH ANGEREGTE PENDEL
47
2. Ein idealer Flummy springe zwischen zwei horizontalen Platten vertikal hin und her.
Wie sehen die Phasendiagramme der möglichen Bewegungen aus?
9 11. JANUAR 2001: EINSCHWINGVORGANG UND PHASENDIAGRAMME
9
48
11. Januar 2001: Einschwingvorgang und Phasendiagramme
9.1
Experimente mit dem Pohl’schen Drehpendel
• Das Drehpendel wurde von dem berühmten Göttinger Experimentalphysiker R. W. Pohl
für die Demonstration gedämpfter und erzwungener harmonischer Schwingungen
entwickelt.
ϕA
ϕ
Das Drehpendel besteht aus einer Unruhe“, die über eine Spiralfeder elastisch an
”
eine Stange gekoppelt ist, die mit einem Exzenter harmonisch verdreht werden kann.
Eingestellt werden können die Dämpfung der Schwingungen über den Strom durch
eine Wirbelstrombremse, die Amplitude der Anregung und die Anregungsfrequenz.
• Demonstrationen:
– Die Schwingungsdauer ist unabhängig von der Amplitude,
T =
9s
,
5
die Schwingung ist also harmonisch.
– Bei Anregung stimmt die Frequenz der stationären Schwingung mit der Anregungsfrequenz überein.
– Bei kleiner Dämpfung schwingt das Pendel lange Zeit scheinbar regellos mit
wechselnder Amplitude hin und her (Einschwingvorgang), bevor es sich in eine
stationäre Schwingung mit konstanter Amplitude einschwingt.
– Bei kleinen Anregungsfrequenzen schwingt das Rad mit kleinen Amplituden in
Phase mit der Anregung.
– Bei großen Anregungsfrequenzen schwingt das Rad mit kleinen Amplituden
gegenphasig zur Anregung.
– Stimmen Anregungsfrequenz und Eigenfrequenz überein, schwingt das Rad
besonders heftig und läuft um ϕ ≈ π2 hinter der Anregung her (Resonanz).
9 11. JANUAR 2001: EINSCHWINGVORGANG UND PHASENDIAGRAMME
9.2
49
Der Einschwingvorgang
Die bisher gefundene Lösung der Bewegungsgleichung des angeregten Pendels beschreibt
nur das Endverhalten: Das Pendel schwingt harmonisch mit der Frequenz der Anregung
und in einer festen Phasenbeziehung zu ihr. Dieses Verhalten nimmt das System unabhängig von den gewählten Anfangsbedingungen an. Man sagt: Das System vergisst
seine Anfangsbedingungen.
Das kompliziert und scheinbar regellose Einschwingverhalten wird also durch diese
Lösung nicht beschrieben. Überraschenderweise lässt sich jedoch auch die Beschreibung
dieses Verhaltens nun sehr leicht finden: Die allgemeine Lösung der Bewegungsgleichung
ist nämlich die Summe aus der speziellen Lösung yi der inhomogenen Gleichung und der
allgemeinen Lösung yh der homogenen Gleichung (ohne Antrieb), die wir bereits kennen
(28):
=⇒
ÿ + ρẏ +
y =
=
=
=
yh + yi
(ÿh + ÿi ) + ρ(ẏh + ẏi ) + ω02 (yh + yi )
(ÿh + ρẏh + ω02 yh ) + (ÿi + ρẏi + ω02yi )
0 + f cos Ωt
ωo2 y
Die allgemeine Lösung ist also eine Superposition aus der gedämpften Schwingung mit
der Frequenz ω und der stationären Schwingung mit der Frequenz Ω der Anregung, also
z.B.:
ρ
y = yh0 e− 2 t cos ωt + yi0 cos(Ωt + ϕ)
Damit haben wir die allgemeine Lösung der Bewegungsgleichung des harmonisch angeregten Pendels gefunden:
Einsetzen der Anfangsbedingungen y(0) = y0 und ẏ(0) = v0 in den allgemeinen Ansatz
ρ
y(t) = e− 2 t (a sin ωt + b cos ωt) + A sin Ωt + B cos Ωt
ergibt:
− ρ2 t
y(t) = e
2v0 + ρ(y0 − B) − 2ΩA
2ω
!
sin ωt + (y0 − B) cos ωt + (A sin Ωt + B cos Ωt)(44)
Dabei sind x0 die Anfangsauslenkung, v0 die Anfangsgeschwindigkeit des Pendels und
ω0 =
A=
s
D
,
m
ω=
,
B=
ρΩf
(ρΩ)2 + (ω02 − Ω2 )2
s
ρ2
,
4
(ω02 − Ω2 )f
ω02 −
(ρΩ)2 + (ω02 − Ω2 )2
Solange die gedämpfte Schwingung noch nicht abgeklungen ist, kommt es zur Interferenz zwischen zwei Schwingungen mit den unterschiedlichen Frequenzen ω und Ω. Dieser
so genannte Einschwingvorgang kann bei schwach gedämpfter Schwingung sehr lange
dauern und ziemlich chaotisch aussehen – insbesondere, wenn die beiden Frequenzen nahe
beieinander liegen (s. Abb. 20).
9 11. JANUAR 2001: EINSCHWINGVORGANG UND PHASENDIAGRAMME
50
y
10
40
80
120
160
t[s]
-10
Abbildung 20: Einschwingvorgang bei schwach gedämpftem Pendel (x0 = 10, v0 = 0, ρ =
0.05ω0 , f = 0.2, Ω = 0.8ω0 , tmax = 200s)
9.3
Übung
• Trajektorien harmonischer Schwingungen mit verschiedenen Anfangsgeschwindigkeiten:
– Alle Trajektorien sind Ellipsen mit demselben Achsenverhältnis von
a
b
=
y0
.
ω0 y 0
– Verschiedene Trajektorien schneiden sich also nicht.
• Aufgabe: Wie sehen die Trajektorien im Phasendiagramm eines gedämpften harmonischen Pendels aus?
Bei Berücksichtigung der Dämpfung spiralt die Trajektorie in den Ursprung (Abbildung 22).
• Aufgabe: Welche Trajektorien können sich bei einem angeregten Pendel ergeben?
Zur stationären Schwingung gehört die Ellipse einer harmonischen Schwingung. Der
Einschwingvorgang, die Überlagerung der beiden Teilschwingungen also, stellt sich
meist als ein Hineinspiralen in diese Ellipse dar (Abbildungen 23 und 24), kann aber
auch ziemlich chaotisch aussehen (Abbildung 25).
• Hüpfender Flummy
– Orientiert man die y-Achse senkrecht nach oben, setzt den Nullpunkt auf die
untere Platte und nennt die Geschwindigkeit des Fluumies beim Absprung von
der unteren Platte v0 , dann gilt:
9 11. JANUAR 2001: EINSCHWINGVORGANG UND PHASENDIAGRAMME
51
vy
y
Abbildung 21: Trajektorien eines ungedämpften harmonischen Pendels für verschiedene
Gesamtenergien
vy
y
Abbildung 22: Trajektorie eines gedämpften harmonischen Pendels
9 11. JANUAR 2001: EINSCHWINGVORGANG UND PHASENDIAGRAMME
52
vy
y
Abbildung 23: Trajektorie eines angeregten harmonischen Pendels
vy
y
Abbildung 24: Trajektorie eines angeregten harmonischen Pendels mit anderen Anfangsbedingungen als in Abb. 23
9 11. JANUAR 2001: EINSCHWINGVORGANG UND PHASENDIAGRAMME
53
vy
y
Abbildung 25: Trajektorie eines angeregten harmonischen Pendels mit anderer Anregungsfrequenz als in Abb. 23
g
y = v0 t − t2
2
vy = v0 − gt
=⇒
q
vy = ± v02 − 2gy
– Die Trajektorien sind also nach links offene Wurzelparabeln, deren Scheitel bei
v2
ymax = 2g0 liegt.
– Die beiden Wände schneiden aus diesen Trajektorien die Teile aus, die zwischen ihnen liegen. An den Wänden wird der Flummy ideal reflektiert, d.h.
seine Geschwindigkeit wechselt das Vorzeichen, d.h. der Zustandspunkt auf
der Trajektorie wird an der y-Achse gespiegelt.
Hausaufgabe: Was bedeuten die Schnittpunkte in der Trajektorie der angeregten
Schwingung (Abb. 25)?
10 18. JANUAR 2001: SIMULATION UND EXPERIMENT
54
vy
d
y
Abbildung 26: Trajektorien eines idealen Flummies, der zwischen zwei horizontalen
Wänden senkrecht hin- und herspringt, für verschiedene Gesamtenergie
10
10.1
18. Januar 2001: Simulation und Experiment
Angeregte Schwingungen im grafischen Modellbildungssystem
• Die Lösung der Bewegungsgleichung (Gleichung (31), S. 39) des angeregten harmonischen Pendels war noch analytisch möglich, aber bereits sehr ziemlich schwierig. Tatsächlich lassen sich kompliziertere Bewegungsgleichungen fast nie analytisch
lösen. Wir werden deshalb von nun an fast ausschließlich numerische Lösungsverfahren anwenden.
• Die numerische Lösung der inhomogenen Bewegungsgleichung ist kaum schwieriger
oder zeitaufwändiger als die der homogenen Gleichung: Wandelt man nämlich die
Differentialgleichung 2. Ordnung in ein System gekoppelter Differentialgleichungen
1. Ordnung um (s. Gleichungen (32), S. 39), dann äußert sich die Anregung in einer
zusätzlichen Gleichung
ṗ = Ω.
• Im grafischen Modell äußert sich das in einer zusätzlichen Zustandsgröße mit entsprechendem Zufluss“ (Abb. 27).
”
• Die zugehörigen Gleichungen lauten:
Zustandsgleichungen
Geschwindigkeit.neu <-- Geschwindigkeit.alt + dt*(ay)
Startwert Geschwindigkeit = 0
Höhe.neu <-- Höhe.alt + dt*(vy)
Startwert Höhe = 0
10 18. JANUAR 2001: SIMULATION UND EXPERIMENT
55
Abbildung 27: Grafisches Modell des gedämpften Pendels (links) und seine Erweiterung
zum angeregten Pendel (rechts)
Phase.neu <-- Phase.alt + dt*(OmegaA)
Startwert Phase = 0
Zustandsänderungen
ay = -Federkonstante/Masse*Höhe-rho*Geschwindigkeit+fA*cos(Phase)
vy = Geschwindigkeit
OmegaA = Omega_omega0*Wurzel(Federkonstante/Masse)
Konstanten
Federkonstante = 1
Masse = 1
rho = 0.05
fA = 1
Omega_omega0 = 0.9
Dabei entsprechen fA der Anregungsamplitude f und OmegaA der Anregungsfrequenz Ω. Die Anregungsfrequenz kann mit dem Parameter Omega omega0 als Vielfaches der Eigenfrequenz ω0 eingegeben werden.
• Mit diesem Modell können die in Abb. 28 oben und Mitte gezeigten Phasendiagramme erzeugt werden.
• Numerisch können die Bewegungsgleichungen auch dann sehr leicht gelöst werden,
wenn sie nichtlinear sind. Als Beispiel betrachten wir eine nichtlineare Feder, bei der
die rücktreibende Kraft nicht proportional zur Auslenkung, sondern proportional
zum Quadrat der Auslenkung ist:
FF = −ω02 x
−→
FF = −ω02 |x|x.
Man kann dabei an eine Feder denken, die bei kleinen Auslenkungen sehr weich ist,
dann aber zunehmend härter wird.
10 18. JANUAR 2001: SIMULATION UND EXPERIMENT
56
Abbildung 28: Mit dem grafikbasierten Modellbildungssystem DYNASYS erzeugte Phasendiagramme (ω02 = 1, ρ = 0.02ω0 ): oben: gedämpfte Schwingung, Mitte: angeregte harmonische Schwingung (Ω = 0.9ω0 , FF = −ω02 x), unten: angeregte anharmonische Schwingung (Ω = 0.9ω0 , FF = −ω02 |x|x)
10 18. JANUAR 2001: SIMULATION UND EXPERIMENT
57
Wie Abbildung 28 unten zeigt, entsteht dabei eine ganz neue – stationäre! – Schwingungsfigur. Solche komplexen Verhaltensmuster werden uns im zweiten Teil dieser
Veranstaltung beschäftigen.
10.2
Phasenraum und Zustandsraum, Attraktoren
Offensichtlich sind in vielen Fällen Phasendiagramme besser als Ort-Zeit-Diagramme geeignet, eine Übersicht über das (Langzeit-) Systemverhalten zu gewinnen. Tatsächlich
werden wir bei der Untersuchung der komplexen Verhaltensmuster nichtlinearer Systeme
sehr häufig Phasendiagramme und Zustandsdiagramme benutzen. Deshalb hier zunächst
einige grundsätzliche Bemerkungen dazu:
• Die Trajektorien sind zusammenhängende Kurven.
Das ist klar: Es wird vorausgesetzt, daß die Zeit kontinuierlich verläuft und die
Ortskoordinaten stetige (sogar zweimal differenzierbare) Funktionen der Zeit sind.
• Die Trajektorien im Phasenraum des gedämpften Pendels können sich nicht schneiden: Ein Schnittpunkt würde ja bedeuten, daß ein und derselbe Anfangszustand zu
zwei verschiedenen Verhaltensweisen des Systems führen würde.
• Das Phasendiagramm des Einschwingvorganges einer erzwungenen Schwingung zeigt
dagegen viele Schnittpunkte (s. Abb. 28, Mitte): Dieselben Werte von Auslenkung
und Geschwindigkeit können offensichtlich zu unterschiedlichem Systemverhalten
führen. Das liegt daran, dass das Verhalten zusätzlich vom momentanen Zustand
der Anregung abhängt! Das zukünftige Verhalten des Systems ist deshalb erst dann
festgelegt, wenn zusätzlich zu Auslenkung und Geschwindigkeit auch der Zustand
der Anregung festgelegt ist. Man sagt: Der Zustandsraum des angeregten Pendels
ist dreidimensional.
Wenn man die Phase der Anregung als zusätzliche Achse dem Phasendiagramm hinzufügt, treten keine Schnittpunkte mehr auf. Abbildung 29 zeigt die Abb. 28 unten
entsprechende Trajektorie eines Einschwingvorganges im Zustandsraum. Da nur die
ersten 20 Anregungsperioden gezeichnet wurden, ist das stationäre Endverhalten
noch nicht gut zu erkennen. Trotzdem ist nur zu ahnen, dass die Trajektorie keinen
Schnittpunkt hat. Ein ähnliches Bild zeigt das Titelbild dieses Vorlesungsskriptes.
• Der Phasenraum wird von den Systemvariablen (Freiheitsgraden) des Systems aufgespannt, die das System vollständig beschreiben, die also eine eindeutige Vorhersage
ermöglichen. Deshalb gilt:
Trajektorien im Zustandsraum schneiden sich nicht.
• Bei Systemen mit nur zwei Freiheitsgraden, wie dem gedämpften Pendel, sind deshalb nur drei verschiedene Langzeitverhaltensweisen möglich:
1. Das System kommt zur Ruhe (genauer: ins Gleichgewicht!): Alle Freiheitsgrade
nehmen konstante Werte an, die Trajektorie zieht sich im Phasenraum auf einen
Punkt zusammen (s. Abb. 22, S. 51).
10 18. JANUAR 2001: SIMULATION UND EXPERIMENT
58
Abbildung 29: Dreidimensionale Darstellung einer Trajektorie im Zustandsraum.
vy
y
Abbildung 30: Sich durch ständig zugeführte Energie aufschaukelnde Schwingung, hier
simuliert durch eine negative Dämpfungskonstante
10 18. JANUAR 2001: SIMULATION UND EXPERIMENT
59
2. Das System divergiert: Mindestens ein Freiheitsgrad des Systems strebt gegen
unendlich. Die Trajektorie läuft wieder gegen einen Punkt – nämlich gegen ∞
(s. Abb. 30).
3. Das System nimmt ein stationäres Verhalten an: Alle Freiheitsgrade variieren periodisch, und die Trajektorie im Phasenraum wird zu einer (einfach)
geschlossenen Kurve (s. Abb. 23, Abb. 24, S. 52).
Da das Systemverhalten von diesen Grenzfiguren im Phasenraum geradezu angezogen wird, nennt man diese Gestalten Attraktoren. Für Systeme mit zwei Freiheitsgraden gibt es nur zwei mögliche Arten von Attraktoren: Den Punktattraktor
(incl. den ∞-Attraktor) und den Grenzzyklus!
10.3
Die Bewegungsgleichung des Drehpendels
Wenn mit Hilfe von Bewegungsgleichungen und ihrer (numerischen oder analytischen)
Integration das Verhalten eines Systems verhergesagt werden soll, dann müssen die Systemparameter, die die Gleichung enthält, mit denen des realen Systems übereinstimmen. Nur dann kann Übereinstimmung zwischen Experiment und Simulation erwartet
bzw. – wenn systematische Abweichungen beobachtet werden – nach Fehlern oder notwendigen Erweiterungen gesucht werden.
Deshalb soll nun am Beispiel des Drehpendels die Aufstellung der angepassten Bewegungsgleichung und, in den folgenden Abschnitten, die Messung der Systemparameter
geübt werden.
• Für Drehbewegungen lautet die Newtonsche Bewegungsgleichung:
M = Θϕ̈.
(45)
Dabei ist Θ das Trägheitsmoment des rotierenden Körpers bezüglich der DrehachP
se (Θ = mi ri2 ), ϕ seine Auslenkung aus der Ruhelage (im Bogenmaß), gemessen
~ = ~r × F~ , |M| =
gegen die Vertikale, und M das angreifende Drehmoment (M
rF sin α)3 .
• Die Unabhängigkeit der Schwingungsdauer von der Amplitude zeigt, dass das von
der Feder erzeugte rücktreibende Drehmoment proportional zur Verformung der
Feder ist (sonst gäbe es keine harmonische Schwingung!):
M = −D∆ϕ
3
(46)
Diese Definition trägt der Erfahrung Rechnung, dass man einen Körper um so schneller in Drehbewegung setzen kann, je größer die Kraft ist, die man auf ihn ausübt, dass die Drehbeschleunigung aber
auch umso größer ist, je weiter von der Drehachse die Kraft angreift und je näher der Winkel zwischen
Kraft und Kraftarm bei π2 liegt.
10 18. JANUAR 2001: SIMULATION UND EXPERIMENT
60
• Im einfachsten Fall (lineares Pendel ohne Dämpfung und Anregung) hat das Rad
also die folgende Bewegungsgleichung:
Θ0 ϕ̈ = −D(ϕ − ϕA )
Dabei ist ϕA die Auslenkung der Anregungsstange aus der Senkrechten, ϕ − ϕA also
die Verformung der Feder.
• Nimmt man geschwindigkeitsproportionale Dämpfung an, dann erweitert sich die
Bewegungsgleichung zu
Θ0 ϕ̈ = −D(ϕ − ϕA ) − β ϕ̇
(Wir haben früher im Experiment gesehen, dass diese Annahme nur sehr grob erfüllt
ist!)
• Regt man das Pendel harmonisch an,
ϕA = α0 cos Ωt,
und führt man die folgenden Hilfsgrößen ein:
ρ :=
β
D
Dα0
, ω02 =
, F =
,
Θ0
Θ0
Θ0
(47)
dann ergibt sich schließlich die Bewegungsgleichung des Rades zu
ϕ̈ + ρϕ̇ + ω02 ϕ = F cos Ωt
10.4
(48)
Übung: Experimentelle Bestimmung der Systemparameter
Um eine realistische Simulation des Pendelverhaltens erzeugen zu können, müssen die
Systemparameter des Pohl’schen Rades zu genau wie möglich experimentell bestimmt
werden:
• Die Federkonstante D kann bestimmt werden, indem das Rad um einen festen Winkel ϕ ausgelenkt wird und dabei die Kraft F mit einem Federkraftmesser und der
Kraftarm (Abstand des Angriffspunktes von der Drehachse) rF gemessen werden.
Dabei ergibt sich typischerweise:
D=
F rF
0.37N · 0.07m
=
= 0.0165Nm.
π
ϕ
2
(49)
• Das Trägheitsmoment des Rades erhält man, indem man die Frequenz ω0 der freien
Schwingung des Rades ohne Unwucht mißt. Dabei ergibt sich (mit T0 = 1.8s) z.B.:
ω02 =
D
Θ0
=⇒
Θ0 =
T02
D = 1.35 · 10−3 kgm2 .
4π 2
(50)
10 18. JANUAR 2001: SIMULATION UND EXPERIMENT
61
• Die Amplitude der Anregung wird gemessen, indem die maximale Auslenkung der
Stange auf beiden Seiten eingestellt und der zugehörige Gleichgewichtswinkel abgelesen wird. Dabei ergeben sich zwei verschiedene extremale Amplituden, da die
Pleuelstange“ an verschiedenen Stellen der Stange befestigt werden kann:
”
- -11 Skt und 2 Skt bzw.
- -7 Skt und 1 Skt.
122 Skt entsprechen einem Winkel von π2 . Damit ergeben sich die extremalen Amplituden zu
α0max =
α0min =
6.5Skt
24.4Skt
π
4Skt
24.4Skt
π
= 0.0837
(51)
= 0.0515
(52)
Das lässt sich auch folgendermaßen schreiben:
α0 =
(
0
0.0193 + 0.0322f
für
f = 0,
für 1 ≤ f ≤ 2.
(53)
• Messung der Dämpfung als Funktion der Stromstärke: ρ = ρ(I)
– Bei I = 0A beträgt die Halbwertzeit der Schwingungsamplitude etwa 80s.
– Bei I = 200mA nimmt die Amplitude nach 10 Schwingungen von 150 Skt auf
73 Skt ab.
– Bei I = 500mA nimmt die Amplitude in 3 Schwingungen von 150 Skt auf 45
Skt ab.
– Bei I = 800mA geht die Amplitude in einer Schwingung von 150 Skt auf 54
Skt ab.
Hausaufgaben:
1. Berechnen Sie unter der Annahme konstanter Schwingungsdauer (wir wissen,
dass diese Annahme recht gut erfüllt ist!) die zugehörigen Werte der Dämpfungskonstanten ρ!
2. Stellen Sie die Abhängigkeit der Dämpfung von der Stromstärke grafisch dar!
3. Finden Sie mit Hilfe eines Potenzreihenansatzes eine Ausgleichskurve ρ = ρ(I)!
11 25. JANUAR 2001: NICHTLINEARITÄT
11
11.1
62
25. Januar 2001: Nichtlinearität
Wiederholung und Ergänzung
• Zustandsraum:
– Der Phasenraum wird aufgespannt von den Orts- und Geschwindigkeitskoordinaten des Systems.
– Der Zustandsraum wird von der kleinsten Zahl von Variablen des Systems aufgespannt, sodass ein Punkt in diesem Raum den Zustand des Systems eindeutig
bestimmt in dem Sinne, dass das zukünftige (und vergangene) Verhalten des
Systems eindeutig vorhergesagt werden kann.
– Die Anzahl der Dimensionen des Zustandsraumes nennt man auch die Anzahl
der Freiheitsgrade des Systems.
Beispiele:
∗
∗
∗
∗
∗
∗
senkrechter Wurf: 2 Freiheitsgrade (y, vy ),
schiefer Wurf: 2 Freiheitsgrade (x, vx , y, vy )
beliebige Bewegungen eines Massenpunktes im Raum: 6 Freiheitsgrade,
radioaktiver Zerfall: 1 Freiheitsgrad (N),
Zwei gekoppelte elektrische Schwingkreise: 4 Freiheitsgrade (I1 , I˙1 , I2 , I˙2 ),
System aus zwei durch Gravitation miteinander wechselwirkenden Körpern:
12 Freiheitsgrade.
– Wie wir sahen, stimmen Phasenraum und Zustandsraum manchmal überein,
aber nicht immer.
• Eigenschaften von Trajektorien:
– Die Bewegung des Systemszustandes auf einer Trajektorie beschreibt die zeitliche Entwicklung des Systems.
– Trajektorien sind stetige (sogar stetig differenzierbare) Kurven.
– Trajektorien im Zustandsraum können sich nicht schneiden. Daraus ergibt sich
eine Möglichkeit zu prüfen, ob der gewählte Raum genügend Dimensionen hat!
– Systeme mit zwei Freiheitsgeraden haben nur zwei mögliche Langzeitverhalten:
Punktattraktor und Grenzzyklus.
• Abbildung 29, S. 58 scheint dieser Aussage zu widersprechen. Zeichnet man die
Bewegung jedoch erst nach Abklingen des Einschwingvorganges auf, dann kann man
durch geeignete Darstellung (Abb. 31, gezeichnet mit ZUSTANDR) deutlich machen,
dass sich die Trajektorie der Bewegung tatsächlich nicht schneidet.
Demonstration: Dreidimensionale Darstellung von Trajektorien im Zustandsraum
(Abb. 31): Programm ZUSTANDR mit
1. 20 angezeigten Perioden
2. mit zusätzlich 200 verdeckten Perioden
11 25. JANUAR 2001: NICHTLINEARITÄT
63
a)
b)
c)
d)
Abbildung 31: Vier Anregungsperioden derselben Bewegung wie der in Abb. 29 gezeigten nach dem Einschwingvorgang (200 Anregungsperioden). Durch verschiedene Tricks
wird der Verlauf der Trajektorie verdeutlicht: b) x(t) wird gepunktet mitgezeichnet. c)
Die Phasenbahn wird zusätzlich gezeichnet. d) Der Zustandsraum wird in Richtung der
Anregungsphase auf [0, 2π] beschränkt.
11 25. JANUAR 2001: NICHTLINEARITÄT
64
3. mit 200 verdeckten und 4 angezeigten Perioden
4. mit zusätzlicher Zeichnung von x(t)
5. mit zusätzlicher Zeichnung von v(t)
6. mit zusätzlicher Zeichnung von x(t) und v(x)
7. mit Beschränkung des Zustandsraumes in Richtung der Anregungsphase auf
[0, 2π].
Bei der letzten Darstellung wird am deutlichsten, dass die Trajektorie keinen Schnittpunkt hat.
11.2
Einführung in die Nichtlinearität
• Einführung von Nichtlinearität in die Bewegungsgleichung des Schraubenfederpendels . . .
– . . . kann motiviert werden durch Federn“, deren Härte von der Dehnung
”
abhängt, z.B. Gummibänder,
– . . . führt zu unübersichtlichen“ Bewegungsformen, die
”
– schließlich die Frage nach der Stabilität und der Ordnung in diesen Bewegungsformen aufwirft. (PHASEND führt bei nichtlinearer Rückstellkraft mit den
Parametern ρ = 0.002, f = 0.2, Ω/ω0 = 0.16 und den Anfangsbedingungen
x0 = 1, vx = 0 (s. Abb.32) nach ca. 2500 Anregungsperioden in eine stationäre
periodische Bewegung! )
• Harmonische Schwingungen bilden in Natur und Technik einen seltenen Idealfall:
Sie treten nur auf bei linearem Kraftgesetz, wenn also die rücktreibende Kraft proportional zur Auslenkung ist.
• Drei Argumente gibt es dafür, sich trotzdem mit ihnen zu befassen:
1. Die analytische Untersuchung ist nur bei linearem Kraftgesetz möglich.
2. Bei kleinen Auslenkungen ist das Kraftgesetz häufig linear (1. Glied der TaylorEntwicklung!).
3. Beliebige periodische Bewegungen lassen sich darstellen als Überlagerung periodischer Schwingungen (Fourierentwicklung).
• Eine offensichtliche Folge der Nichtlinearität ist die Abhängigkeit der Schwingungsdauer von der Amplitude! Z.B. wird das Pendel bei quadratischem Kraftgesetz bei
großen Amplituden viel stärker in die Gleichgewichtslage zurückgezogen als das lineare Pendel. Die Schwingungsdauer nimmt deshalb mit zunehmender Amplitude
ab. (Simulation mit Pendel51: v0 = 0, ρ = 0.05, fA = 0, tmax = 120: Mit den
Anfangsauslenkungen y0 = 0.5, 1.0, 2.0 zeigt das Diagramm in derselben Zeit 7,
10, 14 Schwingungen!)
• Das Entstehen des chaotischen Verhaltens läßt sich damit qualitativ relativ einfach
verstehen:
11 25. JANUAR 2001: NICHTLINEARITÄT
65
Abbildung 32: Bei einem nichtlinearen Pendel kann der Einschwingvorgang sehr (!) lange
dauern und sehr chaotisch aussehen (oben). Trotzdem kann die Bewegung schließlich
stationär werden (unten) – in diesem Fall allerdings sehr kompliziert bleiben.
11 25. JANUAR 2001: NICHTLINEARITÄT
66
– Die Einführung der Nichtlinearität hat zur Folge, daß die Frequenz der Eigenschwingung des Pendels von der Amplitude abhängt: sehr große Frequenz
bei großen Amplituden, immer kleiner werdende Frequenz bei abnehmender
Amplitude.
– Diese Veränderung der Eigenfrequenz kann zur Folge haben, daß sich keine
feste Phasenbeziehung zwischen Schwingung und Anregung einstellen kann.
11.3
Experimente mit dem Fadenpendel
• Freihandexperimente am Fadenpendel:
1. Unabhängigkeit der Frequenz von der (kleinen!) Amplitude,
2. Bei großen Amplituden Beobachtung der Abhängigkeit der Schwingungsdauer
von der Amplitude mit Fadenpendel und Stoppuhr,
• Abhängigkeit der Frequenz f von der Fadenlänge l:
1. je größer l, desto kleiner f ,
2. Vervierfachung von l führt zu Halbierung von f :
f∼
s
1
l
• Abhängigkeit der Frequenz von der Erdbeschleunigung g:
1. Einleuchtend ist, dass die Frequenz zunimmt, wenn die Gravitationskraft wächst.
Also: Je größer g, desto größer f
2. Um die Abhängigkeit der Schwingungsdauer von der Erdbeschleunigung g zu
untersuchen, wird die Schwingungsebene des Pendels um den Winkel β gegen
die Vertikale geneigt. Dadurch wirkt in der Schwingungsebene nur eine Komponente der Schwerkraft, nämlich g cos β.
Folgende Meßergebnisse wurden erhalten:
T0
T
√
β
T
2
0◦
1.3s
33◦
1.43s 0.91
0.92
56◦
1.7s
0.76
0.75
71◦
1.8s
0.72
0.57
cos β
Sie legen, vom letzten abgesehen, die folgende Vermutung nahe:
f∼
q
cos β = gef f
=⇒
f∼
√
g
11 25. JANUAR 2001: NICHTLINEARITÄT
67
Zusammengenommen folgt damit:
f∼
r
g
l
oder
T ∼
s
l
g
• Die Proportionalitätskonstante muss dimensionslos sein. Ein Freihandexperiment
mit einem Fadenpendel ergibt bei einer Fadenlänge von l = 0.835m eine Schwingungsdauer von T = 1.8s.
Damit haben wir experimentell gefunden:
s
s
l
l
T = 6.2
≈ 2π
g
g
(54)
• Eine sorgfältige Messung der Abhängigkeit der Schwingungsdauer von der Amplitude (in Vorlesung aus Zeitgründen diesmal nicht durchgeführt) ergibt die folgenden
Werte:
β
T
2
T
(gemessen)
T0
T
(simuliert)
T0
0◦
655ms
10◦
657ms
1.003
1.002
20◦
659ms
1.006
1.008
30◦
666ms
1.017
1.017
40◦
675ms
1.031
1.031
50◦
684ms
1.044
1.050
60◦
699ms
1.067
1.073
70◦
717ms
1.095
1.102
80◦
738ms
1.127
1.137
90◦
760ms
1.160
1.180
100◦
793ms
1.211
1.232
110◦
835ms
1.275
1.295
120◦
873ms
1.333
1.373
130
◦
938ms
1.432
1.470
140
◦
1020ms
1.557
1.595
Die Werte der letzten Spalte wurden mit einem Simulationsprogramm (PENDEL2)
gemessen“. Sie stimmen sehr gut mit den gemessenen Werten über ein. Man er”
kennt, dass die Schwingungsdauer zunächst kaum merklich, bei größeren Amplituden
aber immer schneller zunimmt. Als Faustregel sollte man sich merken:
Bei Amplituden von nicht mehr als 20◦ (50◦ , 70◦ , 90◦ ändert sich die
Schwingungsdauer nicht mehr als 1%, 5%, 10% bzw. 20%.
11 25. JANUAR 2001: NICHTLINEARITÄT
68
r
α
l
F~F
x
F~s
F~g
α
Abbildung 33: Im Umkehrpunkt ist die Gesamtkraft tangential gerichtet.
11.4
Die Bewegungsgleichung des Fadenpendels
• Wenn sich der Pendelkörper in einem Umkehrpunkt seiner Bewegung befindet, setzt
er sich anschließend in tangentialer Richtung in Bewegung. Er wird also in tangentialer Richtung beschleunigt, die resultierende Kraft F~s muss also tangential gerichtet
sein. Auf den Körper wirkt die Gewichtskraft F~g . Der Aufhängepunkt zieht den
Körper (mit Hilfe des Fadens) in Richtung Zentrum. Andere Körper wirken nicht
auf das Pendel ein. Die Fadenkraft F~F muss also so groß sein, dass sich als Vektorsumme F~g + F~F eine Kraft in Bahnrichtung ergibt:
• Ist die Geschwindigkeit des Pendelkörpers aber von Null verschieden, muss der Faden zusätzlich die Zentripetalkraft aufbringen, um den Körper auf der Kreisbahn
halten zu können (s. Abb. 34). Die Gesamtkraft ist nun nach innen gerichtet. Aber:
Die Kraft in Bewegungsrichtung ist weiterhin die Tangentialkomponente der Schwerkraft!
• Damit kann die Bewegungsgleichung leicht abgeleitet werden:
=⇒
ms̈ = Fg sin α
mlα̈ = mg sin α
(55)
Die Bewegungsgleichung des Fadenpendels lautet also:
α̈ =
g
l
sin α
(56)
• Die Bewegungsgleichung – und damit das Verhalten des (ungedämpften!) Pendels –
erweist sich also als unabhängig von der Masse des Pendelkörpers.
11 25. JANUAR 2001: NICHTLINEARITÄT
69
Abbildung 34: Korrigierte Fassung einer in der Literatur verbreiteten falschen Darstellung
(hier aus Tipler): Wird eine Amplitude von 90◦ angenommen, ist die Fadenkraft – unabhängig von der momentanen Auslenkung! – dreimal so groß wie die Radialkomponente
der Schwerkraft (s. Hausaufgabe)!
• Die Bewegungsgleichung erweist sich – erwartungsgemäß! – als nichtlinear. Da die
Sinusfunktion schwächer als linear wächst, wird der Pendelkörper, im Vergleich zum
harmonischen Pendel, mit zunehmender Amplitude immer schwächer in die Ruhelage zurückgezogen. Das ist die Ursache für die mit der Amplitude zunehmende
Schwingungsdauer!
• Anschaulich ist klar, dass die Schwingungsdauer sogar gegen ∞ streben wird, wenn
die Amplitude gegen π geht: Die rücktreibende Kraft geht dann wie der Sinus gegen
Null. Bei π hat das Pendel also eine zweite Gleichgewichtslage. Wie jedes Kind
weiß, ist diese allerdings instabil : Jede kleinste Abweichung führt dazu, dass sich das
Pendel mit zunehmender Geschwindigkeit aus dieser Lage entfernt ( Balancieren“).
”
11.5
Übung: Die Dämpfung des Drehpendels
• Für die gedämpfte Schwingung ohne Anregung gilt
ρ
α = α0 e− 2 t cos ωt,
für die Maximalausschläge αn gilt also in sehr guter Näherung:
ρ
α0
= e− 2 nT
αn
=⇒
ρ=
2
α0
ln
nT αn
• Damit ergeben sich aus den Messwerten S. 61 die folgenden Werte für ρ:
11 25. JANUAR 2001: NICHTLINEARITÄT
70
ρ[s−1 ]
1.6
2
ρ = (1.8 AI 2 − 0.048 AI + 0.0173)s−1
1.2
r
0.8
r
0.4
r
r
200
400
600
800
I[mA]
Abbildung 35: Anpassung einer quadratischen Funktion an die gemessenen Werte für die
Dämpfungskonstante ρ
I[mA]
0
200
500
800
ρ[s−1 ]
0.0173
0.080
0.446
1.135
• Eine analytische Anpassung (Abb. 35) findet man mit Hilfe des Ansatzes:
ρ(I) = aI 2 + bI + c
Durch Einsetzen dreier Wertepaare ergibt sich:
a = 1.80a−2 s−1 , b = −0.048A−1 s−1 , c = 0.0173s−1.
Auch das 4. Wertepaar liegt nahezu perfekt auf der dadurch definierten Kurve:
ρ = (1.8
I2
I
− 0.048 + 0.0173)s−1
2
A
A
(57)
Hausaufgaben:
1. Welche Kraft muss, verglichen mit der Gewichtskraft des Pendelkörpers, der Faden
eines Pendels am tiefsten Punkt der Bahn aufbringen, wenn die Amplitude der
Schwingung 90◦ beträgt? (Zusatz: Zeigen Sie, dass dieses Ergebnis sogar für jeden
Punkt der Bahn gilt!)
11 25. JANUAR 2001: NICHTLINEARITÄT
71
Nach dem Energieerhaltungssatz ist die kinetische Energie am tiefsten
Punkt gerade gleich der potenziellen Energie am Umkehrpenkt:
m 2
v = mgl
2
Daraus lässt sich sofort die erforderliche Zentripetalkraft berechnen:
v2
FZ = m = 2mg
l
Dies ist die Gesamtkraft auf den Pendelkörper. Da ihn aber die Schwerkraft nach unten zieht, muss der Faden sogar die dreifache Gewichtskraft
aufbringen.
In einem beliebigen Punkt der Bahn gilt entsprechend:
v2
l−h
= 2g
= 2g cos α = 2Fgr
l
l
Die erforderliche Zentripetalkraft ist also an jedem Punkt der Bahn gerade
doppelt so groß wie die Radialkomponente der Schwerkraft.
m
2. Zeigen Sie, dass die Querschwingung eines Körpers, der zwischen zwei Hooke’schen
Federn eingespannt ist, nichtlinear ist! In welchen Grenzfällen ist die Bewegung
trotzdem näherungsweise harmonisch?
3. Verändern Sie das Modell PENDEL51.DYN des angeregten Schraubenfederpendels so,
dass es die Bewegung des Drehpendels so gut wie möglich simuliert! Die Eingabeparameter sollen die Amplitude f der Anregung, die Dämpfungsstromstärke I und
die Anregungsfrequenz als Vielfaches der Eigenfrequenz ωΩ0 sein.
12 1. FEBRUAR 2001: DREHPENDEL MIT UNWUCHT
12
12.1
72
1. Februar 2001: Drehpendel mit Unwucht
Wiederholung
• Geld für Skript einsammeln
• Verteilung des Lernzielkatalogs
• Erinnerung an Fragestunde und Klausur; Taschenrechner!
• Rolle der Nichtlinearität
• Beispiele anharmonischer Schwingungen
• Bewegungsgleichung des Fadenpendels ohne Reibung und kurze Ableitung
12.2
Diskussion der Bewegungsgleichung
• Die Bewegungsgleichung (56) ist nichtlinear, die Schwingungsdauer des Pendels also
abhängig von der Amplitude.
• Da die Sinusfunktion bei α = 0 zwar fast geradlinig beginnt, dann aber immer
schwächer ansteigt, muss die Schwingungsdauer mit der Amplitude zunehmen.
• Die Zunahme der Schwingungsdauer mit der Amplitude lässt sich im Freihandexperiment leicht zeigen. Der Effekt ist jedoch zu klein, um freihändig genügend genau
gemessen werden zu können.
• Die Sinusfunktion hat die folgende (Taylor-) Reihenentwicklung, wenn man den
Winkel im Bogenmaß ausdrückt:
sin α =
∞
X
(−1)n
n=0
α2n+1
α3 α5
=α−
+
− + ...
(2n + 1)!
3!
5!
• Nur für sehr kleine Winkel (dann können die höheren Potenzen von α vernachlässigt
werden) geht (56) in die Bewegungsgleichung einer harmonischen Schwingung über:
α≪1
=⇒
α̈ =
ω02 α
mit
ω0 =
r
g
l
(58)
• Eigenschaften der harmonischen Näherung:
1. Die Schwingungsdauer hängt nicht von der Amplitude ab.
2. Die Schwingungsdauer ist umso
größer, je größer l ist (T ∼
q
1
kleiner, je größer g ist (T ∼ g ).
√
l), und umso
12 1. FEBRUAR 2001: DREHPENDEL MIT UNWUCHT
Abbildung 36: Die Struktur des Fadenpendel-Modells. Die zusätzliche Variable
Ausschlag dient nur der Umrechnung vom Bogenmaß in Grad.
Abbildung 37: Ausgaben des Modells Fadenp.dyn. Bei einem ungedämpften Pendel ist bei einer Amplitude von 179.99◦ die Verlängerung der
Schwingungsdauer sehr deutlich. Die Integrationsschrittweite betrug oben 200 Schritt/Periode, unten nur 20 Schritt/Periode.
73
12 1. FEBRUAR 2001: DREHPENDEL MIT UNWUCHT
12.3
74
Simulation des Fadenpendels
• Das Modell des Federpendels lässt sich leicht so abändern, dass es stattdessen das
Verhalten eines Fadenpendels simuliert. Das wurde in der Vorlesung gemeinsam
durchgeführt. Abbildung 36 zeigt das Modell.
Zustandsgleichungen
Geschwindigkeit.neu <-- Geschwindigkeit.alt + dt*(ay)
Startwert Geschwindigkeit = 0
alpha.neu <-- alpha.alt + dt*(vy)
Startwert alpha = pi/180*179.99
Zustandsänderungen
ay = -g/l*sin(alpha)-rho*Geschwindigkeit
vy = Geschwindigkeit
Konstanten
l = 1
g = 9.81
rho = 0.01
Zwischenwerte
Ausschlag = alpha/pi*180
• Abbildung 37 zeigt das Verhalten bei sehr großer Amplitude. Das Verhalten des
Pendels ist in der Nähe des Überschlagpunktes äußerst sensibel und schwierig zu
simulieren: Selbst bei Integration mit dem Runge-Kutta-Verfahren sind 200 Integrationsschritte pro Periode nötig, um das Verhalten korrekt wiederzugeben (oben).
Bei größeren Integrationsschritten scheint die Amplitude abzunehmen. Es kann auch
leicht passieren, dass das Pendel überzuschlagen scheint.
• Aufgabe: Wie sieht bei einer solchen Schwingung das Phasendiagramm aus? (Hinweis: Das kann man sich überlegen, man kann es aber auch am Computer ausprobieren!)
In der Nähe des labilen Gleichgewichtspunktes hält sich das Pendel lange mit kleinen Geschwindigkeiten auf. Dort muss die Trajektorie deutlich unter der zu einer
harmonischen Schwingung gehörenden verlaufen.
Das Verhalten in der Umgebung von α = π kann man dadurch beschreiben, dass
man eine Variablentransformation nach α′ = α + π durchführt. Dann wird aus der
Bewegungsgleichung
g
g
α̈′ = + sin α′ , bzw. bei kleinen Abweichungen α̈′ = + α′
l
l
Die Lösung dieser Bewegungsgleichung ist eine Exponentialfunktion:
r √
√g
g
g
t
′
l
α ∼e
, α̇ ∼
e l t,
l
′
12 1. FEBRUAR 2001: DREHPENDEL MIT UNWUCHT
75
bei der es offensichtlich einen linearen Zusammenhang zwischen Ausschlag und Geschwindigkeit gibt: Im Phasendiagramm nähern sich die Trajektorien linear der instabilden Gleichgewichtslage.
Bei exakt 180◦ Amplitude würde die Trajektorie bei (180◦ , 0) oder bei (−180◦ , 0)
enden.
12.4
Das Drehpendel mit Unwucht
Das Drehpendel kann nichtlinear gemacht werden, indem bei α = 0 eine Zusatzmasse
angebracht wird (zunächst in Form von Plastillin).
• Diese Zusatzmasse bewirkt ein zusätzliches Drehmoment, durch das das Rad mit
zunehmender Masse immer schwächer in die Nulllage zurückgetrieben wird.
• Als Folge davon wird die Frequenz der Schwingung immer kleiner – und von der
Amplitude abhängig.
• Ab einem gewissen Grenzwert für die Zusatzmasse kommt keine solche Schwinging
mehr zustande. Bei nur etwas größeren Werten ist die Nulllage instabil geworden.
Dafür sind auf beiden Seiten symmetrisch zwei neue stabile Gleichgewichtslagen
entstanden.
• Das Pendel kann nun drei Arten von ungedämpften Schwingungen ausführen:
1. um die linke Gleichgewichtslage,
2. um die rechte Gleichgewichtslage,
3. über die instabile Nulllage hinweg um beide stabilen Gleichgewichtslagen herum.
Die Frequenzen dieser Schwingungen sind unterschiedlich und von der Schwingungsamplitude abhängig.
Das auf diese Weise nichtlinear gemachte Drehpendel wird im zweiten Teil dieser
Vorlesung noch ausführlich experimentell, numerisch und theoretisch untersucht werden.
Hausaufgabe: Erweitern Sie das Simulationsmodell für das Drehpendel um die Unwucht!
12 1. FEBRUAR 2001: DREHPENDEL MIT UNWUCHT
12.5
Übung
12.5.1
Federquerschwingungen
76
• Es war Hausaufgabe, die Bewegungsgleichung für einen Massenpunkt aufzustellen, der zwischen zwei Federn eingespannt ist und quer zur Einspannvorrichtung
schwingt. Die Gleichungen wurden in der Übungssitzung gemeinsam aufgestellt und
untersucht.
}
H
H
HH
HH
HHl
y
HH
HH
α HHHu
u
m
lA
l0
• Sei D die Federkonstante beider Federn, l0 ihre Eigenlänge und lA ihre Länge in der
Gleichgewichtssituation. In einer beliebigen, durch die Koordinate y und die Länge
l der Federn gekennzeichneten Position, zieht also jede Feder den Pendelkörper
mit der Kraft D(l − l0 ) in Richtung Befestigung. Da nur Bewegungen entlang der
Symmetrieachse betrachtet werden sollen (sonst ist die Aufgabe komplizierter!),
kompensieren sich aus Symmetriegründen die Kräfte senkrecht zur y-Achse. Die
rücktreibende Kraft wirkt also in y-Richtung. Für sie gilt offensichtlich:
l − l0
y
F = −2D(l − l0 ) sin α = −2D(l − l0 ) = −2Dy
l
l
Dafür kann man auch schreiben:
F = −2Dy
q
2
y 2 + lA
− l0
q
2
y 2 + lA
• Das Kraftgesetz ist also im Allgemeinen nichtlinear.
In zwei Grenzfällen wird es jedoch linear:
1. Wenn die Federn vernachlässigbare Ruhelängen haben (l0 ≪ lA ), man bezeichnet sie dann als Slinkies“, gilt
”
F = −2Dy,
Die Schwingung ist also harmonisch mit derselben Frequenz wie die Längsschwingung.
2. Bei kleinen Auslenkungen (y ≪ lA ) wird aus dem Kraftgesetz
lA − l0
lA − l0
= −2D ′ y mit D ′ = D
.
lA
lA
Die Schwingung ist wieder harmonisch , aber mit einer kleineren Frequenz als
die Querschwingung.
F = −2Dy
12 1. FEBRUAR 2001: DREHPENDEL MIT UNWUCHT
77
• Im allgemeinen Fall kann man mit den Hilfgrößen l0 = βlA und y ′ =
gesetz umschreiben zu:
F = −2DlA
√
y
lA
das Kraft-
y ′2 + 1 − β ′
√ ′2
y = −2DlA f (y ′)
y +1
Den Verlauf der Funktion f (y ′) zeigt das folgende Bild:
f (y ′)
0.2
β = 0.1
0.4
0.6
D′
β = 0.1
β = 0.5
β = 0.5
β = 0.9
β = 1.0
β = 0.9
β = 1.0
0.8 ′
y
0.2
0.4
0.6
0.8 ′
y
Den Einfluss der Amplitude auf die Schwingungsdauer lässt sich noch besser erken′)
nen, wenn man statt f (y ′) die effektive Federkonstante“ D ′ = 2DlA f (y
aufzeichnet
′
y
”
(rechts): Deutlich ist zu erkennen, dass mit zunehmendem β, d.h. mit zunehmender
Ruhelänge der Federn, die effektive Federkonstante immer kleiner (die Schwingungsdauer also immer größer) und immer weniger konstant wird.
Es wird sich zeigen, dass dieses System ein ganz ähnliches Verhalten hat wie das
Drehpendel mit Unwucht, wenn β > 1 gewählt wird, die beiden Federn in der Mittellage
also sogar zusammengedrückt sind.
12.5.2
Exakte Simulation des Drehpendels
Die Umschreibung des Federpendelmodells zu einem Modell des Drehpendels mit den gemessenen Parametern war Hausaufgabe. Sie wurde in der Übung noch einmal gemeinsam
durchgeführt.
Abbildung 38 zeigt das Modell. Die zugehörigen Gleichungen lauten:
Zustandsgleichungen
wGeschw.neu <-- wGeschw.alt + dt*(ay)
Startwert wGeschw = 0
phi.neu <-- phi.alt + dt*(vphi)
Startwert phi = pi/244*150
Phase.neu <-- Phase.alt + dt*(OmegaA)
Startwert Phase = 0
Zustandsänderungen
12 1. FEBRUAR 2001: DREHPENDEL MIT UNWUCHT
78
Abbildung 38: Grafisches Modell des Pohl’schen Drehpendels. Die wichtigsten experimentell einstellbaren Parameter sind f für die Anregungsamplitude, Omega omega0 für die
Anregungsfrequenz und I für die Dämpfungsstromstärke. Die Funktion AusschlagSkt
dient der Umrechnung der Auslenkung in Skalenteile.
ay = -Quadrat(omega0)*phi-rho*wGeschw+fA*cos(Phase)
vphi = wGeschw
OmegaA = Omega_omega0*omega0
Konstanten
Theta0 = 0.00135
I = 0.500
f = 0
Omega_omega0 = 0.5
D = 0.0165
Zwischenwerte
alpha0 = Wenn(f=0;0;0.0515+0.0322*(f-1))
omega0 = Wurzel(D/Theta0)
fA = D/Theta0*alpha0
rho =1.8*I*I-0.048*I+0.0173
AusschlagSkt = 244/pi*phi
Die Qualität der Simulation wurde untersucht, indem zunächst geprüft wurde, ob das
Modell die Eigenschaften besitzt, die (durch die gemessenen Parameter) hineingesteckt
12 1. FEBRUAR 2001: DREHPENDEL MIT UNWUCHT
79
Abbildung 39: Realistische Simulation des Drehpendels ohne Antrieb bei I =
500mA
wurden. Insbesondere wurde die Abhängigkeit der Dämpfung von der Stromstärke untersucht. Abbildung 39 ist ein Beispiel für die sehr guten Ergebnisse (Man vergleiche mit
dem Messergebnis auf S. 61!).
Anschließend wurde die Dämpfung für eine bisher nicht untersuchte Stromstärke mit
Hilfe des Modells vorhergesagt und anschließend – mit wiederum sehr befriedigendem
Ergebnis! – gemessen.
Die Qualität eines Simulationsmodelles wird geprüft, indem die Übereinstimmung zwischen Simulations- und Messergebnissen untersucht wird. Im Falle
befriedigender Ergebnisse kann man – bis zu einem gewissen Grade – den
Simulationsergebnissen auch dann trauen, wenn man sie experimentell nicht
überprüfen will oder kann.
13 8. FEBRUAR 2001: KLAUSUR
13
80
8. Februar 2001: Klausur
13.1
Fragestunde
13.2
Klausur
1. Harmonische und nicht harmonische Schwingungen
20 P.
Vergleichen Sie harmonische und anharmonische Schwingungen am Beispiel des ungedämpft schwingenden Fadenpendels:
(a) Wie lautet die Bewegungsgleichung? Begründen Sie sie!
5 P.
Der Pendelkörper kann sich nur längs der Kreisbahn bewegen. Tangential dazu wirkt die Kraft F~ = mg sin α (möglichst mit Zeichnung).
Daraus folgt:
ms̈ = −mg sin α
oder
g
α̈ = − sin α
l
(b) Woran bemerkt man im Experiment, dass die Schwingung nicht harmonisch
ist? Unter welchen Umständen ist die Schwingung annähernd harmonisch? Begründen Sie Ihre Aussage!
3 P.
Bei der harmonischen Lösung ist die Schwingungsdauer unabhängig
von der Amplitude, beim realen Pendel jedoch wächst die Schwingungsdauer mit zunehmender Amplitude und strebt sogar gegen unendlich
wenn die Amplitude 180◦ wird.
Bei kleinen Ausschlägen ist die Schwingungsdauer annähernd unabhängig
von der Amplitude.
(c) Nennen Sie die harmonische Näherung der Bewegungsgleichung und eine Lösung dieser Gleichung! Wie groß ist die Schwingungsdauer (Thomsonsche Schwingungsformel)?
4 P.
• harmonische Näherung der Bewegungsgleichung:
Für α ≪ 1 gilt sin α ≈ α und deshalb α̈ = − gl α
• Eine Lösung: α = α0 cos
q
g
t
l
• Thomsonsche Schwingungsformel: T = 2π
q
l
g
• Die Schwingungsdauer hängt nicht ab von der Amplitude und von
der Masse des Pendelkörpers.
(d) Beschreiben Sie
i. qualitative,
ii. halbquantitative und
iii. quantitative
Experimente zur Überprüfung dieser Formel!
i. Qualitativ zu zeigende Aussagen:
• Die Schwingungsdauer hängt von der Pendellänge ab.
8 P.
13 8. FEBRUAR 2001: KLAUSUR
81
• Die Schwingungsdauer hängt von der Erdbeschleunigung ab (z.B.
durch Schrägstellung des Pendels).
• Die Schwingungsdauer hängt nicht von der Masse des Pendelkörpers ab.
• Die Schwingungsdauer hängt nicht von der Schwingungsamplitude ab.
ii. Halbquantitative Aussagen:
• Je größer die Pendellänge, desto größer die Schwingungsdauer.
• Je kleiner die (effektive) Erdbeschleunigung, desto größer die
Schwingungsdauer.
iii. Quantitative Aussagen:
• Vervierfachung der
√Pendellänge führt zu Verdopplung der Schwingungsdauer: T ∼ l
• Kippung des Pendels um 60◦ , Verringerung der effektiven Erdbeschleunigung also um den Faktor 21 , führt zu einer Vergrößerung
q
der Schwingungsdauer um etwa den Faktor 0.7: T ∼ 1g .
2. Numerische Integration
30 P.
(a) Beschreiben Sie die Idee der numerischen Integration von Bewegungsgleichungen, indem Sie das Ganzschritt-Verfahren als Flussdiagramm darstellen.
5 P.
siehe WS 2000/2001, S. 18:
Anfangsbedingungen:
x = v0
v = v0
Bewegungsgleichung:
?
a = a(x, v, t)
-
x = x + v∆t
v = v + a∆t
t = t + ∆t
Zusätzlich sollte eine Abfrage (z.B.: t ≤ tmax ?) und (zwischen Bewegungsgleichung und Integration) eine Ausgabe eingefügt werden.
(b) Eine gleichförmige Kreisbewegung in der (x, y)-Ebene wird durch die folgende Bewegungsgleichung beschrieben:
~¨r = −ω 2~r
Zerlegen Sie diese Vektor-Gleichung in ihre zwei Komponenten, und schreiben
Sie die Bewegungsgleichung so in ein Differentialgleichungssystem 1. Ordnung
um, dass es leicht numerisch integriert werden kann.
5 P.
2
ẍ = −ω x
ÿ = −ω 2 y
)
=⇒









ẋ
v̇x
ẏ
v̇y
=
=
=
=
vx
−ω 2 x
vy
−ω 2 y
-
13 8. FEBRUAR 2001: KLAUSUR
82
(c) Integrieren Sie diese Bewegungsgleichung für den Fall
m
s
numerisch mit dem Ganzschritt-Verfahren zu Fuß“ mit dem Taschenrech”
ner. Rechnen Sie dazu zwei Integrationsschritte mit einer Schrittweite von
∆t = 0.4s.
15 P.
t[s]
0 0.4 0.8
ax [ sm2 ]
-1 -1
x[m] 1
1
1-0.16=0.84
m
vx [ s ] 0 -0.4 -0.4-0.4=0.8
ay [ sm2 ]
0
-0.4
y[m] 0 0.4 0.4+0.4=0.8
vy [ ms ] 1
1
1-0.16=0.84
ω = 1s−1 , x0 = 1m, y0 = 0, vx0 = 0, vy0 = 1
(d) Zusatzaufgabe: Integrieren Sie die Bewegungsgleichung, wieder für dieselben
Parameter und Anfangsbedingungen, numerisch mit dem Halbschritt-Verfahren.
Rechnen Sie dazu einen Integrationsschritt mit der Schrittweite ∆t = 0.8s.
(10 P.)
t[s]
ax [ sm2 ]
x[m]
vx [ ms ]
ay [ sm2 ]
y[m]
vy [ ms ]
0
1
0
0
1
0.4
-1
1
-0.4
0
0.4
1
0.8
-1
1-0.32=0.68
-0.8
-0.4
0.8
1-0.32=0.68
(e) Vergleichen Sie die numerische(n) Lösung(en) mit dem exakten Ergebnis!
Die Bewegung ist eine gleichförmige Kreisbewegung mit dem Radius
r = 1m. Für diese gilt bei den angegebenen Anfangsbedingungen:
α(t) = ωt
~r(t) = r(cos α(t), sin α(t))
~v (t) = ωr(− sin α(t), cos α(t))
Damit ergibt sich sofort:
v = ωr
=⇒
m
s
45.84◦
0.70m
m
−0.72
s
0.72m
m
0.70
s
v = 1
α(0.8s) = 1s−1 0.8s = 0.8
=⇒ α =
x = r cos α =
vx = −v sin α =
y = r sin α =
vy = v cos α =
Die Schrittweite ist mit ∆α ≈ 22.9◦ ziemlich groß. Die numerischen
Ergebnisse stimmen deshalb nicht sehr gut mit der exakten Lösung
5 P.
13 8. FEBRUAR 2001: KLAUSUR
83
überein. Das Ergebnis des Halbschritt-Verfahrens ist trotz der verdoppelten Schrittweite deutlich besser.
3. Der Zustandsraum
30 P.
(a) Wieviele Dimensionen hat der Zustandsraum eines Teilchens, das sich beliebig
durch den Raum bewegen kann? Welche zum Beispiel?
3 P.
6 (z.B. x, vx , y, vy , z, vz )
(b) Welche Eigenschaften haben Trajektorien im Zustandsraum?
5 P.
Die Trajektorien sind stetig differenzierbare Kurven, die sich nicht
schneiden können.
(c) Welche Arten von Langzeitverhalten kann ein System mit 2 Freiheitsgraden
haben? Wie sehen sie als Trajektorien im Zustandsraum aus?
6 P.
• Punktattraktor
• Grenzzyklus
• Divergenz (auch Punktattraktor (gegen ∞))
(d) Wie sehen die Trajektorien im Zustandsraum bei folgenden Bewegungen aus:
i. harmonische (ungedämpfte) Schwingung,
3 P.
achsenparallel Ellipse
ii. Gleiter auf einer horizontalen Luftkissenbahn, der reibungslos zwischen
zwei weit voneinander entfernten elastisch reflektierenden Begrenzungen
hin- und hergleitet,
5 P.
achsenparalleles Rechteck mit leicht gerundeten senkrechten Kanten
iii. freier Fall ohne Reibung?
3 P.
negativer Zweig einer nach links (kleiner werdenden Höhen) geöffneten (Wurzel-) Parabel.
Begründung:
s = s0 − 2g t2
v = −gt
)
=⇒
q
v = ± −2g(s − s0 )
(e) Beschreiben Sie die Bewegung, die im folgenden Phasendiagramm dargestellt
ist! Wie könnte eine solche Bewegung realisiert werden?
5 P.
13 8. FEBRUAR 2001: KLAUSUR
84
Gedämpfte Schwingung um den Nullpunkt, die in der Nähe des Nullpunktes verzögert wird und stabile Gleichgewichtslagen rechts und links
vom Nullpunkt hat.
Realisierungsmöglichkeiten:
a) Kugel in U-förmiger Rinne, die unten einen Hügel“ aufweist.
”
b) lineares Magnetpendel über abstoßendem Magneten.
c) Federquerschwinger, bei dem in der Mittellage die beiden Federn
gespannt sind (s. Vorlesung).
4. Simulation mit grafikbasiertem Modellbildungssystem
20 P.
(a) Zeichnen Sie die grafische Struktur eines Simulationsmodelles, mit dem sich der
reibungsfreie freie Fall simulieren lässt. Schreiben Sie zusätzlich die wichtigsten
Gleichungen auf.
5 P.
Zustandsänderungen
vy = Geschwindigkeit
(b) Ergänzen Sie Struktur und Gleichungen so, dass das Modell Luftreibung in
Form der Luftreibungskraft
1
FR = cW ρLuf t Av 2
2
berücksichtigt.
Dabei sind ρLuf t die Dichte der Luft, A die Querschnittsfläche des fallenden
Körpers und cW der so genannte Widerstandsbeiwert, mit dem die Form (die
Windschlüpfrigkeit“) des Körpers berücksichtigt werden kann.
5 P.
”
13 8. FEBRUAR 2001: KLAUSUR
85
Zustandsänderungen
vy = Geschwindigkeit
ay = g-0.5*cW*rhoLuft*A*vy*abs(vy)
(c) Skizzieren Sie in je einer Zeichnung zwei Graphen, die die Höhe bzw. die Geschwindigkeit als Funktion der Zeit darstellen, für die Fälle vernachlässigbarer
bzw. starker Reibung.
10 P.
h
t
v
t
(d) Zusatzaufgabe: Ergänzen Sie Struktur und Gleichungen so, dass auch ein
Fall aus großer Höhe gut simuliert werden kann.
Hinweis: Dabei muss berücksichtigt werden, dass sich die Erdbeschleunigung g
nach dem Gravitationsgesetz und die Dichte der Luft ρLuf t nach der barometrischen Höhenformel mit der Höhe h ändern:
g = g0
rE2
,
(rE + h)2
−
ρLuf t = ρ0 e
ρ0 g0
h
p0
Dabei sind rE der Erdradius und g0 die Erdbeschleunigung, p0 der Luftdruck
und ρ0 die Luftdichte an der Erdoberfläche.
(5 P.)
13 8. FEBRUAR 2001: KLAUSUR
Zustandsänderungen
vy = Geschwindigkeit
ay = g-0.5*cW*rhoLuft*A*vy*abs(vy)
Konstanten
cW = 0.4
A = 0.01
RE = 6378000
Zwischenwerte
rhoLuft = 1.2*exp(-0.1*Höhe)
g = -9.81*Quadrat(RE)/Quadrat(RE+Höhe)
86
14 15. FEBRUAR 2001: DAS DREHPENDEL MIT UNWUCHT
87
Abbildung 40: Querschwingungen für den Fall β = 1.0: In der Gleichgewichtslage
sind die Federn völlig entspannt.
14
14.1
15. Februar 2001: Das Drehpendel mit Unwucht
noch einmal: Nichtlineare Querschwingungen
• Die in Abschnitt 12.5.1 behandelten Querschwingungen lassen sich sehr leicht simulieren (querschw.dyn):
Zustandsänderungen
vx = Geschwindigkeit
ax = -(Wurzel(Quadrat(Auslenkung)+1)-beta)/
Wurzel(Quadrat(Auslenkung)+1)*Auslenkung
-rho*Geschwindigkeit
Abbildung 40 zeigt den Fall β = 1. Deutlich ist zu erkennen, dass sich das Pendel
in der Nähe der Gleichgewichtslage nahezu gleichförmig bewegt.
• Setzt man in dem Modell β = 1.2, dann simuliert man den Fall, dass der Körper
die Federn sogar zusammendrücken muss, um auf die andere Seite zu gelangen: Die
Gleichgewichtslage ist instabil geworden (Abb. 41).
• Dafür aber sind zwei neue stabile Gleichgewichtspunkte entstanden. Das erkennt
man besonders deutlich, wenn man eine kleine Dämpfung einbaut (Abb. 42): Das
Pendel kommt bei endlicher Auslenkung zur Ruhe!
14 15. FEBRUAR 2001: DAS DREHPENDEL MIT UNWUCHT
Abbildung 41: Querschwingungen für den Fall β = 1.2: Die Federn müssen zusammengedrückt werden, damit der Pendelkörper auf die andere Seite
gelangen kann.
Abbildung 42: Gedämpfte Querschwingungen bei β = 1.2: Der Pendelkörper
kommt in einer neuen Gleichgewichtslage zur Ruhe.
88
14 15. FEBRUAR 2001: DAS DREHPENDEL MIT UNWUCHT
89
• Das Verhalten erinnert sehr an eine Aufgabe der Klausur (3e, S. 83) und an das
Verhalten des Drehpendels mit Unwucht (s. Abschnitt 12.4).
14.2
Phänomene am Drehpendel mit Unwucht
• ohne Anregung:
– Durch eine Zusatzmasse wird ein zusätzliches rücktreibendes Drehmoment angebracht. Dadurch erhält das Pendel zwei stabile Gleichgewichtslagen (und eine
instabile).
– Die Schwingungsdauer wird von der Amplitude abhängig.
– Nach einem Anstoß ist die sich einstellende Ruhelage schwierig vorherzusagen
– ähnlich wie bei einem Würfel!
– Trotzdem kann das Pendel so nicht chaotisch werden: Es hat nur zwei Freiheitsgrade!
• mit Anregung:
– Bei großer Dämpfung schwingt das Rad regulär mit kleiner Amplitude unsymmetrisch auf einer Seite der labilen Gleichgewichtslage.
– Bei kleiner Dämpfung schwingt das Rad regulär mit großer Amplitude symmetrisch über die labile Gleichgewichtslage hinweg.
– Bei mittlerer Dämpfung sind – je nach Anfangsbedingungen - bei gleicher Einstellung der Systemparameter (Anregungsfrequenz und Dämpfung) beide Verhaltensweisen möglich: Zwei oder mehr Schwingungsformen koexistieren!
– Bei mittlerer und kleiner Dämpfung ist außerdem chaotisches Verhalten
möglich: Das Rad überwindet manchmal die instabile Gleichgewichtslage, manchmal nicht. Der genaue Ablauf hängt von den genauen Anfangsbedingungen ab:
Sensitivität
– Bei gewissen Einstellungen der Parameter koexistieren sogar reguläres und
chaotisches Verhalten.
– Wenn das Rad stationär auf einer Seite schwingt und der Nullage recht nahekommt, ohne sie zu überwinden, kann es vorkommen, wenn die Dämpfung
vorsichtig verringert wird, daß sich in der Schwingung des Rades zwei unterschiedliche Amplituden abwechseln: Periodenverdopplung!
14.3
Ergänzung der Bewegungsgleichung des Drehpendels
• Das Zusatzgewicht mit der Masse m übt ein zusätzliches Drehmoment auf das Rad
aus:
Mzus = |~r × F~g | = mg sin ϕ
(59)
14 15. FEBRUAR 2001: DAS DREHPENDEL MIT UNWUCHT
90
• Das zusätzliche Drehmoment durch die Unwucht erweitert die Bewegungsgleichung
zu:
Θϕ̈ = −D(ϕ − ϕA ) + mgr sin ϕ − β ϕ̇
(60)
Dabei ist Θ das Gesamtträgheitsmoment des Rades mit Unwucht:
Θ = Θ0 + mr 2
(61)
• Führt man nun also – diesmal mit dem Gesamtträgheitsmoment! – die folgenden
Hilfsgrößen ein:
ρ :=
D
mgr
Dα0
β
, ω02 = , r0 =
, F =
,
Θ
Θ
Θ
Θ
(62)
dann ergibt sich schließlich die Bewegungsgleichung des Rades zu
ϕ̈ + ρϕ̇ + ω02 ϕ − r0 sin ϕ = F cos Ωt
(63)
Ohne die Zusatzmasse m (⇒ r0 = 0) wäre das die bekannte Bewegungsgleichung
(48) des harmonisch angeregten harmonischen Drehpendels.
14.4
Simulation
• Das Simulationsmodell Pohlrad1 kann leicht um die Unwucht zum Modell Pohlrad2
erweitert werden: Abbildung 43 zeigt das Modell.
Die zugehörigen Gleichungen lauten:
Zustandsgleichungen
wGeschw.neu <-- wGeschw.alt + dt*(ay)
Startwert wGeschw = 0
phi.neu <-- phi.alt + dt*(vphi)
Startwert phi = pi/244*(0)
Phase.neu <-- Phase.alt + dt*(OmegaA)
Startwert Phase = 0
Zustandsänderungen
ay = -Quadrat(omega0)*phi-rho*wGeschw+fA*cos(Phase)+r0*sin(phi)
vphi = wGeschw
OmegaA = Omega_omega0*omega0
Konstanten
14 15. FEBRUAR 2001: DAS DREHPENDEL MIT UNWUCHT
Abbildung 43: Das vollständige System zur Simulation des Drehpendels mit Unwucht (Pohlrad2)
Theta0 = 0.00135
I = 0.07
f = 1.7
Omega_omega0 = 0.5
D = 0.0165
r = 0.085
m = 0.025
g = 9.81
Zwischenwerte
alpha0 = Wenn(f=0;0;0.0515+0.0322*(f-1))
rho = 1.8*Quadrat(I)-0.048*I+0.0173
AusschlagSkt = 244/pi*phi
Theta = Theta0+m*r*r
fA = D/Theta*alpha0
omega0 = Wurzel(D/Theta)
r0 = m*g*r/Theta
• Simulationen:
1. Herausfinden der kritischen Masse
91
14 15. FEBRUAR 2001: DAS DREHPENDEL MIT UNWUCHT
2. Gedämpfte Schwingung für m = 25g
3. Koexistierende Attraktoren
4. Periodenverdopplung
5. chaotische Bewegung
92

Zugehörige Unterlagen

Ubung 2. Kinematik - Universität Potsdam

Physikprüfung III,1 12GE

Dynamische Systeme 1

Zugehörige Unterlagen

Produkte

Unterstützung

Dynamische Systeme 1

Zugehörige Unterlagen

Dieses Dokument Sammlung (en)

Dieses Dokument gespeichert

Schlagen Sie uns vor, wie wir StudyLib verbessern können