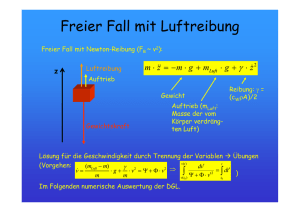
Physikprüfung III,1 12GE

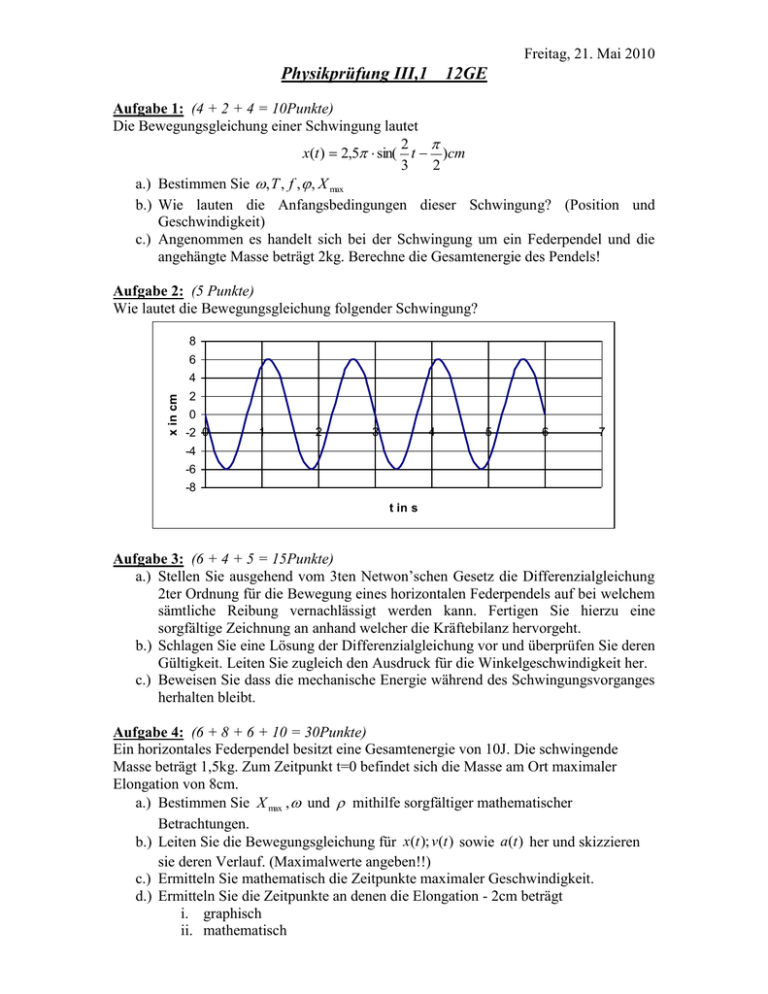
Freitag, 21. Mai 2010
Physikprüfung III,1 12GE
Aufgabe 1: (4 + 2 + 4 = 10Punkte)
Die Bewegungsgleichung einer Schwingung lautet
2 
x(t )  2,5  sin( t  )cm
3
2
a.) Bestimmen Sie , T , f ,  , X max
b.) Wie lauten die Anfangsbedingungen dieser Schwingung? (Position und
Geschwindigkeit)
c.) Angenommen es handelt sich bei der Schwingung um ein Federpendel und die
angehängte Masse beträgt 2kg. Berechne die Gesamtenergie des Pendels!
Aufgabe 2: (5 Punkte)
Wie lautet die Bewegungsgleichung folgender Schwingung?
8
6
x in cm
4
2
0
-2 0
1
2
3
4
5
6
7
-4
-6
-8
t in s
Aufgabe 3: (6 + 4 + 5 = 15Punkte)
a.) Stellen Sie ausgehend vom 3ten Netwon’schen Gesetz die Differenzialgleichung
2ter Ordnung für die Bewegung eines horizontalen Federpendels auf bei welchem
sämtliche Reibung vernachlässigt werden kann. Fertigen Sie hierzu eine
sorgfältige Zeichnung an anhand welcher die Kräftebilanz hervorgeht.
b.) Schlagen Sie eine Lösung der Differenzialgleichung vor und überprüfen Sie deren
Gültigkeit. Leiten Sie zugleich den Ausdruck für die Winkelgeschwindigkeit her.
c.) Beweisen Sie dass die mechanische Energie während des Schwingungsvorganges
herhalten bleibt.
Aufgabe 4: (6 + 8 + 6 + 10 = 30Punkte)
Ein horizontales Federpendel besitzt eine Gesamtenergie von 10J. Die schwingende
Masse beträgt 1,5kg. Zum Zeitpunkt t=0 befindet sich die Masse am Ort maximaler
Elongation von 8cm.
a.) Bestimmen Sie X max ,  und  mithilfe sorgfältiger mathematischer
Betrachtungen.
b.) Leiten Sie die Bewegungsgleichung für x (t ); v (t ) sowie a(t ) her und skizzieren
sie deren Verlauf. (Maximalwerte angeben!!)
c.) Ermitteln Sie mathematisch die Zeitpunkte maximaler Geschwindigkeit.
d.) Ermitteln Sie die Zeitpunkte an denen die Elongation - 2cm beträgt
i. graphisch
ii. mathematisch