Freier Fall mit Luftreibung
Werbung
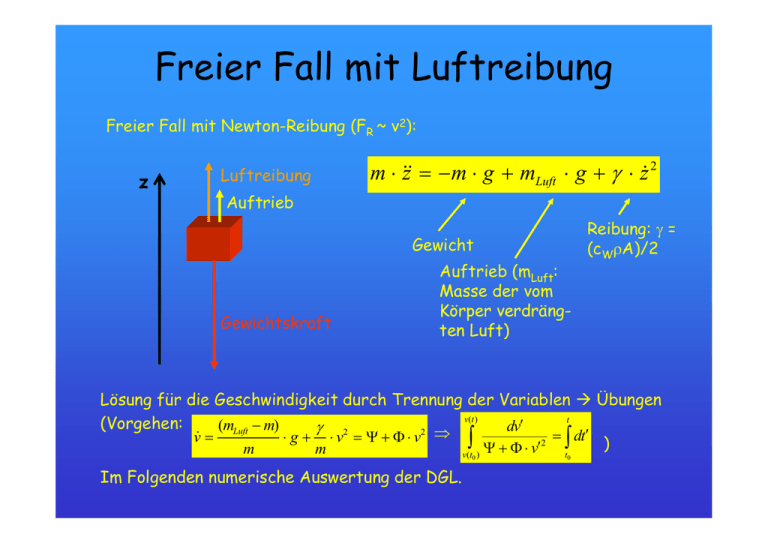
Freier Fall mit Luftreibung Freier Fall mit Newton-Reibung (FR ~ v2): z Luftreibung m ⋅ &z& = −m ⋅ g + mLuft ⋅ g + γ ⋅ z& 2 Auftrieb Gewicht Gewichtskraft Auftrieb (mLuft: Masse der vom Körper verdrängten Luft) Reibung: γ = (cWρA)/2 Lösung für die Geschwindigkeit durch Trennung der Variablen Æ Übungen v (t ) t (Vorgehen: ′ (mLuft − m) d v γ 2 = ∫ dt′ ⋅ g + ⋅ v = Ψ + Φ ⋅ v2 ⇒ ∫ v& = 2 ) ′ Ψ + Φ⋅v m m v (t ) t 0 Im Folgenden numerische Auswertung der DGL. 0 Höhe Freier Fall eines Menschen Geschwindigkeit Höhe Aus Gerthsen - Physik Freier Fall mit Luftreibung Abschätzung der Endgeschwindigkeit aus der Bewegungsgleichung: m ⋅ &z& = −m ⋅ g + mLuft ⋅ g + γ ⋅ z& 2 z γ = (cWρA)/2 Einstellen eines stationären Gleichgewichts, danach gilt: Endgeschwindigkeit vEnde m ⋅ &z& = 0 Einsetzen in die Bewegungsgleichung ergibt für die Endgeschwindigkeit: z&Ende = (m − mLuft ) ⋅ g γ Da sich die Dichte der Luft mit der Höhe ändert, ändert sich auch vEnde. Bei Annäherung an den Erdboden nehmen die Dichte und damit der Reibungskoeffizient γ zu, damit wird die Endgeschwindigkeit kleiner. Ballistische Kurven eines Geschosses r& r & m ⋅ r = m ⋅ g − mLuft r& r r& 2 r ⋅ g − γ ⋅ r ⋅ r& |r| γ = (cWρA)/2 Berechnungen für v0 = n · 170 m/s, n = 1, 2, 3, ... m = 20 g A = 0.5 cm2 cW = 0.2 Höhe in Einheiten von 3 km Aus Gerthsen - Physik x in Einheiten von 3 km Wirbelstrombremse Lichtschranke: gibt Startsignal für Oszilloskop r v (t ) Magnet Kupferblech Luftkissenschlitten Luftkissenschiene Oszilloskopbild: m v 0 Kupferblech erreicht Magnet, Bremswirkung setzt ein t Wirbelstrombremse In der Elektrodynamik-Vorlesung wird gezeigt: Dringt eine Leiterschleife mit der Geschwindigkeit v in ein (homogenes) magnetisches Feld ein, so wird in ihr ein Wirbelstrom hervorgerufen, auf den wiederum eine bremsende Lorentzkraft wirkt: x(t) r B2 ⋅ b2 r ⋅v Bremskraft: FR = − R r r v B T = 2π Bew.gl.: r B2 ⋅ b2 m ⋅ &x& = FR = − ⋅ x& R ⇒ B2 ⋅ b2 ⋅v = 0 m ⋅ v& + R r FR l g Magnetfeldinduzierter Wirbelstrom b R: elektrischer Widerstand der Leiterschleife m: ihre Masse ⇒ v(t ) = v0 ⋅ e − t τ , mit τ = m⋅R B 2 ⋅ b2 Gedämpfte Schwingung ohne treibende Kraft X X0=0 X Auslenkung des Körpers Schwimmkörper, Radius r Dämpfungsvorrichtung: Glycerin, η Kräftebilanz: m ⋅ &x& = − k ⋅ x − γ ⋅ x& Rückstellkraft Bewegungsgleichung: γ Dämpfung, γ = 6πηr k &x& + ⋅ x& + ⋅x = 0 m m Gedämpfte Schwingung ohne treibende Kraft Bewegungsgleichung: &x& + γ m oder üblicherweise in der Form: &x& + 2 τ ⋅ x& + ω 02 ⋅ x = 0 mit ⋅ x& + ω 1 τ k ⋅x = 0 m k = m 2 0 = γ 2m ω0: Eigenfrequenz des ungedämpften Oszillators τ: Dämpfungszeitkonstante Lösungsansatz: eat, ergibt drei zu unterscheidende Fälle: 1. Schwache Dämpfung, Schwingfall, wenn gilt Lösung: Gedämpfte Schwingung x (t ) = x 0 ⋅ e − t τ ω0 ⋅ τ > 1 also : ω0 > ⋅ cos( ω res ⋅ t + ϕ ) mit 1 τ ω res = ω − 2 0 1 τ2 Gedämpfte Schwingung ohne treibende Kraft ω res = ω − 2 0 1 τ2 Eigenfrequenz (Resonanzfrequenz) ωres des gedämpften Oszillators ist gegenüber ω0, der Eigenfrequenz des ungedämpften Oszillators, reduziert (Dämpfung wirkt wie zusätzliche Rückstellkraft). 2. Kritische Dämpfung, Kriechfall, wenn gilt ω0 ⋅ τ = 1 also : ω0 = Lösung: x ( t ) = ( x 01 + x 02 ⋅ t ) ⋅ e 3. Überkritische Dämpfung, aperiodischer Grenzfall, wenn gilt − t τ 1 τ und ωres = 0 Keine Schwingung mehr, kontinuierlicher Rückgang der Auslenkung ω0 ⋅ τ < 1 also : ω0 < Lösung: Keine Schwingung mehr, kontinuierlicher Rückgang der Auslenkung 1 τ und ωres : imaginär Gedämpfte Schwingung ohne treibende Kraft Lösung: x ( t ) = x 01 ⋅ e mit τ± = 1 ω 02 − t τ+ + x 02 ⋅ e ⎛1 ⋅ ⎜⎜ ± ⎝τ − 1 τ2 t τ− ⎞ − ω ⎟⎟ ⎠ 2 0 Experimenteller Vergleich des Abklingverhaltens im Kriechfall und im aperiodischen Grenzfall ergibt: Abklingen im Kriechfall erfolgt schneller. → Wird bei Zeigerinstrumenten zur schnellen Anpassung der Anzeige an sich verändernde Messwerte genutzt.











