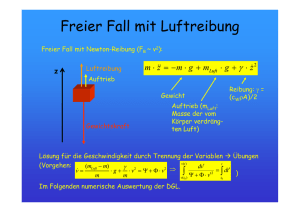
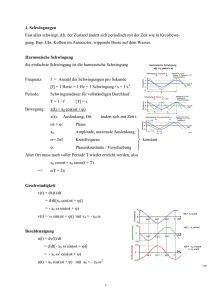
VORBEREITUNG: SCHWINGUNGEN, RESONANZVERHALTEN Im

VORBEREITUNG: SCHWINGUNGEN, RESONANZVERHALTEN
FREYA GNAM, GRUPPE 26, DONNERSTAG
V ERSUCHSAUFBAU
Im Versuch sollen freie, gedämpfte und erzwungene Drehschwingungen an einem
harmonischen Oszillator (Drehpendel nach Pohl) untersucht werden. Dazu steht das
Computer-Messwerterfasssystem CASSY zur Verfügung.
Das Drehpendel. Das Pohlsche Rad ist ein Drehpendel. In dem Versuch handelte es
sich um eine Kupferscheibe mit homogener Massenverteilung und einer an ihr befestigten Spiralfeder, die so angeordnet ist, daß sie der Drehbewegung durch den Schwerpunkt entgegen wirkt. Die Lage kann durch einen Metallzeiger optisch abgelesen werden.
An der Achse des Drehpendels ist ein leichtgängiges Potentiometer angebracht. Damit
wird eine zur Auslenkung proportionalen Spannung erzeugt, die über den Analogeingang des CASSY-Interface als Spannung registriert wird.
Mit einem Elektromagneten, der wie eine Wirbelstrombremse1 wirkt, wird eine zu dϕ
dt
proportionale Dämpfung erzeugt. Je nach Strom durch den Magneten können unterschiedliche Dämpfungen β eingestellt werden.
Das Drehpendel kann durch einen Motor angetrieben werden, dessen Anregungsfrequenz variabel ist. Beim Einschalten treten dabei Einschwingvorgänge auf, die mit der
Zeit abklingen. Erst dann sollten Messungen durchgeführt werden.
Der elektomagnetische Schwingkreis. Ein elektromagnetischer Schwingkreis ist eine Schaltung aus Kondensator C und Induktivität L, in der der Kondensator periodisch
aufgeladen und entladen wird. Der Kondensator C, in dem die elektrische Energie
Wel = 12 CU 2 gespeichert ist, entlädt sich über die Spule L. Der dabei fließende
Strom I = dQ
erzeugt in der Spule ein Magnetfeld B mit der magnetischen Energie
dt
1
2
Wm = 2 LI . Wenn der Strom abzunehmen beginnt, entsteht in der Spule eine Induktionsspannung, welche die Abnahme von I hemmt. Der Kondensator wird umgekehrt
aufgeladen und beginnt dann sich wieder zu entladen...
1
Prinzip einer Wirbelstrombremse: Bewegt sich eine Metallplatte in einem Magnetfeld, werden in
ihr Wirbelströme induziert. Die Ströme erzeugen selbst wieder ein Magnetfeld, das dem äußeren entgegengesetzt ist. Der elektrische Widerstand der Metallplatte bildet für die Wirbelströme einen ohmschen
Verbraucher, wodurch die Bewegungsenergie in Wärme umgesetzt wird.
1
1. D REHPENDEL ,
FREIE
S CHWINGUNGEN
Die Feder erzeugt bei einer Auslenkung des Rings um den Winkel ϕ ein rücktreibendes
2
Drehmoment Mf = Ω ddtϕ2 = −D∗ ϕ.
Freie, ungedämpfte Schwingung. Die Bewegungsgleichung für harmonische Drehschwingungen ohne Dämpfung lautet:
d2 ϕ(t)
dt2
+ ω02 ϕ(t) = 0, wobei ω02 =
D∗
.
Ω
Trägheitsmoment des Drehpendels, einfach abgeschätzt:
Ω = mr2 mit m = ρV = ρπh(ra2 − ri2 ).
Die allgemeine Lösung dieser DGL ist: ϕ(t) = ϕ0 cos(ω0 t + ψ). Amplitude ϕ0 und
Phase ψ werden durch die Anfangsbedingungen festgelegt.
Der Schwingungsvorgang ist auch ohne Wirbelstrombremse nicht ganz dämpfungsfrei:
Das Rad wird durch die Reibung der Achse gebremst. Es wird also ein Amplitudenabfall zu beobachten sein.
2. D REHPENDEL ,
FREIE GEDÄMPFTE
S CHWINGUNGEN
Die Reibung erzeugt ein zusätzliches Moment MR = −2β dϕ
.
dt
Gedämpfte Schwingung. Die Bewegungsgleichung für harmonische Drehschwingungen mit Dämpfung (Dämpfungskraft proportional zu dϕ
) lautet:
dt
d2 ϕ(t)
dt2
+ ω02 ϕ(t) + 2β dϕ(t)
= 0.
dt
Mit dem Ansatz ϕ(t) = ce−λt erhält man λ1,2 = β ±
p
Definiere zudem ω = ω02 − β 2 .
p
β 2 − ω02 .
Unterscheide nach Stärke der Dämpfung
Schwingfall. ω0 > β unterdämpft, ω reell. Gedämpfte periodische Bewegung.
Kriechfall. ω0 < β überdämpft. Konvergiert schnell.
Aperiodischer Grenzfall. ω0 = β Das System kehrt nach einem Ausschlag in seine
Ruhelage zurück.
2
Berechnung des Dämpfungsverhältnisses. Das Dämpfungsverhältnis k beschreibt
das Verhältnis von zwei aufeinander folgenden Ausschlägen der Schwingung:
k=
ϕ(t)
ϕ(t+t)
= eβt .
Für die Berechnung des Dämpfungsverhältnisses stehen zwei Formeln zur Auswahl:
q
n
P
ϕi−1
n ϕ0
k = n1
oder
k
=
ϕi
ϕn
i=1
Die erste Formel verkleinert den statistischen Fehler, das sie einen Mittelwert aus einer
Reihe von Messwerten bildet, für größere Werte von n gestaltet sich die Berechnung
mit der zweiten Formel allerdings als weniger aufwendig.
Güte des Systems. Man charakterisiert die Dämpfung eines schwingungsfähigen Systems im Resonanzbereich oft durch die Güte Q. Wenn ∆Etot der Energieverlust pro
Periode ist, gilt für βT 1:
2
Etot
Q = −2π ∆E
= 2π ϕ(t)2 ϕ(t)
=
−ϕ(t+T )2
tot
2π
1−e−2βt
=≈
ω0
2β
Die Güte bestimmt die Breite der Resonazkurve: Je größer die Güte, desto schärfer
und höher ist die Resonanz.
3. S TATISCHE M ESSUNG DER W INKELRICHTGRÖSSE D∗
Bringt man einen Gegenstand an das Pendel an und misst die Auslenkung in der
Gleichgewichtslage, so kann man daraus die Winkelrichtgröße D∗ der Schneckenfeder des Drehpendels bestimmen: Das Rad wird durch die Kraft F um den Winkel ϕ
ausgelenkt. Greift die Kraft tangential am Rand an, so gilt:
|~r × F~ | = D∗ ϕ, also: D∗ = rF
ϕ
∗
Aus D lässt sich das Trägheitsmoment Ω berechnen: Ω =
der Abschätzung aus Aufgabe 1 vergleichen.2
D∗
,
ω0
mit ω0 =
2π
T
und mit
4. D REHPENDEL , ERZWUNGENE S CHWINGUNGEN
Erzwungender, gedämpfter Fall. Dem schwingfähigen System sei nun ein periodisches äußeres Drehoment M = M0 sin(ωt) aufgeprägt. Die Bewegungsgleichung für
erzwungene, gedämpfte harmonische Drehschwingungen lautet:
d2 ϕ(t)
dt2
+ ω02 ϕ(t) + 2β dϕ(t)
− α sin(ωt) = 0 mit α =
dt
M0
.
Ω
Als eine Lösung findet man ϕ(t) = ϕ0 sin(ωt+ψ) mit der Amplitude ϕ0 = √
und der Phase tan ψ =
−2ωβ
.
ω02 −ω 2
2
T = T (0) Periodendauer bei ungedämpfter Schwingung
3
α
(ω02 −ω 2 )2 +4β 2 ω 2
Die erzwungene Schwingung hat die gleiche Frequenz wie das äußere Drehmoment
und eine zeitlich konstante Amplitude. Äußeres Drehmoment und Auslenkwinkel sind
jedoch um ψ ≤ 0 gegeneinander phasenverschoben. Dabei hinkt der Auslenkungswinkel ϕ(t) dem erregenden Drehmoment M (t) hinterher.
Einige Spezialfälle.
• ω ω0 ψ ≈ 0 in Phase
• ω = ω0 ψ = − π2 Resonanz
• ω → ∞ ψ → −π entgegengesetzt zu M (t)
p
Die maximale Amplitude taucht nicht exakt bei ω = ω0 auf, sondern bei ω = ω02 − β 2 .
Die Resonanz verschiebt sich also in Folge der Dämpfung zu kleineren ω-Werten.
Gütebestimmung. An den √12 -Amplituden-Punkten fällt die Amplitude der angeregten Schwingung auf √12 Ares ab (Ares Amplitude der Resonanzfrequenz). Diese treten
q
auf bei ω1,2 ≈ 1 ± Q1 ω0 (Näherung für große Werte von Q).
Die Differenz dieser Frequenzen bezeichnet man als Bandbreite
q
q
b = ( 1 + Q1 − 1 − Q1 )ω0 . Mit Q 1 ergibt sich b ≈ ωQ0 = 2β
5. S ERIENSCHWINGKREIS , ERZWUNGENE S CHWINGUNGEN
Beim elektromagnetischen Schwingkreis wirken die ohmschen Widerstände R von
Spule und Leitungen als Energieverlustquellen. Es entsteht eine gedämpfte Schwingung, deren Gleichung aus den Kirchhoffschen Regeln hergeleitet werden kann:
U (t) = UL (T ) + UR (T ) + UC (t)
R
I(t)dt
dI(t)
U (t) = L
+ RI(t) +
dt
C
2
1 dU
d I R dI
1
=
+
+
I
2
L dt
dt
L dt CL
Als Lösung erhält man:
r
I(t) = I0 e− 2L t cos(ωt + α) mit ω =
I0 = √
U0
1 2
R2 +(ωl− ωC
)
=
U0
,
Z
q
1
LC
R 2
− ( 2L
) und α = arctan(
1
ωL− ωC
R
).
mit der Impedanz Z (elektrischer Scheinwiderstand).
Mit der Breite b der Resonanzkurve zwischen den √12 -Amplituden-Punkten, bestimmt
sich der Gütefaktor für große Q zu Q = ωb0 . Der Gütefaktor lässt sich auch über die
Resonanzüberhöhung bestimmen: Q = |ULU(ω0 0 )| = |UCU(ω0 0 )| .
4