Ferienkurs Experimentalphysik 1

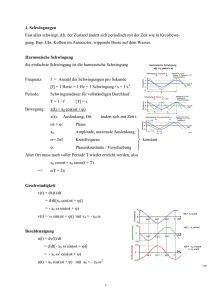
Ferienkurs Experimentalphysik 1
Julian Seyfried
Wintersemester 2015/2016
1
Seite 2
Inhaltsverzeichnis
3 Energie, Arbeit und Leistung
3
3.1
Energie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
3.2
Arbeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
3.3
Leistung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
4 Schwingungen/Oszillationen
4
4.1
freier ungedämpfter Oszillator . . . . . . . . . . . . . . . . . . . . . .
4
4.2
gedämpfter Oszillator
. . . . . . . . . . . . . . . . . . . . . . . . . .
4
4.2.1
schwache Dämpfung . . . . . . . . . . . . . . . . . . . . . . .
5
4.2.2
starke Dämpfung . . . . . . . . . . . . . . . . . . . . . . . . .
5
4.2.3
aperiodischer Grenzfall . . . . . . . . . . . . . . . . . . . . . .
5
5 Systeme von Massenpunkten
6
A Aufgaben
7
A.1 Freier Fall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
A.2 Der Sportwagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
A.3 Schwingung skizzieren . . . . . . . . . . . . . . . . . . . . . . . . . .
7
A.4 Das Federpendel . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
A.5 Das U-Rohr . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
B Musterlösung
9
B.1 Freier Fall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
B.2 Der Sportwagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
B.3 Schwingung skizzieren . . . . . . . . . . . . . . . . . . . . . . . . . .
10
B.4 Das Federpendel . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
B.5 Das U-Rohr . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
Seite 3
3
3.1
Energie, Arbeit und Leistung
Energie
In der Mechanik gilt in einem abgeschlossenen System Energieerhaltung.
Die mechanischen Energieformen werden unterteilt in potentielle Energie und kinetische Energie.
Wird Energie nicht in Wärme oder Verformung umgewandelt, gilt folgende Gleichung:
Eges = Epot + Ekin = konstant
(1)
3.2
Arbeit
Bewegt man sich in einem Kraftfeld, so wird dabei Arbeit verrichtet:
Z
W = F (~r) · d~r
(2)
γ
Da Kraft und infinitesimales Wegstück mit einem Skalarprodukt verknüpft sind,
zählt nur die Kraftkomponente die parallel zum Weg ist.
In einem konservativen Kraftfeld (z.B. Gravitationspotential) ist die Arbeit wegunabhängig.
W = −∆Epot = Epot,1 − Epot,2
(3)
Im Fall konstante Kraft ergibt sich:
W = F~ · |~s| · cos(θ),
(4)
wobei θ der Winkel zwischen Bewegungsrichtung und Kraft ist.
Man kann die wirkende Kraft folgendermaßen aus der potentiellen Energie berechnen:
d
F~ (~r) = −grad Epot (~r) = − Epot (r) · ~er ,
(5)
dr
wobei im letzten Schritt ein radialsymmetrisches Potential angenommen wurde.
3.3
Leistung
Die Leistung ist definiert als Arbeit pro Zeit und daher gegeben als:
P =
dW
dt
Als Beispiele dienen Aufgaben A.1 und A.2
(6)
Seite 4
4
4.1
Schwingungen/Oszillationen
freier ungedämpfter Oszillator
Eine freie ungedämpfte Schwingung wird durch folgende Differentialgleichung beschrieben:
ẍ(t) + ω02 · x(t) = 0
(7)
Differentialgleichungen dieser Art können immer mit folgendem Ansatz gelöst werden:
x(t) = eλ·t
(8)
Daraus erhalten wir:
ẍ(t) = λ2 · eλ·t
(9)
Setzen wir dies in die Differentialgleichung ein, erhalten wir nach dem Kürzen der
e-Funktion das sog. charakteristische Polynom zur Bestimmung von λ:
λ2 + ω02 = 0
(10)
Diese quadratische Gleichung können wir lösen und erhalten:
λ1,2 = ±i · ω0 ,
(11)
d.h. x1 (t) = ei·ω0 ·t und x2 (t) = e−i·ω0 ·t lösen die Differentialgleichung. Eine Differentialgleichung 2. Ordnung hat immer zwei linear unabhängige Lšsungen. Man kann
beweisen, dass eine Differentialgleichung dieser Form auch vom Real- bzw. Imaginärteil einer Lösung gelöst wird. Real- und Imaginärteil stellen zwei linear unabhängige
Lösungen dar. Daher können wir für die allgemeine Lösung der Differentialgleichung
schreiben:
x(t) = A · sin(ω0 · t) + B · cos(ω0 · t) = C · sin(ω0 · t + ϕ)
(12)
Die Bestimmung der beiden unbekannten A & B bzw. C & ϕ erfolgt durch die Anfangsbedingungen.
Schwingungen, die zur Zeit t = 0 eine verschwindende Geschwindigkeit haben, sind
reine Cosinus-Schwingungen. Ist der Oszillator zur Zeit t = 0 in der Gleichgewichtslage und besitzt eine Anfangsgeschwindigkeit, so ist es eine reine Sinus-Schwingung.
4.2
gedämpfter Oszillator
In einem realistischen Fall ist die Schwingung gedämpft. Im Folgenden nehmen wir
eine Reibungskraft proportional zur Geschwindigkeit an.
Seite 5
Wir erarbeiten den gedämpften Oszillator anhand des Federpendels. Unsere wirkende Kraft setzt sich nun zusammen aus Federkraft und Reibungskraft (entgegen der
Bewegung).
m · ẍ = −D · x − b · ẋ,
(13)
wobei b die Stärke der Dämpfung (z.B. Reibung) beschreibt.
b
. Es wird ein Faktor 2
Wir stellen nun die Gleichung um und definieren 2γ := m
gewählt um später ein schöneres Ergebnis zu erhalten.
ẍ + 2γ · ẋ + ω02 · x = 0
(14)
Analog zum vorherigen Kapitel erhalten wir wieder das charakteristische Polynom:
λ2 + 2γ · λ + ω02 = 0
(15)
Mit der Mitternachtsformel erhalten wir für λ folgendes Ergebnis (nun ist auch
offensichtlich warum ein Faktor 2 vor dem γ gewählt wurde):
q
λ1,2 = −γ ± γ 2 − ω02
(16)
Offensichtlich müssen wir drei Fälle unterscheiden:
4.2.1
schwache Dämpfung
In diesem Fall gilt: γ 2 < ω02 . Daher ist die Wurzel rein imaginär und wir erhalten
in der Lösung eine komplexe e-Funktion und damit eine Schwingung. Außerdem
definieren wir ω 2 := ω02 − γ 2 .
x(t) = e−γ·t [A · sin(ω · t) + B · cos(ω · t)] = Ce−γ·t sin(ω · t + ϕ)
(17)
Das Federpendel schwingt also mit Kreisfrequenz ω 6= ω0 und einer exponentiell
abklingenden Amplitude.
4.2.2
starke Dämpfung
In diesem Fall gilt γ 2 > ω02 . Die Wurzel ist also reell und somit findet keine Schwingung statt (α2 := γ 2 − ω02 ):
x(t) = e−γ·t [A · eα·x + B · e−α·x ]
4.2.3
(18)
aperiodischer Grenzfall
Im letzten Fall betrachten wir γ = ω0 . Jetzt fallen die Lösungen der quadratischen
Gleichung zusammen. Da eine Differentialgleichung 2. Ordnung immer zwei Lösungen hat, benötigen wir eine 2. Lösung. Auch in diesem Fall hilft uns ein Satz aus
der Analysis weiter, so dass man die Lösung sofort hinschreiben kann:
x(t) = e−γ·t (c1 + c2 · t)
(19)
Seite 6
5
Systeme von Massenpunkten
Hat man ein System von mehreren Massenpunkten mit Massen mi , Geschwindigkei~ s bestimmen.
ten ~vi und Koordinaten ~ri , so kann man den sog. Schwerpunkt R
P
P
mi · ~ri
mi · ~ri
i
~
Rs = P
= i
(20)
M
i mi
~s angeben:
Man kann damit auch die Geschwindigkeit des Schwerpunkts V
P
~s
mi · ~vi
d
R
~s =
= i
V
dt
M
Der Impuls des Schwerpunkts P~s kann ebenfalls angegeben werden:
X
~s =
P~s = M · V
p~i
(21)
(22)
i
Dieser ist also über die Summe der Einzelimpulse gegeben.
Wirken keine äußeren Kräfte auf das System, so ist der Schwerpunktimpuls eine
Erhaltungsgröße. Dies gilt wegen dem 3. Newtonschen Axiom auch bei Kräften zwischen den einzelnen Massenpunkten.
Als Schwerpunktsystem bezeichnet man das Koordinatensystem, dessen Ursprung
im Schwerpunkt ruht. Falls sich der Schwerpunkt bezüglich des Laborsystems bewegt, so bewegt sich auch das Koordinatensystem.
Das Schwerpunktsystem ist insbesondere bei der Berechnung von Stößen von großer
Bedeutung.
Wir bezeichnen den Ortsvektor eines Teilchens i als ~ri,s . Wir können schreiben:
~ s + ~ri,s
~ri = R
(23)
Auf Grund der Definition des Schwerpunkts verschwindet die Summe über die mit
der Masse gewichteten Koordinaten im Schwerpunktsystem:
X
mi · ri,s = 0
(24)
i
Dementsprechend verschwindet auch die Summe über die Zeitableitungen der Koordinaten im Schwerpunktsystem und es gilt daher:
X
pi,s = 0
(25)
i
Die Geschwindigkeit des Teilchens i kann geschrieben werden als:
~s + ~vi,s
~vi = V
(26)
Seite 7
A
A.1
Aufgaben
Freier Fall
Heiko Hecht springt vom 10m-Turm. Mit welcher Geschwindigkeit taucht er in das
Wasser ein? In welcher Höhe hat er die Hälfte der Geschwindigkeit erreicht?
A.2
Der Sportwagen
Ein Sportwagen der Masse 1500kg wird in 3s aus dem Stand auf 100 km
h beschleunigt.
Welche Leistung erbringt der Motor?
Danach wird der Wagen in 30m zum Stehen gebracht. Wie groß muss die Bremskraft
sein, wenn der Wagen mit konstanter Kraft gebremst wird?
Über das Auto ist bekannt, dass es maximal 300 km
h fährt und die Reibungskraft bei
dieser Geschwindigkeit 3kN beträgt. Welche Leistung bringt der Motor?
A.3
Schwingung skizzieren
Eine Bewegung wird durch folgende Differentialgleichung beschrieben:
1
rad
ẍ + 1 ẋ + 2 · 2 · x = 0
s
s
(27)
Skizziere die Schwingung mit folgenden Anfangsbedingungen:x(0) = 1m, ẋ(0) = 0 ms .
A.4
Das Federpendel
N
Gegeben sei eine Feder mit Federkonstante D = 50 m
, die im entspannten Zustand
an der Zimmerdecke befestigt ist. Zum Zeitpunkt t = 0s wird ein Gewicht der Masse
m = 1kg an die Feder gehängt. Stelle die Differentialgleichung für dieses Problem
auf und löse sie unter den gegebenen Randbedingungen.
A.5
Das U-Rohr
In einem U-Rohr steht eine Flussigkeitssäule. Ihre Gesamtlänge sei L, die Dichte der
Flussigkeit ρ und der Rohrquerschnitt A. Die Flüssigkeit bewegt sich reibungsfrei.
Die Biegung am unteren Ende des U-Rohres werde vernachlässigt. Die Flüssigkeit
wird wie in Abbildung 1 gezeichnet ausgelenkt. Stelle die Bewegungsgleichung für
dieses Problem auf und beschreibe die Bewegung.
Seite 8
Abbildung 1: Skizze des U-Rohrs von Aufgabe A.5
Seite 9
B
B.1
Musterlösung
Freier Fall
In diesem Fall ist die Energie erhalten, es gilt also:
1
· m · v2
2
√
Wir erhalten daher für die Geschwindigkeit: v = 2 · g · h = 14 ms .
Nun berechnen wir die Höhe für die halbe Geschwindigkeit. Es gilt:
m·g·h=
m·g·h=
v2
1
·m·
+ m · g · h∗
2
4
(28)
(29)
Diese Gleichung können wir nun umschreiben in:
g · ∆h =
1 v2
·
2 4
(30)
Mit Gleichung (28) folgt: ∆h = 2, 5m.
B.2
Der Sportwagen
Da wir eine Zeitspanne wissen, benötigen wir noch die erbrachte Arbeit in dieser
Zeitspanne.
Die kinetische Energie, die der Wagen bei 100 km
h hat, wird ihm durch den Motor in
3s zugeführt. Für die Leistung gilt also:
P =
1
2
· m · v2
= 193kW = 262ps
3s
(31)
Nun berechnen wir die benötigte Bremskraft. Die gesamte kinetische Energie muss
in der Strecke von 30m in Wärmeenergie durch Arbeit umgewandelt werden. Es gilt
daher:
1
(32)
W = · m · v2 = F · s
2
1
·m·v 2
Daher erhalten wir für die Kraft: F = 2 s = 19kN.
Nun berechnen wir die Leistung des Motors um die geforderte Geschwindigkeit zu
berechnen:
ds
d
P = (F · s) = F ·
= F · v = 250kW
(33)
dt
dt
Seite 10
B.3
Schwingung skizzieren
l (m)
Es handelt sich um eine gedämpfte Bewegung. Zuerst muss festgestellt werden um
welche Form der Dämpfung es sich handelt.
Aus der Differentialgleichung sehen wir, dass 2γ = 1 1s beträgt und somit γ 2 =
0, 25 s12 < ω02 ist und wir daher eine schwache Dämpfung haben.
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0
1
2
3
4
5
t (s)
Abbildung 2: Plot der Schwingung
B.4
Das Federpendel
Die Differentialgleichung für das System lautet mit ω 2 =
D
m:
ẍ + ω 2 · x = 0
(34)
x(t) = A · cos(ω · t) + B · sin(ω · t)
(35)
Die Lösung lautet:
Für die Geschwindigkeit erhalten wir:
ẋ(t) = −A · ω · sin(ω · t) + B · ω · cos(ω · t)
(36)
Wir wissen, dass zum Anfangszeitpunkt die Masse in Ruhe ist, also ẋ(0s) = 0. Daraus erhalten wir B = 0.
6
Seite 11
Die Feder wird eine Schwingung um die Ruhelage mit angehängtem Gewicht ausführen.
Die Ruhelage berechnen wir durch ein Kräftegleichgewicht:
m · g = D · ∆x
(37)
Der Abstand der Ruhelage von ”ohne Gewicht” und ”mit Gewicht” beträgt also
∆x = m·g
D = 0, 19m.
Somit gilt x(0s) = A = 0, 19m.
B.5
Das U-Rohr
Die Masse des Wassers m kann wie folgt berechnet werden:
m=ρ·L·A
(38)
F = −ρ · A · 2 · h · g
(39)
Für die rücktreibende Kraft gilt:
Wir können also die Bewegungsgleichung aufstellen:
ρ · L · A · ḧ = −ρ · A · 2 · g · h
(40)
Dies lässt sich vereinfachen zu:
ḧ = −
2·g
· h = −ω 2 · h
L
(41)
Die Flüssigkeit
führt demnach eine ungedämpfte Schwingung mit Winkelschwindigq
2·g
keit ω =
L aus.